Highly tunable propagating surface plasmons on supported silver nanowires

Abstract

Surface plasmons, the quanta of the collective oscillations of free electrons at metal surface, can be easily tuned by changing the surrounding dielectric materials, which is well known for metal nanoparticles and metal surfaces, but less is known for one-dimensional metal nanowires. Here, we find an extremely large tunability of surface plasmons on Ag nanowires with a beat period of the near-field distribution pattern increasing by 90 nm per nanometer of Al₂O₃ coating, or by 16 µm per refractive index unit change in the surrounding medium. Such high sensitivity is crucial to directly control the optical signal distribution for various routing and demultiplexing functions in plasmonic circuits and may pave the way to the development of on-chip ultrasensitive biosensing.

The miniaturization of optical devices to the scale compatible with modern nanoelectronic circuits demands the ability to manipulate light at the subwavelength scale. Recently, plasmonics has been a rapidly emerging field that offers various means to manipulate light at the nanometer scale using surface plasmons (SPs) (1–10). SPs can strongly confine electromagnetic fields near metal–dielectric interface to overcome the conventional diffraction limit of dielectric optics. Therefore, SP-based nanophotonic devices are promising to build densely on-chip integrated circuits for next-generation information technology (11, 12). The scaling down of photonic circuits may find applications in quantum information processing as well (13, 14). It is known that the properties of SPs can be strongly affected by the surrounding dielectric materials, e.g., the refractive index of the surrounding material determines the dispersion relations and resonance energies of SPs (15). Although the sensitivity of localized SPs on various metal nanostructures to local dielectric environments has been well studied, less is known for the cases of propagating SPs in plasmonic circuits. It is a challenge to develop advanced plasmonic modulation schemes for designing simple, robust metal–dielectric heteronanostructures suitable for high-performance on-chip plasmonic circuits.

Plasmonic waveguide is one of the key elements for the plasmonic circuits. Different nanostructures have been investigated as waveguides (16–24). Chemically synthesized crystalline silver nanowires (Ag NWs) can support propagating SPs (25–28) with lower losses than lithographically defined NW waveguides (29), and can be easily manipulated to construct complex optical devices (30–33), which make them ideal candidates for proof-of-principle studies of plasmonic circuits. Metal NWs of diameters of tens to hundreds of nanometers and lengths of several to tens of micrometers are mesoscopic systems, which show many novel and valuable properties and may potentially be used in many fields. To investigate the SP propagating properties in metal NWs, both near-field optical microscopy and quantum dots (QDs) fluorescence imaging where QDs are used as local field reporters were applied to produce optical images of plasmon-induced near-field distributions on Ag NWs (29, 32, 34). Near-field distributions of propagating NW plasmons depend strongly on the polarization and phase of the input light, which can be used to realize an entire family of optical Boolean logic gates in NW networks (32). Despite the developments of plasmonic circuits, the key issue is still on how to exactly control and route optical signals in various circuitries with simple design principles. Here, we discover an extremely large tunability of propagating SP near-field pattern on Ag NWs using the QD fluorescence imaging technique. Locally changing the dielectric environment by applying a thin dielectric coating layer of Al₂O₃ results in the period increasing by about 90 nm per nanometer of Al₂O₃. For bulk changes in the surrounding medium, we observe a period increase of about 16 µm per refractive index unit. This high-sensitivity effect is explained by considering the propagation constants and the dispersion curves of NW SPs. We demonstrate that such giant modulation of SPs can be used to design functional plasmonic circuits.

Results

Influence of Dielectric Environment to the Near-Field Distribution Pattern.

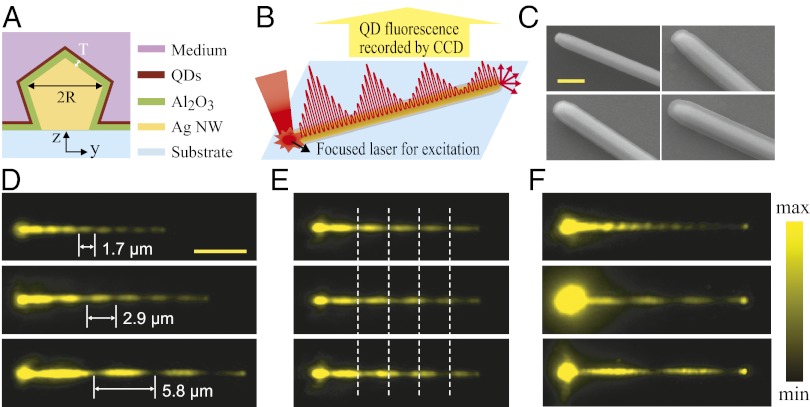
The structure considered here, illustrated in Fig. 1A, consists of Ag NWs of radius R deposited on a glass substrate, and coated with dielectric (Al₂O₃) layers of different thicknesses T and a layer of QDs surrounded by a medium. The laser light was focused through an objective onto one end of the NW and the signal was collected by the same objective. After filtering the laser light, QD fluorescence was recorded by a CCD camera (illustrated in Fig. 1B; see Methods for more details). A HeNe laser operating at a wavelength of 633 nm was used for SP excitation unless specified. Scanning electron microscope (SEM) images of typical NW structures are shown in Fig. 1C, where the smooth Al₂O₃ coating is clearly resolved.

Fig. 1.

Near-field distribution images for NWs with different dielectric environments. (A) Schematic cross-section of the samples. (B) Schematic illustration of the excitation/collection configuration and the plasmons propagating along the NW. (C) SEM images of a typical bare Ag NW (Upper Left) and NWs coated with T = 30 nm (Lower Left), 50 nm (Upper Right), and 80 nm (Lower Right) Al₂O₃ layers. (Scale bar, 500 nm.) (D) QD emission images under excitation at the left ends of the NWs. From Top to Bottom, the radius of the NWs is 160, 155, and 157 nm, and the corresponding Al₂O₃ thicknesses are 30, 50, and 80 nm. (E) QD emission images for a 162-nm radius NW with a 50-nm Al₂O₃ coating measured in air (Top), and then after depositing 5 nm of Al₂O₃ (Middle), and finally with an additional 5 nm of Al₂O₃ (Bottom). The white dashed lines are visual guides to show the shift of the plasmon near-field pattern. (F) QD emission images for a 155-nm radius NW initially coated with 10 nm of Al₂O₃ and QDs, and then capped with another 5 nm of Al₂O₃ to protect the water-soluble QDs from being removed, measured in air (Top), water (Middle), and oil (Bottom). (Scale bar in D for D–F, 5 µm.)

Fig. 1 D–F show typical QD emission images revealing a quasiperiodic oscillation of the near field with a period (Λ) that is highly sensitive to local or bulk changes of the surrounding dielectric materials. In Fig. 1D, Λ increases dramatically with the thickness T of the Al₂O₃ coating: for T = 30 nm (Top) Λ ∼ 1.7 μm, increasing to 2.9 μm for T = 50 nm (Middle), and 5.8 μm for T = 80 nm (Bottom). This high sensitivity to small changes in T is further demonstrated in Fig. 1E where 50 nm of Al₂O₃ was initially deposited on a NW followed by a layer of QDs, and then additional Al₂O₃ in 5-nm increments. Initially, this NW shows a near-field beat period of 2.9 μm (Fig. 1E, Top), increasing to 3.3 μm (Middle) when just 5 nm of Al₂O₃ is added, and to 3.8 µm with an additional 5 nm (Bottom). This corresponds to Λ increasing ∼90 nm when the coating thickness is increased 1 nm. It is interesting that such an increase to each period is cumulative along the NW to make an enormous shift of the last period as N·ΔΛ, where N is the number of total periods. Comparing Fig. 1E Top and Bottom shows that the shift of the last null after depositing an additional 10 nm of Al₂O₃ is 3.6 μm, i.e., ∼360 nm per nanometer of Al₂O₃. Another example with similar high sensitivity of the near-field beat pattern starting from T = 30 nm is shown in Fig. S1.

Immersing the samples in water or oil rather than in air, increasing the refractive index n of the surrounding medium from 1.00 to 1.33 or 1.51, respectively, dramatically changes the near-field pattern as shown in Fig. 1F. In Fig. 1F, Λ increases rapidly from 1.3 μm in air to 4.4 μm in water and 7.2 µm in oil. Expressed as a change in period per refractive index unit (RIU), this corresponds to ΔΛ/Δn = 9.4 µm/RIU from air to water and 16 µm/RIU from water to oil. The total sensitivity of the whole NW will cumulate the sensitivity of each period to be N·ΔΛ/ Δn, where N is the number of total periods. For the case of Fig. 1F, the corresponding sensitivity becomes 3 × 9.4 µm/RIU = 28.2 µm/RIU from air to water and 2 × 16 µm/RIU = 32 µm/RIU from water to oil, respectively. Due to such cumulation effect, in principle, much larger sensitivity can be obtained for longer NWs.

Plasmon Beating and the Mechanism for the High Sensitivity.

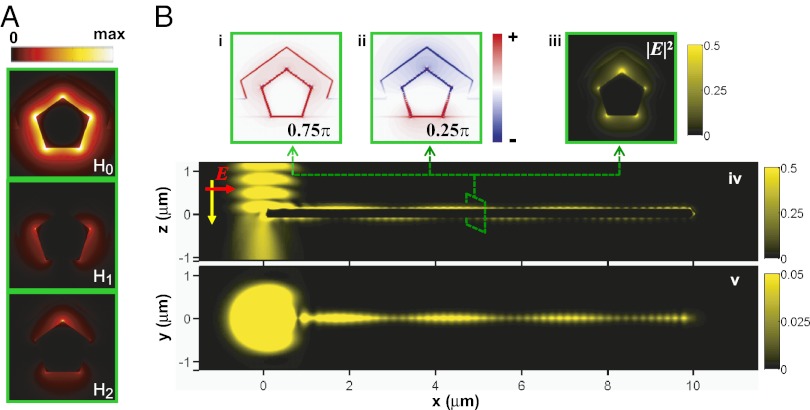
Because the chemically synthesized Ag NWs used here have pentagonal cross-section (35), we used pentagonal wires in the simulation to mimic the real situation. For cylindrical NW, plasmon modes are usually indexed with quantum number “m,” as |m| = 0, 1, 2,… (36, 37). However, here, both the pentagonal shape and the interaction to the dielectric substrate break the perfect symmetry of the cylindrical shape in an ideal system, and “m” is not a good index anymore. As shown in Fig. 2A, three lowest-order SP modes for a coated NW (R = 110 nm, T = 80 nm) on a glass substrate are denoted as H₀, H₁, and H₂. The field distributions of these three modes are obtained from a finite element method (FEM) package (COMSOL Multiphysics 3.5a). To model such large system involving substrate, we performed 3D electrodynamics calculations using another commercial software (Lumerical Solution) based on finite difference time-domain (FDTD) method, as shown in Fig. 2B. For the calculations in Fig. 2B, the laser beam is polarized parallel to the NW. The charge plots in Fig. 2 Bi and Bii and the electric field intensity distribution in Fig. 2Biii clearly reveal that both the H₀ and H₂ modes are excited. The coherent interference of the H₀ and H₂ mode generates plasmon beating along the NW, as shown in Fig. 2 Biv and Bv. The period of the beating is given by Λ = 2π/Re(Δk_//), where Δk_// is the difference of the propagation constant of the H₀ and H₂ mode. The oscillations with a short period are due to the interference between counterpropagating SPs resulting from reflections by the two terminals of the NW, i.e., Fabry–Pérot resonances (29), which is dependent on the length of the wire. The plasmon beating, however, can exist as long as both of the modes are not damped out, independent of the NW length. Because the H₁ mode is not excited in the current configuration, it will not be discussed in the following, but the perpendicular components of the incident electric field to the wire axis, i.e., the change of the incident polarization, can excite H₁ mode and higher-order modes as can be seen in Fig. S2.

Fig. 2.

Excitation of multiple SP modes on supported NWs. (A) Power distribution of three lowest-order modes on supported NW. (Bi and Bii) Charge plot with different initial phase, 0.75π and 0.25π; (Biii–Bv) electric field intensity |E|² distribution on different cross-section of the Ag NW, excited by a Gaussian beam at the left end. The yz plot (Biii)/xz plot (Biv) is cut through the wire at x = 5.0 μm/y = 0 μm, and the xy plot is located 10 nm above the coated NW. The radius of the wire is R = 110 nm, and the coating thickness is T = 80 nm. The incident light, λ = 632.8 nm, is polarized parallel to the wire axis in B.

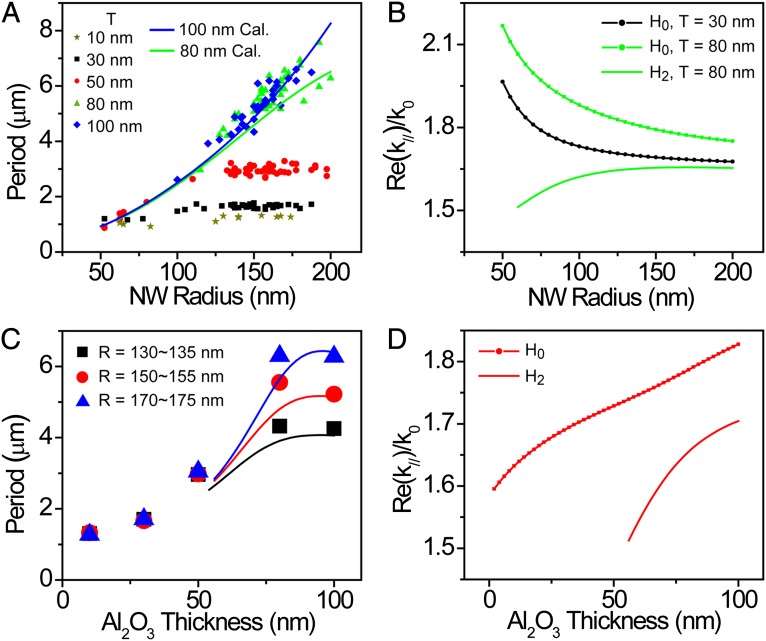
We experimentally measured the beat period of coated NWs of varying radius R and coating thickness T. From Fig. 3A, we can see that the beat period Λ increases with increasing R, and also with increasing T. For the NWs with thick coating (T = 80 and 100 nm), Λ is increased monotonically with the increase of the NW radius, which is reproduced by the calculation. This phenomenon can be explained by the decrease of Re(Δk_//) with the increase of the NW radius as seen in Fig. 3B. For the NWs with thin coating (T ≤ 50 nm), the increase in Λ with radius saturates for R greater than ∼125 nm. Because the propagation constant Re(k_//) of the H₂ mode cannot be obtained by our FEM model for NWs with thinner coating because the mode becomes leaky in this case, a reproduction of the measured beat periods for thin coating was then done using 3D FDTD calculations, as shown in Fig. S3. For very thin wires (R < 50 nm), the interference pattern disappears as the H₂ mode becomes difficult to excite, whereas for wires of larger radiuses (R > 200 nm), higher-order SP modes are also excited so that the quasiperiodic near-field distributions become ill defined (Fig. S4).

Fig. 3.

(A and B) The beat period (A) and the real part of the propagation constant Re(k_//) of the H₀ and H₂ mode (B) as a function of NW radius. (C and D) The beat period (C) and Re(k_//) of the H₀ and H₂ mode (D) as a function of Al₂O₃ coating thickness. The NW radius is 155 nm for the calculation in D. In A and C, the dots are experimental data, and the lines are FEM calculated data.

We extract some data from Fig. 3A to show Λ versus T in Fig. 3C. It is clear that Λ increases at the beginning and becomes saturated for larger T. This result is consistent with the calculated data obtained from the real part of the propagation constant Re(k_//). As can be seen from Fig. 3D, the change of the real part of the propagation constant Re(k_//) is larger for the H₂ mode than the H₀ mode as the thickness of the Al₂O₃ coating T is varied. That is because for a bare NW on top of a dielectric substrate, i.e., without Al₂O₃ coating, the field of the H₀ mode is located at the bottom of the wire, whereas that of the H₂ mode is on the top of the wire (38). As a result, the dielectric screening effect will be more pronounced for the H₂ mode than for the H₀ mode. With the adding of the Al₂O₃ coating onto the NW, the difference between the propagation constant of the H₀ and the H₂ mode becomes smaller. Therefore, the beat period becomes larger. However, increasing the thickness of Al₂O₃ layer tends to reduce the coupling to the substrate because the NW feels a more symmetric dielectric environment for very thick coatings. The increase of the real parts of the propagation constants Re(k_//) of H₁ and H₂ mode becomes saturated when the thickness of Al₂O₃ layer is very thick, which makes the beat period Λ stop increasing and saturate to a value corresponding to the infinite coating thickness. Fig. S5 shows the calculated Re(k_//) of the H₀ and H₂ mode for larger Al₂O₃ coating thickness. For NWs in a homogenous environment, Λ increases monotonically with R as shown in Fig. S6, which is demonstrated in the experimental results measured in oil (Fig. S7).

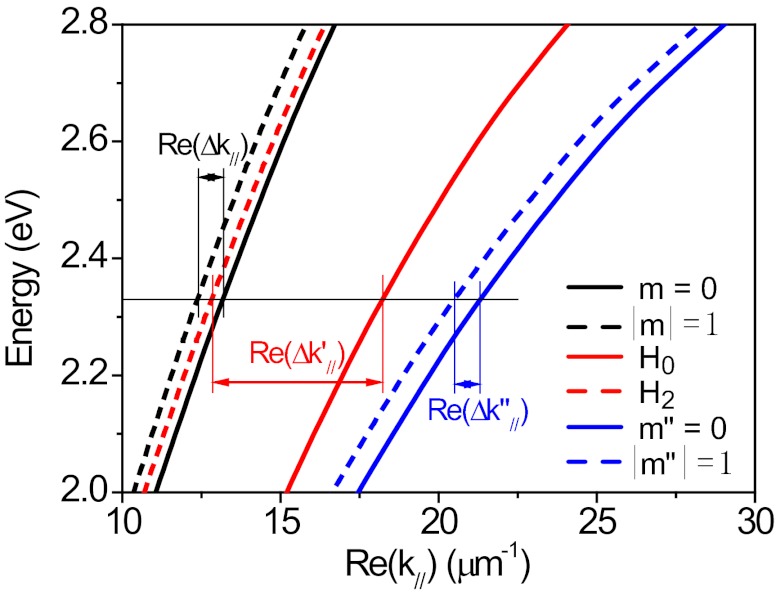
To better understand the physical mechanism of the plasmon beating behavior observed in the experiment and reproduced in the calculation, we examine the dispersion relation for propagating NW SPs. For simplicity, cylindrical NWs are used to obtain the dispersion relation data. The black curves in Fig. 4 show the dispersion relations for the m = 0 (black solid curve) and for the |m| = 1 (black dashed curve) SPs on a bare NW of radius 150 nm in a symmetric dielectric environment (air). When the NWs are deposited on a substrate, the dielectric environment is highly asymmetric. The induced charge on the substrate surface caused by the oscillating charges of different SP modes will change the charge distributions of the primary modes |m| = 0, 1,… to form the asymmetric H₀, H₁, and H₂,… modes and shift the corresponding dispersion relations. Similar to the coupling between two close-packed metal NWs (39), here the wire on the substrate is coupled to its “image” wire in the substrate, and the dispersion relation of the lowest-order mode, i.e., m = 0, will be dramatically red-shifted due to the strong “monopole” coulomb coupling to the substrate. The dispersion relations of the higher-order modes (|m| = 1, 2,…) will be influenced as well, but the corresponding “multipole” couplings decrease with the coupling coulomb potential proportional to ∼r^−(2m+1), where r is the effective distance between two multipole sources, resulting in a less dramatic red shift of the dispersion relation compared with the lowest-order mode. Hence, the substrate-meditated interaction will increase Re(Δk′_//) = Re(k_0//′) − Re(k_1//′) as shown by the red curves in Fig. 4, resulting in a smaller beat period Λ on the substrate (comparing Fig. S6 and Fig. 3A). With increasing thickness of a refractive index-matched coating layer, however, the substrate-meditated interaction will be decreased, and the dielectric screening effect caused by the coating layer will shift the dispersion curves of both H₀ and H₂ to red, but a much faster shift for H₂ mode as seen in Fig. 3D, resulting in a smaller difference between the propagation constants of the two modes. Thus, the beat period Λ is increased with the increase of the coating thickness and saturates for very thick coatings due to the more symmetric dielectric environment. A reduction of the asymmetry can also occur if the air medium is replaced by a medium that more closely index-matches the substrate on which the wires are placed, which is what is observed in Fig. 1F. The blue curves in Fig. 4 show the dispersion relations for the two lowest-order modes on a NW embedded in the glass matrix with a smaller Re(Δk″_//).

Fig. 4.

Dispersion relations for the m = 0 (solid) and |m| = 1 (dash) plasmon modes of a bare Ag NW in air (black) and in glass matrix (blue), and the H₀ and H₂ modes (red) of a NW supported on air–glass interface. The NW (radius R = 150 nm) has a cylindrical cross-section.

Near-Field Distribution Dependence on the Excitation Wavelength and Its Application in Plasmonic Circuits.

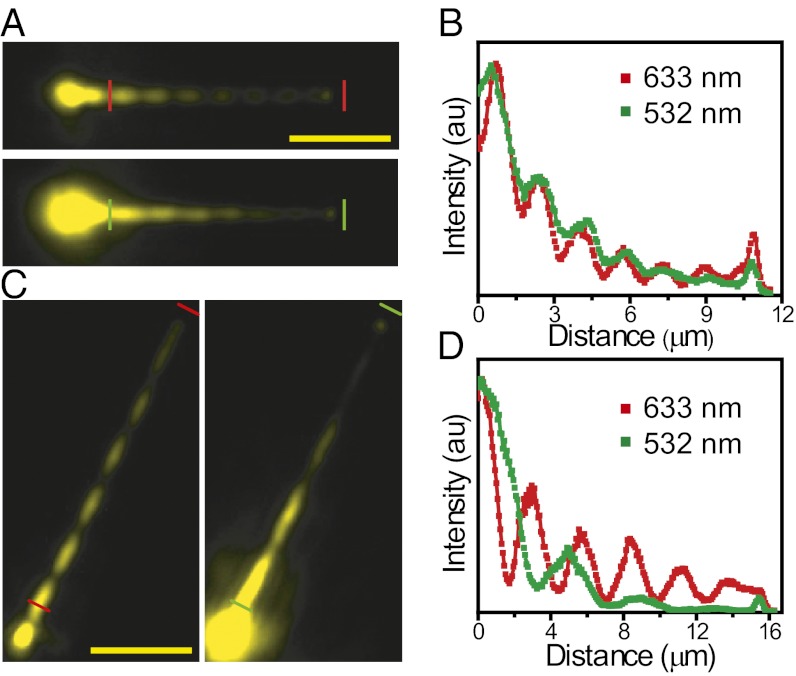
The QDs also fluoresce when excited with a laser of 532-nm wavelength, allowing us to study the effect of excitation wavelength on the beat period. For NWs with T = 30 nm, Λ is similar for both 633- and 532-nm excitation (Fig. 5 A and B), whereas for NWs with T = 50 nm, Λ is larger when excited by 532-nm light (Fig. 5 C and D). It is noted that the change of the beat period is most sensitive to the change of the thickness of the coating layer at about T = 50 nm in Fig. 3C for the excitation by laser light of 633-nm wavelength. The larger increase of the period for 532-nm excitation indicates that the sensitivity to the change of the Al₂O₃ coating thickness is higher for 532-nm excitation than 633-nm excitation in the thickness range considered here. From these results, we can also see that how strongly Λ depends on excitation wavelength can be controlled through the geometry. This flexibility is important for engineering plasmonic circuits where it may be desired to keep signals at different wavelengths together or separate them to follow different paths depending on the device function.

Fig. 5.

Near-field distribution for different excitation wavelengths. (A) QD emission images for a 140-nm radius NW coated with 30 nm of Al₂O₃ for an excitation wavelength of 633 nm (Upper) and 532 nm (Lower). (B) The intensity profiles along the NW between the short bars in A, which are obtained by plotting the intensity of single pixels along the NW as a function of the distance. The intensity is normalized by the maximum of the two curves. (C and D) The corresponding data for a 135-nm radius NW coated with 50 nm of Al₂O₃. (Scale bars, 5 µm.)

To demonstrate how the highly tunable near-field distribution plays an important role in plasmonic devices and circuits, we designed a structure composed of three NWs (Fig. 6A, Left) and coated it with 30-nm Al₂O₃. By adding additional Al₂O₃ in 5-nm increments, we demonstrate that small changes in the coating layer can control the routing of light to different terminals of the device. A supercontinuum light source was used for excitation of propagating plasmons (Fig. 6A, Right), which enables us to study the wavelength response of the structure. The spectrum of the output light at terminal A for the initial structure (black curve in upper panel of Fig. 6B) shows that the transmission of light to terminal A is much higher at wavelengths around 633 and 820 nm compared with 700 nm. The spectrum at terminal B (black curve in lower panel of Fig. 6B) shows similar behavior. Depositing an additional 5 nm of Al₂O₃ results in the output intensity increasing at both terminals A and B across most of the spectrum (red curves in the upper and lower panels of Fig. 6B, respectively). For terminal A, there is a striking increase in the output around 633 nm so that the output around 633 and 800 nm is now equal. Adding an additional 5 nm of Al₂O₃ results in opposite behavior at terminals A and B (blue curves): for terminal A the output decreases dramatically around 800 nm and only light around 633 nm is strongly coupled to this terminal, whereas for terminal B the transmission around 800 nm is unaffected and the transmission around 633 nm is suppressed. The images of QD fluorescence excited by a laser of 633 nm in Fig. 6C show that the plasmon antinode moves to the junction position of the right branch (marked by red dashed line) when the first 5 nm of Al₂O₃ was deposited, which make more light be routed to this branch wire. This observation agrees well with the spectral intensity change in Fig. 6B. These results demonstrate that the tunable plasmon near-field distribution plays a critical role in determining the path light follows through plasmonic circuits.

Fig. 6.

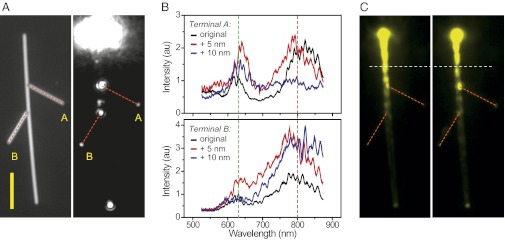
Control the output by controlling the near-field distribution. (A) A structure composed of three NWs was illuminated by the supercontinuum light with the incident polarization parallel to the main NW. (B) The upper panel shows the emission spectra at the terminal A from the right branch for the original structure (black), and for 5 nm (red) and 10 nm (blue) Al₂O₃ layer deposited, respectively. The lower panel is for the terminal B from the left branch. (C) The QD emission images when excited with a laser of 633-nm wavelength for the original structure (Left) and after 5 nm more Al₂O₃ was deposited (Right). The red dashed lines in A and C show the positions of two branch wires. The white dashed line in C is a visual guide to show the shift of the near-field nodes and antinodes due to the addition of 5 nm of Al₂O₃. The batch of NWs used for this structure has the radius of about 150 nm. (Scale bar in A, 5 μm.)

Discussion

We have found extremely large modulation of the near-field distribution of SPs on supported Ag NWs by slightly changing the surrounding dielectric environment. This effect can be understood by examining the dispersion properties of the NW SPs, which are highly sensitive to the change of the surroundings. Such high sensitivity has been demonstrated to design plamonic devices with different routing functions in NW networks by slightly changing the dielectric coating thickness here. This discovery of large tunability of the propagating SPs on Ag NW networks thus provides a simple and robust way for the exact control of plasmon near-field distributions and the precise routing of optical signals in circuitries. Based on the mechanism revealed here, active plasmonic devices can also be designed with carefully selected electro-optical and optical nonlinear coating materials (40, 41). The current study can give the design principle for both passive and active plasmonic devices, which will promote the development of on-chip integrated plasmonic circuits.

Such highly tunable near-field distribution on supported Ag NWs can also be used for new types of ultrasensitive on-chip optical sensors. The dramatic change of the beat period demonstrated here can be caused by the adsorption of tiny amount of molecules on the metal NWs, for example, which changes the local dielectric environment. More importantly, the change of the beat period will cumulate with each period to largely change the position of the last period, and the corresponding total sensitivity will be enlarged for longer wires with more periods. As demonstrated here, the cumulated change ∼360 nm per nanometer of Al₂O₃ coating of the last node position after four-period accumulation, roughly corresponding to a monolayer of small biomolecule adsorption, can be resolved by the ordinary confocal microscopy. By applying the advantages of scanning near-field optical microscopy with the resolution about 10 nm (42, 43), together with longer wires with more beat periods used, hundred times higher sensitivity can be achieved. Hence, ultrasensitive wire plasmon sensors based on the principle discussed here can be developed. In addition, the dramatic changes of the emission spectra and the shift of the fine fringes on the spectra due to Fabry–Pérot resonances (Fig. 6B) can also be used for highly sensitive sensing applications.

Methods

Sample Preparation.

The Ag NWs were prepared by reducing silver nitrate with ethylene glycol in the presence of poly(vinyl pyrrolidone) (44) and washed in ethanol via centrifugation. The Ag NW suspension in ethanol was then deposited on glass slides. Al₂O₃ layers were grown on the NWs using an atomic layer deposition (ALD) system (Cambridge NanoTech; Savannah-100) operating at 200 °C. ZnS-coated CdSe QDs (Invitrogen; Catalog number Q21321MP) were diluted in highly purified water, and then spin-coated on the Al₂O₃ layer. Additional layers of Al₂O₃ may be deposited on top of the QD layer to investigate the effect of small changes in the thickness of the dielectric coating or to protect the QD layer for measurements in a liquid environment. For the deposition of Al₂O₃ on top of the QDs, the ALD system is operated at 80 °C.

Optical Measurements.

Optical measurements were performed using two different but functionally equivalent microscope systems. The optical imaging measurements for Figs. 1 and 5 were performed using an Olympus BX 51 microscope. A 100× objective (N.A. 0.95) was used for excitation and collection of the images measured in air. A 100× objective (N.A. 1.35) and a 60× objective (N.A. 1.2) were used for the measurements in oil and water. For the imaging of the near-field distribution of propagating SPs, a HeNe laser operating at a wavelength of 633 nm or a frequency-doubled Nd:YAG laser for 532 nm was used for excitation at the NW termini. The QD emission images were recorded by a CCD camera (DVC-1412 AM) after the emitted light was transmitted through a long-pass edge filter to block the excitation laser. For Fig. 3A, a Leica DM LM microscope with a 50× (N.A. 0.75) or 100× (N.A. 0.85) objective attached to a Renishaw inVia microRaman system were used to collect optical imaging data. A HeNe laser for 633 nm was used for excitation at the NW termini, and the QD emission imaging data were recorded with a CCD camera (Renishaw RenCam) after the emitted light passed through two long-pass edge filters and a narrow bandpass filter to block the excitation laser and select the QD emission. For Fig. 6B, a supercontinuum light source (Fianium; SC400-PP) was used for excitation through a 100× (N.A. 0.9) objective on an Olympus BX 51 microscope. The output light at NW terminals was directed to a spectrometer (Princeton Instruments; Acton SP-2560) to measure the spectra.

Simulations.

The mode profiles in Fig. 2A and their propagation constants were obtained using the mode solver in COMSOL. These mode analyses were done in the 2D cross-section of the pentagonal NWs. Full-wave electromagnetic simulations were performed using FDTD software (Lumerical Solution). The model used in the calculations is the same as in Fig. 1A, except the QD layer is omitted, and the structural parameters R and T are determined from the experiments. The simulation domain boundaries were extended no less than 1.35 μm away from the wire and perfectly matched layers were used to mimic an infinite substrate and infinite upper half space. A focused Gaussian beam is inserted perpendicular to the wire axis at one of the wire ends. The refractive index of the Al₂O₃ layer and the glass substrate was assumed to be 1.62 and 1.50, respectively. The dielectric permittivity for Ag (ɛ_Ag = −18.36 + 0.48i) was taken from Johnson and Christy (45), corresponding to the vacuum wavelength λ = 632.8 nm. The charge plots in Fig. 2 Bi and Bii were done numerically by calculating the real part of the divergence of the electric field Re(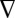·E·e^iφ), where φ represents the initial phase. The dispersion curves of the NW SP modes in Fig. 4 were obtained using the mode solver in the COMSOL multiphysics finite element modeling package.