Scaling body size fluctuations

Abstract

The size of an organism matters for its metabolic, growth, mortality, and other vital rates. Scale-free community size spectra (i.e., size distributions regardless of species) are routinely observed in natural ecosystems and are the product of intra- and interspecies regulation of the relative abundance of organisms of different sizes. Intra- and interspecies distributions of body sizes are thus major determinants of ecosystems’ structure and function. We show experimentally that single-species mass distributions of unicellular eukaryotes covering different phyla exhibit both characteristic sizes and universal features over more than four orders of magnitude in mass. Remarkably, we find that the mean size of a species is sufficient to characterize its size distribution fully and that the latter has a universal form across all species. We show that an analytical physiological model accounts for the observed universality, which can be synthesized in a log-normal form for the intraspecies size distributions. We also propose how ecological and physiological processes should interact to produce scale-invariant community size spectra and discuss the implications of our results on allometric scaling laws involving body mass.

Why should a continuous, gap-free spectrum of organismic sizes emerge from the ecological and evolutionary processes that shape their ecosystems? The origins and the implications of the absence of preferential body sizes, which is routinely observed across a variety of ecosystems regardless of broad differences in climatic and environmental conditions (1–5), have been attracting much interest from field and theoretical ecologists (6–13). Scale invariance, epitomized by power-law probability distributions (9, 12, 14–19), requires regularities of the component parts (the species’ size distributions) making up the whole [the community size spectra (i.e., the probability distributions of size regardless of species)]. In particular, a necessary condition for scaling community size spectra is the lack of peaks that pinpoint frequent occurrences, and therefore excess abundance (and vice versa) within any given range of sizes. Such features are particularly interesting if robust to environmental fluctuations because their dynamic origin could lie in the self-organization of complex adaptive systems (6, 9, 15).

Body size distributions in natural ecosystems are strongly related to the life history of the organisms and to the dynamics of their living communities (18). Thereby, they modulate structure and function of the ecosystem at any scale. Size spectra, which display the relative abundance of organisms of different sizes within or across species, convey a synoptic and possibly taxon-independent image of ecological communities (1, 2, 20, 21). As such, they have long been attracting much interest in ecology because they hold important predictive power (e.g., fish stock projections from planktonic size spectra) (2, 5). Because examples and counterexamples of scaling spectra abound (2, 3, 5, 7, 21–24), it is an unsettled issue as to whether scaling size spectra represent some central tendency of statistically stationary states of natural ecosystems. For instance, the operational computation of mean phytoplankton size was shown to depend on the sample size typically (7) and scaling relationships were documented for interspecific plant biomass (20, 25, 26), whereas some terrestrial ecosystems exhibit ubiquitous gaps in size and uneven relative abundances of organisms (1, 21).

Single species inhabiting communities, however, do exhibit a species-specific mean and variance of their sizes, as even common sense suggests. Thus, there naturally exists the mean size of a particular species, as usually implied by most, if not all, biological scaling laws (10, 27–31), wherein one typical mass subsumes a whole distribution of sizes. One thus wonders how evolutionary and ecological processes interact to modulate species’ abundances, the range of sizes proper to each functional group, and the number of species existing within a given niche or range of sizes to concoct regular, taxon-independent, continuous size spectra. Moreover, one expects that the existence of a range of possible sizes for a species (and how such a range varies for different mean sizes) has to be taken into account when addressing scaling laws in biology (e.g., allometric scaling laws) (10, 11, 27–29, 32–39).

Here, we have precisely measured the intraspecies size distributions of 13 species of protists in isolation or in competition (40–42), covering a relatively broad set of field conditions (Materials and Methods). Examples of such distributions as functions of the linear size in standard environmental conditions are shown in Fig. 1. The corresponding transformed distributions as functions of volume span over four orders of magnitude and are shown in Fig. 2A. Let p_k(m) denote the measured size spectrum of the kth species: Such a p_k(m) measures the relative proportion of individuals of a given species k with mass belonging to (m, m + dm), assuming a continuous distribution of sizes. We tested whether p_k(m) exhibits a finite-size scaling form (22, 30, 36, 43, 44) obtained by the product of two terms, an algebraic power of size multiplied by a suitable scaling function F; that is,

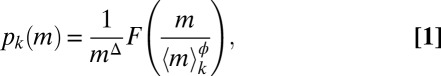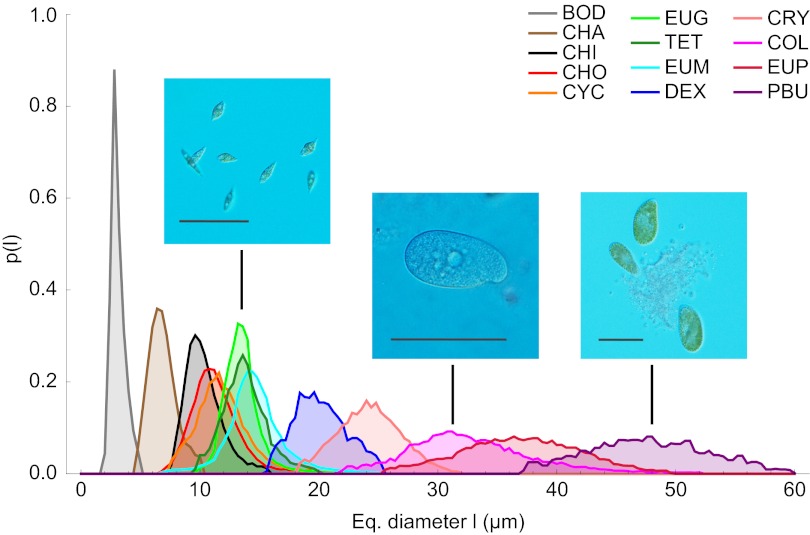
Fig. 1.

Size distributions of 13 protist species as functions of the equivalent (Eq.) diameter (i.e., the diameter a cell would have if it were spherical). (Left to Right) Photographs show individuals of the species E. gracilis, Colpidium sp., and P. bursaria. (Scale bar: 100 μm.) The legend links each color to the corresponding species. (Protist photographs provided by Regula Illi, Eawag: Swiss Federal Institute of Aquatic Science and Technology, Dü\x{0308}bendorf, Switzerland, and F.A.)

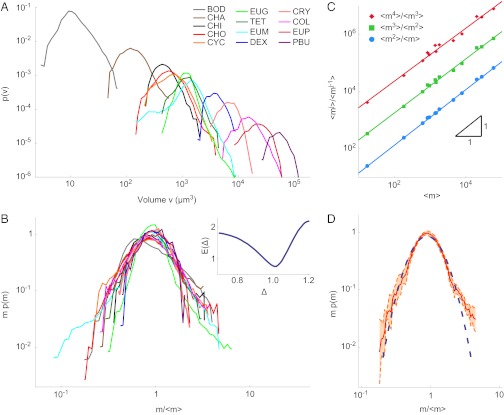
Fig. 2.

Evidence for a universal single-species size distribution. (A) Volume probability distributions of 13 protist species, spanning four orders of magnitude in mass. (B) Data collapse of m^Δp(m) vs. m/〈m〉^ϕ; the best collapse is observed for Δ = ϕ = 1.0. (Inset) Minimum of the functional E(Δ) provides the best estimate for the exponent and the associated error (46) (SI Text). (C) Proportionality of successive moments of m to 〈m〉 is an independent verification of the hypothesis in Eq. 1. (D) Fit of a Gaussian scaling function F as a function of log m/〈m〉 (dashed blue line) contrasting the ensemble average size distribution (red line); the orange region is the 99.7% confidence interval around the average. The scaling function yields a log-normal form for p_k(m) (SI Text).

where 〈m〉_k is the mean mass of the kth species and F(x), critically, is the same scaling function for all species (dimensional analysis and normalization conditions that F must satisfy are discussed in SI Text). Eq. 1 implies that the only species dependence of the size distribution occurs through the average mass 〈m〉_k of species k. Note that the two exponents in Eq. 1, Δ and ϕ, are not independent. This follows from imposing 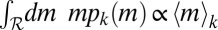(where 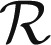is the suitable range of sizes); in fact, 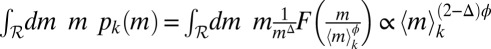is proportional to 〈m〉_k only if the two exponents satisfy (2 − Δ)ϕ = 1 (details concerning constraints on the exponents are provided in SI Text). To verify the hypothesis, we plot m^Δp_k(m) vs. 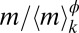for all 13 protist species (Fig. 2B) and vary Δ and ϕ until a satisfactory data collapse (45) is observed. The best collapse is found for Δ = 1.0 (and therefore ϕ = 1.0; Fig. 2B). A quantitative method (46) to produce the best collapse yields Δ = 1.01 ± 0.05 (Fig. 2B, Inset and SI Text). A relevant consequence of Eq. 1, where Δ = ϕ = 1, is that the jth moment 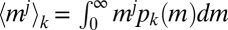is proportional to (〈m〉_k)^j (where j = 1, 2, 3, …). In particular, the variance of the species’ sizes does increase with the mean size. The proportionality of successive moments ratios to 〈m〉_k provides an independent test that further corroborates the validity of Eq. 1 (Fig. 2C and SI Text). We have thus found that a single parameter, the average mass of a species, is sufficient to characterize its size distribution fully. This is far from trivial because, in general, a probability distribution is determined by all its moments (47).

Environmental factors are capable of affecting the size distribution of any given species (48, 49). To test the effects of environmental conditions on Eq. 1, we question whether the measured size distributions might still be described by the universal functional form:

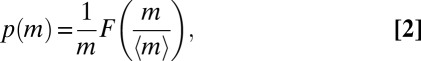where 〈m〉 is the mean mass, critically determined (i) by the species or (ii) by phenotypic plasticity due to environmental factors. To that end, we have investigated a set of manipulated field conditions. Specifically, we grew some of the above protist species at different temperatures, or in pairwise competition with each other, over more than 15 generations to achieve relevant ecological time scales. Although obviously far from exhausting field-like scenarios, a sizeable plasticity was observed (Fig. 3A and SI Text). Crucially, once rescaled by the actual mean body size of the sample, whether constrained by temperature or by competition, all distributions collapse again and the scaling exponent estimate proves to be unaffected (Δ = 1.01 ± 0.10; Fig. 3B, Inset). Significantly, therefore, environmental factors are capable of affecting the size distribution of any given species, although they do not alter its scaling nature because both the exponents and the scaling function F are unchanged.

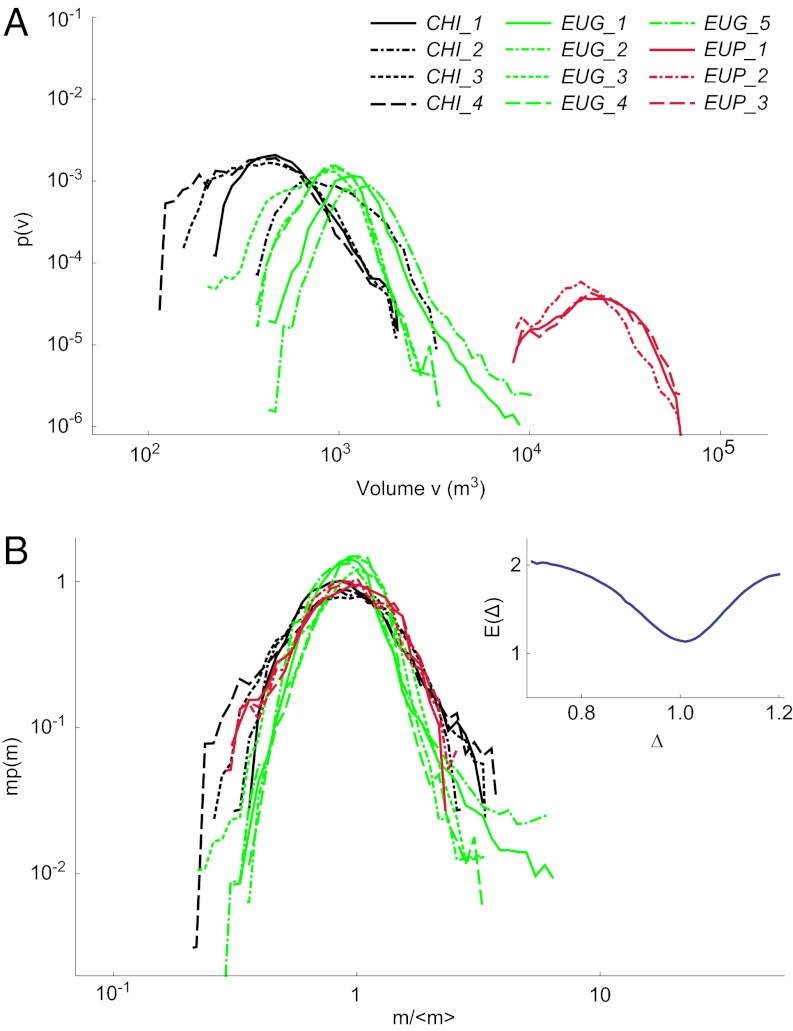
Fig. 3.

Universal form of the single-species size distribution is robust to biotic and abiotic forcings. (A) Volume probability distributions of three protist species in various environmental conditions and competition scenarios; the different colors identify different species. (B) Best data collapse of m^Δp(m) vs. m/〈m〉^ϕ is observed for Δ = ϕ = 1.0. (Inset) Minimum of the functional E(Δ) provides the best estimate for the exponent and the associated error (46) (SI Text).

The observed regularities are compelling, given the profound biological diversity of the species (belonging to the phyla/divisions of Ciliophora, Euglenozoa, Chlorophyta, and Cryptophyta) considered in this study (50). In addition, protists and unicellular algae are of key ecological significance. In fact, they are the basic food source of almost all aquatic food webs, and unicellular algae are responsible for almost 50% of the worldwide biomass production (51). Additionally, the observed universality of eukaryote intraspecies size distributions holds in a range of more than four orders of magnitude in mass. This suggests the existence of a simple underlying mechanism responsible for the empirical patterns observed. One possible explanation for the reported universality may be found in the physiological processes that determine the size of all unicellular species, namely, cellular growth and cell division. We found that a simple mathematical model of these processes (52–54) can justify the scaling form of unicellular eukaryotes’ size distributions without the need to specify further biological details (SI Text). We therefore suggest that the universal features of intraspecies size distributions emerge from fundamental physiological constraints.

The detailed identification of the scaling function F in Eq. 2 is interesting but inessential for our tenet because the collapse of the distributions suffices in documenting the universality sought after. However, a log-normal functional form for p(m) proves admissible and rooted in a theoretical framework for the time evolution of the distribution of body sizes in ecological time scales (Fig. 2D, Inset and SI Text). In this context, the size distribution of organisms of a given species is the stationary distribution of an Ornstein–Uhlenbeck process (55) in the variable x = log(m/〈m〉) (56, 57). A log-normal form for p(m) can also be recovered as a particular case of the physiological model cited above; thus, the two models are not mutually exclusive (SI Text).

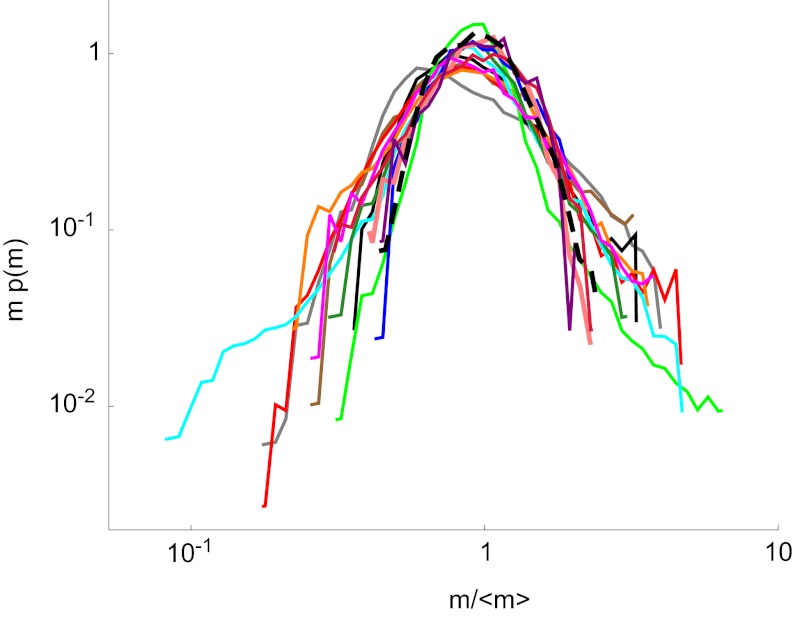
A yet unproven but reasonable ansatz would posit that this behavior might apply to multicellular or arbitrarily complex organisms as well, resulting in even broader validity. An indication supporting this statement is the experimental size distribution of a multicellular organism that we measured with the same methods in our laboratory conditions. In fact, we found that the size distribution of a multicellular species (Cephalodella sp.) showed a very good collapse with the protist size distributions once rescaled according to Eq. 2 (Fig. 4).

Fig. 4.

Collapse of rescaled size distributions as in Fig. 2B, with the superimposed size distribution of a multicellular organism, Cephalodella sp. (black dashed line), whose size distribution collapses well with the others of unicellular protists. Colors are as in Fig. 2A.

The observation of more than 20 orders of magnitude in organismic sizes in natural ecosystems (2, 27) leads to the conclusion that there has been little long-term impediment to the development, on evolutionary time scales, of any particular size. On ecological time scales, however, a characteristic size emerges as a fundamental property of a species, determined by biological constraints and by biotic and abiotic interactions. Such a characteristic size, in turn, modulates the entire size distribution of the species.

Our results have important implications on scaling laws in ecology. They decouple the effects of biotic and abiotic interactions, which regulate abundances and can affect a species’ mean size, from the individuals’ physiology, which shapes intraspecies size distributions. Our replicated, controlled experiments corroborate and extend comparative field findings of marine microbial size spectra to broader size and taxonomic diversity (22). We speculate that such behavior can reasonably be expected to extend over broader domains. Then, theoretical linkages of diverse empirical macroecological relationships, traditionally treated as independent (30, 58), would be substantiated. In fact, because single-species size distributions would be characterized by specific mean values and variances, a precise requirement would be cast on the number of species existing at stationarity within a niche of size, and on the related abundances, to produce community size spectra that lack characteristic scales (SI Text). Ecological interactions among species would consequently adapt to produce thinning laws (i.e., to control the relative abundance of species, given their characteristic sizes) (29, 32). The fact that these thinning laws have been shown to be robust to perturbations further emphasizes their universal character (59).

Finally, a distribution of the form in Eq. 2 implies that the variance of the species’ sizes increases quadratically with the mean size. Because the characteristic mass of a species is frequently adopted as the independent variable in allometric scaling laws (10, 11, 27–29, 32, 34–39), its increasing variance must have an impact on the scaling of the dependent variable, such as metabolic rates in Kleiber’s law. We thus pose the basis for a reexamination of allometric relations by considering appropriate fluctuations in both the dependent (31, 33) (metabolic rate) and independent (mass) variables.

Materials and Methods

Protist Cultures.

Replicated single-species cultures of 13 different protists and unicellular algae (all called “protists”) were initialized with three species of freshwater bacteria (Serratia fonticola, Breviacillus brevis, and Bacillus subtilis) as a food resource in a climatized room at 20 °C under constant fluorescent light 3 wk before the measurements. Previous studies (41, 42) support that the composition and size spectra of these communities are rather stable over this time period; thus, we can assume that cultures were at their carrying capacity while we performed the measurements. Single-species cultures were grown in 500-mL Schott flasks containing a nutrient medium made of sterilized local spring water and Protozoan Pellets (Carolina Biological Supply) at a density of 0.45 g/L. These are referred to as “standard conditions.” The 13 protist species were Bodo saltans (BOD), Chilomonas sp. (CHI), Chlamydomonas sp. (CHA), Chlorogonium euchlorum (CHO), Colpidium sp. (COL), Cryptomonas curvata (CRY), Cyclidium glaucoma (CYC), Dexiostoma campylum (DEX), Euglena gracilis (EUG), Euglena mutabilis (EUM), Euplotes aediculatus (EUP), Paramecium bursaria (PBU), and Tetrahymena sp. (TET). CHI and TET were purchased at Carolina Biological Supply, and BOD, CYC, CHO, CRY, EUM, and DEX were supplied by SAMS Research Services Ltd., whereas all other species were isolated from a natural pond and used in previous studies (41, 42, 60). All species are heterotrophs and feed on bacteria, whereas CHA, CHO, EUG, EUM, EUP, and PBU can also photosynthesize. In a competition scenario, the rotifer Cephalodella sp., also isolated from a natural pond (41, 42), was used.

Environmental Stress and Competition.

In addition to the single-species cultures grown in standard conditions as described in the previous section (which are referred to in Fig. 3 as CHI_1, EUG_1, and EUP_1), we grew CHI, EUG, and EUP at other temperatures and nutrient conditions, or in competition with each other. In the latter case, the two competing species were always sufficiently separated in their size spectrum so that their two distributions did not overlap. We studied the following conditions with at least three replicas each:

• i) Single species at 15 °C (EUG_2, EUP_2)

• ii) Single species at 25 °C (CHI_2, EUG_3, and EUP_3)

• iii) Competition at 20 °C: Two species compete for resources and have been initialized at half of their carrying capacity in 10-mL well plates [Chilomonas sp. with D. campylum (CHI_3), Chilomonas sp. with Colpidium sp. (CHI_4), and E. gracilis with the rotifer Cephalodella sp. (EUG_5)]

• iv) E. gracilis at a low protist medium concentration [0.045 g/L (i.e., 1/10th of the standard conditions concentration (EUG_4)]

Size Distributions.

We performed size distribution measurements with a Cell Counter and Analyzer System (CASY) model TTC (Roche Applied Science). Size measurements were performed by suspending a sample taken from a protist culture in a buffer solution (CASYton), which is developed specifically to aspirate cells through a precision hole in the instrument at a constant speed (61). To perform size measurements of protists, we used capillaries with diameters of 60 μm, 150 μm, and 200 μm depending on the size of the protists under investigation. Smaller capillaries resolve better size distributions at low scale (5–20 μm), but can be blocked if larger particles pass through (it is therefore necessary to use larger capillaries to measure larger species). As a general rule and for each species, we used the smallest capillary that enabled us to separate the protist peak unequivocally from the debris in the instrument output (61) (SI Text). The size spectrum of a sample of living cells is returned by the instrument as a function of the equivalent diameter l of each cell, assuming cells to be spherical. From the definition of size distribution, p(l)dl is the fraction of individuals with an equivalent diameter in (l, l + dl) and p(m)dm is the fraction of individuals with a mass in (m, m + dm). The value of p(m) can then be calculated via the variable transformation p(l)dl = p(m)dm (m = π/6d³). We assume a constant density equal to the density of water (7, 62), and therefore refer to volume and mass without distinction. We also assume that size distributions do not depend on time (i.e., the cultures are in a steady state characterized by size distributions of constant shape). In a typical measurement output for a culture of protists, a peak at small sizes exist due to debris in the culture (SI Text) (61). Peaks at larger sizes are due to protists. To deconvolve the two peaks, we fit the debris peak with an exponential decay (in a region adjacent to the peak, where data lie on a straight line in a log-linear plot; SI Text) and subtracted the resulting curve from the overall spectrum. On the right side of the protist peak, we truncated the data when the measured frequency of a size channel was below 20 occurrences to separate it from the noise. Noise was uniformly distributed on all size channels with a frequency of ∼10–20 counts per channel, as demonstrated by measuring pure buffer solution only. For each species, several measurements of different cultures (grown in the same conditions) were collected and summed to get an ensemble average representative of the species.