Viscoelastic properties of the nematode Caenorhabditis elegans, a self-similar, shear-thinning worm

Abstract

Undulatory motion is common to many creatures across many scales, from sperm to snakes. These organisms must push off against their external environment, such as a viscous medium, grains of sand, or a high-friction surface; additionally they must work to bend their own body. A full understanding of undulatory motion, and locomotion in general, requires the characterization of the material properties of the animal itself. The material properties of the model organism Caenorhabditis elegans were studied with a micromechanical experiment used to carry out a three-point bending measurement of the worm. Worms at various developmental stages (including dauer) were measured and different positions along the worm were probed. From these experiments we calculated the viscoelastic properties of the worm, including the effective spring constant and damping coefficient of bending. C. elegans moves by propagating sinusoidal waves along its body. Whereas previous viscoelastic approaches to describe the undulatory motion have used a Kelvin–Voigt model, where the elastic and viscous components are connected in parallel, our measurements show that the Maxwell model, where the elastic and viscous components are in series, is more appropriate. The viscous component of the worm was shown to be consistent with a non-Newtonian, shear-thinning fluid. We find that as the worm matures it is well described as a self-similar elastic object with a shear-thinning damping term and a stiffness that becomes smaller as one approaches the tail.

The undulatory motion of snakes and fish as they crawl or swim through a medium is considered a superior form of locomotion in terms of its adoption across a broad range of length scales and efficiency (1). Several attempts have been made to achieve the same level of performance artificially (2), but the agility seen in nature is far from being reproduced in manmade systems. A number of experimental model systems have been used to study undulatory motion (3–7). To achieve a deeper understanding of this form of motility, the biomechanics has been studied theoretically for snake-like systems (8, 9). Recently, computational fluid dynamic models of organismal swimming have been developed to simulate fluid–body interactions, including internal forces and body stiffness (10, 11). However, a requirement for a successful, systems-level model is a detailed knowledge of the material properties of the crawler––insight that can only be achieved experimentally.

Caenorhabditis elegans, a millimeter-sized nematode, has been used as a model organism to study undulatory motion experimentally (12–15). One fundamental, unresolved question is how difficult is it for the worm to bend its own body as it moves (16). In other words, what is the bending stiffness of the model organism? Efforts have been made to measure the stiffness of C. elegans (17–20), but a conclusive result is yet to be reached for several reasons.

Direct comparisons between transverse and longitudinal stiffness values have caused confusion. Here, the former quantity is the elasticity probed by a local compression of the worm, whereas the latter corresponds to the stiffness related to a nonlocal bending of the entire worm. As the nematode is known to consist of anisotropic materials (21), the two stiffnesses should not be considered the same. Additionally, the elasticity related to undulatory motion is the longitudinal stiffness, as the worm needs to bend its entire body to swim or crawl. There exist experimental limitations in directly measuring the longitudinal stiffness, and many measurements have been made indirectly through modeling assumptions (18, 19). Models used to elucidate the mechanics of undulatory motion typically involve assumptions of the material properties of C. elegans that are yet to be proven experimentally (22, 23).

Here, we present a method used to probe the dynamic viscoelastic properties of C. elegans at a biologically, physically, and structurally relevant length scale. Direct micromechanical measurements were performed, and a simple elastic model was used to gather results for the bending stiffness of C. elegans at all of its life stages. Furthermore, we have measured the viscoelastic response to bending, and show that commonly used models do not adequately describe the measured material properties of C. elegans. By modeling the viscoelasticity of the worm, our dynamic experiments reveal unexpected viscous properties. The Young’s modulus of the worm as a whole is reported, and an attempt to decouple the contributions from cuticle and muscles to the total stiffness is made.

Results and Discussion

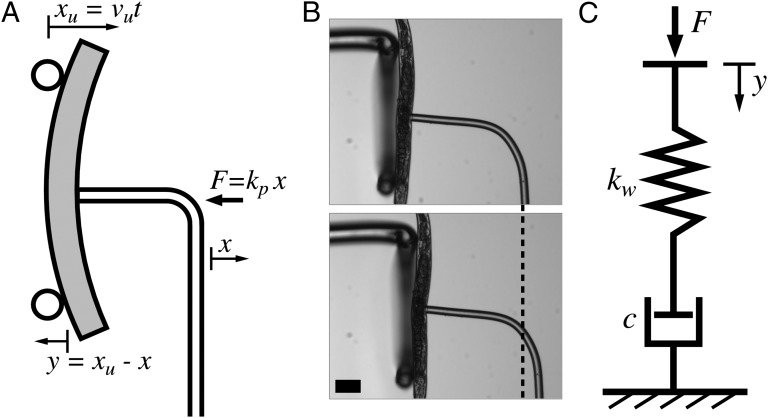
Micropipette deflection (MD) (24) was used to perform three-point bending measurements on anesthetized C. elegans nematodes to probe their force–deflection response. The experiment is illustrated in Fig. 1A, and described in more detail at the end of this paper. In short, the worm was held with a flexible force-calibrated pipette through suction, and bent by moving a simple support toward the “holding” pipette (from left to right in the figure) with a constant speed v_u. The deflection x of the holding pipette produces a certain force F = k_px, where k_p is the spring constant of the pipette. The bending y = x_u − x of the worm is defined as the difference between the motion of the support (x_u) and the deflection of the pipette. Optical microscopy images from the beginning (Upper) and end (Lower) of a bending experiment performed on an adult worm are shown in Fig. 1B. The total deflection of the pipette is indicated by the dashed line.

Fig. 1.

(A) Schematic diagram of the experimental micropipette deflection setup used to study the bending stiffness of C. elegans. A support (two circles) is moved from left to right with a constant speed, v_u. This induces a bending y of the worm due to the force F = k_px applied by the pipette, where k_p is the spring constant of the pipette. The deflection of the pipette and motion of the support are defined as x and x_u, respectively, and the bending y of the worm is defined as the difference between these. (B) Optical microscopy images of an adult worm in the beginning (Upper) and end (Lower) of a bending experiment, with the total pipette deflection indicated by the dashed line. The supporting structure is a thicker, U-shaped glass pipette, into which the worm can be bent as it would be simply supported. Scale bar, 100 μm. (C) Diagram of the worm modeled as a viscoelastic Maxwell material, consisting of a spring (spring constant k_w) and dashpot (damping coefficient c) connected in series. The bending y of the worm corresponds to the compression of the system due to the force F applied by the pipette.

Elastic and Viscoelastic Theoretical Models.

Two different theoretical models were used to achieve an understanding of the worm material. A simple linearized Hookean model was applied to describe the purely elastic properties of C. elegans. To gain deeper insight, a non-Hookean viscoelastic Maxwell model was introduced. In the limit of small deformations and short times these two models are equivalent.

Euler–Bernoulli elastic beam theory (EBT) (25) was used to analyze the elasticity of the worm by approximating it as a spring-like beam. The bending y at the position of the applied force F is given as

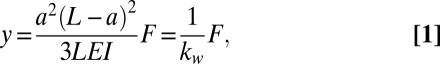where L is the distance between the supports and a is the distance between the upper support and the position of the applied force (pipette). The spring constant k_w of the worm is a function of both the geometry of the experiment, as well as the bending stiffness EI of the worm. The bending stiffness is equivalent to the product of the Young’s modulus E of the material, and the area moment of inertia I of the beam. For simplicity we assume that the cross-sectional distribution of stiff material in C. elegans is cylindrical (17), giving I = (D⁴ − d⁴)π/64 (26), where D and d are the outer and inner diameters of the cylindrical shell, respectively (Supporting Information, Area Moment of Inertia for a Cylinder). We note that much of our data will be reported as EI, because this product is independent of any assumptions in I.

To model the worm as a non-Hookean material, a viscous component was introduced to the system as shown in Fig. 1C. The compression y of the spring and dashpot connected in series corresponds to the bending of our worm. This viscoelastic model is known as the Maxwell model (27), and describes the relationship between force and compression as

where c and k_w are the damping coefficient and spring constant of the material, respectively. By applying the Maxwell model to the geometry of our specific system, the exact solution to Eq. 2 can be solved as (see Supporting Information for a detailed derivation)

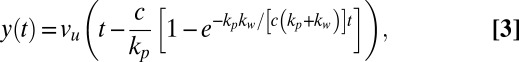where v_u is the speed of the support and k_p is the spring constant of the holding pipette. Furthermore, the force–deformation relationship can be written as

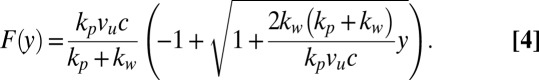The Kelvin–Voigt viscoelastic model, where a spring and a dashpot are connected in parallel (27), has been used by others to describe the material properties of C. elegans (18, 19), based on the theory of snake-like creatures in general (9). The analytical solution of the Kelvin–Voigt model applied to our system is shown in Supporting Information (the derivation is analogous to that sketched above).

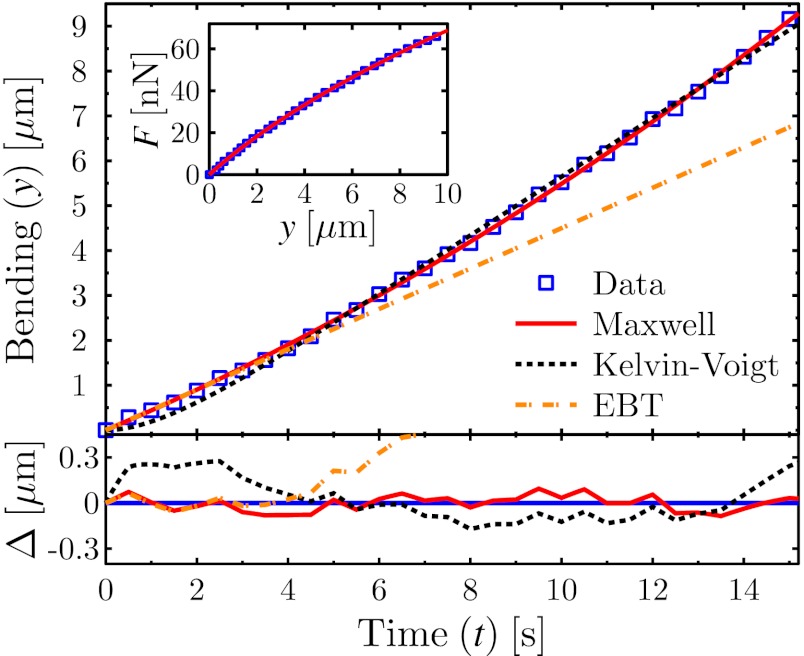
The results from an MD experiment on a young adult worm is shown in the main graph of Fig. 2, where the bending of the worm is plotted as a function of time. The analytical solutions to the theoretical models (EBT, Maxwell, and Kelvin–Voigt) have been fit to the data. The residuals of the fits are shown in the bottom graph, where Δ is the difference between the best-fit line and the data for each case.

Fig. 2.

Comparison between experimental bending results and viscoelastic theories. (Upper) Main graph shows the bending of a young adult worm as a function of time (□). The data have been fitted by the exact solutions from the Maxwell (Eq. 3, solid line) and Kelvin–Voigt (dashed line) models, as well as the EBT (dashed–dotted line). (Lower) Graph shows the difference Δ between theory and experiment (same legend as for Upper), and thus illustrates the quality of the different theoretical models. (Inset) Force is plotted as a function of bending, with the Maxwell force–deformation prediction (Eq. 4) drawn as a solid line.

As expected, the linearized EBT is valid only within the initial time regime, after which it is inadequate as a model due to the apparent viscosity of the material as well as nonlinear bending contributions. The Kelvin–Voigt model shows systematic deviations from the data, whereas the Maxwell model captures the data within the uncertainty of the measurement. Thus, the Maxwell model is a more appropriate method to characterize the viscoelasticity present in the bending of C. elegans. We note that the Maxwell model provided a consistently superior description of the data for all worms studied.

Fig. 2 (Inset) shows the force–deformation data from the same experiment as illustrated in the main graph. The solid line is the best fit of Eq. 4 to the experimental data. The fits used in Fig. 2 only require two fitting parameters c and k_w, because the rest of the constants in Eqs. 3 and 4, such as the speed of the support v_u and spring constant of the pipette k_p are known experimental parameters. By applying the Maxwell model to our data, we therefore obtain values for not only the stiffness, but also for the damping coefficient of C. elegans. The spring constant obtained from the EBT and Maxwell model is the same.

Viscoelastic Properties of C. elegans.

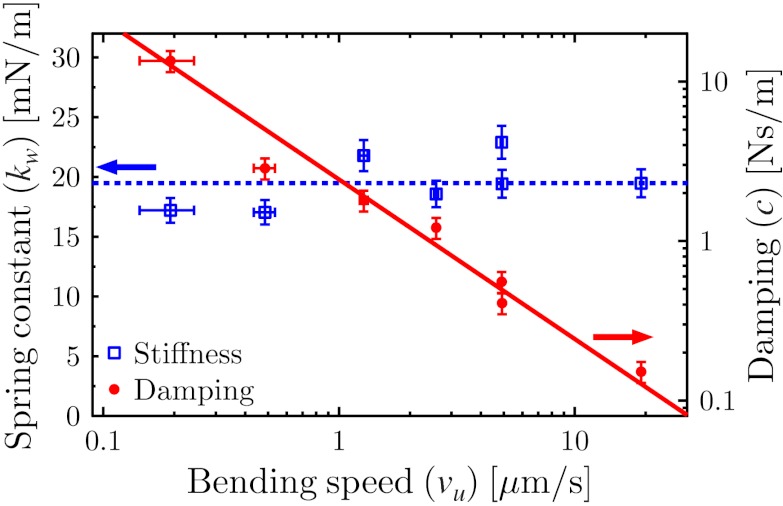
To investigate the viscoelastic properties of C. elegans, bending experiments were performed at different bending speeds v_u. The Maxwell model was used to analyze the data; the resulting speed dependence of the spring constant and damping coefficient of the worm is shown in Fig. 3. The spring constant is independent of speed, which is an expected feature of the elasticity of a material. The viscous component, however, is inversely proportional to the bending speed. This strong decrease of the damping coefficient is a characteristic of a shear-thinning, complex fluid (28). Specifically, the damping coefficient shows a clear power-law dependence over two decades in bending speed: 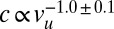. The viscous component of C. elegans should thus be modeled as a power-law fluid, as described by the Ostwald–de Waele model (29).

Fig. 3.

Speed dependence of the spring constant k_w (left y axis), and the damping coefficient c (right y axis), of the worm as a function of bending speed v_u. The damping coefficient is an inversely proportional function of the bending speed.

Shear thinning has been observed in several biological tissue types, such as heart and brain tissue (30) as well as in vocal cords (31). Although the structure and function of these tissue types are vastly different, the gross mechanical behavior is commonly governed by components in the extracellular matrix (ECM) (30, 32). Shear-thinning properties have been measured in the ECM component collagen (33, 34), and, as the cuticle of C. elegans is predominantly composed of cross-linked collagen (35), the non-Newtonian results reported here might be explained by the properties of the cuticle.

Shear-thinning properties have also been noticed in the legs of insects (36). To describe this, a friction-based structural damping model (37) was introduced instead of the more commonly used viscous damping approach. Structural damping cannot, however, describe the relaxation of a stressed material; as we have observed the worm material relax under static conditions (data shown in Supporting Information), the viscoelastic Maxwell model is better suited to describe the inelastic properties of C. elegans.

The implication of the shear-thinning property of C. elegans is that it is easier for the worm to bend its own body quickly rather than slowly. This is because the internal viscous resistance is lower at higher deformation speeds. The shape of an undulating crawler is due to the dynamic balance between elastic, hydrodynamic, and muscular forces. As a result, the shear-thinning property of the worm may influence the dynamics of motility, and shear thinning should be integrated into a full locomotory model. The actual bending speed of an adult C. elegans crawling on an agar surface can be calculated as v_crawl = 104 μm/s, based on the frequency and amplitude of its motion (22). This choice of bending speed is much higher than what was probed in the MD experiment, and corresponds to a speed regime with negligible internal viscous resistance. The gait transition between crawling and swimming can be noted by, among other things, an increase in bending speed (18), which is thought to be made possible by the lower external resistance from a fluid than from a gel substrate. This gait adaptation of C. elegans may, however, be driven to minimize not only external losses, but also internal viscous dissipation.

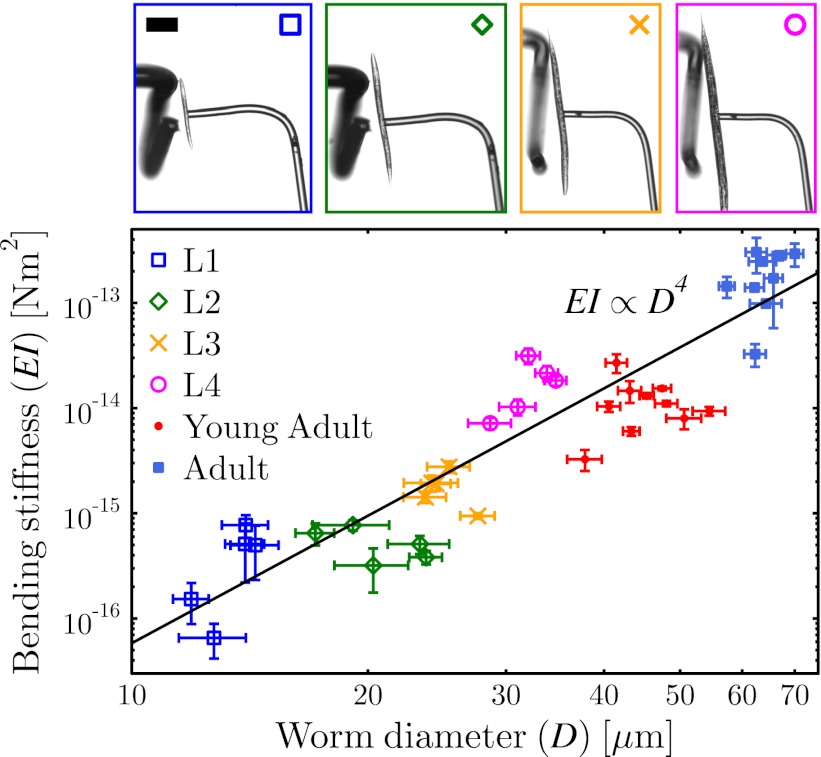
The bending stiffness of C. elegans was measured at all of its life stages, and is shown as a function of worm diameter in Fig. 4. As can be seen in the graph, the bending stiffness of C. elegans increases by almost 4 orders of magnitude as the worm grows from the L1 to the adult stage. The actual values correspond to the spring constant of the worm normalized by the geometry of the system according to Eq. 1, EI = a²(L − a)²k_w/3L. The errors in Fig. 4, as well as in all of the following graphs, are the SDs from several measurements performed on the same worm.

Fig. 4.

Bending stiffness at all life stages of C. elegans as a function of worm diameter. The power-law fit shows a D⁴ dependence, consistent with modeling the stiffness of the worm as a self-similar cylinder. Images on the top show snapshots from the experiments, with an L1, L2, L3, and L4 worm from left to right. Images of experiments done on a young adult and adult worm can be found in Figs. 5A and 1B, respectively. Colors and markers correspond to the respective data sets. Scale bar, 100 μm.

The images at the top of Fig. 4 show snapshots from the MD experiments performed with worms at the L1, L2, L3, and L4 life stages, and the colors and markers correspond to the respective data set plotted in the main graph. The power-law line EI ∝ D⁴ shown in the graph corresponds to the best-fitting function to the data (the exact value of the best-fit exponent is 4.02). As discussed above, if the worm is modeled as a cylindrical tube with an outer and inner diameter of D and d ∝ D, respectively, the bending stiffness will scale as EI ∝ ED⁴, consistent with experimental observations. We conclude that treating the worm as a cylindrical structure, with a stiffness that is self-similar, is a valid approximation––that is, the distribution and amount of stiff material scales with the size of the worm, and can be nondimensionalized by D. Thus, one need not treat the young and adult worms as mechanically different when properly nondimensionalized.

The slope of the power-law line in Fig. 4 can be used to calculate the Young’s modulus E of the nematode. If C. elegans is thought of as a rod-shaped worm consisting of a uniform distribution of “worm material,” the Young’s modulus of this material would be E_rod = 110 ± 30 kPa. When modeling the bending of C. elegans in theory and simulations, this value is what should be used in combination with an area moment of inertia of I = πD⁴/64, where D is the diameter of the worm. In reality, it is well known that the worm does not consist of a uniform distribution of the same material. On the contrary, C. elegans is a complex biological system made up of multiple tissue types, which are organized at different scales (cuticle, muscle, organs). The concept of bending stiffness is robust and independent of these complexities, and is therefore unambiguous when used to describe the complex mechanical structure. The Young’s modulus reported here is only to be used when considering the worm as a whole, without taking substructural components into account. Furthermore, the stiffness measured in this work is the longitudinal stiffness, which is the relevant geometry to consider when studying the bending of C. elegans.

Contributions from the Muscles and Cuticle.

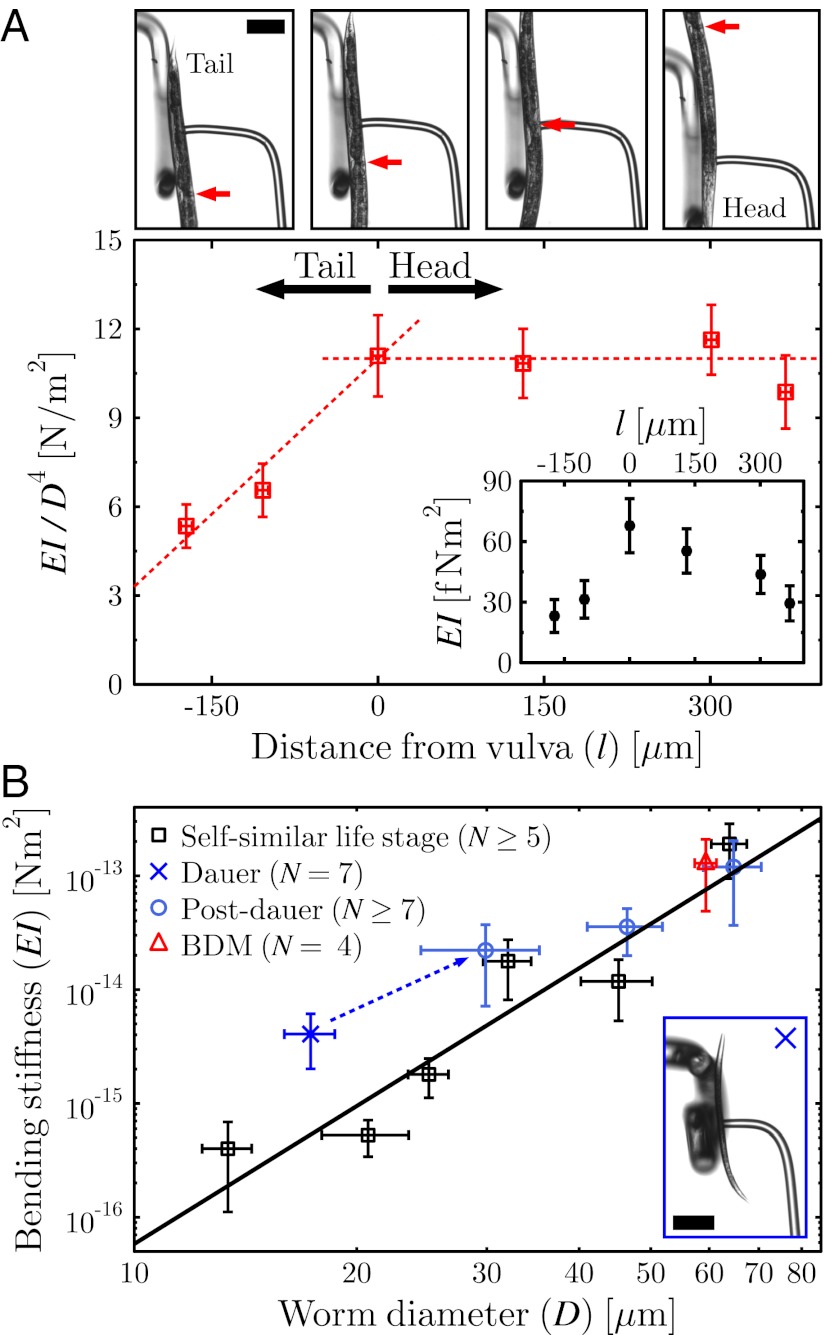
To probe the local stiffness along the body of a young adult worm, a smaller spacing L between the supports was used. The vulva was considered a reference point for the coordinate system due to its visibility in all of the experiments. The distance from the position of the pipette (i.e., the applied force) to the vulva was defined as l, with the head oriented in the positive direction. At the top of Fig. 5A, snapshots from measurements performed at different body positions are shown. The arrows indicate the position of the vulva. To factor out effects from changes in the diameter along the body of the worm, the local bending stiffness was divided by 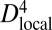for each experiment, where D_local is the local diameter of the worm at the position of the pipette. The resulting “effective” Young’s modulus is shown in the main graph of Fig. 5A, whereas the local bending stiffness is shown in the inset.

Fig. 5.

(A) Bending stiffness along the body of a young adult worm. (Upper) Images show snapshots from experiments performed at different positions (tail on the left, head on the right) of the worm. Arrows indicate the position of the vulva, and l is the distance from this to the middle of the pipette. (Lower) In the main graph, the local D⁴ dependence has been factored out from the bending stiffness, and a local “effective” Young’s modulus is thus plotted. The dashed lines are meant to guide the eye. (Inset) Local bending stiffness as a function of distance from the vulva. (B) Bending stiffness as a function of worm diameter of the self-similar worms (□) averaged over each life stage. N indicates the number of worms per data point, and the line is the same power-law function as used in Fig. 4. Bending stiffness of the dauer-(×) and post-dauer- (○) state worms are shown, and illustrate the deviation from self-similarity of the former. The use of another muscle relaxant (BDM) did not affect the measured bending stiffness of adult worms (△). (Inset) A dauer worm. Scale bar, 100 μm.

From these measurements, it is clear that the tail is significantly (up to 50%) less stiff than the rest of the body. From the vulva to the head, the stiffness was, within error, the same. The strong decrease in relative stiffness of the tail compared with the rest of the body can be explained by the smaller amount of muscles in the tail (21).

The anesthetic sodium azide (NaN₃) used throughout this work acted as a muscle relaxant, resulting in worms that were still and straight. Different concentrations of this drug did not affect the measured bending stiffness of the nematode. To further confirm that the NaN₃ did not affect the material properties of C. elegans, another muscle relaxing drug (2,3 Butanedione monoxime, BDM) was tried. As shown by the triangle in Fig. 5B, the average bending stiffness of adult worms anesthetized with BDM is the same, i.e., independent of choice of drug.

In this work we have probed the passive material properties of a relaxed worm. Having tried two different drugs (NaN₃ and BDM) and studied worms exposed to different concentrations of the anesthetics for different times, we get consistent and reproducible results. Thus, the drug did not affect the probed passive material properties of the nematode. As an active worm moves, the contraction of its muscles could be thought to modify the total bending stiffness of the worm. It is the dynamic modulation of the passive bending stiffness which enables undulatory locomotion.

Under stress, such as lack of food or in environments of high temperatures, the young L1 worms turn into the so-called dauer state, in which they can survive for months (21). It has been shown that dauer-state worms have a thicker cuticle with respect to total body thickness compared with nematodes at normal life stages. Specifically, the fraction between the thickness of the cuticle and the diameter of the worm is 1/36th for a dauer worm, whereas this fraction is 1/88th for all other life stages (35). By measuring the bending stiffness of dauer-state worms, the cuticle contribution to the total stiffness could therefore be studied, as this worm potentially has more stiff material than an equally sized, self-similar worm. The results from MD measurements performed on dauer-state worms (×) are shown in Fig. 5B. The dauer worm is significantly stiffer than what would be the case for a self-similar worm. Thus, the stiffness of C. elegans is highly dependent on the cuticle thickness.

If the cuticle were the only component contributing to the total stiffness of the worm, then the worm’s body could be modeled as a cylindrical shell. The Young’s modulus of this shell would be E_cuticle = 1.3 ± 0.3 MPa, which corresponds to the upper extreme value of this material-specific property of C. elegans. In contrast, the lower limit, obtained above as E_rod = 110 ± 30 kPa, resulted from modeling the worm as a uniform rod. If one were to assign a Young’s modulus to the worm, detailed knowledge of the distribution of the elastic material within the worm would be required. However, the modulus must be bound by these two limiting assumptions.

Measurements were also performed on post-dauer-state worms, as shown by circles in Fig. 5B. The results illustrate how the material properties of C. elegans return back to normal as the nematode exits the dauer state.

Conclusions

Here we have presented the use of a micromechanical technique to probe the viscoelastic material properties of C. elegans. The bending stiffness was measured at all life stages of the worm, and was shown to scale in a self-similar cylindrical way with the diameter of the worm. If assuming a uniform distribution of stiff worm material within the rod-shaped worm, the Young’s modulus of this material was determined to be E_rod = 110 ± 30 kPa. The different stiff body parts contributing to the total stiffness of the worm were investigated, and the cuticle was found to be responsible for a large fraction of the bending stiffness of C. elegans. Furthermore, measurements along the body of the worm showed a higher stiffness of the head than the tail, indicating a strong contribution from the muscles as well.

The viscoelasticity of C. elegans was shown to be best modeled as a Maxwell material. By using this theoretical model, the nematode was found to be shear thinning––a complex fluid property that can be expected to influence the dynamics of motility of the worm. We conclude that the Caenorhabditis elegans nematode can be modeled as a self-similar, shear-thinning object.

Materials and Methods

Bending Measurements.

The micropipette deflection technique was used as described in ref. 24. A flexible micropipette with the length of ∼1 cm and diameter of ∼20 μm was bent into an L shape and used as a spring-like cantilever. The manufacturing and calibration of this force-sensing pipette was performed as in ref. 38. The support used in the bending experiments was a 50-μm-thick micropipette bent into the shape of a U, with which the worm could be supported. The optical microscopy images were analyzed with MATLAB (MathWorks) by performing cross-correlation image analysis on pictures taken at 2 Hz.

Unless mentioned otherwise, all bending experiments were performed in an M9 buffer with a 10-mM concentration of the anesthetic NaN₃. The measurements were performed within 2 h of drugging the worms. Different concentrations of the NaN₃ did not give rise to changes in the measured bending stiffness. To further verify that the drug did not change the bending stiffness of the worm, a buffer of 0.3 M BDM in M9 was used. In this experiment, the worms were studied within 15 min after being put into the buffer, as they lost their rod-like shape after this time.

The results shown from measurements performed on only one worm were all reproduced with several other worms (Supporting Information). All of the worms were bent in the dorsal–ventral plane. Repeated experiments performed on the same worm with different bending speeds were done with enough waiting time (around 3 min) in between measurements to give the worm time to relax. The results from these measurements were independent of changing the speed in an increasing or decreasing fashion. For the results in Fig. 4, at least three measurements were performed per worm.

Worm Strains, Cultivation, and Preparation.

Wild-type worms (N2) were acquired from the Caenorhabditis Genetics Center and were cultivated according to standard methods (39) on Escherichia coli (OP50) nematode growth media (NGM) plates at 20 °C. Dauer-state worms were produced by moving L1 worms to an NGM plate without bacteria, and letting them develop for several weeks. The post-dauer states (first generation) were studied as the dauer worms exited the rest state after they had been moved back to a bacteria-covered NGM plate. All chemicals were sourced from Sigma-Aldrich.