An efficient method to identify differentially expressed genes in microarray experiments

Abstract

Motivation

Microarray experiments typically analyze thousands to tens of thousands of genes from small numbers of biological replicates. The fact that genes are normally expressed in functionally relevant patterns suggests that gene-expression data can be stratified and clustered into relatively homogenous groups. Cluster-wise dimensionality reduction should make it feasible to improve screening power while minimizing information loss.

Results

We propose a powerful and computationally simple method for finding differentially expressed genes in small microarray experiments. The method incorporates a novel stratification-based tight clustering algorithm, principal component analysis and information pooling. Comprehensive simulations show that our method is substantially more powerful than the popular SAM and eBayes approaches. We applied the method to three real microarray datasets: one from a Populus nitrogen stress experiment with 3 biological replicates; and two from public microarray datasets of human cancers with 10 to 40 biological replicates. In all three analyses, our method proved more robust than the popular alternatives for identification of differentially expressed genes.

Availability

The C++ code to implement the proposed method is available upon request for academic use.

1 INTRODUCTION

Analysis of high-throughput microarray data is becoming commonplace with the increase of sequenced genomes and genome-wide investigations of gene expression (Brem et al., 2002; Chesler et al., 2005; Hubner et al., 2005; Mehrabian et al., 2005; Morley et al., 2004; Scheetz et al., 2006; Tsai et al., 2006; Yvert et al., 2003). Low-replication experiments are common in microarray studies (Gadbury et al., 2003) and testing for differential expression of many genes with small samples is problematic (Sima and Dougherty, 2006; Yang and Churchill, 2007). Gene ranking is a fundamental problem in microarray analysis, and great efforts have been devoted to construct powerful statistics. The SAM t in Tusher et al. (2001), the moderated t in Smyth (2004) and the Welch type t in Hu and Wright (2007) are attractive statistics for this purpose. These methods share in common the idea of information pooling across genes, which can be dated back to Chen et al. (1997). Ranking alone does not tell how many or which genes are significantly differentially expressed. Another challenge is to identify, reliably and economically, as many biologically and statistically significant genes as possible while controlling false positives. Some permutation approaches have been developed to empirically estimate the false discovery rate (Storey and Tibshirani, 2003; Tusher et al., 2001; Xie et al., 2005). A permutation based empirical estimate of FDR is a must for SAM t and other statistics with unknown null distributions. However, permutation is not available when the sample size is small.

Many existing approaches ignore the impact of the complex dependence structures in microarray experiments. Several approaches have been proposed (Efron, 2007; Pawitan et al., 2006; Qiu et al., 2005) to address the stochastic dependence between genes to improve statistical inference of microarray data. We focus on the explicit use of gene-to-gene correlation to boost statistical power and prevent false positives in small microarray experiments. We believe that suitable dimension reduction techniques based on clustering can be applied to effectively reduce the number of tests, thereby conserving testing power. Standard clustering analysis forces all data points into groups at the expense of cluster tightness. For microarray experiments, Tseng and Wong (2005) have proposed a method to identify informative, tight and stable clusters to enable statistically valid biological inferences from microarray data. By integrating K-means clustering with resampling, this ‘tight-clustering’ method embodies a novel concept that does not necessitate the estimation of the number of clusters and the assignment of all genes into clusters. Although promising, it is computationally intensive and requires large sample sizes like other resampling-based techniques.

In this article, we propose an efficient method to identify differentially expressed genes. We term the method FCPC, since it is based on a forward search using gene-to-gene correlation and principal component analyses. In FCPC, we first divide genes into co-expression strata using the information conveyed by gene expression. This is analogous to the post-stratification technique commonly used in large scale survey sampling (Cochran, 1977; Feng and Shi, 1996; Holt and Smith, 1979) to improve inference precision. Second, we design a tight clustering method to search within every stratum for tight gene clusters in each of which the minimum gene-to-gene correlation exceeds a predetermined level. The proposed tight clustering approach should be especially suitable for low-replicate experiments. Next, we represent tight clusters by their first principal components (PCs). In terms of mean-square error, principal component analysis is a suitable linear dimension reduction technique for defining a new dimensional space that captures the maximum information in the original dataset. We then pool the information across all PCs and scattered genes using the moderated t by Smyth (2004), which is implemented in the LIMMA package (Wettenhall and Smyth, 2004). The moderated t is attractive in that it does not depend on permutation testing, and thus is suitable for low-replicate experiments. Finally, we screen for significant differential expression among PCs and scattered genes by controlling the FDR (Benjamini and Hochberg, 1995) to the double-sided P-values of the moderated t-statistics. If a PC is found significant, all genes in the cluster are declared to be significant. Simulations based on a clumpy mean–variance model and a real dataset show that FCPC controls FDR and notably outperforms the SAM and the empirical Bayesian approach detailed in Section 2.5. Applications to real microarray datasets also show that our method yields more noteworthy candidate genes for follow-up studies than the popular alternatives.

2 METHODS

Briefly, FCPC is composed of four steps: creating coexpression strata, finding tight clusters, assigning a representative value for each tight cluster by principal component analysis and identifying differentially expressed clusters and/or scattered genes. Details of the four steps are given below.

2.1 Generation of coexpression strata

All genes (probe sets) are initially divided into two strata based on mean expression differences between control and treatment: d_g = x̄_2g − x̄_1g for g = 1,…,G, where x̄_1g and x̄_2g are mean expression indices of the g-th gene in the control and the treatment, respectively, and G is the number of all genes under consideration. We call 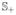= {g: d_g > 0} and 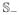= {g: d_g < 0} the upregulated and downregulated strata, respectively, and we screen for up- and downregulated genes from 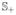and 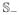. We further stratify 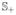using relative expression ratios r_g = x̄_2g/x̄_1g for g ∈ 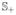. For an integer k ≥ 1, we assign all of the genes with relative expression ratios in [k − 0.5, k +0.5) into substratum k. Similarly, we further stratify 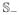using r_g = x̄_1g/x̄_2g for g ∈ 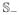. We further break each of the large strata into smaller strata such that each contains L or fewer genes. Based on our simulations, we propose L to be 100 or so in order to balance computational efficiency, power and FDR. In the main text, we will use L = 100 to illustrate the performance of the FCPC.

2.2 Identification of tight clusters

If the smallest gene-to-gene correlation within a cluster is chosen to exceed ρ₀, we identify the cluster as having a tightness ρ₀. We search for tight clusters separately within each stratum. For a given tightness ρ₀, we find tight clusters recursively by a four-step algorithm:

1. Find a cluster core. Search for the gene pair C = (i,j) with the largest sample correlation ρ_max = ρ_ij in the stratum. If ρ_max ≥ ρ₀, then take C as the core of a potential cluster. Otherwise, go to step (4).

2. Extend the core to a cluster. For gene g ∉ C, if min{ρ_gi: i ∈ C} > ρ₀, then add the gene to C and denote as the current cluster; otherwise, search for the next gene ∉ C. Repeat this step until no additional genes can be added. Retain current C as a tight cluster and go to the next step.

3. Remove the tight cluster from the stratum and repeat steps (1) and (2) for the remaining genes in the stratum to find another cluster of tightness ρ₀. Repeat this step until no additional clusters of the same tightness can be found.

4. Reduce the value of ρ₀ and repeat Steps (1) to (3) until ρ₀ falls to a predetermined value. In our simulation studies and real database analyses, we begin with ρ₀ = 0.8, and then reduce it to 0.7, 0.6 and finally 0.5. See Sections 3.4, 3.5 and 5 for the rationale of choosing these values.

2.3 Principal component analysis

For a tight cluster of size m ≥ 2, denote by x^(j) = (x_1j,…,x_mj )^τ the expression indices of m genes in the j-th biological individual. Calculate $\mathrm{\sum }={\sum }_{j=1}^n(x^{(j)}-\overline{x}){(x^{(j)}-\overline{x})}^{\tau }$ where n = n₁ + n₂, n₁ is the sample size of controls, n₂ is the sample size of treatments, and x̄ = n⁻¹(x⁽¹⁾ +···+x⁽ⁿ⁾). All positive eigenvalues of Σ are denoted by λ₁ ≥ ··· ≥ λ_p. The first PC of the j-th biological individual is given by $x_j^{\ast }=e_1^{\tau }{x}^{(j)}$, where e₁ is the eigenvector associating with λ_1. We propose the use of $x^{\ast }={\left(x_1^{\ast },\dots ,x_n^{\ast }\right)}^{\tau }$ to represent this tight cluster. How well the first PC represents this cluster can be measured by the ratio γ = λ₁/(λ₁ + ··· + γ_p) which is the proportion of total variance explained by the first PC. Table 3 and Figure S2 illustrate the representativeness of the first PC.

Table 3.

The representativeness of the first PC

ρ0	nc	γmin	γmax	Mean	Median	cv
0.8	329 978	0.8708	1.0000	0.9491	0.9484	0.0271
0.7	55 367	0.8036	1.0000	0.9266	0.9230	0.0449
0.6	27 452	0.7499	1.0000	0.9009	0.8966	0.0634
0.5	15 009	0.6962	1.0000	0.8753	0.8708	0.0840

ρ₀: level of tightness; n_c: number of clusters; γ_min: minimum of observed γ-values; γ_max: maximum of observed γ-values; cv: coefficient of variance.

2.4 Identification of differentially expressed genes

Suppose there are G₁ tight clusters and G₂ scattered genes. We calculate the double-sided P-values of the moderated t-statistics for the G₁ cluster-specific PCs and G₂ scattered expression vectors. We then sort these P-values as p₍₁₎ < ··· < p_(Ḡ), where Ḡ= G₁ + G₂. For a given nominal FDR α, we identify all clusters and scattered genes with P-values smaller than δ = max{p_(g): p_(g) ≤ gα/Ḡ} to be significant. To find δ, we start at p_(Ḡ) proceed to smaller P-values as long as p_(g) > gα/Ḡ, and stop the procedure as p_(g) ≤ gα/Ḡ with δ = p_(g). All significant scattered genes and the genes in the significant clusters are extracted as differentially expressed candidate genes.

2.5 Methods comparison

We applied the FDR controlling procedure of Benjamini and Hochberg (1995) to the double-sided P-values of the gene-specific moderated t-statistics in Smyth (2004), hereafter referred to as the eBayes. To be specific, we calculated all gene-specific P-values of the moderated t-statistics and sorted them as p̃₍₁₎ < p̃₍₂₎ < ··· < p̃_(G), where G was the number of all genes to be tested. The FDR procedure identifies all genes with P-values smaller than δ̃ = max{p̃_(g): p̃_(g) ≤ gα/G} for the preset nominal α. For the SAM by Tusher et al. (2001), we considered two typical choices of the SD offset in the SAM t-statistic. The median of the gene-specific SDs was adopted in Xu et al. (2005) and Hu and Wright (2007). The corresponding method was referred to as SAM50. Another choice was the coefficient variation minimizer of the SAM t (Hu and Wright, 2007). The corresponding method was referred to as SAMCV.

3 SIMULATION STUDIES

It has been reported that SAM has difficulties in FDR control and estimation (Dudoit et al., 2003; Pan, 2002; Zhang, 2007). For small experiments, the empirical estimate of FDR in SAM may be misleading. We thus adopted average power and FDR as performance criteria. Applying a method to the r-th simulated dataset (1 ≤ r ≤ R), we may claim D_r positives, where D̃_r are among the D differentially expressed genes. We defined power = (RD)⁻¹ (D̃₁ + ··· + D̃_R) as the average probability of rejecting the false null hypotheses, referred to as the average power in Dudoit et al. (2003). Similarly, we calculated $\text{FDR}=1-R^{-1}{\sum }_{r\in \mathfrak{R}}{D}_r^{-1}{\stackrel{\sim }{D}}_r$, where ℜ = {r: D_r > 0, 1 ≤ r ≤ R}. Using common datasets, we calculated average powers and FDRs of SAM along a threshold list, and those of the other two statistical approaches, along a nominal FDR list.

3.1 Clumpy mean–variance model

We designed our simulation dataset based on the fact that genes are usually expressed in functionally relevant patterns, contributing to the mosaic dependence structure of microarray data. Described as ‘clumpy dependence’ by Storey (2003), it depicts the scenario that genes are dependent in small, functionally relevant groups but independent among groups. In actual microarray experiments (or biological systems), the ‘clump’ sizes are likely to vary from a few to several dozens, depending on associated pathways/processes and/or microarray design (e.g. probe redundancy). In addition, as shown in Hu and Wright (2007), different genes may have distinct expression deviations. We therefore simulated gene-expression indices from a clumpy mean–variance model. First, we generated a G×n background matrix X by iterating two steps below: (1) Randomly select clump size m from {1,2,…,100} and clump-wise correlation ρ from U(0.5, 1). (2) For a given (m, ρ) pair, generate m ×1 noise vectors e_·j from $N(0_m,(1-\rho )I_m+\rho 1_m{1}_m^{\prime })$ and let x_·j = μ+diag(σ)e_·j be the expression indices of the m genes in the clump at array j = 1, …, n = n₁ + n₂, where μ is an m × 1 vector of elements ${\mu }_g~1000{\chi }_5^2$, and σ, an m × 1 vector of elements ${\sigma }_g=e^{{\beta }_0/2}{\mu }_g^{{\beta }_1/2}$, and β₀ and β₁ are two constants for all G genes. In this design we set β₀ = −5,β₁ = 2 and n₁ = n₂ = 4. Second, we similarly generated gene clumps containing 150 background expression indices and added 2^−1/2δ_gσ_g to x_gj for all j > 4 to have gene g be upregulated, where δ_g was sampled from U(4,10) such that the true regulation ratio 1+2^−1/2e⁻²δ_g ~ U (1.2322, 1.5804). In a similar way, we generated clumps containing 150 downregulated genes. Finally, we randomly replaced 300 rows of the background matrix X by the 300 differentially expressed genes so that no clumps were enriched by differentially expressed genes. We mimicked gene-expression indices of clump-wise correlations and various gene-specific means and variances. We varied G from 1000 to 50 000 and for each given number we simulated 1000 datasets to calculate the FDR and power for each method.

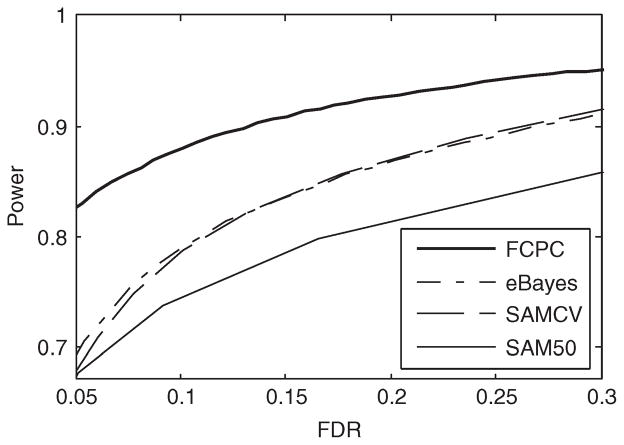
In terms of power for a given FDR, the FCPC notably distinguished itself from the other three methods, with eBayes second, closely followed by SAMCV and SAM50 (Fig. 1). Both the FCPC and the eBayes controlled FDR fairly well, close to the nominal level as shown in Table 1. In contrast, it would be difficult to select the threshold in the SAM approaches to control FDR at a nominal level, especially for very small sample sizes. The FCPC is preferable to the eBayes in terms of the relative power gain defined as (β_FCPC − α_FCPC) × (β_eBayes − α_eBayes)⁻¹ −1, where β’s and α’s were the power and FDR of the specified approaches. Setting nominal FDR at 0.05 and G =20 000, we obtained β_FCPC = 0.785, α_FCPC = 0.032, β_eBayes =0.705 and α_eBayes = 0.054. In such a scenario, the relative power gain of the FCPC over the eBayes was 16%. Under the same nominal FDR, the relative power gain increased as G increased, and approached 34% as G =50 000 (Fig. S1).

Fig. 1.

The power versus the FDR over 1000 simulated datasets from a clumpy mean–variance model. Each dataset contained expression indexes of 20 000 genes at four controls and four treatments, where 300 genes were differentially expressed.

Table 1.

The FDRs of FCPC and eBayes

G	FCPC	eBayes
1000	0.021	0.039
2000	0.029	0.050
3000	0.027	0.051
4000	0.029	0.053
5000	0.030	0.053
6000	0.029	0.055
7000	0.028	0.053
8000	0.029	0.055
9000	0.033	0.056
10 000	0.030	0.054
20 000	0.032	0.054
30 000	0.035	0.056
40 000	0.038	0.056
50 000	0.039	0.054

3.2 Sampling from the colon dataset

The dependence in real datasets should be much more complicated than the clumpy mean–variance model. To illustrate the advantages of the FCPC when sample size is very small, we sampled the colon dataset from Alon et al. (1999). In that dataset, expression indices of 40 tumor and 22 normal colon tissues for 6600 human genes were measured using the Affymetrix GeneChip. A subset of 2000 genes with the highest minimal signal intensity across the samples was chosen by the authors for further analysis. From the subset, we removed 472 genes such that 1 < |ℓ_g| ≤2, where ℓ_g = log(x̄_2g/x̄_1g). For each gene g with ℓ_g > 2 we added 0.6-fold of gene-specific range to every expression index in the treatment to mimic an upregulated gene. At the same time, for each gene g with ℓ_g < −2 we added 0.6-fold of gene-specific range to every expression index in the control to mimic a downregulated gene. As such, we artificially introduced 102 differentially expressed genes and had 1426 stably expressed genes. We randomly sampled 2 out of the 40 tumor arrays and 2 out of the 22 normal arrays for testing with the FCPC and its alternatives. We repeated this procedure 1000 times and calculated the FDR and power of each approach.

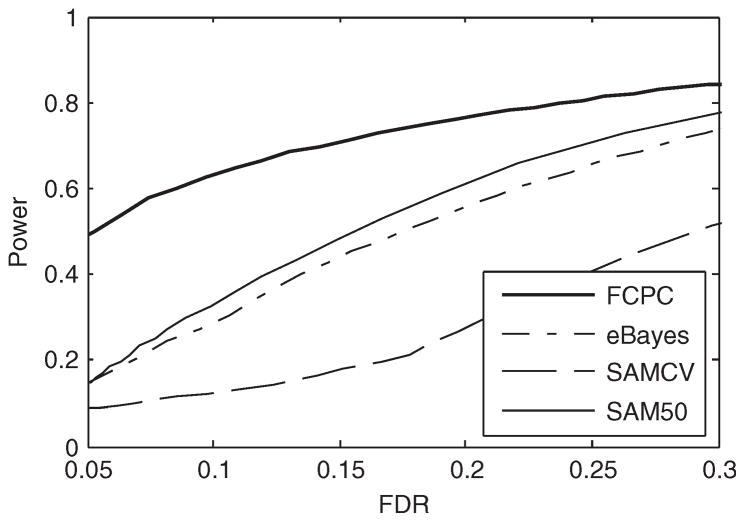
Here again, the FCPC clearly outperformed the other three methods in terms of power, especially at lower FDR levels (Fig. 2). The SAM50 ranked second, closely followed by the eBayes. The SAMCV was the last. At nominal FDR 0.05, the FCPC and eBayes controlled FDR at 0.040 and 0.048 and with a power of 0.433 and 0.141, respectively. The relative power gain of the FCPC over the eBayes was thus 323%. Given the small sample size, the empirical estimate of FDR in SAMCV appears to be unreasonable (Table 2). In some cases, the empirical estimates unacceptably differed from the corresponding FDRs.

Fig. 2.

The power versus the FDR over 1000 subsets randomly sampled from the trimmed colon dataset. Each subset contained expression indexes of 1528 genes at two normal and two tumor arrays, where 102 genes were differentially expressed.

Table 2.

Performance of the SAM to random subsets of the colon data

Δ	SAM50			SAMCV
	eFDR	FDR	Power	eFDR	FDR	Power
0.90	0.175	0.221	0.261	3.151	0.298	0.512
0.75	0.209	0.263	0.332	2.389	0.343	0.594
0.60	0.258	0.316	0.422	1.806	0.406	0.684
0.45	0.338	0.391	0.534	1.386	0.497	0.771
0.30	0.472	0.499	0.670	1.205	0.617	0.850
0.15	0.721	0.680	0.843	1.119	0.783	0.926

For a given value of Δ, the power, FDR and eFDR were computed via 1000 subsets of the reduced colon dataset. Each subset contained the expression indices of 1528 common genes from two normal and two tumor arrays randomly selected from the original 22 normal and 40 tumor arrays. The eFDR was the average of 1000 empirical estimates of FDRs. Each empirical estimate was calculated via balanced permutations as described in Tusher et al. (2001).

3.3 The representativeness of the first PC

The representativeness of the first PC for each tight cluster was evaluated by γ in Section 2.3. Table 3 shows the distribution and certain mathematical characteristics of the γ-values of 427 806 tight clusters produced by 1000 simulated 5000×8 datasets from the clumpy mean–variance model described in Section 3.1. There were 329 978 clusters at tightness ≥0.8, and 55 367 clusters at tightness 0.7 to 0.8 (Table 3). The number of clusters decreased rapidly as the level of tightness declined. At each tightness level, the median and mean were large, and the coefficient of variance was very small. In general, the first PC of a tight cluster represented the cluster fairly well. On average, the first PC explained greater than 87% of the total variance (Table 3, see the smallest mean and median). Additional details for first PCs of tightness ≥ 0.8 are shown in Fig. S2.

3.4 The basis for the forward search tight clustering

The correlations between genes of different expression patterns have distinct properties. Let ρ̂ be a generic notation of the correlation between two genes. We distinguish three hierarchies for ρ̂: (1) between two differentially expressed genes, (2) between a differentially expressed gene and a stably expressed gene and (3) between two stably expressed genes. The proposed tight clustering is based on our simulation studies on gene-to-gene correlations.

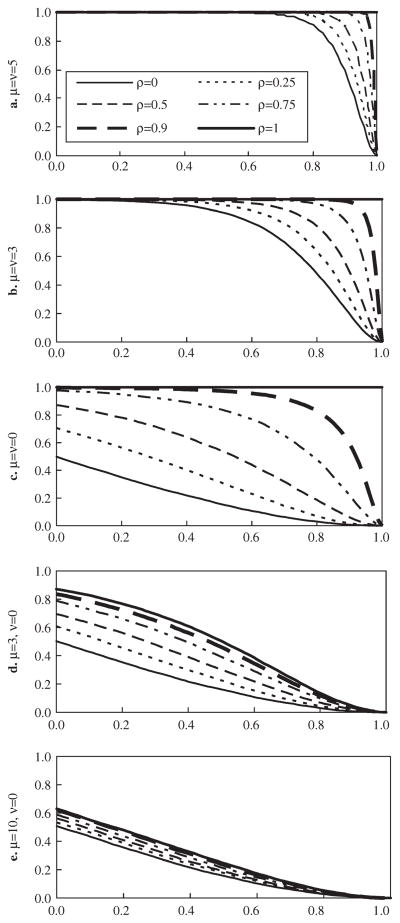
In our method, the probability Pr(ρ̂ > ρ₀) reflects the likelihood of assigning two genes of interest into a cluster of tightness ρ₀. To illustrate the distribution properties of ρ̂, we sampled the expression indices of two genes exhibiting bivariate normal distribution in a control group with mean 0, variance 1 and correlation ρ and bivariate normal distribution in a treatment group with mean (μ, ν)′, variance 1 and correlation ρ. For given differential expression (μ,ν)′ the probability Pr(ρ̂ > ρ₀) increased with residual correlation ρ (Fig. 3 and Fig. S3). This is consistent with classical sample correlation. These figures also show three particular characteristics of gene-to-gene correlations, which clearly differ from classical sample correlations.

Fig. 3.

Horizontal axis: ρ₀ Vertical axis: Pr(ρ̂ > ρ₀) where ρ̂ gene-to-gene correlation. Each curve was based on a gene pair expressed in three controls and three treatments. For a control, the expression of the pair was sampled from the bivariate normal distribution with mean 0, variance 1 and correlation ρ, and for a treatment, the expression of the pair was sampled from the bivariate normal distribution with mean (μ,ν)′, variance 1 and correlation ρ.

First, the distribution of the correlation between two similarly up-or downregulated genes (i.e. μ = ν ≠ = 0) can be dramatically affected by the magnitude of differential μ. The larger the magnitude, the larger the probability Pr(ρ̂ > ρ₀), and the more likely the two genes will be clustered together. As shown in Figure 3a–b and Figure S3a–b, the correlation between two differentially expressed genes was likely to be large if the magnitude of the differential was large. This was also true even if the residual of the two genes were completely independent (ρ = 0). As μ = 5 and ρ = 0, Pr(ρ̂ > 0.8) = 0.9091 in Figure 3a and Pr(ρ̂ > 0.8) = 0.9585 in Figure S3a. The probability decreased as μ decreased. As μ= 3 and ρ = 0, Pr(ρ̂ > 0.8) = 0.4798 in Figure 3b and Pr(ρ̂ > 0.8) = 0.0072 in Figure S3b. Given ρ = 0, Pr(ρ̂ > 0.8) decreased to 0.032 in Figure 3c and to 0 in Figure S3c when μ decreased to 0. Since high gene-to-gene correlations likely occur between similarly up- or downregulated genes with large differentials, the proposed method tends to assign those genes with the largest differentials to a common cluster in early iteration steps.

Second, the correlation between a stably expressed gene and a differentially expressed gene is unlikely to be large. This was especially the case when the magnitude of differential was large, even when the residual correlation ρ was close to 1. As μ = 3, Pr(ρ̂ > 0.8) ≤ 0.1354 in Figure 3d and Pr(ρ̂ > 0.8) ≤ 0.0001 in Figure S2d for ρ ∈ [0,1]. As μ = 10, Pr(ρ̂ > 0.8) ≤ 0.0518 in Figure 3e and Pr(ρ̂ > 0.8) = 0 in Figure S3e for ρ∈ [0,1]. These upper bounds were achieved at ρ = 1, and for fixed μ the probability Pr(ρ̂ ρ₀) declined as ρ decreased. Thus, the proposed forward-search tight clustering method reduced the chance of assigning a stable gene to a differentially expressed cluster, and vice versa.

Third, Figure 3c–e and Figure S3c–e show two properties of the correlation ρ̂ between a stably expressed gene and a differentially expressed gene: (1) The distribution of ρ̂ is invariant to μ if the two genes are independent (ρ = 0). Precisely, independence means τ = (n−2)^1/2 ρ̂(1 − ρ̂²)^−1/2 ~ t_n−2 (the student t with n − 2 degrees of freedom) for arbitrary μ. (2) For arbitrary ρ∈ [0,1],τ converges in distribution to t_n−2 as μ → +∞. As μ increases, the curves with respect to positive residual correlations decline toward the benchmark curve of an independent stably expressed pair. By these properties, one may control the possibility of clustering a gene of fixed differential expression with a stably expressed gene by choosing a suitable tightness correlation threshold.

Classical correlation theory applies for the correlation ρ̂ between two stably expressed genes (μ = ν = 0). In such a case, ρ̂ is well-known to converge in probability to the residual correlation ρ as sample size increases. The distribution of ρ̂ is mainly affected by ρ for a finite sample size. The larger the residual correlation, the more likely ρ̂ exceeded a given threshold (Fig. 3c and Fig. S3c). In microarray experiments, there are more stably expressed genes than differentially expressed genes in general. Hence, the forward-search tight clustering is especially efficient as there are large residual correlations among stably expressed genes.

3.5 Parameters that affect FCPC

Two user-defined parameters, the maximum substratum size L and the tightness level T impact the tight cluster sizes and hence the sensitivity, specificity and the computational efficiency of the FCPC. In our simulations, we investigated four sets of tightness levels: T1 ={0.9, 0.8, 0.7, 0.6} and Ti = T 1− 0.1×(i −1) for i = 2,3,4. For each Ti we calculated the power and FDR of the FCPC with L =50, 100, 1000, 2000 and 5000 as applicable. The power of the FCPC appeared robust as L changed for a given T (Figs S4a and S5a). In general, using large L would reduce computational efficiency and increase the possibility of mixing noise genes and genes that are only marginally differentially expressed. We recommend performing tight clustering within substrata of sizes 100 or so. Using less stringent tightness levels could boost statistical power at the expense of inflating FDR, especially for a very small nominal FDR. In our simulations, T 1 yielded the most stringent control of FDR and was the most computationally demanding. T 2 controlled FDR very well even as G = 50 000 (Table 1), with considerably improved computational efficiency.

4 APPLICATIONS TO REAL MICROARRAY DATASETS

4.1 Nitrogen deficiency in Populus

We applied FCPC and eBayes to analyze the transcriptomic response of Populus fremontii × angustifolia to nitrogen deficiency using the GeneChip® Poplar Genome Array (Affymetrix). Raw hybridization signals were processed by the Affymetrix MAS 5.0 software, and only probe sets identified as ‘present’ in all three control and three nitrogen stress replicates were analyzed further. The resultant 13 507 probe sets were separated into up- (6202) and downregulated (7305) strata. Of the 6202 probe sets in the upregulated stratum, 5368 were represented by 2206 tight clusters, likewise, 6478 of the 7305 probe sets in the downregulated stratum were covered in 2196 tight clusters, and we had 1630 scattered genes. At the nominal FDR α =0.05, the FCPC method detected 410 significantly up- and 189 significantly downregulated genes, and eBayes identified 143 up-and 90 downregulated genes.

Further examination of the significant results from each procedure revealed discrepancies in terms of the genes identified. Table 4 lists the 10 downregulated discoveries based on the highest expression differentials and the 10 downregulated discoveries based on the smallest expression differentials found by eBayes and FCPC. Half of the discoveries by FCPC from the most significantly downregulated stratum were not captured by eBayes (see the genes and relative expression ratios in boldface in panel a of Table 4). FCPC also outperformed eBayes in capturing weakly but statistically significantly downregulated genes (Table 4, panel b). For instance, the 10 most weakly downregulated genes discovered by FCPC were completely missed by eBayes. All 10 FCPC discoveries shown in panel b of Table 4 were ≤ 1.3-fold downregulated, versus only 1 by eBayes. We also analyzed this dataset using various tightness levels (Tables S1 and S2). Using less stringent tightness levels had no effect on strongly downregulated genes (Table S2a), but captured more genes with weak expression differentials (Table S2b). Although biological significance of these weakly downregulated candidate genes requires follow-up analysis, FCPC nevertheless provides a more sensitive means than eBayes in capturing more candidate genes for subsequent investigations.

Table 4.

Partial lists of downregulated candidate genes in nitrogen-stressed Populus

eBayes		FCPC
Gene name	RR	Gene name	RR
Panel a. The 10 significant discoveries with the largest relative expression ratios
Ptp.2165.1.S1_at	19.7	PtpAffx.71066.2.A1_at	60.9
PtpAffx.73917.1.S1_at	19.6	Ptp.2165.1.S1_at	19.7
PtpAffx.158518.3.S1_a_at	15.1	PtpAffx.73917.1.S1_at	19.6
Ptp.7001.1.S1_at	15.0	PtpAffx.158518.3.S1_a_at	15.1
PtpAffx.204261.1.S1_at	12.8	Ptp.7001.1.S1_at	15.0
PtpAffx.42221.1.A1_s_at	8.6	PtpAffx.24775.1.A1_x_at	14.6
PtpAffx.200453.1.S1_at	7.5	Ptp.2598.1.S1_at	14.1
PtpAffx.143356.1.S1_at	6.3	PtpAffx.204261.1.S1_at	12.8
PtpAffx.4337.1.A1_s_at	5.9	PtpAffx.71066.7.A1_at	10.3
PtpAffx.21075.1.S1_at	5.8	PtpAffx.22847.2.A1_a_at	10.3
Panel b. The 10 significant discoveries with the smallest relative expression ratios
PtpAffx.12016.2.S1_a_at	1.6	PtpAffx.222420.1.S1_at	1.3
PtpAffx.144999.1.A1_s_at	1.6	Ptp.817.1.S1_a_at	1.3
PtpAffx.51612.1.A1_at	1.6	PtpAffx.130633.1.S1_at	1.3
Ptp.288.1.A1_s_at	1.5	Ptp.6011.1.S1_at	1.3
PtpAffx.128269.1.S1_s_at	1.5	PtpAffx.215038.1.S1_at	1.3
Ptp.6204.2.S1_at	1.5	PtpAffx.5907.1.A1_at	1.2
Ptp.5434.1.A1_at	1.4	Ptp.6067.1.S1_s_at	1.2
Ptp.6046.1.A1_at	1.4	Ptp.902.1.S1_s_at	1.1
Ptp.4006.1.S1_at	1.4	PtpAffx.213776.1.S1_at	1.1
Ptp.2332.2.A1_a_at	1.3	Ptp.3777.1.S1_s_at	1.1

RR: Relative expression ratio r_g = x̄_1g/x̄_2g.

4.2 Human diseases

Having applied the FCPC method to the low-replicate plant microarray experiment, we then turned to investigate its performance in microarray datasets of human cancers (colon cancer and leukemia), in which there were more biological replicates. The basic features of the colon data were described in Section 3.2. The leukemia dataset was from Golub et al. (1999). This dataset contained expression indices of 7129 genes of 11 AML and 27 ALL, where 3051 genes remained after filtering and preprocessing as done by the authors. We applied FCPC and eBayes to the filtered genes as summarized in panel a of Table 5.

Table 5.

Basic features and significant gene discoveries of colon and leukemia at nominal FDR 0.05

Panel a		Numbers of
	Cancers	filtered genes		Controls		Treatments
	Colon	2000		22		40
	Leukemia	3051		11		27
Panel b		eBayes			FCPC
	Cancers	Up	Down	Total	Up	Down	Total
	Colon	173	274	447	203	293	496
	Leukemia	357	312	669	394	329	723

FCPC claimed 49 and 54 more genes to be differentially expressed than eBayes in the colon and leukemia datasets, respectively, as shown in panel b of Table 5. Using the leukemia dataset as an example, eBayes discovered 357 significantly upregulated genes and 312 significantly downregulated genes, while FCPC discovered 394 and 329, respectively. As with the low-replicate experiment reported above, lowering the tightness levels led to more significant gene discoveries, as shown in Table S3. Taken together, these analyses showed that FCPC performs as well as, or slightly better than eBayes when applied to microarray experiments with high biological replication. However, FCPC is substantially more robust than eBayes for significant gene discoveries in low-replicate experiments.

5 DISCUSSION

In this article, we present a powerful and computationally simple method, FCPC, to detect differentially expressed genes from microarray data. The method integrates the strengths of stratification,

tight clustering, data compression, information pooling and standard Benjamini–Hochberg FDR correction. We evaluated FCPC by simulation studies as well as by application to a real dataset. Simulation results show that FCPC controls FDR and is much more powerful than the popular approaches when the number of genes is large. The basis for the FCPC approach is 2-fold. First, expression indices that vary between different experimental conditions can reveal certain regulatory strata. Genes within one common stratum may be more related functionally, at the organismal level, than genes from different strata. This serves as the basis for stratification. Second, gene-expression indices are correlated in various clumps (Qiu et al., 2005; Storey, 2003). This serves as the basis for correlation-based clustering.

The rational of the iterative clustering method we employed deserves special mention. Clustering was done progressively, and with a correlation threshold in order to maximize the tightness of early formed clusters. We designed the method according to our observations on the sampling distributions of gene-to-gene correlation. A correlation threshold can be chosen such that the sample correlation between similarly up- or downregulated genes will most likely exceed that threshold, while the correlation between a stably expressed gene and a differentially expressed gene is unlikely to meet the threshold. Therefore, the proposed clustering method can distinguish differentially expressed genes from stably expressed genes during the early iterations, and organize them into tight clusters. In addition, the correlation between two stably expressed genes is likely larger than a threshold if the residual correlation is strong. This integration proved to efficiently prevent loss of statistical power and the flood of false discoveries.

The observations in Section 3.4 are helpful for defining the tightness parameters to find stable clusters. It is very difficult to find the optimal set of tightness levels without information about the residual correlations. According to our simulations and observations of the properties of gene-to-gene correlation, T1 and T2 are reasonable choices. Analysis of real data as in Section 4 appeared to validate the dependence between genes, as use of these tightness levels resulted in the clustering of most genes. The gene-to-gene correlation is affected by many factors such as expression differential, residual correlations and the variance deviation across conditions, but the theoretical basis remains under-investigated. Nevertheless, the proposed FCPC approach provides a powerful and efficient means for assessing the various parameters as part of the microarray data analysis for identification of differentially expressed genes.