Abstract
Bluetongue is an arboviral disease of ruminants causing significant economic losses. Our risk assessment is based on the epidemiological key parameter, the basic reproduction number. It is defined as the number of secondary cases caused by one primary case in a fully susceptible host population, in which values greater than one indicate the possibility, i.e., the risk, for a major disease outbreak. In the course of the Bluetongue virus serotype 8 (BTV-8) outbreak in Europe in 2006 we developed such a risk assessment for the University of Veterinary Medicine Vienna, Austria. Basic reproduction numbers were calculated using a well-known formula for vector-borne diseases considering the population densities of hosts (cattle and small ruminants) and vectors (biting midges of the Culicoides obsoletus spp.) as well as temperature dependent rates. The latter comprise the biting and mortality rate of midges as well as the reciprocal of the extrinsic incubation period. Most important, but generally unknown, is the spatio-temporal distribution of the vector density. Therefore, we established a continuously operating daily monitoring to quantify the seasonal cycle of the vector population by a statistical model. We used cross-correlation maps and Poisson regression to describe vector densities by environmental temperature and precipitation. Our results comprise time series of observed and simulated Culicoides obsoletus spp. counts as well as basic reproduction numbers for the period 2009–2011. For a spatio-temporal risk assessment we projected our results from the location of Vienna to the entire region of Austria. We compiled both daily maps of vector densities and the basic reproduction numbers, respectively. Basic reproduction numbers above one were generally found between June and August except in the mountainous regions of the Alps. The highest values coincide with the locations of confirmed BTV cases.
Introduction
Veterinary authorities are generally interested in a spatio-temporal risk assessment to establish efficient protection and control measures when facing diseases with high economic impact such as caused by the Bluetongue virus (BTV). Such risk assessments are frequently based on one common epidemiological parameter, the basic reproduction number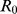 
. It describes the number of secondary cases caused by a primary case in a completely susceptible population at the beginning of an epidemic. Thus, 
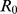may be interpreted as a threshold parameter: a major disease outbreak may only occur for R
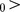1, while for R
1 the disease will fade out [1].
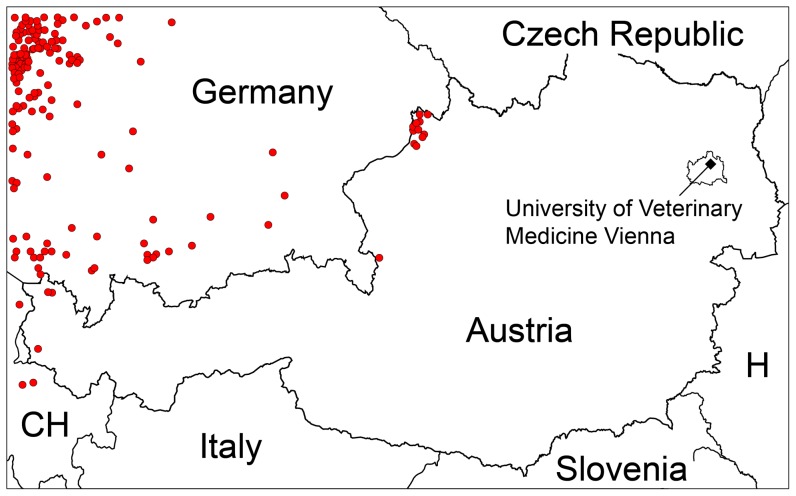
The motivation for this study was the Bluetongue virus serotype 8 (BTV-8) epidemics in Europe, which emerged in 2006 at the border triangle of Belgium, Germany and the Netherlands [2], [3]. Within a few years this arboviral disease rapidly spread across North-western and Central Europe [4], [5] and caused substantial losses in agriculture amounting to millions Euro [6]. Beside movement restrictions and surveillance, the main veterinary measure was to vaccinate the susceptible populations beginning in 2008 [7]. In Austria, only a few cattle near the border to Germany were confirmed to be BTV-8 seropositive. Due to the German vaccination campaigns achieving a coverage of 78% [8] and preventive vaccination in Austria the eastwards spread of the Bluetongue disease could be stopped at the German-Austrian border (Figure 1).
Figure 1. Reported locations of BTV-8 cases between 2006 and 2009 in Germany [8], Austria [43] and Switzerland [44].
In the course of the European BTV-8 outbreak several methods for the calculation of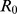 
have been proposed. Some of these methods are based on data from surveillance and monitoring programmes. For example, [9] estimated 
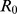between herds for the Netherlands. Furthermore, a theoretical study on 
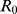using a deterministic epidemic model was introduced by [10] to investigate the seasonal spread of BTV over several years and to evaluate the effectiveness of vaccination strategies. Most approaches presented so far considered temperature dependent vector parameters as well as host and vector densities. While [11] presented a general concept on the calculation of 
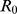for which they discussed the influence of temperature on the transmission cycle, [12] and [13] generated spatial 
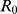maps for the Netherlands and Switzerland, respectively. Furthermore, the uncertainty and sensitivity of such temperature-dependent models have been analysed and temperature turned out to be the most dominant factor for determining the magnitude of 
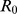[14]. [15] estimated the possible impact of past and future climates on the basic reproduction number 
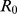on an European scale. For their study they used input data from climate model runs applied to different emission scenarios of the Intergovernmental Panel on Climate Change (IPCC). The authors have used a similar approach for modelling another mosquito-borne disease outbreak, the Usutu virus epidemics in Vienna [16]. Here we present a predictive risk assessment method based on the basic reproduction number 
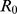after [12] applied to a potential Bluetongue outbreak in Austria. Results comprise regions at risk on a spatio-temporal scale representative for a resolution of 10 km and 1 day.
In general, BTV circulates in a natural transmission cycle between vectors (Culicoides biting midges) and hosts (ruminants: mainly cattle, sheep, and goats). For risk assessment using the concept of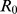 
the knowledge of both the vector and the host densities are of fundamental importance. While the population densities of farm animals are well documented in national veterinary databases or available worldwide on a regular grid [17], the vector density is generally not well known or rather unknown. Therefore, a central part of our study is concerned with the estimation of the vector population. We established a continuously operating daily Culicoides spp. monitoring at the University of Veterinary Medicine Vienna, Austria, to quantify the seasonal abundance for at least three years. This approach is in contrast to former - mainly weekly - monitoring programs, such as the large-scale entomological surveillance program throughout the European Union to investigate the occurrence and geographical distribution of Culicoides spp. ([18]; results were published e.g. by [19], [20]).
Methods
Vector monitoring
For the Culicoides spp. monitoring a black light suction trap of Onderstepoort type, as described by [21], was placed next to an automatic weather station at the university campus (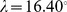
E geographical longitude and 
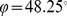N geographical latitude). The location in Vienna is characterised by a temperate, fully humid climate with warm summers, corresponding to Cfb climate following the Köppen-Geiger climate classification [22]. This standardized trap is commonly used in monitoring and surveillance programs, because it is very efficient compared to other suction light traps [23]. Following the guideline of [24], the trap was hung at a height of 1.5 m above the ground. The distance to the stables and paddocks with cattle, sheep, and horses was less than 20 m. A collection bottle rotator (model 1512, John W. Hock Company, FL, USA) with eight beakers was used to segregate collections at 24 h intervals. For species evaluation the catches were separated first in Culicoides spp. and other insects (bycatches) under a stereomicroscope. Afterwards the Culicoides species complexes were determined by the characteristic pattern and coloration of the wings according to [24]–[26].
During the monitoring period 2009–2011 a total of 18,952 Culicoides spp. were captured, in which the predominantly trapped complex was C. obsoletus (85.7%). The C. obsoletus complex comprises C. obsoletus, C. scoticus, C. dewulfi, and C. chiopterus. In addition we identified midges of the C. pulicaris complex (9.8%), amongst others (4.5%). In this study we used only the most frequent vectors, i.e. those of the C. obsoletus complex.
Vector modelling
The aim of our vector modelling is to statistically describe the midge catches by operationally available meteorological quantities. Assuming that the relationship between meteorological quantities and C. obsoletus abundance is location-independent (but not independent on the host density), the model will be used to estimate the spatial distribution of C. obsoletus. Additionally, the C. obsoletus abundance may be projected into the future by using meteorological output parameters from numerical weather prediction models. The development of the statistical model was carried out in two steps. In the first step, we performed a cross correlation map (CCM) analysis to investigate which of the meteorological quantities correlates best with the observed C. obsoletus counts. In the second step, we used these meteorological quantities in a Poisson regression model. This procedure was done first for Vienna to demonstrate the performance of the statistical model by comparing it's output with observations and subsequently applied for the entire region of Austria.
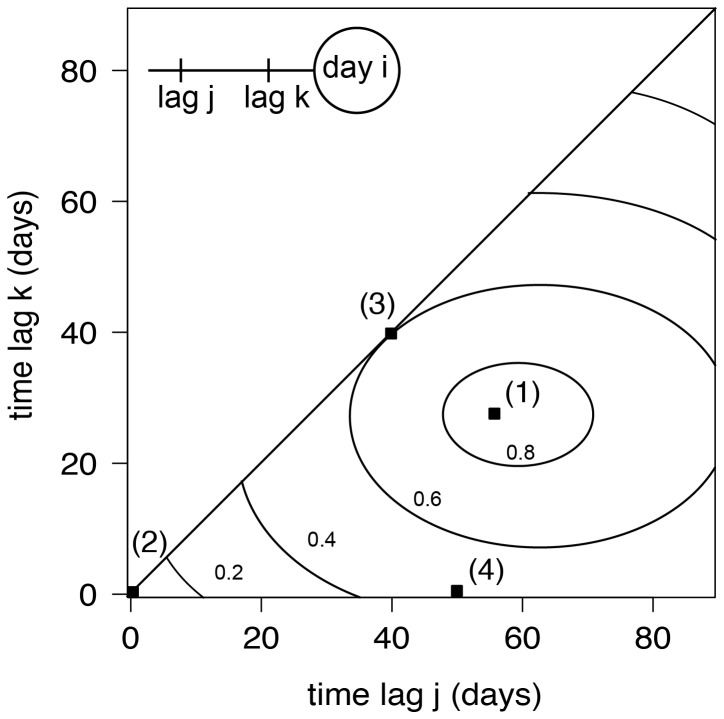
The CCM analysis is an extension of the ordinary cross-correlation by introducing a second time lag. This second time lag is used to average or accumulate meteorological quantities over a period beginning at time lag 1 and ending at time lag 2. Correlation coefficients are then calculated for these averaged quantities, in which the CCMs depict the averaging period resulting in the highest correlation coefficient (Figure 2). CCMs were adopted for example by [27] to investigate the relationship between Ochlerotatus sollicitans abundance and environmental parameters. Further applications comprise studies on Aedes sollicitans [28] as well as Aedes sollicitans and Culex salinarius [29].
Figure 2. Schematic illustration of a cross correlation map (CCM).
(1) Maximum correlation of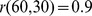 
for a dependent vs. an independent quantity. The latter averaged over the period of preceding days j = 60 to k = 30. (2) Commonly used correlation coefficient (without time lags, j = k = 0) of 
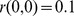. (3) Cross-correlation (with one time lag, j = k = 40) of 
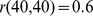, which is equal to a cross correlation with a single time lag. (4) Cross correlation of r(50,0), the independent quantity was averaged over the preceding 50 days.
Using a more mathematical notation, the statistical analysis reads as follows: For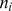 
representing a time series of the observed population of midges and 
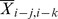a meteorological quantity with time index 
, the CCM considers 
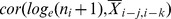for each time lag 
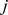and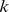 
, at which 
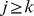. Generally, the population data were normalized using a 
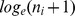-transformation and 
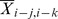is averaged over the time interval ranging from 
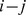to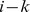 
. The correlations for all possible time intervals are displayed in a CCM with the time lags 
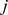and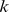 
range along the two axes. Note, that for the special case of 
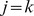(45
-line in a CCM), the correlation coefficients are equal to those of a cross-correlogram. We developed a source code for the calculation of CCMs using the R statistical computing environment [30].
Based on the correlations found by CCMs, a Poisson regression was applied to describe daily vector abundance by meteorological quantities. Again, the analysis was performed using the R statistical computing environment.
Risk assessment
For the different tasks we used vector densities, estimated from both observed and simulated counts of midges, to assess the risk of a potential BTV-8 outbreak in cattle and small ruminants. Therefore, we applied the basic reproduction number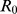 
, which may be interpreted as a threshold value for the possibility of a major outbreak (
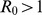). An analytical solution for 
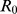is generally derived from epidemic differential equation models. Here the formula used in recent studies by [12], [15] and [31] is applied, which may be traced back to the historical developments by Ronald Ross and George Macdonald [32].
 |
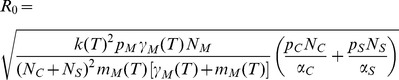(1) |
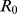equations given by [12], [15] and [31] are formally equivalent but differ in the complexity of parameter formulation. The most comprehensive formulation by [31] provides a gamma distribution for the extrinsic incubation period, which reduces to equation (1) by setting the scale parameters for the gamma distributions to one. Model parameters are probabilities for an infection of cattle 
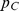, small ruminants 
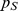and midges 
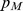, the removal rate (recovery or death rate) for cattle 
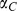and small ruminants 
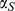, as well as some functions describing the temperature dependent behaviour of midges. The latter comprise the biting rate of midges 
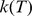, the virus reproduction rate in midges 
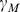(T), i.e. the reciprocal of the extrinsic incubation period, and the mortality rate of midges 
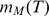. All constant parameters as well as temperature dependent parameter functions were taken according to [12] and are summarized in Table 1. Note that the temperature dependent parameter functions are not well defined for low temperatures. Therefore, we calculated 
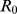only for threshold values of 
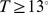C. Note further that several other functions were proposed in the literature. A sensitivity study performed by [33] using alternative functions for midge mortality, extrinsic incubation period and biting rate results in similar 
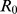values (see Text S1 for details). Additionally, the basic reproduction number depends on the host and vector densities. We distinguish between cattle 
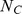, small ruminants 
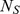and midges 
.
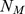Table 1. Parameters and parameter functions as applied to calculate the basic reproduction numbers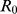 
.
| Parameter | Symbol | Value/Function | Reference |
| transmission probability to midges |
|
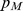
1.00 | [12] |
| transmission probability to hosts |
|
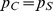
0.05 | [12] |
| removal rate of cattle |
|
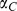
0.055 | [31] |
| removal rate of small ruminants |
|
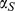
0.125 | [12] |
| biting rate of midges |
|
|
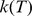
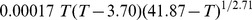
[45] |
| virus reproduction rate in midges |
|
|
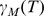
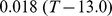
[46] |
| mortality rate of midges |
|
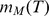
0.0089 exp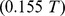
|
[47] |
Results
Simulated vector population
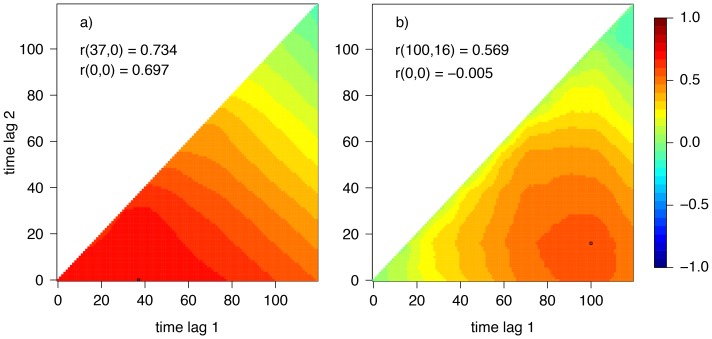
In a first step we investigated the correlations between time series of midges of the Culicoides obsoletus complex and environmental quantities measured by the automatic weather station beside the light trap. The latter comprise amongst others air temperature, precipitation, wind speed and relative humidity. CCMs as discussed above were compiled. In accordance with the life cycle of midges we considered time frames of 120 days (4 months) preceding the catches. From all investigated quantities only temperature and precipitation were found to correlate quite well with the daily midge counts. Note that daily precipitation has a skewed frequency distribution and was normalized by log-transformation before CCMs were calculated (Figure 3).
Figure 3. Cross correlation maps (CCMs) for daily time series in Vienna, Austria: Midges vs. temperature (a) and midges vs. precipitation (b).
Note that midge counts and precipitation values were normalized by log-transformation. Period: Jan. 2009 to Dec. 2011.
We found a maximum correlation for midges vs. temperature averaged over the preceding 37 days of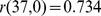 
(Figure 3 left). This correlation is slightly higher than the corresponding day-to-day correlation of r(0,0) = 0.697. Between midges and precipitation we found no day-to-day correlation, but for the precipitation averaged over the period between the preceding days 100 to 16 a correlation of r(100,16) = 0.569 was calculated (Figure 3 right). Inserting these three positive correlations into the Poisson regression model leads to
 |
(2) |
with the daily temperature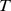 
, the mean temperature 
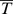, and the mean logarithmic precipitation 
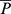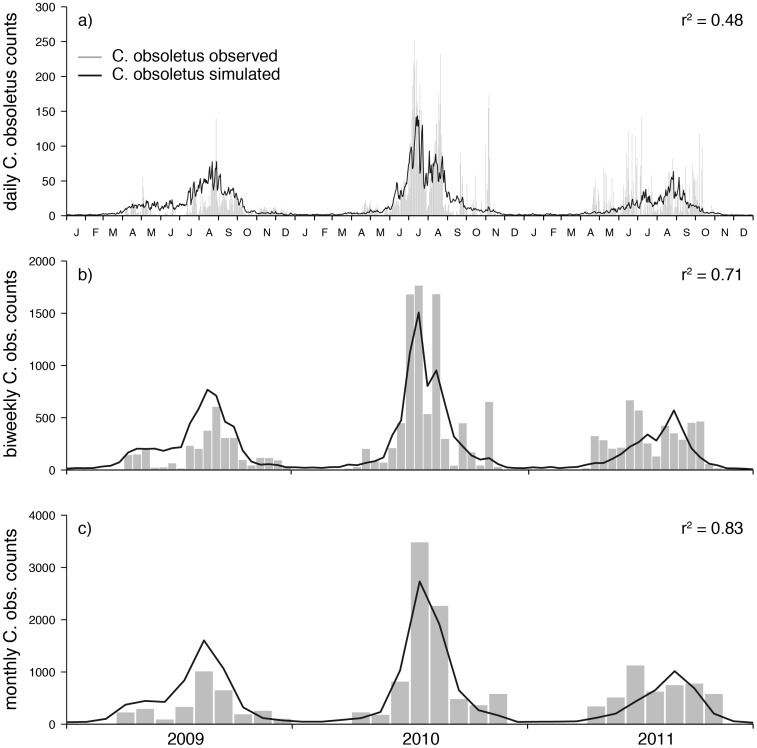
(contribution of all coefficients significant with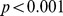 
). As a result, observed vs. predicted daily Culicoides counts for Vienna are depicted in Figure 4. According to that, temperature and precipitation explain about 48.1% of the daily variance of the C. obsoletus counts. We plotted also bi-weekly and monthly time series, although it is clear that the explained variances are higher for accumulated data, because they are usually appropriate for many epidemiological applications. For monthly data, for example, the explained variance increases up to 83.3%.
Figure 4. Daily (a), biweekly (b) and monthly (c) Culicoides obsoletus complex counts observed with the black-light trap (bars) vs. predicted by the Poisson regression model (lines).
Period: January 2009 to December 2011; Vienna, Austria.
Dynamic Bluetongue risk assessment for Vienna
We calculated the daily reproduction number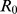 
for Vienna by applying Eq. 1, in which vectors and hosts may be alternatively inserted as absolute numbers or densities. Assuming our university campus covers an area of 1 km
, values given in absolute numbers or densities are equal. We used an average host density of cattle and small ruminants of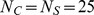 
animals/km
. The true vector density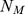 
, however, is unknown. In every case it is much higher than the number of midges caught at the location of the light trap. In the absence of any other estimate we applied the reasonable assumption proposed by [12]. Accordingly, the trapped midges were assumed to reflect 1% of the local vector population, i.e. our catches were multiplied by a factor of 100 before entering Eq. 1 (
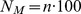). Additionally, the temperature dependent functions given in Table 1 are defined for temperatures 
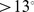C, hence 
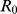is calculated for only 46.3% of the days (mainly between April and October).
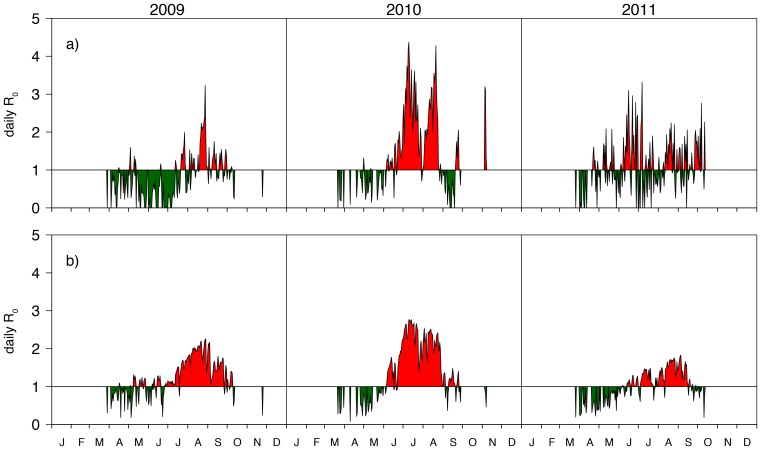
Figure 5 depicts the time series of the daily reproduction number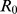 
for Vienna. While in Figure 5a the observed numbers of midges were used, Figure 5b depicts 
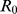values based on the simulated numbers of midges. Taking the first as a gold standard we evaluated the influence of simulated midges 
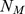on the calculation of 
by using the two verification measures sensitivity and specificity. We calculated a sensitivity of 0.81 (probability that days with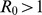 
were correctly realized using 
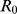estimates based on simulated 
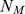) and a specificity of 0.53 (probability that days with 
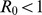were correctly realized).
Figure 5. Daily basic reproduction number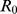
for Vienna based on observed (a) and simulated (b) Culicoides obsoletus time series.
Red and green bars indicate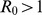 
and 
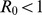, respectively.
Spatio-temporal Bluetongue risk assessment for the entire region of Austria
Assuming that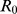 
calculations in Vienna based on simulated 
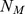values satisfy our requirements concerning the accuracy, we applied the 
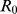estimation method to the entire region of Austria. Therefore we defined a grid with 10 km spacing, equidistant in geographical longitude (
) and latitude (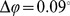
). Gridded data of temperature and precipitation were taken from the Austrian meso-scale numerical weather prediction model ALADIN [34]. Only data for the period 2010–2011 were used, because data for earlier years were not available. The advantage of ALADIN data over observations (in situ or satellite data) is that they are available on a higher temporal resolution, will be available in near future also on a much higher spatial resolution and gives us the opportunity to project 
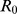values to the future. It should be mentioned that we found a few extraordinary high precipitation values within the ALADIN data leading to unrealistic high numbers of midges simulated by Eq. 2. To avoid such artefacts we applied a truncation for the accumulated logarithmic precipitation of 
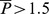mm/day. This cut-off coincides with annual precipitation maxima of about 1200 mm/year as observed in high Alpine regions [35].
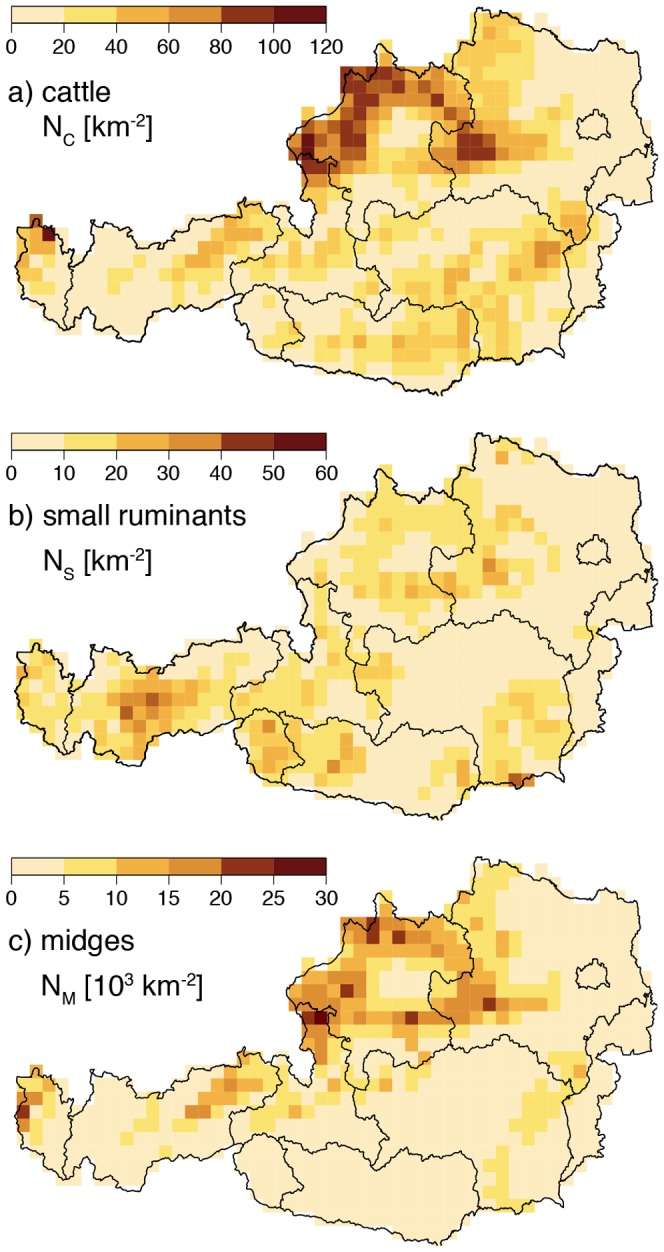
Host and vector densities used for the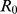 
calculation over Austria are depicted in Figure 6. The constant densities of cattle 
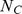(Figure 6a) and small ruminants 
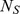(Figure 6b) were taken from the Austrian veterinary database. The spatial distribution of the vector density 
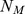, a function of temperature, precipitation, 
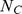and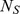 
, is given in units of 
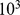midges/km
. Again we assumed that the simulated midges reflect 1% of the real vector population. Further we adjusted the vector density for host densities following the findings of [36]. Thus, the vector density at a grid point with geographical coordinates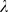 
and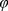 
is calculated from the simulated vectors at this coordinate 
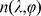multiplied by a factor of 100 as discussed above and normalized by the host density at the location of the University of Veterinary Medicine Vienna (with 50 ruminants/km
).
 |
(3) |
Figure 6. Constant host densities for cattle (a) and small ruminants (b), both given in animals/km 
, and simulated vector densities for 11 July 2010 in 10
midges/km
(c).
Note that the vector density varies temporally and spatially, because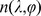 
is a function of temperature and precipitation. As an example, Figure 6c depicts the vector density for 11 July 2010.
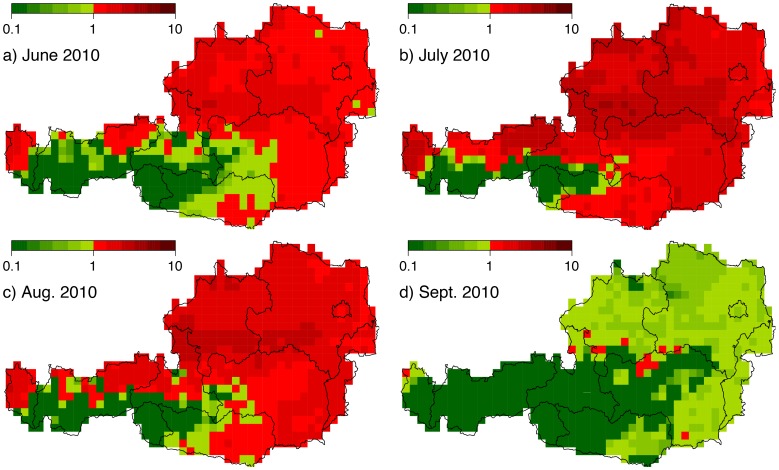
Using these daily vector densities, the host densities as well as the parameters and temperature dependent parameter functions we compiled daily risk maps for the period 2010–2011. Movies of simulated daily vector densities and Bluetongue risk maps are provided as supporting information (see Videos S1 and S2) or on our website http://epidemic-modeling.vetmeduni.ac.at/btvmodel.htm. Figure 7 depicts mean daily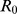 
maps for June, July, August, and September 2010. While red areas indicate a potential risk for a major outbreak (
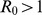), green areas are associated with minor or no risk at all (
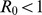). For example, the 
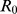values for July 2010 are within the range 
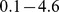, in which the maximum indicates that from one infected animal on average 4.6 animals may be newly infected with BTV. Interestingly areas with a high vector density coincided with high host densities, even without the adjustment after [36]. Verification of the 
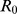maps is currently not possible, because so far no major BTV outbreaks occurred in Austria. However, the regions with BTV-8 seropositive cases at the Austrian-German border (Figure 1) coincide with regions of high 
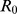values.
Figure 7. Mean daily basic reproduction number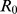 
for June to September 2010.
The different maps represent the spatio-temporal distribution of the potential risk for a BTV outbreak in Austria. Green colours depict areas not under risk, red under moderate risk and dark red under high risk (note the logarithmic scaling).
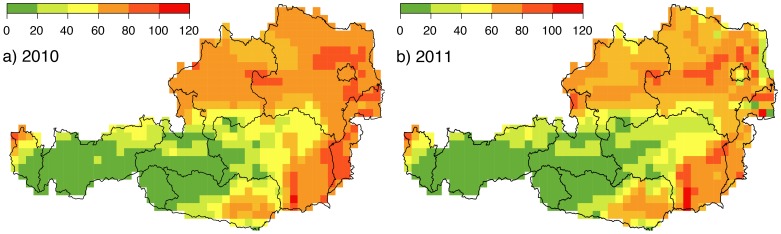
A visual comparison of the total numbers of days with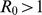 
between 2010 (Figure 8a) and 2011 (Figure 8b) shows that in 2010 many regions are at risk for longer, indicating a high inter-annual variation of the 
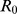values.
Figure 8. Numbers of days with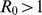 
for 2010 (a) and 2011 (b) demonstrating significant differences caused by inter-annual climate fluctuations.
Regions with maxima of more than 100 days in the west and north-west of Austria coincide well with confirmed BTV cases depicted in Figure 1.
Discussion
We presented a risk assessment for a potential Bluetongue disease outbreak in Austria depicted by time series and maps of the basic reproduction number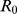 
. Input data were constant host densities and fluctuating vector densities simulated by a Poisson regression model using temperature and precipitation fields from the Austrian numerical weather prediction model ALADIN. Although the methodology presented here is generally accepted and was recently applied to BTV by [13], [12] and [15], there are some uncertainties in estimating 
.
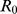First of all, the applied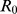 
formula is originated from an epidemic model, usually formulated by differential equations, by determining the largest eigenvalue of the so-called next-generation matrix. In the case of BTV it has never been verified by comparison with real outbreak data. Such a verification should demonstrate that the observed BTV-8 dynamics may be approximately reproduced by the underlying epidemic model with the parameter functions selected. Reasons for a missing verification may be due to the fact that it is extremely time-consuming, complex and expensive. However, other epidemic models for arboviral diseases were successfully verified against outbreak data, e.g. for the well-documented Usutu virus outbreak in Vienna [37].
Further, it is difficult to estimate vector densities, even if numbers of trapped midges from a monitoring programme are available. We noticed that the official monitoring data sampled at 54 Austrian locations once a week according to the regulation of the European Union [18] provide an excellent overview on the species composition and on the seasonal activity of our native midge populations. Both were hitherto unknown or at least remain undocumented. A quantitative interpretation of the monitoring data, however, is hardly applicable. This is documented by the following small statistical experiment, where we compiled weekly time series based on Monday catches (after [18]) and compared them with weekly time series based on all daily catches. An explained variance of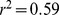 
indicates that the numbers of midges sampled according to [18] were afflicted with significant undersampling errors. Further, the official sampling locations were neither representative for their vicinity nor comparable among each other. Also weather stations at short distances to the sampling locations were missing. Therefore, we established our own monitoring with continuously daily observations of midges and environmental parameters from 2009 to present. It allows us to calculate plausible 
values, although they should be interpreted with care. Due to the generally unknown magnitude of the vector density (we assumed numbers of midges per square kilometre to be two orders of magnitude higher than sampled at a point location), our 
values should be interpreted as relative rather than absolute measures.
Another uncertainty in the vector monitoring lies in the nature of the trapping method. [38] indicated that black light traps are adequate for measuring relative abundance, but not species composition. Further, we don't take into account that midges themselves can be transported by wind over considerable distances, although several models have been developed to investigate this wind-borne spread of BTV [39], [40]. An alternative study on C. obsoletus modelling applied a negative binomial regression model (see also Text S1) to simulate the seasonal cycle of daily catches at several locations in England [41]. It distinguishes between the influence of seasonality and meteorological quantities (temperature, precipitation and wind), but does not consider accumulated quantities as defined by CCMs. Further differences comprise the fraction of trapped midges of the C. obsoletus complex, which is 86% in Vienna and 48% in England. Unfortunately, due to differences in visualization and verification an objective comparison between [41] and the results presented here is not possible. Both approaches underestimate the extremely high variance of the observations, which is a general problem in vector modelling.
Similar to domestic ruminants most species of wild ruminants, e.g. red deer, are susceptible to BTV infection. We neglected the influence of these potential host species due to their still unclear epidemiological role in BTV transmission [42].
Supporting Information
Sensitivity study for the extrinsic incubation period and C. obsoletus models.
(PDF)
Daily maps of C. obsoletus densities simulated for May to November 2010 (left) and 2011 (right).
(MOV)
Daily maps of potential Bluetongue outbreak risk simulated for May to October 2010 (left) and 2011 (right).
(MOV)
Acknowledgments
We are grateful to C. Rath for supporting the Culicoides monitoring, to K. Wimmer (Vetmeduni Vienna) for servicing the black-light trap, to A. Schmalwieser (Vetmeduni Vienna) and S. Schneider (ZAMG) for providing weather data, and to K. Fuchs (AGES) for providing gridded data of animal densities.
Funding Statement
The research was supported by the PL2 Start-up project bluetongue disease model of the University of Veterinary Medicine Vienna. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Diekmann O, Heesterbeek J (2000) Mathematical epidemiology of infectious diseases. Chichester: Wiley.
- 2. Saegerman C, Berkvens D, Mellor PS (2008) Bluetongue epidemiology in the European Union. Emerg Infect Dis 14: 539–544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Carpenter S, Wilson A, Mellor PS (2009) Culicoides and the emergence of bluetongue virus in northern Europe. Trends Microbiol 17: 172–178. [DOI] [PubMed] [Google Scholar]
- 4. Mehlhorn H, Walldorf V, Klimpel S, Jahn B, Jaeger F, et al. (2007) First occurrence of Culicoides obsoletus-transmitted Bluetongue virus epidemic in Central Europe. Parasitol Res 101: 219–228. [DOI] [PubMed] [Google Scholar]
- 5. Conraths FJ, Gethmann JM, Staubach C, Mettenleiter TC, Beer M, et al. (2009) Epidemiology of bluetongue virus serotype 8, Germany. Emerg Infect Dis 15: 433–435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Wilson A, Mellor P (2008) Bluetongue in Europe: vectors, epidemiology and climate change. Parasitol Res 103 Suppl 1S69–S77. [DOI] [PubMed] [Google Scholar]
- 7. Caporale V, Giovannini A (2010) Bluetongue control strategy, including recourse to vaccine: a critical review. Rev Sci Tech 29: 573–591. [DOI] [PubMed] [Google Scholar]
- 8. Gethmann J, Hoffmann B, Probst C, Beer M, Conraths F, et al. (2010) A survey on three years with bluetongue disease serotype 8 in Germany (in German). Tierärztl Umschau 64: 4–12. [Google Scholar]
- 9. de Koeijer AA, Boender GJ, Nodelijk G, Staubach C, Meroc E, et al. (2011) Quantitative analysis of transmission parameters for Bluetongue virus serotype 8 in Western Europe in 2006. Vet Res 42: 53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Charron MVP, Seegers H, Langlais M, Ezanno P (2011) Seasonal spread and control of Bluetongue in cattle. J Theor Biol 291: 1–9. [DOI] [PubMed] [Google Scholar]
- 11.de Koeijer AA, Elbers A (2007) Modelling of vector-borne diseases and transmission of bluetongue virus in North-West Europe. Wageningen: Wageningen Academic Publishers.99-112.
- 12. Hartemink NA, Purse BV, Meiswinkel R, Brown HE, de Koeijer A, et al. (2009) Mapping the basic reproduction number (R0) for vector-borne diseases: a case study on bluetongue virus. Epidemics 1: 153–161. [DOI] [PubMed] [Google Scholar]
- 13. Racloz V, Venter G, Griot C, Stärk KDC (2008) Estimating the temporal and spatial risk of bluetongue related to the incursion of infected vectors into Switzerland. BMC Vet Res 4: 42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Gubbins S, Carpenter S, Baylis M, Wood JLN, Mellor PS (2008) Assessing the risk of Bluetongue to UK livestock: uncertainty and sensitivity analyses of a temperature-dependent model for the basic reproduction number. J R Soc Interface 5: 363–371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Guis H, Caminade C, Calvete C, Morse AP, Tran A, et al. (2012) Modelling the effects of past and future climate on the risk of Bluetongue emergence in Europe. J R Soc Interface 9: 339–350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Brugger K, Rubel F (2009) Simulation of climate-change scenarios to explain Usutu-virus dynamics in Austria. Prev Vet Med 88: 24–31. [DOI] [PubMed] [Google Scholar]
- 17. Robinson TP, Franceschini G, Wint W (2007) The Food and Agriculture Organization's gridded livestock of the world. Vet Ital 43: 745–751. [PubMed] [Google Scholar]
- 18.EU (2007) Commission Regulation (EC) No 1266/2007.Official Journal of the European Union.
- 19. Anderle F, Sehnal P, Schneemann Y, Schindler M, Wöss G, et al. (2008) Culicoides surveillance in Austria (Diptera: Ceratopogonidae) - a snap-shot. Beiträge zur Entomofaunistik 9: 67–79. [Google Scholar]
- 20. Clausen PH, Stephan A, Bartsch S, Jandowsky A, Hoffmann-Köhler P, et al. (2009) Seasonal dynamics of biting midges (Diptera: Ceratopogonidae, Culicoides spp.) on dairy farms of Central Germany during the 2007/2008 epidemic of Bluetongue. Parasitol Res 105: 381–386. [DOI] [PubMed] [Google Scholar]
- 21. Venter GJ, Meiswinkel R (1994) The virtual absence of Culicoides imicola (Diptera: Ceratopogonidae) in a light-trap survey of the colder, high-lying area of the eastern Orange Free State, South Africa, and implications for the transmission of arboviruses. Onderstepoort. J Vet Res 61: 327–340. [PubMed] [Google Scholar]
- 22. Kottek M, Grieser J, Beck C, Rudolf B, Rubel F (2006) World map of the Köppen-Geiger climate classification updated. Meteorol Z 15: 259–263. [Google Scholar]
- 23. Venter GJ, Labuschagne K, Hermanides KG, Boikanyo SNB, Majatladi DM, et al. (2009) Comparison of the efficiency of five suction light traps under field conditions in South Africa for the collection of Culicoides species. Vet Parasitol 166: 299–307. [DOI] [PubMed] [Google Scholar]
- 24. Goffredo M, Meiswinkel R (2004) Entomological surveillance of bluetongue in Italy: methods of capture, catch analysis and identification of Culicoides biting midges. Vet Ital 40: 260–265. [PubMed] [Google Scholar]
- 25.Delécolle JC (1985) Nouvelle contribution a l'etude systématique et iconographique des espèces du genre Culicoides (Diptera: Ceratopogonidae) du Nord-Est de la France [Ph.D. thesis]. Universitè Louis Pasteur de Strasbourg. 283 pp.
- 26. Rawlings P (1996) A key, based on wing patterns of biting midges (Genus: Culicoides Latreille - Diptera: Ceratopogonidae) in the Iberian Peninsula, for use in epidemiological studies. Graellsia 52: 57–71. [Google Scholar]
- 27. Curriero FC, Shone SM, Glass GE (2005) Cross correlation maps: a tool for visualizing and modeling time lagged associations. Vector Borne Zoonotic Dis 5: 267–275. [DOI] [PubMed] [Google Scholar]
- 28. Shone SM, Curriero FC, Lesser CR, Glass GE (2006) Characterizing population dynamics of Aedes sollicitans (Diptera: Culicidae) using meteorological data. J Med Entomol 43: 393–402. [DOI] [PubMed] [Google Scholar]
- 29. Walsh A, Glass G, Lesser C, Curriero F (2008) Predicting seasonal abundance of mosquitoes based on off-season meteorological conditions. Environ Ecol Stat 15: 279–291. [Google Scholar]
- 30.R Development Core Team (2012) R: A Language and Environment for Statistical Computing, version 2.14.1. R Foundation for Statistical Computing (Vienna, Austria). Available: http://www.R-project.org/.
- 31. Gubbins S, Hartemink N, Wilson A, Moulin V, Vonk Noordegraaf C, et al. (2012) Scaling from challenge experiments to the field: Quantifying the impact of vaccination on the transmission of bluetongue virus serotype 8. Prev Vet Med 105: 297–308. [DOI] [PubMed] [Google Scholar]
- 32. Smith DL, Battle KE, Hay SI, Barker CM, Scott TW, et al. (2012) Ross, Macdonald, and a theory for the dynamics and control of mosquito-transmitted pathogens. PLoS Pathog 8: e1002588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Jungblut C, Schober S (2012) Risk assessment methods for bluetongue disease (in German). Rubel F, Brugger K, editors. Austrian Contributions to Veterinary Epidemiology, volume 7 . Austria: Vetmeduni Vienna. 91 pp.
- 34. Wang Y, Bellus M, Wittmann C, Steinheimer M, Weidle F, et al. (2011) The Central European limited-area ensemble forecasting system: ALADIN-LAEF. Q J R Meteorol Soc 137: 483–502. [Google Scholar]
- 35. Frei C, Schär C (1998) A precipitation climatology of the Alps from high-resolution rain-gauge observations. Int J Climatol 18: 873900. [Google Scholar]
- 36. Garcia-Saenz A, McCarter P, Baylis M (2011) The influence of host number on the attraction of biting midges, Culicoides spp., to light traps. Med Vet Entomol 25: 113–115. [DOI] [PubMed] [Google Scholar]
- 37. Rubel F, Brugger K, Hantel M, Chvala-Mannsberger S, Bakonyi T, et al. (2008) Explaining Usutu virus dynamics in Austria: model development and calibration. Prev Vet Med 85: 166–186. [DOI] [PubMed] [Google Scholar]
- 38. Carpenter S, Szmaragd C, Barber J, Labuschagne K, Gubbins S, et al. (2008) An assessment of Culicoides surveillance techniques in northern Europe: have we underestimated a potential bluetongue virus vector? J Appl Ecol 45: 1237–1245. [Google Scholar]
- 39. Ducheyne E, Lange M, Van der Stede Y, Meroc E, Durand B, et al. (2011) A stochastic predictive model for the natural spread of bluetongue. Prev Vet Med 99: 48–59. [DOI] [PubMed] [Google Scholar]
- 40.Burgin LE, Gloster J, Sanders C, Mellor PS, Gubbins S, et al. (2012) Investigating incursions of bluetongue virus using a model of long-distance Culicoides biting midge dispersal. Transbound Emerg Dis. doi:10.1111/j.1865-1682.2012.01345.x. [DOI] [PubMed]
- 41. Sanders CJ, Shortall CR, Gubbins S, Burgin L, Gloster J, et al. (2011) Influence of season and meteorological parameters on flight activity of Culicoides biting midges. J Appl Ecol 48: 1355–1364. [Google Scholar]
- 42. Falconi C, López-Olvera JR, Gortázar C (2011) BTV infection in wild ruminants, with emphasis on red deer: a review. Vet Microbiol 151: 209–219. [DOI] [PubMed] [Google Scholar]
- 43.Loitsch A, Sehnal P, Schneemann Y, Winkler M, Revilla-Fernández S, et al. (2009). Durchführung der Bluetongue Überwachung in Österreich - BTV-Abschlussbericht 2008 & 2009 (in German). Austrian Agency for Health and Food Safety (AGES).
- 44.Schorer M, Schwermer H (2012) Blauzungenüberwachung in der Schweiz: Erklärung der Seuchen3 freiheit (in German). Federal Veterinary Office (FVO).
- 45. Mullens B, Gerry A, Lysyk T, Schmidtmann E (2004) Environment effects on vector competence and virogenesis of bluetongue virus in Culicoides: interpreting laboratory data in a field of context. Veter Ital 40: 160–166. [PubMed] [Google Scholar]
- 46. Carpenter S, Wilson A, Barber J, Veronesi E, Mellor P, et al. (2011) Temperature dependence of the extrinsic incubation period of orbiviruses in Culicoides biting midges. PLoS ONE 6: e27987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Gerry A, Mullens B (2000) Seasonal abundance and survivorship of Culicoides sonorensis (Diptera: Ceratopogonidae) at a south California dairy, with reference to potential bluetongue virus transmission and persistence. J Med Entomol 37: 675–688. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Sensitivity study for the extrinsic incubation period and C. obsoletus models.
(PDF)
Daily maps of C. obsoletus densities simulated for May to November 2010 (left) and 2011 (right).
(MOV)
Daily maps of potential Bluetongue outbreak risk simulated for May to October 2010 (left) and 2011 (right).
(MOV)