Abstract
Arteries are under significant mechanical loads from blood pressure, flow, tissue tethering, and body movement. It is critical that arteries remain patent and stable under these loads. This review summarizes the common forms of buckling that occur in blood vessels including cross-sectional collapse, longitudinal twist buckling, and bent buckling. The phenomena, model analyses, experimental measurements, effects on blood flow, and clinical relevance are discussed. It is concluded that mechanical buckling is an important issue for vasculature, in addition to wall stiffness and strength, and requires further studies to address the challenges. Studies of vessel buckling not only enrich vascular biomechanics but also have important clinical applications.
Keywords: instability, collapsible tube, bent buckling, twist buckling, kinking, folding, blood flow, arteries, veins, blood vessels
1. Introduction
Arteries and veins in vivo are subjected to significant mechanical stresses generated by lumen blood flow, pressure, surrounding tissue tethering, and body movement.31, 47 It has been well documented that mechanical stresses play important roles in regulating vascular cell biology, the vascular function, and the pathological development of vascular diseases such as atherosclerosis.61, 65, 75 A high mechanical stress can lead to injury to the cells and damage to the vascular wall. Excessive stress has also been considered as a risk factor for aneurysm rupture and atherosclerotic plaque rupture.12, 98 Arteries and veins, like water hoses or pipelines may also lose their mechanical stability under mechanical loads. The stability of blood vessels under in vivo loads is essential to maintain their physiological function.
While the strength and stiffness of the arterial wall are important and have been studied extensively,30, 52 the mechanical stability of arteries under mechanical load is also an important issue but less studied. A complete understanding of arterial function and disease cannot be achieved without understanding the mechanical stability of arteries under in vivo loads.
This review summarizes the state of the art studies regarding the stability of arteries and veins. We will first review the stability of the vessel due to low lumen pressure and then focus on the stability of long vessel segments under high lumen pressure and twisting. The challenges and potential future directions will also be discussed.
2. Mechanical Stability of Blood Vessels
Buckling is the loss of mechanical stability, which generates large deformation and failure in structures. Generally speaking, arteries and veins are under complex mechanical loads, including a lumen pressure, outer pressure, axial tension due to tissue tethering, and twisting and bending due to body movement (Figure 1). From an engineering perspective, blood vessels can be considered cylindrical structures subject to combined loads including tension, bending, and torsion. The tubular arteries may buckle under these loads and deform from their normally straight cylindrical shape. Different buckling phenotypes can occur, as depicted in Table 1. The most common buckling phenotypes are described in the following sections, including cross-sectional buckling, lateral bent buckling, and axial twist buckling.
Figure 1.
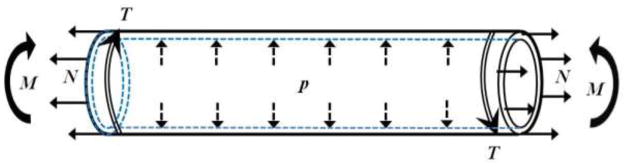
Schematic of an artery segment illustrating the complex loads an artery is subjected to in vivo, including transmural pressure (p), axial tension (N), bending moment (M), and axial torque (T).
Table 1.
Phenotypes of blood vessel buckling.
| Description | Sketch | Example Conditions |
|---|---|---|
| Lumen collapse |
|
arteries – stenoses,22, 97 veins – surface compression, 21 internal jugular vein – catheter insertion,56 coronary arteries – cardiac contraction 81 |
| Axial bent buckling |

|
carotid artery – aging, hypertension,19, 55 retinal arteries and veins – retinopathy,60, 95 vein grafts – over length4 |
| Twist buckling |

|
anastomoses, 53, 86, 88 coronary vessels – cardiac contraction,80 vein grafts,20, 26 vertebral artery – head rotation3, 59 |
| Kinking |

|
iliac arteries,87 internal carotid arteries79, 108 |
| Helical buckling |

|
vein grafts114 “corkscrew” collaterals91 |
3. Cross-Sectional Stability: Collapse of Vessel Lumen
It has been well documented that blood vessels buckle radially and vessel lumens collapse when internal lumen pressure is too low or the external pressure exceeds the internal pressure by a critical value.31 Collapse is a common occurrence in veins located above the level of the heart and in veins squeezed by skeletal muscle contractions to return blood to the heart from the feet of upright mammals.5, 81 In clinical settings, use of real-time ultrasound-assisted guidance during insertion of a central venous catheter into the internal jugular vein can cause collapse of the vein due to transcutaneous pressure produced by the ultrasound probe, which results in failure of venous puncture for catheter insertion.56 Pulmonary veins do not collapse with negative transmural pressure (internal pressure minus external pressure) due to tethering to interalveolar septa that stabilize vessel walls.31 Collapse of veins has also been shown to be beneficial in regulating the flow rate during raising of the head for giraffes.9
While veins often collapse due to low internal pressure, arteries are normally free from collapse due to their high lumen blood pressure and thicker walls.31 However, arteries may collapse under certain conditions. For example, intramyocardial coronary arteries collapse during left ventricle contraction.81 Arteries also collapse due to blood pressure cuffs,81 and it has been suggested that arteries may collapse at regions immediately downstream of a stenosis.22, 97
Collapsible Tube Models and Buckling Equation
Collapsible tube models have been developed based on the theory of elastic instability to determine the critical pressure at which a blood vessel collapses.22, 31 For example, Fung31 concisely illustrated the buckling equation for thin-walled circular cylindrical tubes of linear elastic material and uniform wall thickness subjected to transmural pressure. Using the equilibrium equations of forces and moments and their relations to the change in wall curvature, he established a second order linear differential equation for curvature change. Then, based on the periodic feature of the curvature and observing that the basal buckling mode occurs at a wavenumber n = 2, the buckling equation for the critical transmural pressure was obtained as 31
| (1) |
where pe is external pressure, p is internal lumen pressure, E′I= Et3/(12(1−ν2)) is the flexural rigidity of the thin-walled tube. E is Young’s modulus of the material, I is cross-sectional area moment of inertia per unit length, I= t3/12, t is wall thickness, ν is Poisson’s ratio, and R is tube median radius at zero transmural pressure, Although this critical buckling pressure equation was derived for linear elastic materials, the equation is used to estimate the buckling pressure for arteries and especially for veins with thinner walls. In addition, Fung noted that the incremental modulus E that corresponds to the working stress level in an artery can be used in this equation to obtain an estimation of the critical buckling pressure for arteries.31 However, we have seen no buckling equation that takes into account the nonlinear anisotropic properties of arterial walls. Further study is needed to extend the collapsible tube model to include these properties to better predict the critical load.
The post-buckling behavior of collapsible tubes was illustrated by the classic work of Flaherty, Keller, and Rubinow.28 They used a similar approach based on equilibrium and curvature equations as described by Fung to numerically determine the cross-sectional shapes of long, inextensible, elastic thin-walled circular tubes at a broad range of transmural pressures (the tube law, Figure 2). In the range when the two opposite sides can contact, as negative transmural pressure decreased, the cross section was reduced in size while it remained similar in shape. Their work and the experimental results of Shapiro established the tube law, which describes the cross-sectional area of collapsible tubes post-buckling as a function of transmural pressure given by:28,31
Figure 2.
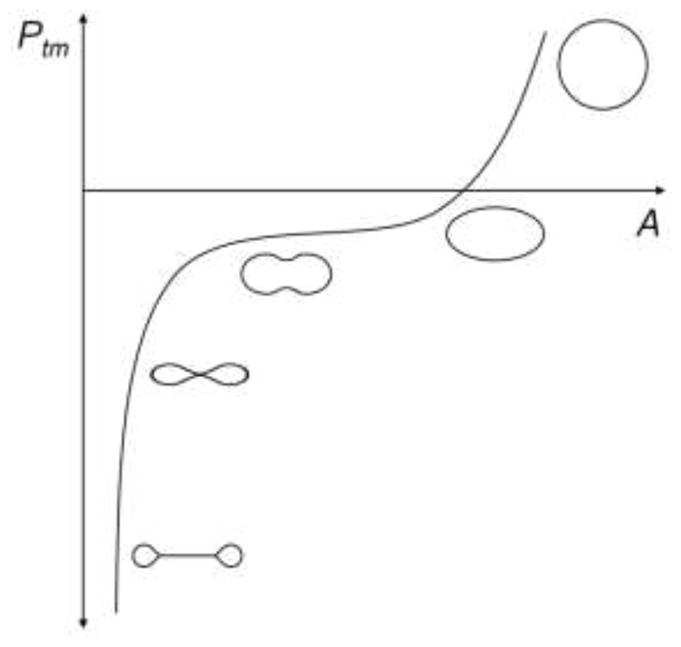
Sketch of transmural pressure (Ptm) versus cross-sectional area (A) showing cross-sectional shape for five regions of the curve for a collapsible tube, recreated based on Shapiro.89
| (2) |
where non-dimensional transmural pressure is p̃= (p− pe) /(E′I/R3), non-dimensional cross-sectional area is α= A /(πR2) and A is the cross-sectional lumen area. This equation accounts for large deformation and is thus directly applicable to collapse of veins and other thin-walled tubes, but it only gives a general estimation for collapse in arteries because of the linear elastic and thin-wall assumptions.
To better describe the pressure-area relationship, it is necessary to develop models accounting for the nonlinear anisotropic behavior of the arterial wall. Using an exponential stress-strain law, Drzewiecki et al. developed a pressure-lumen relationship for arteries as given by23
| (3) |
where m is a constant. C1 and C2 are material constants. A is the cross-sectional area, Ab is the cross-sectional area at critical buckling pressure, and Pb is the critical buckling pressure. They demonstrated a good fit of this equation with their experimental data of carotid arteries.23
Collapsible Tubes under Fluid Flow
Collapse of veins occurs under flow conditions in vivo with the vessel and flow interacting in a coupled way. Collapsible tube models have thus been studied under steady or pulsatile flow conditions by many groups.6, 38 The classic work by Shapiro89 presented a theoretical analysis of one-dimensional, steady flow through thin-walled, collapsible tubes. The analysis included physical mechanisms that are present in physiologic flows, which include friction, gravity, inertial forces, and axial variations in external pressure, muscular tone, tension, curvature, and reference cross-sectional area. This theory demonstrated the tight coupling of the tube structural mechanics to the fluid mechanics and showed that specific features were opposite for subcritical flows compared with supercritical flows. For example, internal pressure and cross-sectional area decreased with increasing external pressure for subcritical flows, but increased for supercritical flows. Since then, numerous models have been developed to investigate tube collapse under fluid flow. For example, Chow and Mak14 simulated steady flow through a collapsible vein using a two-dimensional unidirectional model. They determined the pressure versus cross-sectional area and pressure versus flow rate curves, and shapes of the vein during collapse. Marzo et al.73 illustrated differences in location and shape of the collapsed region of a thick-walled tube compared with a thinner-walled tube using a three-dimensional simulation under steady flow conditions. For unsteady flow, Bertram and Pedley5 developed a lumped parameter, mathematical model of a collapsible thick-walled tube. This model was used to demonstrate the importance of the unsteady jet head loss at the throat on oscillations of flow properties and cross-sectional area. The model also showed the importance of the physical properties upstream and downstream of the collapsible tube section.
In contrast to the studies above in which collapse was mainly induced by negative transmural pressure as occurs in veins, Ku, Tang, and colleagues demonstrated that stenoses caused collapse of arteries just downstream of stenoses, and that collapse was oscillatory under unsteady flow.22, 96, 97, 99 For example, Tang et al.99 developed a three-dimensional, fluid-structure interaction, computational model that combined a modified tube law and thin-shell model for collapse of elastic tubes. This study found that for arteries under cyclic pressure, severe stenoses induced negative transmural pressure at the stenosis throat and for some distance downstream, which produced collapse at a distance of about one artery diameter downstream of the throat. This and other results of the study showed good agreement with experimental results of a polyvinyl alcohol hydrogel stenosis model that had mechanical properties close to those of bovine carotid arteries.97 In addition, some fluid-structure interaction studies have modeled the arterial wall as a multilayer nonlinear anisotropic structure.39, 102
On the other hand, experimental work on tube collapse due to low transmural pressure has validated some model predictions and revealed some limitations. Elad et al.25 developed an experimental technique to measure the geometry, transmural pressure, and flow rate for collapsible tubes during static loading or steady flow. Measurements for tube laws under static loading compared well with previous experimental and theoretical studies. Experimental pressure and flow measurements were significantly different than predictions from one-dimensional steady flow models such as that of Shaprio.89 Drzewiecki and Pilla24 measured the transmural pressure versus lumen area of the human brachial artery using an occlusive pressure cuff. Transmural pressure for complete collapse was found to be between −50 to −40 mmHg. At the onset of collapse, transmural pressure was mainly a small positive value and was higher compared to previous in vitro data of canine blood vessels, which the authors suggested was likely due to axial tension in vivo. The authors also noted that unlike elastic tubes, blood vessel resistance to collapse remained small until the lumen area was nearly zero.
Numerous theoretical, numerical, and in vitro experimental studies have been done under various underlying assumptions and for specific conditions. These studies have helped elucidate the structural mechanics of collapsible tubes under pressure, as well as the inseparable coupling of structural mechanics and fluid mechanics of collapsible tubes. Our knowledge in this field will continue to evolve under fewer assumptions and for more physiological circumstances, especially as additional in vivo experimental methods are developed, 36 which can also validate and improve modeling efforts. Aspects of fluid-structure interaction models that are important for future studies include nonlinear viscoelastic and/or non-uniform wall properties and the two-phase nature of blood. These aspects will allow more detailed simulation and examination of pathological and physiological conditions that may be associated with vessel collapse.
4. Longitudinal Stability: Bent Buckling under Lumen Pressure
Arteries are commonly considered stable under lumen pressure and axial tension.40, 47, 48, 76 However, Han and colleagues recently demonstrated that long vessel segments can become unstable when the lumen pressure exceeds a critical value or the axial tension is reduced.42–45 The phenomenon was termed “artery buckling” because of its similarity to column-beam buckling (Figure 3).45
Figure 3.

A porcine carotid artery buckled under lumen pressure, within a gelatin matrix simulating surrounding tissue support. A multiple wave tortuous shape is formed.
Blood vessels, such as retinal arteries and veins, often become tortuous along their paths associated with hypertension, diabetes, and retinopathy.49, 95 Tortuous carotid arteries are often associated with aging, atherosclerosis, and hypertension.19, 47, 79 In a rabbit carotid artery grafting model, Jackson and colleagues demonstrated that reducing axial tension in arteries can lead to the development of tortuous shape.55 Elastin deficiency due to genetic defect, flow increase, or other vascular diseases can lead to weaker walls and tortuous arteries.16, 95, 106
In efforts to explain the tortuous shape of retinal arteries under hypertensive pressure, Kylstra et al., Stelson et al., and Brossollet and Vito modeled blood vessels as closed-ended vessel segments under axial compression and used the linear elastic Euler buckling equation to estimate the critical pressure.10, 60, 93 However, there was no justification for the unrealistic “closed-ends” and “axial compression” assumptions. On the other hand, axial length growth and elongation were thought to be the reasons for artery bent buckling. However, the paradox is that arteries remain under axial tension even with growth and elongation. So the classic Euler column buckling (under axial compression) cannot explain the bent buckling phenomenon.
Buckling Model and Equations
The paradox was resolved in 2007 by Han using a buckling model based on adjacent equilibrium.42, 44 It was shown that a lateral load could be generated by lumen pressure due to surface area difference between the convex and concave sides when a vessel bends. The lateral load could balance the axial tension when the pressure is high enough. Thus the vessel can reach equilibrium and buckling occurs. Using both adjacent equilibrium and potential energy approaches, Han established an artery buckling model for nonlinear anisotropic arterial walls (thick-walled) that predicted the critical load for artery bent buckling under lumen pressure. The model first determined the lateral distributed load generated by the lumen pressure due to surface area difference on convex and concave sides of a deflected artery.77 Then using the Bernoulli beam-column bending moment equation for the artery subjected to the lateral distributed load and the axial tension, as well as elastic support from the surrounding matrix, yielded a fourth order differential equation for the deflection as a function of axial position. Solving this differential eigenvalue equation yielded a periodic deflection curve and a buckling equation for a long vessel segment within a soft elastic matrix given by:44–46
| (4) |
where pcr is the critical buckling pressure, ks is the modulus of the surrounding matrix, N is the axial force, ÊÎ is the cross-sectional bending modulus of the vessel, l is the vessel length, ri is the lumen radius, and n is the wave number of the buckling mode shape. Note that ÊÎ cannot be separated as Ê and Î for nonlinear arterial wall and in fact ÊÎ =H (“bending stiffness”) as given in the Appendix of Lee et al.64 Both N and ÊÎ are functions of the transmural pressure and the strains for nonlinear anisotropic arterial walls.44, 64 So determination of pcr requires iterations using equation (4).
This model equation and experimental measurements demonstrated that arteries buckle when lumen pressure exceeds a critical pressure. The critical pressures of blood vessels are determined by vessel dimensions, wall stiffness, axial tension, and surrounding tissue stiffness.42, 44 Both experiments64, 70 and model simulations42, 43, 45 have demonstrated that artery critical buckling pressure decreased with the decrease of axial tension (axial stretch ratio). This conclusion is also true for thin-walled veins.62, 72 In addition, degradation of elastin, an important extracellular matrix component, by using elastase significantly reduced arterial critical buckling pressure associated with reduced wall stiffness.63, 64 Furthermore, growth and remodeling in collateral arterioles can lead to buckling of arterioles and make them tortuous.71 In contrast, a stronger surrounding tissue support (bigger ks) lead to a higher critical buckling pressure and a higher wave shape mode.44, 64 Further model analysis demonstrated that geometric variations such as initial curvature, tapering, eccentric or oval cross sections, stenosis, and aneurysm often reduced the stability as indicated by the reduced critical pressures.17, 44, 46, 77, 78
It is worth noting that although the classic linear elastic Euler column buckling model predicts a sudden, large, catastrophic increase of deflection with buckling, arteries do not show a sudden large deflection and catastrophic failure, but only a small deflection at buckling due to geometric nonlinearity.45, 100 The deflection of a buckled artery increases post-buckling with increasing lumen pressure, in a nonlinear fashion.63, 64
Bent Buckling under Pulsatile Flow
Arteries in vivo are under pulsatile flow. In 2009, Rachev extended the static buckling model into a dynamic buckling model and mathematically analyzed the dynamic stability of arteries.83 It was suggested that an increase in the mean pressure, pulse pressure, or pulse frequency of the pulsatile flow will cause the loss of stability. Recent experimental studies and model simulations by Liu and Han70 indicated that arteries under pulsatile pressure would buckle when the lumen pressure exceeded a critical pressure, consistent with arteries under static pressure. However, when buckling occurs under pulsatile flow, arteries flex periodically with the oscillation of lumen pressure.70 Furthermore, model simulations showed that the effect of excitation frequency on artery buckling was small at low excitation frequencies (< 5 Hz), arteries would buckle when the peak pressure (mean pressure + pulse pressure) reached the same critical pressure obtained under static or steady condition, and accordingly, the critical mean pressure increased almost linearly with the decrease of the pulse pressure. However, the dynamic effect became greater at excitation frequency > 5 Hz, the relation of mean pressure and pulse pressure became nonlinear, and the artery would buckle at a lower peak pressure than the critical pressure values under static or steady condition. In addition, it has been shown that ideal or viscous fluids had the same influence on the dynamics of arteries, and the centrifugal force induced by blood flow velocity acted in the same manner as the axial force.83 It is well known that the pulse pressure in humans increases significantly while axial tension decreases in the aged population.54, 76 These changes would make aged arteries vulnerable to instability and buckling. This may be a reason for the high occurrence of tortuous arteries in the aged population.
Artery buckling changes artery shape and thus alters lumen blood flow and wall stress, which can induce thrombosis.13, 69 The cyclic bending of arteries under pulsatile pressure can also affect matrix and gene expression,105 which are related to atherosclerosis.92 Bent buckling of arteries can also increase the local stress in atherosclerotic plaques and aneurysms and cause rupture.63, 78, 98 The long-term effects of artery buckling remain unclear.
5. Longitudinal Stability: Twist Buckling under Torque
Blood vessels often experience torsion and twist along their axes. Twisting of blood vessels can occur naturally with body movement and due to surgical procedures requiring blood vessel manipulation (e.g., vascular graft implantation, microanastomosis, skin grafting).3, 26 Excessive torsion can initiate a loss in stability in which the vessel buckles, characterized by the formation of a single wave distributed over the vessel’s long axis or a concentrated twist at a focal point (twist-kink).88 The twist is similar to that sometimes seen in a twisted garden hose. A twisted vessel can disrupt normal blood flow, damage the endothelial lining, and increase the risk for thrombosis.26 In vivo arteriographs have shown that rotation of the head to the left and right positions can initiate obstruction or kinking of the vertebral artery at the atlantoaxial joint and is implicated in vertebrobasilar symptoms.3, 59 Similarly, the internal jugular vein can also become obstructed with head rotation, which presents a risk for hydrocephalus if the contralateral vein is also obstructed.35
Buckling Model and Experiments
Arteries and veins are often considered as long cylinders subject to combined loads of pressure inflation, axial tension, and torsion (see Figure 1). Mechanical models have been developed for twist buckling of elastic cylindrical vessels under torsion. A classical model includes a thin-walled long cylinder of linear elastic material under a torque at the ends as given in Flugge29 and Timoshenko and Gere.100 The critical buckling torque Tcr was given by
| (5) |
This equation was obtained by utilizing the equilibrium equation for elastic thin cylindrical shells and presuming that the buckling pattern (displacement) was periodic. It is applicable to long cylinders under a torque alone and in the small deformation domain. For finite deformations, the theory of small deformations superposed on large elastic deformations was proposed to study bifurcations from known equilibrium states.37 Using this approach, Ertepinar and Wang27 developed a model for torsion of thick-walled cylinders of hyperelastic materials while under external pressure and axial compression. Further analysis by Zubov and Sheidakov showed that cylindrical vessels with nonlinear material could buckle under a combination of torsion, tension, and inflation.115 However, for blood vessels with nonlinear orthotropic walls subjected to torsion, lumen pressure and axial stretch that undergo large pre-buckling deformation, there is no appropriate model to describe the twist buckling behavior or to predict the critical torque and critical twist angle.
In surgical procedures, blood vessels may be either intentionally or unintentionally rotated upon implantation causing the vessel to become twisted or twist-kinked. However, there are some discrepancies among the reports on the critical twist angles at which the patency becomes significantly reduced.26, 88 For example, the rat femoral artery was used to study the rotation angle at which patency is significantly reduced in microvessels and was reported to be anywhere from 90 – 270 degrees, while other studies reported no significant reduction even at 360 degrees of rotation.53, 86, 101 The critical twist angles resulting in significant patency reduction in rat femoral veins has been reported to be between 90 – 180 degrees.7, 86 For vascular grafts, Endean et al. found that flow through superficial canine veins decreased sharply between 140 to 180 degrees of rotation and stopped completely between 175 to 200 degrees.26 The discrepancy among these results for arteries or veins can be attributed to the differences in vessel dimensions (especially the length), loading conditions, and animal models (e.g., Sprague-Dawley vs. Wistar rats or canine vs. rats). Thus, it is necessary to normalize these parameters, such as by using twist angle (rotation per unit vessel length) in describing the twist behavior of blood vessels.
Experimental measurements and model analyses have shown that the critical buckling loads and buckling shapes are affected by vessel dimensions, wall material properties, and boundary conditions. Dobrin et al.20 performed a study to identify key determinants for vascular graft kinking under torsion using synthetic and native vein grafts. They concluded that graft length, thickness, diameter, and material stiffness were all important factors for determining kinking behavior and that grafts having a shorter length, thinner wall, larger diameter, and stiffer material were more vulnerable to kinking. Similar conclusions were made in a numerical study by Wong et al.,110 in which perforator vessels were subjected to twist. However, Dobrin et al.20 found that lumen pressure had no significant influence on the number of turns required to produce a kink, while Wong et al.110 reported lumen pressure to be the main factor in resisting venous deformation.
Recently, the authors’ lab has investigated the in vitro buckling behavior of blood vessels under torsion using a custom built torsion machine capable of generating simultaneous axial tension, internal pressure, and torsion.32, 34 Porcine arteries and veins were rotated at various axial stretch and lumen pressure combinations while the torque and axial force were measured. The results demonstrated that the torsional resistance increased linearly with rotation until suddenly dropping upon kinking of the blood vessel (Figure 4). The critical buckling torque and critical buckling twist angle were obtained at this point of instability. For porcine common carotid arteries, twist buckling required a larger torque load with increased axial stretch ratio and lumen pressure. The critical twist angle for buckling was significantly reduced with increased axial stretch ratio but was not affected by the lumen pressure, in agreement with the conclusions for vein grafts.20 Torsional buckling tests have also been conducted on porcine internal jugular veins and similar buckling shapes were observed at lower critical loads.33
Figure 4.
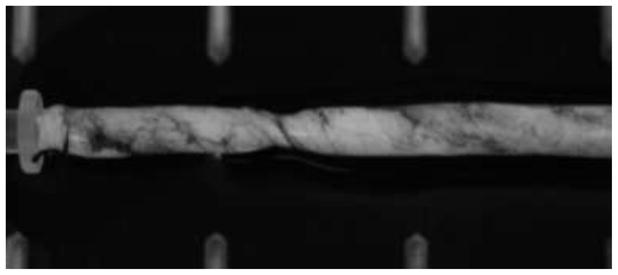
A porcine carotid artery buckled under axial torque. A kink is formed due to twist buckling. The ink smear was used to better visualize the twist deformation.
A very recent work by Garcia et al. showed an empirical equation linking the critical torque Tcr to arterial wall dimensions and shear modulus G for porcine carotid arteries.34
| (6) |
where α is a dimensionless constant (=17.6). This equation provides an estimation of the experimental measurement for critical torque of all tested arteries under various lumen pressures and axial stretch ratios. However, this equation is empirical in nature and a mechanics based theoretical model is needed to better predict the critical torque and twist angle.
6. Helical Buckling
A less studied buckling mode of cylinders is the generation of a helical configuration, or a three-dimensional spiral shape while the cross section remains open (Table 1). Helical buckling typically occurs when a cylinder is constrained within an enclosure such as in drilling operations where the drill string is surrounded by another cylinder. In these drilling applications, the drill string initially buckles into a sinusoidal shape under combined axial compression and torque, followed by a transition to a helical configuration upon further loading.74 Torsional buckling of carbon nanotubes within a matrix has also been demonstrated to form helical configurations.51, 90 We have observed in vitro that porcine carotid arteries would buckle into helical shapes when subject to a high lumen pressure (bend-buckling) in combination with an axial torque (Figure 5). Helical arterial paths have been reported in carotid arteries, umbilical cords, collateral arteries and grafts.57, 94, 114 However, it is not clear whether the helical paths were due to buckling alone or other processes. More studies are needed to better understand the occurrence of helical buckling in arteries.
Figure 5.
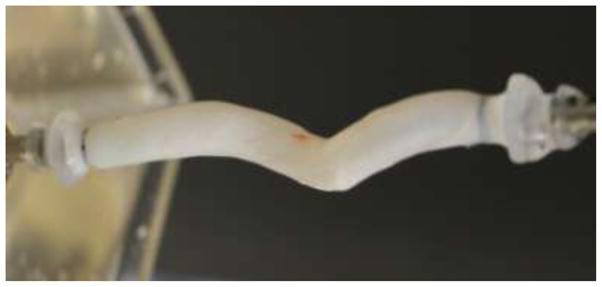
A porcine carotid artery buckled under combined lumen pressure and axial torque. A helical shape is formed.
7. Effects of Buckling on Blood Flow
Buckled blood vessels exhibit various changes in shape, including lumen collapse, curvature, twist, and kinking. These shape changes may be transient or become permanent and will result in changes in lumen blood flow, which include alterations to flow patterns and fluid shear stress, as well as restriction or complete occlusion of flow. Such flow modifications produce various physiological and pathological effects.
Upon loss of cross-sectional stability of a vessel, such as partial or full collapse of the lumen (see Figure 2), flow becomes restricted or blocked.81, 97 Brook and Pedley9 performed computational simulations in uniform collapsible tubes to illustrate the benefits of collapse, showing that time-dependent collapse of the giraffe jugular vein regulated flow rate during raising of the head. Additionally, as a prophylactic, compression of leg veins by graduated compression stockings or intermittent pneumatic compression is commonly used for hospital patients to prevent deep vein thrombosis and pulmonary embolism that arise from venous flow stasis. A combined in vivo and computational study by Downie et al.21 showed that compression of large deep and superficial veins in the calf by elastic compression stockings was effective in prevention of flow stasis in humans. Moreover, the stockings increased wall shear stresses, compared with controls, to become closer to physiological levels that protect against thrombosis. On the other hand, low wall shear stresses were close to zero in controls, which could promote venous thrombosis as well as atherosclerosis. Another phenomenon observed under certain transmural pressures and flow rates in collapsible tubes, and possibly veins, is self-excited, self-sustaining oscillation of outflow rate despite a constant inflow rate.5
Loss of longitudinal stability of a vessel by bent buckling can lead to a curved or tortuous vessel shape, thus changing the spatial path of blood flow. Back and colleagues examined the flow in a human femoral artery model with reverse curvature and measured the flow in a sinusoidal coronary artery model.1, 2 These and many other studies have shown that vessel curvature has significant effects on blood flow by increasing pressure loss, flow resistance, and secondary flow, as well as increasing pressure and lumen shear stress on the outer curvature.111 In “S-shaped” arteries, computational simulations of Qiao et al.82 showed that in the systolic phase, maximum velocity occurred at the inner bend (convex side of the lumen) of the upstream portion of the curve during the acceleration period and then moved through the centerline to the outer bend of the upstream portion of the curve before the deceleration period began. Secondary flow was also observed. Additionally, wall shear stresses of nearly 200 dyn/cm2 were achieved at both inner and outer bends, which is an order of magnitude larger than those in normal arteries. In curved venules, steady flow computational simulations of Chesnutt and Han13 and Liu et al. 69 demonstrated a shift of maximum velocity and streamlines toward the inner bend, and wall shear stresses that were higher at the inner bend and larger than that in straight venules. A consequence of high shear stresses, as produced by curvature in the above artery and venule simulations, is the possibility of platelet activation and subsequent thrombus formation, as seen in in vivo experiments in rats69 and computational simulations.13 More studies are needed for flows in severely and continuously tortuous arteries.
Twist buckling or twist-kinking of arteries and veins also alters blood flow. Kinking of internal carotid arteries in patients has reduced cerebral blood flow and produced symptoms such as hemiplegia, hemiparesis, syncope, transient vision loss, poor coordination, and ischemic stroke.104 Schep et al.87 used echo-doppler examination and magnetic-resonance angiography to observe that kinking of iliac arteries caused restricted blood flow in athletes who reported pain and lack of leg power while active in endurance sports. In another study, Salgarello et al.86 demonstrated that twisted vessels in vivo due to free flap or replantation surgery produced thrombosis, which may be partly ascribed to altered blood flow. In addition, computational simulations of flow in helical vessels demonstrated a screwed velocity profile and increased local wall shear stress.57, 114
As illustrated in this section, blood vessel buckling modifies blood flow to produce numerous effects. Some of these effects are beneficial, while others are detrimental. In many cases, detrimental outcomes can be alleviated by surgery in which the vessel is returned to a more physiological shape.87, 94, 104
8. Other Buckling Phenotypes
Other forms of buckling may also occur in arteries. Although a barrel-like buckling pattern is possible,107 there have been no reports of barrel-shape buckling in arteries in the literature. It has been noticed that an arterial lumen may buckle into a wavy shape (folding) when the lumen pressure is low or when the artery is excised from the body.41 Folding of the lumen of arteries has been analyzed numerically.50 In addition, when arteries are under severe bending, a local kink may occur on the inner curve (see Table 1). The kinking happens often in carotid and iliac arteries. 18, 79, 87, 94 A kink could significantly restrict or even completely occlude blood flow.18, 19, 79
9. Buckling of Other Organs and Organisms
Similar to arteries, cross-sectional buckling and collapse also occur in other tubular organs such as esophagus, trachea, ureters, and intestine.50, 66, 68, 113 The collapse instability also occurs in other organelles such as sclera, alveoli, and red blood cells.30, 85 Buckling is also seen in cytoskeletons. Microtubule and microfilament buckling has been reported in cells during cell movement and contraction.8, 15
Folding in tubular organs such as intestine and esophagus has also been related to buckling. Folding of the mucosal layer and lumen of biological vessels (e.g., artery, intestine, esophagus, and airway) has been examined through experimental measurements and numerical simulations.50, 66, 68, 109, 113 Buckling has been proposed as a mechanism in forming gyrus during the brain folding process.84, 103 Folding and wrinkling in living tissues and fruits have been widely observed and modeled as the result of buckling due to growth, and have been considered as mechanisms for pattern formation in organs.11, 66, 67 Pattern formation in flowers, leaves and fruits has been attributed to buckling due to non-uniform growth.11, 58
10. Future Directions
While significant progress has been made in measuring and modeling the buckling behavior of arteries and veins, many challenging problems remain to be investigated. Buckling of arteries changes the profiles of blood flow, pressure, and stresses (shear stress and wall stress), which regulate endothelial cells, smooth muscle cells, and extracellular matrix, and therefore buckling affects vascular function and causes arterial remodeling. While we have gained some understanding of the conditions that lead to artery buckling, we know very little about the adaptation of the arterial wall after buckling occurs. For example, bent buckling yields tortuous vessels and changes the flow path, lumen shear stress, and wall tensile stresses. In vitro experiments have demonstrated different amounts of cell proliferation at inner and outer walls in buckled arteries.112 However, long-term wall remodeling in buckled arteries needs further investigation. While buckling causes variations in wall stress and lumen shear stress that lead to non-uniform wall remodeling, the remodeling would further change the vessel geometry and buckling mode and thus affect the hemodynamics and wall stresses. The dynamic interaction between arterial mechanics, buckling and vessel remodeling needs further study in order to understand the dynamic development process of tortuous blood vessels. Another area that needs further study is the twist buckling behavior of arteries. First, as stated above, a theoretical model is needed to predict the critical torque and twist angle. Second, the effects of surround tissue support and the effects of arterial wall remodeling due to aging and vascular diseases need to be investigated.
While buckling represents an initial loss in stability, the mechanisms leading to spatial buckling or tortuosity are not well understood. The post-buckling behavior of arteries under pressure, axial tension and torque needs further investigation. In addition, for arteries under complex loads, models are needed to capture the combined bent-twist buckling or helical buckling behavior of the nonlinear tubular vessels and to predict the critical buckling loads.
In conclusion, various buckling patterns occur in arteries under in vivo mechanical loads. Mechanical buckling is an important aspect of vascular mechanics, physiology and pathology. Further studies are needed to better understand the buckling behavior of arteries and its physiopathological effects.
Acknowledgments
This work was supported by the National Heart, Lung, and Blood Institute (R01 HL095852 to HCH, T32 HL04776 to JKWC), the MBRS-RISE program of the National Institutes of Health (Predoctoral fellowship to JG under grant GM60655), and the National Science Foundation (CAREER award 0644646 to HCH).
Footnotes
12. Conflict of interest statement
The authors have no conflict of interests.
References
- 1.Back LH, Back MR, Kwack EY, Crawford DW. Flow measurements in a human femoral artery model with reverse lumen curvature. J Biomech Eng. 1988;110(4):300–9. doi: 10.1115/1.3108446. [DOI] [PubMed] [Google Scholar]
- 2.Back LH, Liem TK, Kwack EY, Crawford DW. Flow measurements in a highly curved atherosclerotic coronary artery cast of man. J Biomech Eng. 1992;114(2):232–40. doi: 10.1115/1.2891377. [DOI] [PubMed] [Google Scholar]
- 3.Barton JW, Margolis MT. Rotational obstructions of the vertebral artery at the atlantoaxial joint. Neuroradiology. 1975;9(3):117–20. doi: 10.1007/BF00332957. [DOI] [PubMed] [Google Scholar]
- 4.Beris AE, Soucacos PN, Touliatos AS. Experimental evaluation of the length of microvenous grafts under normal tension. Microsurgery. 1992;13(4):195–9. doi: 10.1002/micr.1920130410. [DOI] [PubMed] [Google Scholar]
- 5.Bertram CD, Pedley TJ. A mathematical model of unsteady collapsible tube behaviour. J Biomech. 1982;15(1):39–50. doi: 10.1016/0021-9290(82)90033-1. [DOI] [PubMed] [Google Scholar]
- 6.Bertram CD. Flow-induced oscillation of collapsed tubes and airway structures. Respir Physiol Neurobiol. 2008;163(1–3):256–65. doi: 10.1016/j.resp.2008.04.011. [DOI] [PubMed] [Google Scholar]
- 7.Bilgin SS, Topalan M, Ip WY, Chow SP. Effect of torsion on microvenous anastomotic patency in a rat model and early thrombolytic phenomenon. Microsurgery. 2003;23(4):381–386. doi: 10.1002/micr.10150. [DOI] [PubMed] [Google Scholar]
- 8.Brangwynne CP, MacKintosh FC, Kumar S, Geisse NA, Talbot J, Mahadevan L, Parker KK, Ingber DE, Weitz DA. Microtubules can bear enhanced compressive loads in living cells because of lateral reinforcement. J Cell Biol. 2006;173(5):733–41. doi: 10.1083/jcb.200601060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Brook BS, Pedley TJ. A model for time-dependent flow in (giraffe jugular) veins: uniform tube properties. J Biomech. 2002;35(1):95–107. doi: 10.1016/s0021-9290(01)00159-2. [DOI] [PubMed] [Google Scholar]
- 10.Brossollet LJ, Vito RP. An alternate formulation of blood vessel mechanics and the meaning of the in vivo property. J Biomech. 1995;28(6):679–87. doi: 10.1016/0021-9290(94)00119-o. [DOI] [PubMed] [Google Scholar]
- 11.Chen X, Yin J. Buckling patterns of thin films on curved compliant substrates with applications to morphogenesis and three-dimensional micro-fabrication. Soft Matter. 2010;6(22):5667–5680. [Google Scholar]
- 12.Cheng GC, Loree HM, Kamm RD, Fishbein MC, Lee RT. Distribution of circumferential stress in ruptured and stable atherosclerotic lesions. A structural analysis with histopathological correlation. Circulation. 1993;87(4):1179–87. doi: 10.1161/01.cir.87.4.1179. [DOI] [PubMed] [Google Scholar]
- 13.Chesnutt JKW, Han HC. Tortuosity triggers platelet activation and thrombus formation in microvessels. J Biomech Eng. 2011;133:121004-1-11. doi: 10.1115/1.4005478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chow KW, Mak CC. A simple model for the two dimensional blood flow in the collapse of veins. J Math Biol. 2006;52(6):733–44. doi: 10.1007/s00285-005-0351-5. [DOI] [PubMed] [Google Scholar]
- 15.Costa KD, Hucker WJ, Yin FC. Buckling of actin stress fibers: a new wrinkle in the cytoskeletal tapestry. Cell Motil Cytoskeleton. 2002;52(4):266–74. doi: 10.1002/cm.10056. [DOI] [PubMed] [Google Scholar]
- 16.Coucke PJ, Willaert A, Wessels MW, Callewaert B, Zoppi N, De Backer J, Fox JE, Mancini GM, Kambouris M, Gardella R, Facchetti F, Willems PJ, Forsyth R, Dietz HC, Barlati S, Colombi M, Loeys B, De Paepe A. Mutations in the facilitative glucose transporter GLUT10 alter angiogenesis and cause arterial tortuosity syndrome. Nat Genet. 2006;38(4):452–7. doi: 10.1038/ng1764. [DOI] [PubMed] [Google Scholar]
- 17.Datir P, Lee AY, Lamm SD, Han HC. Effects of geometric variations on the buckling of arteries. Int J Appl Mech. 2011;3(2):385–406. doi: 10.1142/S1758825111001044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Dawson DL, Hellinger JC, Terramani TT, Najibi S, Martin LG, Lumsden AB. Iliac artery kinking with endovascular therapies: technical considerations. J Vasc Interv Radiol. 2002;13(7):729–33. doi: 10.1016/s1051-0443(07)61852-1. [DOI] [PubMed] [Google Scholar]
- 19.Del Corso L, Moruzzo D, Conte B, Agelli M, Romanelli AM, Pastine F, Protti M, Pentimone F, Baggiani G. Tortuosity, kinking, and coiling of the carotid artery: expression of atherosclerosis or aging? Angiology. 1998;49(5):361–71. doi: 10.1177/000331979804900505. [DOI] [PubMed] [Google Scholar]
- 20.Dobrin PB, Hodgett D, Canfield T, Mrkvicka R. Mechanical determinants of graft kinking. Ann Vasc Surg. 2001;15(3):343–9. doi: 10.1007/s100160010078. [DOI] [PubMed] [Google Scholar]
- 21.Downie SP, Raynor SM, Firmin DN, Wood NB, Thom SA, Hughes AD, Parker KH, Wolfe JH, Xu XY. Effects of elastic compression stockings on wall shear stress in deep and superficial veins of the calf. Am J Physiol Heart Circ Physiol. 2008;294(5):H2112–20. doi: 10.1152/ajpheart.01302.2007. [DOI] [PubMed] [Google Scholar]
- 22.Downing JM, Ku DN. Effects of frictional losses and pulsatile flow on the collapse of stenotic arteries. J Biomech Eng. 1997;119(3):317–24. doi: 10.1115/1.2796096. [DOI] [PubMed] [Google Scholar]
- 23.Drzewiecki G, Field S, Moubarak I, Li JK. Vessel growth and collapsible pressure-area relationship. Am J Physiol. 1997;273(4 Pt 2):H2030–43. doi: 10.1152/ajpheart.1997.273.4.H2030. [DOI] [PubMed] [Google Scholar]
- 24.Drzewiecki G, Pilla JJ. Noninvasive measurement of the human brachial artery pressure-area relation in collapse and hypertension. Annals of Biomedical Engineering. 1998;26(6):965–74. doi: 10.1114/1.130. [DOI] [PubMed] [Google Scholar]
- 25.Elad D, Sahar M, Avidor JM, Einav S. Steady flow through collapsible tubes: measurements of flow and geometry. J Biomech Eng. 1992;114(1):84–91. doi: 10.1115/1.2895454. [DOI] [PubMed] [Google Scholar]
- 26.Endean ED, DeJong S, Dobrin PB. Effect of twist on flow and patency of vein grafts. J Vasc Surg. 1989;9(5):651–5. doi: 10.1067/mva.1989.vs0090651. [DOI] [PubMed] [Google Scholar]
- 27.Ertepinar A, Wang ASD. Torsional buckling of an elastic thick-walled tube made of rubber-like material. Int J Solids Struct. 1975;11(3):329–337. [Google Scholar]
- 28.Flaherty JE, Keller JB, Rubinow SI. Post Buckling Behavior of Elastic Tubes and Rings with Opposite Sides in Contact. Siam J Appl Math. 1972;23(4):446–455. [Google Scholar]
- 29.Flugge W. Stress in Shells. Chapters 2 & 8. New York: Springer-Verlag; 1973. [Google Scholar]
- 30.Fung YC. Biomechanics: Mechanical Properties of Living Tissues. 2. New York: Springer Verlag; 1993. [Google Scholar]
- 31.Fung YC. Biomechanics: Circulation. 2. Chapter 4. New York: Springer; 1997. [Google Scholar]
- 32.Garcia J, Lamm SD, Han HC. Buckling behavior of arteries under torsion. ASME Summer Bioeng Conf; 2011; Farmington, PA. [Google Scholar]
- 33.Garcia J, Han HC. The stability of veins under torsion. ASME Summer Bioeng Conf; 2012; Fajardo, Puerto Rico. [Google Scholar]
- 34.Garcia JR, Lamm SD, Han HC. Twist buckling behavior of arteries. Biomech Model Mechanobiol. 2012 doi: 10.1007/s10237-012-0453-0. (In press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gooding CA, Stimac GK. Jugular vein obstruction caused by turning of the head. AJR Am J Roentgenol. 1984;142(2):403–6. doi: 10.2214/ajr.142.2.403. [DOI] [PubMed] [Google Scholar]
- 36.Gorenberg M, Rotztein H, Marmor A. A new noninvasive device for measuring central ejection dP/dt mathematical foundation of cardiac dP/dt measurement using a model for a collapsible artery. Cardiovasc Eng. 2009;9(1):27–31. doi: 10.1007/s10558-009-9064-5. [DOI] [PubMed] [Google Scholar]
- 37.Green AE, Rivlin RS, Shield RT. General Theory of Small Elastic Deformations Superposed on Finite Elastic Deformations. Proc Roy Soc London A-Math Phys Sci. 1952;211(1104):128–154. [Google Scholar]
- 38.Grotberg JB, Jensen OE. Biofluid mechanics in flexible tubes. Annual Review of Fluid Mechanics. 2004;36:121–147. [Google Scholar]
- 39.Hamadiche M, Kizilova N, Gad-El-Hak M. Suppression of absolute instabilities in the flow inside a compliant tube. Communications in Numerical Methods in Engineering. 2009;25(5):505–531. [Google Scholar]
- 40.Han HC, Fung YC. Longitudinal strain of canine and porcine aortas. J Biomech. 1995;28(5):637–41. doi: 10.1016/0021-9290(94)00091-h. [DOI] [PubMed] [Google Scholar]
- 41.Han HC, Fung YC. Direct measurement of transverse residual strains in aorta. Am J Physiol. 1996;270(2 Pt 2):H750–9. doi: 10.1152/ajpheart.1996.270.2.H750. [DOI] [PubMed] [Google Scholar]
- 42.Han HC. A biomechanical model of artery buckling. J Biomech. 2007;40(16):3672–8. doi: 10.1016/j.jbiomech.2007.06.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Han HC. Nonlinear buckling of blood vessels: a theoretical study. J Biomech. 2008;41(12):2708–13. doi: 10.1016/j.jbiomech.2008.06.012. [DOI] [PubMed] [Google Scholar]
- 44.Han HC. Blood vessel buckling within soft surrounding tissue generates tortuosity. J Biomech. 2009;42(16):2797–2801. doi: 10.1016/j.jbiomech.2009.07.033. [DOI] [PubMed] [Google Scholar]
- 45.Han HC. The theoretical foundation for artery buckling under internal pressure. J Biomech Eng. 2009;131(12):124501. doi: 10.1115/1.4000080. [DOI] [PubMed] [Google Scholar]
- 46.Han HC. Determination of the critical buckling pressure of blood vessels using the energy approach. Annals of Biomedical Engineering. 2011;39(3):1032–40. doi: 10.1007/s10439-010-0212-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Han HC. Twisted Blood Vessels: Symptoms, Etiology and Biomechanical Mechanisms. J Vasc Res. 2012;49(3):185–197. doi: 10.1159/000335123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Han HC, Jiang Z. Vascular remodeling under axial tension. J Med Biomech [Chinese] 2012;27(1):1–6. [Google Scholar]
- 49.Hayreh SS, Servais GE, Virdi PS. Retinal arteriolar changes in malignant arterial hypertension. Ophthalmologica. 1989;198(4):178–96. doi: 10.1159/000309998. [DOI] [PubMed] [Google Scholar]
- 50.Hrousis CA, Wiggs BJ, Drazen JM, Parks DM, Kamm RD. Mucosal folding in biologic vessels. J Biomech Eng. 2002;124(4):334–41. doi: 10.1115/1.1489450. [DOI] [PubMed] [Google Scholar]
- 51.Huang X, Yuan HY, Hsia KJ, Zhang SL. Coordinated Buckling of Thick Multi-Walled Carbon Nanotubes Under Uniaxial Compression. Nano Research. 2010;3(1):32–42. [Google Scholar]
- 52.Humphrey JD. Cardiovascular Solid Mechanics: Cells, Tissues, and Organs. Chapters 8 & 9. New York: Springer; 2002. [Google Scholar]
- 53.Izquierdo R, Dobrin PB, Fu KD, Park F, Galante G. The effect of twist on microvascular anastomotic patency and angiographic luminal dimensions. J Surg Res. 1998;78(1):60–63. doi: 10.1006/jsre.1997.5228. [DOI] [PubMed] [Google Scholar]
- 54.Izzo JL, Jr, Levy D, Black HR. Clinical Advisory Statement. Importance of systolic blood pressure in older Americans. Hypertension. 2000;35(5):1021–4. doi: 10.1161/01.hyp.35.5.1021. [DOI] [PubMed] [Google Scholar]
- 55.Jackson ZS, Dajnowiec D, Gotlieb AI, Langille BL. Partial off-loading of longitudinal tension induces arterial tortuosity. Arterioscler Thromb Vasc Biol. 2005;25(5):957–62. doi: 10.1161/01.ATV.0000161277.46464.11. [DOI] [PubMed] [Google Scholar]
- 56.Joo WJ, Fukui M, Kooguchi K, Sakaguchi M, Shinzato T. Transcutaneous pressure at which the internal jugular vein is collapsed on ultrasonic imaging predicts easiness of the venous puncture. J Anesth. 2011;25(2):308–11. doi: 10.1007/s00540-010-1077-0. [DOI] [PubMed] [Google Scholar]
- 57.Kaplan AD, Jaffa AJ, Timor IE, Elad D. Hemodynamic analysis of arterial blood flow in the coiled umbilical cord. Reprod Sci. 2010;17(3):258–68. doi: 10.1177/1933719109351596. [DOI] [PubMed] [Google Scholar]
- 58.Klein Y, Efrati E, Sharon E. Shaping of elastic sheets by prescription of non-Euclidean metrics. Science. 2007;315(5815):1116–1120. doi: 10.1126/science.1135994. [DOI] [PubMed] [Google Scholar]
- 59.Kuether TA, Nesbit GM, Clark WM, Barnwell SL. Rotational vertebral artery occlusion: A mechanism of vertebrobasilar insufficiency. Neurosurgery. 1997;41(2):427–432. doi: 10.1097/00006123-199708000-00019. [DOI] [PubMed] [Google Scholar]
- 60.Kylstra JA, Wierzbicki T, Wolbarsht ML, Landers MB, 3rd, Stefansson E. The relationship between retinal vessel tortuosity, diameter, and transmural pressure. Graefes Arch Clin Exp Ophthalmol. 1986;224(5):477–80. doi: 10.1007/BF02173368. [DOI] [PubMed] [Google Scholar]
- 61.Langille BL. Arterial remodeling: relation to hemodynamics. Can J Physiol Pharmacol. 1996;74(7):834–41. [PubMed] [Google Scholar]
- 62.Lee A, Han HC. A thin-walled nonlinear model for vein buckling. Cardiovasc Eng & Tech. 2010;1(4):282–289. doi: 10.1007/s13239-010-0024-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Lee AY. Biomedical Engineering. University of Texas at San Antonio; San Antonio, TX: 2011. Determining the Critical Buckling of Blood Vessels Through Modeling and In Vitro Experiments. [Google Scholar]
- 64.Lee AY, Han B, Lamm SD, Fierro CA, Han HC. Effects of elastin degradation and surrounding matrix support on artery stability. Am J Physiol Heart Circ Physiol. 2012;302(4):H873–84. doi: 10.1152/ajpheart.00463.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Lehoux S, Tedgui A. Cellular mechanics and gene expression in blood vessels. J Biomech. 2003;36(5):631–43. doi: 10.1016/s0021-9290(02)00441-4. [DOI] [PubMed] [Google Scholar]
- 66.Li B, Cao YP, Feng XQ. Growth and surface folding of esophageal mucosa: a biomechanical model. J Biomech. 2011;44(1):182–8. doi: 10.1016/j.jbiomech.2010.09.007. [DOI] [PubMed] [Google Scholar]
- 67.Li B, Cao YP, Feng XQ, Gao H. Mechanics of morphological instabilities and surface wrinkling in soft materials: a review. Soft Matter. 2012;8:5728–5745. [Google Scholar]
- 68.Liao D, Zhao J, Yang J, Gregersen H. The oesophageal zero-stress state and mucosal folding from a GIOME perspective. World J Gastroenterol. 2007;13(9):1347–51. doi: 10.3748/wjg.v13.i9.1347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Liu Q, Mirc D, Fu BM. Mechanical mechanisms of thrombosis in intact bent microvessels of rat mesentery. J Biomech. 2008;41(12):2726–34. doi: 10.1016/j.jbiomech.2008.06.013. [DOI] [PubMed] [Google Scholar]
- 70.Liu Q, Han HC. Mechanical buckling of artery under pulsatile pressure. J Biomech. 2012;45(7):1192–8. doi: 10.1016/j.jbiomech.2012.01.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Liu Q, Han HC. Mechanical buckling of arterioles in collateral development. J Theor Biol. 2013;316C:42–48. doi: 10.1016/j.jtbi.2012.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Martinez R, Fierro CA, Shireman PK, Han HC. Mechanical buckling of veins under internal pressure. Annals of Biomedical Engineering. 2010;38(4):1345–53. doi: 10.1007/s10439-010-9929-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Marzo A, Luo XY, Bertram CD. Three-dimensional collapse and steady flow in thick-walled flexible tubes. J Fluids Struct. 2005;20(6):817–835. [Google Scholar]
- 74.Mitchell RF. Tubing Buckling-The State of the Art. Spe Drill & Completion. 2008;23(4):361–370. [Google Scholar]
- 75.Nerem RM. Role of mechanics in vascular tissue engineering. Biorheology. 2003;40(1–3):281–7. [PubMed] [Google Scholar]
- 76.Nichols WW, O’Rourke MF. Experimental, and Clinical Principles. 4. Chapter 16. London: Arnold Publisher; 1998. McDonald’s Blood Flow in Arteries: Theoretical. [Google Scholar]
- 77.Northcutt A, Datir P, Han HC. Computational simulations of buckling of oval and tapered arteries. In: Chien S, et al., editors. Tributes to Yuan-Cheng Fung on His 90th Birthday. World Scientific Publishing; New Jersey: 2009. [Google Scholar]
- 78.Northcutt A, Han HC. Finite element analysis of buckling of arteries with aneurysms. ASME Summer Bioeng Conf; 2009; Lake Tahoe, CA. [Google Scholar]
- 79.Pancera P, Ribul M, Presciuttini B, Lechi A. Prevalence of carotid artery kinking in 590 consecutive subjects evaluated by Echocolordoppler. Is there a correlation with arterial hypertension? J Intern Med. 2000;248(1):7–12. doi: 10.1046/j.1365-2796.2000.00611.x. [DOI] [PubMed] [Google Scholar]
- 80.Pao YC, Lu JT, Ritman EL. Bending and Twisting of an Invivo Coronary-Artery at a Bifurcation. J Biomech. 1992;25(3):287–295. doi: 10.1016/0021-9290(92)90026-w. [DOI] [PubMed] [Google Scholar]
- 81.Pedley TJ, Luo XY. Modelling flow and oscillations in collapsible tubes. Theoret Comp Fluid Dynamics. 1998;10:277–294. [Google Scholar]
- 82.Qiao AK, Guo XL, Wu SG, Zeng YJ, Xu XH. Numerical study of nonlinear pulsatile flow in S-shaped curved arteries. Med Eng & Phys. 2004;26(7):545–552. doi: 10.1016/j.medengphy.2004.04.008. [DOI] [PubMed] [Google Scholar]
- 83.Rachev A. A theoretical study of mechanical stability of arteries. J Biomech Eng. 2009;131(5):051006. doi: 10.1115/1.3078188. [DOI] [PubMed] [Google Scholar]
- 84.Richman DP, Stewart RM, Hutchinson JW, Caviness VS., Jr Mechanical model of brain convolutional development. Science. 1975;189(4196):18–21. doi: 10.1126/science.1135626. [DOI] [PubMed] [Google Scholar]
- 85.Rosenzweig J, Jensen OE. Capillary-elastic instabilities of liquid-lined lung airways. J Biomech Eng. 2002;124(6):650–5. doi: 10.1115/1.1516811. [DOI] [PubMed] [Google Scholar]
- 86.Salgarello M, Lahoud P, Selvaggi G, Gentileschi S, Sturla M, Farallo E. The effect of twisting on microanastomotic patency of arteries and veins in a rat model. Ann Plastic Surg. 2001;47(6):643–646. doi: 10.1097/00000637-200112000-00011. [DOI] [PubMed] [Google Scholar]
- 87.Schep G, Bender MHM, van de Tempel G, Wijn PFF, de Vries WR, Eikelboom BC. Detection and treatment of claudication due to functional iliac obstruction in top endurance athletes: a prospective study. Lancet. 2002;359(9305):466–473. doi: 10.1016/s0140-6736(02)07675-4. [DOI] [PubMed] [Google Scholar]
- 88.Selvaggi G, Salgarello M, Farallo E, Anicic S, Formaggia L. Effect of torsion on microvenous anastomotic patency in rat model and early thrombolytic phenomenon. Microsurgery. 2004;24(5):416–417. doi: 10.1002/micr.20085. [DOI] [PubMed] [Google Scholar]
- 89.Shapiro AH. Steady flow in collapsible tubes. J Biomech Eng. 1977;99(3):126–147. [Google Scholar]
- 90.Shen HS, Zhang CL. Torsional buckling and postbuckling of double-walled carbon nanotubes by nonlocal shear deformable shell model. Composite Struct. 2010;92(5):1073–1084. [Google Scholar]
- 91.Shireman PK, Quinones MP. Differential necrosis despite similar perfusion in mouse strains after ischemia. J Surg Res. 2005;129(2):242–50. doi: 10.1016/j.jss.2005.06.013. [DOI] [PubMed] [Google Scholar]
- 92.Stein PD, Hamid MS, Shivkumar K, Davis TP, Khaja F, Henry JW. Effects of cyclic flexion of coronary arteries on progression of atherosclerosis. Am J Cardiol. 1994;73(7):431–7. doi: 10.1016/0002-9149(94)90671-8. [DOI] [PubMed] [Google Scholar]
- 93.Stelson KA, Blackshear PL, Jr, Wirtschafter JD. On the tortuosity of the veins of the retina. Microvasc Res. 1983;26(1):126–8. doi: 10.1016/0026-2862(83)90062-6. [DOI] [PubMed] [Google Scholar]
- 94.Szekely G, Csecsei GI. Anteposition of the internal carotid artery for surgical treatment of kinking. Surg Neurol. 2001;56(2):124–6. doi: 10.1016/s0090-3019(01)00512-2. [DOI] [PubMed] [Google Scholar]
- 95.Taarnhoj NC, I, Munch C, Sander B, Kessel L, Hougaard JL, Kyvik K, Sorensen TI, Larsen M. Straight versus tortuous retinal arteries in relation to blood pressure and genetics. Br J Ophthalmol. 2008;92(8):1055–60. doi: 10.1136/bjo.2007.134593. [DOI] [PubMed] [Google Scholar]
- 96.Tang D, Yang J, Yang C, Ku DN. A nonlinear axisymmetric model with fluid-wall interactions for steady viscous flow in stenotic elastic tubes. J Biomech Eng. 1999;121(5):494–501. doi: 10.1115/1.2835078. [DOI] [PubMed] [Google Scholar]
- 97.Tang D, Yang C, Kobayashi S, Ku DN. Steady flow and wall compression in stenotic arteries: a three-dimensional thick-wall model with fluid-wall interactions. J Biomech Eng. 2001;123(6):548–57. doi: 10.1115/1.1406036. [DOI] [PubMed] [Google Scholar]
- 98.Tang D, Yang C, Kobayashi S, Zheng J, Woodard PK, Teng Z, Billiar K, Bach R, Ku DN. 3D MRI-based anisotropic FSI models with cyclic bending for human coronary atherosclerotic plaque mechanical analysis. J Biomech Eng. 2009;131(6):061010. doi: 10.1115/1.3127253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Tang DL, Yang C, Walker H, Kobayashi S, Ku DN. Simulating cyclic artery compression using a 3D unsteady model with fluid-structure interactions. Computers & Structures. 2002;80(20–21):1651–1665. [Google Scholar]
- 100.Timoshenko SP, Gere JM. Theory of Elastic Stability. 2. New York: McGraw-Hill; 1963. [Google Scholar]
- 101.Topalan M, Bilgin SS, Ip WY, Chow SP. Effect of torsion on microarterial anastomosis patency. Microsurgery. 2003;23(1):56–9. doi: 10.1002/micr.10092. [DOI] [PubMed] [Google Scholar]
- 102.Valencia A, Baeza F. Numerical simulation of fluid-structure interaction in stenotic arteries considering two layer nonlinear anisotropic structural model. International Communications in Heat and Mass Transfer. 2009;36(2):137–142. [Google Scholar]
- 103.Van Essen DC. A tension-based theory of morphogenesis and compact wiring in the central nervous system. Nature. 1997;385(6614):313–8. doi: 10.1038/385313a0. [DOI] [PubMed] [Google Scholar]
- 104.Vannix RS, Joergenson EJ, Carter R. Kinking of Internal Carotid-Artery - Clinical Significance and Surgical Management. Am J Surg. 1977;134(1):82–89. doi: 10.1016/0002-9610(77)90288-4. [DOI] [PubMed] [Google Scholar]
- 105.Vorp DA, Peters DG, Webster MW. Gene expression is altered in perfused arterial segments exposed to cyclic flexure ex vivo. Ann Biomed Eng. 1999;27(3):366–71. doi: 10.1114/1.158. [DOI] [PubMed] [Google Scholar]
- 106.Wagenseil JE, Nerurkar NL, Knutsen RH, Okamoto RJ, Li DY, Mecham RP. Effects of elastin haploinsufficiency on the mechanical behavior of mouse arteries. Am J Physiol Heart Circ Physiol. 2005;289(3):H1209–17. doi: 10.1152/ajpheart.00046.2005. [DOI] [PubMed] [Google Scholar]
- 107.Waxman AM. Blood vessel growth as a problem in morphogenesis: a physical theory. Microvasc Res. 1981;22(1):32–42. doi: 10.1016/0026-2862(81)90109-6. [DOI] [PubMed] [Google Scholar]
- 108.Weibel J, Fields WS. Tortuosity, Coiling, and Kinking of the Internal Carotid Artery. I. Etiology and Radiographic Anatomy. Neurology. 1965;15:7–18. doi: 10.1212/wnl.15.1.7. [DOI] [PubMed] [Google Scholar]
- 109.Wiggs BR, Hrousis CA, Drazen JM, Kamm RD. On the mechanism of mucosal folding in normal and asthmatic airways. J Appl Physiol. 1997;83(6):1814–21. doi: 10.1152/jappl.1997.83.6.1814. [DOI] [PubMed] [Google Scholar]
- 110.Wong CH, Cui F, Tan BK, Liu Z, Lee HP, Lu C, Foo CL, Song C. Nonlinear finite element Simulations to elucidate the determinants of perforator patency in propeller flaps. Ann Plastic Surg. 2007;59(6):672–678. doi: 10.1097/SAP.0b013e31803df4e9. [DOI] [PubMed] [Google Scholar]
- 111.Wood NB, Zhao SZ, Zambanini A, Jackson M, Gedroyc W, Thom SA, Hughes AD, Xu XY. Curvature and tortuosity of the superficial femoral artery: a possible risk factor for peripheral arterial disease. J Appl Physiol. 2006;101(5):1412–8. doi: 10.1152/japplphysiol.00051.2006. [DOI] [PubMed] [Google Scholar]
- 112.Xiao Y, Zhao Y, Hayman D, Han HC. Arterial buckling promotes NF-κB activation associated with cell proliferation in porcine carotid arteries perfused ex vivo. Ann Meeting Biomed Eng Soc (BMES 2011); 2011; Hartford, CT. [Google Scholar]
- 113.Yang W, Fung TC, Chian KS, Chong CK. Three-dimensional finite element model of the two-layered oesophagus, including the effects of residual strains and buckling of mucosa. Proc Inst Mech Eng [H] 2007;221(4):417–26. doi: 10.1243/09544119JEIM47. [DOI] [PubMed] [Google Scholar]
- 114.Zheng T, Fan Y, Xiong Y, Jiang W, Deng X. Hemodynamic performance study on small diameter helical grafts. ASAIO J. 2009;55(3):192–9. doi: 10.1097/MAT.0b013e31819b34f2. [DOI] [PubMed] [Google Scholar]
- 115.Zubov LM, Sheidakov DN. Instability of a hollow elastic cylinder under tension, torsion, and inflation. J Appl Mech. 2008;75(1) [Google Scholar]


