Generating reservoir conformations for replica exchange through the use of the conformational space annealing method

Abstract

Temperature replica exchange molecular dynamics (T-REM) has been successfully used to improve the conformational search for model peptides and small proteins. However, for larger and more complicated systems, the use of T-REM is computationally intensive since the complexity of the free energy landscape and number of replicas required increase with system size. Achieving convergence of systems with slow transition kinetics is often difficult. Several methods have been proposed to overcome the size and convergence speed issues of standard T-REM. One of these is the Reservoir Replica Exchange Method (R-REM), in which the conformational search and temperature equilibration are separated by exchanging with a pre-existing reservoir of structures. This approach allows the integration of computationally efficient search algorithms with replica exchange. The Conformational Space Annealing (CSA) method has been shown to be able to determine the global energy minimum of proteins efficiently and has been used in structure prediction successfully. CSA uses a genetic algorithm to generate a diverse set of conformations to determine the minimum energy structure. We combine these methods by using conformations generated by the CSA method to build a reservoir. R-REM is then used to seed the top replica with the structures from the reservoir; fast convergence at every temperature is observed. The efficiency of this method is then demonstrated with model peptides and small proteins, and significant improvement of efficiency is observed while maintaining the overall shape of the free energy landscape.

Introduction

Conformational sampling is one of the most important challenges in simulating biologically relevant events in atomistic detail. Since the potential energy landscape for biological molecules is rugged, simulations tend to get trapped in local minima, which prohibits thorough exploration of the conformational space, even with accurate, state of the art force fields. Over the years, significant effort has been put into improving conformational sampling methods to overcome such traps and improve transitions between minima; these have been summarized in the recent review by Zuckerman.¹

Temperature replica exchange (T-REM),^2–4 where high temperatures are used to speed up conformational transitions while preserving the canonical ensemble, has become a popular method used to enhance sampling. In T-REM, multiple simulations (called replicas) of the system are conducted simultaneously at different temperatures. At regular intervals, exchanges between neighboring replicas are attempted, and at every successful attempt the structures are exchanged. This scheme allows the simulations at lower temperatures to exchange to higher temperatures where, with the added thermal kinetic energy, they will be able to overcame barriers, escape local minima and explore the free energy landscape. While low temperature replicas are heated to enhance the sampling, the high temperature replicas are cooled down to where they can explore the current minima they visit. When a T-REM simulation is converged, temperature dependent properties can be calculated since each replica will show the equilibrium properties corresponding to its assigned temperature.^5–9

Even though T-REM is very successful in enhancing conformational sampling, it still has some problems. It is not size extensive, meaning that as the number of degrees of freedom in the system increase, more replicas are required to cover the same temperature range. Added with the fact that a system with many degrees of freedom will have a more complex free energy landscape requiring more simulation time to reach convergence, the computational cost for larger and biologically more relevant systems often increases drastically. Another problem with T-REM is that while the high temperature replicas search for new conformations, the low temperature ones get stuck and oversample their current minima. Until proper sampling across all of the temperatures is achieved, none of the replicas represent a Boltzmann distribution and can be considered converged. In other words, at the beginning of the T-REM simulations during the search phase, the sampled states, especially at lower temperatures, are most likely to be trapped and should be ignored for analysis, which may mean that a large portion of the collected data may have to be discarded. Several improvements have been reported that overcome the increased computational cost of T-REM with large systems.^10–20

One of the enhanced replica methods is called the Reservoir Replica Exchange Method (R-REM).^15,16 The R-REM scheme separates the conformational search phase from thermal equilibration by performing an extensive conformational search that generates many structures representing all accessible local minima. These conformations are then collected in a structure reservoir and used to seed the REM simulation by having the highest temperature replica make “exchange” attempts with a random conformation from the reservoir. Upon a successful “exchange,” the selected reservoir conformation replaces the one from the highest temperature replica and the simulation resumes. R-REM assumes that the reservoir is completely converged and every possible minima is represented. Since the conformational search and the thermal reweighting are separated, the aforementioned oversampling problem at lower temperatures is eliminated. Coupled to a proper reservoir, the replicas quickly converge to their equilibrium values, reducing the computational cost. Initial tests with simple systems show a 5–20 fold increase in convergence speed over standard T-REM simulations.¹⁵

A key assumption of R-REM approach is that the sampling performed prior the REM step is completely converged and the structures in the reservoir represent a Boltzmann distribution, meaning that for each accessible minimum correct relative populations are needed at the reservoir temperature. In the original implementation of the R-REM, simple test cases were used so that achieving a “perfect” reservoir with conventional methods such as high temperature molecular dynamics were possible. For larger systems with many degrees of freedom and complex energy landscapes, it may be impossible to generate such a reservoir.

However, if the distribution of the reservoir is known, the exchange criterion between the reservoir and the highest temperature replica can be adjusted, eliminating the need to generate a Boltzmann weighed reservoir. This concept, called non-Boltzmann Reservoir Replica Exchange (nBR-REM),¹⁶ was introduced with a reservoir having a flat distribution (e.g. one representative conformation for each local minimum). The flat distribution was obtained via performing cluster analysis of the original reservoir and only selecting the representative conformations for each cluster. Using the modified exchange potential, the results were in excellent agreement with standard T-REM simulations while still showing the same enhanced convergence speed of R-REM.^15,16 The advantage of nBR-REM is that since only representative conformations are needed for each accessible minimum; it is possible to use many different and efficient methods for generating the reservoir. The reservoir generation and R-REM are independent from each other, allowing any enhanced and efficient sampling method to be used for conformational search.

Over the years many structure prediction methods have emerged and proven successful in blind prediction of native states in the Critical Assessment of Techniques for Protein Structure Prediction (CASP) experiments.^21,22 Shenoy and Jayaram summarize the advancements in structure prediction algorithms and describe the current state in their excellent review.²³ Many such methods perform extensive conformational search to identify the global energy minimum via physics and knowledge based potentials.

One of these methods is called Conformational Space Annealing (CSA),^24,25 where conformational search is performed by generating a set of trial conformations and using a genetic algorithm to modify and score them according to the energy function used. A distance metric is chosen to ensure that the search space is expanded at each cycle and different conformations are explored through the algorithm. Once the calculation is finished, the lowest energy structures are taken for further evaluation and prediction. The CSA method has been very successful in de novo structure prediction, and has been one of the most successful methods in recent CASP^21,22 competitions. The CSA method has also been implemented in finding lowest energy configurations of Lennard-Jones clusters,²⁶ off-lattice protein AB models,²⁷ molecular docking,²⁸ and multiple sequence alignment.²⁹ The CSA method has recently been implemented in the CHARMM³⁰ molecular simulation program.

The CSA method is mainly used for structure prediction purposes where only the lowest energy structures are selected for further analysis. However, the algorithm generates many structures representing conformations for local minima with higher energies than the global energy minimum. It is possible to direct the algorithm to generate a large enough set of structures to determine numerous minima on a complex energy landscape, which can be used as reservoir conformations. Since the structures are generated and ranked based on the potential energy function used, it is not straightforward to obtain free energies for each conformation. Through REM, it is possible to explore the energy landscape and calculate relative probabilities of each local minimum. The implementation of CSA in CHARMM enables the use of exactly the same parameters (force field, implicit solvent, same non-bond parameters etc.) with CSA and REM, ensuring that an identical Hamiltonian is used in reservoir generation and thermal reweighting.

In this study the CSA method implemented in CHARMM is used to generate structure reservoirs for simple model systems, which are used to run non-Boltzmann Replica Exchange (CSA-nBR-REM) simulations. The free energy profiles generated via CSA-nBR-REM are compared to standard T-REM. Simple model systems such as Alanine Tetrapeptite (Ala₃), Alanine-10 (Ala₁₀), and the Trpcage³¹ mini-protein are used to make sure that the available conformation space can be explored with traditional methods such as T-REM. Sampling qualities of each system are investigated by comparing free energy profiles generated by T-REM and R-REM on chosen reaction coordinates. Both alanine peptides are small and topologically simple enough that transitions between different conformations are relatively quick and obtaining converged simulations is straightforward even with conventional MD. For Ala₃ identical free energy profiles are obtained from T-REM and CSA-nBR-REM simulations using different reservoirs. For Ala₁₀, similar free energies are also obtained, although CSA-nBR-REM simulations have more coverage of higher energy minima and more transitions between each minima. Faster folding times and convergence between independent simulations are observed with Trpcage. These results are consistent with the observations previously reported on reservoir replica exchange methods.^15,16

Methods

Temperature Replica Exchange

Standard temperature replica exchange (T-REM) simulations for all model systems (Ala₃, Ala₁₀ and Trpcage) were performed to generate the benchmark results that were used to validate the CSA-nBR-REM scheme. In the T-REM simulations exchanges were attempted every 1000 molecular dynamics steps with a 1 fs timestep. For each system, the number of replicas and their temperatures were selected to ensure an ~20% exchange probability between neighboring replicas while covering a temperature range of 300–550K. Exchanges were attempted using the standard exchange criterion^3,4 (Equation 1), where $X_j^s$ represents conformation j at temperature s with energy E_j, and $X_k^t$ represents conformation k at temperature t and with energy E_k and β = 1/kT. The Langevin thermostat was used to maintain temperature with a collision frequency of 2 ps⁻¹ and SHAKE³² was used to constrain bonds involving hydrogen atoms. Each simulation was run with the CHARMM22³³ protein force field with CMAP corrections,³⁴ and the SCPISM³⁵ method was used to include the solvent effects implicitly. All replica exchange simulations were run with the distributed replica “REPDstr” functionality in CHARMM.³⁰

$$\frac{W(X_j^s,X_k^t\to X_j^t,X_k^s)}{W(X_k^s,X_j^t\to X_k^t,X_j^s)}=e^{({\beta }_t-{\beta }_s)(E_k-E_j)}$$ (1)

Conformational Space Annealing

Conformational Space Annealing (CSA), developed by Lee et. al.,^24,25 uses a genetic algorithm to perform the conformational search. At the beginning of the CSA process a random set of trial structures are generated, minimized, and ranked based on their potential energies. The bottom half of the conformations are kept, and the top half with higher energies are modified by changing dihedral angles. The distances D_ij between each pair of conformations are calculated by comparing dihedral angles and root mean square deviations, and if the distance is smaller than a cutoff value D_cut then the two conformations are assumed to be of the same family. At each iteration, the lowest energy members of each family are kept and the others are modified and again minimized. The value of D_cut is initially set to a large number and gradually reduced throughout the calculation; this has the effect of forcing the structures apart, which increases the structural diversity and overcome barriers. The algorithm finishes once each conformation generated can be classified as a unique family (i.e. for each conformation D_ij ≥ D_cut).

Reservoir generation via Conformational Space Annealing

The Conformational Space Annealing (CSA) method has been implemented in the CHARMM Molecular Modeling Program.³⁰ The same force field and implicit solvent models were used as in the T-REM simulations (CHARMM22/CMAP and SCPISM). All CSA calculations were started with nearly linear extended conformations. None of the final generated conformations retains the initial linear conformation. For the Alanine Tetrapeptide (Ala₃) system, we generated 64 and 256 conformations, for the Alanine-10 (Ala₁₀) system we generated 256 conformations, and for Trpcage we generated 1024 conformations to build the reservoirs.

The CSA method is very efficient in overcoming energy barriers regardless of their height. During the reservoir generation stage many conformations with incorrect chiralities and cis-trans isomerization on peptide bonds were observed, making validation against traditional methods impossible. Improper dihedral angle restraints were added to prevent chirality flips, and flat bottomed (180° ± 60°) harmonic dihedral restraints were used to keep the peptide bonds in their trans conformations and limit the CSA search space to that of T-REM. It is very important to restrict the conformational space of the CSA generated structures to those that are relevant to a particular study. The effects of having a reservoir with D-amino acids and cis-peptide bonds is explained in the discussion section.

Non-Boltzmann Reservoir Replica Exchange

Both the Boltzmann and non-Boltzmann reservoir replica exchange schemes have been implemented in the “REPDstr” module in CHARMM. CSA generates conformations representing different minima via the distance criterion used in the algorithm, corresponding to a flat distribution (1/N, N = Number of reservoir conformations) instead of a Boltzmann distribution. The results are one representative structure for each minimum found. This allows us to use the non-Boltzmann Reservoir Replica Exchange (nBR-REM) method exactly as it was described in Roitberg et. al.¹⁶

Because of the assumption of a flat reservoir distribution, 2 can be used as the exchange criterion. The exchanges depend solely on the potential energy differences between the replica and reservoir conformations. It should be noted that this equation is only valid when there is one structure per minimum in the reservoir. Any deviations from this assumption (such as duplicate conformations etc.) would lead to wrong population distributions at every temperature.

Even though the reservoir temperature does not appear explicitly in the nBR-REM exchange equation (Equation 2), where $X_j^R$ represents conformation j at reservoir R, the reservoir structures still have to be thermally equilibrated to obtain an accurate ΔE between the reservoir and highest temperature replica.

$$\frac{W(X_j^R,X_k^t\to X_j^t,X_k^R)}{W(X_k^R,X_j^t\to X_k^t,X_j^R)}=e^{{-\beta }_t(E_j-E_k)}$$ (2)

The CSA method produces minimized conformations, which have to be equilibrated to the correct reservoir temperature. Different equilibration schemes involving short MD runs at reservoir temperature using weak positional restraints were tried, but noticeable changes in the reservoir conformations were observed, causing a change in the energy-based ranking of structures compared to initial reservoir set. Therefore, we decided to skip the equilibration altogether and add $\frac{k_{B}T}{2}$ for each degree of freedom to the minimized CSA energies for each system. The number of degrees of freedom is calculated after all the simulation parameters such as SHAKE are defined, and the resulting energy correction factors are shown in Table 1.

Table 1.

Number of degrees of freedom and energy corrections for each simulated system with respect to reservoir temperatures.

System	Degrees of Freedom	Energy added (kcal/mol)
Ala3	104	41.33 (400K)
Ala10	279	117.81 (425K)
Trpcage	762	333.13 (440K)

Even though the energies are corrected to represent realistic values for the reservoir temperatures, the structures themselves are taken directly from CSA and are minimized. To ensure proper equilibration, different values of the Langevin collision frequency were investigated, it was seen that for frequencies above 2 ps⁻¹ identical potential energy histograms to standard T-REM simulations were obtained. Therefore, collision frequency of 2 ps⁻¹ was used for each T-REM and CSA-nBR-REM simulations.

The highest temperature replica of the nBR-REM simulations were run coupled to the CSA generated reservoirs using the exchange criterion described in Equation 2. All other exchanges between replicas use the standard exchange equation (Equation 1). As with T-REM, for each system two independent simulations with different initial conformations were run, where for alanine peptides simulations were started from all extended and all helical conformations and for Trpcage simulations were started from all extended and native conformations. The same simulation parameters used for the CSA were used during replica exchange runs. Exchanges between replicas were attempted every 1000 dynamics step.

Data analysis

Dihedral angles, end-to-end distances, radii of gyration and root mean square deviations (RMSD) were calculated using CHARMM’s “CORRel” functionality. End-to-end distances were calculated as the distance between C_α atoms of the first and last residue for each peptide. Ramachandran free energy lanscapes were constructed through 2-D histograms of dihedral angles using 5° by 5° windows. The window with the highest population (minimum free energy) was assigned a free energy of 0 kcal/mol and contour lines were drawn in 0.5 kcal/mol intervals. The end-to-end distance and radius of gyration data were divided into 100 bins between their minimum and maximum values, and again the bin with the highest population was assigned a free energy of 0 kcal/mol. The first 10000 snapshots of each simulation were discarded to eliminate starting structure bias. For Trpcage simulations, conformations were designated as native if their backbone RMSD was less than 2.5 Å with respect to the published structure (1L2Y.pdb³¹). All histograms and resulting free energies were calculated using the “numpy” module, and the free energy landscapes were plotted using the “matplotlib” module of Python version 2.6.5.

Results and Discussion

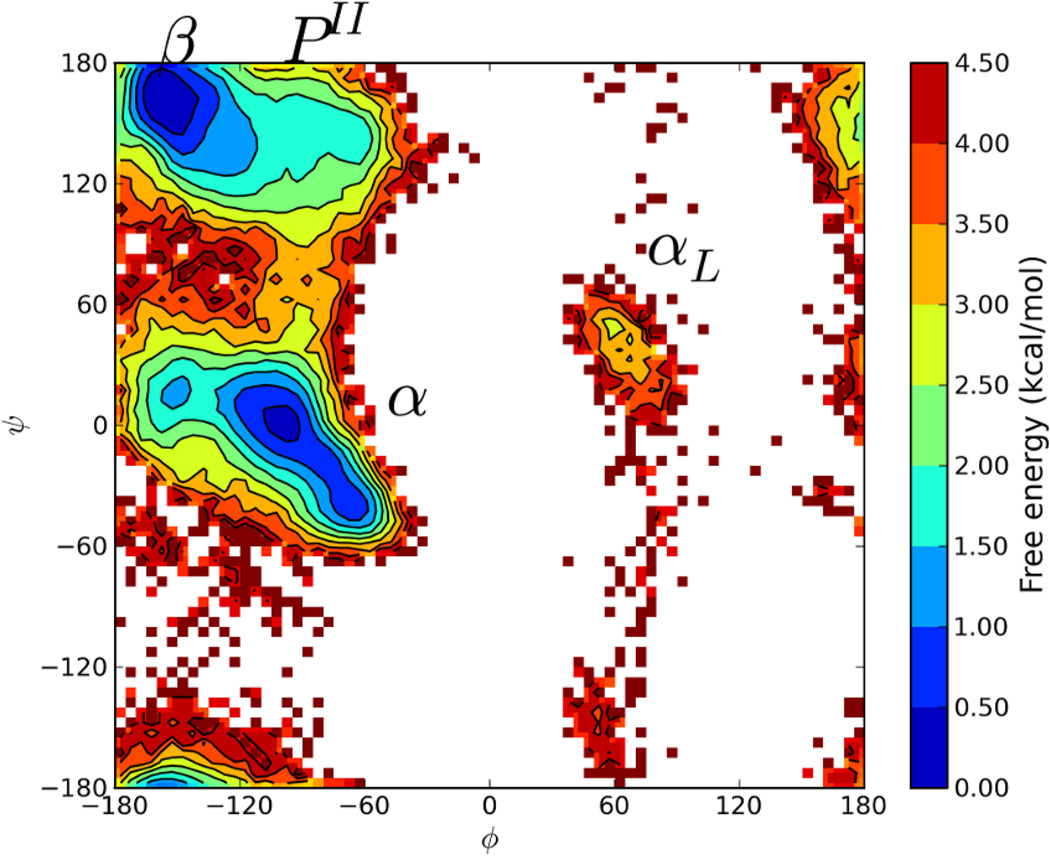
To test the applicability of a new enhanced sampling method, a simple enough system is needed that the accessible energy landscape can be explored through conventional methods such as MD or T-REM so that the new method can be compared against their results. Alanine tetrapeptide (Ala₃) is an established test system with few degrees of freedom, allowing such a comparison. To ensure full coverage of the accessible free energy landscape, standard T-REM simulations were run for 200000 exchange attempts (200 ns/replica) using 8 replicas where all replicas were started from the linear conformation. The Ramachandran free energy landscape of the dihedral angles of the central Alanine residue was constructed (Figure 1) at 300K, which will be the baseline for comparison. Multiple transitions between conformational regions were observed in every replica, suggesting that convergence in sampling was achieved for this residue.

Figure 1.

Ramachandran Free Energy profile for the central Alanine residue in Ala₃ from standard T-REM simulations at 300K. Major conformational regions are labeled.

As seen in Figure 1, good coverage for each secondary structure was observed since the free energy for α and β regions are within 0.5 kcal/mol with a 3.0–3.5 kcal/mol barrier between them. The Polyproline-II (P^II) region is about 1.5–2.0 kcal/mol higher than the α and β regions, and the left handed helix region (α_L), which is around 2.5–3.0 kcal/mol higher in free energy, has some coverage. For the nBR-REM simulations with a CSA generated reservoir, this plot will be used as a baseline and the free energies for each region and the barriers between them will be compared. When the same Hamiltonian is used for reservoir generation and R-REM, identical free energy profiles are expected if all minima are represented in the reservoir. Since Ala₃ is a small system, relatively few reservoir conformations should be needed to generate an accurate free energy profile. Two reservoirs, containing 64 and 256 structures respectively, were constructed via CSA to be used for nBR-REM simulations.

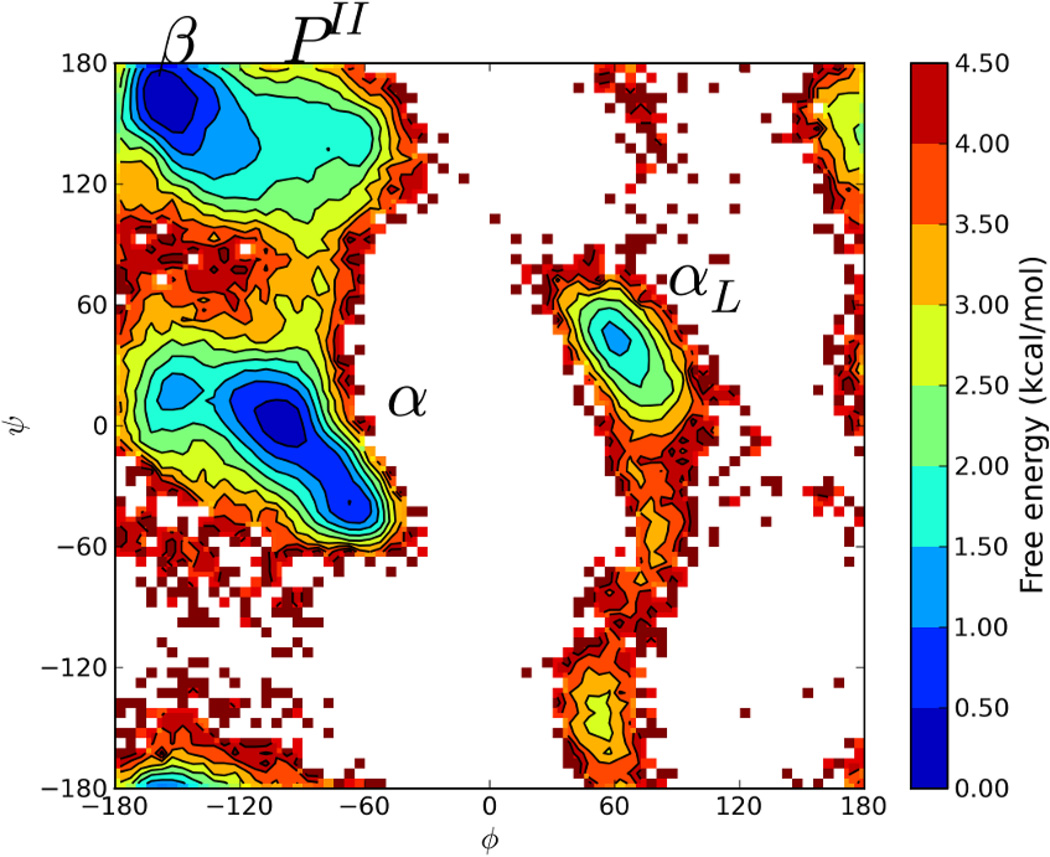
For both reservoirs (64 and 256 CSA generated structures), nBR-REM simulations were run for 200000 exchange attempts as in standard the T-REM simulations. The reservoir temperature was determined to be 400K, and 4 replicas were run under 400K, with the highest temperature replica (375K) attempting exchanges with the reservoir based on Equation 2. The resulting free energy profile for the nBR-REM run with 64 reservoir conformations for the central Ala residue at 300K is plotted in Figure 2.

Figure 2.

Ramachandran Free Energy Profile for central Alanine residue from CSA-nbR-REM simulations at 300K. Similar profile to T-REM for α, β and P^II regions. The α_L region has significantly more population compared to T-REM.

Figure 2 shows that the free energy profiles are similar between T-REM and CSA-nBR-REM simulations. Two major minima (the α and β conformations) are again within 0.5 kcal/mol with a 3.0–3.5 kcal/mol barrier separating them. The P^II region id about 1.5–2.0 kcal/mol higher than the α and β regions, which is in excellent agreement with T-REM. However, at the left handed helix region (α_L) has a much higher population and significantly lower free energy (0.5–1.0 kcal/mol) as compared to T-REM simulations (2.5–3.0 kcal/mol). The simulations using 256 reservoir structures have near identical results to those using a reservoir size of 64 (data not shown). Even though the R-REM approach increases the speed of conformational transitions, enabling transiently sampled states to get more coverage, such a drastic change in free energy is not expected. Upon careful analysis of the trajectories, uncommon conformations where peptides with incorrect chiralities and cis-conformations along peptide bonds were observed. These are high free energy barriers to cross even for enhanced techniques such as replica exchange, and further analysis revealed that such conformations were produced by the CSA algorithm and were present in the reservoir set. Using an enhanced algorithm is important for generating a low energy conformations quickly and efficiently, but it became apparent that the CSA method is very powerful in crossing such high barriers, resulting the presence of D-peptides and cis-peptides in the reservoir. While crossing both barriers is theoretically possible and there are naturally occurring cis-peptides,^36,37 it is highly unlikely that conventional methods such as T-REM would be able to sample such transitions. The presence of these “unusual” structures makes it nearly impossible to validate a new enhanced sampling approach against standard T-REM. The CSA method can efficiently overcome such high barriers and might be a good tool to investigate such transitions in future studies. An additional problem is that the force field used (CHARMM22+CMAP) is not optimized for D-peptides in that the CMAP term is dependent on specific chirality.

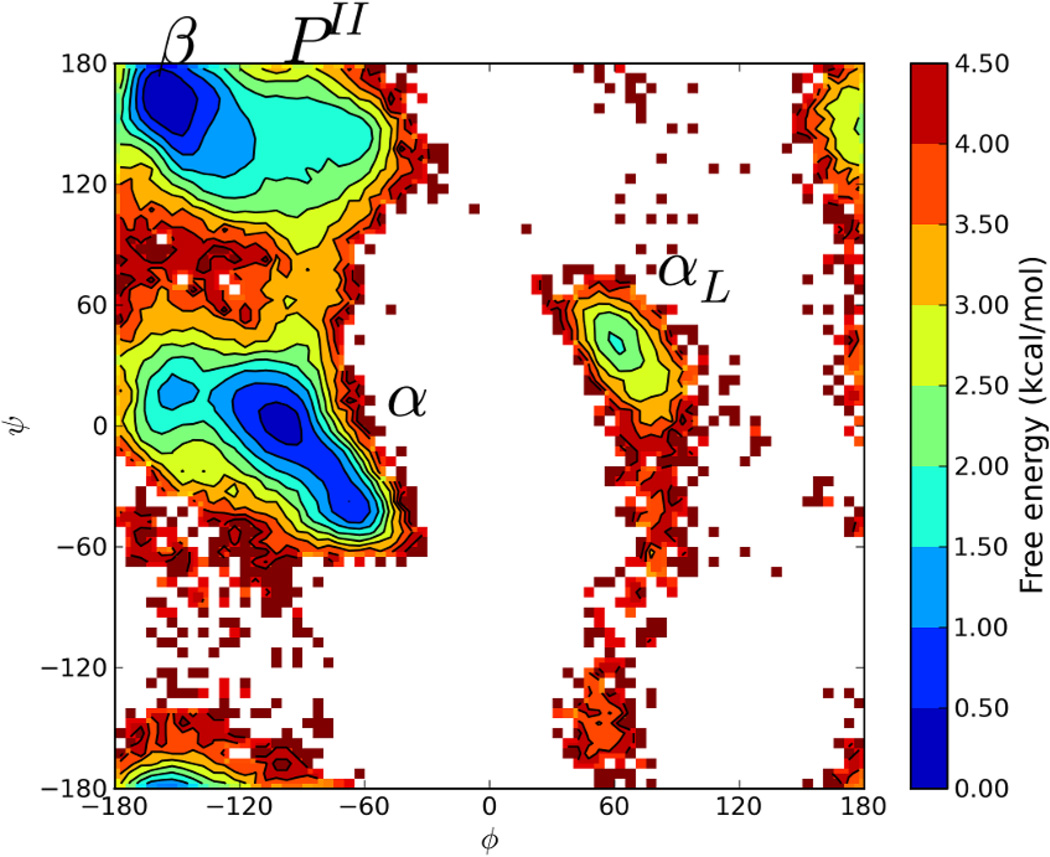
For this study, it was decided to focus the search space to MD accessible minima and to eliminate D-peptide and cis-peptide conformations. Therefore, improper dihedral angle restraints to prevent chirality flips and additional restraints to prevent cis-trans isomerisation around the peptide bond were added as described in the Methods section, and CSA calculations were repeated to generate new reservoirs (again containing 64 and 256 structures). A flat bottomed harmonic restraint function around the peptide bond was used to make sure that no additional energy was introduced while the peptide was in its correct trans conformation. Once new reservoirs were generated and all the reservoir conformations were checked to make sure that all residues had correct chiralities and trans peptide bonds, the nBR-REM simulations were repeated. The resulting free energy profile for the reservoir with 64 structures is shown in Figure 3.

Figure 3.

Ramachandran Free Energy Profile for the central Alanine residue from CSA-nbR-REM simulations with 64 reservoir conformations at 300K. The simulations were repeated with the newly generated reservoir containing no D- and cis-peptides. An almost identical free energy landscape as standard T-REM simulations were observed, however the α_L region has around 1 kcal/mol lower free energy.

Once a “proper” reservoir is generated, an almost identical free energy landscape as the benchmark T-REM simulations can be obtained. Once the efficient CSA algorithm is restricted to the accessible minima by T-REM, both methods show the same free energy values for each observed minimum and the same barriers between the α and β regions. However, even with a “correct” reservoir, the α_L region shows more population with a free energy about 1 kcal/mol lower than T-REM. The α_L region is separated by a large barrier from other regions with negative ϕ values, so it is possible that the use of CSA generated reservoir increased conformational transitions over this large barrier.

Ala₃ is a very small system with a limited number of degrees of freedom, and generating a reservoir for it with a method like CSA takes only a few minutes on a modern computer. Since the accessible free energy landscape is simple, Ala₃ simulations converge very quickly even with unenhanced molecular dynamics, making direct efficiency comparisons on convergence speed very difficult. However, since the reservoir generation is almost instantaneous and fewer replicas (4 instead of 8) were used for CSA-nBR-REM simulations, the computational cost was reduced by ~50% to generate data of the same quality.

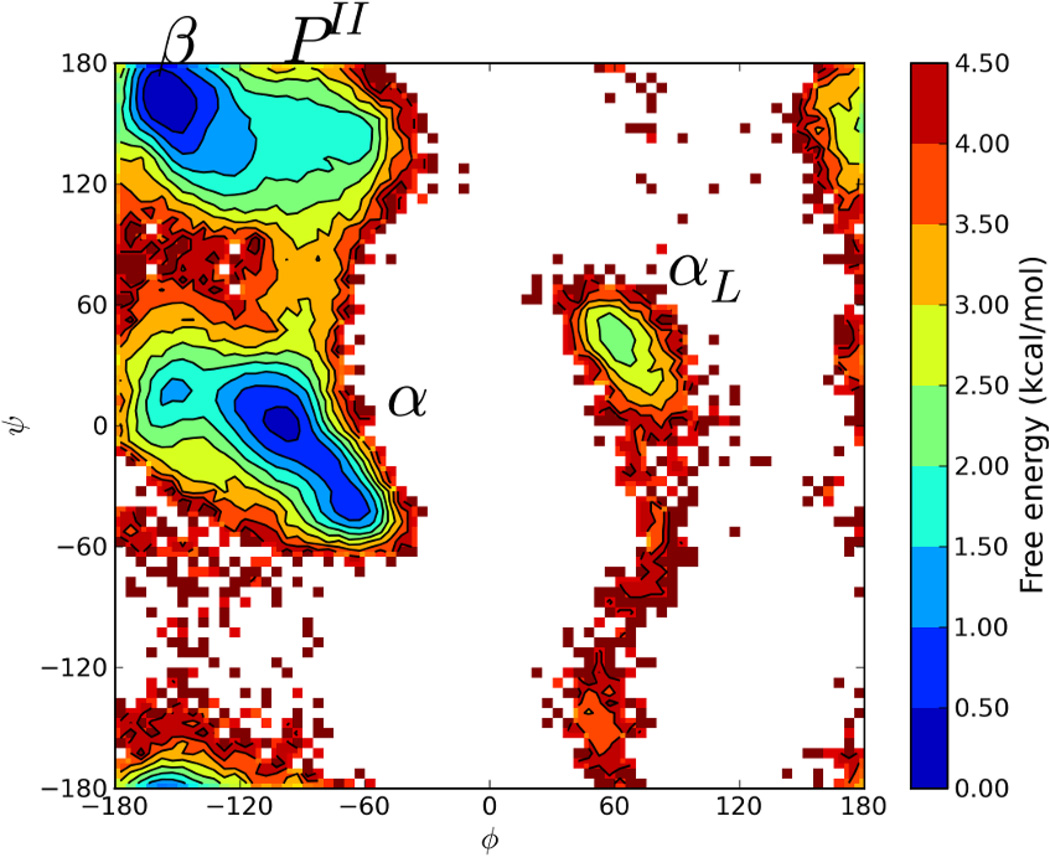
One other important variable to consider is the size of the reservoir. The main assumption of the reservoir replica exchange approach is that the reservoir contains representative conformations for every accessible minima. Not having enough structures in the reservoir could leave out important regions in the free energy landscape leading to skewed results. To test if a reservoir size of 64 structures was sufficient for Ala₃, the same calculations were repeated while using a new reservoir of 256 conformations. As before, the same restraints were applied during the CSA step to prevent chirality flips and cis-trans isomerizations. Figure 4 shows the free energy landscape, which is very similar to the T-REM and the CSA-nBR-REM simulations with 64 conformations, meaning that 64 CSA generated structures are enough to build a reservoir for a simple model system like Ala₃.

Figure 4.

Ramachandran Free Energy Profile for central Alanine residue from CSA-nbR-REM simulations. 256 CSA generated conformations were used as reservoir. Essentially identical free energy landscape as standard T-REM and CSA-nbR-REM simulations with a 64 structure reservoir were observed.

The consistency in results between R-REM simulations using reservoirs with 64 and 256 structures is expected since Ala₃ is a small system. The addition of extra conformations in CSA expands the search space, and more local minima with higher energies are found and reported. Table 2 shows the energies for the highest and lowest potential energy structures found by CSA. As seen from the table, both CSA calculations find the same global energy minimum. The larger calculation has an expanded search space, and as a result minima with higher energies were found. When used as reservoir conformations, these higher energy structures have very low probability to be selected (via Equation 2) when compared to the lower energy ones, and the overall free energy landscape at 300K is not affected. However, it should be noted that for larger and more complicated systems there will be many minima with similar energies and one should probably generate a reservoir as big as can be computationally afforded.

Table 2.

Energies of the minimum and maximum energy conformations for Ala₃ CSA calculations generating 64 and 256 structures. Both calculations find same energy minimum. A higher number of conformations expands the search space and minima corresponding to higher energy states are also found.

Number of CSA Generated Conformations	Emin (kcal/mol)	Emax (kcal/mol)
64	−265.19	−251.93
256	−265.19	−242.69

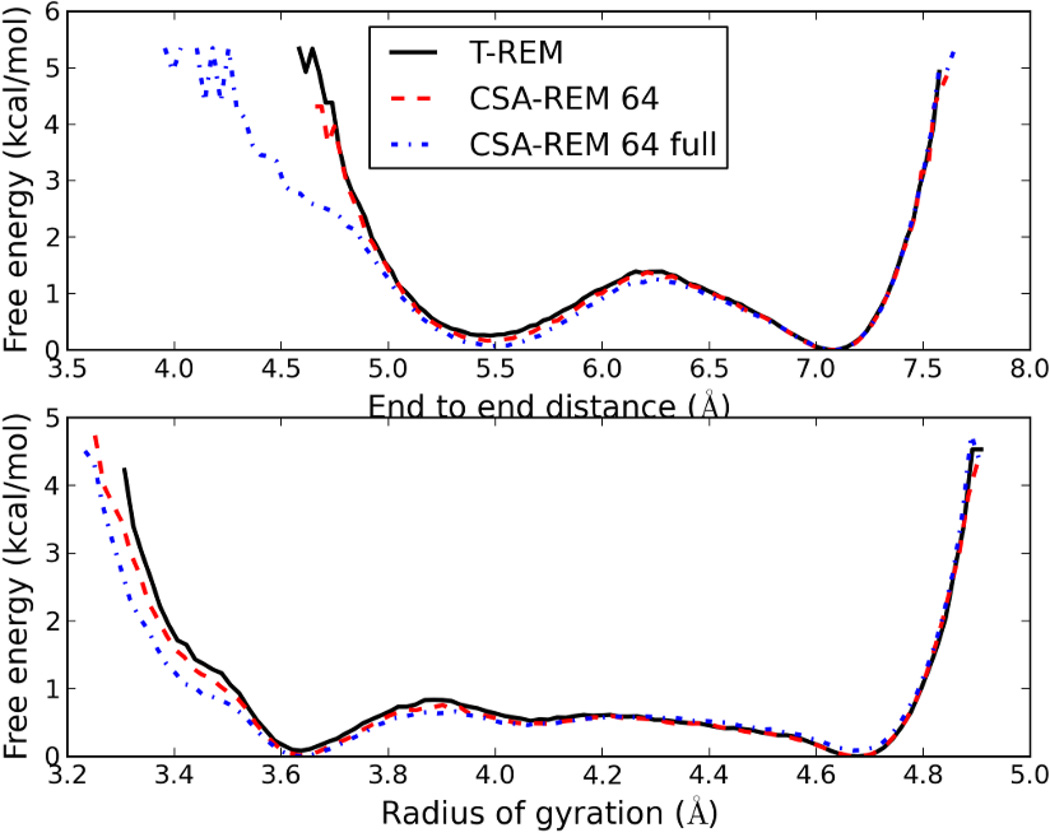
Up until this point dihedral angles of the central alanine residue have been used for comparing free energy profiles between T-REM and CSA-nBR-REM. Obtaining converged results for one residue is straightforward, and the resulting free energy landscapes can conveniently be used for comparison. However, when evaluating the accuracy of a model, more than one order parameter should be used for comparison to eliminate any potential bias. Therefore, the free energy profiles of two commonly used order parameters, end-to-end distance and radius of gyration, were also used for comparison. Both of these parameters take into account the whole system and can be assumed to represent global properties of the system. Figure 5 shows the comparisons of the free energy profiles for both parameters. As can be seen from the figure, when a reservoir containing representative conformations accessible via T-REM is generated, identical free energy profiles are observed. It is evident that when a full reservoir containing uncommon peptide conformations is used, the shape of the free energy profiles change significantly while maintaining the two minima. The addition of cis and D-peptides cause the presence of more compact conformations and lower free energies for structures with low end-to-end distances and radius of gyration.

Figure 5.

Free energy comparison for T-REM and CSA-REM simulations using end-to-end distances and radius of gyration. CSA-REM simulations using the new reservoir show identical behavior compared to standard T-REM. The simulations using the full reservoir containing cis-peptides and D-peptides still show same major minima, but explore compact conformations not observed in T-REM as well.

As mentioned before, Ala₃ is a simple system whose conformational space can be investigated easily via normal molecular dynamics. It is a great candidate for model validation and obtaining accurate results from it is a necessary test for each new method to pass. However, obtaining good Ala₃ results cannot be assumed to be conclusive, and further validation with larger systems having more complex and rugged energy landscapes is needed. Therefore, the CSA-nBR-REM calculations were repeated with Ala₁₀ using a reservoir with 256 conformations. As with Ala₃, improper dihedral restraints and restraints on the peptide bond were used to limit the search space. Like before CSA-nBR-REM simulations were run using 4 replicas, and the results were compared to standard T-REM simulations with 8 replicas. For Ala₁₀ 2 sets of simulations with different initial conformations (all linear and all helical) were run for T-REM and CSA-nBR-REM, each with 500000 exchange attempts. Instead of looking at dihedral angles of individual residues, radius of gyration and end-to-end distances were calculated and a 2-D free energy landscape was constructed. The free energy landscapes shown in Figure 6 are used for comparison.

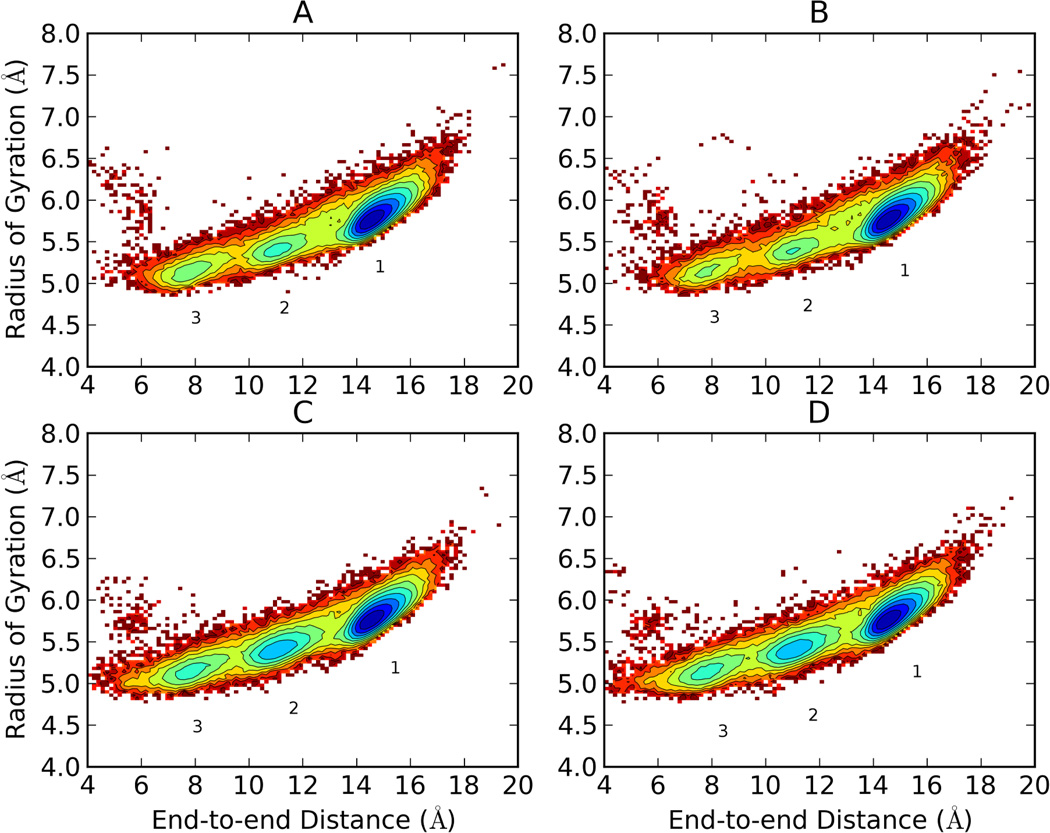
Figure 6.

Free energy landscapes of the 300K replica of Ala₁₀ via T-REM (starting from linear (A) and starting from helical (B) conformations) and CSA-nBR-REM (starting from linear (C) and starting from helical (D) conformations) simulations using radius of gyration and end-to-end distances as coordinates. Contour lines are drawn for every 0.5 kcal/mol. Three broad free energy minima were observed for both T-REM and CSA-nBR-REM simulations. The lowest energy conformation (1) has a uniform α-helical conformation. The other minima (2 and 3) still have many residues in helical form but with kinks and turns resulting in a more compact overall structure. There are more observed transitions between minima when CSA-nBR-REM is used.

As shown in Figure 6, Ala₁₀ has three distinct minima. The lowest free energy state (minimum 1) corresponds to a uniform α-helical conformation. The other minima, (2 and 3) with free energies of 1.5–2.0 kcal/mol and 2.0–2.5 kcal/mol, represent more compact but still helical conformations, with some kinks and more flexibility at the terminal residues. The two profiles obtained from independent T-REM simulations (Figure 6-A and B) with different initial starting structures show minor differences in the shape and depth of the minima 2 and 3. The same analysis with CSA-nBR-REM yields a free energy profile similar to T-REM (Figure 6-C and D).With this method the barriers between minima are lower, indicating faster transitions between them as compared to the T-REM simulations. The free energies for minima 2 and 3 seem to be about 0.5 kcal/mol lower than they are in the T-REM simulations. Even though CSA-nBR-REM simulations were started from two different initial starting structures, identical free energy profiles were observed since they are bound to the same reservoir.

Figure 6 shows the overall free energy profile for each simulation and that the three dominant minima are clearly separated. To get a better idea of the speed of conformational transitions and convergence, we calculated the relative free energies for all three minima by population for smaller portions of the trajectories. For each simulation, the trajectories at 300K were divided into 10 equal parts of 50000 frames each, and average relative free energies, standard deviations and the average number of barrier crossing events for each minima were calculated. The resulting free energy values are summarized in Table 3. As indicated by Figure 6, the T-REM simulations show slightly different free energies between each minima, with larger standard deviations compared to CSA-nBR-REM simulations. This suggests that 50000 exchange attempts may not be enough to obtain converged results with T-REM even for a simple system like Ala₁₀. CSA-nBR-REM simulations show almost identical free energies with small standard deviations between different parts of the trajectory, suggesting frequent barrier crossings and quick convergence. Comparing the number of barrier crossing events shows that on average using the CSA-nBR-REM method yields twice as many transitions as using T-REM.

Table 3.

Free energies and standard deviations for each observed minimum. The lowest free energy conformation (minimum 1) is selected as a reference. Averages and standard deviations for each run were calculated by dividing the 300K trajectory in 10 equal pieces (50000 frames each). CSA-nBR-REM simulations show more consistent free energy values between each run and lower free energies than T-REM, which suggests more frequent barrier crossings.

Method	Starting structure	Minimum 1	Minimum 2	Minimum 3	Number of barrier crossings
T-REM	Linear	0.0	1.83 (0.12)	2.32 (0.23)	2291.60 (366.53)
T-REM	Helical	0.0	1.70 (0.08)	2.13 (0.24)	2732.20 (264.84)
CSA-nBR-REM	Linear	0.0	1.13 (0.04)	1.63 (0.05)	5065.70 (191.83)
CSA-nBR-REM	Helical	0.0	1.13 (0.04)	1.64 (0.08)	4931.90 (215.15)

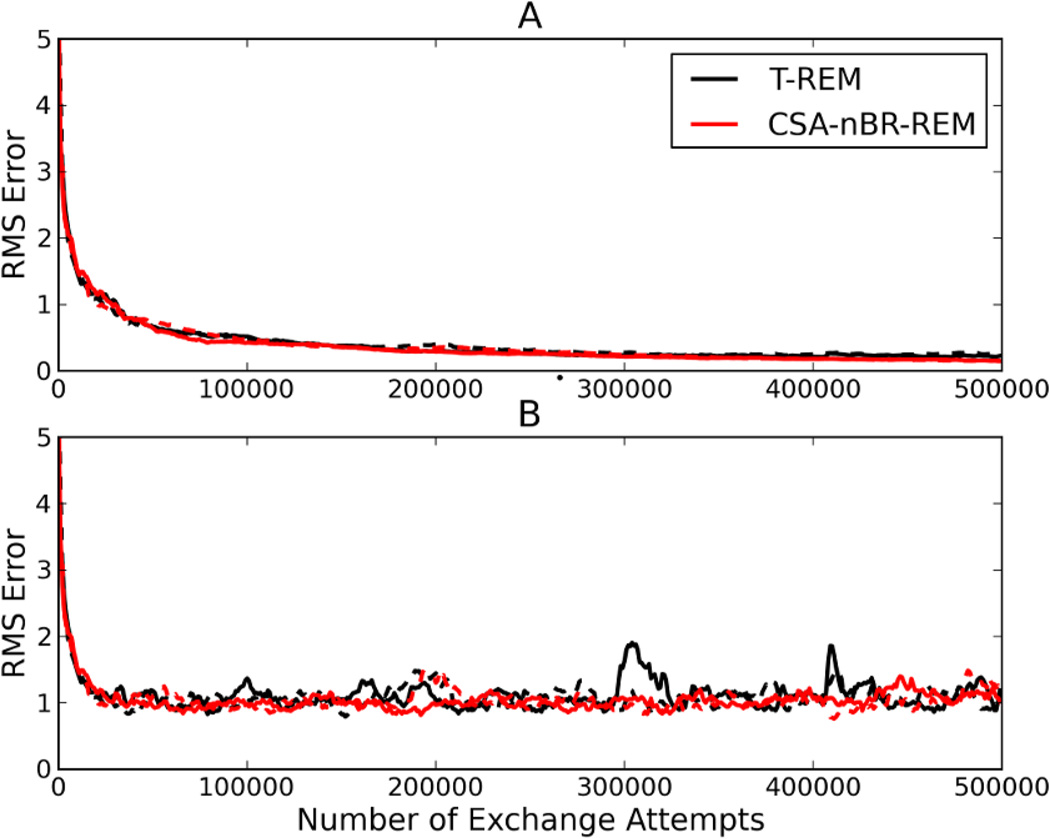
To investigate relative the convergence speeds of the T-REM and CSA-nBR-REM simulations further, the free energy histograms of all the simulations started from both conformations were compared every 250 exchange attempts. Each histogram was compared to the equilibrium histogram, generated by combining both of the T-REM simulations used to generate the free energy landscapes shown in Figure 6, and the resulting differences are plotted in Figure 7. By comparing the entire landscape, it is possible to show differences in the convergence speeds of higher energy states. However, Figure 7-A shows that both the T-REM and CSA-nBR-REM simulations converge to their final equilibrium values at similar rates. This is because the helical conformation has a much lower free energy, and therefore both methods sample it extensively at similar rates, which dominates the shape of the curve. Figure 7-A shows the average root mean square (RMS) error throughout the trajectory, which smooths out the local fluctuations. To make such fluctuations visible, running averages over 25000 exchanges are shown in Figure 7-B. This analysis yields similar conclusions, with the T-REM simulations having larger fluctuations. Since CSA-nBR-REM simulations cross barriers more frequently, any 25000 exchange section of the trajectory would give similar ensemble averages. These observations are consistent with the earlier studies of reservoir replica exchange methods.^15,16

Figure 7.

RMS Error with respect to simulation time for T-REM (black) and CSA-nBR-REM (red) simulations for Ala₁₀ starting from all helical (solid lines) and all linear (dashed lines) initial conformations. RMS errors are calculated by comparing histograms at each 250 ps window with the equilibrium histogram used to construct the free energy landscapes in Figure 6. The overall error (A) and the running average error over 25000 exchange attempts (B) are shown for both simulations.

Ala₁₀ has a simple topology with three well defined free energy minima. When using an enhanced sampling method like T-REM, the peptide quickly folds to the helical structure, even when starting from the all extended conformation. However, when the overall free energy landscape is investigated, T-REM shows differences in populations of the other minima having higher free energy even after 500000 exchange attempts (500ns per replica). This is seen in Figure 6, where minima 2 and 3 have slightly different shapes and in Table 3, where minima 2 and 3 have slightly different free energies and standard deviations. When a reservoir generated via CSA is used, all minima are populated quickly and many transitions between minima are observed.

The Ala₁₀ results clearly indicate that the combination of CSA and reservoir REX is a very effective strategy for crossing free energy barriers. To test this on a more realistic system, we used CSA-nBR-REM on the Trpcage³¹ mini-protein. Trpcage has 20 amino acid residues with a more diverse set of side chains than alanine polypeptides, and it has been studied extensively experimentally and computationally.^38–49 Because of the increased system size and number of degrees of freedom, it was necessary to generate 1024 conformations via CSA to find the native conformation, employing the same type of chiral and dihedral restraints as before. These conformations were used as a reservoir at a temperature of 440K. 6 replicas were run under the reservoir temperature for 100000 exchange attempts (100ns/replica). As before, reservoir results were compared to standard T-REM simulations using 8 replicas. Two sets of simulations were run for each method, starting from the native and fully extended conformations.

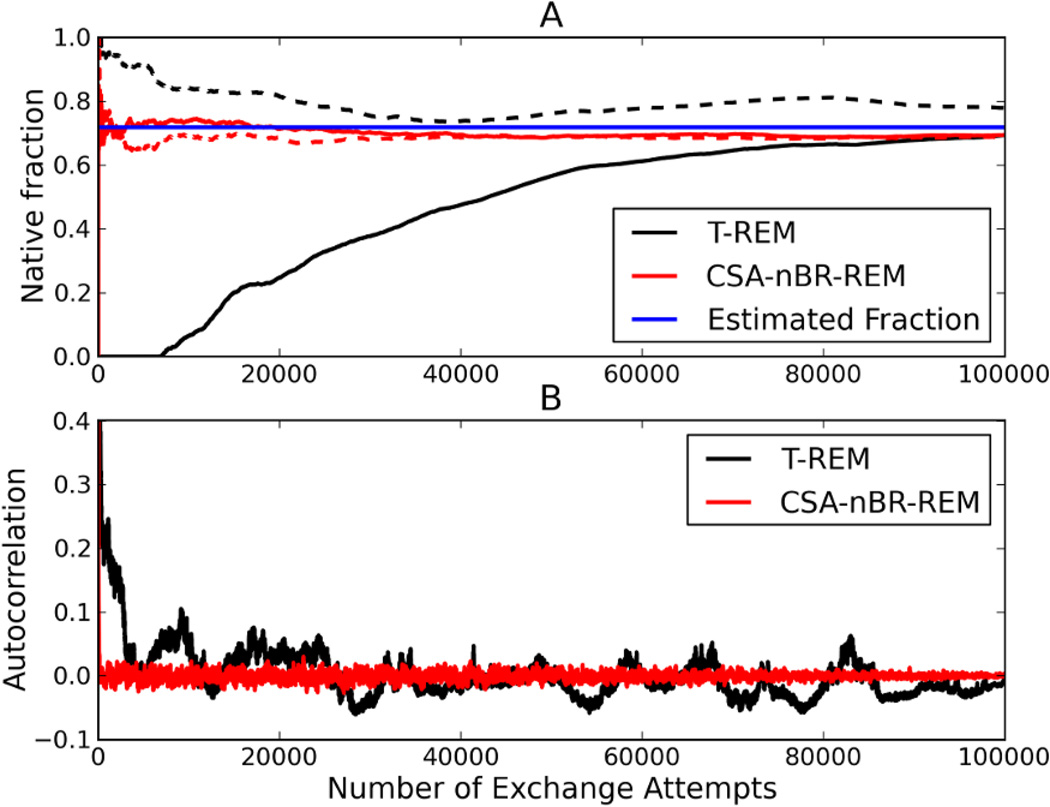
Trpcage is a relatively large system, and T-REM simulations of 100ns/replica are not sufficient to fully explore the free energy landscape, but it is possible to make qualitative observations comparing the populations of the lowest energy states. Figure 8-A shows the fractional population of the native state conformation throughout the simulations, showing that the T-REM simulations slowly converge towards each other. The simulation starting from the linear conformation finds and starts populating the native conformation after around 10000 exchange attempts. The CSA-nBR-REM simulations almost immediately find the native state and both simulations reach their equilibrium native populations within first few thousand exchange attempts and retain them. The end-to-end distance autocorrelations (Figure 8-B) show a similar picture, in which the T-REM trajectories slowly converge towards their equilibrium value. As expected, instant equilibration with CSA-nBR-REM was observed.

Figure 8.

Fraction Native (A) vs. number of exchange attempts for Trpcage. Black curves show the evolution of the native population via T-REM simulations and red curves show CSA-nBR-REM simulations. For both methods, solid lines are simulations starting from linear conformation and the dashed lines are those starting from native conformation. The blue line represents the average native population calculated after first the 25000 exchanges were dropped from both linear and native T-REM simulations. The end-to-end distance autocorrelation is also shown in (B) where the black curve is obtained from T-REM and the red curve is from CSA-nBR-REM simulations both starting from linear conformation.

As seen in Figure 8 the T-REM simulations start to show similar populations for the native conformation after 100000 exchange attempts. Using 8 replicas, it took about 3000 CPU hours per starting conformation to generate this data, resulting in 6000 CPU hours of total computer time. We needed about 1350 CPU hours to generate the 1024 reservoir conformations with CSA. Even though we ran the CSA-nBR-REM simulations to 100000 exchange attempts for better comparison with T-REM, the simulations converged in under 10000 exchange attempts. The cost for running 6 replicas for 10000 attempts is about 250 CPU hours per simulation per starting conformationm resulting in 500 CPU hours. The total computer time spent by CSA-nBR-REM scheme is about 1850 CPU hours to obtain converged data, making it more than 3 times more efficient than T-REM.

Conclusions

Obtaining converged sampling for biomolecular simulations at atomic detail is still a formidable problem. While there are advanced methods available, many of them rely on changing the Hamiltonian during sampling. In most cases equilibrium properties can be back calculated, however errors can be introduced during the sampling and reweighting steps. We have introduced an enhanced method combining two of the most powerful sampling methods, Conformational Space Annealing and Reservoir Replica Exchange, and obtain identical sampling to standard methods on model peptides. Since both the CSA and R-REM methods use the same Hamiltonian during reservoir generation and replica exchange, no additional energy terms or forces are introduced, meaning that no extra reweighting and correction steps are necessary. Once a large enough reservoir is generated, containing representative conformations for each accessible minimum, the replica exchange step quickly yields correct populations for each minimum.

CSA is a very powerful tool for conformational search and finding the global energy minimum as well as for generating structures corresponding to many local minima. While having minimum energy structures is extremely useful, especially in structure prediction, there is no direct and efficient way of calculating free energies via CSA. By using the CSA generated conformations as a reservoir for replica exchange simulations, free energy profiles for systems of interest can be calculated quickly and a much clearer overall picture of the relationships between various minima can be obtained. We have tested this approach with small model peptides where we compared resulting free energy profiles to those generated via conventional methods, obtaining effectively identical results. Simulations on a larger system showed significantly increased sampling efficiency through the combining CSA and R-REM.

The combination of CSA and R-REM is very powerful in exploring conformational space and should be a valuable tool in investigating peptide and protein folding at all atom resolution. However, except for small systems such as Alanine polypeptides or Trpcage, current all-atom force fields, solvation models, and other parameters may not be fully adequate for such a task yet. Furthermore, it should be noted that the overall free energy landscape strongly depends on the sampling quality of the CSA calculations. The user should be very careful interpreting the results. For larger systems as many conformations as the user can computationally afford should be generated to minimize errors. If enough structures are generated to capture all relevant minima, CSA-nBR-REM can very efficiently estimate the free energies of each. If used carefully such an efficient method can help in developing and testing new force field parameters or other simulation methods.

Even though no additional energy terms are used for the CSA-nBR-REM scheme, it still relies on the very important assumption that the reservoir sampling is complete and all the conformations visited during the replica exchange can be classified as part of one of the structure families already present in the reservoir. There is always the possibility that the reservoir may have multiple conformations for one minimum or have implausible structures such as cis-peptides, introducing bias towards a particular state. Ideally we would like to devise an adaptive R-REM scheme allowing the reservoir to expand if new structures are discovered during the replica exchange stage. Such a scheme would be able to converge to the true distribution in the long time limit and correct potential errors introduced by the initial reservoir. We have developed a transition state based method called the Molecular Dynamics Meta Simulator (MDMS) model to develop such schemes in an efficient way.⁵⁰ We will be investigating different reservoir generation schemes and other tools for R-REM methods in the future.