IQ-Motif Proteins Influence Intracellular Free Ca²⁺ in Hippocampal Neurons Through Their Interactions With Calmodulin

Abstract

Calmodulin (CaM) is most recognized for its role in activating Ca²⁺–CaM-dependent enzymes following increased intracellular Ca²⁺. However, CaM’s high intracellular concentration indicates CaM has the potential to play a significant role as a Ca²⁺ buffer. Neurogranin (Ng) is a small neuronal IQ-motif–containing protein that accelerates Ca²⁺ dissociation from CaM. In cells that contain high concentrations of both Ng and CaM, like CA1 pyramidal neurons, we hypothesize that the accelerated Ca²⁺ dissociation from CaM by Ng decreases the buffering capacity of CaM and thereby shapes the transient dynamics of intracellular free Ca²⁺. We examined this hypothesis using a mathematical model constructed on the known biochemistry of Ng and confirmed the simulation results with Ca²⁺ imaging data in the literature. In a single-compartment model that contains no Ca²⁺ extrusion mechanism, Ng increased the steady-state free Ca²⁺. However, in the presence of a Ca²⁺ extrusion mechanism, Ng accelerated the decay rate of free Ca²⁺ through its ability to increase the Ca²⁺ dissociation from CaM, which in turn becomes subject to Ca²⁺ extrusion. Interestingly, PEP-19, another neuronal IQ-motif protein that accelerates both Ca²⁺ association and dissociation from CaM, appears to have the opposite impact than that of Ng on free Ca²⁺. As such, Ng may regulate, in addition to the Ca²⁺–CaM-dependent process, Ca²⁺-sensitive enzymes by influencing the buffering capacity of CaM and subsequently free Ca²⁺ levels. We examined the relative impact of these Ng-induced effects in the induction of synaptic plasticity.

INTRODUCTION

Synaptic spines are small compartments (~1 μm in diameter) connected to the dendrites of a neuron through a thin shaft (~0.1 μM) (Nimchinsky et al. 2002). One proposed functional role of spine architecture is to biochemically isolate the compartment from the dendrite and vice versa, permitting each spine to serve as independent functional units relative to intracellular Ca²⁺ (Majewska et al. 2000; Nimchinsky et al. 2002; Sabatini et al. 2002; Yang et al. 1999). In hippocampal CA1 pyramidal neurons, the elevation of Ca²⁺ in the postsynaptic spine results in the induction of synaptic plasticity, e.g., long-term potentiation (LTP) and long-term depression (LTD). More specifically, the amplitude, duration, and temporal profile of local Ca²⁺ signals in the spine are important determinants of the selective induction of either LTP or LTD (Yang et al. 1999). However, the factors that control local Ca²⁺ in the spine under physiological conditions, such as Ca²⁺ influx dynamics (by ion channels), Ca²⁺ buffers, and Ca²⁺ extrusion mechanism, are largely unknown (Majewska et al. 2000; Sabatini et al. 2002; Scheuss et al. 2006).

Calmodulin (CaM) is a key regulator of the Ca²⁺ signaling system of the postsynaptic spine important for LTP and LTD induction (Malenka et al. 1989; Xia and Storm 2005). Besides its role as a signal transduction molecule, CaM also functions as a ubiquitous endogenous Ca²⁺ buffer in neurons (Baimbridge et al. 1992). Interestingly, most CA1 pyramidal neurons contain CaM but not other EF-hand Ca²⁺-binding proteins (e.g., parvalbumin and calretinin; reviewed in Bainbridge et al. 1992). An exception is calbindin-D28K, which is expressed in a subpopulation of CA1 pyramidal neurons but only in rat (Guadano-Ferraz et al. 2005; Singec et al. 2004). The function of CaM as a buffer is frequently overlooked but a review of experimental evidence reinforces that CaM is a primary Ca²⁺ buffer in CA1 pyramidal neurons. The concentration of total (soluble and membrane bound) CaM in hippocampal neurons is 0.25–0.67% of the total protein (Kakiuchi et al. 1982; Klee and Vanaman 1982; Popov et al. 1988). This corresponds to about 37–100 μM of CaM (assuming the protein content is 0.25 g/ml cell volume as in Huang et al. 2004). CaM binds four Ca²⁺ ions: two Ca²⁺ ions bind in a cooperative fashion to each lobe (Babu et al. 1985; Gaertner et al. 2004; Putkey et al. 2003). Therefore CaM equips hippocampal neurons with about 148–400 μM of Ca²⁺-binding sites. Using this information, one can calculate a Ca²⁺ buffering capacity (κ_E) of about 32–87 (see Ca²⁺ buffering capacity and Ng in METHODS). This value exceeds the (endogenous) Ca²⁺ buffering capacity estimated in the small dendrites and spine (κ_E ~ 20) (Sabatini et al. 2002) and is close to or slightly lower than the buffering capacity in the proximal apical dendrite (κ_E ~ 44–80) of CA1 pyramidal neurons (Helmchen et al. 1996; Lee et al. 2000a; Maravall et al. 2000). Furthermore, the diffusion coefficient of CaM in neurites is about 2–20 μm²/s (Kim et al. 2006), which is close to the estimated diffusion coefficients (~10–50 μm²/s) of the dominant endogenous Ca²⁺ buffer at excitatory hippocampal synapses (Murthy et al. 2000). These data strongly suggest that CaM is a primary, albeit not the only, endogenous Ca²⁺ buffer in dendritic spines of CA1 pyramidal neurons.

If CaM plays a significant role as an endogenous Ca²⁺ buffer, then proteins that bind CaM and tune CaM’s Ca²⁺-binding kinetics must have an impact on the local Ca²⁺ dynamics. Neurogranin (Ng) is such a protein and its effect on the Ca²⁺-binding kinetics of CaM was recently identified (Gaertner 2004; Gaertner et al. 2004; Putkey et al. 2003). Neurogranin (Ng) and a related protein, PEP-19, are members of the IQ-motif family of CaM-binding proteins that interact with apo-CaM and Ca²⁺–CaM. Both proteins appear to specifically affect Ca²⁺ binding to the C-terminal lobe of CaM, with no apparent effect on Ca²⁺ binding to the N-terminal lobe. Ng is a 78 amino acid neuronal protein highly enriched in the postsynaptic spines of CA1 pyramidal neurons (minimally ~65 μM) (Huang et al. 2004). On binding, Ng accelerates the dissociation of Ca²⁺ from the C-lobe of CaM (Gaertner et al. 2004). Ng may well play a significant role in the local Ca²⁺ handling in the spine by controlling the Ca²⁺-binding capacity of CaM (Gerendasy 1999; Gerendasy et al. 1994; Huang et al. 2004; Krucker et al. 2002; van Dalen et al. 2003). As mentioned, calbindin-D28K, another major EF-hand family Ca²⁺-binding protein, is not expressed in most excitatory neurons in the hippocampal CA1 region (Guadano-Ferraz et al. 2005; Singec et al. 2004) and Ng and calbindin-D28K do not colocalize in CA1 pyramidal cells (Guadano-Ferraz et al. 2005). Because Ng’s only known biochemical function is binding CaM, this observation leads to the core hypothesis of the present work: Ng will control the Ca²⁺ buffering capacity and Ca²⁺ transient dynamics by its interactions with CaM in CA1 pyramidal neurons.

Here we use a simple but realistic mathematical model constructed on experimental data of Ca²⁺–CaM–Ng and Ca²⁺–CaM–PEP-19 interactions and investigate kinetic mechanisms through which these IQ-motif proteins regulate the steady-state level and the temporal profiles of intracellular free Ca²⁺. The paper is organized as follows. We first describe an experimentally constrained mathematical model of Ca²⁺–CaM–Ng interactions (see Mathematical model in METHODS, Fig. 1, and Table 1). We also introduce a simple single-compartment model of Ca²⁺ dynamics with or without Ca²⁺ injection and extrusion mechanisms (see Compartment model of spine Ca²⁺ dynamics in METHODS and Fig. 2). In Ca²⁺ buffering capacity and Ng (METHODS) and Fig. 3, we calculate the buffering capacity of CaM and explain the mechanistic principle through which Ng influences the Ca²⁺ buffering capacity. We then use a kinetic model to dissect the mechanism by which IQ-motif proteins control the steady-state level of free Ca²⁺ concentration (Fig. 4 and Table 1 for the parameter values). Using the simple single-compartment model with Ca²⁺ injection and extrusion mechanisms, we study how Ng regulates the temporal profile of free Ca²⁺ during oscillatory Ca²⁺ stimulations (Fig. 5). We also include results using a mutant Ng (PEP-19–like protein) to understand the kinetic mechanism by which Ng controls the free Ca²⁺ transient. These simulation results demonstrate that both association and dissociation pathways of Ca²⁺ from CaM influence the temporal dynamics of free Ca²⁺. In particular, the model shows that PEP-19–like protein produces an impact that is significantly different from that of Ng on the intracellular free Ca²⁺ dynamics (Fig. 6). Our analysis indicates Ng has the potential to shape the intracellular Ca²⁺ profile in neurons through its effects on the Ca²⁺-binding properties of CaM.

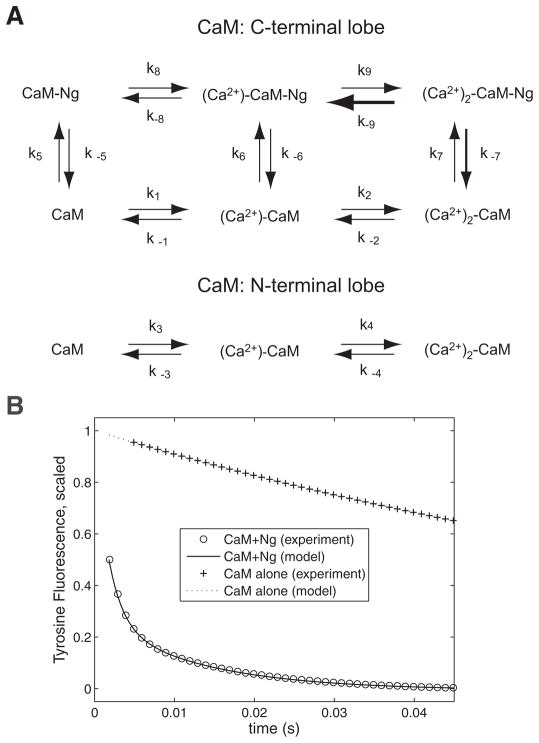
FIG. 1.

Mathematical model. A: reaction scheme of the neurogranin–calmodulin (Ng–CaM) interactions. C-terminal lobe and N-terminal lobe of CaM bind 2 Ca²⁺ ions (horizontal arrows). We assume the binding of Ca²⁺ to each lobe is relatively independent (C-lobe: top; N-lobe: bottom). Ng interacts with and binds the C-domain of CaM and accelerates Ca²⁺ dissociation from it (thick horizontal arrow in top panel). There is presently no experimental result indicating that Ng binds to or affects Ca²⁺-binding to the N-lobe of CaM. Therefore we assume no binding of Ng to the N-terminal lobe (i.e., no vertical arrows in bottom panel). Each arrow in the figure is marked by symbols, k₁, k₋₁, k₂, k₋₂, k₃, k₋₃, k₄, k₋₄, k₅, k₋₅, k₆, k₋₆, k₇, k₋₇, k₈, k₋₈, k₉, and k₋₉, which we also use to indicate the corresponding reaction rate. Positive number subscript indicates a binding reaction, whereas the negative number subscript is for a dissociation reaction (Table 1). Units of reaction rates are μM⁻¹ · s⁻¹ for association and s⁻¹ for dissociation rate constants, respectively. B: parameter optimization of the model for Ng-induced Ca²⁺ dissociation from CaM shown in A. Experimental data shown were accomplished by rapidly mixing CaM (2 μM) and Ca²⁺ (100 μM) with (black open circles) or without (black plus signs) 50 μM of Ng, with 5 mM EGTA and the Tyr fluorescence signal from CaM was measured as an indication of Ca²⁺ dissociation specifically from the C-terminal lobe. See Gaertner et al. (2004) for more details. Results shown are from the ordinary differential equation (ODE) model using the parameter values listed in Table 1. Solid and dotted lines are simulations with 50 and 0 μM of Ng, respectively. Note, data shown from each experiment are from 5 stopped-flow injections, averaged, and then fit with single- or double-exponential curves. Relative error of the final model as compared with the “fitted curve” is <0.5% and they are virtually indistinguishable. For this reason, we chose to plot the “fitted curve” as circle/crosses (at discrete time points) and overlay them with the simulation results (solid/dotted lines). Ca²⁺-binding kinetics of EGTA used in the simulation were as follows: EGTA binds Ca²⁺ with a 1:1 stoichiometry and the Ca²⁺ association and dissociation rates are 55.8 μM⁻¹ × s⁻¹ and 2.12 s⁻¹, respectively (Schuhmeier et al. 2003).

TABLE 1.

Parameters used in the model for Ng and PEP-19–like protein

Parameter	Symbol	Ng	PEP-19	Unit
C-lobe of CaM
Ca2+ binding to CaM	k1	426	426	μM−1 · s−1
	k2	21	21	μM−1 · s−1
Ca2+ binding to CaM–Ng	k8	426	426	μM−1 · s−1
	k9	21.5	630	μM−1 · s−1
Ca2+ dissociation from CaM	k −1	5,115	5,115	s−1
	k −2	8.5	8.5	s−1
Ca2+ dissociation from CaM–Ng	k −8	5,830	5,115	s−1
	k −9	418	255	s−1
Ng binding to apo-CaM	k5	28	28	μM−1 · s−1
Ng binding to (Ca2+)-CaM	k6	23	28	μM−1 · s−1
Ng binding to (Ca2+)2-CaM	k7	2	28	μM−1 · s−1
Ng dissociation from apo-CaM	k −5	36	36	s−1
Ng dissociation from (Ca2+)-CaM	k −6	35	36	s−1
Ng dissociation from (Ca2+)2-CaM	k −7	136	36	s−1
N-lobe of CaM
Ca2+ binding to CaM	k3	500	500	μM−1 · s−1
	k4	500	500	μM−1 · s−1
Ca2+ dissociation from CaM	k −3	16,000	16,000	s−1
	k −4	2,000	2,000	s−1

N-terminal kinetic rates are not affected by IQ-motif proteins. Symbols for each kinetic rate are indicated in Fig. 1A.

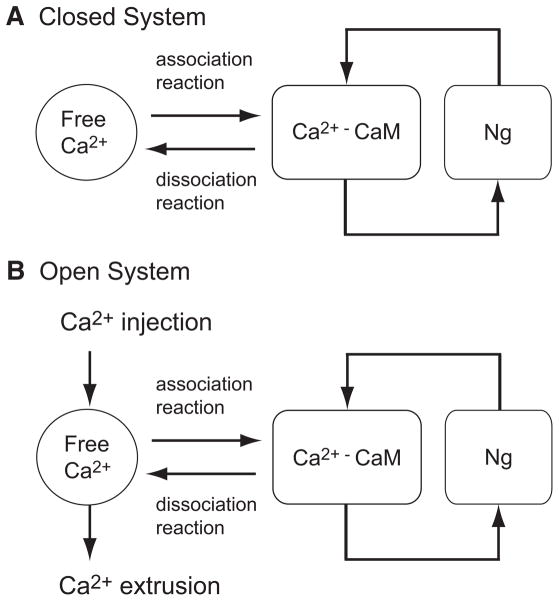
FIG. 2.

Single-compartment model of the Ca²⁺, CaM, and Ng system. A: closed system has no Ca²⁺ injection or extrusion pathways. B: open system with Ca²⁺ injection and extrusion mechanisms. Ca²⁺ injection was modeled by an N-methyl-D-aspartate (NMDA) receptor like Ca²⁺ channel found in the postsynaptic spine of hippocampal CA1 pyramidal neurons. We model extrusion as a simple Ca²⁺ decay term.

FIG. 3.

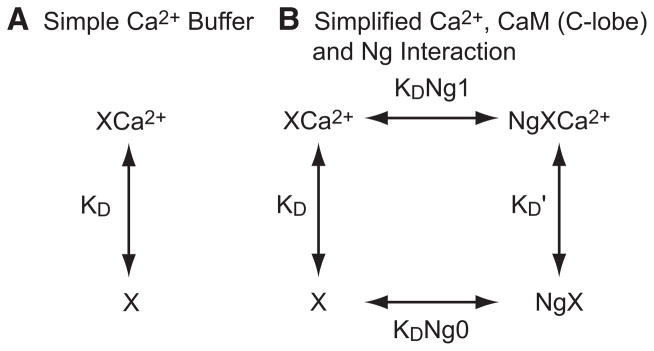
Modulation of Ca²⁺ buffering by Ng. A: Ca²⁺-binding protein X alone or (B) with interacting Ng. B: XCa²⁺, Ng · X, and Ng · XCa²⁺ represent Ca²⁺-bound buffer X, Ng–X complex (Ca²⁺ free), and Ng–Ca²⁺–X complex, respectively. Ng binds both apo- and Ca²⁺-bound buffer X with different dissociation constants K_DNg1 and K_DNg0 (μ M), respectively. Ca²⁺ dissociation constant of X and Ng· X are K_D and K′_D (μM), respectively. Free Ca²⁺ and free Ng are omitted for the purpose of illustration.

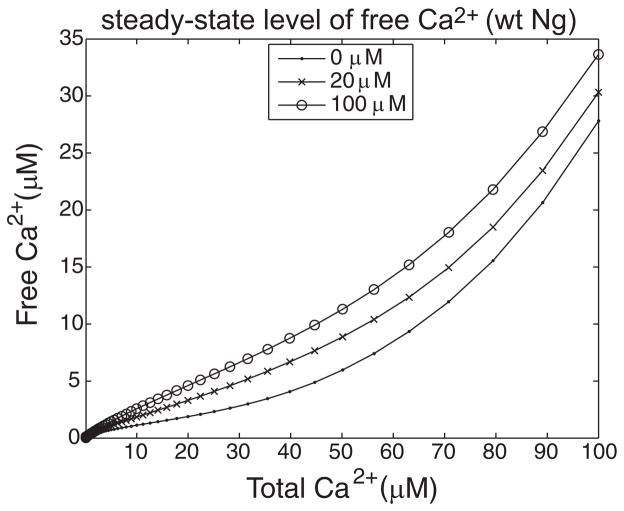
FIG. 4.

Ng increases the steady-state level of free Ca²⁺ concentration. 20 μM CaM and 0 μM (dots), 20 μM (crosses) and 100 μM (open circles) of Ng were mixed in the presence of varying concentrations of Ca²⁺ (x-axis, 0.1–100 μM). Steady-state level of free Ca²⁺ was plotted against the total Ca²⁺ in the simulation (CaM bound or free). Accelerated Ca²⁺ dissociation from CaM induced by Ng resulted in an increased steady-state level of free Ca²⁺. Increasing Ng concentration led to increased amounts of free Ca²⁺. This effect of Ng, however, becomes saturated for Ng ≳ 100 μM (data not shown).

FIG. 5.

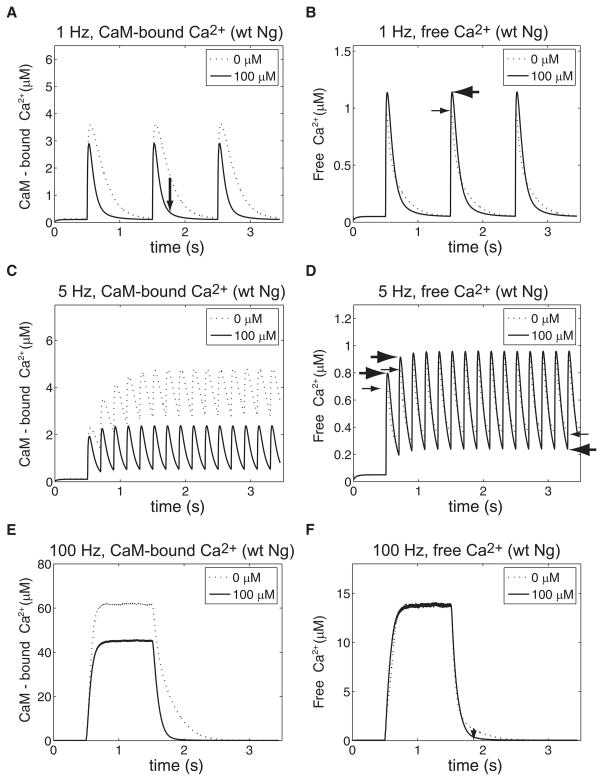
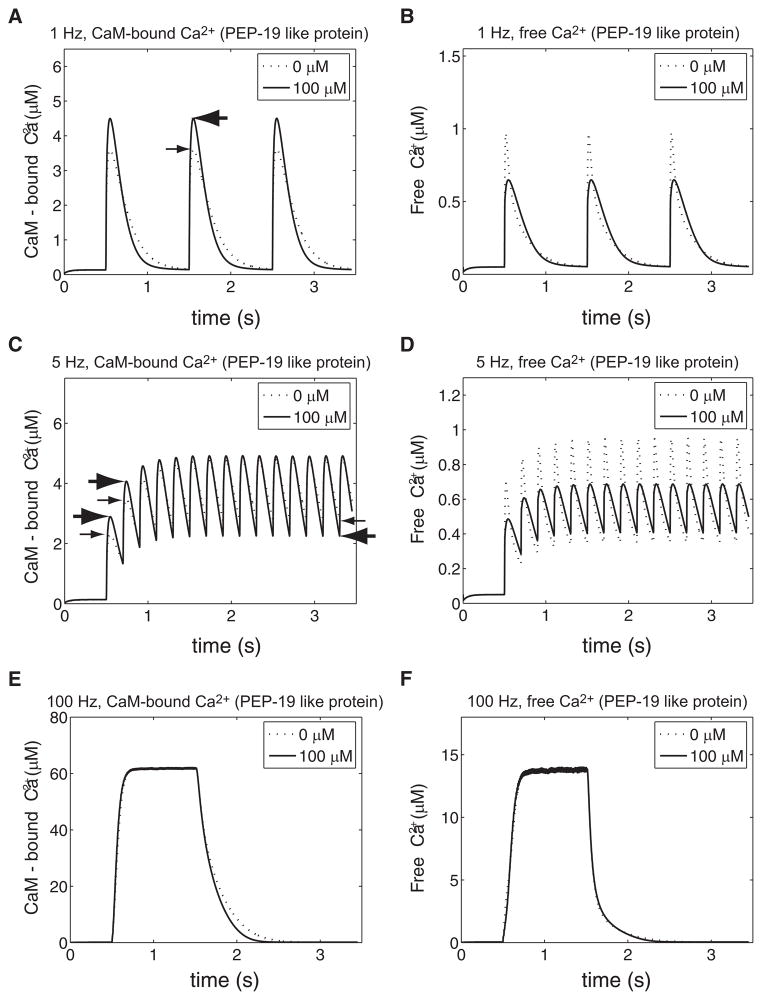
Free Ca²⁺ and CaM-bound Ca²⁺ dynamics driven by oscillatory Ca²⁺ injections of different frequencies. 20 μM of CaM and 100 μM (solid line) or 0 μM (dotted line) of wild-type Ng were included in the single-compartment model of postsynaptic spine Ca²⁺ dynamics (see Compartment model of spine Ca²⁺ dynamics in METHODS; see Fig. 2B). Ca²⁺ ions were introduced to the compartment by NMDA-receptor–like current injections at the identified frequencies [1 Hz (A and B), 5 Hz (C and D), and 100 Hz (E and F)]. Temporal evolutions of the CaM-bound Ca²⁺ (A, C, and E) and free Ca²⁺ (B, D, and F) are shown. CaM-bound Ca²⁺ here also includes the CaM–Ng–Ca²⁺ triple complex.

FIG. 6.

Free Ca²⁺ and CaM-bound Ca²⁺ dynamics driven by oscillatory Ca²⁺ injections of different frequencies in the presence of PEP-19 (like protein). 20 μM of apo-CaM and 100 μM (solid line) or 0 μM (dotted line) of PEP-19 (like protein) were included in the single-compartment model of postsynaptic spine Ca²⁺ dynamics (Fig. 2B). Ca²⁺ ions were introduced to the compartment by NMDA-receptor–like current injections at 1 Hz (A and B), 5 Hz (C and D), and 100 Hz (E and F). Temporal evolutions of the CaM-bound Ca²⁺ (A, C, and E) and free Ca²⁺ (B, D, and F) are shown. CaM-bound Ca²⁺ here also includes CaM–PEP-19 (like protein)–Ca²⁺ triple complex. Note the dotted lines in Fig. 6 are identical to those of Fig. 5 (without Ng).

Finally, we compare the model predictions with two genetic knockout studies of Ng (Gerendasy et al. 1994; Huang et al. 2004; Krucker et al. 2002; van Dalen et al. 2003). The free Ca²⁺ dynamics measured in neurons from these two genetic strains of mice and the model predictions from our work are all in agreement. The present modeling work indicates Ng increases the peak or rising phase of free Ca²⁺ concentrations, whereas it reduces the peak of Ca²⁺–CaM activation (Fig. 5). We evaluate the outcome of these seemingly opposite impacts of Ng on the induction of synaptic plasticity and the results identify that Ng may function as a key regulator of synaptic metaplasticity.

METHODS

Mathematical model

CaM is a bilobed molecule that has two Ca²⁺-binding sites within each lobe and Ng interaction with CaM was shown experimentally to increase the rate of Ca²⁺ dissociation from the sites in the C-terminal lobe (Gaertner et al. 2004). Figure 1A shows how this kinetic mechanism is modeled. Each lobe of Ng-free CaM has three different states dependent on the number of bound Ca²⁺ ions: (apo)-CaM, (Ca²⁺)-CaM, and (Ca²⁺)₂-CaM (horizontal arrows in Fig. 1A). Ng binds each of these three states of the C-lobe of CaM with different affinities (vertical arrows in the top diagram of Fig. 1A). Ng changes CaM’s affinity toward Ca²⁺ by increasing the dissociation rate (k₋₉, the thick horizontal arrow in the C-lobe kinetic pathway; Fig. 1A) but it does not change the Ca²⁺ association rate (Gaertner et al. 2004). We assume Ng affects only the C-lobe of CaM, as supported by present experimental evidence (Gaertner et al. 2004; Putkey et al. 2003). Thus each CaM molecule undergoes transitions between 18 (6 × 3) activation states involving association and dissociation of Ca²⁺ and Ng (6 different states for the C-terminal lobe and 3 for N-lobe). We constructed an ordinary differential equation (ODE)–type model based on this kinetic scheme.

The parameter values were optimized for experimental data in a systematic manner. The kinetic parameters for Ca²⁺–CaM interaction (k₁, k₋₁, k₂, k₋₂, k₃, k₋₃, k₄ and k₋₄ in Fig. 1A) were determined from experimental data (Gaertner et al. 2004). For Ng, the following data are available: the forward and backward reaction rates of 1) apo-CaM binding to Ng and 2) Ca²⁺ association to and dissociation from CaM in the presence of Ng. All parameter values are constrained by microscopic reversibility and this thermodynamic principle helped reduce the number of unknown parameters. Because Ng did not change the Ca²⁺ association rates, we were left with four unknown parameters (k₋₈, k₋₉, k₆, and k₇ in Fig. 1A). The rates k₋₆ and k₋₇ were calculated from microscopic reversibility. We used a brute force stochastic parameter search from a slate of 10⁸ different parameter sets followed by nonlinear least-square methods (e.g., Levenberg–Marquardt and trust region method implemented in the MATLAB Optimization Toolbox, The MathWorks). The final 100 candidate parameter values were tested against experimental data and the best parameter set was chosen (Table 1). Figure 1B illustrates the goodness of fit of the model (solid and dashed line) with experimental data of EGTA-induced Ca²⁺ dissociation from CaM (circles and squares) with or without Ng. Note that the experimental data shown in Fig. 1B generate the double-exponential curve fit to the average of five stopped-flow injections collected at room temperature (see Gaertner et al. 2004). All parameter optimizations were accomplished by using “fitted curves” from the raw data.

Compartment model of spine Ca²⁺ dynamics

The resultant ODE model from the previous section is a closed system. There is no Ca²⁺ injection or Ca²⁺ extrusion mechanism (Fig. 2A). Ca²⁺ is removed from the free Ca²⁺ pool by the association reaction (i.e., CaM binding) and increased through the dissociation reaction. Note the total amount of Ca²⁺ in the system remains constant. The ODE equation for the free Ca²⁺ is

$$\frac{\text{d}[{Ca}^{2+}]}{\text{d}t}=-(\mathit{association}\mathit{reaction})+(\mathit{dissociation}\mathit{reaction})$$ (1)

in which Ca²⁺ association reaction removes free Ca²⁺ and the free Ca²⁺ increases when Ca²⁺ dissociates from proteins.

On the other hand, the Ca²⁺–CaM–Ng dynamics in a postsynaptic spine (=nonequilibrium system), may be significantly different from that in a closed system. A model of Ca²⁺–CaM–Ng interaction that contains Ca²⁺ injection and Ca²⁺ extrusion mechanisms is required. However, the spine Ca²⁺ dynamics is a dauntingly complex process involving a large number of channels, pumps, and signaling molecules and we do not intend to model all of these processes. In particular, CaM interacts with channels and pumps and modulates their function (Liang et al. 2003; Penniston and Enyedi 1998). How and to what extent Ng influences CaM–pump and CaM–channel interaction is still unknown. For these reasons, we constructed a simple model of spine Ca²⁺ dynamics for the purposes of this study (Fig. 2B) similar to that used previously (Cai et al. 2006; Shouval et al. 2002). In this model, a single compartment of homogeneous spine Ca²⁺ dynamics was formulated under two assumptions. First, the primary Ca²⁺ source is through N-methyl-D-aspartate (NMDA) receptors. The kinetics of NMDA current is characterized by a double exponential of the form

$$I_{\mathit{NMDA}}(t)=G_{\mathit{NMDA}}\left[I_f\theta (t)exp\left(-\frac{t}{{\tau }_f}\right)+(1-I_f)\theta (t)exp\left(-\frac{t}{{\tau }_s}\right)\right]B(V)(V-V_r)$$ (2)

where t is time and V ≡ V(t) is the (time-varying) postsynaptic membrane potential. The voltage dependence of NMDA channels is described by B(V) (Jahr and Stevens 1990; Shouval et al. 2002), and parameters used are I_f = 0.7, τ_f = 0.032 s, and τ_s = 0.16 s (fast and slow time constants) (Cai et al. 2006), with approximate calcium reversal potential V_r = 130 mV and a conductance G_NMDA that was defined in Shouval et al. (2002). θ(t) = 1 when t ≥ 0; otherwise θ(t) = 0. Second, the Ca²⁺ dynamics is modeled by a single first-order ODE

$$\frac{\text{d}[{Ca}^{2+}]}{\text{d}t}=I_{\mathit{NMDA}}(t)-\frac{[{Ca}^{2+}]}{{\tau }_{Ca}}$$ (3)

with the time constant τ_Ca = 0.02–0.05 s (Majewska et al. 2000; Sabatini et al. 2002; Scheuss et al. 2006). In Fig. 2B, we use a modified version of this single-compartment model. First, we use the same Ca²⁺ injection mechanism (Eq. 2) as Shouval et al. (2002). As stated, Shouval et al. (2002) collapsed all Ca²⁺ extrusion processes, which include Ca²⁺ buffers, Ca²⁺ pumps, and diffusion-dependent escape of Ca²⁺ ions, into a single empirical decay term (the second term on the right-hand side of Eq. 3). Combining this single-compartment model with our Ca²⁺–CaM–Ng ODE model requires a careful adjustment of the Ca²⁺ decay term because CaM is a major endogenous Ca²⁺ buffer of the spine. We decided to use τ_Ca = 0.015 s as our decay time constant so that the overall Ca²⁺ decay profile of the model becomes consistent with experimental measurement (Majewska et al. 2000; Sabatini et al. 2002; Scheuss et al. 2006). The resultant equation for the free Ca²⁺ is

$$\frac{\text{d}[{Ca}^{2+}]}{\text{d}t}=I_{\mathit{NMDA}}(t)-\frac{[{Ca}^{2+}]}{{\tau }_{Ca}}-(\mathit{association}\mathit{reaction})+(\mathit{dissociation}\mathit{reaction})$$ (4)

The first and second terms on the right side of Eq. 4 correspond to Ca²⁺ injection and Ca²⁺ extrusion, respectively (vertical arrows, Fig. 2B). Once fixed, these parameter values were unchanged throughout all simulation experiments. The steady-state free Ca²⁺ concentration (Fig. 3) was calculated by running a long simulation and/or by numerical bifurcation analysis (e.g., XPP-Auto and MATCONT) (Dhooge et al. 2003; Ermentrout 2002). All methods converge to the same steady-state value.

Ca²⁺ buffering capacity and Ng

How does the Ca²⁺ buffering capacity of CaM influence transient dynamics of free Ca²⁺ and to what extent does Ng modulate free Ca²⁺ transients through interacting with CaM? Numerical simulation is the most accurate way to address these questions; however, simple mathematical formulas will be useful to gain insight and understand the qualitative influence that Ng and CaM have on free Ca²⁺ transients. As in the classical theory of Ca²⁺ buffering (Neher and Augustine 1992), we assume Ca²⁺ equilibrates with an endogenous Ca²⁺-binding protein X much faster than the rest of the Ca²⁺ dynamics, such as Ca²⁺ extrusion. Here we introduce the Ca²⁺ buffering capacity (κ_E, unitless) of endogenous buffer X (Neher and Augustine 1992)

$${\kappa }_{\text{E}}\equiv \frac{\partial [{\mathit{XCa}}^{2+}]}{\partial [{Ca}^{2+}]}=\frac{[X_T]K_{\text{D}}}{{([{Ca}^{2+}]+K_{\text{D}})}^2}$$ (5)

where [X_T] is the total concentration (μM) of endogenous buffer, [XCa²⁺] is the concentration of Ca²⁺ bound buffer (μM) and K_D is the dissociation constant (μM) and [XCa²⁺] ≡ [X_T] · [Ca²⁺]/([Ca²⁺] + K_D) (Fig. 3A). In other words, the buffering capacity (k_E) is the ratio of the change in [XCa²⁺] and the change in free Ca²⁺ concentration

$$\frac{\text{d}[{\mathit{XCa}}^{2+}]}{\text{d}t}\approx {\kappa }_{\text{E}}\frac{\text{d}[{Ca}^{2+}]}{\text{d}t}$$ (6)

If X is the only Ca²⁺-binding protein in the system, we replace the last two terms in Eq. 4 [i.e., − (association reaction) + (dissociation reaction)] with [−(d[XCa²⁺]/dt)] and rearrange the equation to obtain

$$\begin{array}{c}\frac{\text{d}[{Ca}^{2+}]}{\text{d}t}=\frac{1}{\beta }\left[I_{\mathit{NMDA}}(t)-\frac{{Ca}^{2+}}{{\tau }_{Ca}}\right]\\ \beta =1+{\kappa }_{\text{E}}\end{array}$$ (7)

Here we approximate the buffering capacity as a constant within the dynamic range of Ca²⁺ signals. If we have more than one, say N number of, Ca²⁺ buffers (or Ca²⁺-binding sites), we replace β = 1 + κ_E with $\beta =1+{\sum }_{i=1}^N{k}_{Ei}$ in Eq. 7, a linear sum of buffering capacity for all Ca²⁺-binding proteins (or binding sites) (see Eq. 13 for cooperative Ca²⁺ binding).

Equation 7 can be solved and we have

$$[{Ca}^{2+}]=\frac{1}{\beta }{\int }_0^t\text{d}{sI}_{\mathit{NMDA}}(s)exp\left[\frac{-(t-s)}{\beta {\tau }_{Ca}}\right]+{[C{a}^{2+}]}_0$$ (8)

where [Ca²⁺]₀ is the basal Ca²⁺ concentration (at time t = 0). Equation 8 is a key formula describing the effect of buffering capacity (κ_E in β =1 + κ_E) on the Ca²⁺ transient for a given Ca²⁺ injection [e.g.,I_NMDA(t)]. For the simplicity of the theory, the NMDA current defined in Eq. 2 can be approximated by a double-exponential function

$$I_{\mathit{NMDA}}(t)\approx Q_{f}exp\left(-\frac{t}{{\tau }_f}\right)+Q_{s}exp\left(-\frac{t}{{\tau }_s}\right)$$ (9)

where Q_f and Q_s represent the amplitude of the fast and slow components of NMDA currents and τ_f and τ_s are the corresponding time constants, respectively. By plugging this equation in Eq. 9, the [Ca²⁺] transient is

$$[C{a}^{2+}]=\frac{Q_f}{(\beta /{\tau }_f)-(1/{\tau }_{Ca})}\left[exp\left(-\frac{t}{\beta {\tau }_{Ca}}\right)-exp\left(-\frac{t}{{\tau }_f}\right)\right]+\frac{Q_s}{(\beta /{\tau }_s)-(1/{\tau }_{Ca})}\left[exp\left(-\frac{t}{\beta {\tau }_{Ca}}\right)-exp\left(-\frac{t}{{\tau }_f}\right)\right]+{[C{a}^{2+}]}_0$$ (10)

The resultant Ca²⁺ transient has three decay time constants, one of which depends linearly on the buffering capacity (κ_E) as β = 1 + κ_E. The peak amplitude of the Ca²⁺ transient is inversely proportional to the linear function of the buffering capacity as well. This equation suggests higher buffering capacity leads to lower peak amplitude and slower decay rate of the free Ca²⁺ transient.

What is the effect of Ng? What will Eq. 8 or Eq. 10 look like if we add Ng? As explained in Fig. 1, the interaction of Ng and CaM (C-lobe) is complicated. Intuitively, the decrease in Ca²⁺ affinity of CaM in the presence of Ng implies Ng also decreases the Ca²⁺ buffering capacity of CaM. To explain this mechanism, we use a simplified kinetic scheme to derive a mathematical formula (Fig. 3B). Here we can think of Ca²⁺ buffer X as the Ca²⁺-binding sites in the C-lobe of CaM. Ng binds this buffer X in the presence and absence of Ca²⁺ but with dissociation constants K_DNg1 and K_DNg0 (μM), respectively (the horizontal arrows in Fig. 3B). The Ca²⁺ dissociation constants of Ng free and Ng-bound buffer X are K_D and K′_D (μM), respectively (the vertical arrows in Fig. 3B). Applying microscopic reversibility (K_D · K_DNg1 = K′_D · K_DNg0) and simple steady-state analysis, we have

$$[{\mathit{XCa}}^{2+}]+[Ng·{\mathit{XCa}}^{2+}]=\frac{[C{a}^{2+}][X_{\tau }]}{[C{a}^{2+}]+\frac{\left(1+\frac{[Ng]}{K_{\text{D}}Ng0}\right)K_{\text{D}}}{\left(1+\frac{[Ng]}{K_{\text{D}}N{g}_1}\right)}}$$ (11)

where [Ng] and [Ng · XCa²⁺] represent the concentration (μM) of (free) Ng and Ng–X–Ca²⁺ complex, respectively. In other words, the “bulk” Ca²⁺ dissociation constant K of CaM in the presence of Ng is

$$K=\frac{\left(1+\frac{[Ng]}{K_{\text{D}}Ng0}\right)K_{\text{D}}}{\left(1+\frac{[Ng]}{K_{\text{D}}N{g}_1}\right)}$$ (12)

which is usually larger than K_D because apo-CaM has a higher affinity toward Ng than Ca²⁺ bound CaM (K _DNg0 < K_DNg1). Plugging Eq. 12 in Eq. 5 gives an approximate buffering capacity of CaM in the presence of Ng and explains why Ng reduces the buffering capacity. Going back to Eq. 10, this simple theory indicates that Ng will increase the peak amplitude and Ca²⁺ decay rate for a single NMDA stimulation. We will subsequently test this prediction (see, for example, 1-Hz stimulation in Fig. 5B).

So far, we have derived the buffering capacity (κ_E) for single or multiple independent Ca²⁺-binding sites. We have not considered the case where the binding of first Ca²⁺ ion increases the affinity for the second Ca²⁺ as in CaM. This process is modeled as a sequential Ca²⁺ binding to each lobe (see the horizontal arrows without Ng in Fig. 1B). The extension of Eq. 5 is straightforward from the steady-state analysis of this kinetic scheme. The new formula for the buffering capacity (κ_E) of the C- or N-terminal lobe of CaM (represented by X) is

$${\kappa }_{\text{E}}=\frac{[X_T]K_{\text{D}2}({[C{a}^{2+}]}^2+4K_{\text{D}1}[C{a}^{2+}]+K_{\text{D}1}{K}_{\text{D}2})}{{({[C{a}^{2+}]}^2+K_{\text{D}2}[C{a}^{2+}]+K_{\text{D}1}{K}_{\text{D}2})}^4}$$ (13)

where [X_T] is the total concentration (μM) of C-terminal or N-terminal lobe of CaM and K_D1 and K_D2 are the two macroscopic dissociation constants (μM) of each lobe (K_D1 = k₋₁/k ₁ and K_D2 = k₋₂/k₂ for C-terminal lobe and K_D1 = k₋₃ /k₃ and K_D2 = k₋₄/k₄ for N-terminal lobe; see Fig. 1). Using the estimated CaM concentrations in CA1 pyramidal neurons (~37–100 μM; see INTRODUCTION) and Eq. 5, we estimate the buffering capacity due to CaM is about 32–87 ([Ca] = 0.1 μM). If we use Eq. 13, the buffering capacity is about 12–33. The former is higher than and the latter is close to the experimentally measured buffering capacity in the dendrites of CA1 neuron (κ_E = 20) (Sabatini et al. 2002).

Synaptic weight function

In the present work, we use the “synaptic weight function” developed in Shouval et al. (2002) to assess the impact that Ng might have on the induction of synaptic plasticity. This is a simple mathematical formalism that was shown to explain the relation between synaptic Ca²⁺ (or Ca²⁺–CaM) input and bidirectional synaptic plasticity. This formalism is based on the Ca²⁺ control hypothesis: the elevation of Ca²⁺ is the primary signal for synaptic plasticity. The validity of this formalism has been tested with diverse induction protocols (Cai et al. 2006; Shouval et al. 2002). In this formalism, a new variable W (synaptic weight, unitless) is introduced that obeys a first-order ODE

$$\frac{\text{d}W}{\text{d}t}=\eta ([C{a}^{2+}])[\mathrm{\Omega }([C{a}^{2+}])-W]$$ (14)

where η determines a Ca²⁺-dependent “learning rate” (i.e., speed at which the synaptic weight W approaches the steady state), which in turn is determined by a nonlinear function of Ca²⁺ (Ω). These Ca²⁺-dependent functions are defined as follows

$$\mathrm{\Omega }(x)={\alpha }_0-{\alpha }_0·\mathit{sig}(x-{\alpha }_1,{\beta }_1)+\mathit{sig}(x-{\alpha }_2,{\beta }_2)$$ (15)

and

$$\eta (x)=p_1\frac{{(x+p_4)}^{p_3}}{{(x+p_4)}^{p_3}+{(p_2)}^{p_3}}$$ (16)

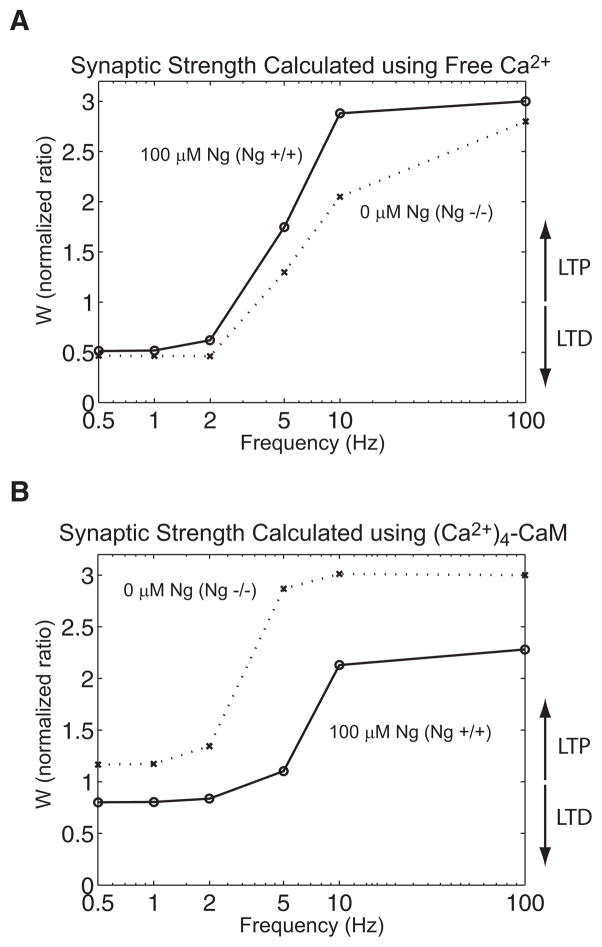
where sig (x, β) = exp(βx)/[1 + exp(βx)], α₀ = 0.333, α₁ = 0.8, α₁ =1.2, β₁ = 32, β₂ = 16, p₁ = 1, p₂ = 2.8, p₃ = 3, and p₄ = 0.00001 (partially modified from Cai et al. 2006 and used for Fig. 7A). In the present work, we use the free Ca²⁺ transient (Fig. 7A) or CaM-bound Ca²⁺ (Fig. 7B) as an input to Eq. 14 and calculate the ratio of the weight function W before [i.e., W(0) = 1] and after the Ca²⁺ stimulations (900 pulses for 0.5, 1, 2, 5, and 10 Hz; 100 pulses for 100 Hz). In Fig. 7B, we set α₀ = 0.333, α₁ = 2.5, α₂ = 4, β₁ = 2, β₂ = 1, p₁ = 1, p₂ = 10, p₃ = 3, and p_{4 ­}= 0.00001 as we change the input from free Ca²⁺ to CaM-bound Ca²⁺. The parameters α₁ and α₂ can be determined by the peak value of free Ca²⁺ (Fig. 7A) or CaM-bound Ca²⁺ (Fig. 7B) at 1 Hz (Fig. 5, A and B): α₁ is set lower than the peak values with or without Ng and α₂ is higher than both of these peak values. The parameters β₁ and β₂ determine the sharpness of the Ω function (Eq. 15). The higher the β₁ (and β₂), the sharper the curve of the omega function (i.e., the deeper the depression). If β₁ and β₂ are too small, the omega function becomes shallow and there would be no LTD induction (Shouval et al. 2002). This defines the lower limit for beta parameters (β₁ and β₂). For each value of β₁ and β₂, we needed to calibrate the p₂ value to avoid undesirable rapid declines and oscillations of the synaptic weight function (Shouval et al. 2002). The remaining parameter values are the same as in Cai et al. (2006). We also impose that β₁ = 2β₂ as in Cai et al. (2006). As long as α₁, α₂, β₁, β₂, and p₂ obey these constraints (α₁ = 0.8, α₂ = 1.2, 2.5 < β₂ [< 40, and 1 < β₂ = 3.5 for Fig. 7A and α₁ = 2.5, α₂ = 4, 0.7 < β₂ < 40, and 1 < p₂ < 11 for Fig. 7B), the qualitative results presented in Fig. 7, A and B are robust.

FIG. 7.

Frequency-dependent induction of synaptic plasticity simulated with and without Ng. y-axis represents normalized synaptic weight (final/initial) at the end of the induction protocol used in the simulated gene knockout experiments. Values <1 are indicative of depression, whereas those >1 are indicative of potentiation. Synaptic strength function (W) was calculated either from the free Ca²⁺ transient (A) or Ca²⁺-saturated CaM (B) as inputs. Single-compartment model that contains 100 μM of Ng (circles and solid line) was compared with a model without Ng (crosses and dashed line). Former model is analogous to data examining the induction of synaptic plasticity in wild-type mice and the latter represents data from the Ng knockout mice. Synaptic strength was calculated for 0.5, 1, 2, 5, 10, and 100 Hz. Low-frequency induction protocol (0.5–10 Hz) was simulated for 900 pulses, whereas 100 pulses were applied at 100 Hz.

RESULTS

Steady-state analysis of the free Ca²⁺

Having established the kinetic pathway and the corresponding parameter values (see Mathematical model in METHODS), we investigated the influence of Ng on the equilibrium steady-state free Ca²⁺. In this series of numerical simulations, the model is a closed system and does not contain Ca²⁺ injection or extrusion mechanisms (Fig. 2A). In Fig. 4, we mixed 20 μM of CaM and a fixed (total) amount of Ca²⁺ (0–100 μM) in the presence of 0 μM (dots and line), 20 μM (crosses and line), and 100 μM (open circles and line) Ng at the beginning of the simulations. The final steady-state level of free Ca²⁺ (the vertical axis) was then plotted against the total amount of Ca²⁺ (the horizontal axis) injected at time = 0. The range of (total) Ca²⁺ concentrations used here spans the levels of Ca²⁺ transients measured in the dendritic spine (Majewska et al. 2000; Sabatini et al. 2002; Scheuss et al. 2006).

As shown in Fig. 4, Ng increases the steady-state level of free Ca²⁺ in an Ng-concentration–dependent manner. Even in the presence of 20 μM Ng, this effect is prominent for all total Ca²⁺ concentrations tested (0–100 μM). On the other hand, there is no further increase in the free Ca²⁺ even if we raise the Ng concentration beyond about 100–120 μM (data not shown). In other words, under these system parameters, the effect of Ng is saturated at about 100 μM. For perspective, the estimated concentration of Ng in the dendritic spine is ≳ 65 μM (Huang et al. 2004). Note, however, Ng is subject to various posttranslational modifications including oxidation and protein kinase C (PKC)–mediated phosphorylation, both of which reduce its interaction with CaM (Gerendasy et al. 1994; Huang et al. 2004; Krucker et al. 2002; van Dalen et al. 2003). These posttranslational modifications will influence the intracellular free Ca²⁺ by tuning Ng’s capacity to bind CaM.

What is the mechanism by which Ng controls the free Ca²⁺? We have indicated that Ng, on binding the C-lobe of CaM, increases the Ca²⁺ dissociation (thick leftward horizontal arrow in the top diagram, Fig. 1A). This leads to a reduced amount of Ca²⁺-bound CaM; as a result, it increases the free Ca²⁺. In other words, the change in Ca²⁺ dissociation constant at the C-lobe (=k₋₉/k₉) will influence the free Ca²⁺ concentration. In fact, Gerendasy (1999) has already confirmed this view. An interesting example is PEP-19, another IQ-motif protein that has an impact on the Ca²⁺-binding properties of CaM different from that of Ng. PEP-19 increases (~30- to 40-fold) both the Ca²⁺ association rate (k₉) and dissociation rate (k₋₉) of CaM to a similar degree (see Table 1) (Putkey et al. 2003). Because PEP-19 does not change the dissociation constant (k₋₉/k ₉), the steady-state level of free Ca²⁺ will remain the same. The numerical simulation of PEP-19–like protein confirmed this conclusion as well (data not shown).

Ng accelerates the free Ca²⁺ decay dynamics

So far, we have analyzed the behavior of the Ca²⁺–CaM–Ng system in a closed compartment. The system has neither time-varying Ca²⁺ injection nor Ca²⁺ extrusion pathways (Fig. 2A). In addition, we have focused only on the steady state but not the transient dynamics of the system. In this section, we investigate the role of IQ-motif proteins (Ng and PEP-19) in regulating the level of free Ca²⁺ during oscillatory Ca²⁺ stimulations.

Figure 5A shows the temporal evolution of CaM-bound Ca²⁺ during 1-Hz NMDA-receptor–like Ca²⁺ stimulation with different concentrations of Ng: 0 μM (dotted line) and 100 μM (solid line). In these analyses, CaM-bound Ca²⁺ indicates all Ca²⁺ ions bound to CaM molecules irrespective of whether they are associated with Ng. As explained earlier, Ng increases the Ca²⁺ dissociation rate from the C-lobe of CaM. In this open system, once released from CaM, Ca²⁺ becomes available for the Ca²⁺ extrusion mechanism (Fig. 2B). Thus the peak amplitude of CaM-bound Ca²⁺ is lower and its decay dynamics is faster in the presence of Ng (see the downward arrow during the second Ca²⁺ pulse in Fig. 5A). On the other hand, Fig. 5B shows that the peak amplitude of the free Ca²⁺ is higher with Ng (100 μM, the solid line) than without Ng (the dotted line). The difference is indicated by the thick leftward horizontal arrow for 100 μM Ng and the thin rightward horizontal arrow for CaM alone. This result occurs because more Ca²⁺ ions remain CaM bound when Ng is absent (Fig. 5A). Equations 10 and 12 in METHODS also predicted the same outcome. Ng reduces the buffering capacity of CaM and thereby influences both the amplitude and decay rate of Ca²⁺ transients. Biochemical insight from Fig. 5A and the mathematical formula converge to the same free Ca²⁺ dynamics (Fig. 5B). Note that the total amount of CaM in the system is 20 μM, which binds 80 μM of Ca²⁺ and, at 1-Hz stimulation, the Ca²⁺-binding capacity of CaM was not saturated (see Fig. 5A). Note the binding capacity used here to quantify the total number of available Ca²⁺-binding sites on CaM is different from the “buffering capacity” defined in METHODS. Again, as predicted, the decay of the free Ca²⁺ is also faster in the presence of Ng: the decay starts from a higher level and reaches the basal level in a shorter time window (Fig. 5B).

What if we change the frequency of Ca²⁺ stimulation? In the mathematical formula presented in METHODS (Eq. 10), we have explored Ca²⁺-influx due to only a single NMDA current injection, which may be relevant during 1-Hz stimulation (Fig. 5, A and B) where temporal summation is not evident. In Fig. 5, C and D we examine the temporal dynamics of CaM-bound and free Ca²⁺ when 5-Hz stimulation is applied. Under this condition, the average level of CaM-bound Ca²⁺ transient is higher without Ng (dotted line in Fig. 5C) than with Ng (100 μM, solid line in Fig. 5C). The decay dynamics of CaM-bound Ca²⁺ is slightly faster in the presence of Ng, although not as prominent as that in Fig. 5A (1 Hz). The binding capacity of CaM for Ca²⁺ (total amount 20 μM, which binds 80 μM of Ca²⁺) is not saturated at this frequency. The free Ca²⁺ dynamics requires a careful inspection at 5 Hz (Fig. 5D). During the first four to five Ca²⁺ spikes, the peak value of the free Ca²⁺ in the presence of Ng exceeds that of CaM alone (see two thick rightward arrows for Ng plus CaM and two thin rightward arrows for CaM alone for the first two spikes, Fig. 5D). After this initial phase, the peak amplitudes of the free Ca²⁺ with or without Ng converge to the same value. However, the decay of the free Ca²⁺ is consistently faster with Ng; therefore the minimum level of the free Ca²⁺ concentration is lower with Ng (see leftward arrows in the figure; a thin leftward arrow for CaM alone and a thick leftward arrow for 100 μM Ng plus CaM).

The dynamics of the system under 100-Hz Ca²⁺ stimulation (for a total of 100 pulses) was next examined. As shown in Fig. 5E, the CaM-bound Ca²⁺ is lower in the presence of 100 μM (solid line) Ng than without Ng (dotted line). The total amount of Ca²⁺ injected during this higher-frequency stimulation is larger than that at lower frequencies (Fig. 5, A–D) but CaM’s Ca²⁺-binding capacity (total CaM concentration = 20 μM, which binds 80 μM Ca²⁺) has still not been exceeded (Fig. 5E). In fact, the plateau levels of CaM-bound Ca²⁺ and free Ca²⁺ are consistent with the bulk Ca²⁺ dissociation constant of CaM. The peak amplitudes of the free Ca²⁺ are the same with Ng (solid line in Fig. 5F) or CaM alone (dotted line in Fig. 5F). Again, the decay dynamics of the free Ca²⁺ is faster in the presence of Ng at the end of the 100-Hz stimulation noted by the small downward arrow between the dotted and solid lines during the declining phase of the free Ca²⁺.

In total, Ng increases the steady-state equilibrium level of free Ca²⁺ in a closed system (Fig. 2A). Ng accelerates the decay dynamics of the free Ca²⁺ in an open nonequilibrium system that contains a Ca²⁺ extrusion mechanism (Fig. 2B). As mentioned earlier, Ng increases the Ca²⁺ dissociation rate from the C-lobe of CaM. This kinetic mechanism of Ng–CaM interaction seems to underlie two opposite observations: one in a closed and the other in an open nonequilibrium system. Note that the total amount of Ca²⁺ influx is the same for 0 and 100 μM Ng in Fig. 5. In the absence of Ng, Ca²⁺ remains bound to CaM for a longer period of time, preventing its extrusion. Whereas the Ca²⁺ extrusion is significantly faster in the presence of 100 μM Ng (see the areas below dashed line and solid line in Fig. 5, A, C, and E; compare them with those in Fig. 5, B, D, and F).

PEP-19–like protein dampens the free Ca²⁺ response during low to intermediate frequencies of Ca²⁺ stimulation

What happens if we change both association and dissociation rates of Ca²⁺ binding to the C-lobe of the CaM–Ng complex while maintaining all other reaction rates the same? The PEP-19–like protein we discussed earlier represents such a simulated mutant molecule that interacts with CaM. PEP-19–like protein does not change the steady-state equilibrium of the free Ca²⁺. However, the accelerated Ca²⁺-binding rate of CaM–PEP-19–like protein (k₉ = 630 μM⁻¹ · s⁻¹ in Table 1) may have a significant impact on the Ca²⁺ dynamics in a nonequilibrium system: it may increase the amount of Ca²⁺ absorbed by CaM during the rising phase of Ca²⁺ spike and thus reduce the free Ca²⁺ concentration.

Figure 6, A–F tests this possibility in the open system. All simulation conditions are otherwise the same as in Fig. 5. At 1-Hz Ca²⁺ stimulation, PEP-19–like protein increases the peak amplitude of CaM-bound Ca²⁺ (Fig. 6A; see the thick leftward and thin rightward horizontal arrows indicating the peak value with or without PEP-19–like protein, respectively). The CaM–Ca²⁺ decay dynamics is faster with PEP-19–like protein than without it: the decay starts from a higher level and reaches the basal level in a shorter time window (Fig. 6A). Consistent with an increased amount of CaM-bound Ca²⁺, PEP-19–like protein (100 μM) dampens the free Ca²⁺ response: the peak amplitude of the free Ca²⁺ is smaller than that without PEP-19–like protein (Fig. 6B).

This blunted response of the free Ca²⁺ becomes more prominent at 5-Hz Ca²⁺ stimulation (Fig. 6, C and D). For the first four to five spikes, the amount of CaM–Ca²⁺ with PEP-19–like protein (100 μM, solid line in Fig. 6C) exceeds that of CaM alone (dotted line in Fig. 5C; see two thick rightward arrows for PEP-19–like protein plus CaM and two thin right-ward arrows for CaM alone during the first two spikes). After this initial transient phase, the system reaches its asymptotic periodic dynamics and the peak CaM–Ca²⁺ values converge to the same level with or without PEP-19–like protein. Note this transient dynamics of CaM-bound Ca²⁺ is similar to the free Ca²⁺ dynamics in the presence of wild-type Ng (Fig. 5D). During the rising phase of the Ca²⁺ spike, PEP-19–like protein accelerates Ca²⁺ association to CaM (Fig. 6C), whereas wild-type Ng accelerates the accumulation of free Ca²⁺ (Fig. 5D) by increasing the Ca²⁺ dissociation from CaM. The dissociation of Ca²⁺ from the C-lobe of CaM is faster and the minimum level of CaM–Ca²⁺ is lower with PEP-19–like protein than with CaM alone (see two horizontal arrows in Fig. 6C: the thin leftward arrow for no PEP-19–like protein and the thick leftward arrow for 100 μM of PEP-19). Correspondingly, the peak of the free Ca²⁺ is lower and the minimum of the free Ca²⁺ is higher in the presence of PEP-19–like protein than with CaM alone (Fig. 6D). The response of free Ca²⁺ is “blunted” in the presence of PEP-19–like protein.

This effect of PEP-19–like protein is less significant at 100-Hz stimulation (100 pulses, Fig. 6, E and F). With a large influx of Ca²⁺ during this high-frequency stimulation, the system quickly approaches its steady-state level where PEP-19 (like protein) has no significant impact. Only the decay dynamics is faster with PEP-19 because the dissociation rate of Ca²⁺ from the C-lobe CaM–PEP-19 is increased approximately 30-fold (Fig. 6E). In summary, the effect of PEP-19–like protein is prominent at low (1 Hz) or intermediate (~5 Hz) Ca²⁺ stimulation and its effect is different from that of wild-type Ng.

Note that the PEP-19–like protein does not change the Ca²⁺ dissociation constant of CaM. The classical theory (see Ca²⁺ buffering capacity and Ng in METHODS) predicts no change in the buffering capacity of CaM in the presence of PEP-19–like protein (Eqs. 5 and 12). Equation 10 predicts no major change in Ca²⁺ transients. However, we have observed a significant impact of PEP-19–like protein in the numerical simulations. The peak amplitude of Ca²⁺ transients is decreased (Fig. 6B), which, according to the theory, looks as if PEP-19–like protein has increased the buffering capacity of CaM. The latter observation is not surprising because PEP-19 increases the association rate of Ca²⁺ to CaM. This accelerated Ca²⁺ binding results in a transient increase of CaM-bound (buffer-bound) Ca²⁺ before it relaxes to the equilibrium. In other words, the “rapid equilibrium” assumption (and/or subsequent approximation made in Eq. 6)—a critical prerequisite for the classical theory—is violated in the presence of PEP-19. This is why the classical theory fails to predict and is inconsistent with the numerical simulations.

Ng genetic knockout studies

Finally, we sought to compare the model predictions (Fig. 5) with experimental data. Two genetic knockout studies in mice (Huang et al. 2004; Krucker et al. 2002; van Dalen et al. 2003) confirmed that deletion of Ng reduced the free Ca²⁺ response. In one experiment (van Dalen et al. 2003), Ca²⁺ dynamics was measured in cultured neuron from wild-type and KO mice using fura-2–based microscopic imaging. The averaged peak amplitudes of Ca²⁺ during spontaneous and NMDA-receptor–activated stimulations were about 20% higher in the wild-type than in KO neurons. In Fig. 5B, we observed a similar (~20%) increase in the Ca²⁺ peak in the presence of Ng. Using independently produced Ng KO mice, Huang et al. (2004) measured fluorescence Ca²⁺ signals in the dendrites of hippocampal neurons. They found Ca²⁺ transients were about two- to threefold higher in wild-type than those of the mutants during both 100- and 5-Hz stimulations. Although the single-compartment model is oversimplified and the experimental conditions in these studies are different from our simulations, Fig. 5 qualitatively agrees with these Ca²⁺ imaging data.

DISCUSSION

In the present work, we have investigated several possible consequences of the biochemistry of IQ-motif–containing CaM-binding proteins. Ng and PEP-19 are the members of the IQ-motif protein family and these two proteins accelerate the Ca²⁺ dissociation from the C-terminal lobe of CaM (Gaertner et al. 2004; Putkey et al. 2003). We hypothesized these proteins may have a significant impact on the intracellular free Ca²⁺ by regulating the Ca²⁺ buffering capacity of CaM. The high concentration of CaM in hippocampal CA1 pyramidal neurons strongly suggests such a control mechanism may be important in these neurons. In a single-compartment closed model that has no Ca²⁺ extrusion mechanism, Ng increases the steady-state equilibrium free Ca²⁺ concentration (Fig. 4). With a Ca²⁺ extrusion mechanism present, Ng accelerates the decay dynamics of the free Ca²⁺ (Fig. 5). On the other hand, another IQ-motif binding protein, PEP-19, which does not change CaM affinity but speeds up both Ca²⁺ association and dissociation kinetics, leads to more efficient damping of the Ca²⁺ oscillations, but no changes in the steady-state Ca²⁺ levels.

The effect of Ca²⁺ buffer on the transient dynamics of free Ca²⁺ has important implications in cellular physiology and it has been a subject of numerous mathematical modeling studies (Franks and Sejnowski 2002; Gamble and Koch 1987; Gerendasy 1994; Gold and Bear 1994; Holcman et al. 2005; Holmes and Levy 1990; Lee et al. 2000b; Zador et al. 1990). Early modeling works (Gamble and Koch 1987; Gold and Bear 1994; Holcman et al. 2005; Holmes and Levy 1990; Zador et al. 1990) have suggested an impact that the endogenous buffer, especially CaM, may have on nonlinear Ca²⁺ dynamics in the dendritic spine. These modeling works, however, did not address a potential role of IQ-motif protein. On the other hand, Gerendasy (1999) explored the potential role of IQ-motif proteins and their impacts on the steady-state level of free Ca²⁺. This work suggested Ng might increase the free Ca²⁺ level, thereby activating Ca²⁺-dependent enzymes such as PKC. The present work extended the work by Gerendasy (1999) to a time-varying Ca²⁺ signal in a nonequilibrium system with the Ca²⁺ extrusion mechanism. Finally, the present work demonstrated a limitation of classical (linear) theory of Ca²⁺ buffering (PEP-19 in Fig. 6). The limitation of classical theory has been pointed out in several modeling works including that of Lee et al. (2000b) who investigated the influence that parvalbumin might have on Ca²⁺ decay dynamics in chromaffin cells. We have presented another example of a failure of classical theory caused by the CaM–IQ-motif protein interaction (Fig. 6).

The potential impact of Ng on the free Ca²⁺ concentration implicated by the modeling work is particularly intriguing. The free Ca²⁺ dynamics in the spine is the critical determinant of induction of either LTP or LTD (Yang et al. 1999). The impact of Ng on the Ca²⁺ dissociation rate from CaM strongly suggests that Ng plays an important role in synaptic plasticity. Interestingly, two knockout studies in mice confirmed that genetic disruption of Ng reduced the Ca²⁺ response to NMDA-receptor agonist (Huang et al. 2004; Krucker et al. 2002). In the simulations (Fig. 5, B, D and F), the removal of Ng attenuated the free Ca²⁺ response. Therefore with regard to the free Ca²⁺ dynamics, two knockout studies and the simulation results all agree.

What is the role that Ng plays in the induction of synaptic plasticity? The genetic knockout studies do not provide a clear answer to this question. One knockout study (Huang et al. 2004) showed a deficit in high-frequency–induced LTP, whereas the other knockout mice (Krucker et al. 2002) showed enhanced LTP induction. A brief discussion of the intertwined biochemical network that involves Ng might help illustrate the complexity of the problem. First and most important, Ng is phosphorylated by PKC (Huang et al. 2004; Xia and Storm 2005) and is dephosphorylated by PP2B and/or PP1 (Seki et al. 1995). Here we have a kinase–phosphatase system acting on the same substrate, Ng, and this system may exhibit zero-order ultrasensitivity (Goldbeter and Koshland 1981). Phosphorylation of Ng by PKC attenuates its interaction with CaM. Figure 5 suggests Ng increases free Ca²⁺ and decreases CaM-bound Ca²⁺ that would activate PKC and blunt the activation of PP2B, respectively. Ng occupies a key position of the nested signaling feedback loop in which CaM-dependent and CaM-independent Ca²⁺ signals intersect and influence each other. Thus Ng has a potential to shift the entire system dynamics toward LTP induction or to LTD induction through the CaM-dependent and CaM-independent signaling cascades.

Figure 7, A and B illustrates this point. Here we calculate the changes in synaptic strength using as input either free Ca²⁺ (Fig. 7A) or fully Ca²⁺ saturated CaM (Fig. 7B) during the induction protocol of plasticity. In other words, these simulations represent two extreme outcomes that Ng might have on the induction of plasticity. For this purpose, we used our current data (Fig. 5) and used an empirical mathematical formalism that has been tested with various induction protocols (Cai et al. 2006; Shouval et al. 2002) to estimate Ng’s impact on the induction of plasticity. This mathematical formalism (Eqs. 14–16, METHODS) was used to explain the relation between the input Ca²⁺ (or Ca²⁺–CaM) signal and bidirectional synaptic plasticity.

Figure 7A shows the ratio of synaptic strength before and after the induction of plasticity at different frequencies (0.5, 1, 2, 5, 10, and 100 Hz). In this figure, we calculate the synaptic weight function using the free Ca²⁺ transient as an input. A ratio >1 indicates LTP induction and <1 implies LTD induction. The crosses and dashed line indicate no Ng present (i.e., knockout animal), whereas the circles and solid line represent a model with 100 μM Ng (i.e., wild-type). In this simulation, Ng enhances LTP at higher frequencies (5, 10, 100 Hz). Ng does not influence LTD induction at lower frequencies. Figure 7A is reminiscent of the knockout study by Huang et al. (2004). On the other hand, Fig. 7B calculates the changes in the synaptic weight using CaM-bound Ca²⁺ as an input. In this case, LTP at high-input frequencies is attenuated by Ng. This result is reminiscent of that in Krucker et al. (2002), although their knockout mice show no change in low-frequency–induced LTD.

Note, in these simulations, we artificially uncoupled the CaM-dependent and CaM-independent Ca²⁺ signaling systems to independently assess each one’s potential role in modifying synaptic strength. This way, Fig. 7, A and B can represent two extreme impacts that Ng might have on LTP/LTD induction. If these two results were identical, we would be able to suggest a robust role of Ng in LTP/LTD induction despite the complex feedback network that involves Ng. However, these two simulations show almost opposite impacts on LTP induction. In other words, Ng could be a key (tunable) regulator of synaptic metaplasticity (Abraham and Bear 1996) and can differentially control the LTP/LTD threshold by potentially balancing the relative impact of two different Ca²⁺ signaling pathways: one CaM independent and one CaM dependent.

Finally, another implication of our modeling work is the difference between Ng and PEP-19. Ng is enriched in CA1 hippocampal pyramidal neurons, whereas PEP-19 is highly expressed in cerebellar Purkinje cells (Putkey et al. 2003; Xia and Storm 2005). In contrast to Ng, PEP-19 increases the dissociation rate as well as the association rate of Ca²⁺ to the same degree (Putkey et al. 2003). We found the impact of such a PEP-19–like protein is significantly different from that of Ng in both temporal and steady-state dynamics of free Ca²⁺, suggesting that Ng and PEP-19 may have distinctive effects on the intracellular metabolism of Ca²⁺ and that the physiological role of PEP-19 in cerebellar Purkinje cells (and other cells that contain PEP-19) may be different from that of Ng in hippocampal CA1 neurons. Purkinje cells contain large amounts of other Ca²⁺-binding proteins such as calbindin (Bainbridge et al. 1992) and simulation experiments with these Ca²⁺-binding proteins will be necessary to clarify their role in Purkinje cells. It would also be interesting to see how GAP43 (neuromodulin) (Xia and Storm 2005), another neuronal IQ-motif protein enriched in the presynaptic terminal, regulates the free Ca²⁺ dynamics.