ESTIMATING STRAIN-SPECIFIC AND OVERALL EFFICACY OF POLYVALENT VACCINES AGAINST RECURRENT PATHOGENS FROM A CROSS-SECTIONAL STUDY

Summary

Evaluating vaccine efficacy for protection against colonisation with bacterial pathogens is an area of growing interest. Colonisation of the nasopharynx is an asymptomatic carrier state responsible for person-to-person transmission. It differs from most clinical outcomes in that it is common, recurrent and observed only in its prevalent state. To estimate rates of acquisition and clearance of colonisation requires repeated active sampling of the same individuals over time, an expensive and invasive undertaking. Motivated by feasibility constraints in efficacy trials with colonisation endpoints, investigators have been estimating vaccine efficacy from cross-sectional studies without principled methods. We present two examples of vaccine studies estimating vaccine efficacy from cross-sectional data on nasopharyngeal colonisation by Streptococcus pneumoniae (pneumococcus). This study presents a framework for defining and estimating strain-specific and overall vaccine efficacy for susceptibility to acquisition of colonisation (VE_acq) when there is a large number of strains with mutual interactions and recurrent dynamics of colonisation. We develop estimators based on one observation of the current status per study subject, evaluate their robustness, and re-analyse the two vaccine trials. Methodologically, the proposed estimators are closely related to case-control studies with prevalent cases, with appropriate consideration of the at-risk time in choosing the controls.

1. Introduction

Vaccine efficacy (VE) is generally defined as a relative reduction in some measure of risk in the vaccinated group compared to the unvaccinated group (Halloran, Longini, and Struchiner, 2010). When a vaccine is polyvalent, that is, it contains antigens against two or more, but not necessarily all, related strains of a microorganism, assessing both the strain-specific efficacies and the overall (aggregate) efficacy against all strains is of interest. Some bacterial pathogens asymptomatically colonise the nasopharyngeal passages, called the carrier state. Colonisation with any strain may be cleared and recur repeatedly. Colonisation only rarely leads to manifest disease, such as bacteremia or meningitis, but it is a prerequisite for disease and the only source of transmission. Thus, the effect of vaccination on colonisation is of interest. Examples of such bacterial pathogens with polyvalent vaccines either available or under development include Streptococcus pneumoniae (pneumococcus), Neisseria meningitidis (Tan, Carlone, and Borrow, 2010), and group B streptococci (Edwards, 2008). Current formulations of pneumococcal conjugate vaccine contain antigens of 7, 10 or 13 of the known 93 serotypes (MMWR, 2010).

A straightforward approach to define and estimate vaccine efficacy for susceptibility based on the hazard rate of acquiring colonisation (VE_acq) for individual strains would be to treat colonisation by each strain as separate and independent outcomes. To estimate rates of acquisition and clearance of colonisation requires repeated active sampling of the same individuals over time, an expensive and invasive undertaking. Thus, investigators have turned to using cross-sectional data to estimate vaccine efficacy without, however, explicitly defining the estimand of interest and its underlying assumptions (Rinta-Kokko et al. 2009).

We present two randomised controlled trials of polyvalent pneumococcal vaccines in which assessment of serotype-specific and overall vaccine efficacy is based on cross-sectional data (Table 1). In a vaccine study in South Africa (Mbelle et al., 1999), 500 infants were randomised to either a 9-valent pneumococcal conjugate vaccine or control vaccine and given 3 doses at 6, 10, and 14 weeks of age. Serotype-specific colonisation was measured once at the age of 9 months. Samples were available from 481 children. In a vaccine trial in Finland in 1995–1999 (Kilpi et al., 2001), 2497 children were randomised to a 7-valent pneumococcal conjugate vaccine or control and given 3 doses at 2, 4 and 6 months of age, and a booster at 12 months of age. Serotype-specific colonisation was measured before the booster at 12 months of age and approximately 6 months after the booster at 18 months of age. Here we analyse measurements made at least 6 months after the booster (2403 children).

Table 1.

Vaccine efficacy against colonisation in two vaccine studies. Upper part. Data from a randomised, double-blind vaccine study on the effect of an experimental 9-valent pneumococcal conjugate vaccine on colonisation in Soweto, South Africa (Mbelle et al., 1999). Altogether 500 infants were recruited; 481 completed the 9-month follow-up. Children received either pneumococcal vaccine (Wyeth Lederle Vaccines, n=242) or placebo (n=239). The vaccine was given at 6, 10 and 14 weeks of age and the estimates of vaccine efficacy are based on measurements of colonisation at 9 months of age. Estimates are shown individually for seven of the nine vaccine serotypes (serotypes 1 and 5 were not found at all in the study), for all vaccine serotypes and for all non-vaccine serotypes. Lower part: Data from a randomised, double-blind vaccine study on the effect of a 7-valent pneumococcal conjugate vaccine on colonisation in Finland (Kilpi et al., 2001). Children received either of two pneumococcal vaccines (Wyeth Lederle Vaccines, n=831, or Merck Sharp and Dohme, n=835), or HBV vaccine (Merck Sharp and Dohme, n=831) as a control. The vaccine was given at 2, 4, 6 and 12 months of age and the estimates of vaccine efficacy are based on measurements of colonisation at 18 months of age. Estimates are shown individually for the seven vaccine serotypes (in the South African dataset, there were no samples with two of the vaccine serotypes, 1 and 5), for all vaccine serotypes, and for all non-vaccine serotypes. For both studies, the estimates of vaccine efficacy are determined against all vaccine serotypes and non-vaccine serotypes using estimators (4) and (5) for VE_W|0 and VE_V̄|0, respectively. For comparison, the last column shows estimates of vaccine efficacy (HRK), based on simple odds ratios (Rinta-Kokko et al., 2009; see text)

Serotype	Number of samples		Estimates of vaccine efficacy
	Vaccinees	Controls	VEW|0 (90% CI†)	HRK (90% CI†)
South Africa
4	3	5	0.54 (−0.54, 0.86)	0.41 (−0.97, 0.82)
6B	8	28	0.78 (0.57, 0.89)	0.74 (0.49, 0.87)
9V	1	2	0.62 (−1.89, 0.95)	0.51 (−2.71, 0.93)
14	3	6	0.62 (−0.24, 0.88)	0.51 (−0.58, 0.85)
18C	2	0	–	–
19F	19	32	0.55 (0.25, 0.73)	0.45 (0.09, 0.67)
23F	7	14	0.62 (0.17, 0.83)	0.52 (−0.04, 0.78)
Vaccine types	43	87	0.62 (0.46, 0.74)	0.62 (0.46, 0.74)
Non-vaccine types	87	58	−0.26 (−0.81, 0.12)*	−0.75 (−1.44, −0.26)
0	112	94
Finland
4	1	2	0.77 (−0.76, 0.97)	0.75 (−0.87, 0.97)
6B	44	39	0.47 (0.24, 0.64)	0.45 (0.20, 0.62)
9V	4	4	0.53 (−0.50, 0.85)	0.50 (−0.60, 0.84)
14	13	10	0.39 (−0.22, 0.70)	0.35 (−0.30, 0.68)
18C	6	4	0.30 (−1.03, 0.76)	0.25 (−1.17, 0.74)
19F	44	32	0.36 (0.05, 0.56)	0.32 (0.00, 0.54)
23F	47	34	0.35 (0.06, 0.56)	0.32 (0.01, 0.53)
Vaccine types	159	125	0.41 (0.27, 0.52)	0.41 (0.27, 0.52)
Non-vaccine types	268	111	−0.16 (−0.42, 0.06)*	−0.25 (−0.52, −0.02)
0	1176	564

^*For vaccine efficacy against non-vaccine strains, the reference state is 0 and estimator (5) was used.

^†CI = confidence interval.

Rinta-Kokko et al. (2009) proposed to estimate VE_acq based on one cross-sectional study under stationary conditions using simple ratios of the odds of vaccination in those colonised with the types targeted by the vaccine versus those not colonised. However, that analysis was not adjusted for the possible difference in the times spent susceptible by the vaccinees and controls. Colonisation is usually common and recurrent even on the strain level. In addition, the time spent at-risk for acquiring a new colonisation is affected by between-strain interactions induced by intra-species competition (Lipsitch et al., 2000; Melegaro et al., 2007). Any reduction in colonisation within a vaccinated host by pneumococcal strains targeted by the vaccine is thus counterbalanced by an increase in non-vaccine type colonisation (e.g. Mbelle et al., 1999), a phenomenon we call within-host replacement. For these reasons, the vaccine efficacy estimands may have to be conditioned on the appropriate states of colonisation in which an individual is susceptible to colonisation by the strain(s) targeted by the vaccine. Without such adjustment, the biological protective efficacy on the causal pathway and the estimated (outcome) efficacy may be different, confounding the interpretation and comparability of estimates of vaccine efficacy across different epidemiologic settings (cf. Struchiner et al., 1994).

Here we present a framework for defining vaccine efficacy for multiple interacting strains which can be acquired and carried repeatedly. We develop two new estimands of VE_acq in the multi-type setting. We propose estimators of VE_acq for individual strains as well as for any collection of select (target) strains based solely on one measurement per study subject. We generalise the model to allow estimation of combined efficacy against acquisition and duration of colonisation as a more general estimand within a broader class of vaccine efficacy on colonisation. We present simulations and discuss robustness of estimation to departures from model assumptions.

2. Models of colonisation and vaccine effects

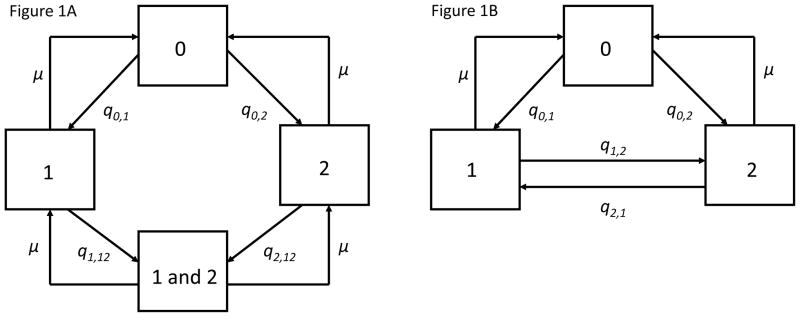
Figure 1A depicts two alternative models (A and B) to describe recurrent colonisation and competition among multiple strains of a pathogen within an individual (Lipsitch, 1997; Melegaro et al. 2007; Auranen et al., 2010).

Figure 1.

1A. Model A of colonisation. The model has two strains and four states of colonisation. The states are uncolonised (0), colonised with strain 1, colonised with strain 2, and colonised with both strains (1 and 2). The model is governed by eight transition hazards, which fulfil conditions (A1) and (A2) if q_{1, 12}/q_{2, 12} = q_{0, 2}/q_{0, 1}. In the text, this model is considered for an arbitrary number of strains, separately for the vaccinated (T) and control (C) individuals. 1B. Model B of colonisation. The model has two strains and three states of colonisation. The states are uncolonised (0), colonised with strain 1, and colonised with strain 2. The model is governed by six transition hazards, which fulfil conditions (B1) and (B2) if q_{1, 2}/q_{2, 1} = q_{0, 2}/q_{0, 1}. In the aggregated model, states 0, 1 and 2 correspond to aggregated states 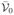, 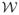and 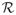(see Section 5).

In model A for two strains, an individual can be either susceptible (i.e., uncolonised in state 0) or colonised with either of the two strains (in states 1 or 2). In addition, the individual may be simultaneously colonised by both strains (co-colonised state 1&2). Figure 1A presents the model only for two strains, but we consider it for an arbitrary number of distinguishable strains. However, in this paper we do not allow simultaneous colonisation with more than two strains, which is supported by the rarity of such multiple colonisation by pneumococci (Kaltoft et al., 2008). For n strains, the set of n(n+1)/2+1 possible states of colonisation is denoted by 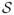= {0} ∪ S ∪ {(1, 2), (1, 3), …, (1, n), (2, 3), …, (n−1, n)} where S = {1, …, n} is the index set of the strains.

There are altogether 2n² transition hazards between the directed pairs of states in 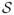. For clarity, we index the individual states explicitly by strain indices, i.e., q_{i, j} denotes the hazard of transition from state i to state j, i, j ∈ S ∪ {0}, i ≠ j, and q_{i, ij} and q_{ij, i} denote the hazards of the two reverse transitions between states i and (i, j), i, j ∈ S, i ≠ j. Occasionally, it is more convenient to use an alternative naming convention in which the states are enumerated as {[1], …, [n(n + 1)/2 + 1]}. Then q_[h][k] denotes the hazard of transition from state [h] to state [k] ([h], [k] ∈ 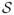, [h] ≠ [k]).

We assume the hazards of transition in the unvaccinated subjects (“C” for controls) under model A fulfil two conditions:

$$q_{j,ij}^C/q_{i,ij}^C=q_{0,i}^C/q_{0,j}^C\text{for}\text{all}i,j\in S,i\ne j,$$ (A1)

$$q_{i,0}^C=q_{ij,j}^C\equiv \mu \text{for}\text{all}i,j\in S,i\ne j.$$ (A2)

For any two strains, assumption (A1) states the ratio of their two hazards of acquisition to the doubly-colonised state (j to (i, j) vs. i to (i, j)) equals the ratio of the respective hazards of colonisation from state 0 (0 to i vs. 0 to j). Competition between strains is quantified in terms of relative hazards $q_{j,ij}^C/q_{0,i}^C$, values < 1 indicating reduced acquisition of strain i due to the currently colonising strain j. Consequently, we refer to condition (A1) as symmetry in competition because it implies $q_{j,ij}^C/q_{0,i}^C=q_{i,ij}^C/q_{0,j}^C$ for any given pair of strains i and j.

Conditions (A1) and (A2) still allow each strain i to have its own hazard of colonisation q_{0, i}. According to (A2), however, the hazards of clearance from the singly-colonised states to state 0 and the hazards of clearance from doubly-colonised states to singly-colonised states are equal for all strains and denoted by μ. In Sections 5 and 6 we relax this assumption.

Illustration

To illustrate these concepts, assume there were four strains, with the vaccine containing antigens of two strains, called the vaccine strains. The other two are non-vaccine strains. Denote the two vaccine strains 1 and 2, and the non-vaccine strains 3 and 4. Let the hazards of colonisation in uncolonised, unvaccinated individuals be q_{0, 1} = 0.07, q_{0, 2} = 0.06, q_{0, 3} = 0.05, and q_{0, 4} = 0.04 per time unit. Assume the hazard of clearance (μ) is 0.17 per time unit. Let the relative hazards for acquisition of double carriage (q_j,ij/q_0,i) be 0.4 for all i, j, according to eq. (A1). The value 0.4 < 1 indicates considerable competition against double colonisation. For example, if a person is already colonised with strain 1, 3, or 4, the hazard of becoming doubly colonised with strain 2 would be 0.06 · 0.4 = 0.024.

Model B

Figure 1B presents model B for two strains. Again, an individual can be either susceptible or colonised with either of the two strains, but there is no co-colonisation. In a model for n strains, the conditions corresponding to (A1) and (A2) are:

$$q_{j,i}^C/q_{i,j}^C=q_{0,i}^C/q_{0,j}^C,i,j\in S,i\ne j,$$ (B1)

$$q_{i,0}^C=\mu ,i\in S.$$ (B2)

Under model B, competition between strains is described in terms of the ratios $q_{j,i}^C/q_{0,i}^C$ of the reverse transition hazards between the singly colonised states, values < 1 again indicating competition. Although many results derived in this paper are applicable for any number of strains also under model B, the main use of this model is with three states only, obtained by aggregating states of model A (see Section 5).

The vaccine model

We assume the direct biological effect of vaccination acts on susceptibility to acquisition of colonisation, the primary estimand of interest thus being VE_acq. Under model A a strain-specific efficacy estimand VE_{acq, i} is defined as the relative reduction in the hazard of acquisition of strain i if vaccinated (T) compared to if receiving control (C):

$${\text{VE}}_{\text{acq},i}=1-q_{0,i}^T/q_{0,i}^C=1-q_{j,ij}^T/q_{j,ij}^C,i,j\in S,i\ne j.$$ (A3)

VE_{acq, i} is defined separately for each state from which a transition is possible to state i or (i, j), i.e., for all states in which an individual is susceptible to acquisition of strain i. The definition assumes no interaction between the current state of colonisation and vaccine efficacy for strain i.

Illustration, cont'd

In the four strain example above, let VE_{acq, 1} = 0.7 and VE_{acq, 2} = 0.4. Under (A3), the efficacy against colonisation by strain 1 is the same whether an individual is uncolonised or colonised with strain 2, 3, or 4. The hazard of an uncolonised vaccinated person being colonised with strain 1 would be (1 − 0.7)0.07 = 0.21 (per time unit). However, due to the competition described above, the hazard of a colonised vaccinated person being colonised with strain 1 would be (1 − 0.7)0.4 · 0.07 = 0.064. The same arguments hold for strain 2. The hazards of the non-vaccine strains 3 and 4 are unaffected by vaccination.

Initially we assume that vaccination does not affect the hazard of clearance of colonisation:

$$q_{i,0}^T=q_{ij,j}^T=\mu ,i,j\in S,i\ne j.$$ (A4)

Under model B, the analogous vaccine efficacy estimand is

$${\text{VE}}_{\text{acq},i}=1-q_{0,i}^T/q_{0,i}^C=1-q_{j,i}^T/q_{j,i}^C,i,j\in S,i\ne j,$$ (B3)

and the assumption about the hazard of clearance is (B4) $q_{i,0}^T=\mu ,i\in S$. It is straightforward to show that with the assumed vaccine models, (A3)–(A4) or (B3)–(B4), the respective conditions (A1)–(A2) or (B1)–(B2) hold for the vaccinated individuals as well. In the sequel, we drop “acq” in the notation for VE_acq,i, if not required for clarity.

3. Overall vaccine efficacy for multiple strains

We denote the index sets of the non-vaccine and vaccine strains by V̄ and V, so S = V̄ ∪ V. We also define the set V̄₀ = V̄ ∪ {0} as the index set of those (single) states against which the vaccine does not confer direct biological protection. In particular, when conditioning on the current state of colonisation, assuming no cross-reactivity of immunity between strains, the true direct biological vaccine efficacy against a non-vaccine strain is zero, i.e., VE_i = 0 for i ∈ V̄. In contrast, the efficacy against any vaccine strain is a priori unknown. We denote the index set of these target strain(s) in a vaccine study by W ⊆ V. Typically W = {i} separately for each i ∈ V (for strain-specific estimates for vaccine efficacy) or W = V (for overall efficacy against all vaccine-strains). However, there may be interest in a proper subset of (vaccine) strains as the target, e.g., “new” strains in a vaccine with a larger valency.

Partition of the states of colonisation

To define the estimands of overall efficacy, we need to specify a partition of the states of colonisation into three disjoint sets (Figure 2). The sets correspond to (a) states in which none of the vaccine-strains is involved, denoted 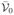; (b) states in which any one of the target strains of the vaccine is involved either alone or with any of the non-vaccine strains, denoted 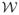; and (c) the rest 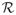= 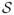\( 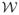∪ 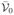). The sets 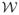and 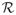generally depend on the choice of target strains W against which vaccine efficacy is considered. For W = V, 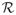contains only the doubly-colonised states with two vaccine-strains (Figure 2A). These states are not included in because our definition of vaccine efficacy does not involve acquisition of secondary vaccine strains (see below). For strain-specific efficacy, also includes all states with non-target vaccine-strains (Figure 2B).

Figure 2.

Partition of states for estimation of vaccine efficacy. The figure presents the seven states of colonisation in model A for three strains. Strains 1 and 2 are vaccine strains and strain 3 is a non-vaccine strain, i.e., S = {1, 2, 3} and V = {1, 2}. 2A. Overall vaccine efficacy. The figure shows the partition for estimation of overall vaccine efficacy against strains 1 and 2. Here = {1, 2, (1, 3), (2, 3)} and 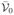= {0, 3}. The complement 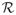= {(1, 2)} consists of the (only) doubly-colonised state with two vaccine strains. The aggregate model has a chain structure 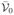↔ ↔ 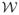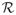. 2B. Strain-specific vaccine efficacy. The figure shows the partition for vaccine efficacy against strain 1. Here 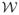= {1, (1, 3)}, 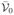= {0, 3}, and 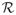= {2, (1, 2), (2, 3)}. Generally, for an individual strain i ∈ S, define 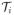= {i} ∪ {(i, j); j ∈ V̄, j ≠ i} as the set of those states in which strain i is involved either alone or with any of the non-vaccine strains. Then 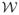= ∪_i∈W 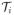and 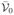= (∪_i∈V̄ 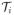) ∪ {0}.

Overall vaccine efficacy

Generalising the strain-specific estimands in (A3) and (A4), we define overall (aggregate) vaccine efficacy against all strains in a target set W as the relative reduction in their overall hazard of acquisition. To make this definition precise in a multi-state setting, we specify a distribution for the time spent at risk to acquire the target strains among the non-vaccine states. We consider two estimands based on transitions either from state 0 only, or alternatively from any of the non-vaccine states V̄₀.

The first estimand specifies the overall vaccine efficacy against a given collection of target strains as the relative reduction in their overall hazard of acquisition from state 0. The target states W then include all states to which there is a direct transition (“arrow”) from state 0 and the overall hazard is simply the sum of the hazards of colonisation q_{0, i}, i ∈ W. For a given set of vaccine-strains W (⊆ V), the overall vaccine efficacy estimand is thus defined as

$${\text{VE}}_{W\mid 0}:=1-\sum _{i\in W}{q}_{0,i}^T/\sum _{i\in W}{q}_{0,i}^C=\left\{\sum _{i\in W}{q}_{0,i}^C·{\text{VE}}_i\right\}/\sum _{i\in W}{q}_{0,i}^C.$$ (1)

The rightmost equation expresses overall efficacy as a weighted average of strain-specific efficacies, the weights being the hazards of colonisation. In a strain-specific analysis, i.e., when W = {i}, it holds naturally that VE_{i}|0 = VE_i as in the left part of (A3) and (B3).

The second estimand considers vaccine efficacy based on transitions from set V̄₀, i.e., from state 0 or any of the singly-colonised states with a non-vaccine strain. This seems a natural extension of the “susceptibility set” from state 0 to states against which the vaccine does not have a biological effect mechanism. The set of target states 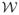now includes all states to which there is a direct transition (“arrow”) from any of the states in V̄₀. To define a unique, time-independent hazard of transition between the two collections of states (V̄₀ and 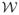), we need in addition to specify a mixing distribution for the time spent among the states in V̄₀. It proves useful to apply the stationary distribution. For a given set W of target strains, the alternative overall vaccine efficacy estimand is then defined as:

$${\text{VE}}_{W\mid {\overline{V}}_0}:=1-\sum _{[h]\in {\overline{V}}_0}{\overline{p}}_{[h]\mid {\overline{V}}_0}^T\left(\sum _{[k]\in \mathcal{W}}{q}_{[h][k]}^T\right)/\sum _{[h]\in {\overline{V}}_0}{\overline{p}}_{[h]\mid {\overline{V}}_0}^C\left(\sum _{[k]\in \mathcal{W}}{q}_{[h][k]}^C\right),$$ (2)

where p̄ _[h]|V̄0 denotes the stationary probability of state [h], conditioned upon being in V̄₀.

Expression (2) is also a weighted average of strain-specific efficacies (see Web Appendix A). The two definitions thus fully agree for any strain-specific efficacy as in (A3). Moreover, for the overall efficacy they will yield similar numerical values if between-strain competition is homogeneously symmetric across all strains or acquisition of double colonisation is not common (see Web Appendix A).

Analogous to (1), we also define vaccine efficacy against the non-vaccine strains as the relative reduction in the overall hazard of acquisition of any of the non-vaccine strains from the uncolonised state:

$${\text{VE}}_{\overline{V}\mid 0}:=1-\sum _{j\in \overline{V}}{q}_{0,j}^T/\sum _{j\in \overline{V}}{q}_{0,j}^C.$$ (3)

By the assumption VE_i = 0 for any non-vaccine strain, the theoretical value of VE_V̄|0 is 0. The estimand can naturally be restricted to any individual non-vaccine strain.

Illustration cont'd

In the four strain example, the overall vaccine efficacy against the two vaccine strains, based on definition (1), is VE_{{1, 2}|0} = (0.07·0.7+0.06·0.4)/(0.07+0.06) = 0.56. Based on definition (2), the overall vaccine efficacy VE_{{1, 2}|{0, 3, 4}} is also 0.56, calculated as

$$1-\frac{{\overline{p}}_{0\mid {\overline{V}}_0}^T\left((1-0.7)0.07+(1-0.4)0.06\right)+{\overline{p}}_{\{3,4\}\mid {\overline{V}}_0}^T·0.4\left((1-0.7)0.07+(1-0.4)0.06\right)}{{\overline{p}}_{0\mid {\overline{V}}_0}^C(0.07+0.06)+{\overline{p}}_{\{3,4\}\mid {\overline{V}}_0}^C·0.4(0.07+0.06)},$$

where $(p_{0\mid {\overline{V}}_0}^T,p_{\{3,4\}\mid {\overline{V}}_0}^T)=(0.253,0.134)/0.387$ and $(p_{0\mid {\overline{V}}_0}^C,p_{\{3,4\}\mid {\overline{V}}_0}^C)=(0.197,0.103)/0.3$ are the conditioned stationary probabilities of states 0 and {3, 4} in the vaccinees and controls. In this model, the competition parameter has the same value (0.4) for all pairs of strains and the overall efficacies based on (1) and (2) are thus equivalent (cf. Web Appendix A).

Throughout, we assume no interference among study subjects, and that the rate of exposure to colonisation does not change. This would be plausible if a small proportion of the population took part in the trial, such as a portion of infants. Under randomisation, expected exposure to colonisation would be the same in vaccinees and non-vaccinees. However, even under these circumstances, the hazards of acquiring non-vaccine strains would differ between vaccinees and non-vaccinees if not conditioned on current state of colonisation, because total time at-risk is distributed differently among the states of colonisation. The very motivation of this research is to elucidate the definition and estimation of vaccine efficacy in such situations.

4. Cross-sectional estimation of vaccine efficacy against colonisation

Here we present the main results of this paper by formulating expressions for VE_acq in (1) and (2) in terms of the stationary distribution, the stationarity requirement being imposed separately on the unvaccinated and vaccinated groups. Estimation of vaccine efficacy can then be based on these expressions, relying solely on cross-sectional measurement of colonisation. The following results are valid under model A. Derivation of results, proofs, and applicability under model B are shown in Web Appendix A. Let $p_{[k]}^C$ and $p_{[k]}^T$ denote the stationary probabilities of state [k] ∈ 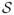in the non-vaccinated (C) and vaccinated groups (T).

Result 1

The overall vaccine efficacy against a collection of vaccine strains W (⊆ V), as defined by (1), can be expressed in terms of the stationary probabilities as

$${\text{VE}}_{W\mid 0}=1-\frac{p_W^T/p_{{\overline{\mathcal{V}}}_0}^T}{p_W^C/p_{{\overline{\mathcal{V}}}_0}^C}\equiv 1-\frac{\left({\displaystyle \sum _{[k]\in W}}{p}_{[k]}^T\right)/\left({\displaystyle \sum _{[k]\in {\overline{\mathcal{V}}}_0}}{p}_{[k]}^T\right)}{\left({\displaystyle \sum _{[k]\in W}}{p}_{[k]}^C\right)/\left({\displaystyle \sum _{[k]\in {\overline{\mathcal{V}}}_0}}{p}_{[k]}^C\right)}.$$ (4)

Expression (4) for VE_W|0 has the form `one minus an odds ratio’. The odds of being vaccinated (T vs. C) are compared between those colonised with the target strains and those colonised with the non-vaccine strains. The possible target states W include all singly-colonised states for any target strain. The reference states 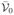involve all states in which no vaccine-strain is involved.

Instead of using 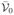as the reference set, it is possible to restrict the comparisons to state 0 (uncolonised). With this choice and using the non-vaccine strains as the target set, we obtain the following expression for vaccine efficacy against the non-vaccine strains to estimate (3):

$${\text{VE}}_{\overline{V}\mid 0}=1-\left\{\left(\sum _{[k]\in \overline{V}}{p}_{[k]}^T\right)/p_0^T\right\}/\left\{\left(\sum _{[k]\in \overline{V}}{p}_{[k]}^C\right)/p_0^C\right\}.$$ (5)

If the model is correctly specified, the theoretical value of (5) is 0, so the estimate of VE_V̄|0 should be close to zero (see Web Appendix A).

Result 2

The overall vaccine efficacy against a collection of vaccine strains W (⊆ V), as defined by (2), can be expressed in terms of the stationary probabilities as

$${\text{VE}}_{W\mid {\overline{V}}_0}=1-\frac{p_{\mathcal{W}}^T/p_{{\overline{\mathcal{V}}}_0}^T}{p_{\mathcal{W}}^C/p_{{\overline{\mathcal{V}}}_0}^C}\equiv 1-\frac{\left({\displaystyle \sum _{[k]\in \mathcal{W}}}{p}_{[k]}^T\right)/\left({\displaystyle \sum _{[k]\in {\overline{\mathcal{V}}}_0}}{p}_{[k]}^T\right)}{\left({\displaystyle \sum _{[k]\in \mathcal{W}}}{p}_{[k]}^C\right)/\left({\displaystyle \sum _{[k]\in {\overline{\mathcal{V}}}_0}}{p}_{[k]}^C\right)}.$$ (6)

As with VE_W|0 in (4), the reference set 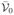includes all those states in which no vaccine-strain is involved. Instead of the singly colonised states W, the target states 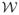now include all those states in which one of the target strains is involved either alone or together with a non-vaccine strain (Figure 2).

Expressions (4)–(6) provide estimators in terms of proportions of the subjects in different states of colonisation in the stationary phase. Thus, under stationary conditions both strain-specific efficacies and overall efficacy can be estimated without expensive and invasive longitudinal observation using standard methods for estimating odds ratios.

Illustration, cont’d

Table 2 demonstrates how to calculate estimates based on VE_W|V̄0 in (6) from observed strain distributions.

Table 2.

Estimation of vaccine efficacy from cross-sectional data. The table presents one simulated data set for 1000 vaccinated and 1000 control (non-vaccinated) individuals at the stationary phase in model A for two vaccine strains (1 and 2) and two non-vaccine strains (3 and 4), with hazards of colonisation 0.07, 0.06, 0.05, and 0.04 per time unit. The hazard of clearance (μ) was 0.17 per time unit, and the relative hazards for acquisition of double carriage (q_{j, ij}/q_{0, i}) was 0.4 for all i; j, see eq. (A1). For each strain, the numbers of observations are given for the singly and the three doubly-colonised states with that strain. The last column shows how to calculate vaccine efficacy against individual and all vaccine-strains (VS) by using estimator (6) for VE_W|V̄0, and vaccine efficacy against individual and all non-vaccine strains (NVS) by using estimator (5). The true values of vaccine efficacy are given in the first column. The true value of the overall efficacy against the vaccine-strains is VE_{V| V̄0} = VE{1;2}|{0, 3, 4} = 0.56, based on definition (2) and equation (E1)

True efficacy	States of colonisation	Numbers of samples in vaccinees	Numbers of samples in controls	Estimates of vaccine efficacy VEW|V̄0
0.70 (VE1)	1+1&2+1&3+1&4	61 + 4 + 7 + 6	162 + 29 + 18 + 9	$1-\frac{(61+7+6)/(522+260+13)}{(162+18+9)/(403+207+9)}=0.70$
0.40 (VE2)	2+1&2+2&3+2&4	107 + 4 + 12 + 8	136 + 29 + 17 + 10	$1-\frac{(107+12+8)/(522+260+13)}{(136+17+10)/(403+207+9)}=0.39$
0.00 (VE3)	3+1&3+2&3+3&4	131 + 7 + 12 + 13	111 + 18 + 17 + 9	$1-\frac{131/522}{111/403}={0.09}^{\ast }$
0.00 (VE4)	4+1&4+2&4+3&4	129 + 6 + 8 + 13	96 + 9 + 10 + 9	$1-\frac{129/522}{96/403}=-{0.04}^{\ast }$
0.56 (all VS)	VS+VS& NVS+VS&VS†	168 + 33 + 4	298 + 54 + 29	$1-\frac{(168+33)/(522+260+13)}{(298+54)/(403+207+9)}=0.56$ ††
0.00 (all NVS)	NVS+VS & NVS+NVS& NVS†	260 + 33 + 13	207 + 54 + 9	$1-\frac{260/522}{207/403}={0.03}^{\ast }$
0	–	522	403	–

^*For efficacy against non-vaccine strains, the reference state is 0 and estimator (5) was used.

^†VS&NVS is the number of subjects colonised with a vaccine-strain and a non-vaccine strain, VS&VS is the number of subjects colonised with two vaccine-strains, NVS&NVS is the number of subjects colonised with two non-vaccine strains.

^††For the vaccine-strains, the overall estimate is based on eq. (6) for VE_V|V̄0 = VE_{{1, 2}|{0, 3, 4}}. An alternative estimate given by eq. (4) is VE_V|0 = VE_{{1, 2}|0} = 1− (168/(522+260+13))/(298/(403+207+9)) = 0.56.

5. The aggregated model and sufficient conditions

To analyse the robustness of the proposed estimators to departures from the assumptions in Section 2, we formulate a sufficient set of conditions that still allows valid estimation of VE_acq from cross-sectional data. Consider the partition of the original set of colonisation states into three aggregated states (Figures 2A and 2B). The partition consists of the reference set 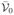, i.e., the colonisation states, including state 0, for which the vaccine has no direct effect on the hazard of entering these states, the target set 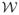, and the “rest” 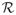. We specify a new Markov model for the three aggregated states by defining the hazards of transition from one aggregate state to another in terms of the underlying transition hazards as follows:

$$q_{U,P}=\sum _{[h]\in U}{\overline{p}}_{[h]U}\left(\sum _{[k]\in P}{q}_{[h][k]}\right),U,P\in \{{\overline{\mathcal{V}}}_0,\mathcal{W},\mathcal{R}\},U\ne P,$$ (7)

where p̄ _[h]|U denotes the stationary probability of the state [h], conditioned upon the aggregate state U, and q_[h][k] is the transition hazard from state [h] to state [k] (see Deng et al. (2009) for theoretical justification).

Under the aggregated model, it is natural to define another VE_acq for susceptibility of acquisition of strains in set W as

$${\text{VE}}_{W\mid {\overline{V}}_0}=1-q_{{\overline{\mathcal{V}}}_0,\mathcal{W}}^T/q_{{\overline{\mathcal{V}}}_0,\mathcal{W}}^C,$$ (8)

i.e., the relative reduction in the hazard 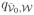due to vaccination. This estimand is equivalent to (2) (see Web Appendix A for details). In addition, expression (6) for VE_W|V̄0 can be interpreted as based on the aggregated model since the stationary distribution of the aggregated process is obtained by summing up the respective stationary probabilities under model A. It follows that, for any choice of the target strains, it is possible to formulate a smaller set of conditions directly in the context of the aggregated model that allows cross-sectional estimation of VE_acq. In the following we summarise these conditions.

For W = V, i.e., when estimating overall efficacy against all vaccine strains, the aggregated model has a simple chain structure of three states: 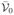↔ ↔ 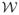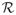(Figure 2A). It is then easy to show by the reversibility of chain models that the only condition required for cross-sectional estimation is the similarity of clearance hazards of the aggregate states 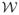in the vaccinees and controls: (B5) $q_{\mathcal{W},{\overline{\mathcal{V}}}_0}^C=q_{\mathcal{W},{\overline{\mathcal{V}}}_0}^T$.

Likewise, if the reverse hazards 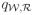and 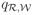satisfy the symmetry condition ( 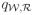/ 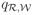= 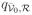/ 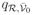), the essential model structure at stationarity is again a chain between three states: 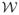↔ ↔ 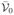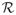and (B5) is sufficient to estimate vaccine efficacy against any collection of vaccine strains (W ⊂ V). Only when W is a strict subset of V and the competition is not symmetric, the aggregated model has the triangle structure (Figure 1B), and the conditions are more restrictive. Specifically, they are (B1)–(B4) for model B with three states corresponding to 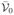, , 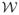and 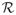(see Web Appendix A for more details).

6. Simulations, sensitivity analyses, and data analyses

Simulated examples

We conducted a simulation study with four vaccine and five non-vaccine strains under model A to examine the performance of the proposed cross-sectional estimators. We chose the hazards of colonisation, q_{0, i}, i = 1, …, 9, and the hazard of clearance μ so the stationary strain distribution mimics that typical of serotypes of S. pneumoniae, with prevalence ranging from approximately 20% for the most common type to < 2% for rare types. Repetitions of samples in a cohort of 1000 vaccinees and 1000 unvaccinated controls were taken at the stationary phase of the process satisfying conditions (A1)–(A4).

Estimates of VE_acq based on VE_W|V̄0 or VE_W|0 were similar (Table 3), with both producing estimates close to the true values. Coverage probabilities are almost equal to the nominal confidence interval (90%). The use of VE_W|V̄0 produces somewhat more precise estimates because a larger portion of the data is used. The slightly negative bias in the point estimates is due to bias in odds-ratio estimates from finite samples (see Web Appendix C Table C1).

Table 3.

Performance of cross-sectional estimators of vaccine efficacy assuming perfect detection of the singly and doubly-colonised states. The results are based on 1000 simulated data sets, each with 1000 vaccinees and 1000 controls. The model consisted of 4 vaccine (shown in boldface) and 5 non-vaccine strains, with hazards of colonisation 0.0075, 0.003, 0.002, 0.001, 0.005, 0.003, 0.0009, 0.0005, and 0.0003 per time unit (day). The relative hazard for acquisition of double carriage (q_{j, ij}/q_{0, i}) was 0.4 for all i, j. The hazard of clearance μ was 0.017 per day. The simulation was started from state 0 (uncolonised) for each individual and the sample for calculating the vaccine efficacy was taken at day 183. The true vaccine efficacy was 0.70 against strains 1 and 3, and 0.40 against strains 2 and 4. The true value of the overall efficacy is VE_V|V̄0 = 0:61, based on definition (2) and equation (E1). The program code to analyse an example data with 9 strains is provided in a Web Appendix B.

Strain	True efficacy	No. of singly and doubly colonised samples† (% of all samples)		Estimates of vaccine efficacy (SE log(OR); 90 % cov. prob.)††
		Vaccinees	Controls	VEW|V̄0	VEW|0
1	0.7	66 + 19(8.5)	166 + 61(22.7)	0.70(0.14; 0.91)	0.70(0.16; 0.91)
2	0.4	53 + 16(6.9)	66 + 31(9.7)	0.39(0.18; 0.90)	0.39(0.19; 0.90)
3	0.7	18 + 6(2.4)	44 + 22(6.6)	0.70(0.27; 0.90)	0.69(0.29; 0.91)
4	0.4	17 + 6(2.3)	22 + 11(3.3)	0.38(0.30; 0.91)	0.37(0.33; 0.92)
5	0	146 + 34(18.0)	110 + 46(15.6)	−0.01(0.14; 0.90)*	−0.01(0.14; 0.90)*
6	0	88 + 24(11.2)	66 + 31(9.7)	−0.01(0.18; 0.92)*	−0.01(0.18; 0.92)*
7	0	26 + 9(3.5)	20 + 10(3.0)	−0.06(0.31; 0.92)*	−0.06(0.31; 0.92)*
8	0	15 + 5(2.0)	11 + 6(1.7)	−0.13(0.42; 0.90)*	−0.13(0.42; 0.90)*
9	0	9 + 3(1.2)	6 + 4(1.0)	−0.18(0.56; 0.92)*	−0.18(0.56; 0.92)*
Vaccine strains	0.61	154 + 41(19.5)	298 + 96(39.4)	0.61(0.10; 0.90)	0.61(0.11; 0.89)
Non-vaccine strains	0	284 + 55(33.9)	213 + 82(29.5)	0.00(0.11; 0.91)*	0.00(0.11; 0.91)*
0		501(50.1)	378(37.8)	–	–

^*For efficacy against non-vaccine strains, the reference state is 0 and estimator (5) was used.

^†The mean number of samples in the 1000 simulated data sets.

^††The average standard error of the log odds ratio, based on the 1000 simulated data sets. The coverage probability of a 90% confidence interval, based on the 1000 simulated data sets.

Table 4 presents estimates of VE_acq in a similar scenario, except the observed data for any individual included at most one strain. This was achieved by randomly dropping one strain in any simulated sample with two simultaneous strains (approximately 20% of positive samples) and using estimator (4). As a general finding, this type of symmetry in missing data does not appear to affect the efficacy estimates. The estimates were not biased under heterogeneous clearance rates across individuals either (data not shown).

Table 4.

Performance of cross-sectional estimation of vaccine efficacy under imperfect detection of double colonisation. The simulated complete data were the same as used in Table 3. Consequently, all doubly-colonised states were recorded as singly-colonised, with 50% chance of either of the colonising strains being detected.

Strain	True efficacy (VEi)	No. of colonised samples† (% of all samples)		Estimates of vaccine efficacy (SE log(OR); 90% cov. prob.)††
		Vaccinees	Controls	VEW|V̄0	HRK
1	0.7	75(7.5)	196(19.6)	0.70(0.15; 0.90)	0.66(0.14; 0.78)
2	0.4	61(6.1)	82(8.2)	0.42(0.18; 0.90)	0.27(0.18; 0.72)
3	0.7	21(2.1)	55(5.5)	0.71(0.27; 0.89)	0.64(0.27; 0.84)
4	0.4	20(2.0)	28(2.8)	0.40(0.30; 0.90)	0.24(0.30; 0.83)
5	0	163(16.3)	133(13.3)	0.07(0.14; 0.85)*	−0.28(0.13; 0.40)
6	0	100(10.0)	81(8.1)	0.07(0.16; 0.86)*	−0.27(0.16; 0.59)
7	0	31(3.1)	25(2.5)	0.05(0.28; 0.88)*	−0.27(0.28; 0.82)
8	0	17(1.7)	14(1.4)	0.00(0.38; 0.91)*	−0.34(0.38; 0.86)
9	0	10(1.0)	8(0.8)	−.06(0.50; 0.91)*	−0.42(0.49; 0.88)
Vaccine strains	0.61	177(17.7)	361(36.1)	0.62(0.11; 0.88)	0.62(0.11; 0.88)
Non-vaccine strains	0	321(32.1)	261(26.1)	0.08(0.11; 0.80)*	−0.33(0.10; 0.11)
0		502(50.2)	378(37.8)

^*For efficacy against non-vaccine strains, the reference state is 0 and estimator (5) was used.

^†The mean number of samples in the 1000 simulated data sets.

^††The average standard error for the log odds ratio, based on the 1000 simulated data sets. The coverage probability of a 90% confidence interval, based on the 1000 simulated data sets.

The last column in Table 4 presents the estimates of VE_acq proposed by Rinta-Kokko et al. (2009) (HRK), based on simple odds ratios obtained by splitting the observations into two complementary categories for each choice of the target strain(s). Such estimates are straightforward to calculate in a setting in which observations do not record double colonisation. However, this estimator does not take into account interactions between strains, thus systematically underestimates the strain-specific efficacies. In particular, estimates for the non-vaccine strains are grossly negative. Only the overall efficacy against all vaccine-strains agrees with the true value, which follows directly from the fact that expression (6) is equivalent to the simple odds ratio in this case.

Sensitivity to model assumptions

To study sensitivity of the cross-sectional estimates to departures from model assumptions, we performed a simulation study for 9 strains, similarly as in Table 3. To estimate overall vaccine efficacy, the only assumption required is (B5). When vaccine enhances clearance of vaccine strains, violating (B5), the mean of the cross-sectional estimator (6) was close to a combined efficacy 1 − (1 − VE_{W| V̄0})(1−VE_D) where VE_D is one minus the ratio of mean duration of colonisation in vaccinees to that in controls (Web Appendix C Table C2). The combined efficacy could not be estimated as well if vaccine decelerates clearance, which, however, is an implausible assumption. The estimate based on (6) can thus be interpreted more generally as a summary measure of the effect of being vaccinated on susceptibility to acquisition and on duration of colonisation. If individuals are infectious throughout colonisation, this quantity is related to the transmission potential of the strain in question (Rinta-Kokko et al. 2009; Becker and Starczak 1998). Similar results were obtained in extensive simulation studies for strain-specific efficacy against the transmission potential under symmetric competition between strains.

The theoretical results of Section 5 further mean the cross-sectional estimators for overall and strain-specific efficacy are also applicable with any difference in the clearance rates of the target strain and those in the class “rest”, at least under symmetric competition. We verified this by simulations in which the ratio of clearance rates for the target and the rest was as large (small) as 2 (0.5) (Web Appendix C Table C3). The same finding applies to the combined efficacy when the vaccine affects clearance (data not shown).

Analysis of two pneumococcal vaccine trials

We used the cross-sectional estimators of vaccine efficacy to analyse data from the two randomised, controlled trials of the effect of pneumococcal conjugate vaccination on colonisation (Table 1). In both studies, double colonisation had not been recorded and, consequently, we calculated estimates based on (4) (for the vaccine types) and (5) (for the non-vaccine types). These can be interpreted as estimates of VE_acq in those individuals susceptible to acquisition. In both studies, vaccine efficacy against colonisation is estimated to be in the range 0.4–0.8 for most serotypes, although confidence intervals are wide. The overall efficacy against the non-vaccine types does not differ from 0 in either of the studies. The HRK efficacy estimates based on the simple odds ratios that do not adjust for within-host replacement in the last column are consistently smaller, demonstrating that the adjustment for time at-risk makes a difference.

7. Discussion

In this paper we consider estimation of VE_acq, vaccine efficacy against susceptibility to asymptomatic infection by a microorganism with multiple interacting strains, from cross-sectional data. We propose two estimands of VE_acq which differ in the way they condition on being at-risk to acquire the target strains. Specifically, VE_W|0 is based on the relative reduction in the overall hazard of acquiring the target strains in an uncolonised individual whereas VE_W|V̄0 is based on the corresponding hazard in all those susceptible to acquiring the target strains. The first has an individual level interpretation and would ideally be estimated from longitudinal data in the context of a (Markov) transition model. The second has a population level interpretation as the average efficacy under stationary conditions. Both estimands can be used for any set of strains and are coherent in the sense that the efficacy against all target strains is a weighted average of the respective strain-specific efficacies.

In practice, estimates of VE_W|0 and VE_W|V̄0 are similar when double colonisation is un-common. Moreover, we showed assuming symmetry in competition, the two estimands are equivalent in any strain-specific analysis. For better statistical efficiency, estimates of VE_W|V̄0 seem therefore preferable on most occasions. Under quite general conditions, the estimators yield the combined efficacy against susceptibility to acquisition and duration of colonisation. In particular, no assumption is needed about the clearance rates of the target strains and the rest. If the overall clearance rate of the target strains is not affected by vaccination, both estimators collapse to VE_acq. When competition between the target strain and the other vaccine-strains is not very asymmetric, the key assumption is stationarity.

Pneumococcal vaccine trials are most often conducted in infants, in whom a relatively stationary colonisation is achieved in unvaccinated individuals a few months after birth (e.g. Granat et al., 2007). In vaccinees, such data are more scarce, but it is plausible that a similar time period is sufficient to achieve stationarity (Nohynek et al., 2008). In our simulations, taking samples six months after vaccination was enough for successful cross-sectional estimation of vaccine efficacy. If using the proposed method in a specific epidemiologic setting, the appropriate sampling time should be examined by simulation.

To differentiate the effect of vaccination on acquisition and clearance rates requires longitudinal data. Vaccine-induced changes in the average clearance rate of vaccine strains through direct biological enhancement by vaccination on clearance is not supported by available data in the pneumococcal context (O’Brien et al., 1997; Dagan et al., 2002). Vaccination could also affect average clearance rates by changing the within-host mixture of vaccine-strains. This situation would require large differences in strain-specific efficacy for susceptibility and a wide distribution of clearance rates across different strains. Such differences are not evident between the pools of pneumococcal vaccine and non-vaccine serotypes although differences exist among individual serotypes (e.g. Lipsitch et al., 2012). Nevertheless, in these situations, we show the combined efficacy against susceptibility and duration is estimable from cross-sectional data if vaccination does not markedly lengthen duration of vaccine-strain colonisation.

The difference between estimates of VE_W|V̄0 and the simple HRK estimates can be considerable for strain-specific efficacies (Tables 1 and 4). For pivotal trials with colonisation endpoints, VE_W|V̄0 appears more justifiable as a measure of the biological effect of the vaccine on transmission potential or susceptibility to acquisition. This estimand is also more likely comparable across epidemiological settings with differing levels of competing exposure by non-vaccine strains. By contrast, the simpler HRK estimate with an anticipated negative efficacy for non-vaccine strains may be more informative about the extent of replacement colonisation. Furthermore, a difference between the HRK estimate and the adjusted one for overall non-vaccine strains could give an indication of between-strain competition.

The a priori partition of strains into vaccine and non-vaccine strains is important in choosing the appropriate reference set of colonisation states ( ). Some non-vaccine pneumococcal serotypes, however, may be affected by the vaccine through cross-immunity (Dagan et al., 2002). In this case, we showed the comparison set can be restricted to a smaller set of non-vaccine strains or even to the uncolonised state. The same argument can be applied in trials in which the control vaccine is another pneumococcal vaccine with a possibly different composition of vaccine-strains compared to the experimental vaccine.

A potential caveat in all approaches to estimating vaccine efficacy for multiple strains is the sensitivity of detection is less than perfect. In this study, the robustness of the suggested aggregation was shown with regard to complete insensitivity to detect double colonisation. However, the situation could be different with differential sensitivity across strains and under asymmetric competition between strains.

The proposed method of cross-sectional measurement of hazard ratios has a close connection to risk-set sampling in nested case-control studies. In particular, hazard ratios can be estimated by selecting controls from those at risk of the event of interest at the incident times of the cases (Wacholder et al., 1998). In the current setting with many states, the at-risk set corresponds to states from which there are arrows to the target states (Lubin, 1986). Specifically, although the setting in this paper is prospective, it can be cast as a case-control study. The “cases” are prevalent, i.e., subjects colonised with the target strains, while the “controls” are those in states from which a transition to the target state is possible or, more generally, states upon which the exposure (vaccine) does not have a direct effect. In contrast to nested case-control studies, cases themselves must not be included in the risk set.

Open questions for future research include incorporating asymmetric competition, heterogeneous response to vaccination, and allowing hazard rates of colonisation to change during the study. In the meantime, we have demonstrated under broadly general conditions, cross-sectional data can be used to estimate the protective effect of vaccination on colonisation.