Distinct Mutational Behaviors Differentiate Short Tandem Repeats from Microsatellites in the Human Genome

Abstract

A tandem repeat’s (TR) propensity to mutate increases with repeat number, and can become very pronounced beyond a critical boundary, transforming it into a microsatellite (MS). However, a clear understanding of the mutational behavior of different TR classes and motifs and related mechanisms is lacking, as is a consensus on the existence of a boundary separating short TRs (STRs) from MSs. This hinders our understanding of MSs’ mutational properties and their effective use as genetic markers. Using indel calls for 179 individuals from 1000 Genomes Pilot-1 Project, we determined polymorphism incidence for four major TR classes, and formalized its varying relationship with repeat number using segmented regression. We observed a biphasic regime with a transition from a faster to a slower exponential growth at 9, 5, 4, and 4 repeats for mono-, di-, tri-, and tetranucleotide TRs, respectively. We used an in vitro mutagenesis assay to evaluate the contribution of strand slippage errors to mutability. STRs and MSs differ in their absolute polymorphism levels, but more importantly in their rates of mutability growth. Although strand slippage is a major factor driving mononucleotide polymorphism incidence, dinucleotide polymorphism incidence is greater than that expected due to strand slippage alone, indicating that additional cellular factors might be driving dinucleotide mutability in the human genome. Leveraging on hundreds of human genomes, we present the first comprehensive, genome-wide analysis of TR mutational behavior, encompassing several motif sizes and compositions.

Introduction

Tandem repeats (TRs) of short (1–6 bp) DNA sequences constitute approximately 3% of the human genome (Lander et al. 2001). Microsatellites (MS) are TRs that have high germline mutation rates in humans (10⁻² to 10⁻⁴ per locus per generation [Ellegren 2004]), resulting in high polymorphism levels at such loci across populations. As a consequence, MSs have become useful markers for population genetics, forensics, and association studies (Ellegren 2004). Although many MSs are thought to evolve neutrally, some play an important role in the regulation of gene activity and in protein function, particularly by encoding amino acid repeats (Li et al. 2004; Kelkar et al. 2011). Indeed, MS polymorphisms can affect gene expression (reviewed in Gemayel et al. [2010]) and approximately 17% of human genes contain MSs within their open reading frames. Polymorphic MSs are significantly enriched within human genes involved in transcriptional regulation, chromatin remodeling, morphogenesis and neurogenesis (Legendre et al. 2007), and MS allele variants are implicated in over 40 human neurological/neuromuscular diseases (reviewed in Pearson et al. [2005]).

The expansion and contraction of TRs are largely attributed to strand slippage during DNA synthesis associated with replication, repair, and/or recombination (Levinson and Gutman 1987; Ellegren 2000). The propensity of TRs to mutate increases with their repeat number, likely to reflect the increased probability of strand slippage with length (Ellegren 2000; Ellegren 2004; Kelkar et al. 2008). Several studies have shown that starting at a certain repeat number, a TR can acquire mutation rates greater than those of non-repetitive loci and/or loci with just two repeats (Messier et al. 1996; Eckert et al. 2002; Eckert and Hile 2009; Kelkar et al. 2010). These observations form the basis of the threshold hypothesis, which proposes the existence of a critical repeat number or length at which a short TR (STR) becomes an MS—a hotspot for DNA mutation. Although the idea of an MS threshold has been investigated by numerous studies and approaches, a consensus on its existence, exact value(s), and differences across TRs of different motifs is yet to be reached (Jurka and Pethiyagoda 1995; Messier et al. 1996; Bell and Jurka 1997; Cox and Mirkin 1997; Dechering et al. 1998; Field and Wills 1998; Rose and Falush 1998; Dieringer and Schlotterer 2003; Lai and Sun 2003). Moreover, several studies offered evidence of slippage and slippage-like processes contributing to expansions and contractions of very STRs (Zhu et al. 2000; Dieringer and Schlotterer 2003; Messer and Arndt 2007), which has led some investigators to question the very notion of an MS threshold (Pupko and Graur 1999; Noor et al. 2001; Sokol and Williams 2005; Leclercq et al. 2010). Although slippage does occur at very STRs, its rate at such repeats is extremely low (Kunkel 1990; Eckert et al. 2002; Garcia-Diaz and Kunkel 2006).

Recently, we reported the results of a computational procedure to assess the effect of length on polymorphisms (a proxy for slippage rates) for TRs identified in human populations, and an experimental procedure to determine in vitro polymerase DNA error rates at these TRs (Kelkar et al. 2010). Polymorphism rates for (A/T)_n and (GT/CA)_n were estimated from 10 Encyclopedia of DNA elements (ENCODE) regions sequenced for 48 human genomes, and compared with background slippage rates. Remarkably, the computational and experimental findings for (GT/CA)_n repeats were in strong agreement, indicating that slippage rates are significantly elevated above background slippage rates at 10 bps (repeat number 5)—which we proposed as the MS threshold for these repeats. Computational findings for (A/T)_n repeats also identified their MS threshold at a length of approximately 10 bps (repeat number 10), suggesting that length in base pairs, and not just repeat number, might affect MS mutational behavior.

In this study, we examine how the mutational behavior of a TR depends on its length, motif size, and sequence composition. This pursuit is of paramount importance; determining the length at which MSs become highly mutable is crucial for computational and statistical analyses of their genomic occurrence, distribution, and mutational properties (mechanisms and rate variation). In turn, an accurate assessment of MS mutational properties is essential for their effective use as genetic markers. The availability of sequenced human genomes from the Pilot 1 phase of the 1000 Genomes Project (The 1000 Genomes Project Consortium 2010) provides an excellent opportunity to study the incidence of TR polymorphism and changes in mutational behavior that occur on a genome-wide scale and across human populations. We used this rich data set of 179 individual human genomes from East Asian (JPT and CHB, referred to as JPTCHB henceforth), European (CEU) and African (YRI) populations to compute polymorphism incidence of four TR classes (mono-, di-, tri-, and tetranucleotides) and subclasses (by motif composition and repeat secondary structure potential), and formalized the relationship between polymorphism incidence and repeat number with segmented regression models. Moreover, we used an in vitro assay to assess the contribution of DNA polymerase strand slippage errors to polymorphism incidence for mono- and dinucleotide TRs, and thus shed light on mechanisms underlying the mutational behavior of TRs. Taken together, our results indicate that STRs and MSs differ not only in their absolute levels of polymorphism, but also in the rate of exponential growth of polymorphism incidence with repeat number. Paradoxically, although MSs mutate at higher rates than do TRs before the threshold, mutability grows at a slower rate after crossing the threshold (after STRs become MSs). The change points in mutational behavior that we identify here correspond to previously defined MS threshold values. Our results also indicate that mono- and dinucleotide TRs may be differentially modulated by slippage and other biochemical processes.

Materials and Methods

Identification of TRs

The indels called by the Pilot 1 of the 1000 Genome Project using Dindel (indels for the two sex chromosomes were not available due to lack of imputation and polarization on these chromosomes using chimpanzee, gorilla, orangutan, and macaque genomes; the Y chromosome data are missing for several of these genomes [Montgomery et al. 2013]) were intersected with a comprehensive list of TRs identified via a custom script in the March 2006 assembly of the human genome (hg18). Compound TRs (i.e., those containing different repeated motifs) and TRs within 10-bp of each other were filtered out, and the final list consisted of simple TRs (containing a single repeated motif).

Identification of Polymorphic TRs

Putative TR-containing indels (obtained earlier) were filtered to retain only those containing repeat number alterations. This resulted in a set of polymorphic TR loci that have undergone expansion or contraction in the populations under consideration. The allele frequencies of the indels were then used to adjust the repeat numbers of these polymorphic TRs. This adjusted repeat number was equated to the repeat number of the TR allele created by indel polymorphism if the allele frequency of the indel was ≥0.05, and to that of the hg18 TR otherwise. The 5% allele frequency cut-off ensures that a TR allele is supported by at least three individuals in each population (the number of samples per indel was in the range of 58–60, 51–52, and 57–58 for over 90% of the indels in YRI, CEU, and JPTCHB, respectively).

Estimation of Polymorphism Incidence at TR Loci

Polymorphism incidence was estimated as the proportion of polymorphic TRs present at each repeat number bin. Only bins containing at least 100 TR loci were considered to minimize estimation biases due to small sample sizes. To obtain bootstrap bands around polymorphism incidence curves, the TR loci within each bin were sampled with replacement 1,000 times, polymorphism incidence values were computed for each bootstrap sample, and 95% bands were then extended from the 2.5th to the 97.5th percentiles of these values.

Polymorphism incidence of nonrepetitive loci (NR) was computed as the proportion of NR loci containing indels, and polymorphism incidence of SNPs was computed as the proportion of genome-containing SNPs. Data for these were obtained from Montgomery et al. 2013.

Dindel

As mentioned earlier, we used indel calls produced by Dindel on the 1000 Genome Pilot 1 data (Montgomery et al. 2013). Dindel is a software program, which uses a Bayesian approach to call short (≤50 bp) indels from short-read sequencing data (Albers et al. 2010). The version of Dindel we employed incorporates an error model for homopolymer TRs. The current implementation of Dindel produces only one alternative allele per locus.

Segmented Regression

In symbols, a segmented regression model (Muggeo 2003) comprising one predictor and one change point, can be written as:

The R package “segmented” (http://cran.r-project.org/web/packages/segmented/index.html; [Muggeo 2008]) provides functions to fit segmented regressions with one or more predictors, including the estimation of change points, and to assess through statistical tests whether differences in slope before and after change points are significant. We used the segmented() function to fit segmented regressions for polymorphism incidence (response) on repeat number (predictor), and estimate change points, for various classes of TRs. We also used the davies.test() function to test differences in slopes before and after the change points.

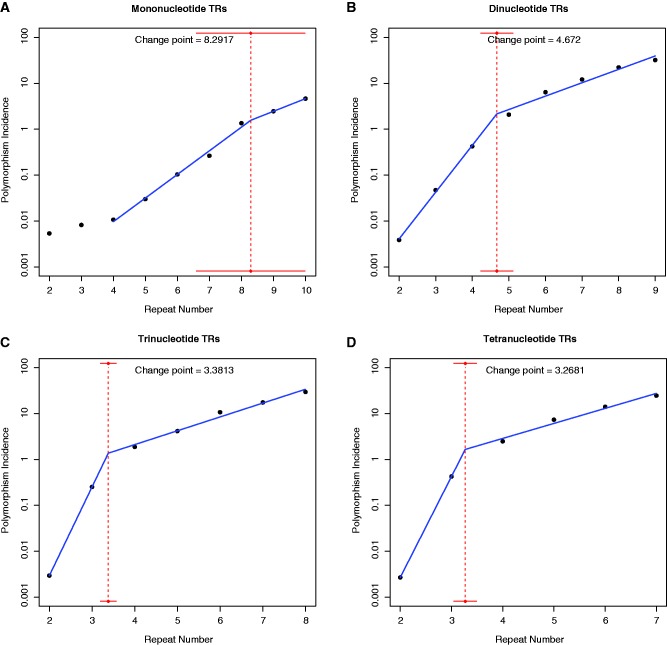
The accuracy of change point estimation depends on sample size, location of the change point, and extent to which the relationship is modified before and after the change point. Large sample size, a change point in the mid-range of x, and a high (absolute value) difference in slopes all contribute to estimation accuracy. Although in our application sample sizes for all TR classes are small (9,8,7, and 6 for mono-, di-, tr-, and tetranucleotide TRs, respectively), we observe a substantial (and statistically significant) difference in slopes, and a change point located in the mid-range of repeat numbers, for di, tri, and tetranucleotide TRs; our change point estimation in these cases is accurate (low standard error; tight confidence intervals). For mononucleotide TRs, the segmented regression for mononucleotides encounters two issues: 1) Convergence: When attempting to fit a segmented regression on the entire range of repeat numbers (2–10) the algorithm fails to converge (technically, this is due to the fact that the “gap” between the straight lines before and after the change point fails to reach zero). Convergence is achieved when limiting the range to 4–10 repeats. Thus, we fitted the segmented regression for mononucleotides in the repeat range 4–10. 2) Change point estimation: The change point estimate exhibits large standard error (broad confidence intervals in fig. 2A). Indeed, the difference in slopes, albeit statistically significant, is smaller than for di-, tri-, and tetranucleotide TRs, and most importantly, the change point lies closer to the upper limit of the observed repeat number range (our data set does not contain mononucleotide TRs above 10 bps due to high sequencing errors, so we cannot adequately capture the polymorphism incidence variation at longer repeats). The small difference in slope and the peripherally located change point likely contribute to the large standard error in change point estimation.

Fig. 2.—

European (CEU) population: log of polymorphism incidence (see also fig. 1, black symbols) against repeat number, with fits from segmented regression (blue), for (A) mono-, (B) di-, (C) tri-, and (D) tetranucleotide TRs. Dotted vertical red lines show the location of the change points. Horizontal red lines represent 90% confidence intervals for change points. For mononucleotides, values at repeat number 2 and 3 were not included in the segmented regression fit due to convergence issue (see Materials and Methods for details).

Secondary Structures for Tri- and Tetranucleotide TRs

We compiled a list of all motifs for which secondary DNA structures have been determined by previous studies (Wang et al. 2008; Zhao et al. 2010). For the remaining motifs, the structure was designed as 1) triplex if the resulting repeat contained homopurine or homopyrimidine sequences with mirror symmetry (Wang et al. 2008; Zhao et al. 2010); 2) hairpin/cruciform if the resulting repeat contained inverted bases which could base-pair with one another (Wang et al. 2008; Zhao et al. 2010); and 3) lacking secondary structure if it could not be classified as triplex or hairpin.

Estimation of θ

Stepwise mutation models, which allow for stepwise changes of repeat size of alleles, have been extensively used to study MSs. The sample homozygosity model is one of such stepwise models, and incorporates information on both number of alleles and allele frequency (Xu and Fu 2004). Using this model, we can estimate the composite parameter θ = 0.5 (1/F² − 1), where F is the sample homozygosity defined as F = n (Σ_{(i = 1…k)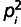} − 1)/(n − 1), and p_i is the allele frequency of the ith allele in the sample, k is the number of alleles, and n is the number of samples. We estimated θ for various population-locus combinations, and averaged θs of a population by motif type and repeat number (separately for each population).

Computation of Recombination Rates of TRs

We obtained sex-averaged standardized recombination maps (partitioned into 10-kb intervals) from (Kong et al. 2010). Using tools from Galaxy (Giardine et al. 2005; Blankenberg et al. 2010; Goecks et al. 2010), each TR locus was assigned a recombination rate based on the 10-kb interval it belonged to. For every motif size (mono-, di-, tri-, and tetra-) and repeat number bin, the mean and median recombination rates of all TRs in the bin were computed. The polymorphism incidence values were then regressed against mean recombination rates to determine the contribution of recombination rate to TR mutability. Next, we separately pooled polymorphic and non-polymorphic loci in each TR class and compared the mean recombination rates of the two pools using a two-sample t test.

In vitro DNA Polymerase Assay

Polymerase MS unit-based indel error frequencies were determined as described (Eckert et al. 2002; Kelkar et al. 2010). The Pol EF values for (GC/CG)₂ dinucleotides, and two-, three-, and four- mononucleotide repeats (A, T, C, and G) were derived for sequences endogenous to the HSV-tk coding sequence. For all other TR motifs and lengths, pSStu1-based vectors (Hile and Eckert 2008) were constructed to contain TR sequences of varying length in-frame within the HSV-tk gene, as described (Kelkar et al. 2010). Some constructs required alteration of immediately flanking sequences to maintain the wildtype HSV-tk gene reading frame. A summary of the construct sequences is given in supplementary figure S5, Supplementary Material online. HSV-tk function of all constructs was confirmed by selective plating in the presence of trimethoprim, which selects for plasmids bearing wildtype plasmid HSV-tk, as described (Eckert et al. 1997). Gapped duplex molecules for each TR construct were generated from linear DNA fragments and single-stranded DNA (Eckert et al. 2002; Hile and Eckert 2008). In vitro primer extension reactions were carried out with 1 pmol DNA template and 10 pmol of recombinant DNA polymerase β (as described in Eckert et al. [2002]) or 15 units of human DNA polymerase α-primase (Chimerx, Madison, WI; as described in Hile and Eckert [2004, 2008]). Small fragments were generated from polymerase reaction products by Mlu I and Stu I restriction digest, and were hybridized to the appropriate gapped duplex molecule. Small fragment to gap hybridization was confirmed by agarose gel electrophoresis, and a sample was transformed by electroporation into E. coli strain FT334. Mutant selection was carried out by plating bacteria in the presence of 40 µM FUdR and 50 µg/ml chloramphenicol. The HSV-tk mutant frequency was determined as the number of FUdR-resistant + Cm^R colonies, divided by the total number of Cm^R colonies. Independent mutants were isolated from two separate polymerase reactions, and analyzed by dideoxy sequencing to identify mutations within the HSV-tk target sequence. The overall Pol EF and Pol EF for unit-based indel errors were calculated as described (Kelkar et al. 2010). To determine the combined indel Pol EF for all motifs at a particular TR length (n), TR indel mutants and total mutants (with mutations anywhere within the target) were pooled from all reactions with constructs containing TR_n. The pooled Pol indel EF was calculated as: 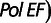for all reactions containing constructs with TR_n. The primary data are provided for mononucleotide and dinucleotide TRs in supplementary tables S7A and B, Supplementary Material online, respectively.

Results

TRs and Their Polymorphisms in the 1000 Genomes Project Data

Using the March 2006 assembly of the human genome (hg18), we identified approximately 500 million TRs (supplementary table S1, Supplementary Material online) comprising perfectly repeated sequences (simple TRs; see Methods). An analysis of interrupted TRs is the subject of another study. We focused on the four most abundant classes of TRs, namely mono-, di-, tri-, and tetranucleotide repeats, considering all loci with at least two repeats. To assess the polymorphism status of these TRs, we utilized genome-wide indel calls from the Illumina-generated Pilot 1 data of the 1000 Genomes Project, which provide a catalog of approximately 1.6 million indels identified in 179 human genomes belonging to three populations (East Asian, JPTCHB; European, CEU; and African, YRI) (Montgomery et al. 2013). These indel calls are the result of rigorous processing steps, including alignment with the indel-sensitive read-mapper Stampy (Lunter and Goodson 2011); variant calling with Dindel, which incorporates information about known variants, error models in homopolymer contexts and base quality scores (Albers et al. 2010); and polarization of identified indels using primate alignments (Montgomery et al. 2013). These processing steps ensured high specificity and sensitivity in indel variant calls, and minimized sequencing artifacts. Among Dindel’s high quality indel calls, approximately 40% were located within TRs (Montgomery et al. 2013), notwithstanding the fact that TRs cover only approximately 3% of the human genome (Lander et al. 2001). This provides a clear demonstration of polymorphism enrichment within repeat contexts. The share of TRs located in intergenic and intronic regions of the genome was approximately 93.2%, with the remaining 6.8% located in exonic and regulatory regions (including coding exons, untranslated region [UTR] exons, and 5-kb upstream and downstream from transcript boundaries), consistent with the genomic coverage of the two types of regions (92.8% vs. 7.2%; supplementary table S2, Supplementary Material online).

Modeling TR Polymorphism Incidence as a Function of Repeat Number

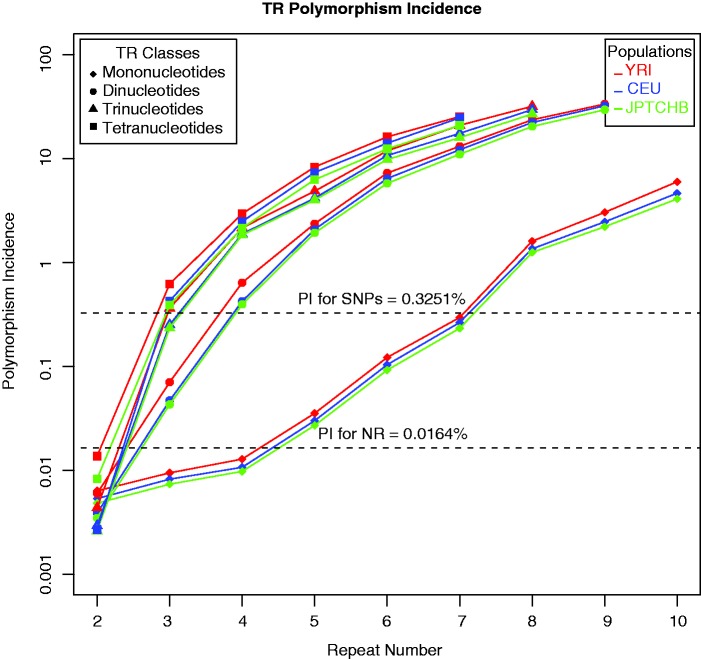
For each TR locus, we determined presence/absence of TR polymorphism, and for each polymorphic locus, we found a modal repeat number (a proxy for the most frequent, and thus likely ancestral, allele). Only indels consisting of an entire (and not partial) repeated motif were considered here. To summarize these data genome-wide, TR loci of the same motif size (e.g., dinucleotide repeats) were binned based on their modal repeat number, and for each such bin, the proportion of polymorphic loci was computed as the proportion of TRs containing an indel with an allele frequency ≥5% (see Materials and Methods). This was done separately for each population, resulting in log-scale polymorphism incidence curves versus repeat number (or length) for mono-, di-, tri-, and tetra-nucleotide repeats, as reported in figure 1A.

Fig. 1.—

East Asian (JPTCHB), European (CEU), and African (YRI) populations: polymorphism incidence (PI) curves (proportion of polymorphic TRs by increasing repeat number), separately for mono-, di-, tri-, and tetranucleotide TRs—on the log-scale.

For all four classes of TRs, polymorphism incidence increases with repeat number. However, this trend is reversed when reaching lengths close to the read length of the sequencing technology used—mainly 35-bp Illumina reads (supplementary fig. S1, Supplementary Material online). Therefore, we analyzed mono-, di-, tri-, and tetranucleotide TRs up to repeat number 10, 9, 8, and 7 (i.e., tract length 10, 18, 24, and 28 bp), respectively. The unavailability of indel calls for mononucleotide TRs over 10-bp is due to high sequencing error rates in these contexts (Albers et al. 2010; Montgomery et al. 2013). Nearly identical polymorphism incidence curves were obtained from randomly sampled subsets of individuals (of sizes ranging from 10 to 60 individuals; supplementary fig. S2, Supplementary Material online, data shown for CEU only), suggesting that our polymorphism incidence estimates are robust to differences in sample size.

To investigate how the propensity to mutate is affected by TR length, we modeled polymorphism incidence, used here as a proxy for mutability (Kelkar et al. 2010), as a function of repeat number, separately for each TR class. Previous studies have suggested that mutability grows nearly exponentially as a function of length—that is, in an almost linear way on the log-scale (Ellegren 2004; Eckert and Hile 2009). Although polymorphism incidence clearly increases with repeat number for all TR classes, we found that linear regression models for the logarithm of polymorphism incidence versus repeat number, albeit explaining large shares of the variability (R² = 82–98%, supplementary table S3A, Supplementary Material online), fail to properly recapitulate the observed data. Indeed, for all TR classes except mononucleotides, residuals show a discernable inverted U pattern (supplementary fig. S3A, Supplementary Material online). This suggests that the relationship between polymorphism incidence and repeat number may be biphasic, with shorter and longer TRs characterized by different rates of exponential growth, and need to be modeled accordingly.

Segmented Regression for TR Polymorphism Incidence

Segmented (or piece-wise) regression allows the relationship between a response variable y and a predictor variable x to vary at different ranges of the predictor, and to estimate change point(s), that is, the predictor value(s) at which a switch occurs from one relationship to another (Muggeo 2003). Here, we applied segmented regression to allow for a switch in the exponential growth rate of polymorphism incidence as a function of repeat number, using the model:

Fitting this model to each of the four classes of TRs separately, we estimate change points (c) along with intercepts (a₁, a₂) and slopes (b₁, b₂) below and above the change point, respectively, corresponding to low and high repeat numbers (fig. 2 and table 1 for CEU, see supplementary table S4, Supplementary Material online, for JPTCHB and YRI). The fits provide extremely high R² values (above 99.6% in all four cases). Intriguingly, at repeat numbers below the change point (c), the rate of polymorphism incidence growth (b₁) is high, although the absolute values of polymorphism incidence are low (0.01–1%), whereas at repeat numbers above the change point the rate of polymorphism incidence growth (b₂) is low, although the absolute values of polymorphism incidence are high (>1%). The change points estimated for mono-, di-, tri-, and tetranucleotide TRs are 8.29, 4.67, 3.38, and 3.27, respectively (fig. 2). Rounding these up to the subsequent integer, one can think of 9, 5, 4, and 4 as the repeat numbers at which mono-, di-, tri-, and tetranucleotide TRs start displaying the slowed down exponential growth regime. The evidence for a biphasic relationship between polymorphism incidence and repeat number is less clear-cut for mononucleotide TRs—with a smaller difference between the two slopes, and a less accurate estimate of the change point (large confidence interval for the change point in fig. 2A; see Materials and Methods for details). However, this is most likely due to the fact that the change point for mononucleotide TRs occurs near the end of the available range of repeat numbers (recall mononucleotides >10 repeats long were excluded from our analysis due to sequencing errors; Montgomery et al. 2013). Additionally, visual inspection of the polymorphism incidence curve for mononucleotide TRs may suggest the existence of two change-points, and to examine this we fitted a triphasic-segmented regression for mononucleotide TRs (supplementary fig. S3B, Supplementary Material online), which resulted in two change points at 4.314 and 8.184. Although the R² of the triphasic segmented regression is slightly higher than that of the biphasic segmented regression (R² = 99.83% vs. 99.64%), the confidence intervals for the two change points (horizontal red lines in supplementary fig. S3B, Supplementary Material online) are very broad and very close to each other; roughly, the first phase change occurring between repeat numbers 3 and 6 and the second between 6 and 10. This lack of a clear separation indicates a weak, but ambiguous triphasic relationship for mononucleotides—the lack of longer mononucleotides in our data set hinders a satisfactory resolution of this issue.

Table 1.

Segmented Regression Model for Log Polymorphism Incidence as a Function of Repeat Number for Mono-, Di-, Tri-, and Tetranucleotide TRs in the CEU Population

TR Class	Log (Polymorphism Incidence) ∼ Repeat Number						Polymorphism Incidence at the Change Point (%)
	Change Point	Intercept (P value)	Slope below Change Point	Slope above Change Point	P Value for Difference in Slope	R2 (%)
Mono	8.292	−4.075 (1.5E−04)	0.515	0.276	0.0082	99.64	1.57
Di	4.672	−4.431 (3.1E−05)	1.02	0.292	2.20E−16	99.73	2.16
Tri	3.381	−6.398 (1.6E−04)	1.933	0.302	2.20E−16	99.86	1.37
Tetra	3.268	−6.97 (1.9E−03)	2.2	0.327	2.20E−16	99.87	1.66

In summary, our segmented regression models provide a way to demarcate the boundary between STRs (TRs below the change-point) and MSs (TRs above the change-point) in terms of the relationship between polymorphism incidence and repeat number. Note that our change points in repeat number decrease with motif size. Furthermore, at a given motif length and repeat number, Africans had the highest polymorphism incidence levels, followed by Europeans and finally East Asians; these differences were particularly significant at shorter di-, tri-, and tetranucleotide TRs, and at all mononucleotide TRs considered here (fig. 1 and supplementary fig. S4, Supplementary Material online). Change points were found to be invariant across populations (table 1 and supplementary table S4, Supplementary Material online). Finally, θ values computed for putatively neutral TRs found in intergenic and intronic regions show the same change points as polymorphism incidence (9, 5, 4, and 4 for mono-, di-, tri-, and tetranucleotide TRs, respectively; supplementary tables S5 and S6, Supplementary Material online).

Inspection of the slope estimates obtained from fitting the segmented regression models (table 1) reveals large differences in slopes below the change point among the four motif sizes, with mononucleotide repeats having the smallest slope (0.52) and tetranucleotide repeats the highest (2.2). However, after the change point, the slopes become more similar, ranging from 0.28 to 0.33 (table 1). The different rates of exponential growth in polymorphism incidence below and above the change point potentially reflect the varying contribution of different mechanisms to the mutability of STRs and MSs (discussed later).

Contribution of Slippage to Mononucleotide TR Mutability

The TR polymorphism incidence values computed above from the genome-wide 1000 Genomes Project Pilot 1 sequencing data (The 1000 Genomes Project Consortium 2010) reflect the net result of several cellular pathways controlling genome stability such as replication, recombination, and repair. We used our established in vitro HSV-tk mutagenesis assay (Messier et al. 1996; Eckert et al. 2002; Eckert and Hile 2009; Kelkar et al. 2010) to evaluate experimentally the specific contribution of polymerase strand slippage errors during DNA synthesis to the observed mutational behavior of TRs in the human genome. In vitro DNA polymerase reactions were conducted using DNA polymerase β (Pol β) to derive the frequency of unit-based indel errors (polymerase error frequency [Pol EF]), which presumably result from slippage, for TRs at varying motif size, sequence and repeat number (supplementary fig. S5, Supplementary Material online). Unit-based indel mutations are defined as polymerase errors that result in the insertion or deletion of an entire TR motif. The average Pol β EF for mononucleotide TRs of repeat number 4 was 1.0 × 10⁻⁴, a 2-fold increase over that measured for TRs of repeat number 2 (table 2 and supplementary table S7A, Supplementary Material online). However, the average Pol β EF increased approximately 170-fold between repeat numbers 4 and 8, a two orders of magnitude increase per doubling of repeat number (table 2). Indeed, the indel error frequency within mononucleotides of 8–10 repeats was 1.5–2.0 × 10⁻², demonstrating the high frequency of slippage within longer mononucleotide TRs.

Table 2.

Experimentally Derived Pol β Indel Error Frequencies at Varying Repeat Numbers for Mono- and Dinucleotide TRs

TR Class	Repeat Number	Motifs Analyzed (Number of Sites)	Average Pol-β EF (Per Site)a
Mono	2	A, T, C, G (52)	6.06 × 10−5
	3	A, T, C, G (16)	1.14 × 10−4
	4	A, T, C, G (8)	1.05 × 10−4
	8	A, T (2)	1.74 × 10−2
	10	C, G (2)	1.53 × 10−2
Di	2	GC, CG (2)	5.74 × 10−5
	3	TA, TC, AG (3)	1.05 × 10−4
	4	TA, TC, AG, GT, CA (5)	1.45 × 10−4
	5	TA, TC, AG, GT, CA (5)	1.99 × 10−4
	6	TA, GT, CA (3)	1.11 × 10−3
	8	TC, AG, GT, CA, TA (5)	7.8 × 10−4
	9	GT,CA (2)	1.26 × 10−3

Note.—Values for mononucleotides of repeat number 2 are derived from the data in (Kelkar et al. 2010); values for mononucleotides of repeat numbers 3 and 4 are derived from the data in (Eckert et al. 2002).

^aCalculated as .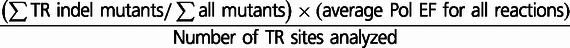

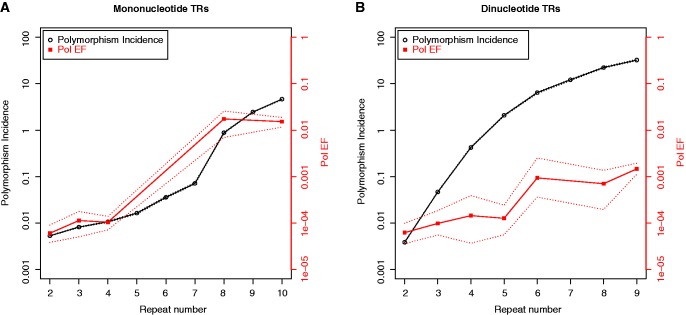
Next, we compared the experimental Pol EF values to the polymorphism incidences computed from the 1000 Genomes Project Pilot 1 data (fig. 3A). For mononucleotide TRs, the experimental Pol EF curve (which is a function of polymerase slippage errors alone) is consistent with the curve obtained from the 1000 Genomes data. The differences observed between the two curves likely reflect the lack of experimental data for mononucleotides at certain repeat numbers (5–7, 9), as well as fluctuations due to the limited number of TRs differing in motif composition examined experimentally at repeat numbers 8 and 10. Because of these limitations, we also cannot reliably fit a segmented regression model to capture a change point in the experimental Pol EF. However, modeling the logarithm of Pol EF as a function of repeat number by simple linear regression (supplementary fig. S6A, Supplementary Material online) led to a slope estimate of 0.3485 (supplementary table S3B, Supplementary Material online), which lies between the slope estimates before and after the change point in the segmented regression model for mononucleotides (table 1). Together, these observations suggest that strand slippage-mediated polymerase errors are a major driver of mononucleotide TR polymorphism incidence.

Fig. 3.—

European (CEU) population: Polymorphism incidence curves (see also fig. 1, black symbols) and experimentally based Pol EF values (as fractions, red), both on log scale, for (A) mono- and (B) dinucleotide TRs.

Contribution of Slippage to Dinucleotide TR Mutability

We experimentally examined the contribution of polymerase slippage errors to dinucleotide TR mutability for (GC)_n, (AT)_n, (TC)_n, and (AG)_n motifs ranging from 2 to 14 repeats, inserted within the same sequence context of the HSV-tk gene. The new results were combined with our previous data for (GT)_n and (CA)_n alleles ((Messier et al. 1996; Eckert et al. 2002; Eckert and Hile 2009; Kelkar et al. 2010) to estimate the average Pol β EF for all dinucleotide TRs of a given repeat number (tables 2 and supplementary table S7B, Supplementary Material online). Similar to mononucleotides, we observed an approximately 2-fold increase in Pol β EF between repeat numbers 2 and 4. The Pol EF continued to increase with length, and between repeat numbers 3 and 9, the polymerase strand slippage frequency increased approximately 10-fold, from approximately 1 × 10⁻⁴ to 1 × 10⁻³ (table 2).

Comparing the dinucleotide TR Pol EF and 1000 Genome data polymorphism incidence curves (fig. 3B) led to different observations than the corresponding mononucleotides curve comparison (fig. 3A). In particular, for dinucleotide TRs, polymorphism incidence was higher than experimental Pol EF at all repeat numbers starting at 3. We considered whether this discordance could be due to the fact that (GC)_n TRs with >2 repeats were not included in our experimental analyses. However, omitting (GC)_n TRs and re-computing polymorphism incidences from the 1000 Genomes data produced almost exactly the same curve (data not shown), because there are few of these repeats in the genome (Ellegren 2004).

We also modeled the logarithm of Pol EF as a function of dinucleotide repeat number by simple linear regression, obtaining a slope estimate of approximately 0.2 (supplementary table S3B and fig. S6B, Supplementary Material online). Interestingly, this value is similar to the slope estimate after the change point in the segmented regression model for dinucleotides (∼0.3, table 1) and substantially lower than the regression model slope before the change point (1.0, table 1). These observations suggest that the rate of exponential growth of dinucleotide MSs (after the change point) might be driven by slippage-mediated mechanisms.

The observed differences in levels and growth behavior between Pol EF and polymorphism incidence curves for dinucleotides could be due to limitations of our experimental approach, as we examined TRs in a single sequence context and used only one polymerase (Pol β) to examine slippage-based errors. To assess the influence of polymerase identity on slippage-mediated mutations at dinucleotide TRs, we determined the replicative Pol α-primase EF within (AT)_n dinucleotide TRs of repeat numbers 3 through 6. Again, we observed an increase in Pol EF with repeat number for (AT)_n dinucleotides, although Pol α-primase displayed lower Pol EFs than did Pol β at all repeat numbers examined (supplementary fig. S7, Supplementary Material online). For the same (AT)_n templates, the Pol EF for the human Pol δ holoenzyme, which functions in lagging-strand DNA synthesis during bulk genome replication (Loeb and Monnat 2008), was of the same or lower magnitude compared with Pol α-primase (data not shown). Previously, we observed that the variation in Pol EF for indel errors within a (GT)₁₀ allele varied by a factor of only 2- to 3-fold among Pols α-primase, β and δ (Hile et al. 2012). Our observations suggest that although polymerase identity does affect the absolute frequency of slippage errors within TRs, it is not sufficient to explain the higher mutation frequency of small dinucleotide TRs in human genomes.

Association between TR Polymorphism Incidence and Recombination

Recombination might also affect TR mutability and could contribute to the observed differences between dinucleotide Pol EF and polymorphism incidence curves (Wahls et al. 1990; Dutreix 1997; Benet et al. 2000; Majewski and Ott 2000; Ellegren 2004; Pearson et al. 2005; Brandstrom et al. 2008; Kelkar et al. 2008). To examine this potential association, each TR was assigned a recombination value from fine-scale deCODE data (Kong et al. 2010) (see Methods). Running simple linear regressions for TR polymorphism incidence on recombination rate for mono-, di-, tri-, and tetranucleotides, we observed positive slopes but very weak correlations (R² = 4.62%, 0.81%, 1.48%, and 1.17% for mono-, di-, tri-, and tetranucleotide TRs, respectively; see supplementary table S8, Supplementary Material online, for details). However, when comparing mean recombination rates between polymorphic and nonpolymorphic TRs, the rates for the former were found to be significantly greater than the latter (P value for two-sample t test for means = 2.2E−16, 1.4E−07, 8.4E−09, and 2.1E−08 for mono-, di-, tri-, and tetranucleotide TRs, respectively; supplementary table S9, Supplementary Material online). In summary, while we find some evidence of a positive association between TR polymorphism status and recombination (positive slope values in supplementary table S8, Supplementary Material online, and significant differences in supplementary table S9, Supplementary Material online), this association is weak (very low R² values in supplementary table S8, Supplementary Material online).

Effect of Motif Composition on Polymorphism Incidence and Polymerase Slippage

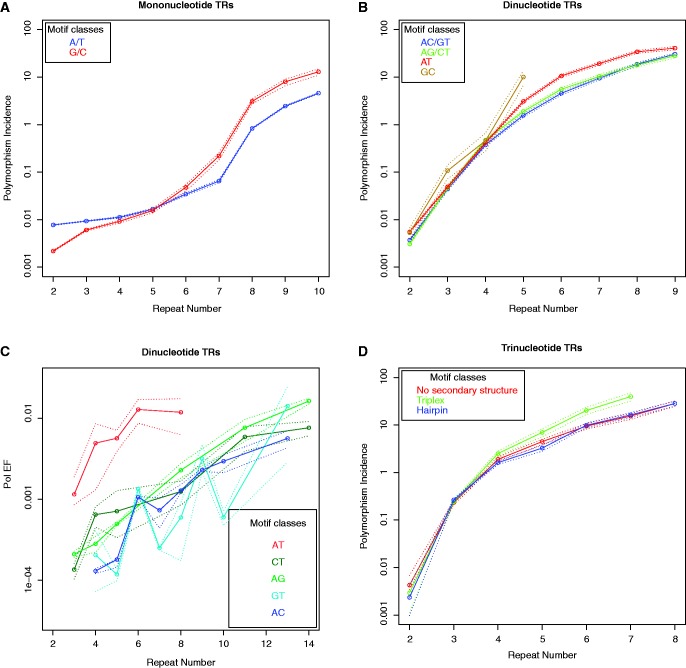
We examined whether polymorphism incidence curves estimated from the 1000 Genomes Project Pilot 1 data are motif-specific. For mononucleotide TRs, long (G/C)_n repeats were found to have a higher incidence of polymorphism than long (A/T)_n repeats (fig. 4A; data shown for CEU only). In terms of segmented regression fits, statistically significant change points could not be detected in the observed repeat number range for either (A/T)_n or (G/C)_n repeats (supplementary table S10, Supplementary Material online).

Fig. 4.—

European (CEU) population: Polymorphism incidence curves (log scale) with bootstrap bands for (A) mononucleotide TRs and (B) dinucleotide TRs, separately for different motif composition. (C) Pol β unit-based indel error frequencies (log scale) with bootstrap bands, separately for different motif composition; data for GT and AC motifs are taken from (Kelkar et al. 2010). (D) Polymorphism incidence curves (log scale) with bootstrap bands for trinucleotide TRs, separately for different secondary structures.

Change point and slope estimates for (AC/TG)_n, (AG/TC)_n, and (AT/TA)_n were fairly similar (supplementary table S10, Supplementary Material online), indicating comparable polymorphism incidence growth rates. However, the levels of polymorphism incidence differed between these motifs after the change point (fig. 4B; data shown for CEU only); the polymorphism incidence of (GC/CG)_n was highest, followed by that of (AT/TA)_n, whereas those of (AG/TC)_n and (AC/TG)_n were lowest and comparable with each other. These results were confirmed in the HSV-tk in vitro assay, where Pol EF was highest for (AT)_n dinucleotide repeats, while it was lower and similar among (TC)_n, (AG)_n, (GT)_n, and (AC)_n motifs (fig. 4C). (GC)_n repeats were not investigated using this assay, due to their low abundance genome wide.

No significant differences either in change points or in polymorphism incidence patterns were observed for tri- and tetranucleotide TRs, as studied from the 1000 Genomes Project Pilot 1 data, when they were divided by GC-content (supplementary fig. S8, Supplementary Material online). We also classified tri- and tetranucleotide motifs into three secondary structure based groups—hairpin-forming motifs, triplex-forming motifs, and motifs with no secondary structure (see “Secondary structures for tri- and tetranucleotide TRs” under Materials and Methods section; fig. 4D and supplementary fig. S9 and table S10, Supplementary Material online). Interestingly, for trinucleotide TRs, the incidence of polymorphism for motifs with the potential to form triplex secondary structures was significantly higher than that for either hairpin-forming motifs or motifs without a secondary structure (as indicated by nonoverlapping bootstrap bands in fig. 4D). No significant difference in incidence of polymorphism was observed for secondary structure classes among tetranucleotide TRs at most repeat numbers examined (supplementary fig. S9, Supplementary Material online).

Discussion

Biphasic Behavior of TR Polymorphism Incidence and Change Points

We analyzed the genomic sequences of 179 humans from the 1000 Genomes Project Pilot 1 to investigate the relationship between polymorphism incidence and repeat number for four classes of TRs (mono-, di-, tri-, and tetra-nucleotides). To assess whether the observed polymorphism incidence patterns may reflect a transition in TR mutational behavior, we modeled the logarithm of polymorphism incidence as a function of repeat number using segmented regression. For all TR classes, we found a biphasic characterization demarcating STRs from MSs: lower polymorphism levels (0.01–1% on the linear scale) yet faster exponential growth in the first phase, followed by higher polymorphism levels (>1% on the linear scale) and paradoxically slower exponential growth in the second phase (fig. 2 and table 1). Interestingly, the change point estimates produced by these models differ by repeat type (mono-, di-, tri-, and tetranucleotides), and correspond to MS thresholds determined previously by us and others (Messier et al. 1996; Dechering et al. 1998; Rose and Falush 1998; Dieringer and Schlotterer 2003; Lai and Sun 2003; Brandstrom and Ellegren 2008; Kelkar et al. 2010). We note that the biphasic characterization for mononucleotides is weaker than that for di-, tri-, and tetranucleotides, likely because the change point (9 repeats) is very close to the end of the range of repeat numbers available for these TRs.

The observed biphasic behavior of TR polymorphism incidence could be explained by two nonmutually exclusive mechanisms involving the probability of slippage events as a function of repeat number. First, a greater rate of exponential growth in polymorphism incidence of STRs (prior to the change point) may reflect the greater proportional change in total allele length that occurs for STRs as they add repeats, and this might increase slippage probability more dramatically. For instance, a dinucleotide STR change from repeat number 2–3 represents a 50% allele length increase (4–6 bp), whereas a change from repeat number 8–9 is only a 12.5% increase in length (16–18 bp). Past the change point, the probability of strand slippage is sufficient to drive a high polymorphism incidence, but the exponential growth in polymorphism incidence per additional repeat might not be as consequential, because tract length changes are proportionately smaller. Second, above the change point, deletion and insertion mutations might occur back and forth within a population at an increasing rate. Although the polymorphism incidence increases with repeat number, a proportion of polymorphisms might go undetected due to such dynamic mutational events (i.e., homoplasy), driving the observed exponential growth of polymorphism incidence of MSs down.

Further, in all four TR classes, polymorphism incidence values below the change point are <1%, comparable with those of single nucleotide polymorphisms (SNPs) and indels in nonrepetitive regions, which have polymorphism incidence values of 0.3251% and 0.0164%, respectively. Polymorphisms incidence values for TRs above the change point increase by several-fold (fig. 1). This observation suggests that while slippage may be the major driver of MS mutability at larger TRs, additional mechanisms associated with SNPs including, but not limited to chromatin compaction (Prendergast et al. 2007), CpG effect (Cooper and Krawczak 1989), and telomere-associated aberrant repair (Linardopoulou et al. 2005) may be more prevalent at STRs. This hypothesis corroborates our recent study of MS birth and death dynamics in which we demonstrated the importance of nucleotide substitutions for TRs with small repeat numbers (Kelkar et al. 2010).

Finally, change points in TR mutational behavior (as measured by polymorphism incidence or θ values) are identical across the populations studied (table 1 and supplementary table S4, Supplementary Material online)—suggesting that the change points are defined at a species level. Nevertheless, the values of polymorphism incidence are usually highest for Africans, intermediate for Europeans, and lowest for East Asians (fig. 1), reflecting differences in the history of these populations (Watkins et al. 2001; Amos and Hoffman 2009; The 1000 Genomes Project Consortium 2010).

Mechanisms Underlying Polymorphism Incidence Patterns

DNA Strand Slippage

To determine the contribution of polymerase strand slippage errors to the population polymorphism incidence values, we measured the production of unit-based indel errors within mono- and dinucleotide TRs. For mononucleotide TRs, we observed relatively low error frequencies (∼10⁻⁴) for short (2–4) repeat numbers (table 2), similar to the observed low polymorphism incidence values. At longer mononucleotide repeat numbers (8 and 10), we measured dramatically increased error frequencies (∼10⁻²). Our results corroborate a previous study of T7 DNA polymerase error rates within mononucleotide TRs as a function of repeat number (Kroutil et al. 1996). Strikingly, for mononucleotides, we observed concordance between the polymorphism incidence curves derived from 1000 Genome Project data and those based on polymerase indel error frequencies measured experimentally (fig. 3A), suggesting that polymerase strand slippage errors largely drive polymorphism within mononucleotide TRs.

Intriguingly, for dinucleotide TRs, the polymorphism incidence curves derived from 1000 Genome Project data rise more rapidly than experimental Pol EF curves (fig. 3B). Modeling of the latter produced a slope that is very similar to that of the former above the change point (segmented regression). Therefore, the rate of change in polymorphism incidence for dinucleotide MSs appears to correspond to strand slippage errors during DNA synthesis, whereas other cellular mechanisms likely contribute to polymorphism incidence of dinucleotide STRs.

Recombination

Population polymorphism incidence reflects the combined effects of multiple cellular mechanisms, including DNA replication, repair, and recombination pathways. In particular, mutability of MSs has been associated with recombination rates in previous studies (Wahls et al. 1990; Dutreix 1997; Benet et al. 2000; Majewski and Ott 2000; Ellegren 2004; Pearson et al. 2005; Brandstrom et al. 2008; Kelkar et al. 2008). We examined the effect of genome-wide recombination rates directly, and observed a weak correlation between TR polymorphism incidence and recombination rates (supplementary table S8, Supplementary Material online). Similarly, in previous studies (Kelkar et al. 2008; Ananda et al. 2011), regional genomic landscape features (including recombination rates) were found to have only minor effects on MS mutability. Thus recombination is unlikely to be a major player in determining the observed differences between dinucleotide polymorphism incidence and Pol EF values.

DNA Synthesis-Specific Mechanisms

Cellular TR mutability might be affected by the temporal order of DNA replication during the S-phase of the cell cycle. TRs are typically enriched within early replicating regions of the genome, with dinucleotides being an exception (Cohen et al. 2006). Perhaps late-replicating TRs have higher mutability due to the accumulation of single-stranded DNA that might occur within late-replicating regions (Stamatoyannopoulos et al. 2009) and/or the progressive reduction in DNA repair activities with replication timing (Chen et al. 2010). Furthermore, some genomic regions can remain unreplicated into G2 phase, and the mutagenic specificity of DNA translesion synthesis has recently been shown to differ between S- and G2-phase (Diamant et al. 2012). Thus, the higher polymorphism incidence of dinucleotide TRs relative to Pol EF might be associated with the potentially elevated propensity for mutations of late-replicating regions. The higher polymorphism incidence of short dinucleotide TRs, relative to Pol EF, also may result from the efficient extension of slipped intermediates through nonreplicative DNA synthesis pathways. The ability to extend slipped intermediates is an intrinsic property of DNA polymerases and varies among polymerases (Doublie et al. 1998; Franklin et al. 2001; Garcia-Diaz et al. 2005). Further experiments are needed to identify potential DNA polymerases, possibly those associated with error-prone repair, that may generate a high rate of slippage-based errors within short repeat tracts. For example, nonhomologous end-joining in Saccharomyces cerevisiae has been shown recently to be a replication-independent mechanism of generating indels in short repeats (Lehner et al. 2012).

Sequencing Artifacts

Because of the repetitive nature of TRs, they are particularly susceptible to sequencing artifacts (McIver et al. 2011) and issues in downstream processing (e.g., reduced sensitivity in alignment of short reads with repeat content). Therefore, here we took careful measures to distinguish real biological variants from sequencing artifacts. These included mapping with an indel-sensitive read-mapper, incorporation of information on known errors in homopolymer contexts and quality scores during variant calling, and polarization of identified indels using primate alignments (Montgomery et al. 2013). Nevertheless, although dinucleotide TRs are less prone to sequencing and genotyping errors compared with mononucleotide TRs (Ellegren 2004; Albers et al. 2010; Luo et al. 2012), one cannot completely rule out the existence of such errors specific to these repeats.

Effect of Motif Size on Polymorphism Incidence

When comparing TRs of an equivalent number of repeat units, mononucleotides have an overall lower polymorphism incidence than do di-, tri-, and tetranucleotides TRs. Moreover, the different change points for mono-, di-, tri-, and tetranucleotide TRs (9, 5, 4, and 4 repeats, respectively) suggest that not only repeat number but also motif size (and thus tract length) affect TR mutability, corroborating our previous observations (Kelkar et al. 2008). The effect of motif size is also apparent when comparing slopes generated by the segmented regression modeling (table 1 and supplementary table S4, Supplementary Material online). Mononucleotide TRs, in particular, have the lowest rate of change and tetranucleotide TRs the highest rate of change below the change point. These results indicate that at a given repeat number, mutations (expansions/contractions) are more pronounced for TRs with larger motif sizes and thus larger tract lengths. Future in vitro experiments are required to investigate the frequencies of strand slippage errors within tetranucleotide TRs of varying sequence and length.

The differences in mutational behavior between TR classes could be due, in part, to differences in the efficiency of cellular mismatch repair (MMR). Experimental studies have shown that the relative order of MMR efficiency is mono- > dinucleotide repeats, the inverse of the observed differences in polymorphism incidence. Comparing MMR-deficient and MMR-proficient colorectal cancer cell lines, the mutation rate of a (G/C)_n mononucleotide TR varied over 200-fold while that measured for a (AC/GT)_n dinucleotide TR varied only approximately 25-fold (Campregher et al. 2010). Similar results were observed in Escherichia coli, in which the mutation frequency measured within a (G/C)₁₀ MS varied >10⁴-fold between MMR-proficient and deficient cells, but that measured within a (AC/GT)₁₀ MS varied 10³-fold (Jacob and Eckert 2007). Although a general trend towards more efficient MMR of mononucleotide versus dinucleotide repeats has been observed, it is important to note that some of these results depended on motif identity (Jacob and Eckert 2007; Campregher et al. 2010).

Effect of Motif Composition and DNA Secondary Structure Potential on Polymorphism Incidence

For mono- and dinucleotide TRs, we observed significant effects of motif sequence composition on the levels of polymorphism incidence, although polymorphism incidence growth rates were comparable (fig. 4A–C). Our observations indicate difference in polymorphism incidence levels between (G/C)_n and (A/T)_n mononucleotides at repeat-number as low as 6 (fig. 4A). For dinucleotides, polymorphism incidence levels were found to be highest for (GC/CG)_n, followed by (AT/TA)_n, and finally (AG/TC)_n and (AC/TG)_n (fig. 4B). The mutability order observed here for dinucleotide motifs agrees closely with previous observations based on human–chimpanzee comparison (Kelkar et al. 2008). Pol EF measured at different dinucleotide motifs confirmed our computational findings.

Repetitive DNA motifs are known to adopt non-canonical DNA structures, including hairpins, triplexes, Z-DNA, and G-quadraplexes, which can cause mutations and increase genome instability (Zhao et al. 2010). We considered whether TR secondary structure potential could influence polymorphism incidence. (G/C)_n mononucleotides have the potential to form both triplex and four-stranded structures (Sinden 1994), and this may explain, in part, the increased polymorphism incidence of (G/C)_n compared with (A/T)_n repeats, which only can form triplex structures. Similarly, (AT/TA)_n dinucleotides form stronger hairpins and contain a smaller number of hydrogen bonds making them more vulnerable to slippage, compared with (AG/CT)_n and (AC/TG)_n TRs (Casasnovas et al. 1993; Sinden 1994). This may contribute to the increased polymorphism incidence of (AT/TA)_n repeats compared with those of (AG/CT)_n and (AC/GT)_n repeats. Our dinucleotide polymorphism results corroborate our recent finding that the intensity of DNA replication for stalling within long dinucleotides motifs follows the order: GC/CG > AT/TA > (AG/TC and AC/TG), consistent with a role of secondary structure formation in repeat instability (Eckert KA and Krasilnikova M, unpublished data). Our observation that triplex-forming motifs in trinucleotide TRs had a significantly higher incidence of polymorphism than either hairpin-forming motifs or motifs without any secondary structure (fig. 4D; see “Secondary structures for tri- and tetranucleotide TRs” under Materials and Methods section) reinforces the hypothesized role of DNA triplex structures in blocking replication forks, and thereby causing mutations (Zhao et al. 2010 and references therein).

Supplementary Material

Supplementary figures S1–S9 and tables S1–S10 are available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).