Abstract
We describe a simple framework for teaching the principles that underlie the dynamical laws of transport: Fick’s law of diffusion, Fourier’s law of heat flow, the Newtonian viscosity law, and the mass-action laws of chemical kinetics. In analogy with the way that the maximization of entropy over microstates leads to the Boltzmann distribution and predictions about equilibria, maximizing a quantity that E. T. Jaynes called “caliber” over all the possible microtrajectories leads to these dynamical laws. The principle of maximum caliber also leads to dynamical distribution functions that characterize the relative probabilities of different microtrajectories. A great source of recent interest in statistical dynamics has resulted from a new generation of single-particle and single-molecule experiments that make it possible to observe dynamics one trajectory at a time.
I. INTRODUCTION
We describe an approach for teaching the principles that underlie the dynamical laws of transport of particles (Fick’s law of diffusion), energy (Fourier’s law of heat flow), momentum (the Newtonian law for viscosity),1 and mass-action laws of chemical kinetics.2 Recent experimental advances now allow for studies of forces and flows at the single-molecule and nanoscale level, representative examples of which may be found in Refs. 3-10. For example, single-molecule methods have explored the packing of DNA inside viruses7 and the stretching of DNA and RNA molecules.9,10 Similarly, video microscopy now allows for the analysis of trajectories of individual submicron size colloidal particles,11 and the measurement of single-channel currents has enabled the kinetic studies of DNA translocation through nanopores.3,6
One of the next frontiers in biology is to understand the “small numbers” problem: how does a biological cell function given that most of its proteins and nucleotide polymers are present in numbers much smaller than Avogadro’s number?12 For example, one of the most important molecules, a cell’s DNA, occurs in only a single copy. Also, it is the flow of matter and energy through cells that makes it possible for organisms to maintain a relatively stable form.13 Hence, cells must be in this stable state far from equilibrium to function. Thus, many problems of current interest involve small systems that are out of equilibrium.
Our interest here is twofold: to teach students a physical foundation for the phenomenological macroscopic laws, which describe the properties of averaged forces and flows, and to teach them about the dynamical fluctuations away from those average values for systems with small numbers of particles.
In this article we describe a simple way to teach these principles. We start from the “principle of maximum caliber” first described by E. T. Jaynes.14 It aims to provide the same type of foundation for the dynamics of systems with many degrees of freedom that the second law of thermodynamics provides for the equilibria of such systems. To illustrate the principle, we use a slight variant of one of the oldest and simplest models in statistical mechanics, the dog-flea or two urn model.15-17 Courses in dynamics often introduce Fick’s law, Fourier’s law, and the Newtonian-fluid model as phenomenological laws, rather than deriving them from some deeper foundation. We describe an unified perspective that we have found useful for teaching these laws from a foundation in statistical dynamics. In analogy with the role of microstates as a basis for the properties of equilibria, we focus on microtrajectories as the basis for predicting dynamics.
One argument that might be leveled against the kind of framework we present here is that in the cases we consider it is not clear that it leads to anything different from what one obtains using conventional nonequilibrium thinking. On the other hand, restating the same physical result in different language often can provide a better starting point for subsequent reasoning. This point was well articulated by Feynman in his Nobel lecture:18
“Theories of the known, which are described by different physical ideas may be equivalent in all their predictions and are hence scientifically indistinguishable. However, they are not psychologically identical when trying to move from that base into the unknown. For different views suggest different kinds of modifications which might be made and hence are not equivalent in the hypotheses one generates from them in one’s attempt to understand what is not yet understood.”
We begin with the main principle embodied in Fick’s law. Why do particles and molecules in solution flow from re-gions of high concentration toward regions of low concentration? To keep it simple, we consider one-dimensional diffusion along a coordinate x. The diffusion is described by Fick’s first law of particle transport,1,2 which says that the average flux 〈J〉 is given in terms of the gradient of the average concentration ∂〈c〉/∂x by
| (1) |
where D is the diffusion coefficient. To clearly distinguish quantities that are dynamical averages from those that are not, we indicate the averaged quantities explicitly by angular brackets, 〈…〉. Before we describe the nature of this averaging and the nature of the dynamical distribution functions over which the averages are taken, we briefly review the standard derivation of the diffusion equation. We combine Fick’s first law with particle conservation,
| (2) |
and obtain Fick’s second law, which is also known as the diffusion equation:
| (3) |
The solution of Eq. (3) subject to two boundary conditions and one initial condition gives 〈c(x,t)〉, the average concentration in time and space, and the average flux 〈J(x,t)〉 when no other forces are present. The generalization to situations involving additional applied forces is the Smoluchowski equation.2
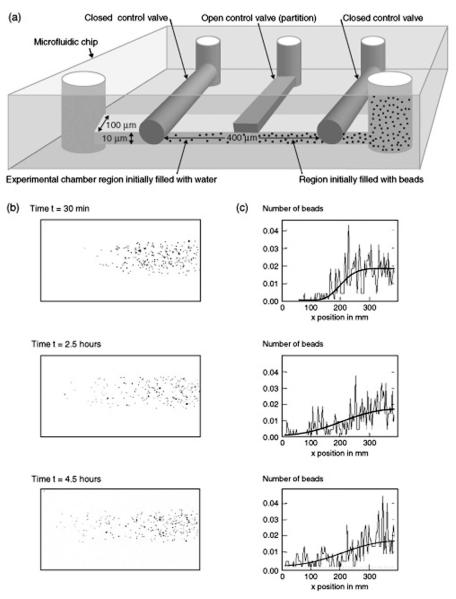
A simple experiment shows the distinction between averaged quantities and individual microscopic realizations. By using a microfluidics chip like that shown in Fig. 1(a), it is possible to create a small fluid chamber divided into two regions by control valves. The chamber is filled on one side with a solution containing a small concentration of micronscale colloidal particles. The other region contains just water. The three control valves on top of that microfluidic chamber serve two purposes: The two outer ones are used for isolation so that no particles can diffuse in and out of the chamber, while the middle control valve provides the partition between the two regions. The evolution of the system is then monitored after the removal of the partition [see Fig. 1(b)]. The time-dependent particle density is determined by dividing the chamber into a number of equal sized boxes in thelong direction and by computing histograms of the numbers of particles in each slice as a function of time. This system is a colloidal solution analog of the gas diffusion experiments of classical thermodynamics. The corresponding theoretical model usually used is the diffusion equation. Figure 1(c) shows the solution to the diffusion equation as a function of time for the geometry of the microfluidics chip. The initial condition is a step function in concentration at x=200 μm at time t=0.
Fig. 1.
Colloidal free expansion setup to illustrate diffusion involving small numbers of particles. (a) Schematic of experimental setup. (b) Several snapshots from the experiment. (c) Normalized histogram of particle positions during the experiment. The solution to the diffusion equation for the microfluidic “free expansion” experiment is superposed for comparison.
We use this simple experiment to illustrate one main point. The key distinction is that the theoretical curves are very smooth, while there are very large fluctuations in the experimentally observed dynamics of the particle densities. The fluctuations are large because the number of colloidal particles is small, tens to hundreds. The experimental data show that the particle concentration c(x,t) is a highly fluctuating quantity. It is not well described by the standard smoothed curves that are calculated from the diffusion equation. Of course, when averaged over many trajectories or when particles are at high concentrations, the experimental data should approach the smoothed curves that are predicted by the classical diffusion equation.
II. THE EQUILIBRIUM PRINCIPLE OF MAXIMUM ENTROPY
Because our strategy follows so closely the Jaynes derivation of the Boltzmann distribution law of equilibrium statistical mechanics,2,19 we first show the equilibrium treatment. To derive the Boltzmann law, we start with a set of equilibrium microstates i=1,2,3, …, N that are relevant to the problem at hand. Our aim is to calculate the probabilities pi of these microstates in equilibrium. We define the entropy S of the system as
| (4) |
where kB is Boltzmann’s constant. The equilibrium probabilities, are those values of pi that cause the entropy to be a maximum, subject to two constraints:
| (5) |
which is a normalization condition that ensures that the probabilities pi sum to one, and
| (6) |
which says that the energies, when averaged over all the microstates, sum to the macroscopically observable average energy.
By using Lagrange multipliers λ and β to enforce the first and second constraints, respectively, we obtain an expression for the values that maximize the entropy:2,19
| (7) |
The result is that
| (8) |
where Z is the partition function, defined by
| (9) |
After a few thermodynamic arguments, the Lagrange multiplier β can be shown to be equal to 1/kBT.19 This derivation, first given in this simple form by Jaynes,19 identifies the probabilities that are both consistent with the observable average energy and that otherwise maximize the entropy. Jaynes justified this strategy on the grounds that it would be the best prediction that an observer could make, given the observable mean energy, if the observer is ignorant of all else. Although this derivation of the Boltzmann law is now popular, its interpretation as a method of prediction, rather than as a method of physics, is controversial. Nevertheless, for our purposes here, it does not matter whether we regard this approach as a description of physical systems or as a strategy for making predictions.
We switch from the principle of maximum entropy to the principle of maximum caliber.14 In particular, rather than focusing on the probability distribution p(Ei) for the various microstates, we seek p[{σi(t)}], where σi(t) is the ith microscopic trajectory of the system. Again we maximize an entropy-like quantity obtained from p[{σi(t)}] to obtain the predicted distribution of microtrajectories. If there are no constraints, this maximization results in the prediction that all the possible microtrajectories are equally likely during the dynamical process. In contrast, certain microtrajectories will be favored if there are dynamical constraints, such as may be specified in terms of the average flux.
III. FICK’S LAW FROM THE DOG-FLEA MODEL
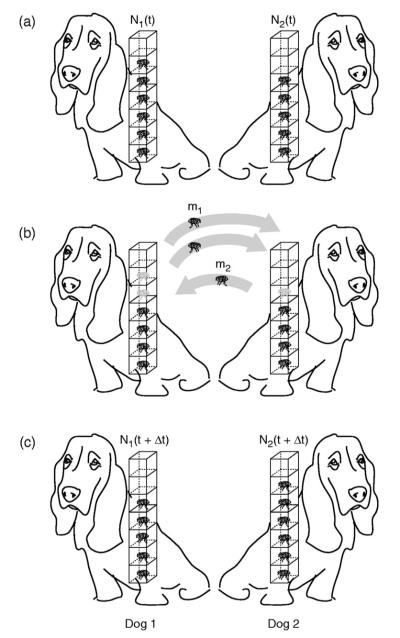
We want to determine the diffusive evolution of particles in a one-dimensional system. The key features of this system are revealed by considering two columns of particles separated by a plane, as shown in Fig. 2. The left-hand column 1 has N1(t) particles at time t and the right-hand column 2 has N2(t) particles. This system is a simple variant of the famous “dog-flea” model of Ehrenfest’s introduced in 1907.15,17 Column 1 corresponds to dog 1, which has N1 fleas on its back at time t, and column 2 corresponds to dog 2, which has N2 fleas at time t. In the time interval between time t and t +Δt, a flea can either stay on its current dog or jump to the other dog. This model has been used extensively to study the Boltzmann H-theorem and to understand how the time asymmetry of diffusion processes arises from the underlying time symmetry in the laws of motion.15,17,20 We use this model for a slightly different purpose. In particular, our aim is to take a well-characterized problem like diffusion and to reveal how the principle of maximum caliber may be used in a concrete way.
Fig. 2.
Schematic of the simple dog-flea model. (a) State of the system at time t; (b) a particular microtrajectory in which two fleas jump from the dog on the left and one flea jumps from the dog on the right; (c) occupancies of the dogs at time t+Δt.
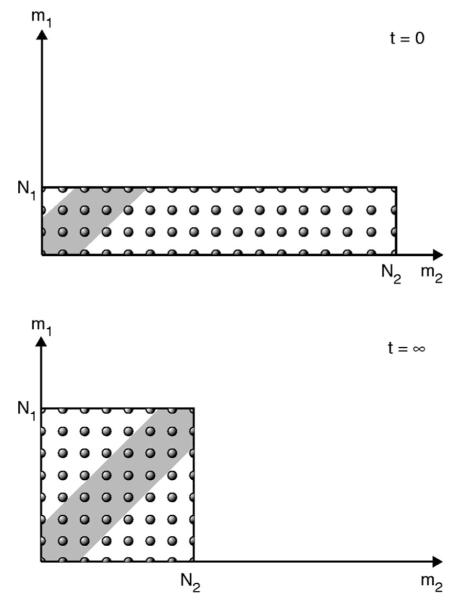
First consider the equilibrium state of the dog-flea model. The total number of ways of partitioning the (N1+N2) fleas is
| (10) |
The state of equilibrium is that for which the entropy, S=kB ln W, is a maximum. A simple calculation shows that the entropy is a maximum when the value is as nearly equal to as possible. In short, at equilibrium, both dogs will have approximately the same number of fleas, in the absence of any bias.
Our focus here is on how the system reaches equilibrium. We discretize time into a series of intervals Δt. We define a dynamical quantity p, which is the probability that a particle (flea) jumps from one column (dog) to the other in any time interval Δt. Thus, the probability that a flea stays on its dog during the time interval is q=1-p. We assume that p is independent of the time t and that all the fleas and jumps are independent of each other.
In equilibrium statistical mechanics, the focus is on the microstates. However, for dynamics we focus on processes, which at the microscopic level we call the microtrajectory. Characterizing the dynamics requires more than just information about the microstates; we must also consider the processes. Let m1 represent the number of particles that jump from column 1 to 2 and m2 represent the number of particles that jump from column 2 to 1 between time t and t+Δt. There are many possible values of m1 and m2: it is possible that no fleas will jump during the interval Δt, or that all the fleas will jump, or that the number of fleas jumping will be in between these limits. Each one of these different situations corresponds to a distinct microtrajectory of the system in this idealized dynamical model. We need a principle to tell us what number of fleas will jump during the time interval Δt at time t. Because the dynamics of this model is so simple, the implementation of the caliber idea is reduced to a simple exercise in enumeration and counting using the binomial distribution.
A. The dynamical principle of maximum caliber
The probability Wd(m1,m2|N1,N2) that m1 particles jump to the right and that m2 particles jump to the left in a time interval Δt, given that there are N1(t) and N2(t) fleas on the dogs at time t, is
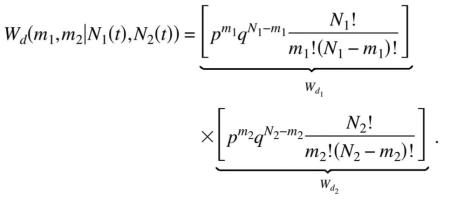 |
(11) |
Wd counts microtrajectories in dynamics in the same spirit that W counts microstates for equilibrium. In the same spirit of the second law of thermodynamics, we maximize Wd over all the possible microtrajectories (that is, over m1 and m2) to predict the flux of fleas between the dogs. This maximization is the implementation of the principle of maximum caliber for this model. Maximizing Wd over all the possible processes (different values of m1 and m2) gives our prediction (right flux and left flux ) for the macroscopic flux that we should observe experimentally. (We follow the usual definition of flux, the number of particles transferred per unit time and per unit area. For simplicity, we take the cross-sectional area to be unity.)
Because the jumps of the fleas from each dog are independent, we find the predicted macroscopic dynamics by maximizing Wd1 and Wd1 separately, or for convenience their logarithms:
| (12) |
The application of Stirling’s approximation to Eq. (11) gives
| (13) |
We call the caliber. Maximizing with respect to m gives
| (14) |
This result may be simplified to yield
| (15) |
which implies that the most probable jump number is simply given by
| (16) |
Because our probability distribution Wd is nearly symmetric about the most probable value of flux, the average number and the most probable number are approximately the same. Hence, the average net flux to the right is
| (17) |
which is Fick’s law for this simple model with the diffusion coefficient given by D=pΔx2/Δt. We have rewritten N1−N2=−ΔcΔx.
This approach gives us a simple explanation for why there is a net flux of particles diffusing across a plane down a concentration gradient: more microscopic trajectories lead downhill than uphill. It shows that the diffusion coefficient D is a measure of the jump rate p. This model does not assume that the system is near-equilibrium, for example, it does not utilize the Boltzmann distribution law, and thus it indicates that Fick’s law should also apply far from equilibrium. We might have imagined that for very steep gradients, Fick’s law might have been only an approximation and that diffusion is more accurately represented as a series expansion of higher derivatives of the gradient. But at least for the present model, Fick’s law is a general result that emerges from counting microtrajectories. On the other hand, we would expect Fick’s law to break down when the particle density becomes so high that the particles start interacting with each other, thus spoiling the assumption of independent particle jumps.
B. Fluctuations in diffusion
We have shown that the most probable number of fleas that jump from dog 1 to dog 2 between time t and t+Δt is . The model also tells us that sometimes we will have fewer fleas jumping during this time interval and sometimes we will have more fleas. These variations are a reflection of the fluctuations resulting from the system following different microscopic pathways.
We focus now on predicting the fluctuations. To illustrate, we first construct a table of Wd, the different numbers of possible microtrajectories, for all the values of m1 and m2. To keep the illustration simple, we consider the special case N1(t)=4 and N2(t)=2. We also assume p=q=1/2. Table I lists the multiplicities of all the possible routes of flea flow. A given entry tells us how many microtrajectories correspond to the value of m1 and m2.
Table I.
Trajectory multiplicity for the case where N1(t)=4 and N2(t)=2. Each entry corresponds to the total number of trajectories for the particular values of m1 and m2.
| m 1 | m2=0 | m2=1 | m2=2 |
|---|---|---|---|
| 0 | 1 | 2 | 1 |
| 1 | 4 | 8 | 4 |
| 2 | 6 | 12 | 6 |
| 3 | 4 | 8 | 4 |
| 4 | 1 | 2 | 1 |
Table I confirms our previous discussion. The dynamical process for which Wd is a maximum (12 microtrajectories in this case) occurs when , and . You can calculate the probability of this flux by dividing Wd=12 by the sum of entries in Table I, which is 26=64, the total number of microtrajectories. The result, which is the fraction of all the possible microtrajectories that have and , is 0.18. We have chosen an example in which the particle numbers are very small, so the fluctuations are large; they account for more than 80% of the flow. In systems with large numbers of particles, the relative fluctuations are much smaller.
Now look at the top right entry of Table I. This entry says that there is a probability of 1/64 that both fleas on dog 2 will jump to the left while no fleas will jump to the right, implying that the net flux for this microtrajectory is backward relative to the concentration gradient. We call these “bad actor” microtrajectories. In these cases, particles flow to increase the concentration gradient, not decrease it.21 At time t, there are four fleas on the left dog, and two on the right. At the next instant, t+Δt, all six fleas are on the left dog, and no fleas are on the right-hand dog.
Similarly, if you look at the bottom left entry of Table I, you see a case of superflux: a net flux of four particles to the right, whereas Fick’s law predicts a net flow of only two particles to the right. Table I illustrates that Fick’s law is only a description of the average or most probable flow and that Fick’s law is not always exactly correct at the microscopic level. However, such violations of Fick’s law are of low probability, a point that we will make more quantitative in the following. Such fluctuations have been experimentally measured in small systems.23
We can elaborate on the nature of the fluctuations by defining the “potencies” of the microtrajectories. We define the potency to be the fraction of all the trajectories that lead to a substantial change in the macrostate. The potencies of trajectories depend on how far the system is from equilibrium. To see this, we continue our consideration of the simple system of six particles. The total number of microscopic trajectories available to this system at each instant in our discrete time picture is 26=64. Suppose that at t=0 all six of these particles are on dog 1. The total number of microscopic trajectories available to the system can be classified using m1 and m2, where in this case m2=0 because there are no fleas on dog 2 (see Table II).
Table II.
Trajectory multiplicity for N1(t)=6 and N2(t)=0 when the system is far from macroscopic equilibrium. In this case m2=0.
| m 1 | m2=0 |
|---|---|
| 0 | 1 |
| 1 | 6 |
| 2 | 15 |
| 3 | 20 |
| 4 | 15 |
| 5 | 6 |
| 6 | 1 |
What fraction of all microtrajectories changes the occupancies of both dogs by more than some threshold value, say ΔNi>1? In this case, we find that 57 of the 64 microtrajectories cause a change greater than this value to the current state. We call these potent trajectories.
Now let us look at the potencies of the same system of six particles in a different situation, N1=N2=3 when the system is in macroscopic equilibrium (see Table III). In this case only the trajectories with (m1,m2) pairs given by (0,2), (0,3), (1,3), (2,0), (3,0), and (3,1) satisfy our criterion. Summing over all of these outcomes shows that just 14 of the 64 trajectories are potent in this case.
Table III.
Trajectory multiplicity for N1(t)=3 and N2(t)=3 when the system is at macroscopic equilibrium.
| m 1 | m2=0 | m2=1 | m2=2 | m2=3 |
|---|---|---|---|---|
| 0 | 1 | 3 | 3 | 1 |
| 1 | 3 | 9 | 9 | 3 |
| 2 | 3 | 9 | 9 | 3 |
| 3 | 1 | 3 | 3 | 1 |
There are two key observations conveyed by these arguments. For a system far from equilibrium the vast majority oftrajectories at that time are potent and move the system significantly away from its current macrostate. Also when the system is near equilibrium, the vast majority of microtrajectories leave the macrostate unchanged. We now generalize from the tables to see when fluctuations will be important.
Fluctuations and potencies
A simple way to characterize the magnitude of the fluctuations is to look at the width of the Wd distribution.2 It is shown in standard texts that for a binomial distribution for which the mean and most probable value both equal , the variance is . The variance characterizes the width. Moreover, if Ni is sufficiently large, a binomial distribution can be well-approximated by a Gaussian distribution
| (18) |
a convenient approximation because it leads to simple analytic results. However, this distribution function is not quite the one we want. We are interested in the distribution of flux, P(J)= P(m1-m2), not the distribution of right-jumps m1 or left-jumps m2 alone.
Due to a remarkable property of the Gaussian distribution, it is simple to compute the quantity we want. If you have two Gaussian distributions, one with mean 〈x1〉 and variance and the other with mean 〈x2〉 and variance , then the distribution function, P(x1-x2) for the difference will also be a Gaussian distribution with mean 〈x1〉-〈x2〉 and variance .
For our binomial distributions, the means are and and the variances are and . Hence the distribution of the net flux, J=m1-m2 is
| (19) |
where N=N1+N2.
Figure 3 shows an example of the distributions of fluxes at different times using p=0.1 and starting from N1=100, N2=0. We update each time step using an averaging scheme, N1(t+Δt)=N1(t)-N1(t)p+N2(t)p. Figure 3 shows how the mean flux is large at first and decays toward equilibrium, J=0. This result could also have been predicted from the diffusion equation. Equally interesting are the wings of the distributions, which show the deviations from the average flux; these deviations are not predictable from the diffusion equation.
Fig. 3.
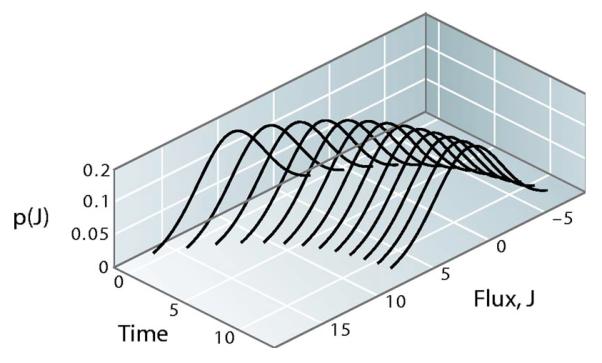
Schematic of the distribution of fluxes for different times as the system approaches equilibrium.
One measure of the importance of the fluctuations is the ratio of the standard deviation σ to the mean, . In the limit of large N1, reduces to
| (20) |
In a typical bulk experiment, the particle numbers are large, of the order of Avogadro’s number 1023. In such cases, the width of the flux distribution is exceedingly small, and it becomes overwhelmingly probable that the mean flux will be governed by Fick’s law. However, within biological cells and in applications involving small numbers of particles, the variance of the flux can become significant. It has been observed that both rotary and translational single motor proteins sometimes transiently step backward relative to their main direction of motion.24
As a measure of the fluctuations, we now calculate the variance in the flux. It follows from Eq. (19) that 〈J2〉=Npq, where N=N1+N2. Thus, we can represent the magnitude of the fluctuations as
| (21) |
where N=N1+N2 is the total number of fleas and f=(N1-N2)/(N) is the normalized concentration difference. The quantity δ is also a measure of the degree of backflux. In the limit of large N, δ goes to zero. That is, the noise diminishes with system size. However, even when N is large, δ can still be large (indicating the possibility of backflux) if the concentration gradient, N1-N2, is small.
Another measure of fluctuations is the potency. Trajectories that are not potent should have |m1-m2|≈0, which corresponds to a negligible change in the current state of the system as a result of a given microtrajectory. In Fig. 4 the impotent microtrajectories are shown as the shaded band for which m1≈m2. We define impotent trajectories as those for which |m1-m2|≤h (h⪡N). In the Gaussian model, the fraction of impotent trajectories is
| (22) |
| (23) |
and corresponds to summing over the subset of trajectories that have a small flux. To keep it simple, we take p=q=1/2 for which the probability distribution for the microscopic flux m1-m2 is given by Eq. (19). The choice of h is arbitrary and we choose h to be one standard deviation, . Figure 5 shows the potencies for various values ofN1 and N2. When the concentration gradient is large, most trajectories are potent, leading to a statistically significant change of the macrostate, whereas when the concentration gradient is small, most trajectories have little effect on the macrostate.
Fig. 4.
Schematic of which trajectories are potent and which are impotent. The shaded region corresponds to the impotent trajectories for which m1 and m2 are either equal or approximately equal and hence make relatively small change in the macrostate. The unshaded region corresponds to potent trajectories.
Fig. 5.

Illustration of the potency of the microtrajectories associated with different distributions of N particles on the two dogs. The total number of particles N1+N2=N=100.
As another measure of the fluctuations, let us now consider the “bad actors” (see Fig. 6). If the average flux is in the direction from dog 1 to dog 2, what is the probability we will observe flux in the opposite direction (bad actors)? We use Eq. (19) for P(J) to obtain
| (24) |
| (25) |
which amounts to summing up the fraction of trajectories for which J⪡0. Figure 7 shows the fraction of bad actors for p=q=1/2. Bad actors are rare when the concentration gradient is large, and highest when the gradient is small. The discontinuity in the slope of the curve in Fig. 7 at N1/N=1/2 is a reflection of the fact that the mean flux abruptly changes sign at that value.
Fig. 6.
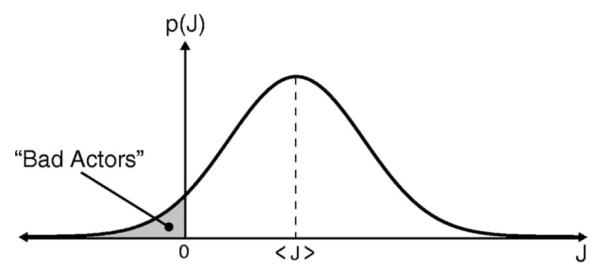
Illustration of the notion of bad actors. Bad actors are the microtrajectories that contribute net particle motion that has the opposite sign from the macroflux.
Fig. 7.
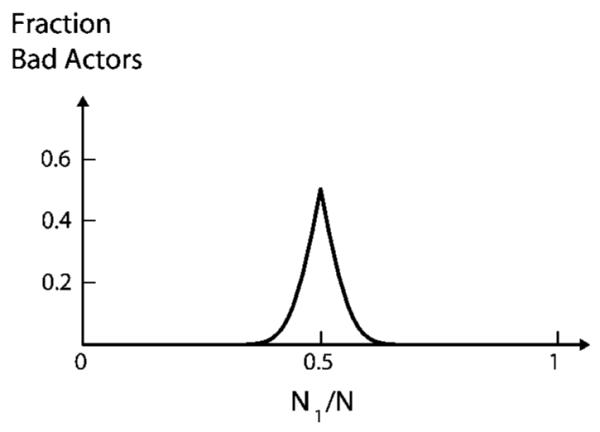
The fraction of all possible trajectories that go against the direction of the macroflux for N=100. The fraction of bad actors is highest at N1=N/2=50.
IV. FOURIER’S LAW OF HEAT FLOW
Although particle flow is driven by concentration gradients according to Fick’s law, 〈J〉=−D∂c/∂x, energy flow is driven by temperature gradients according to Fourier’s law:1
| (26) |
Here, Jq is the energy transferred per unit time and per unit cross-sectional area and ∂T/∂x is the temperature gradient that drives it. The thermal conductivity1 κ plays the role that the diffusion coefficient plays in Fick’s law.
To explore a simplified version of Fourier’s law that depends only on particle transport, we return to the dog-flea model as described in Sec. III. Now columns 1 and 2 can differ not only in their particle numbers, N1(t) and N2(t), but also in their temperatures, T1(t) and T2(t). For simplicity, we assume that each column is at thermal equilibrium and thateach particle that jumps carries with it the average energy 〈mv2/2〉=kBT/2 from the column it left. We again take the cross-sectional area to be unity. In this simple model all energy is transported by hot or cold molecules switching dogs. The average heat flow at time t is
| (27) |
where and are as defined in Sec. III A the numbers of particles jumping from each column at time t. If the particle numbers are identical, N1=N2=N/2, then
| (28) |
which is Fourier’s law for the average heat flux for this two-column model. The model predicts that the thermal conductivity is κ=(pkBNΔx)/(Δt), which can be expressed in a more canonical form as κ=pkBnvavΔx in terms of the particle density n=N/Δx and the average velocity, vav=Δx/Δt. Our model gives a value for the thermal conductivity similar to that found in the kinetic theory of gases,1 κ=(1/3)kBnνavl, if Δx in our model corresponds to l, the mean free path.
The factors of p and 1/3 in our model and kinetic theory, respectively, can be reconciled by the following observation. Kinetic theory deals with the motion of particles in three dimensions so that each particle can move in six possible directions (±x, ±y, ±z). As a result, only 1/6 of the particles will contribute to the heat flux in our direction of interest. Also, on the plane of interest there are particles coming in from the positive and negative directions. So the factor of 1/6 is increased by two to 1/3. In contrast, in our model, the particles move with probability p or stay with probability 1-p. So the contribution to the flux comes from a fraction p of the particles. The origin of the numerical factors is thus clear.
The numerical factors of 1/3 or p are not really important to the point we are trying to make. It is also not fair to read too much into this simple but illustrative model. The key point is that the simple model captures the main physical features of heat flow by appealing to the idea of summing over the weighted microtrajectories available to the system.
V. NEWTONIAN VISCOSITY
Another phenomenological law of gradient-driven transport is that of Newtonian viscosity,1
| (29) |
where τ is the shear stress that is applied to a fluid, dvy/dx is the resultant shear rate, and the proportionality coefficient η is the viscosity of a Newtonian fluid. Whereas Fick’s law describes particle transport and Fourier’s law describes energy transport, Eq. (29) describes the transport (in the x direction, from the top moving plate toward the bottom fixed plate) of linear momentum in the y direction (parallel to the plates)(see Fig. 8). In the same spirit as our simplified treatment of Fourier’s law, the dog-flea model can be used as the basis of a particle transfer version of momentum transport. Suppose each particle in column 1 of Table I carries momentum mvy1 along the y axis, and particles hop from column 1 to 2 at time t carrying with them some linear momentum. As before, we consider the simplest model for which every particle carries the same average momentum from the column it leaves to its destination column.
Fig. 8.
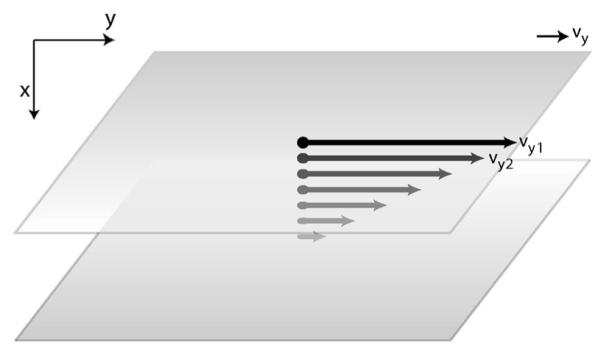
Illustration of Newton’s law of viscosity. The fluid is sheared with a constant stress. The fluid velocity decreases continuously from its maximum value at the top of the fluid to zero at the bottom. There is thus a gradient in the velocity which can be related to the shear stress in the fluid.
The flux Jp is the amount of y-axis momentum that is transported from one plane to the next in the x direction per unit area:
| (30) |
If the number of particles is the same in both columns, N/2=N1=N2, Eq. (30) simplifies to
| (31) |
which is the Newtonian law of viscosity for this two-column model. The viscosity is predicted by this model to be η=(pmNΔx)/(Δt). If we convert this result to the more canonical form, we have η=pmnvavΔx, where n=N/Δx is the particle density, and vav=Δx/Δt is the average velocity. This form is equivalent to the value given by the kinetic theory of gases,1 η=(1/3)mnlvav from our model equals l. The numerical factors of 1/3 and p in the kinetic theory and our model, respectively, have the same origin as discussed in the context of heat flow. Note that this simple model based on molecular motions will clearly not be applicable to complex fluids where the underlying molecules possess internal structure.
VI. CHEMICAL KINETICS WITHIN THE DOG-FLEA MODEL
Let us now look at chemical reactions using the dog-flea model. Chemical kinetics can be modeled using the dog-flea model when the fleas have preference for one dog over the other. Consider the reaction
| (32) |
The time-dependent average concentrations, [A](t) and [B](t) are often described by chemical rate equations,2
| (33a) |
| (33b) |
where kf is the average conversion rate of an A to a B, and kr is the average conversion rate of a B to an A. These rate expressions describe only average rates; they do not give the distribution of rates. Some A’s will convert to B’s faster than the average rate kf[A] predicts, and some will convert more slowly. Again we use the dog-flea model and consider the average concentrations and the fluctuations in concentrations. A particularly fruitful area for applications of the A⇋B dynamics considered here is to problems involving molecular motors and ion channels.
We assume that dog 1 represents chemical species A and dog 2 represents chemical species B. The net chemical flux from 1 to 2 is given by . What is different about our model for these chemical processes than in our previous situations is that now the intrinsic jump rate from column 1 (species A), p1, is different than the jump rate from column 2, p2. This difference reflects the fact that a forward rate can differ from a backward rate in a chemical reaction. We assume that the fleas have a different escape rate from each dog. Fleas escape from dog 1 at rate p1 and fleas escape from dog 2 at rate p2. Maximizing Wd gives and , so the average flux (which is almost the same as the most probable flux because of the approximately symmetric nature of the binomial distribution) at time t is
| (34) |
which is just the standard mass-action rate law, expressed in terms of the mean concentrations. The mean values satisfy detailed balance at equilibrium (〈J〉=0 implies that N2/N1=p1/p2=kf/kr
More interesting than the behavior of the mean chemical reaction rate is the behavior of the fluctuations. For example, if the number of particles is small, then even when kf[A]−kr[B]>0, indicating an average conversion of A’s to B’s, the reverse can happen occasionally. When will these fluctuations be large? As in Sec. III, we first determine the probability distribution of the flux J. In this case, the probability distribution becomes
| (35) |
We use this flux distribution function to consider the fluctuations in the chemical reaction. The relative variance in the flux is
| (36) |
As before, the main message is that when the system is not yet at equilibrium (that is, the denominator is nonzero), macroscopically large systems will have negligibly small fluctuations. The relative magnitude of the fluctuations scales approximately as N-1/2. Let us also look at the potencies of microtrajectories as another window into the fluctuations. If we use Eq. (23) with p1 and p2, we find that the fraction of trajectories that are impotent is
| (37) |
| (38) |
For N1+N2=N=100 and p1=0.1 and p2=0.2, Φpotent=1−Φimpotent is shown in Fig. 9 as a function of N1/N.
Fig. 9.
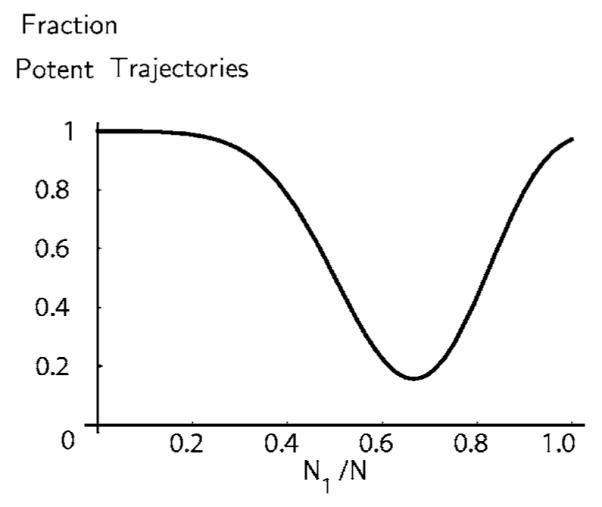
The fraction of potent trajectories Φpotent as a function of N1/N for N1+N2=N=100, and p1=0.1 and p2=0.2. The minimum value of the potency does not occur at N1/N=0.5, but at N1/N=0.66. This value of N1/N also corresponds to its equilibrium value given by p2/(p1+p2).
VII. DERIVATION OF THE DYNAMICAL DISTRIBUTION FUNCTION FROM MAXIMUM CALIBER
We have used the binomial distribution function Wd as the basis for our treatment of stochastic dynamics. The maximum caliber assumption is that if we find the value of Wd that is a maximum with respect to the microscopic trajectories, this value will give the macroscopically observable flux. We now restate this assumption more generally in terms of the probabilities of the trajectories.
Let P(i) be the probability of a microtrajectory i during the interval from time t to t+Δt. A microtrajectory is a specific set of fleas that jump; for example microtrajectory i=27 might be the case for which fleas 4, 8, and 23 jump from dog 1 to 2. We take as a constraint the average number of jumps, 〈m〉, the macroscopic observable. The quantity mi=3 in this case indicates that trajectory i involves three fleas jumping. We express the caliber as
| (39) |
where λ is the Lagrange multiplier that enforces the constraint of the average flux and α is the Lagrange multiplier that enforces the normalization condition that the P(i)’s sum to one. Maximizing the caliber gives the populations of the microtrajectories,
| (40) |
Note that the probability P(i) of the ith trajectory depends only on the total number mi of the jumping fleas. Also, all trajectories with the same mi have the same probabilities. In the same way that it is sometimes useful in equilibrium statistical mechanics to switch from microstates to energy levels, we now express the population P(i) of a given microtrajectory in terms of ρ(m), the fraction of all the microtrajectories that involve m jumps during this time interval,
| (41) |
where g(m)=N!/[m!(N-m)!] is the density of trajectories with flux m (in analogy with the density of states for equilibrium systems), and Q(m) is the probability P(i) of microtrajectory i with mi=m. In other words, i denotes a microtrajectory (a specific set of fleas jumping) and m denotes a microprocess (the number of fleas jumping). The total number of i’s associated with a given m is g(m). It can also be easily seen that
| (42) |
| (43) |
Thus the distribution of jump-processes written in terms of the jump number m is
| (44) |
The Lagrange multiplier α can be eliminated by summing over all trajectories and requiring that , that is,
| (45) |
We combine Eqs. (44) and (45) to obtain
| (46) |
If we now let
| (47) |
we obtain
| (48) |
and
| (49) |
If we combine Eqs. (46), (48), and (49), we find the simple form
| (50) |
which appears in Eq. (11) and which we have used throughout this paper.
VIII. SUMMARY AND COMMENTS
We have shown how to derive the phenomenological laws of nonequilibrium transport, including Fick’s law of diffusion, Fourier’s law of heat conduction, the Newtonian law of viscosity, and the mass-action laws of chemical kinetics from a simple physical foundation that can be taught in undergraduate courses. We used the dog-flea model for describing how particles, energy, or momentum can be transported across a plane. We combined this model with the principle of maximum caliber, a dynamical analog of the principle of maximum entropy for the laws of equilibrium. For dynamics we focus on microtrajectories rather than microstates and maximize a dynamical entropy-like quantity, subject to an average flux constraint. In this way maximizing the caliber is the dynamical equivalent of minimizing a free energy for predicting equilibria. A particular value of this approach is that it also gives us fluctuation information, not just averages. In diffusion, for example, sometimes the flux can be a little higher or lower than the average value expected from Fick’s law. These fluctuations can be important for biology and nanotechnology, where the numbers of particles can be very small, and therefore where there can be significant fluctuations in rates, around the average.
ACKNOWLEDGMENTS
It is a pleasure to acknowledge the helpful comments and discussions with Dave Drabold, Mike Geller, Jané Kondev, Stefan Müller, Hong Qian, Darren Segall, Pierre Sens, Jim Sethna, Ron Siegel, Andrew Spakowitz, Zhen-Gang Wang, and Paul Wiggins. We would also like to thank Sarina Bromberg for help with the figures. K.A.D. and M.M.I. would like to acknowledge support from NIH Grant No. R01 GM034993. R.P. acknowledges support from NSF Grant No. CMS-0301657, CIMMS, the Keck Foundation, NSF NIRT Grant No. CMS-0404031, and NIH Director’s Pioneer Award Grant No. DP1 OD000217.
Contributor Information
Kingshuk Ghosh, Department of Biophysics, University of California, San Francisco, California 94143.
Ken A. Dill, Department of Biophysics, University of California, San Francisco, California 94143
Mandar M. Inamdar, Division of Engineering and Applied Science, California Institute of Technology, Pasadena, California 91125
Effrosyni Seitaridou, Division of Engineering and Applied Science, California Institute of Technology, Pasadena, California 91125.
Rob Phillips, Division of Engineering and Applied Science and Kavli Nanoscience Institute, California Institute of Technology, Pasadena, California 91125.
References
- 1.Reif F. Fundamentals of Statistical and Thermal Physics. McGraw-Hill; New York: 1965. [Google Scholar]
- 2.Dill K, Bromberg S. Molecular Driving Forces: Statistical Thermodynamics in Chemistry and Biology. Garland Science; New York: 2003. [Google Scholar]
- 3.Kasianowicz J, Brandin E, Branton D, Deamer D. Characterization of individual polynucleotide molecules using a membrane channel. Proc. Natl. Acad. Sci. U.S.A. 1996;93:13770–13773. doi: 10.1073/pnas.93.24.13770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lu HP, Xun L, Xie XS. Single molecule enzymatic dynamics. Science. 1998;282:1877–1882. doi: 10.1126/science.282.5395.1877. [DOI] [PubMed] [Google Scholar]
- 5.Reif M, Rock RS, Mehta AD, Mooseker MS, Cheney RE, Spudich JA. Myosin-V stepping kinetics: A molecular model for processivity. Proc. Natl. Acad. Sci. U.S.A. 2000;97:9482–9486. doi: 10.1073/pnas.97.17.9482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Meller A, Nivon L, Branton D. Voltage-driven DNA translocations through a nano-pore. Phys. Rev. Lett. 2001;86:3435–3438. doi: 10.1103/PhysRevLett.86.3435. [DOI] [PubMed] [Google Scholar]
- 7.Smith DE, Tans SJ, Smith SB, Grimes S, Anderson DL, Bustamante C. The bacteriophage [H9278]29 portal motor can package DNA against a large internal force. Nature (London) 2001;413:748–752. doi: 10.1038/35099581. [DOI] [PubMed] [Google Scholar]
- 8.Li H, Linke WA, Oberhauser AF, Carrion-Vazquez M, Kerkvliet JG, Lu H, Marszalek P, Fernandez JM. Reverse engineering of the giant muscle protein. Nature (London) 2002;418:998–1002. doi: 10.1038/nature00938. [DOI] [PubMed] [Google Scholar]
- 9.Liphardt J, Dumont S, Smith SB, Tinocho I, Bustamante C. Equilibrium information from nonequilibrium measurements in an experimental test of Jarzynski’s equality. Science. 2002;296:1832–1835. doi: 10.1126/science.1071152. [DOI] [PubMed] [Google Scholar]
- 10.Bustamante C, Bryant Z, Smith SB. Ten Years of tension: single-molecule DNA mechanics. Nature (London) 2003;421:423–427. doi: 10.1038/nature01405. [DOI] [PubMed] [Google Scholar]
- 11.Dufresne ER, Altman D, Grier DG. Brownian dynamics of sphere in a slit pore. Europhys. Lett. 2001;53:264–270. [Google Scholar]
- 12.Alberts B, Bray D, Johnson A, Lewis J, Raff M, Roberts K, Walter P. Essential Cell Biology: An Introduction to the Molecular Biology of the Cell. Garland; New York: 1997. [Google Scholar]
- 13.Kondepudi D, Prigogine I. Modern Thermodynamics: From Heat Engines to Dissipative Structures. Wiley; New York: 1998. [Google Scholar]
- 14.Jaynes ET, Jaynes ET, Rosenkrantz RD. Papers on Probability, Statistics and Statistical Physics. Kluwer Academic; 1980. Chap. 14. [Google Scholar]
- 15.Klein M. Entropy and the Ehrenfest urn model. Physica (Amsterdam) 1956;22:569–575. [Google Scholar]
- 16.Ambegaokar V, Clerk A. Entropy and time. Am. J. Phys. 1999;67:1068–1073. [Google Scholar]
- 17.Emch GG, Liu C. The Logic of Thermostatistical Physics. Springer-Verlag; New York: 2002. [Google Scholar]
- 18.Feynman RP. Nobel Lectures in Physics: 1901-1995. World Scientific; Singapore: 1998. [Google Scholar]
- 19.Reference 14, Chap. 1.
- 20.Kac M. Random walk and the theory of Brownian motion. Am. Math. Monthly. 1947;54:369–391. [Google Scholar]
- 21.The Maxwell demon is an imaginary microscopic object that was invoked in similar situations in heat flow processes, that is, where heat flows from a colder object to a hotter one, albeit with low probability (Ref. 22). In particular, the demon is supposed to capture the bad actor microtrajectories.
- 22.Gamow G. One Two Three … Infinity. Dover; New York: 1988. [Google Scholar]
- 23.Wang GM, Sevick EM, Mittag E, Searles DJ, Evans DJ. Experimental verification of the fluctuation theorem. Phys. Rev. Lett. 2002;89:050601–1. doi: 10.1103/PhysRevLett.89.050601. [DOI] [PubMed] [Google Scholar]
- 24.Howard J. Mechanics of Motor Proteins and the Cytoskeleton. Sinauer Associates; 2001. [Google Scholar]