Abstract
We propose a two-stage approach to analyze genome-wide association (GWA) data in order to identify a set of promising single-nucleotide polymorphisms (SNPs). In stage one, we select a list of top signals from single SNP analyses by controlling false discovery rate (FDR). In stage two, we use the least absolute shrinkage and selection operator (LASSO) regression to reduce false positives. The proposed approach was evaluated using simulated quantitative traits based on genome-wide SNP data on 8,861 Caucasian individuals from the Atherosclerosis Risk in Communities (ARIC) Study. Our first stage, targeted at controlling false negatives, yields better power than using Bonferroni corrected significance level. The LASSO regression reduces the number of significant SNPs in stage two: it reduces false positive SNPs and it reduces true positive SNPs also at simulated causal loci due to linkage disequilibrium. Interestingly, the LASSO regression preserves the power from stage one, i.e., the number of causal loci detected from the LASSO regression in stage two is almost the same as in stage one, while reducing false positives further. Real data on systolic blood pressure in the ARIC study was analyzed using our two-stage approach which identified two significant SNPs, one of which was reported to be genome-significant in a meta-analysis containing a much larger sample size. On the other hand, a single SNP association scan did not yield any significant results.
Keywords: LASSO, FDR, multi-marker, association, power
Introduction
Genome-wide association studies (GWAS) have achieved great successes during the past years with more than 3,000 genetic variants found to be associated with complex traits [Hindorff et al., 2009]. There is a convergence of knowledge that common complex traits derive from etiologic factors with multiple loci whose genetic main effects are typically small, therefore, require substantial sample sizes for discovery as well as replication. For recently discovered loci associated with blood pressures and hypertension, phenotypic variation explained by each locus varies from 0.03% to 0.09% [Levy et al., 2009; Newton-Cheh et al., 2009]. In the GWAS of serum lipid phenotypes, about 100 loci have been identified with a sample size larger than 100,000 [Kathiresan et al., 2008; Kathiresan et al., 2009; Teslovich et al., 2009]. With millions of single-nucleotide polymorphisms (SNPs) under tests in GWAS, the power of identifying signals with such small effect sizes at the genome-wide significance level [Pe’er et al., 2008] is typically small for many established studies. In order to find signals showing genome-wide statistical significance, seeking evidence outside of the study is necessary. Nowadays, large consortia have been established to find common genetic variants mostly targeted at common complex traits. As a result, genome-wide meta-analysis has become a common practice. On the other hand, for those complex traits or ethnic groups that have not been widely studied, finding large number of samples through such collaborative effort may not be feasible. GWAS have to rely upon studies with relatively small sample sizes, hence requires exploiting information in a very efficient manner. Although it is almost a common belief that large sample sizes are crucial for identifying most, if not all, genetic components of complex diseases, recent genome-wide association (GWA) results [Adeyemo et al., 2009; Asano et al., 2009; Schaefer et al., 2010; Tanaka et al., 2010] show-case the successes of finding some variants with sample sizes in the thousands or even hundreds. With complex genetic architecture and heterogeneity of complex traits, effect sizes of underlying genetic variants vary across populations. It is likely that for a particular study sample some loci will have relatively larger effect sizes than in the general population. In this case, the so-called “winner’s curse” [Capen et al., 1971; Yu et al., 2007] for replication is indeed a “complexity’s blessing” at the discovery phase. In addition, longitudinal data that measure phenotypes on the same subjects repeatedly can be used for GWAS, which have much better overall signal-to-noise ratio than the same sample with cross-sectional snapshot data. As shown in Shi et al. [2009], using simulated phenotypes from the Genetic Analysis Workshop 16 Problem 3 [Kraja et al., 2009], statistical power of longitudinal analysis of a phenotype with three-visit data is substantially greater than analysis based on any single visit. Longitudinal data have also been considered as being more powerful and providing much better information on individual changes than cross-sectional data, thus providing a good opportunity to test for age depedent genetic effects, i.e., gene-age interactions. In this work, we propose a two-stage approach for GWA analysis aiming to identify a promising set of SNPs that can be used for independent replication or for seeking additional statistical evidence through meta-analysis. In stage one, GWA analysis will be based on regular single SNP tests as conducted in many genome-wide scans. Instead of applying type I error based thresholds such as Bonferroni corrected or genome-wide significance thresholds, we subset SNPs by controlling false discovery rate (FDR) [Benjamini and Hochberg, 1995] to minimize false negatives meanwhile controlling false positive results. In stage two, we analyze the selected top SNPs jointly with the least absolute shrinkage and selection operator (LASSO) regression [Tibshirani, 1996; Efron et al., 2004] and reduce false positives further.
Methods
The proposed two-stage approach is illustrated in Supplementary Figure S1. Analysis starts by running a genome-wide scan with a regular single SNP association test. A variety of statistical tests can be applied at this step depending on the study design and the nature of the phenotype. In this work, we focused on quantitative traits from a population-based study. For dichotomous traits or other types of study designs, appropriate tests can be adopted accordingly. Haplotype-based multi-marker tests can also be applied in the proposed two-stage approach without loss of generality. With the results from the GWA scan, a set of top SNPs will be determined via a FDR approach [Benjamini and Hochberg, 1995] at end of the first stage. Different from traditional significance tests that control family-wise type I error rate, i.e., the probability of having one or more false positive results, FDR approaches particularly address the multiple comparison issue by controlling the expected false discovery rate, defined as
where S represents the total number of declared positive hypotheses, and F stands for the number of false positives among the declared positives. Many variations of the FDR methods have been proposed [Benjamini and Liu, 1999; Yekutieli and Benjamini, 1999; Benjamini and Hochberg, 2000; Benjamini and Yekutieli, 2001; Storey, 2002; Storey, 2003; Storey et al., 2004; Gordon et al., 2007] and this concept was further extended to the so-called q value [Storey, 2002; Storey, 2003]. FDR approaches have been widely used in gene expression micro-array data analysis [Tusher and Tibshirani, 2001; Reiner et al., 2003; Storey and Tibshirani, 2003; Zhang, 2007], genome-wide linkage analysis [Benjamini and Yekutieli, 2005], and most recently investigated in the context of genome-wide association [Marenne et al., 2009]. After the FDR procedure, genome-wide SNPs would fall into two sets: one consists of declared significant SNPs and the other consists of declared negative SNPs. Among the significant SNPs, error rate is controlled at a pre-set FDR level. FDR approaches are considered to be more powerful than controlling family-wise error rate especially when a large number of hypotheses are under examination and multiple hypotheses are expected to be true alternatives [Storey, 2003]. If all hypotheses are truly under null, controlling of FDR is equivalent to controlling family-wise error rate [Benjamini and Hochberg, 1995].
With the significant SNPs from stage one, we analyzed them jointly using LASSO regression [Tibshirani, 1996; Efron et al., 2004]. The LASSO regression is a constrained multiple linear regression method whose L1 norm of regression coefficients is restricted to be less than or equal to a specified value. In LASSO regression, model parameters are estimated such that
where μ is the intercept, βj are regression coefficients, and t is the bound on the L1 norm of regression coefficients. From another point of view, this is an optimization problem with the quadratic object function defined on a hypersphere with Manhattan distance. As a result of such L1 constraint, LASSO regression has the so-called shrinkage property and is able to yield a parsimonious model with many regression coefficients forced to zero. Unlike regular regression, the optimization problem is well-defined even when the number of SNPs is larger than the number of subjects. Hence, LASSO regression is a natural solver for variable selection, especially for high-dimensional problems. Alternatively, the mathematical equivalent of the LASSO regression can be formulated as
Therefore, LASSO regression is also a penalized regression approach. Ridge regression, a regression with penalty on the L2 norm of regression coefficients, has been proposed as a multi-marker approach for analyzing dense SNPs in linkage disequilibrium in order to overcome multicollinearity issue [Malo et al., 2008; Sun et al., 2009]. LASSO penalized logistic regression was applied in the GWA analysis of case-control gene mapping problem [Shi et al., 2007; Wu et al., 2009]. Most recently, LASSO regression was used as a multi-marker association method for a family-based study [Sung et al., 2009] and LASSO logistic regression was used for detecting gene×gene interaction in a population-based case control study [D’Angelo et al., 2009]. Elastic net, a hybrid version of ridge and LASSO regressions, was proposed for protein structure prediction [Ball et al., 2002] as well as GWAS [Cho et al., 2009]. In this work, we applied the LASSO technique in the second stage as a tool for trimming false positive results from stage one.
Simulation Study
To evaluate the proposed two-stage GWA method, we simulated quantitative traits using genome-wide SNP data on 8,861 individuals from the Atherosclerosis Risk in Communities (ARIC) study [The ARIC investigators, 1989]. Affymetrix 6.0 array genotypes were obtained in the 8,861 self-identified whites of European descent. To avoid any missing data issues, we used imputed genotypes [Pfeufer et al., 2009] in the simulation study, which were conducted with high quality genotyped SNPs and HapMap CEU samples using a hidden Markov model implemented in MACH [Li and Abecasis, 2006]. After quality control filters, only those SNPs which are in both Affymetrix 6.0 array and the HapMap SNP panel were used in this simulation study, which corresponds to a total of 610,018 SNPs. When simulating quantitative traits, 25 SNPs were selected as being “causal” SNPs, which have a genotyping missing rate of less than 1%, Hardy-Weinberg P values larger than 0.1, and minor allele frequencies (MAFs) close to the following five values: 2.5%, 5%, 10%, 20%, and 40%. Five SNPs were selected for each MAF value and simulated with different effect sizes measured as R-squared, i.e., portions of phenotypic variance. The R-squared takes five discrete values: 0.25%, 0.5%, 1%, 2%, and 4% for every MAF value. A summary of the 25 selected “causal” SNPs are shown in Supplementary Table S1. Genetic effects of the 25 SNPs were simulated to be additive without interactions among them, and the total genetic effects account for 38.75% of the variance of the simulated phenotype. The rest of the 61.25% phenotypic variation was simulated to be additive, normally and independently distributed random noise. The 25 SNPs spread over 22 autosomes, six of them are located on chromosomes 1, 2, and 3 with two SNPs each, and the others reside on distinct chromosomes. Physical distances between the two SNPs on chromosomes 1, 2, and 3 are 81.6 Mbp, 177.0 Mbp, and 29.7 Mbp, respectively. To simulate samples with different sample sizes, subjects were drawn randomly from the total ARIC sample without replacement.
The two-stage GWA approach was used to analyze the simulated phenotype and the 610,018 SNPs. Sample size was varied from 1,000 to 8,000 incrementally by 1,000, each with 100 replications. In stage one, single SNP association analyses were conducted using PLINK [Purcell et al., 2007] with the “--assoc” option under the additive model, FDR analyses were conducted with SAS PROC MULTTEST and “FDR” option, and a LASSO regression was conducted using the LARS package [Efron et al., 2004] under R [R Development Core Team, 2007].
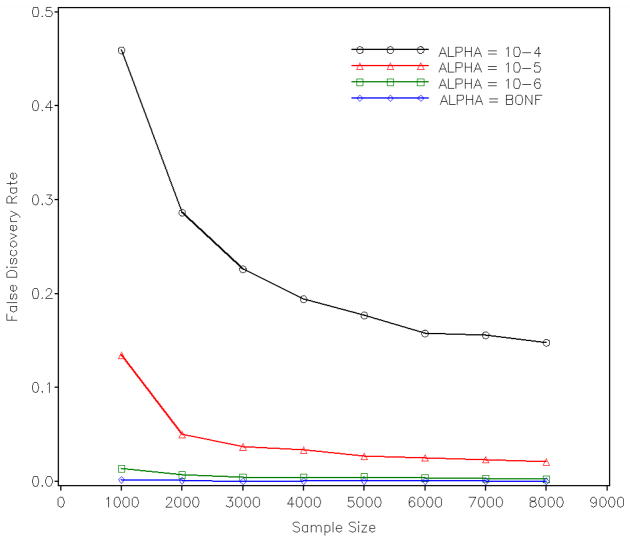
Supplementary Figure S2 shows the empirical power of detecting each of the 25 “causal” SNPs with sample sizes varying from 1,000 to 8,000 and with a Bonferroni-corrected type I error threshold. It is easy to see that with a sample size of 1,000, only SNPs explaining 4% phenotypic variances were detected with sufficient power (larger than 0.8). With a sample size of 2,000, most SNPs with R-squared larger than 2% were detected with sufficient power. A sample size of 8,000 had enough power to detect most SNPs with R-squared above 0.5%. SNPs that explained a quarter percent of phenotypic variation had power less than 0.5 even with 8,000 samples. MAF shows no systematic impact on the power, and variations of empirical power results among SNPs having the same effect sizes are mostly due to the limited number of replications. These results agree with the power from theoretic predictions using Quanto [Gauderman and Morrison, 2006], which are shown in Table I. Supplementary Figure S3 demonstrates the average number of “causal” SNPs detected with different sample sizes and type I error thresholds. The results of applying a step-up FDR controlling procedure [Benjamini and Hochberg, 1995] are also shown in the same figure. As we can see, controlling FDR at 0.05 is more powerful than controlling family-wise error rate at 0.05 (same as Bonferroni corrected), both of which are expected to yield the same family-wise error rate when all hypotheses are truly under the null [Benjamini and Hochberg, 1995]. Under our simulation setup, controlling FDR at the 0.05 level with a sample size of 8,000 is approximately equivalent to controlling type I error at some level between 10−4 and 10−5; the equivalent type I error rate, however, becomes more stringent when using a sample size of 1,000. Viewing the relationship from another point of view, Figure 1 shows the empirical FDR when controlling type I error at different levels. It is obvious to see that if we lower the type I error threshold to 10−4 for a sample of 1,000, almost half of the positive results will be false discoveries under our simulation setup. For studies with smaller sample sizes, it is a common practice to lower the type I error threshold in the hope of avoiding possible false negatives, which may, however, increase the FDR substantially.
TABLE I.
Empirical power for detecting simulated “causal” SNPs and theoretical power predicted by Quanto. Type I error threshold 8.2×10−8 (Bonferroni corrected) was used.
| Sample Size | Effect Size (R2)
|
||||
|---|---|---|---|---|---|
| 0.25% | 0.5% | 1% | 2% | 4% | |
| 1,000 | 0.00/0.00 | 0.00/0.00 | 0.01/0.01 | 0.15/0.19 | 0.88/0.85 |
| 2,000 | 0.00/0.00 | 0.02/0.01 | 0.19/0.19 | 0.78/0.84 | 1.00/1.00 |
| 4,000 | 0.02/0.03 | 0.20/0.19 | 0.86/0.84 | 1.00/1.00 | 1.00/1.00 |
| 8,000 | 0.19/0.19 | 0.86/0.83 | 1.00/1.00 | 1.00/1.00 | 1.00/1.00 |
The first number represents empirical power from simulation study; and the second stands for theoretical power from Quanto. Empirical power results were averaged over SNPs with the same R2 value.
Fig. 1.
Empirical FDR for controlling type I error rates at 10−4, 10−5, 10−6, and 8.2×10−8 (Bonferroni corrected).
To verify the FDR and type I error controlling procedures, we compared empirical FDR and type I error rates with their targeted nominal values for different sample sizes. Since the simulated “causal” SNPs may be in linkage disequilibrium with adjacent SNPs, significant SNPs adjacent to “causal” SNPs should be considered as true positives instead of false ones. We define the false positives as SNPs being significant and located 5 Mbp or further away from any simulated “causal” SNPs. Supplementary Figure S4 and S5 show the empirical results of FDR and type I error rate, respectively. Both FDR and type I error rates are close to their controlled nominal values. For a small sample size such as 1,000, empirical results of the two error rates are slightly smaller than their nominal values.
At the end of stage one, a set of SNPs will be declared to be significant, among which the false discovery rate is controlled at a pre-determined level. The average number of significant SNPs from stage 1 for different sample sizes and FDR thresholds are shown in Supplementary Figure S6. The number of true positive results, defined as SNPs within 5 Mbp distance from any “causal” SNPs, are shown in Supplementary Figure S7, and the number of false positive SNPs, the difference between total positives and true positives, are shown in Supplementary Figure S8. It can be seen that the number of true positive SNPs is much larger than the number of simulated “causal” SNPs. Not surprisingly, this is due to the correlation between the “causal” SNPs and their neighboring SNPs. The “inflation” of true positive results becomes higher when sample size is larger. False positive SNPs, after examining their genomic locations, seem to distribute randomly and without obvious clusters observed.
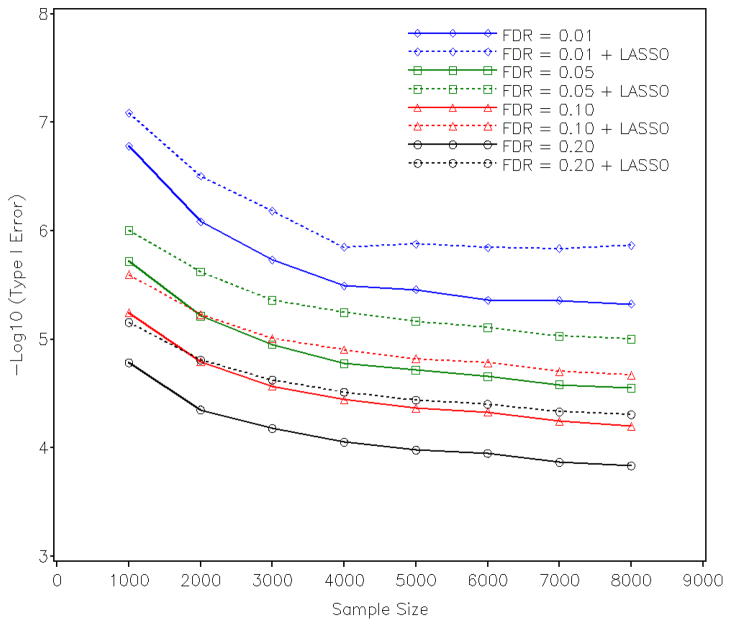
SNPs significant in stage 1 were simultaneously analyzed with the multi-marker LASSO regression in stage 2. In this simulation evaluation, we used Cp [Mallows, 1973; Efron et al., 2004] to choose the constraint on L1 norm of regression coefficients. The model with the smallest Cp value is finally chosen and the SNPs that stay in the final model (with minimum Cp value) are considered “significant” in the second stage. The number of significant SNPs, true positives, and false positives in the second stage were compared with results from stage 1 and shown in Supplementary Figure S6–S8. From Figure S7, we can see that the LASSO regression reduces the number of SNPs dramatically. For the case with a sample size of 8,000 and an FDR of 0.05, the number of significant SNPs was reduced from 327.7 in stage 1 to 63.7 in stage 2. Supplementary Figure S7 and S8 show the number of true positive SNPs and false positive SNPs after the LASSO regression, respectively; both numbers dropped substantially. For the same case with a sample size of 8,000 and an FDR of 0.05, the number of false positive SNPs was reduced from 17.1 in stage 1 to 6.1 in stage 2. As a result, type I error rate was reduced after the LASSO regression. See Figure 2 for the empirical type I error rates at the two stages.
Fig. 2.
Empirical type I error rate in stage 1 and stage 2.
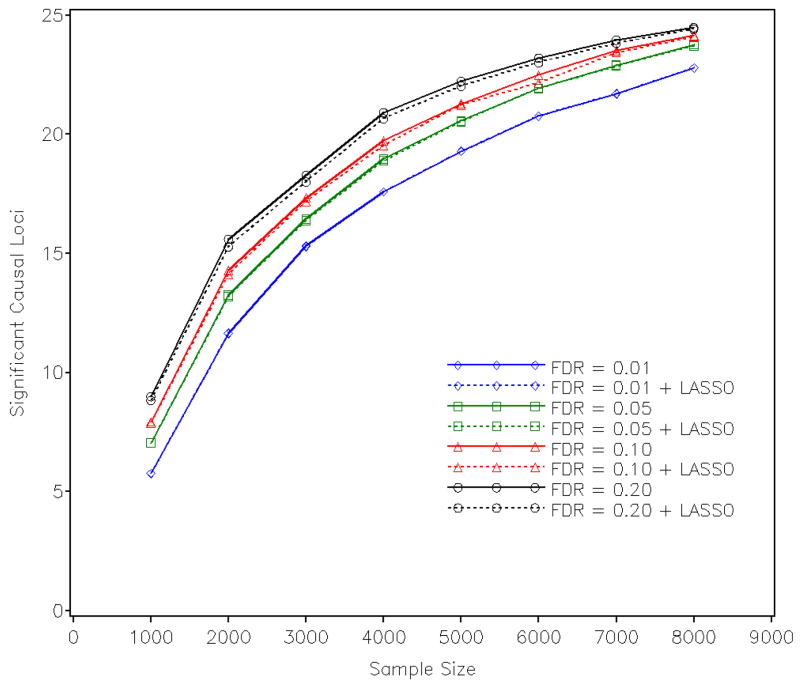
Since true positive results include multiple SNPs from the same loci, it would be interesting to know how many true “causal” loci that were significant in stage 1 remain significant in stage 2. We define a “causal” locus to be significant if any SNP within 5 Mbp distance from the simulated “causal” SNP at this locus is significant. In Figure 3, we show the numbers of “causal” loci as a function of sample size that were significant in two stages. Interestingly, the two sets of results are very close. Hence, even though the LASSO regression reduces the significant SNPs substantially, it keeps almost all the “causal” loci identified from stage 1. The two-stage approach was also examined by using different definitions of finding the “causal” signals. In a stricter sense, the successful detection requires the “causal” SNP itself to be significant. Corresponding results are summarized in Supplementary Figure S9. Most “causal” SNPs stay significant after the LASSO regression, but there were some “causal” SNPs that were missed in the second stage. From Figure 3, we know that for those “causal” SNPs losing significance in stage 2, there are some other SNPs from the same loci that survived the LASSO regression. From the most stringent standard, a successful detection requires the “causal” SNP not only to be significant but also to have the smallest P value among all neighboring SNPs. Supplementary Figure S10 shows the results by this definition, in which the LASSO regression shows no evidence of affecting the number of signals detected. We summarized the empirical power of the two-stage method by the three definitions in Table III. Compared with the results in Table II, which is based on controlling Bonferroni-corrected type I error rate, we can see that the proposed two-stage method improves power substantially, especially when the sample size is large and effect sizes of SNPs are small. For example, for SNPs with an R-squared of 0.25%, the two-stage approach has a power of 0.63 for identifying the “causal” SNPs with a sample size of 8,000, however, when controlling for type I error rate it shows a power of only 0.19.
Fig. 3.
Number of “causal” loci significant in stage 1 and stage 2.
TABLE III.
Top SNPs from the first and second stage of analyzing ARIC SBP (FDR=0.2). SNPs significant in stage 2 (LASSO regression) are in bold.
| SNP | Chr | Pos | P* | PFDR† |
|---|---|---|---|---|
| rs17155179 | 8 | 8,975,232 | 7.58×10−7 | 0.17 |
| rs17155181 | 8 | 8,975,595 | 8.43×10−7 | 0.17 |
| rs6987277 | 8 | 8,977,241 | 4.96×10−7 | 0.17 |
| rs6601286 | 8 | 8,977,445 | 4.98×10−7 | 0.17 |
| rs7818455 | 8 | 8,977,779 | 5.04×10−7 | 0.17 |
| rs2681472 | 12 | 88,533,090 | 6.94×10−7 | 0.17 |
| rs11105354 | 12 | 88,550,654 | 7.84×10−7 | 0.17 |
| rs12579302 | 12 | 88,574,634 | 8.63×10−7 | 0.17 |
| rs17249754 | 12 | 88,584,717 | 6.61×10−7 | 0.17 |
| rs11105364 | 12 | 88,593,407 | 7.91×10−7 | 0.17 |
| rs11105368 | 12 | 88,598,572 | 9.44×10−7 | 0.17 |
| rs11105378 | 12 | 88,614,872 | 9.12×10−7 | 0.17 |
| rs12230074 | 12 | 88,614,998 | 8.75×10−7 | 0.17 |
| rs9533040 | 13 | 41,694,721 | 1.17×10−6 | 0.20 |
| rs942188 | 14 | 89,613,556 | 8.37×10−7 | 0.17 |
P: P value from single SNP test;
PFDR: FDR corrected P value.
TABLE II.
Empirical power of the two-stage approach for detecting simulated “causal” signals with three different definitions. False discovery rate 0.05 was used.
| Sample Size | Effect Size (R2)
|
||||
|---|---|---|---|---|---|
| 0.25% | 0.5% | 1% | 2% | 4% | |
| 1,000 | 0.00/0.00/0.00 | 0.00/0.00/0.00 | 0.06/0.06/0.06 | 0.38/0.29/0.25 | 0.96/0.86/0.78 |
| 2,000 | 0.02/0.01/0.01 | 0.12/0.10/0.06 | 0.54/0.51/0.48 | 0.95/0.79/0.69 | 1.00/0.91/0.82 |
| 4,000 | 0.16/0.12/0.09 | 0.64/0.57/0.45 | 0.98/0.91/0.87 | 1.00/0.88/0.79 | 1.00/0.93/0.85 |
| 8,000 | 0.76/0.63/0.48 | 0.99/0.93/0.78 | 1.00/0.95/0.89 | 1.00/0.90/0.89 | 1.00/0.93/0.90 |
The first number represents empirical power of detecting the “causal” loci; the second stands for power of detecting the “causal” SNPs; and the third is power for detecting the “causal” SNPs with the smallest P values at their loci. Power estimates were averaged over SNPs with the same R2 value.
Analysis of Real Data in the ARIC Study
We applied the two-stage method in analyzing systolic blood pressure (SBP) in the ARIC data. The ARIC study is a prospective epidemiologic study sponsored by National Heart, Lung, and Blood Institute (NHLBI). A total of 15,792 subjects aged between 45 and 64 were recruited at baseline (1987–89). Subjects were chosen by probability sampling from 4 US communities, see the ARIC study website (http://www.cscc.unc.edu/aric) for the study design and protocol. There were four clinic examinations conducted three years apart between 1987 and 1998. Mean of the last two measurements of SBP during the first visit was used in the analysis. Phenotypic outliers, defined as 4 standard deviations (SDs) away from the respective mean, were excluded from the analysis. For subjects on anti-hypertensive medication, 10 mm Hg was added to the observed SBP value value [Cui et al., 2003]. In stage one, about 2.5 million imputed SNPs based on HapMap CEU samples (release 22 build 36) were tested assuming an additive genetic model; sex, body mass index, age, square of age, and field center were used as covariates. In the single-SNP association analysis, no SNP showed genome-wide significance with a P value smaller than 5×10−8 [Pe’er et al., 2008], the SNP with the smallest P value was rs6987277 (P value= 4.96×10−7) on chromosome 8p23.
After controlling FDR at 0.2, top SNPs from stage one included 15 SNPs distributed on four chromosome loci 8p23, 12q21, 13q14, and 14q32. No SNPs were significant at FDR=0.05 or FDR=0.1 levels in the first stage. Details on the top SNPs are shown in Table III. After analyzing the 15 SNPs using LASSO regression, 2 of them were significant in the second stage: rs6987277 on chromosome 8p23 and rs2681472 on chromosome 12q21. Interestingly, the chromosome 12q21 SNP rs2681472 has been recently reported to be associated with SBP (P value=2.5×10−11) in the CHARGE meta-analysis with a total sample size of 29,136 [Levy et al., 2009]. This demonstrates the efficacy of our approach for finding signals with small effect sizes. Although SNP rs6987277 was not found in the recent GWAS of blood pressures, SNP rs11775334 from the same 8p23 region was reported to be associated with hypertension status (P value 4.05×10−6) [Levy et al., 2009] when combing more than 60,000 samples from the CHARGE and Global BPgen consortia.
Discussion
In our simulation work, we employed the step-up FDR procedure [Benjamini and Hochberg, 1995] that was originally developed for controlling FDR with independent test statistics, and was later shown to be applicable to some positively dependent tests [Benjamini and Yekutieli, 2001; Sarkar, 2003]. In GWAS, millions of dense SNPs are examined, hence test statistics of SNPs within linkage disequilibrium blocks could be correlated. Simulation evaluation showed good FDR control with the existence of linkage disequilibrium. Without loss of generality, any appropriate FDR procedure can be used in our proposed two-stage approach. It is worth mentioning that unlike controlling family-wise type I error rate whose significance threshold depends on the number of tests only, the FDR approach is data-driven, and its significance threshold depends on the distribution of the observed P values from all tests. For the same reason, although the FDR approach is more powerful than controlling family-wise type I error as reported in many FDR type publications, the absolute magnitudes of improvement depends on the number of true “causal” SNPs, their effect sizes, sample size, and the number of SNPs being analyzed.
LASSO regression solves least-squares regression with constraint on the L1 norm of the regression coefficients. Due to the nature of the L1 penalty, the LASSO approach provides a sparse selection of independent variables by shrinking most of the regression coefficients to zero. The number of variables that can be handled by LASSO is not limited by sample size and it is able to solve under-determined problems, hence providing an appealing approach for analyzing a large number of markers from genome-wide association studies. In our simulation study, LASSO reduced the number of correlated SNPs from the same locus showing the capability to handle potential multicollinearity issues. A common question for LASSO or other penalized regression methods, e.g., ridge regression, is what the “right” or “best” penalty or constraint should be. In simulations, we used the Mallows’ Cp, which provides a balance between model fitness and the number of variables, much as many other model selection criteria do, and is readily available in the publicly available LARS package we used. In some literature, it was reported that the Cp criterion tends to over-fit in some situations [Stine, 2004; Ishwaran, 2004], and this issue can be solved with a modified degrees of freedom term in the Cp formula [Stine, 2004] or the use of Cp with a stochastic variable selection technique [Ishwaran, 2004]. Cross-validation approach is another attractive criterion for determining the constraint parameter. However, splitting samples for cross-validating may jeopardize the chance of discovery especially for those already under-powered GWAS. Although it is technically feasible to apply the cross-validation criterion in our two-stage GWA strategy, it will not be recommended for real data analysis unless it is with a sufficiently large sample size. Most recently, the penalty parameter was used to tune LASSO regression for selecting a predetermined number of SNPs [Wu et al., 2009]. Not surprisingly, the order of SNP entering the model when relaxing the penalty would depend on the marginal significance of those SNPs under general scenarios. This is particularly useful when the resources for follow-up investigation are limited by the number of SNPs. We also want to mention that LASSO regression can handle when the number of SNPs is larger than the sample size, and hence, theoretically it could handle all the GWA SNPs simultaneously in a single model. However, it would be computationally more efficient to first screen a subset of SNPs most of which are likely to be true signals, and then follow with LASSO regression to reduce false positives further.
We selected 25 SNPs as “causal” SNPs in our simulation, and the simulated phenotype was generated based on the genotypes of the subjects. Due to linkage disequilibrium, these “causal” SNPs are correlated with many other SNPs in their neighborhoods and so are their association results. As commonly seen in GWA literature, reported signals show clusters of SNPs with high or moderate statistical evidence. We know that there is only one “causal” SNP at each locus that is “biologically” associated with our simulated phenotype, hence all other SNPs should be “biologically” false positives since they are not “functional”. Whereas, from a statistical point of view, all significant SNPs from the same locus should be treated as “statistically” true positives since their statistical evidence come from the correlation with the true “causal” SNPs. We used 5 Mbp distance from “causal” SNPs as a threshold to determine true and false positives in simulation evaluations, which is obviously much larger than the usual linkage disequilibrium block lengths or haplotype lengths [Reich et al., 2001]. We want to argue that the common linkage disequilibrium range, measured by linkage disequilibrium block or haplotype lengths, characterizes the scope of SNPs with relatively strong correlations. Some SNPs may have relatively weaker correlations at much longer distances than the usual linkage disequilibrium block or haplotype lengths. In this case, SNPs may still be significant due to their weak correlation with a “causal” SNP that has a large effect size and strong statistical significance. Supported from a real data example, with 868 cases and 1,194 controls from Genetic Analysis Workshop 16 Problem 1 [Amos et al., 2009], a top SNP in the famous HLA region associated with rheumatoid arthritis on chromosome 6p21 shows a P value less than 1×10−100. There are 339 genotyped SNPs at this locus having P values smaller than 5×10−8 and they spread over a region larger than 4 Mbp. The strengths of linkage disequilibrium between the top SNP and other significant SNPs, measured by R-squared, are even less than 0.01. To what extent genotypic correlation will affect the error rates depends on a number of factors: the strength of linkage disequilibrium between “causal” SNP and adjacent SNPs, sample size, as well as effect size of the “causal” SNP. In this study, using 5 Mbp threshold appeared to account for this issue well. However, this does not imply that the same threshold will serve as a universal standard in real data analysis.
We computed empirical type I error and false discovery rates with 500 Kbp distance from “causal” SNPs as the threshold for determining true and false positives, the results are shown in Supplementary Figure S11 and S12. Both results were significantly inflated from their nominal values especially when the sample size is large. With the 5 Mbp threshold, about 250 Mbp chromosome regions, which is less than 10 percent of human genome, will be considered as having no false positives by default. Hence, empirical false positives or false discovery rates may be smaller than they actual are, but this downward bias is limited to be less than 10%. From Supplementary Figure S4 and S5, we observed that the empirical false positive and false discovery rates with a sample size of 1,000 are slightly smaller than their nominal values. This discrepancy can be explained by the bias due to the 5 Mbp distance threshold used.
In the simulation study, we looked at three different definitions of finding a “causal” signal: (1) any SNP adjacent to the “causal” SNP is significant; (2) the “causal” SNP itself is significant but does not necessarily have the smallest P value at its locus; and (3) the “causal” SNP is significant and has the smallest P value. Obviously, the last criterion is the most stringent and represents the ideal case that we wish to find when analyzing real data. This requires that the “causal” SNP is genotyped, statistically significant, and has the most significant statistical evidence at its locus. Comparing results on Supplementary Figure S9 and S10, it is easy to find that “causal” SNPs actually have a good chance to be the most significant ones if they were indeed tested. On the other hand, commercial SNP arrays cover only a small fraction of the total human SNPs; even with imputed genotypes from the HapMap SNP panel, the coverage is still limited to the most common ones. Identifying associated locus instead of pinpointing the causal SNP(s) would be the practical objective for most GWAS. Thus, the Figure 3 represents the most likely situation when analyzing real data.
We showed that false positive SNPs are actually true positives in a statistical sense (due to their correlations with “causal” SNPs), hence the FDR could be larger if computed according to the number of loci instead of SNPs. Haplotype-based tests account for linkage disequilibrium implicitly and can effectively reduce the dependence in genome-wide scan, hence will yield better control of FDR measured by locus. Due to the extensive computational burden involved, in this work we focused on a single SNP test only. Haplotype-based tests can be readily applied in the proposed two-stage approach as well.
In summary, we proposed a two-stage method for analyzing GWA data. The FDR approach in the first stage is more powerful than using stringent family-wise type I error rate and can avoid excessive type I errors by arbitrarily lowering the type I error threshold. The multi-marker LASSO regression in the second stage can reduce redundant SNPs in the true signal regions due to linkage disequilibrium and effectively reduce false positives further. The two-stage approach provides a trade-off between false negatives and false positives in GWAS and can be used for mining loci with relatively small effect sizes, the so-called “gold dust” [Province and Borecki, 2008], which are often below the genome-significance level thereby escaping discovery.
Supplementary Material
Acknowledgments
This work was supported by grants 5R01GM028719, 5U01HL054473, and 5R01HL086694.
References
- Adeyemo A, Gerry N, Chen G, Herbert A, Doumatey A, Huang H, Zhou J, Lashley K, Chen Y, Christman M, Rotimi C. A genome-wide association study of hypertension and blood pressure in African Americans. PLoS Genet. 2009;5:e1000564. doi: 10.1371/journal.pgen.1000564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amos CI, Chen WV, Seldin MF, Remmers EF, Taylor KE, Criswell LA, Lee AT, Plenge RM, Kastner DL, Gregersen PK. Data for Genetic Analysis Workshop 16 Problem 1, association analysis of rheumatoid arthritis data. BMC Proc. 2009;3(Suppl 7):S2. doi: 10.1186/1753-6561-3-s7-s2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asano K, Matsushita T, Umeno J, Hosono N, Takahashi A, Kawaguchi T, Matsumoto T, Matsui T, Kakuta Y, Kinouchi Y, Shimosegawa T, Hosokawa M, Arimura Y, Shinomura Y, Kiyohara Y, Tsunoda T, Kamatani N, Iida M, Nakamura Y, Kubo M. A genome-wide association study identifies three new susceptibility loci for ulcerative colitis in the Japanese population. Nat Genet. 2009;41:1325–1329. doi: 10.1038/ng.482. [DOI] [PubMed] [Google Scholar]
- Ball KD, Erman B, Dill KA. The elastic net algorithm and protein structure prediction. J Comput Chem. 2002;23:77–83. doi: 10.1002/jcc.1158. [DOI] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J Roy Stat Soc Ser B. 1995;57:289–300. [Google Scholar]
- Benjamini Y, Liu W. A step-down multiple hypotheses testing procedure that controls the false discovery rate under independence. J Stat Plan Infer. 1999;82:163–170. [Google Scholar]
- Benjamini Y, Hochberg Y. On the adaptive control of the false discovery rate in multiple testing with independent statistics. J Educ Behav Stat. 2000;25:60–83. [Google Scholar]
- Benjamini Y, Yekutieli D. The control of the false discovery rate in multiple testing under dependency. Ann Stat. 2001;29:1165–1188. [Google Scholar]
- Benjamini Y, Yekutieli D. Quantitative trait loci analysis using the false discovery rate. Genetics. 2005;171:783–790. doi: 10.1534/genetics.104.036699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Capen EC, Clapp RV, Campbell WM. Competitive bidding in high-risk situations. J Petrol Technol. 1971;23:641–653. [Google Scholar]
- Cho S, Kim H, Oh S, Kim K, Park T. Elastic-net regularization approaches for genome-wide association studies of rheumatoid arthritis. BMC Proc. 2009;3(Suppl 7):S25. doi: 10.1186/1753-6561-3-s7-s25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cui JS, Hopper JL, Harrap SB. Antihypertensive treatments obscure familial contributions to blood pressure variation. Hypertension. 2003;41:207–210. doi: 10.1161/01.hyp.0000044938.94050.e3. [DOI] [PubMed] [Google Scholar]
- D’Angelo GM, Rao DC, Gu CC. Combining least absolute shrinkage and selection operator (LASSO) and principal-components analysis for detection of gene-gene interactions in genome-wide association studies. BMC Proc. 2009;3(Suppl 7):S62. doi: 10.1186/1753-6561-3-s7-s62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron B, Hastie T, Johnstone I, Tibshirani R. Least angle regression. Ann Stat. 2004;32:407–451. [Google Scholar]
- Gauderman WJ, Morrison JM. QUANTO 1.1: A computer program for power and sample size calculations for genetic-epidemiology studies. 2006 http://hydra.usc.edu/gxe.
- Gordon A, Glazko G, Qiu X, Yakovlev A. Control of the mean number of false discoveries, Bonferroni and stability of multiple testing. Ann Appl Stat. 2007;1:179–190. [Google Scholar]
- Hindorff LA, Sethupathy P, Junkins HA, Ramos EM, Mehta JP, Collins FS, Manolio TA. Potential etiologic and functional implications of genome-wide association loci for human diseases and traits. Proc Natl Acad Sci USA. 2009;106:9362–9367. doi: 10.1073/pnas.0903103106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishwaran H. [Least angle regression]: Discussion. Ann Stat. 2004;32:452–458. [Google Scholar]
- Kathiresan S, Melander O, Guiducci C, Surti A, Burtt NP, Rieder MJ, Cooper GM, Roos C, Voight BF, Havulinna AS, Wahlstrand B, Hedner T, Corella D, Tai ES, Ordovas JM, Berglund G, Vartiainen E, Jousilahti P, Hedblad B, Taskinen MR, Newton-Cheh C, Salomaa V, Peltonen L, Groop L, Altshuler DM, Orho-Melander M. Six new loci associated with blood low-density lipoprotein cholesterol, high-density lipoprotein cholesterol or triglycerides in humans. Nat Genet. 2008;40:189–197. doi: 10.1038/ng.75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kathiresan S, Willer CJ, Peloso GM, Demissie S, Musunuru K, Schadt EE, Kaplan L, Bennett D, Li Y, Tanaka T, Voight BF, Bonnycastle LL, Jackson AU, Crawford G, Surti A, Guiducci C, Burtt NP, Parish S, Clarke R, Zelenika D, Kubalanza KA, Morken MA, Scott LJ, Stringham HM, Galan P, Swift AJ, Kuusisto J, Bergman RN, Sundvall J, Laakso M, Ferrucci L, Scheet P, Sanna S, Uda M, Yang Q, Lunetta KL, Dupuis J, de Bakker PI, O’Donnell CJ, Chambers JC, Kooner JS, Hercberg S, Meneton P, Lakatta EG, Scuteri A, Schlessinger D, Tuomilehto J, Collins FS, Groop L, Altshuler D, Collins R, Lathrop GM, Melander O, Salomaa V, Peltonen L, Orho-Melander M, Ordovas JM, Boehnke M, Abecasis GR, Mohlke KL, Cupples LA. Common variants at 30 loci contribute to polygenic dyslipidemia. Nat Genet. 2009;41:56–65. doi: 10.1038/ng.291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kraja AT, Culverhouse R, Daw EW, Wu J, Van Brunt A, Province MA, Borecki IB. The Genetic Analysis Workshop 16 Problem 3: simulation of heritable longitudinal cardiovascular phenotypes based on actual genome-wide single-nucleotide polymorphisms in the Framingham Heart Study. BMC Proc. 2009;3(Suppl 7):S4. doi: 10.1186/1753-6561-3-s7-s4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy D, Ehret GB, Rice K, Verwoert GC, Launer LJ, Dehghan A, Glazer NL, Morrison AC, Johnson AD, Aspelund T, Aulchenko Y, Lumley T, Köttgen A, Vasan RS, Rivadeneira F, Eiriksdottir G, Guo X, Arking DE, Mitchell GF, Mattace-Raso FU, Smith AV, Taylor K, Scharpf RB, Hwang SJ, Sijbrands EJ, Bis J, Harris TB, Ganesh SK, O’Donnell CJ, Hofman A, Rotter JI, Coresh J, Benjamin EJ, Uitterlinden AG, Heiss G, Fox CS, Witteman JC, Boerwinkle E, Wang TJ, Gudnason V, Larson MG, Chakravarti A, Psaty BM, van Duijn CM. Genome-wide association study of blood pressure and hypertension. Nat Genet. 2009;41:677–687. doi: 10.1038/ng.384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Ding J, Abecasis GR. Mach 1.0: rapid haplotype reconstruction and missing genotype inference. Am J Hum Genet. 2006;S79:2290. [Google Scholar]
- Mallows CL. Some comments on cp. Technometrics. 1973;15:661–675. [Google Scholar]
- Malo N, Libiger O, Schork NJ. Accommodating linkage disequilibrium in genetic-association analyses via ridge regression. Am J Hum Genet. 2008;82:375–385. doi: 10.1016/j.ajhg.2007.10.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marenne G, Dalmasso C, Perdry H, Génin E, Broët P. Impaired performance of FDR-based strategies in whole-genome association studies when SNPs are excluded prior to the analysis. Genet Epidemiol. 2009;33:45–53. doi: 10.1002/gepi.20355. [DOI] [PubMed] [Google Scholar]
- Newton-Cheh C, Johnson T, Gateva V, Tobin MD, Bochud M, Coin L, Najjar SS, Zhao JH, Heath SC, Eyheramendy S, Papadakis K, Voight BF, Scott LJ, Zhang F, Farrall M, Tanaka T, Wallace C, Chambers JC, Khaw KT, Nilsson P, van der Harst P, Polidoro S, Grobbee DE, Onland-Moret NC, Bots ML, Wain LV, Elliott KS, Teumer A, Luan J, Lucas G, Kuusisto J, Burton PR, Hadley D, McArdle WL, Brown M, Dominiczak A, Newhouse SJ, Samani NJ, Webster J, Zeggini E, Beckmann JS, Bergmann S, Lim N, Song K, Vollenweider P, Waeber G, Waterworth DM, Yuan X, Groop L, Orho-Melander M, Allione A, Di Gregorio A, Guarrera S, Panico S, Ricceri F, Romanazzi V, Sacerdote C, Vineis P, Barroso I, Sandhu MS, Luben RN, Crawford GJ, Jousilahti P, Perola M, Boehnke M, Bonnycastle LL, Collins FS, Jackson AU, Mohlke KL, Stringham HM, Valle TT, Willer CJ, Bergman RN, Morken MA, Döring A, Gieger C, Illig T, Meitinger T, Org E, Pfeufer A, Wichmann HE, Kathiresan S, Marrugat J, O’Donnell CJ, Schwartz SM, Siscovick DS, Subirana I, Freimer NB, Hartikainen AL, McCarthy MI, O’Reilly PF, Peltonen L, Pouta A, de Jong PE, Snieder H, van Gilst WH, Clarke R, Goel A, Hamsten A, Peden JF, Seedorf U, Syvänen AC, Tognoni G, Lakatta EG, Sanna S, Scheet P, Schlessinger D, Scuteri A, Dörr M, Ernst F, Felix SB, Homuth G, Lorbeer R, Reffelmann T, Rettig R, Völker U, Galan P, Gut IG, Hercberg S, Lathrop GM, Zelenika D, Deloukas P, Soranzo N, Williams FM, Zhai G, Salomaa V, Laakso M, Elosua R, Forouhi NG, Völzke H, Uiterwaal CS, van der Schouw YT, Numans ME, Matullo G, Navis G, Berglund G, Bingham SA, Kooner JS, Connell JM, Bandinelli S, Ferrucci L, Watkins H, Spector TD, Tuomilehto J, Altshuler D, Strachan DP, Laan M, Meneton P, Wareham NJ, Uda M, Jarvelin MR, Mooser V, Melander O, Loos RJ, Elliott P, Abecasis GR, Caulfield M, Munroe PB Wellcome Trust Case Control Consortium. Genome-wide association study identifies eight loci associated with blood pressure. Nat Genet. 2009;41:666–676. doi: 10.1038/ng.361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pe’er I, Yelensky R, Altshuler D, Daly MJ. Estimation of the multiple testing burden for genomewide association studies of nearly all common variants. Genet Epidemiol. 2008;32:381–385. doi: 10.1002/gepi.20303. [DOI] [PubMed] [Google Scholar]
- Pfeufer A, Sanna S, Arking DE, Müller M, Gateva V, Fuchsberger C, Ehret GB, Orrú M, Pattaro C, Köttgen A, Perz S, Usala G, Barbalic M, Li M, Pütz B, Scuteri A, Prineas RJ, Sinner MF, Gieger C, Najjar SS, Kao WH, Mühleisen TW, Dei M, Happle C, Möhlenkamp S, Crisponi L, Erbel R, Jöckel KH, Naitza S, Steinbeck G, Marroni F, Hicks AA, Lakatta E, Müller-Myhsok B, Pramstaller PP, Wichmann HE, Schlessinger D, Boerwinkle E, Meitinger T, Uda M, Coresh J, Kääb S, Abecasis GR, Chakravarti A. Common variants at ten loci modulate the QT interval duration in the QTSCD Study. Nat Genet. 2009;41:407–414. doi: 10.1038/ng.362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Province MA, Borecki IB. Gathering the gold dust: methods for assessing the aggregate impact of small effect genes in genomic scans. Pac Symp Biocomput. 2008:190–200. [PubMed] [Google Scholar]
- Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MA, Bender D, Maller J, Sklar P, de Bakker PI, Daly MJ, Sham PC. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet. 2007;81:559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Development Core Team. R: A language and environment for statistical computing. R Foundation for Statistical Computing; Vienna, Austria: 2007. URL http://www.R-project.org. [Google Scholar]
- Reich DE, Cargill M, Bolk S, Ireland J, Sabeti PC, Richter DJ, Lavery T, Kouyoumjian R, Farhadian SF, Ward R, Lander ES. Linkage disequilibrium in the human genome. Nature. 2001;411:199–204. doi: 10.1038/35075590. [DOI] [PubMed] [Google Scholar]
- Reiner A, Yekutieli D, Benjamini Y. Identifying differentially expressed genes using false discovery rate controlling procedures. Bioinformatics. 2003;19:368–375. doi: 10.1093/bioinformatics/btf877. [DOI] [PubMed] [Google Scholar]
- Sarkar SK. Some results on false discovery rate in stepwise multiple testing procedures. Ann Stat. 2002;30:239–257. [Google Scholar]
- Schaefer AS, Richter GM, Nothnagel M, Manke T, Dommisch H, Jacobs G, Arlt A, Rosenstiel P, Noack B, Groessner-Schreiber B, Jepsen S, Loos BG, Schreiber S. A genome-wide association study identifies GLT6D1 as a susceptibility locus for periodontitis. Hum Mol Genet. 2010;19:553–562. doi: 10.1093/hmg/ddp508. [DOI] [PubMed] [Google Scholar]
- Shi G, Rice T, Gu CC, Rao DC. Application of three-level linear mixed-effects models incorporating gene-age interactions for association analysis of longitudinal family data. BMC Proc. 2009;3(Suppl 7):S89. doi: 10.1186/1753-6561-3-s7-s89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi W, Lee KE, Wahba G. Detecting disease-causing genes by LASSO-pattern search algorithm. BMC Proc. 2007;1(Suppl 1):S60. doi: 10.1186/1753-6561-1-s1-s60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stine RA. [Least angle regression]: Discussion. Ann Stat. 2004;32:475–481. [Google Scholar]
- Storey JD. A direct approach to false discovery rates. J Roy Stat Soc B. 2002;64:479–498. [Google Scholar]
- Storey JD. The positive false discovery rate: A Bayesian interpretation and the q-value. Ann Stat. 2003;31:2013–2035. [Google Scholar]
- Storey JD, Taylor JE, Siegmund D. Strong control, conservative point estimation and simultaneous conservative consistency of false discovery rates: a unified approach. J Roy Stat Soc Ser B. 2004;66:187–205. [Google Scholar]
- Storey JD, Tibshirani R. Statistical significance for genome-wide studies. Proc Nat Acad Sci USA. 2003;100:9440–9445. doi: 10.1073/pnas.1530509100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun YV, Shedden KA, Zhu J, Choi NH, Kardia SL. Identification of correlated genetic variants jointly associated with rheumatoid arthritis using ridge regression. BMC Proc. 2009;3(Suppl 7):S67. doi: 10.1186/1753-6561-3-s7-s67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sung YJ, Rice TK, Shi G, Gu CC, Rao DC. Comparison between single-marker analysis using Merlin and multi-marker analysis using LASSO for Framingham simulated data. BMC Proc. 2009;3(Suppl 7):S27. doi: 10.1186/1753-6561-3-s7-s27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanaka T, Roy CN, Yao W, Matteini A, Semba RD, Arking D, Walston JD, Fried LP, Singleton A, Guralnik J, Abecasis GR, Bandinelli S, Longo DL, Ferrucci L. A genome-wide association analysis of serum iron concentrations. Blood. 2010;115:94–96. doi: 10.1182/blood-2009-07-232496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teslovich TM, Musunuru K, Smith AV, Ripatti S, van Duijn C, Rotter J, Chasman D, Boerwinkle E, Cupples LA, Krauss R, Gudnason V, Rader D, Sandhu M, Kooner J, Borecki I, Munroe P, Pentonen L, Boehnke M, Abecasis G, Kathiresan S Global Lipids Genetics Consortium. Meta-analysis of >100,000 individuals identifies 63 new loci associated with serum lipid concentrations. Am J Hum Genet. 2009;S82:4. [Google Scholar]
- The ARIC investigators. The Atherosclerosis Risk in Communities (ARIC) Study: design and objectives. Am J Epidemiol. 1989;129:687–702. [PubMed] [Google Scholar]
- Tibshirani R. Regression shrinkage and selection via the lasso. J Roy Stat Soc Series B. 1996;58:267–288. [Google Scholar]
- Tusher VG, Tibshirani R, Chu G. Significance analysis of microarrays applied to the ionizing radiation response. Proc Nat Acad Sci USA. 2001;98:5116–5121. doi: 10.1073/pnas.091062498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu TT, Chen YF, Hastie T, Sobel E, Lange K. Genome-wide association analysis by lasso penalized logistic regression. Bioinformatics. 2009;25:714–721. doi: 10.1093/bioinformatics/btp041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yekutieli D, Benjamini Y. Resampling based false discovery rate controlling procedure for dependent test statistics. J Stat Plan Infer. 1999;82:171–196. [Google Scholar]
- Yu K, Chatterjee N, Wheeler W, Li Q, Wang S, Rothman N, Wacholder S. Flexible design for following up positive findings. Am J Hum Genet. 2007;81:540–551. doi: 10.1086/520678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang S. A comprehensive evaluation of SAM, the SAM R-package and a simple modification to improve its performance. BMC Bioinformatics. 2007;8:230. doi: 10.1186/1471-2105-8-230. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.