Abstract
Small regulatory RNAs are central players in the regulation of many cellular processes across all kingdoms of life. Experiments in mouse and human have shown that a typical small RNA may regulate the expression of many different genes, suggesting that small RNAs act as global regulators. It is noted though that most targets respond only weakly to the presence of the small RNA. At the same time, evidence in bacteria and animals suggest that the phenotypes associated with small RNA mutants are only due to a few of their targets. Here we assume that targets regulated by a small RNA to control function is in fact small, and propose that the role of the many other weak targets is to confer robustness to the regulation of these few principal targets. Through mathematical modeling we show that auxiliary targets may significantly buffer both number and kinetic fluctuations of the principal targets, with only minor slowdown in the kinetics of response. Analysis of genomic data suggests that auxiliary targets experience a nonspecific evolutionary pressure, playing a role at the system level. Our work is of importance for studies on small RNA functions, and impacts on the understanding of small RNA evolution.
Introduction
Small RNA molecules play critical regulatory roles in many different organisms, from small regulatory RNAs regulating stress response in bacteria to microRNAs regulating development and homeostasis in mammals (1,2). Many small RNA families achieve target-specificity at the posttranscriptional level via basepairing of a very short (6–8 nucleotides) region with the targeted microRNA. Consequently, one predicts that a particular binding sequence could appear at random in multiple loci across the genome, which may explain why many genes carry binding sites in their 3′UTR. Sequence pairing, however, may not be sufficient for successful interaction, and one might expect that most of these putative sites are nonfunctional, and would be lost during evolution. Surprisingly, bioinformatic searches for microRNA targets that focus on highly conserved sites still predict a large number of target genes per microRNA (3). In addition, recent experiments in mouse (4) and in humans (5) demonstrate that the transfection of a single microRNA affects the expression of many genes that carry a seed match, although most of these genes respond to the microRNA very weakly. It is therefore reasonable to hypothesize that these many binding sites mediate real interactions and have some functionality within the cellular context. One tempting interpretation is that microRNAs act as global regulators, affecting directly genes across pathways or modules of the cellular network.
On the other hand, detailed studies focused on particular small regulatory RNAs (srRNAs) draw a very different picture. Studies in bacteria and animals (6–16) suggest that the phenotype associated with mutating srRNAs is due only to few of their targets. For example, the lethal phenotype associated with mutating the recognition sequence in the heterochronic microRNA let-7 of Caenorhabditis elegans (6,7) is rescued by a compensating mutation in only one gene (lin-41). Similarly, concurrent reexpression of only three targets of the human microRNA miR-31 (10) (out of the hundreds predicted) is enough to abrogate the metastasis suppression phenotype associated with overexpression of the microRNA. These and other examples suggest that only few targets are directly involved in the cellular response to the level of the srRNA.
As the functions of more and more srRNAs are being elucidated in a variety of organisms and tissues, the mystery remains: what is the role of the many weakly interacting conserved targets (17)? Recently, it has been proposed that the number of phenotypically relevant targets regulated by a srRNA is in fact small (18,19) and that the many other weak targets which we accordingly term auxiliary might be competitive inhibitors for the srRNA by preventing the srRNA binding to the few principal targets. In this article we propose that the role of these auxiliary targets is to confer robustness and suppress both number and kinetic fluctuations. Through dynamical analysis we show that auxiliary targets can strongly suppress intrinsic fluctuations in their target levels with only minor effect on the kinetics of response. We support these predicted functional role of auxiliary targets by analyzing their conservation across vertebrates, and show that auxiliary targets experience a nonspecific evolutionary pressure, suggesting that their role is at the system level. With small RNAs acting in development and response pathways, these features are expected to be of major physiological consequence.
Materials and Methods
Unified model for srRNA regulation
General description of the model
In absence of auxiliary targets, the general picture of srRNA posttranscriptional regulation is well described by modeling the dynamics of the number of free srRNA s, of the number of principal target mRNAs m, and of the number of principal target proteins p, by a set of mass-action equations (20):
| (1) |
| (2) |
| (3) |
Here αs (αm) refers to the transcriptional rate of srRNA (mRNA) and βs (βm) to its degradation or turnover rate. The value k represents the interaction rate between the srRNA and its target mRNA. The target proteins are produced at a rate γ per mRNA molecule and self-degrade at a rate βp. Equations 1 and 2 assume that the pairing between the srRNA and the mRNA either leads to degradation of the complex or sequesters it (e.g., while blocking translation) for considerable time. Active codegradation is believed to occur for many prokaryotic small RNA-mRNA couples (1), while titration may be a more dominant mode of action of eukaryotic miRNAs (2). Within the same framework, it is easy to generalize the model and allow a fraction of the srRNA to be recycled. This does not affect the main results of our work (see the Supporting Material).
We generalize this model by accounting for the interaction between the srRNA and the auxiliary targets, leading to the formation of a transient complex (Fig. 1). The kinetics of the number of free auxiliary target mRNAs n and of complexed srRNAs c follow the mass-action equations
| (4) |
| (5) |
where αn is the total production rate over all auxiliary targets and βn is their average turnover rate. The value ka is the association rate between the srRNA and the auxiliary targets and kd the dissociation rate of the transient complex which is degraded at a rate βc ≪ kd. To account for the effect of the auxiliary targets on the srRNA level, one has to augment Eq. 1 by
with pd the probability that the srRNA is also eliminated during the complex degradation.
Figure 1.
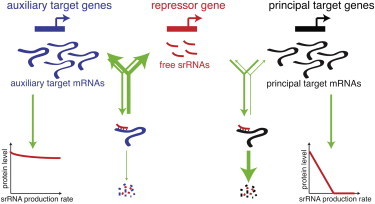
Interactions of a srRNA with its targets. In the pathway, the main difference between auxiliary and principal targets resides in the fate of the mRNA-srRNA complexes: for principal targets, the complexes are rapidly degraded leading to a strong effect on the overall principal protein level, whereas for auxiliary targets, the complexes preferentially dissociate, leading to only a weak effect on the auxiliary protein level.
Accounting for stochasticity
Stochasticity of the underlying biochemical reactions, including the transcriptional burstiness (21,22) and the effect of transport by diffusion of the interacting molecules (23,24), is accounted for by augmenting the previous set of mass-action equations with Langevin terms (25,26) which captured the intrinsic fluctuations of each reaction (see the Supporting Material for a detailed description of the full stochastic model).
Analysis of steady-state properties
We analyzed the steady-state properties of srRNA regulation in absence or in presence of auxiliary targets within the limit of small noise, using the linear noise approximation (25). The mean steady-state levels were estimated by solving the mass-action equations (Eqs. 1–5). Fluctuations were analyzed by solving the fluctuation-dissipation relation
| (6) |
with C as the covariance matrix of the system, J as the Jacobian of the set of mass-action equations (Eqs. 1–5), and N as a diagonal matrix whose entries are the amplitudes of the noise (Langevin) terms (see the Supporting Material).
Efficacy of the srRNA regulation and limit between slow and fast transport modes
As a robust measure of the efficacy of the srRNA regulation, we choose an information theory-based measure, which considers the interactions between a regulator and its target as a communication channel, and measure the information capacity of this channel (27,28). The major advantage of this choice is that it does not require any specific knowledge of the function of the regulator or the precise signal it transduces. Moreover, this measure is insensitive to the particular form of the response function, and can therefore be applied across the entire range of parameters in our model.
In the limit of low noise, the information capacity for srRNA pathways can be approximated by (see the Supporting Material)
| (7) |
where 〈p〉 and σp are, respectively, the steady-state mean and standard deviation of the principal target level. At a fixed set of parameters the impact of auxiliary targets on this information-based efficacy strongly depends on the mobility of the molecules: auxiliary targets increase the capacity of the channel if they diffuse rapidly, but decrease its capacity if diffusion is slow. One can therefore define a critical diffusion rate that marks the boundary between these two behaviors (see the Supporting Material).
Analysis of kinetic properties
The kinetic response of the pathway was studied using stochastic Gillespie simulations (29), where, for simplicity, we neglect fluctuations in the total number of auxiliary targets. Each simulation starts with a configuration sampled from the steady-state distribution of principal targets (Poissonian distribution with mean αm/βm). At t = 0 the transcription of srRNA is switched on, and the kinetic response is assessed by measuring the distribution of the first-passage time when the number of principal mRNAs reaches zero.
Choice of parameter values
Typical values for parameters are only known for bacterial srRNA pathways (20,30). We choose to use these ranges of values (given in the Supporting Material) to plot our figures. However, Fig. S2 in the Supporting Material shows that the effects described in the article are robust over a wide range of parameter values that likely also include the eukaryotic pathways.
Analysis of genomic data
The conservation of microRNA targets was studied for a set of 87 microRNAs conserved among vertebrates (see Table S1 in the Supporting Material) and compared with an artificially generated set of 1000 mock-microRNAs (see Table S2). Seeds of the mock microRNAs were generated as 7-mers that obey the same dinucleotide statistics as the 87 conserved microRNAs in our sample (31). See the Supporting Material for details.
For each microRNA, a list of predicted targets in 12 vertebrates (Homo sapiens, Pan troglodytes, Macaca mulatta, Mus musculus, Rattus norvegicus, Canis familiaris, Equus caballus, Bos taurus, Monodelphis domestica, Ornithorhynchus anatinus, Gallus gallus, and Xenopus tropicalis) was obtained using the TargetScan algorithm and the aligned 3′UTRs dataset available at the TargetScan website (32). The number of targets Ni,s per microRNA i in each species s was normalized by the total number of genes per species Ntot,s in the alignment. Conservation of the number of targets was quantified by computing for each microRNA the relative fluctuations of {Ni,s/Ntot,s} across species (see the Supporting Material).
Taking the list of human targets as reference, we represent TargetScan predictions by a binary array xti,s, where xti,s = 1 if gene t is a target of microRNA i in human and in species s, and 0 otherwise. The observed frequency fti is then defined as the mean value of xti,s across species. The corresponding conservation score Cti is obtained by normalizing fti by the number of species that carry a homolog of gene t (see the Supporting Material). For example, Cti = 1 means that gene t is a target of microRNA i in every species where t is present.
To investigate the conservation of principal and auxiliary targets, we use published experimental data that measured global proteome response to transfection of a microRNA (miR-1, miR-124, and miR-181) in (human) HeLa cells (4). For each transfected microRNA, we extract from the experimental dataset the protein level change of each of its target genes (as defined above), if it had been measured. Table S3 contains the list of these genes for miR-1 (382 genes), miR-124 (249 genes), and miR-181 (345 genes), as well as the corresponding fold-change in protein level (in log2 unit).
The distributions of fold-repression do not offer a natural separation between principal and auxiliary targets in HeLa cells. We therefore split the targets based on their fold-change into an subset of strong targets, representing targets with a fold-repression below a given arbitrary limit (log2 of the fold-change ≤−0.6) and the complementary subset of weak targets. We verified that our conclusions do not depend on the choice of this limit (see the Supporting Material).
Results
Simple model for srRNAs with two classes of targets
Although it is still unclear which factors determine the efficiency of a given srRNA on a particular target, experiments on mammalian somatic tissues have revealed that most of the putative targets are only weakly affected by the transfection of a single microRNA, and only a small proportion is more significantly repressed (4,5). Below we identify the phenotypically relevant srRNA targets with this limited subset of strongly affected targets. This assumption may not always be justified, as in some cases small modulation may have strong physiological impact (see Table 2 in Seitz (18)), and conversely one could imagine an auxiliary role even for a strongly suppressed target (17,33) (see the Supporting Material).
Despite the fact that small RNA pathways differ in many details (including their biogenesis and mechanism of action), at an abstract level they can all be described by a unified model (20,26,30,34–38), which accounts for synthesis of all RNA species, interaction of the srRNA with its targets, and the consequential suppression of translation and/or promotion of degradation of the mRNA (and, perhaps, the small RNA molecule itself). This model can be translated into a simple mathematical framework (20) that we augment to describe the interactions with two classes of targets: the principal targets and the auxiliary targets (Fig. 1). Within a Langevin formalism, our model accounts for the stochastic nature of the underlying biochemical reactions, including the effect of transport by diffusion of the interacting molecules, by taking the limit of weak noise (for details, see Materials and Methods as well as the Supporting Material).
Auxiliary targets can finely tune the expression of principal targets
In absence of auxiliary targets, the effect of srRNAs on the mean level of principal targets falls into one of three categories (20), depending on the relative strength of the small RNA expression compared with that of the target (Fig. 2 A, black line). For efficient srRNA production (i.e., in cases where the synthesis rate of mature srRNAs αs is much larger than that of mRNA, αm), most of the mRNAs are targeted by the large srRNA pool, leading to complete silencing. Conversely, under conditions where the production of the srRNA is less efficient (αs ≪ αm) the target is almost unaffected by the presence of the small RNA and is normally expressed. Intermediate scenarios, where the production rates of the srRNA and of the mRNA are comparable (αs ∼ αm), allow fine-tuning of the target expression. Under these conditions, quantitative changes in the transcription rate of the srRNA correspond to quantitative changes in the target level. The sharpness of the transition between silenced and expressed regimes is controlled by the strength of the interaction between srRNA and mRNA. For strong interactions, the regulatory logic is a sharp linear-threshold response (see Fig. S1 A).
Figure 2.
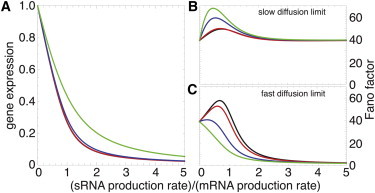
Steady-state properties of the principal targets in absence or presence of auxiliary targets. (A) Mean protein level of the principal targets as a function of the ratio αs/αm between the production rates of srRNA and principal mRNAs, and for different numbers n of auxiliary mRNA molecules (black, 0; red, 100; blue, 1000; green, 10,000). (B and C) Effect of the number of auxiliary targets on the noise/signal ratio (Fano factor) of the principal target proteins in the slow (B) and fast (C) transport limit.
Additional targets may affect the level of srRNA available for regulating the principal targets in many ways, and one possibility is that auxiliary targets could significantly change this simple picture. At steady state, auxiliary targets can be interpreted as stoichiometric weak targets with an effective interaction constant keff = kapd(βc/kd)/(1 + βc/kd) (see the Supporting Material). The fact that the auxiliary targets are, by definition, weakly affected by the srRNA suggests that keff ≪ k. The level of auxiliary targets would therefore play a measurable role on the principal one only at keff αn ≳ k αm (20). In this situation, the auxiliary targets modify the steady-state level of the srRNA and then indirectly that of principal targets. This could help in finely tuning the position of the transition between the expressed and silent regimes (Fig. 2 A) but does not change the regulatory logic of the posttranscriptional regulation. Typical parameters (20,30) suggest that this effect starts to be significant for thousands of auxiliary target molecules.
This characteristic regulatory logic has been verified experimentally in vivo for bacterial small RNA pathways in Escherichia coli (20) and for the mammalian microRNA pathway in HeLa cells (38). These results allow us to characterize the effect of a small RNA on a target in terms of three qualitatively different operating regimes: the silencing regime, the tuning (or crossover) regime, and the expression regime. In this language, one may deduce that the effect of many mammalian microRNAs at their normal expression level lies within the tuning category. Indeed, on one hand, overexpression experiments show at most a twofold repression compared to wild-type (4,5), suggesting that in normal tissues the targets are not completely silenced. On the other hand, knockdown of the same microRNA leads to, at most, a twofold upregulation (5), suggesting that targets are already somewhat suppressed in normal tissues. It is therefore possible that many microRNA-target pairs act in the crossover regime, which—as we discuss next—exposes them to amplified fluctuations.
Auxiliary targets reduce the intrinsic noise of the principal targets
The stochastic nature of the biochemical reactions composing gene regulation pathways leads to intrinsic fluctuations around the mean signal levels (39–41). A canonical way to appreciate the strength of protein fluctuations is to consider the Fano factor ν = σ2p/〈p〉, with σ2p the variance and 〈p〉 the mean level of the principal protein number p at steady-state. The value ν is a measure of the noise/signal ratio, which confers two advantages: in simple cases it does not depend on the transcription rate; and it allows comparison of the fluctuations in a particular system to a simple memoryless Poisson process, where ν = 1. For example, in the absence of srRNA regulation, the noise/signal ratio is mainly driven by the burstiness of the protein translation and ν ≈ 1 + b (39) with b = γ/βm the protein burst size, which is the average number of protein translated from a single mRNA molecule.
Models of posttranscriptional regulation by srRNAs suggest that this mode of regulation is particularly effective in suppressing intrinsic fluctuations in the silenced regime (26,35) (Fig. 2 C, black lines). Indeed, in the limit of efficient transport, the effective lifetime of an active mRNA ([βm + k〈s〉]−1) is dramatically reduced through the interaction with the srRNA and ν ≈ 1 + b∗ with b∗/b = 〈p〉/〈p〉max = βm /[βm +k〈s〉] ≪ 1 and 〈p〉max = (γαm)/(βmβp), the expression level in absence of srRNA (see the Supporting Material). If transport is inefficient, the slow stochastic diffusion of a very low number of mRNA molecules can lead to relatively high fluctuations in the local mRNA concentration and diffusion noise may dominate (Fig. 2 B, black lines).
In the crossover regime, where synthesis of srRNA and mRNA are similarly efficient, the ultrasensitivity of the stoichiometric system leads to a high correlation between the abundance of the srRNA and that of its principal target (42). The cell state becomes broadly distributed and alternates between unrepressed and repressed states, yielding a large distribution for the protein level with a high noise/signal ratio (26,35,42) (Fig. 2 C, black lines). These fluctuations are enhanced by strong RNA-RNA interaction (Fig. S1 B) and amplified by stochasticity in active gene copy number and transcriptional bursting (26,35). The presence of such large fluctuations deems small RNAs unsuitable for fine-tuning gene expression, and has adverse impact on their suitability for patterning gene expression during development (43). As discussed above, it is likely that many mammalian microRNA-target pairs act within the tuning regime and are therefore exposed to these amplified fluctuations. In what follows we suggest that the role of auxiliary targets is to suppress these fluctuations, making the tuning regime operational.
Our key observation is that the presence of auxiliary targets serves to diminish the correlation between the free srRNA copy number and that of its principal target, thus reducing fluctuations significantly (Fig. 2 C). By following the propagation of fluctuations within the model, we find that large intrinsic fluctuations in the srRNA level are quickly absorbed by the dynamic equilibrium between free and complexed srRNAs. To appreciate the effect of auxiliary targets on the fluctuations of principal targets, we first simplify the model by assuming that auxiliary targets have no effect on the mean steady-state level of principal targets (βc/kd → 0). We will return to this point at the end of this section.
Consider first the case of efficient transport. The presence of auxiliary targets has a weak impact on the steady-state level of free srRNA while creating a pool of complexed srRNA. This pool plays the role of particle reservoir that absorbs srRNA fluctuations (due, e.g., to transcriptional burstiness or ultrasensitivity of the interaction with the principal targets). In particular, for a high number of auxiliary targets, the noise/signal ratio of the principal targets is given by ν ≈ 1 + b∗ (see the Supporting Material). To appreciate this result we call the reader’s attention to the fact that in the absence of auxiliary targets this expression is only valid in the repressed regime. The presence of auxiliary targets reduces the fluctuations for any level of the srRNA, even in the noise-sensitive crossover regime, thus permitting fine-tuning and better control.
Interaction between srRNAs and their targets occur in a complex environment in the cytoplasm, perhaps in dedicated bodies (44). We reason that the presence of auxiliary targets may alter the delivery of a srRNA to its principal targets and consequently increases fluctuations. We therefore depart from the limit of efficient diffusion, and study the model over a range of diffusion constants governing the srRNA mobility. As suspected, when transport is slower, the presence of auxiliary targets yields a notable increase in fluctuations (Fig. 2 B). Indeed, the stochastic diffusion of a small number of free srRNAs (compared with the high number of free auxiliary targets) impacts on the noisy formation of the srRNA-auxiliary target complexes, leading to an increase of the srRNA fluctuations which propagates into that of principal targets.
We conclude that auxiliary targets have two opposing effects on the fluctuations in the level of a principal targets: they buffer number fluctuations due, for example, to bursty transcription or chromatin fluctuations, while increasing noise due to slow transport. Using the notions of efficacy and information capacity of the regulatory pathway (27) (see Materials and Methods and the Supporting Material), we show that the competition between these two effects is mainly settled by comparing the diffusibility of the RNA molecules and their half-lives (see Fig. 3 and Fig. S2). Based on these two parameters (which may be srRNA- and condition-specific), the principal targets of a srRNA may benefit or suffer from the presence of auxiliary targets. Interestingly, the boundary between these two situations does not depend significantly on the microscopic details of the various interactions in the model. For bursty promoters, the buffering of fluctuations is even stronger and auxiliary targets help in maintaining a low noise level even for slow transport.
Figure 3.
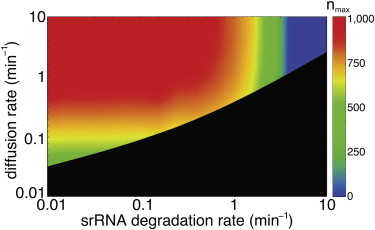
Impact of the srRNA degradation rate on the transition between fast and slow diffusion limit in the presence of auxiliary targets. In the fast transport region (colored zone), auxiliary targets help in maintaining a low noise level for the principal targets. In the slow transport region (black zone), diffusion noise dominates and the presence of auxiliary targets increases the internal fluctuations of the principal targets. (Colors) Upper bound of the number of auxiliary targets nmax imposed by limiting the slow-down in temporal response (see text).
Which regime characterizes the behavior of naturally occurring small RNAs? It has long been assumed (and in some cases verified experimentally) that srRNAs are stable (45,46), and that they are actively mobile (46). We therefore expected srRNA to be in the fast diffusion-slow decay regime, which is favorable for auxiliary targets. Indeed, estimating typical parameters for small RNAs in bacteria, yeast, and metazoan taken from the BioNumbers website (47) (see Table 1) suggests that they all sit safely in the region where auxiliary targets serve to suppress fluctuations. This observation can explain the ability of natural microRNAs present in somatic tissues to regulate their principal targets with low noise, even in the crossover regime.
Table 1.
Diffusion mode in different organisms
| Escherichia coli | Budding yeast | HeLa cells | |
|---|---|---|---|
| D (μm2 s−1) | 5 | 60 | 100 |
| Ω (μm3) | 0.7 | 33 | 2000 |
| β (min−1) | 1/10 | 1/20 | 1/600 |
| β/d | 0.05 | 0.09 | 0.11 |
Estimation of typical parameters for different organisms. The transition between fast and slow diffusion modes is mainly controlled by the ratio between the RNA self-degradation rate β and the diffusion rate d ≡ Dℓ/Ω with D the effective diffusion constant, Ω the volume of the cell (or of the cytoplasm), and ℓ ∼ 5 nm the length-scale of the reaction volume (see the Supporting Material). A small (high) ratio means fast (slow) transport mode. Numbers are taken from the BioNumbers database (47).
To complete our discussion of noise attenuation we comment that the general picture presented above is not changed when allowing the srRNA-auxiliary target complexes to have a short but finite lifetime (see the Supporting Material). However, in this case, the presence of auxiliary targets may affect the efficacy of the regulation. Indeed, under these conditions auxiliary targets effectively reduce the numbers of srRNA that are presented to their principal targets. In principle, one could have used this feature to impose a bound on the number of allowed auxiliary targets. However, as discussed in the next section, auxiliary targets act also as kinetic traps for the srRNAs and slow down the regulation process. As it turns out, this imposes an even stronger bound on the number of auxiliary targets.
Auxiliary targets maintain a robust kinetic response
In response to changes in environmental signals or development transitions, cells may need to adapt by stopping the expressions of specific proteins. Posttranscriptional regulation has been suggested as a mechanism to accelerate the response of gene expression to changes in the input signals (26,30). Indeed, in the absence of auxiliary targets newly produced srRNAs are directly used for depleting the pool of principal mRNA targets. However, it is natural to assume that auxiliary targets could act as kinetic traps and decelerate the adaptation of principal targets to signals that affect the srRNA production. The number of auxiliary targets exceeds significantly that of the principal target (4,5), and one may wonder if this would not result in an impossible hindrance of cellular response.
To address this question, we compare the kinetic response of two simple scenarios. In Scenario I, the srRNA bears sole responsibility for suppression of the target. Transcription of the mRNA is unaffected while the production of the srRNA is turned on at a high rate (αs ≫ αm), thus switching from the expressed to the repressed regime of Fig. 2 A. In Scenario II, which is srRNA-free, transcription of mRNA is stopped (e.g., by binding of transcription factors (TF)) and the remaining mRNAs and proteins are allowed to self-degrade. As we just mentioned, in the absence of auxiliary targets the response time is much faster in the srRNA-based Scenario I than in the TF-based Scenario II (Fig. 4, green arrow), and the question is whether this effect is wiped out by the presence of auxiliary targets. To answer this question we extend the analysis by measuring the statistics of the first passage time when the number of principal target mRNAs reaches zero, using exact stochastic simulations (29) (for details, see the Supporting Material).
Figure 4.
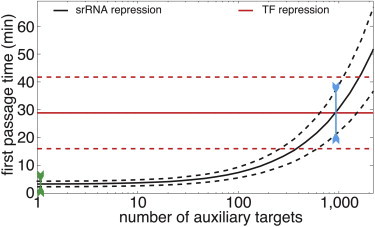
Impact of auxiliary targets on the temporal response of the principal targets. The temporal response is quantified by the first passage time, when the number of principal target mRNAs reaches zero. (Solid lines) Mean first passage time for the srRNA-based Scenario I and the TF-based Scenario II, as a function of the number of auxiliary targets. (Dashed lines) Standard deviation from the mean.
Our results suggest that the presence of auxiliary targets does not represent an overwhelming limitation to the reactivity of principal targets. As expected, the mean first passage time increases as the number of auxiliary targets is increased, imposing an upper bound on that number. To quantify it, we define nmax as the number of auxiliary target molecules that slow down the response time such that it is comparable with the response time in the TF-based Scenario II. Fig. 3 depicts this number for typical sets of parameters. We find that in a significant part of the parameter space this number can be very large (1000 auxiliary target molecules and more).
What determines the magnitude of nmax are the characteristics of the interaction between auxiliary targets and the srRNA. In particular, the rates of association and dissociation of srRNAs from their auxiliary targets turn out to be crucial for setting an upper bound on the number of auxiliary targets allowed without dramatically affecting the response time (Fig. 5 A). For example, if the srRNA-auxiliary target complex is very unstable (high dissociation constant Kd ≡ kd/ka), the effect of these targets on the response time is weak, and even a high number of targets can be present with no slow-down in response. On the other hand, if this complex is stable (low Kd), the dynamics is strongly affected even by a small number of auxiliary targets. Typical numbers for the association and dissociation rates (ka ≈ k and Kd ≈ 10–100 (30)) suggest that the number of auxiliary target molecules should be ∼103–104 to significantly slow down the kinetic response of the principal targets.
Figure 5.
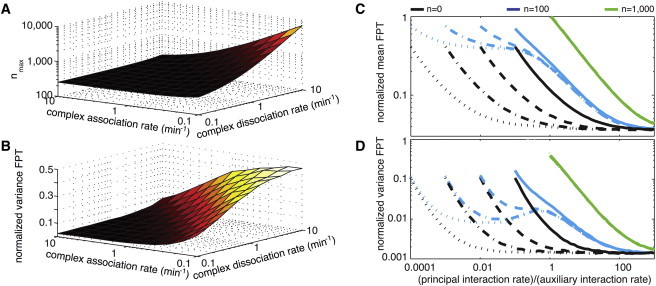
Impact of kinetic parameters on the efficiency of the temporal response of the posttranscriptional repression. (A and B) Number nmax of auxiliary targets (A) at which the mean time required for full suppression of the principal target by the srRNAs is equal to the corresponding time required by TF-based regulation, and the uncertainty in the response time (B) of the posttranscriptional regulation for n = nmax (normalized by the corresponding value for the transcriptional regulation). (C and D) Mean and variance of the first passage time as a function of the ratio k/ka between the interaction rate of the principal targets and the one of the auxiliary targets, for different numbers of auxiliary target molecules n and different values of the dissociation constant for the formation of the srRNA-auxiliary target complexes Kd = 10 (full line), 1 (dashed line), 0.1 (dotted and dashed line), and 0.01 (dotted line). Results are normalized by the corresponding values for the TF repression.
The statistics of first passage times allows us to consider another aspect of fluctuations that is typically ignored. In a fluctuating environment like the cell, the time at which all mRNA molecules initially present are degraded, bears some uncertainty: this time can be longer in one cell than in another. Looking back at the two scenarios described above, we notice that in the absence of auxiliary targets not only is the response time significantly reduced, but the uncertainty as well (Fig. 4, green arrow). This is yet another aspect of the robustness that small RNAs confer with their regulatory logic. Once again, one may be worried that the presence of auxiliary targets might reverse this outcome, and make the response time not only longer but also significantly less predictable.
Our model shows that this is not the case (Figs. 4 and 5 B). For example, consider the extreme case where the number of auxiliary targets is nmax, such that the mean response time is the same as in the TF-based Scenario II (Fig. 4, blue arrow). We find that the variance of this first passage time is still significantly smaller (at least twofold) in Scenario I than in Scenario II. Indeed, over the relevant range of parameters, and for any number of auxiliary targets below nmax, the uncertainty in the response time in Scenario I is significantly reduced compared to Scenario II.
Buffering of environmental noise by auxiliary targets
The cellular regulatory network is responsive to environmental changes, such that a change in the environment should lead to a robust response in gene expression. At the same time it is possible that a transient change in the environment should be ignored. We have previously suggested that small RNAs offer an inherent mechanism to buffer transient environmental changes that would result in the activation of a target gene (35). In this mechanism, the accumulation of target mRNAs is delayed with respect to the activation of transcription. Accumulation of the mRNA only starts after the pool of free srRNAs, which exists when the mRNA transcription is reactivated, is depleted. The size of the srRNA pool in the repressed state dictates the time window during which the changes in environmental signals are buffered.
Here we propose that the existence of auxiliary targets offers a similar mechanism in the opposite direction, i.e., when a change in environmental signals should result in suppression of the target (Scenario I above). We observe that under certain choices of parameters, the auxiliary targets provide the same kind of buffer for the srRNAs (Fig. 5, C and D). When the formation of auxiliary complexes is kinetically favored compared to the formation of principal complexes, srRNAs are first drawn to the pool of free auxiliary targets. Only after a significant fraction of these have been integrated into complexes can the srRNAs efficiently interact with the principal targets and silence their expression. This introduces a delay in the response time, followed by an abrupt repression of the principal targets. Both parts of this kinetic process are relatively noise-free, and together do not take longer than the more continuous (but slower) degradation occurring in Scenario II. This highlights a potential role for the auxiliary targets to delay the onset of the cell response without significantly affecting its efficiency.
Not surprisingly, the buffering effect exists when the rate of complex formation with auxiliary targets ka is somewhat larger than the corresponding rate for principal targets k. The relevant range of parameters can be identified by observing the plateaus in the mean and the variance of the response time when plotted as a function of k. Such a range can be found for intermediate values of the association rate ka and of the number of auxiliary targets n, such that (kan) is comparable with k, but no fine-tuning is required (Fig. 5, C and D, cyan lines).
Nonspecific evolutionary pressure on auxiliary targets
In our model, the precise identity of the auxiliary targets is not significant for their role in suppression of noise. Indeed, the only requirement is that these targets would not be sensitive to a minor downregulation by their ineffective interactions with the srRNA, and that they would be coexpressed (at least partially) with the principal targets. The one important property for the functionality of the auxiliary targets is at the system level: the number of auxiliary targets should be large enough to create a noise-suppressing reservoir, and on the other hand not too large to titrate the srRNA away from its principal targets or to significantly slow down their temporal response. A prediction of this model is that the evolutionary force to maintain the interaction between auxiliary targets and the srRNA is nonspecific, and permits replacement of one target by another. We therefore ask if one could observe this evolutionary signature in available genomic data.
We focus on the conservation of microRNA targets across vertebrates for a set of 87 conserved microRNAs (see Table S1). Using the bioinformatic target prediction tool TargetScan (32), we generated a list of predicted targets for each microRNA in a set of 12 genomes. As a control, we employed the same procedure for a set of 1000 mock-microRNAs that were generated to mimic real microRNAs in many ways, but carry a random seed (see Table S2).
To explore the conservation of target identities, we focused on microRNA-target pairs in human. For each such pair we computed the probability that the target gene interacts with the microRNA in the other 11 species. Fig. 6 B shows the cumulative distribution of conservation scores. As expected, predicted targets of real microRNAs are slightly but significantly more conserved than those of mock microRNAs, suggesting a selection pressure acting on the interaction between natural microRNAs and their targets. Importantly, we observe that the total number of targets of each microRNA (but not their identity) remains strongly conserved among the 12 species (Fig. 6 A).
Figure 6.
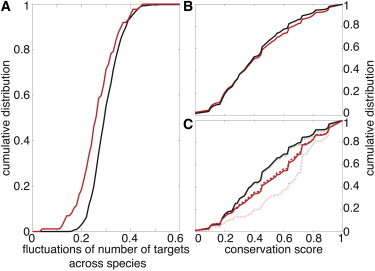
Conservation of microRNA targets across vertebrates. (A) Cumulative distributions for the relative fluctuations of the number of targets per microRNA across species for natural (red) and fake (black) microRNAs. Differences between the two distributions are significant (p-value < 10−4 for the Kolmogorov-Smirnov test). Number of targets is more conserved for natural microRNAs. (B) Cumulative distributions for the conservation scores of predicted targets of natural (red) and fake (black) microRNAs. Differences between the two distributions are small but significant (p-value < 10−10, Kolmogorov-Smirnov test). Proportion of conserved targets is slightly more important for natural microRNAs. (C) Cumulative distributions for the conservation scores of a subset of genes that are weak (red dashed line) or strong (red dotted line) targets of three natural microRNAs (miR-1, miR-124, and miR-181) in human (see Materials and Methods). (Red solid line) Distribution for the merged ensemble (weak and strong). (Black lines) Corresponding cumulative distributions for the same genes but when associated with fake microRNAs. Differences between natural and random microRNAs are always significant (p-values < 10−10, Kolmogorov-Smirnov test). Proportion of conserved targets is larger for strong targets of natural microRNAs, then for weak targets of natural microRNAs, then for targets of fake microRNAs.
To classify the predicted targets as principal and auxiliary, we used published experimental data following the change in the proteome in human HeLa cells after transfection of three different microRNAs (4) (see Table S3). Targets that were strongly repressed (based on some arbitrary threshold) were classified as principal targets, whereas the many predicted targets that showed little or no response were classified as auxiliary. We note that in this approximation we do not use—or have—any information about the physiological significance of the different targets.
As observed previously (48), our data suggests that targets in the principal group are more conserved than those in the auxiliary group. Indeed, the data of Fig. 6 C, comparing the conservation of these two subsets of targets to those of mock microRNA, supports this claim. This reflects the strong evolutionary pressure that acts to conserve the interactions between microRNAs and their principal targets.
Taken together, we find that the number of targets for each microRNA is highly conserved, and that for principal targets this probably comes from the fact that the targets themselves are conserved. For the auxiliary targets, however, this target-number conservation is stronger than the conservation of target identity, supporting the notion that it is their collective effect that is important, not their individual regulation.
Discussion
Single microRNAs have been shown to regulate the expression of many different target genes (hundreds if not thousands), although most of them very weakly (4,5). This seems to be a universal feature, applicable to many small RNA pathways (including those acting in bacteria) that rely on a very short seed for specificity. These findings stimulated the contemporary view in the field, that small RNAs act as global modulators of gene expression at a network scale, rather than gene-by-gene.
On the other hand, in all cases we are aware of, where the functionality of a small RNA has been carefully studied, only a small number of target genes were identified as being phenotypically relevant (6–15). If this is the rule rather than the exception, one is led to ask what is the function of the many other weak targets of a srRNA. One possibility is that seed matching between most of the targets and a srRNA are completely coincidental and neutral (49). However, it has been reported that most of these interactions are evolutionarily conserved, suggesting possible functionality (3,18).
Our results support an elegant viewpoint of the relationships among srRNA targets, initially formulated by Seitz (18), which is unique to srRNA regulation, but not limited to a particular pathway or organism. Even if the precise molecular mechanisms that control the actual strength of the srRNA regulation on a specific target remain unclear (50), evidence suggest a hierarchy among srRNA targets. Principal targets are the ones behind the physiological role of the srRNA. Examples of such targets include the cancer-related proteins Suz12 for miR-200 (13), ANP32A and SMARCA4 for miR-21 (11), or integrin-α5, radixin, and RhoA for miR-31 (10). In contrast, auxiliary targets are not functionally regulated by the srRNA. In addition to the sponge-like effect (51) which allows a fine-tuning of the expression of principal targets (18), our model suggests functional roles for auxiliary targets in conferring robustness to the regulation and the kinetics of the principal targets. At an affordable price of slowing down the (already accelerated) reactivity of regulation, auxiliary targets significantly reduce fluctuations in the level of the principal targets, while maintaining the sensitivity of the regulatory logic. This observation is robust over the large range of in vivo parameters and does not depend on the details of the model. The buffer effect induced by the presence of auxiliary targets may not be limited to srRNA regulation and has also been suggested as a functional role for the many decoy binding sites of transcription factors along a genome (52).
These features may explain the wide spread of srRNAs in development and stress response pathways (1,2) where a precise but reactive response is needed. Specificity of each posttranscriptional pathway may have governed the evolution of the number of auxiliary targets for a given srRNA to find a compromise between the loss in reactivity and the gain in fidelity.
What are the auxiliary targets? The emerging picture suggests that auxiliary targets should be coexpressed with the principal targets of a srRNA. For a srRNA with multiple principal targets that are not coexpressed, we expect a set of auxiliary targets associated with each principal target. Any gene that share a pattern of expression with a principal target can be recruited as an auxiliary target, because the expression of these genes is hardly affected by the srRNA. Our results indicate that the exact number of auxiliary targets and their exact level of expression is of little consequence.
The role of most srRNA targets as auxiliary targets predicts that the evolutionary pressure in place to maintain the interaction between a srRNA and its auxiliary targets is nonspecific (18), and cannot be explained in evolutionary models that account for targets one at a time (53). The pressure to maintain auxiliary targets should also be contingent on the conservation of the principal targets. This type of evolutionary pressure should have unique fingerprints, and we expect it to be detectable as more whole-genome sequences become available.
Acknowledgments
The authors thank Craig Hunter, Philip Zamore, David Bartel, and Benedikt Obermayer for discussions.
This work was supported by the National Science Foundation under grant No. MCB1121057.
Footnotes
Daniel Jost’s present address is Laboratoire de Physique de l’ENS Lyon, Université de Lyon, CNRS UMR 5672, Lyon, France.
Supporting Material
References
- 1.Gottesman S. Micros for microbes: non-coding regulatory RNAs in bacteria. Trends Genet. 2005;21:399–404. doi: 10.1016/j.tig.2005.05.008. [DOI] [PubMed] [Google Scholar]
- 2.Ghildiyal M., Zamore P.D. Small silencing RNAs: an expanding universe. Nat. Rev. Genet. 2009;10:94–108. doi: 10.1038/nrg2504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Thomas M., Lieberman J., Lal A. Desperately seeking microRNA targets. Nat. Struct. Mol. Biol. 2010;17:1169–1174. doi: 10.1038/nsmb.1921. [DOI] [PubMed] [Google Scholar]
- 4.Baek D., Villén J., Bartel D.P. The impact of microRNAs on protein output. Nature. 2008;455:64–71. doi: 10.1038/nature07242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Selbach M., Schwanhäusser B., Rajewsky N. Widespread changes in protein synthesis induced by microRNAs. Nature. 2008;455:58–63. doi: 10.1038/nature07228. [DOI] [PubMed] [Google Scholar]
- 6.Reinhart B.J., Slack F.J., Ruvkun G. The 21-nucleotide let-7 RNA regulates developmental timing in Caenorhabditis elegans. Nature. 2000;403:901–906. doi: 10.1038/35002607. [DOI] [PubMed] [Google Scholar]
- 7.Slack F.J., Basson M., Ruvkun G. The lin-41 RBCC gene acts in the C. elegans heterochronic pathway between the let-7 regulatory RNA and the LIN-29 transcription factor. Mol. Cell. 2000;5:659–669. doi: 10.1016/s1097-2765(00)80245-2. [DOI] [PubMed] [Google Scholar]
- 8.Massé E., Vanderpool C.K., Gottesman S. Effect of RyhB small RNA on global iron use in Escherichia coli. J. Bacteriol. 2005;187:6962–6971. doi: 10.1128/JB.187.20.6962-6971.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Liu K., Liu Y., He R. MiR-124 regulates early neurogenesis in the optic vesicle and forebrain, targeting NeuroD1. Nucleic Acids Res. 2011;39:2869–2879. doi: 10.1093/nar/gkq904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Valastyan S., Benaich N., Weinberg R.A. Concomitant suppression of three target genes can explain the impact of a microRNA on metastasis. Genes Dev. 2009;23:2592–2597. doi: 10.1101/gad.1832709. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- 11.Schramedei K., Mörbt N., Brocke-Heidrich K. MicroRNA-21 targets tumor suppressor genes ANP32A and SMARCA4. Oncogene. 2011;30:2975–2985. doi: 10.1038/onc.2011.15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hyun S., Lee J.H., Kim V.N. Conserved MicroRNA miR-8/miR-200 and its target USH/FOG2 control growth by regulating PI3K. Cell. 2009;139:1096–1108. doi: 10.1016/j.cell.2009.11.020. [DOI] [PubMed] [Google Scholar]
- 13.Iliopoulos D., Lindahl-Allen M., Struhl K. Loss of miR-200 inhibition of Suz12 leads to polycomb-mediated repression required for the formation and maintenance of cancer stem cells. Mol. Cell. 2010;39:761–772. doi: 10.1016/j.molcel.2010.08.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Melton C., Judson R.L., Blelloch R. Opposing microRNA families regulate self-renewal in mouse embryonic stem cells. Nature. 2010;463:621–626. doi: 10.1038/nature08725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zhao C., Sun G., Shi Y. MicroRNA let-7b regulates neural stem cell proliferation and differentiation by targeting nuclear receptor TLX signaling. Proc. Natl. Acad. Sci. USA. 2010;107:1876–1881. doi: 10.1073/pnas.0908750107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Mavrakis K.J., Wolfe A.L., Wendel H.G. Genome-wide RNA-mediated interference screen identifies miR-19 targets in Notch-induced T-cell acute lymphoblastic leukemia. Nat. Cell Biol. 2010;12:372–379. doi: 10.1038/ncb2037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Flynt A.S., Lai E.C. Biological principles of microRNA-mediated regulation: shared themes amid diversity. Nat. Rev. Genet. 2008;9:831–842. doi: 10.1038/nrg2455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Seitz H. Redefining microRNA targets. Curr. Biol. 2009;19:870–873. doi: 10.1016/j.cub.2009.03.059. [DOI] [PubMed] [Google Scholar]
- 19.Swami M. Small RNAs: pseudogenes act as microRNA decoys. Nat. Rev. Genet. 2010;11:530–531. doi: 10.1038/nrg2835. [DOI] [PubMed] [Google Scholar]
- 20.Levine E., Zhang Z., Hwa T. Quantitative characteristics of gene regulation by small RNA. PLoS Biol. 2007;5:e229. doi: 10.1371/journal.pbio.0050229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chubb J.R., Trcek T., Singer R.H. Transcriptional pulsing of a developmental gene. Curr. Biol. 2006;16:1018–1025. doi: 10.1016/j.cub.2006.03.092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.So L.-H., Ghosh A., Golding I. General properties of transcriptional time series in Escherichia coli. Nat. Genet. 2011;43:554–560. doi: 10.1038/ng.821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Berg H.C., Purcell E.M. Physics of chemoreception. Biophys. J. 1977;20:193–219. doi: 10.1016/S0006-3495(77)85544-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bialek W., Setayeshgar S. Physical limits to biochemical signaling. Proc. Natl. Acad. Sci. USA. 2005;102:10040–10045. doi: 10.1073/pnas.0504321102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.van Kampen N. North-Holland; Amsterdam, The Netherlands: 2001. Stochastic Processes in Physics and Chemistry. [Google Scholar]
- 26.Mehta P., Goyal S., Wingreen N.S. A quantitative comparison of sRNA-based and protein-based gene regulation. Mol. Syst. Biol. 2008;4:221. doi: 10.1038/msb.2008.58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Tkacik G., Callan C.G., Jr., Bialek W. Information flow and optimization in transcriptional regulation. Proc. Natl. Acad. Sci. USA. 2008;105:12265–12270. doi: 10.1073/pnas.0806077105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cover T., Thomas J. John Wiley and Sons; New York: 1991. Elements of Information Theory. [Google Scholar]
- 29.Gillespie D. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977;81:2340–2361. [Google Scholar]
- 30.Shimoni Y., Friedlander G., Margalit H. Regulation of gene expression by small non-coding RNAs: a quantitative view. Mol. Syst. Biol. 2007;3:138. doi: 10.1038/msb4100181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gentles A.J., Karlin S. Genome-scale compositional comparisons in eukaryotes. Genome Res. 2001;11:540–546. doi: 10.1101/gr.163101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lewis B.P., Burge C.B., Bartel D.P. Conserved seed pairing, often flanked by adenosines, indicates that thousands of human genes are microRNA targets. Cell. 2005;120:15–20. doi: 10.1016/j.cell.2004.12.035. [DOI] [PubMed] [Google Scholar]
- 33.Bartel D.P., Chen C.-Z. Micromanagers of gene expression: the potentially widespread influence of metazoan microRNAs. Nat. Rev. Genet. 2004;5:396–400. doi: 10.1038/nrg1328. [DOI] [PubMed] [Google Scholar]
- 34.Mitarai N., Andersson A.M.C., Sneppen K. Efficient degradation and expression prioritization with small RNAs. Phys. Biol. 2007;4:164–171. doi: 10.1088/1478-3975/4/3/003. [DOI] [PubMed] [Google Scholar]
- 35.Levine, E., M. Huang, …, T. Hwa. 2008. On noise and silence in gene regulation by small RNA. http://matisse.ucsd.edu/hwa/pub/sRNA-noise.pdf.
- 36.Mitarai N., Benjamin J.-A.M., Sneppen K. Dynamic features of gene expression control by small regulatory RNAs. Proc. Natl. Acad. Sci. USA. 2009;106:10655–10659. doi: 10.1073/pnas.0901466106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Jost D., Nowojewski A., Levine E. Small RNA biology is systems biology. BMB Rep. 2011;44:11–21. doi: 10.5483/BMBRep.2011.44.1.11. [DOI] [PubMed] [Google Scholar]
- 38.Mukherji S., Ebert M.S., van Oudenaarden A. MicroRNAs can generate thresholds in target gene expression. Nat. Genet. 2011;43:854–859. doi: 10.1038/ng.905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Thattai M., van Oudenaarden A. Intrinsic noise in gene regulatory networks. Proc. Natl. Acad. Sci. USA. 2001;98:8614–8619. doi: 10.1073/pnas.151588598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Elowitz M.B., Levine A.J., Swain P.S. Stochastic gene expression in a single cell. Science. 2002;297:1183–1186. doi: 10.1126/science.1070919. [DOI] [PubMed] [Google Scholar]
- 41.Paulsson J. Summing up the noise in gene networks. Nature. 2004;427:415–418. doi: 10.1038/nature02257. [DOI] [PubMed] [Google Scholar]
- 42.Elf J., Paulsson J., Ehrenberg M. Near-critical phenomena in intracellular metabolite pools. Biophys. J. 2003;84:154–170. doi: 10.1016/S0006-3495(03)74839-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Levine E., McHale P., Levine H. Small regulatory RNAs may sharpen spatial expression patterns. PLOS Comput. Biol. 2007;3:e233. doi: 10.1371/journal.pcbi.0030233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Goldie B.J., Cairns M.J. Post-transcriptional trafficking and regulation of neuronal gene expression. Mol. Neurobiol. 2012;45:99–108. doi: 10.1007/s12035-011-8222-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Le Derout J., Boni I.V., Hajnsdorf E. Hfq affects mRNA levels independently of degradation. BMC Mol. Biol. 2010;11:17. doi: 10.1186/1471-2199-11-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Krol J., Loedige I., Filipowicz W. The widespread regulation of microRNA biogenesis, function and decay. Nat. Rev. Genet. 2010;11:597–610. doi: 10.1038/nrg2843. [DOI] [PubMed] [Google Scholar]
- 47.Milo R., Jorgensen P., Springer M. BioNumbers—the database of key numbers in molecular and cell biology. Nucleic Acids Res. 2010;38(Database issue):D750–D753. doi: 10.1093/nar/gkp889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Friedman R.C., Farh K.K.-H., Bartel D.P. Most mammalian mRNAs are conserved targets of microRNAs. Genome Res. 2009;19:92–105. doi: 10.1101/gr.082701.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Chen K., Rajewsky N. The evolution of gene regulation by transcription factors and microRNAs. Nat. Rev. Genet. 2007;8:93–103. doi: 10.1038/nrg1990. [DOI] [PubMed] [Google Scholar]
- 50.Grimson A., Farh K.K.-H., Bartel D.P. MicroRNA targeting specificity in mammals: determinants beyond seed pairing. Mol. Cell. 2007;27:91–105. doi: 10.1016/j.molcel.2007.06.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Ebert M.S., Sharp P.A. Emerging roles for natural microRNA sponges. Curr. Biol. 2010;20:R858–R861. doi: 10.1016/j.cub.2010.08.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Burger A., Walczak A.M., Wolynes P.G. Abduction and asylum in the lives of transcription factors. Proc. Natl. Acad. Sci. USA. 2010;107:4016–4021. doi: 10.1073/pnas.0915138107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Shomron N., Golan D., Hornstein E. An evolutionary perspective of animal microRNAs and their targets. J. Biomed. Biotechnol. 2009;2009:594738. doi: 10.1155/2009/594738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Berg O.G. On diffusion-controlled dissociation. Chem. Phys. 1978;31:47–57. [Google Scholar]
- 55.Hao Y., Xu L., Shi H. Theoretical analysis of catalytic-sRNA-mediated gene silencing. J. Mol. Biol. 2011;406:195–204. doi: 10.1016/j.jmb.2010.12.008. [DOI] [PubMed] [Google Scholar]
- 56.Walczak A.M., Tkacik G., Bialek W. Optimizing information flow in small genetic networks. II. Feed-forward interactions. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2010;81:041905. doi: 10.1103/PhysRevE.81.041905. [DOI] [PubMed] [Google Scholar]
- 57.Mugler A., Grinshpun B., Wiggins C.H. Statistical method for revealing form-function relations in biological networks. Proc. Natl. Acad. Sci. USA. 2011;108:446–451. doi: 10.1073/pnas.1008898108. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


