Cell Cycle-Dependent Binding Modes of the Ran Exchange Factor RCC1 to Chromatin

Abstract

The formation of an activity gradient of the small G-protein Ran around chromatin depends on the differential partitioning of the opposing enzyme activities of the Ran guanine nucleotide exchange factor RCC1 that resides on chromatin, and the cytoplasmic Ran GTPase activating protein RanGAP. We studied the time-dependent interaction kinetics between RCC1 and chromatin and the mobility of the Ran-RCC1 complex in living cells by fluorescence correlation spectroscopy to investigate whether binding of RCC1 to chromatin regulates the exchange activity of RCC1, and whether the stability of the RCC1-chromatin interaction is regulated during the cell cycle. We found that RCC1 mobility is dominated by two states: a highly mobile state that is trapped within chromatin, and a transiently immobilized state that is stabilized during mitosis. We show that only the immobilized state of RCC1 interacts with Ran and conclude that its guanine nucleotide exchange activity is restricted to specific sites on chromatin.

Introduction

An activity gradient of the small G-protein Ran emanating from chromatin underlies essential cellular processes such as nucleo-cytoplasmic transport, mitotic spindle assembly, and formation of the nuclear envelope (1,2). Formation of this gradient depends on the spatial partitioning of the opposing enzyme activities of the Ran guanine exchange factor, the regulator of chromosome condensation (RCC1), and the Ran GTPase activating protein, RanGAP (3). This partitioning is established by the binding of RCC1 to chromatin (4–6). However, there is little information on whether and how the interaction of RCC1 and chromatin is regulated during the cell cycle, and on how chromatin binding of RCC1 and its interaction with Ran are coupled. To address these questions, we quantitatively measured the dynamics of the RCC1-chromatin interaction at different stages of the cell cycle.

RCC1 has a compact structure, classified as a seven bladed β-propeller fold (7). One face of the protein binds to Ran (8), whereas binding to chromatin occurs via the N-terminal tail of the protein in addition to one of the loop regions connecting the β-sheets (9,10). The flexible N-terminal tail, which is not part of the rigid core structure, contains a nuclear localization sequence as well as a DNA-binding site (11,12). The N-terminal tail is also the site of multiple posttranslational modifications, which affect chromatin-binding affinity. Most notably, methylation of the N-terminal serine residue increases the affinity for double-stranded DNA and is required for proper mitotic spindle assembly (13).

Chromatin binding is not only required for the localization of RCC1, but might also affect its catalytic activity. In vitro, binding to histones H2A/H2B moderately enhances the nucleotide exchange rate (4). In living cells, one study employed fluorescence recovery after photobleaching (FRAP) experiments and microinjection of the nucleotide free mutant RanT24N to show that the binary complex of RCC1 and nucleotide free Ran binds more tightly to chromatin (6). By the increased affinity of this complex to chromatin, the exchange reaction is effectively coupled to chromatin, which allows for the localized activation of Ran. This model also suggests that the residence time of RCC1 on chromatin is an important kinetic parameter of the guanine nucleotide exchange reaction.

An article from 2009 has demonstrated that phosphorylation of histone H2B immobilizes RCC1 on chromatin, which leads to reduced levels of GTP-bound Ran in early stages of apoptosis (14). This indicates a connection between RCC1’s chromatin binding affinity and the regulation of apoptosis, and also underscores the connection between the kinetics of chromatin association and enzymatic activity of RCC1.

Binding of RCC1 to chromatin in living cells has so far been studied by fluorescence redistribution after photobleaching/photoactivation experiments (15–17). All these studies showed the interaction between chromatin and RCC1 to be transient. One study measured kinetic parameters in interphase cells and provided a lower limit to the dissociation rate of chromatin binding (17).

The N-terminus of RCC1 is phosphorylated during mitosis. This phosphorylation inhibits binding to importins (16). However, there are conflicting results on whether phosphorylation also affects the affinity for chromatin. According to Hutchins et al. (16), phosphorylation ensures that RCC1 retains a dynamic binding to chromatin during mitosis rather than a stable, immobile binding. On the other hand, Li and Zheng (15) have concluded from fluorescence loss in photobleaching experiments that phosphorylation results in a more stable binding to chromatin.

FRAP has been a popular technique for measuring the intracellular mobility of fluorescent proteins, and is considered to be particularly useful for the analysis of molecules whose mobility is decreased due to interactions with cellular structures. Materials and Methods have been developed to quantify interactions of proteins with immobile binding sites, in particular the interaction of transcription factors with chromatin (18,19). These methods, however, assumed a cylindrical symmetry in the distribution of fluorescent molecules, and have not been applied for chromatin binding proteins in mitosis so far.

Fluorescence correlation spectroscopy (FCS) provides information about the mobility and photophysical properties of fluorescent molecules by a statistical analysis of the fluorescence fluctuations emitted from a diffraction-limited sample volume (20,21). In contrast to FRAP, FCS is especially useful for the analysis of rapid molecular dynamics down to the timescale of photophysical processes such as fluorophore blinking.

Given the central role of the Ran system for morphogenetic processes during different stages of the cell cycle, such as spindle organization, it is an interesting question whether RCC1’s chromatin affinity is concomitantly regulated. Up to this point, however, it was not possible to measure exact kinetic parameters of the RCC1-chromatin interaction during mitosis. We therefore set out to precisely measure the dynamics of chromatin binding in living cells. Using FCS, we show that the mobility of RCC1-EGFP is largely dictated by two processes that take place at different timescales and are characterized by different temperature dependencies. This allowed us to ascribe the faster component to a process akin to diffusion within chromatin and the slower to release from binding to chromatin. To parameterize the FCS autocorrelation data we applied a binding-diffusion model accounting for diffusion and transient interaction of RCC1 with immobile nucleosomes (22). We find that the interaction between chromatin and RCC1 is more stable during metaphase of mitosis than during interphase and that N-terminal phosphorylation has no direct effect on the stability of chromatin binding. Dual-color fluorescence cross-correlation spectroscopy measurements indicate that Ran interacts predominantly with the immobile fraction of RCC1, which points at catalytic sites on chromatin. Combining our FCS analysis with quantitative imaging, we deduce that a large part of the mobile fraction of RCC1 is trapped within chromatin due to highly transient interactions.

Materials and Methods

DNA constructs

pRCC1-EGFP was constructed by inserting the coding sequence of the γ-isoform of human RCC1 (kind gift from J. Ellenberg) into the XhoI and AgeI sites of pEGPF-N1 (Clontech, Mountain View, CA), thus creating a SPVAT linker between the two proteins. pRCC1-Δ27-EGFP was made by deleting the first 27 codons from pRCC1-EGFP. All point mutations were introduced into pRCC1-EGFP by DpnI-mediated site-directed mutagenesis. pH2B-EGFP was constructed by inserting the coding sequence for human histone H2B from pH2B-diHcRed (gift from J. Ellenberg (23)) into the SalI and BamHI sites of pEGFP-N1.

Cell culture

HeLa cells were grown at 37°C and 5% CO₂ in DMEM (PAN-Biotech, Aidenbach, Germany) supplemented with 10% fetal calf serum and 2 mM L-glutamine. Two days before the experiments, cells were seeded on LabTek II chambered No. 1 cover glass (Nalge Nunc International, Rochester, NY) and transfected using FuGENE 6 (Roche, Mannheim, Germany) according to the manufacturer’s instructions. For microscopy, cells were kept in phenol red-free DMEM supplemented with 25 mM HEPES, 10% fetal calf serum, and 2 mM L-glutamine.

Fluorescence correlation spectroscopy

Fluorescence correlation spectroscopy (FCS) was performed on a LSM 510 Meta confocal microscope (Carl Zeiss Jena, Jena, Germany) equipped with a ConfoCor 3 unit and a C-Apochromat 40×/1.2 NA W Corr water-immersion objective. During measurements, the sample and the objective were kept at the desired temperature using an incubation box. If not noted otherwise, measurements were carried out at 37°C.

For single-color autocorrelation measurements, the sample was excited with the 488-nm line of an argon laser through an HFT 405/488/561 beam splitter (Carl Zeiss Jena). The emitted fluorescence was collected through an LP 505 long-pass filter, and was detected in confocal mode with a 70-μm pinhole using an avalanche photodiode detector. In dual-color cross-correlation measurements, the sample was simultaneously excited with the 488-nm line of an argon laser and the 561-nm line of a diode-pumped solid-state laser through an HFT 405/488/561 beam splitter (Carl Zeiss Jena). The emitted fluorescence was separated through an NFT 565 beam splitter (Carl Zeiss Jena) onto two avalanche photodiode detectors equipped with a BP 505-540 IR (EGFP channel) and a BP 615-680 IR (mCherry channel) band-pass filter, respectively. The pinhole diameter was set to 72 μm (corresponding to 1.09 Airy units for the EGFP channel and 0.95 Airy units for the mCherry channel).

Calibration measurements were performed on aqueous solutions of Alexa Fluor 488 or Alexa Fluor 546 (Molecular Probes, Eugene, OR) on LabTek II chambered No. 1 cover glass (Nalge Nunc International) to determine the geometrical parameters of the observation volume in the EGFP and mCherry channel, respectively. At the beginning of each day of experimentation, the objective correction ring and the lateral pinhole position were optimized to yield the maximal count rate from Alexa Fluor 488 excited with 488 nm. After this optimization, the excitation power was attenuated to give an average molecular brightness of 15 kHz for Alexa Fluor 488 and 11 kHz for Alexa Fluor 546 to record the calibration autocorrelation curves.

For live cell measurements of EGFP and mCherry, the excitation power was attenuated to give an average molecular brightness of 1 kHz per molecule for EGFP and 0.4 kHz per molecule for mCherry. Cells were selected for the expression level of EGFP- and mCherry-tagged proteins based on the averaged count rate measured at the point of interest. FCS measurements were taken over an average count rate range of 10–200 kHz. This corresponds to an average concentration of labeled proteins in the range 6–130 nM.

The raw intensity data were auto- and cross-correlated using the microscope manufacturer’s software. Typically, the correlation curves of 2–5 consecutive 20-s intensity recordings were averaged for one measurement, except for calibration measurements where 10 consecutive 10-s recordings were averaged. Individual correlation curves were discarded when strong drift or bleaching was apparent in the intensity trace.

FCS data analysis

Fitting of model equations to the correlation curves was performed using nonlinear least-squares minimization of the unweighted sum of the squared-fit residuals. The fitting procedure was implemented in MATLAB 7 R2010b (The MathWorks, Natick, MA) on the basis of the lsqnonlin function of the MATLAB optimization toolbox.

Correlation curves of fluorescent proteins recorded in living cells were fit only for correlation times above 10 μs. On this timescale, fluorophore blinking effects could be neglected and were not accounted for in the fitting models. Autocorrelation curves were fit either with an equation for binding and diffusion or for diffusion only.

The model for binding and diffusion takes into account unhindered three-dimensional diffusion of a labeled and transient binding of labeled molecules to immobile binding sites (see Fig. S1 in the Supporting Material). Diffusion is assumed to follow Ficks’s law, whereas binding is modeled as a single-step bimolecular binding reaction, where the concentration of binding sites is assumed to be much larger than the concentration of the labeled molecule. Autocorrelation curves for molecules undergoing binding and diffusion are fit with the following model equation:

$$G\left(\tau \right)=\frac{1}{{\left(2\pi \sum _j^2\langle C_j\rangle \right)}^2}\underset{0}{\overset{\mathrm{\infty }}{\int }}d{q}_r\underset{0}{\overset{\mathrm{\infty }}{\int }}d{q}_{z}r\exp \left(-\frac{r_0^2{q}_r^2}{4}-\frac{z_0^2{q}_z^2}{4}\right)\sum _j^2\sum _{l\le j}\left(2-{\delta }_{jl}\right)\langle C_j\rangle \sum _{s=1}^2{X}_l^{\left(s\right)}\exp \left({\lambda }^{\left(s\right)}\tau \right){\left(X^{-1}\right)}_j^{\left(s\right)}.$$

Here, 〈C₁〉 and 〈C₂〉 are the average concentrations of bound and unbound molecules, r₀ is the width of the focal volume, and z₀ is the height of the focal volume. λ^(s) is the sth eigenvalue of the matrix M. X is the matrix of eigenvectors of the matrix M and X^(s) is the sth eigenvector from the matrix X. The matrix M is given by

$$M=\left(\begin{array}{cc}-k_{\text{on}}\left[B\right]-\left(q_r^2+q_z^2\right)D& k_{\text{off}}\\ k_{\text{on}}\left[B\right]& -k_{\text{off}}\end{array}\right),$$

wherein k_on is the association rate constant (in M⁻¹ s⁻¹), k_off is the dissociation rate constant (in s⁻¹), [B] is the concentration of binding sites (in M), and D is the diffusion constant (in μm²/s). 〈C₁〉 and 〈C₂〉 are calculated as a function of the total concentration of labeled molecules, C_total = 〈C₁〉 + 〈C₂〉, and the fraction, F, of unbound molecules: 〈C₁〉 = FC_total, and 〈C₂〉 = (1 – F)C_total. The term k_on[B] can be calculated from F and k_off according to $k_{\text{on}}\left[B\right]=k_{\text{off}}/F-k_{\text{off}}$. Hence, the model is dependent on the fitting parameters C_total, F, k_off, and D.

For unhindered three-dimensional diffusion, the following model equation was used (21):

$$G\left(\tau \right)=\frac{1}{N}\frac{1}{\left(1+\tau /{\tau }_D\right)}\sqrt{\frac{1}{1+\tau /\left({\tau }_D{S}^2\right)}}.$$

Here, N is the average number of fluorescent particles in the focal volume, and τ_D = r₀²/4D is the correlation time (in microseconds), which is a function of the diffusion constant D and the width of the focal volume, r₀. S = z₀/r₀ is the structural parameter, giving the ratio of the axial and the transversal dimension of the focal volume.

The geometrical parameters S and r₀ of the focal volume were determined from calibration measurements of Alexa 488, assuming a diffusion constant of 400 μm² s⁻¹ at 25°C (24), extrapolated to 536 μm² s⁻¹ at 37°C (25). Calibration curves were fit for correlation times above 1 μs with a modified version of the model for unhindered three-dimensional diffusion, which accounted for fluorophore blinking (21):

$$G\left(\tau \right)=\left(1+\frac{F_T\exp \left(-\tau /{\tau }_T\right)}{1-F_T}\right)\frac{1}{N}\frac{1}{\left(1+\tau /{\tau }_D\right)}\sqrt{\frac{1}{1+\tau /\left({\tau }_D{S}^2\right)}}.$$

Here, F_T is the fraction of molecules in a dark state, and τ_T is the dark state’s relaxation rate.

Calculation of the apparent interaction strength

To calculate the apparent interaction strength in fluorescence cross-correlation spectroscopy (FCCS) experiments, auto- and cross-correlation amplitudes were estimated by calculating the average correlation value between 1 μs and 100 μs. In a dual-color FCCS experiment, the correlation amplitudes are related to the total concentration of each labeled species and to the concentration of their complex. Assuming that the two species A and B form a complex with 1:1 stoichiometry, the following expression for the dissociation constant of the interaction can be derived:

$$K_D=\frac{G_X}{V_{\text{eff}}{G}_A{G}_B}\left(\frac{G_A}{G_X}-1\right)\left(\frac{G_B}{G_X}-1\right).$$

Here, G_X is the cross-correlation amplitude and G_A and G_B are the autocorrelation amplitudes of the two species A and B, respectively. V_eff is the effective overlap of the two observation volumes.

The calculation of a K_D for two interacting proteins A and B is complicated by two characteristic features of live cell measurements: First, the interaction takes place in the presence of a potentially large number of competing interactors. Second, in addition to the labeled proteins, which are encoded by the DNA plasmid used for transfection, there is an unknown fraction of unlabeled proteins expressed from their genomic location that participate in the binding equilibrium. It is therefore not possible to calculate an absolute K_D for the binary interaction of A and B. Hence, cross-correlation experiments were quantified by calculating a dimensionless apparent interaction strength to compare the extent of interaction in different samples. This also allowed us to neglect the effect of an impartial overlap of the two observation volumes, which should be the same in all samples. The apparent interaction strength was calculated as the inverse of the K_D, with V_eff = 1. As described in Results and Discussion, the apparent interaction strength was normalized between the highest and lowest mean values observed.

Statistical analysis

Fitting results for k_off and D were compared using two-sided mean difference tests based on a Student’s t-distribution. The p-values of individual pairwise comparisons were Bonferroni-corrected.

Confocal microscopy

Confocal microscopy was performed on the same instrument and with equivalent filter sets as the FCS measurements, except that a PMT detector was used. Single confocal slices were recorded. Images were processed using the software IMAGEJ (NIH, Bethesda, MA). For publication purposes, the image brightness was linearly adjusted.

To calculate the fraction of unbound molecules in mitotic cells, mean fluorescence intensities were measured in a cytoplasmic region and in a region occupied by chromatin as derived from images of mitotic cells. The mean fluorescence intensities were corrected by subtracting the mean background intensity measured in a region outside of the cell. The fraction of unbound molecules was calculated as F = I_cytoplasm/I_chromatin, where I_cytoplasm and I_chromatin were the background-corrected mean fluorescence intensities in the cytoplasm and on chromatin, respectively.

Results and Discussion

To gain insight into the molecular mobility of RCC1, we analyzed autocorrelation curves derived from fluorescence fluctuations of RCC1-EGFP transiently expressed in HeLa cells. Our analysis revealed that the mobility of RCC1-EGFP on chromatin is significantly different from its mobility in the cytoplasm. Visual inspection of autocorrelation curves recorded in the nucleus of interphase cells or on chromatin in mitotic cells revealed two inflection points pointing at two components with approximate correlation times of ∼1 ms and ∼100 ms. In contrast, in the cytoplasm of interphase and mitotic cells the autocorrelation curves had a single inflection point at a correlation time of ∼1 ms (Fig. 1). Autocorrelation curves of RCC1-EGFP in the cytoplasm could be well described by a model for unhindered three-dimensional diffusion (see Materials and Methods). Fitting of this model to the measured autocorrelation curves gave a diffusion constant of 27.11 ± 5.35 μm² s⁻¹ (mean ± standard deviation, SD; N = 15 cells) in interphase and 11.05 ± 1.66 μm² s⁻¹ (N = 15) in mitosis. We also measured autocorrelation curves of monomeric EGFP as a control in all four compartments (see Fig. S2).

Figure 1.

Autocorrelation curves of RCC1-EGFP on chromatin and in the cytoplasm of HeLa cells at different stages in the cell cycle. Representative measured in the nucleus of an interphase HeLa cell (A), the cytoplasm of an interphase HeLa cell (B), on chromatin in a HeLa cell in metaphase (C), and in the cytoplasm of a HeLa cell in metaphase (D). (Curves in panels A and C were fit with the binding-diffusion model; curves in panels B and D were fit with a model for free diffusion.) (Upper panel of each graph) Fit residuals. (Insets) Confocal images of RCC1-EGFP expressing HeLa cells, with measurement positions indicated (open crosses). Scale bars: 5 μm.

Although anomalous diffusion has previously been reported for EGFP (26), autocorrelation data of EGFP could be fit by a model for unhindered three-dimensional diffusion in all four compartments, yielding the diffusion constants given in Table 1. We estimated the molecular mass of RCC1-EGFP from the measured diffusion constants based on the Stokes-Einstein relation, assuming that RCC1-EGFP alone or the complex with other proteins has an approximately spherical shape. The measured diffusion constants for the 27-kDa EGFP were taken as reference. This led to the conclusion that RCC1-EGFP diffuses as fast as a 63-kDa spherical particle in the interphase cytoplasm and as fast as a 932-kDa spherical particle in the mitotic cytoplasm. In the interphase cytoplasm this estimated mass agrees well with the actual mass of RCC1-EGFP (72 kDa), indicating that RCC1-EGFP diffuses as a monomer in interphase cells. In contrast, RCC1- EGFP diffuses much slower in the mitotic cytoplasm, suggesting that it is bound to a high molecular-weight multiprotein complex, possibly reflecting its interaction with karyopherins (27,28). We also noted that the diffusion of EGFP was significantly slowed down in mitotic chromatin as compared to interphase chromatin, indicating that the highly condensed mitotic chromatin acts as a barrier to restrict diffusion of EGFP (29).

Table 1.

Diffusion constants of EGFP, RCC1-EGFP, and NT-EGFP measured in different compartments of HeLa cells

Protein	Compartment	D/μm2 s−1	N
EGFP	Nucleus	37.79 ± 4.37	15
	Interphase cytoplasm	35.12 ± 6.31	15
	Mitotic chromatin	26.64 ± 4.36	14
	Mitotic cytoplasm	35.95 ± 6.94	14
RCC1-EGFP	Interphase cytoplasm	27.11 ± 5.35	15
	Mitotic cytoplasm	11.05 ± 1.66	15
NT-EGFP	Nucleus	16.8 ± 4.06	15
	Mitotic chromatin	12.9 ± 5.32	10
	Mitotic cytoplasm	17.94 ± 2.83	10

Diffusion constants were determined by fitting a model for free diffusion to the autocorrelation data. NT-EGFP refers to a fusion protein comprising the first 27 amino acids of RCC1γ fused to EGFP. Values given are mean ± SD calculated from measurements in N different cells.

The two-component autocorrelation curves of RCC1-EGFP on chromatin suggested that binding interactions such as those between RCC1 and chromatin contributed to the shape of the autocorrelation curves. We therefore hypothesized that the fast autocorrelation component reflects diffusion of unbound RCC1, whereas the slow component reflects the kinetics of RCC1 release from chromatin. To test this hypothesis, we derived theoretical autocorrelation curves by following and extending an approach originally developed by Elson and Magde (20) and then later by Michelman-Ribiero et al. (22). The theory was based on a model of fluorescent molecules that undergo unhindered three-dimensional diffusion and transiently interact with immobile binding sites. This reaction-diffusion model could readily be described with the mathematical framework provided by Elson and Magde (for a detailed derivation of the model, see the Supporting Material and Fig. S1).

In this model, diffusion and binding kinetics are described by three parameters: the diffusion constant D of unbound molecules, the dissociation rate constant k_off of the interaction with the binding sites, and the fraction F of unbound molecules. Fig. S3 shows theoretical autocorrelation curves for varying the parameters D, k_off, and F in an expected physiological range. These calculations exemplify that in this parameter regime the process of protein diffusion and the kinetics of binding are separable by analyzing autocorrelation curves. However, if the dissociation rate is very large, the intensity fluctuations are dominated by diffusion and only an effective diffusion constant can be derived from the autocorrelation curves that, in this case, exhibit a single inflection point. Autocorrelation curves recorded in interphase nuclei and on mitotic chromatin were fitted with this binding-diffusion model, allowing the determination of D, k_off, and F. For RCC1-EGFP in interphase nuclei we found D = 6.16 ± 1.52 μm² s⁻¹, k_off = 4.58 ± 0.94 s⁻¹, and F = 0.41 ± 0.02 (N = 21) (Table 2, see Fig. S4 C). We also did not observe any correlation between the particle number of RCC1-RCC1 and any of the parameters D, k_off, and F determined for individual cells (see Fig. S5). This allowed us to rule out an influence of ectopic expression of RCC1 on the fitting results.

Table 2.

Binding-diffusion model parameters of RCC1-EGFP, wild-type protein, and mutants, measured by fitting autocorrelation data with the binding diffusion model

Data type	Notation	Nucleus		Mitotic chromatin
		Mean ± SD	N	Mean ± SD	N
D/μm2 s−1	WT	6.16 ± 1.52	21	6.28 ± 2.3	15
	Δ27	8.57 ± 2.17	15	7.36 ± 2.08	14
	S2,11A	8.1 ± 2.58	15	7.59 ± 1.8	15
koff/s−1	WT	4.58 ± 0.94	21	2.43 ± 1.44	15
	Δ27	14.8 ± 4.47	15	5.39 ± 2.23	14
	S2,11A	3.82 ± 1.15	15	2.0 ± 0.66	15
F	WT	0.41 ± 0.02	21	0.36 ± 0.1	15
	Δ27	0.5 ± 0.04	15	0.44 ± 0.04	14
	S2,11A	0.4 ± 0.02	15	0.4 ± 0.03	15

D is the diffusion constant, k_off the dissociation rate constant of chromatin-bound RCC1, and F is the fraction of unbound RCC1. Values given are mean ± SD from N cells.

We measured fluorescence fluctuations with histone H2B-EGFP to rule out that nucleosome movement occurs on the timescale of the FCS recording (20 s) and thereby gives rise to an apparent slow component in the autocorrelation curves. Fast bleaching of H2B-EGFP fluorescence indicated that nucleosomes were immobile on the timescale of our FCS recording, which is in contrast to a previous report on the diffusional dynamics of unbound H2B-EGFP in the nucleus as measured by FCS (30) (see Fig. S6).

To investigate whether binding kinetics indeed contributed to the slow component in the autocorrelation curves, we exploited the difference in the temperature dependence of the diffusion and the dissociation rate constants. The dissociation rate constant is an exponential function of the temperature according to Arrhenius’ law, whereas the diffusion constant is linearly dependent on temperature according to the Stokes-Einstein equation. Consequently, the dissociation rate constant is expected to be more sensitive to small changes in temperature. Diffusion constants and dissociation rate constants of RCC1-EGFP were therefore derived from FCS measurements in nuclei of HeLa cells at different temperatures ranging from 22°C to 37°C (relative change of ΔT/T0 = 0.05 on the absolute temperature scale) (Fig. 2). No change in the diffusion constants of RCC1-EGFP or EGFP alone could be observed in this temperature range, whereas the k_off as well as the free fraction determined for RCC1-EGFP clearly increased with temperature. This shows that the slow component in the autocorrelation curves reflects dissociation kinetics. Based on the observed relative change of Δk/k₀ = 0.56, the dissociation has an estimated activation energy of 27.5 kJ mol⁻¹.

Figure 2.

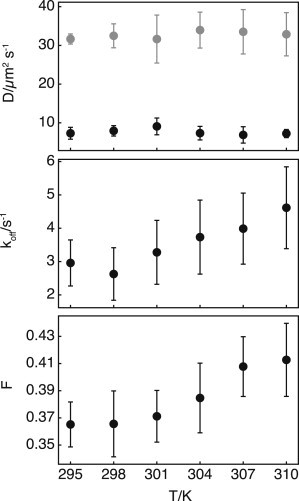
Diffusion constant and off-rate constant of RCC1-EGFP as function of temperature measured in nuclei of HeLa cells. (Top panel) Diffusion constant of RCC1-EGFP (solid) and EGFP (shaded) as a function of temperature. (Center panel) Dissociation rate constant of RCC1-EGFP as a function of temperature. (Bottom panel) Free fraction as a function of temperature. Error bars indicate the SD from measurements in at least four cells.

To further investigate whether binding to chromatin contributed to the slow component in the autocorrelation curves, we studied the mobility of the chromatin-binding deficient mutant RCC1-Δ27-EGFP that lacks the first 27 amino-terminal amino acid residues, which mediate binding to DNA (12). We observed that this mutation strongly affected the k_off but not the diffusion constant, which confirms that binding of RCC1 to chromatin is reflected in the slow component of the autocorrelation curves. From fits to the binding-diffusion model, we found: D = 8.57 ± 2.17 μm² s⁻¹, k_off = 14.8 ± 4.47 s⁻¹, and F = 0.5 ± 0.04 in interphase nuclei (N = 15). The residual chromatin affinity that was still observed for this mutant agrees with the previous finding that RCC1 interacts with chromatin not only via its N-terminal tail but also via interaction sites in its β-propeller domain (9,10).

The analysis above shows that one can extract chromatin binding kinetics of RCC1-EGFP from FCS autocorrelation curves using the reaction-diffusion model, which allowed us to address whether RCC1’s chromatin-binding affinity is regulated during the cell cycle. For this, we compared the chromatin-dissociation rate constant of RCC1 in nuclei of interphase cells to that from chromatin of mitotic cells (Table 2). Reaction-diffusion analysis of autocorrelation curves derived from FCS measurements on mitotic chromatin yielded a lower dissociation rate constant but a similar diffusion constant as compared to interphase chromatin (D = 6.28 ± 2.3 μm² s⁻¹, k_off = 2.43 ± 1.44 s⁻¹, and F = 0.36 ± 0.1, N = 15). These results indicate that RCC1’s residence time on chromatin is increased during metaphase of mitosis, which indicates that its binding to chromatin is regulated during the cell cycle. Interestingly, RCC1-Δ27 also showed an increased chromatin affinity during mitosis. Fitting FCS data of RCC1-Δ27 on mitotic chromatin resulted in D = 7.36 ± 2.08 μm² s⁻¹, k_off = 5.39 ± 2.23 s⁻¹, and F = 0.44 ± 0.04 (N = 14). Thus, even RCC1-Δ27 exhibits a twofold reduction of its dissociation rate during mitosis just as the wild-type protein, although its interaction with chromatin is overall weaker. We conclude that whatever mechanism stabilizes the interaction of RCC1 with chromatin during mitosis does not depend on the N-terminus of RCC1. This would also rule out a regulatory effect of phosphorylation of N-terminal serine residues on chromatin binding (15,16). Indeed, a nonphosphorylatable mutant of RCC1, in which Serine 2 and Serine 11 are mutated to alanine (RCC1-S2,11A), did not show any differences compared to the wild-type protein in chromatin-binding dynamics, neither in interphase nor during mitosis (see Table 2).

We noted a striking difference between the unbound fraction of roughly 0.4 that we measured for RCC1-EGFP in the nucleus by FCS and the unbound fraction of only 0.02 that has been inferred from photoactivation experiments (17). An explanation for this might be that the free fraction of RCC1-EGFP was affected by the amount of ectopically expressed labeled RCC1. However, the concentration of RCC1-EGFP in our FCS experiments was in the range of 6–130 nM (see Materials and Methods), which is much lower than the estimated 2 μM endogenous concentration of RCC1 in the nucleus (3). The concentration of ectopically expressed protein therefore adds <10% to the endogenous protein concentration and should, therefore, not have a strong effect on the chromatin binding equilibrium. We then performed fluorescence imaging experiments on mitotic cells expressing RCC1-EGFP to get another independent measure for the partitioning of RCC1 between cytoplasm and chromatin.

These measurements were performed on mitotic cells, because RCC1-EGFP molecules are able to freely equilibrate between chromatin and cytoplasm without interference by the nuclear envelope and the cytoplasmic fluorescence intensity should be approximately proportional to the concentration of unbound molecules. The fluorescence intensity on chromatin should be proportional to the sum of the concentrations of bound and unbound molecules. Therefore, the fraction of unbound molecules should be equal to the ratio of the cytoplasmic fluorescence intensity to the fluorescence intensity on chromatin. We arrested mitotic cells in metaphase by nocodazole treatment and measured the free fraction over a longer time (Fig. 3). We found that the free fraction stayed constant over a period of >70 min and concluded that RCC1 is in equilibrium with the cytoplasmic pool in mitotic cells. To directly determine the time it takes for RCC1 to equilibrate with the cytoplasm, we performed photoactivation experiments in which we selectively photoactivated RCC1-paGFP on chromatin of mitotic cells. We found that the average cytoplasmic intensity of RCC1-paGFP increased and reached a steady state within seconds after the photoactivation pulse. This demonstrates that equilibration of unbound RCC1 should occur directly after nuclear envelope breakdown and certainly has reached steady state by the time of metaphase.

Figure 3.

Equilibration of RCC1 between chromatin and cytoplasm in mitotic cells. (A and B) A HeLa cell expressing RCC1-EGFP (green) and Tubulin-mCherry (red) was arrested in metaphase with 100 ng/mL nocodazole and fluorescence was imaged over a period of over 1 h. Scale bar: 5 μm. Average cytoplasmic and chromatin fluorescence intensities of RCC1-EGFP were used to calculate the fraction of unbound RCC1 at each time point (B). RCC1-paGFP was photoactivated on mitotic chromatin and the cytoplasmic fluorescence intensity of photoactivated RCC1-paGFP followed in time (C).

By measuring the cytoplasmic image intensity relative to the average intensity of the chromatin region, we determined a free fraction of 0.04 ± 0.01 for RCC1-EGFP expressed in HeLa cells (N = 5 cells, see Fig. 4). For RCC1-Δ27, the free fraction determined by this approach was 0.21, consistent with the reduced chromatin affinity found for this mutant. These results show a strong discrepancy between the fraction of unbound RCC1 molecules as determined by FCS and fluorescence imaging. Two explanations may resolve this discrepancy.

Figure 4.

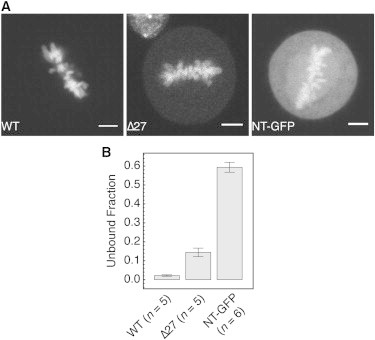
Determination of the fraction of unbound RCC1 in mitotic cells by fluorescence imaging. (A) Mitotic cells expressing different constructs of RCC1-EGFP were imaged using confocal fluorescence microscopy. (B) Fraction of unbound protein was calculated from average fluorescence intensity in cytoplasm and on chromatin. Error bars indicate SD from measurements in n cells. Scale bars: 5 μm.

The first explanation is that, in a three-state model of RCC1 mobility, separate mobile diffusing states can be distinguished: a freely diffusing RCC1 that does not interact with chromatin; and a chromatin-bound RCC1 that moves along it by one-dimensional diffusion. These diffusing states cannot be distinguished by our FCS measurements because they take place on similar length-timescales.

This explanation is, however, unlikely in light of the finding that sliding distances for DNA binding proteins are ∼50–100 bp (31,32). This gives a sliding distance on extended linear DNA that is an order-of-magnitude smaller than what is expected to cover an FCS spot.

The second (and more likely) explanation is that the large fraction of highly mobile RCC1 in FCS measurements originates from a population that transiently and unspecifically binds to chromatin, thereby slowing down the apparent diffusion (19). When the concentration of RCC1 in the cytoplasm is larger than the dissociation constant for the chromatin interaction, this can result in a high fraction of RCC1 molecules on chromatin at equilibrium, even for low-affinity binding. On top of this, chromatin-binding proteins might also undergo compact exploration (29) in a confined chromatin environment with a high density of low-affinity binding sites. This means that they will temporarily be trapped within a small compartment. Therefore, transient binding as well as compact exploration might account for the high fraction of RCC1 on chromatin as observed in the imaging experiments.

To further study this transient binding of RCC1 to chromatin, the N-terminus of RCC1 (amino-acid positions 1–27) fused to EGFP (NT-EGFP) was expressed in HeLa cells. By fluorescence imaging in mitotic cells, we determined a bound fraction of 50%, demonstrating that the N-terminus retains some of the chromatin-binding ability of full-length RCC1 (Fig. 4). However, we could not distinguish a tightly bound, low mobile fraction in the autocorrelation curves of NT-EGFP. Instead, a model for a single diffusing species could fit autocorrelation data of NT-EGFP in all three compartments (see Fig. S7). This yielded diffusion constants of 16.8 ± 4.06 μm² s⁻¹ in the interphase nucleus (N = 15), 12.9 ± 5.32 μm² s⁻¹ on mitotic chromatin (N = 10), and 17.94 ± 2.83 μm² s⁻¹ in the mitotic cytoplasm (N = 10) (Table 1). The slower apparent diffusion constant of NT-EGFP with respect to EGFP is consistent with highly transient, low-affinity binding to chromatin mediated by the N-terminal domain of RCC1. The fast decaying component in the autocorrelation curves of RCC1 therefore likely represents an effective diffusion constant that is the convolution of free diffusion and rapid transient binding to chromatin.

It has been hypothesized that the binary complex of RCC1 and nucleotide-free Ran is bound to chromatin and that this interaction is a mechanism to couple nucleotide-exchange activity to chromatin binding (6). This hypothesis implicates that a fraction of Ran should be immobilized on chromatin and should display mobility characteristics similar to RCC1. Interestingly, a model for pure diffusion was not sufficient to fit autocorrelation curves of EGFP-tagged Ran expressed in nuclei of HeLa cells (Fig. 5). Instead, these data could be fit with a binding-diffusion model giving parameters of D = 14.34 ± 1.06 μm² s⁻¹, k_off = 7.08 ± 0.99 s⁻¹, and F = 0.94 ± 0.04 (N = 6), indicating that a small fraction of Ran (roughly 6%) was transiently immobilized by binding to chromatin. This fraction was substantially increased without affecting the other parameters for the dominant negative RanT24N mutant (D = 12.42 ± 2.23 μm² s⁻¹, k_off = 6.86 ± 1.31 s⁻¹, F = 0.46 ± 0.08, N = 12), which is known to sequester RCC1 in an unproductive catalytic intermediate (Fig. 5). This indicated that the RCC1-mediated guanine nucleotide exchange reaction of Ran takes place on chromatin. The interaction between RCC1 and Ran using dual-color FCCS was therefore measured. The cross-correlation data were quantified by calculating an apparent association constant (see Materials and Methods) that was normalized to a negative control consisting of coexpressed freely diffusing EGFP and mCherry, and a positive control consisting of a tandem fusion of EGFP, p38 MAP kinase, and mCherry (see Fig. S8). The effective association constant of the negative and positive controls was set to 0 and 1, respectively (Fig. 6). A strong cross-correlation between RCC1-EGFP and mCherry-RanT24N (apparent association constant of 0.1 ± 0.04, N = 14) was observed. This is indicative of a specific interaction and supports the hypothesis that the reduced mobility of RanT24N is due to its interaction with RCC1. Furthermore, we observed that the cross-correlation curve is dominated by a prominent slow component with a correlation time on the order of several hundred milliseconds. The cross-correlation curves could be fit with the binding-diffusion model, yielding D = 6.9 ± 1.13 μm² s⁻¹, k_off = 3.51 ± 1.36 s⁻¹, and F = 0.24 ± 0.05 (N = 11) (Fig. 7), demonstrating that most of the RCC1-RanT24N complex is immobilized on chromatin.

Figure 5.

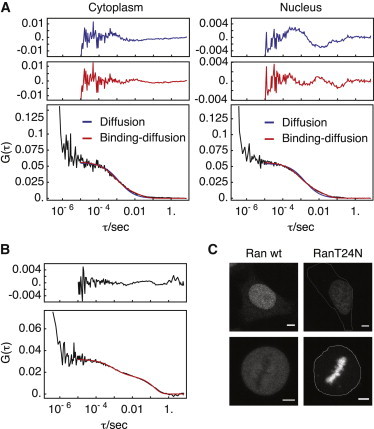
Autocorrelation curves of EGFP-Ran and EGFP-RanT24N in the nucleus and in the cytoplasm of HeLa cells during interphase. (A) Autocorrelation curves of EGFP-Ran recorded in the cytoplasm (left) or the nucleus (right) of HeLa cells during interphase were fit with either a model for free diffusion (blue) or the binding diffusion model (red). (Upper panels) Fit residuals for each model. (B) Autocorrelation curve of EGFP-RanT24N recorded in the nucleus of an interphase HeLa cell and fit with the binding diffusion model. (Upper panel) Fit residuals. (C) Confocal images of HeLa cells expressing either EGFP-Ran (left column) or EGFP-RanT24N (right column) during interphase (top row) or mitosis (bottom row). Cell borders are outlined (thin white line). Scale bars: 5 μm.

Figure 6.

Normalized interaction strengths for RCC1-Ran and RCC1-RanT24N complexes as determined by dual-color fluorescence cross-correlation spectroscopy. Measurements were taken either in interphase nuclei (I) or on mitotic chromatin (M). (Each box-and-whisker chart represents measurements from N different cells.)

Figure 7.

Cross-correlation curves of RCC1-EGFP and mCherry-RanT24N on chromatin. Representative cross-correlation curves recorded in interphase nuclei (A) or on mitotic chromatin (B) of HeLa cells coexpressing RCC1-EGFP and mCherry-RanT24N were fit with the binding diffusion model (red curves) to determine the diffusion and dissociation rate of the RanT24N-RCC1 complex.

This provides further evidence that the interaction of RCC1 and Ran occurs on chromatin, and suggests that the exchange reaction is spatially coupled to sites on nucleosomes. On mitotic chromatin, we observed a decrease in the relative amount of RCC1-RanT24N complex (0.04 ± 0.04, N = 12) with respect to interphase nuclei. The complex was, however, more tightly bound to chromatin as evidenced by the decrease in F and k_off (D = 6.73 ± 0.76 μm² s⁻¹, k_off = 0.63 ± 0.41 s⁻¹, and F = 0.09 ± 0.02, N = 4) that were obtained from fitting the cross-correlation curves to the binding-diffusion model. This is consistent with the view that the association of RCC1 is regulated during the cell cycle, where it is more tightly bound to chromatin during metaphase of mitosis. No significant cross-correlation signal was detected for RCC1 and wild-type Ran, which indicates that only a small fraction of both proteins interact at steady state in the catalytic cycle. This is also consistent with the observed small fraction of immobilized Ran on chromatin.

Conclusion

FCS measurements of RCC1 in living cells revealed two distinct components of RCC1 mobility on chromatin. A similar observation has previously been reported for the nuclear mobility of histone H1, another chromatin-binding protein, but has not been analyzed in great quantitative detail (30). Here, we have used and validated a binding-diffusion model of RCC1 mobility to analyze FCS data (22), which allowed us to determine an apparent diffusion constant, the steady-state bound fraction, and a dissociation rate constant of RCC1. These experiments demonstrated that ∼40% of highly mobile RCC1 originates from a population that transiently and unspecifically bind to chromatin, thereby slowing down its apparent diffusion (19), as well as uncovering a large fraction of RCC1 that is tightly bound to chromatin. Based on this, one could speculate that the unspecific recruitment to chromatin followed by short-range, one-dimensional diffusion is a possible mechanism to increase the encounter rate of Ran and RCC1 and consequently the turnover rate of the guanine nucleotide-exchange factor (GEF) reaction (33). This would also require Ran to weakly associate to chromatin before its association with RCC1, for which evidence has been provided by the RCC1-independent binding of Ran to chromatin via histones H3/H4 (34). Another possible consequence of the short- and long-lived species of chromatin-associated RCC1 is that the GEF reaction on Ran is tightly coupled to specific sites on chromatin, where RCC1 has a relatively long dwell time. This idea is consistent with the high fraction of long-lived RCC1-RanT24N complexes on chromatin as was observed by FCCS in this study.

There is also an apparent correlation between the k_off of the Ran-chromatin interaction as measured by FCS, and the stability of the Ran-RCC1 interaction. For wild-type Ran, the stability of the Ran-RCC1 interaction is determined by the rate-limiting step of the GEF reaction. This step is the nucleotide dissociation with a rate constant of 14.9 s⁻¹ in vitro (35). Given the approximately twofold stimulation of nucleotide dissociation in the presence of histones (4), this rate is of similar order of magnitude to the k_off of the Ran-chromatin interaction. For RanT24N, the k_off of the Ran-chromatin interaction is of similar order of magnitude to the dissociation rate constant of the RanT24N-RCC1 interaction, which is estimated to be ∼2 s⁻¹ on the basis of the K_D of the RanT24N-RCC1 interaction and the association rate constant of nucleotide-bound Ran and RCC1 (35). Thus, our data are consistent with a model, in which Ran dissociates from chromatin once the GEF reaction is completed by nucleotide binding to Ran and dissociation of the Ran-RCC1 complex.

Our FCS measurements also demonstrate that the dynamics of the RCC1-chromatin interaction and of the RanT24N-RCC1 complex on chromatin are different between interphase and mitosis. Specifically, the k_off for RCC1 is decreased during mitosis. Interestingly, this decrease in the dissociation rate constant was not accompanied by a significant decrease in the mobile fraction. The same effect was observed for RCC1-Δ27. As the mobile fraction can be either a convolution of a freely diffusing and a transiently bound, or a freely diffusing and a one-dimensionally diffusing species, the parameter F is an integrated parameter. We do not know how a change in k_off affects such an integrated parameter, but one possible explanation is that both the association and the dissociation rates are reduced during mitosis and that there is a higher activation energy barrier between the mobile and immobile states of RCC1. Furthermore, our data suggest that the regulation of the association and dissociation rates during mitosis do not depend on modifications at the N-terminus of RCC1. We also observed that the lifetime of the RanT24N-RCC1 complex on chromatin is increased with respect to the wild-type Ran complex. From these observations, we speculate that efficient catalytic turnover of the Ran GTPase on chromatin requires RCC1 to optimally switch between its exploratory mobile and its catalytically competent immobilized state. This might explain the correlation between a decrease in the mobility of RCC1 and a decrease in its catalytic efficiency that has been observed during apoptosis (14).