Turning Oscillations Into Opportunities: Lessons from a Bacterial Decision Gate

Abstract

Sporulation vs. competence provides a prototypic example of collective cell fate determination. The decision is performed by the action of three modules: 1) A stochastic competence switch whose transition probability is regulated by population density, population stress and cell stress. 2) A sporulation timer whose clock rate is regulated by cell stress and population stress. 3) A decision gate that is coupled to the timer via a special repressilator-like loop. We show that the distinct circuit architecture of this gate leads to special dynamics and noise management characteristics: The gate opens a time-window of opportunity for competence transitions during which it generates oscillations that are turned into a chain of transition opportunities – each oscillation opens a short interval with high transition probability. The special architecture of the gate also leads to filtering of external noise and robustness against internal noise and variations in the circuit parameters.

Genetically identical cells have the capacity to stochastically differentiate into various phenotypes each with it own with unique attributes. This hedge survival strategy allows the population to continuously deploy specialized cells in response to, and in anticipation of, possible drastic changes in conditions¹,²,³,⁴,⁵,⁶,⁷,⁸,⁹,¹⁰,¹¹. The stochastic phenotype differentiations (or stochastic fate determinations) involve cell-cell communication and coordination and provide each cell with the flexibility and freedom to select its own phenotype according to the specific conditions it encounters but in harmony with the other cells. A variety of different phenotypes interact and contribute for the well-being of the colony by performing different tasks¹²,¹³.

The phenotypical diversity arising from isogenic populations leads to the question, how random these individual decisions are. On one hand, neighbors exposed to the same environment need to make different decisions about their fates, in order to achieve diversity at the local level. On the other hand, the individual cell decisions must be collectivley regulated and coordinated carefully to garantee the optimal distribution of phenotypes for the colony as a whole. That means that even though there is need for randomness in the decision process to break symmetry, the probabilities of the possible outcomes must be carefully regulated by sensorial inputs and cell-cell communication.

The challenge is to reveal the principles governing how individual cells sense their environment and communicate with their neighbors before their own fate determination. And how, at the same time, these same individuals leave the final decision to chance in order to avoid the choice of the same phenotype by the whole population? To do so, the decision circuits must have a special capacity (yet not understood) for noise managment, allowing the bacteria to detemine fate by “playing dice with controled odds”¹. Cellular capacity to manage the odds should entail both means to program and regulate the noise level and means to program the effect of the noise on the gene circuit performance⁵,⁶,⁷,⁸,⁹,¹⁰,¹⁴. Several studies have shown that circuit architecture (the connectivity map between the circuit genes) can encode distinct noise behaviors critical to the function implemented by the circuit⁴,⁵,⁶,¹⁵,¹⁶,¹⁷.

A prototypic example of how genetic networks harness noise for performance of cellular differentiation is the fate determination between sporulation and competence in Bacillus subtilis. Many bacteria strains, in response to severe starvation, can form endospores – dormant cells that are remarkably resistant to many hazards like heat, radiation and toxic chemicals. The process of sporulation is accompanied eventually by termination of metabolic activity in one daughter cell (the spore) and death by lysis of the other (the ‘mother cell’). Sporulation is not initiated automatically upon nutrient limitation, but instead it is a last resort. Initially, a variety of other tactics to survive the stress can be employed. Up to eight different phenotypes have been identified in Bacillus subtilis when facing starvation, including differentiation into higher flagellated motile phenotype seeking new food niches, differentiation into phenotypes mastering in the secretion of hydrolytic enzymes to scavenge extracellular proteins and polysaccharides and differentiation into cannibal phenotype feeding on its peers¹²,¹³. When other tactics fail in lifting the stress, sporulation is the cell fate chosen by a majority of the cells. The material released by lysis of the sporulating cells is not wasted but can be taken up by a minority of competent cells. On the path towards sporulation, the individual cells can switch (escape) into competence and become able to uptake the genetic material from lysed cells which can be used as a food sources, for DNA repair and occasionally even as new genetic information to enable resisting the encountered stress. The competent cells can switch back (after about a day) into vegetative growth and proceed towards sporulation¹⁸.

The network performing the decision between sporulation competence is a complex one, involving several modules and inputs. Many different stress signals are integrated into a phosphorelay leading to the phosphorylation of the sporulation master regulator Spo0A which have been show to act as a timer with adaptable clock rate - the production rate of Spo0A* (phosphorylated Spo0A)¹⁹,²⁰. The process terminate upon comitment to sporulation when Spo0A* exceeeds a thereshold level. In order to regulate this process, pheromones are sent and received by the cell to indicate not only the local population density, but also information on stress levels sensed by the neighbors, which indicate their propensities of entering competence or sporulation²¹. The transition into competence requires noise in the expression of its master regulator ComK. A positive feedback loop on ComK is activated when fluctuations lead its concentration to cross a certain threshold. By interfering with the active degradation of ComK by MecA, a peptide ComS linked to the quorum sensing response sets the threshold for self-activation of ComK.

The stand-alone operations of the two modules – the sporulation timer and the competence switch - are well understood. The next challenge requires understanding of the interplay between the operations of the two modules, which determines the way bacteria decide between the two phenotypes. The AbrB-Rock decison gate is at the core of the sporulation-competence interplay²²,²³. However, the operational principles of this gate, which couples the opening of the stochastic switch with the state of the timer, are still not understood and subject to an ongoing debate.

Here we reveal the connection between the distinct circuit architecture of this gate and its special dynamics and noise management characteristics. Our starting point is the realization that the gate has intriguing dynamics since AbrB forms, together with Spo0A* and Spo0E, a special repressilator-like motif²⁴. This leads to new operational principles: 1. “Inhibition of inhibition” – inhibition of the gate by Spo0A* and inhibition of ComK by the gate. 2. “Window of opportunity” with oscillating dynamics that generates a chain of short intervals with high probability of transition into competence – a chain of opportunities. We propose that the “inhibition of inhibition” and the “chain of opportunities” are essential principles for collective decision-making in general.

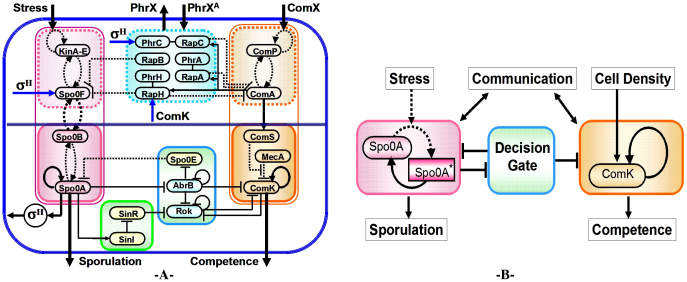
Global view of the decision-making system: Considerable research effort has been devoted to untangling the components of the genetic decision–making system which allows an individual cell to decide whether to wait, go through a competence cycle or commit to sporulation. It is now understood that the decision follows an elaborate assessment of its individual stress level, the colony density, stress signals from other cells and a memory of previously encountered stress and colony state. Years of intensive experimental studies identified the tens of key regulatory genes and measured several of the associated physiological parameters that are involved in the sporulation-competence decision process of the domesticated B. subtilis 168. More recently, these findings led to the development of tractable quantitative model of some of the elements (or module circuits) of this highly interconnected genetic network shown in Figure 1.

Figure 1. Global presentation of the sporulation/competence decision system.

(A) Representation of the complete network. The sporulation module is shown on the left (red), and the competence module is shown on the right (orange). The other modules process and transmit information between these two modules, coordinating the decision between sporulation and competence. (B) Representation of the module composed by Spo0E, AbrB and Rok as the decision gate, processing information from the sporulation module, and gating the competence module.

In this approach the operation of the competence module is modeled as a stochastic switch whose transition rate is controlled by a quorum sensing unit, and the operation of the sporulation module as an adaptable timer whose clock rate is adjusted by stress signals and signals sent from other cells. More specifically, Spo0A* accumulation is determined by a cascade of kinases transferring phosphate to the sporulation master regulator Spo0A²⁵,²⁶,²⁷,²⁸,²⁹. Phosphate is transferred down the relay, leading to the accumulation of Spo0A*. The outcome is that the clock rate of the sporulation timer is adjusted by the cell stress. Spo0A* acts as a transcriptional activator of both Spo0A and Spo0F via the sigma factor σ^H.

The competence stochastic switch consists of a self-activator master regulator ComK and a degradation complex MecA/ClpP/ClpC which continuously acts to keep ComK at low levels³⁰,³¹. This degradation is regulated by competitive binding of peptide ComS. It has been proposed that the ComK-ComS-MecA circuit can act as an excitable system, a bi-stable system or both, depending on parameters³,⁴,⁶,⁷,³². The transition probability is regulated by the cell density in response to the level of quorum sensing pheromone ComX³³ which activates the production of ComS via the competence and the ComP-ComA two component quorum sensing system.

The interplay between the timer and stochastic switch master modules is regulated by the operation of the Rap communication module and the AbrB-Rok decision gate. The Rap module³⁴,³⁵ acts as the central cell-cell communication and information possessing system of the decision-making network. Generally speaking, Rap decreases the clock rate of the sporulation timer and increases the waiting time of the competence switch by dephosphorylation of Spo0F* and inactivation of ComA, respectively. The module is up-regulated by the quorum sensing signal (via ComA) and down-regulated by the external peptide pheromones secreted by the neighboring cells and the cell itself. Rap is also regulated by Spo0A* which enhances the production of some of the pheromones (e.g. PhrC) via σ^H. More recently, it was discovered that the Rap system provides the means to prevent sporulation during competence. ComK activates RapH, which dephosphorylate phosphorelay component Spo0F³⁵.

The AbrB-Rok gate, described in greater details in the next section, acts as an inhibitory gate (repressor) of ComK, which blocks competence transitions, unless high levels of Spo0A* make the levels of both AbrB and Rok sufficiently low, as detailed further below.

The AbrB-Rok decision gate: Previously, Schultz et al¹⁴ proposed that the combined task of the AbrB-Rok module is gating the competence transitions to be allowed only between two values of Spo0A* - the “window of opportunity”. AbrB is repressed by the sporulation master regulator Spo0A* and also by itself, in a negative feedback loop that prevents overexpression. Due to the instability of the protein, AbrB concentration responds quickly to transcriptional repression, dropping its levels quickly in the presence of Spo0A*. Lower AbrB concentrations allow increase in the expression of Spo0E, a phosphatase that acts directly on Spo0A*, slowing down its accumulation.

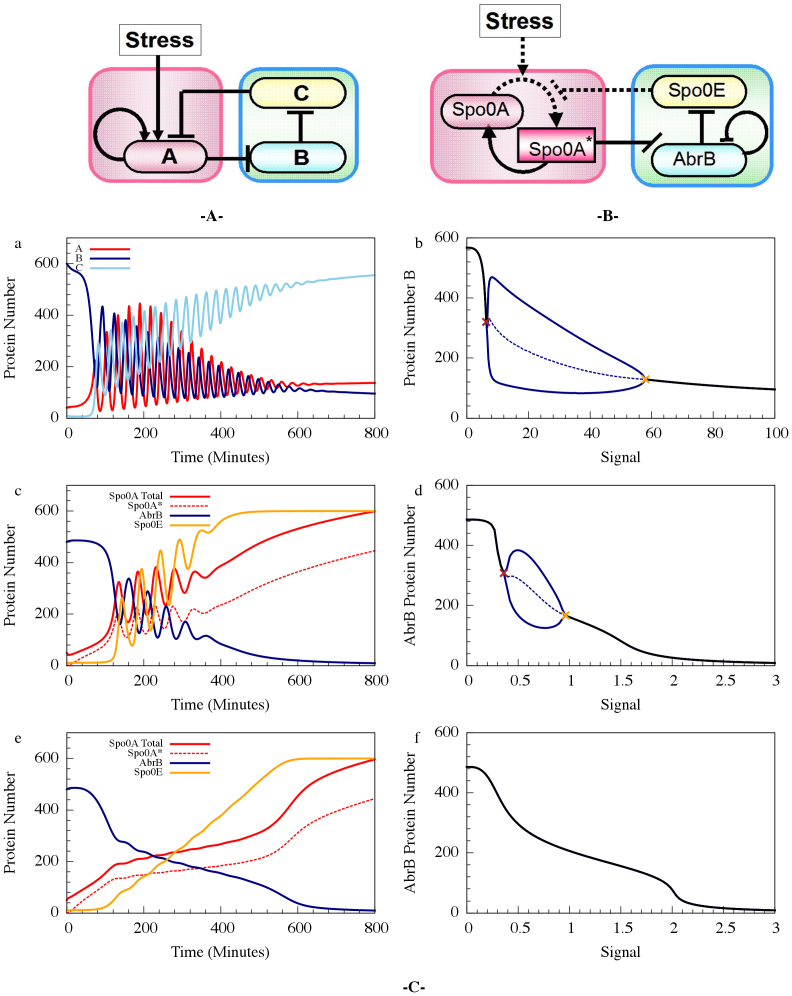
The Spo0A-AbrB-Spo0E part of the decision gate regulates the clock rate of the sporulation timer (the rate of accumulation of Spo0A*). Since Spo0A* is dephosphorylated by Spo0E which is inhibited by AbrB which is inhibited by Spo0A*, these three genes form a special repressilator circuit²⁴. Hence, the clock rate is regulated via a special repressilator-like dynamic. For some input signals, this repressilator can cause the concentration of the components of the decision module to oscillate. The oscillations of the protein levels lead to short intervals with elevated probability of transition into competence (“chain of opportunities”) when the levels of both AbrB and Rock are below some threshold.

The repressilator is a well studied network motif consisting of three genes that repress each other in sequence and in a loop - A represses B, B represses C, C represses A (ABC for short). This circuit, when implemented experimentally in a cell, showed oscillatory behavior. The Spo0A*-AbrB-Spo0E (ABE for short) circuit is a variant of the classical repressilator, where one of the repressions (Spo0E- Spo0A*) is mediated via dephosphorylation, rather than a transcriptional repression, and two of the components show regulatory feedback loops, one negative (AbrB represses its own transcription), and one positive (Spo0A* activates its own transcription indirectly through σ^H transcription activation of Spo0A). In addition, unlike the classical repressilator, the circuit studied here is driven by an input signal: the rate of phosphorylation of Spo0A that is determined by the stress level. As we show in the next sections, the outcome of this driven repressilator is not only directly responsible for entrance into sporulation, but it also intermediates the sporulation pathway and the competence pathway by translating oscillations in the driven repressilator into windows of opportunity.

Results

The modeling approach and the definition of the activation and inhibition Hill functions are presented in the Methods section via the example of a variant of the classical ABC repressilator that is transcription driven by an external signal. To better understand the functional role of the various features of the Spo0A*-AbrB-Spo0E circuit, we also inspect in the Methods section the dynamics of a variant of the classical ABC repressilator in which A (the gene stimulated by the external signal) is self-activated. The models studied here involve a large number of parameters (e.g. transcription and degradation rates of the various genes, the rank of the various inhibitory and excitatory Hill functions, etc.). Since only some of the parameters are known, and even those ones have uncertainty regarding the exact values, the challenge is to choose a “realistic” set of parameters for meaningful predictions and sound testing of the model predictions. The way the parameters were selected is described in the Methods section and SI6 where we also detail all the parameters. For the sake of clarity, we present the models with real rather than dimensionless units – concentrations are represented by the number of molecules in the cell of each of the proteins, time is measured in minutes, and production and degradation rates are measured in number of molecules per minute.

Phosphorylation driven repressilator

The Spo0A*-AbrB-Spo0E circuit employed by the bacteria can be viewed as a phosphorylation driven self-activated repressilator in which A* (Spo0A*), the phosphorylated version of the protein A (Spo0A), inhibits B (AbrB) which inhibits E (Spo0E). E dephosphorylates A* and the input signal phosphorylates A which is activated by A*. The deterministic dynamics of the circuit is described by the following equations for A, A*, B and E:

where 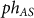= 0.00375 (1/molecule)/minute is the rate constant of the phosphorylation of Spo0A by the input signal I_S = S is measured in number of molecules (see SI6), and 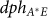= 0.00155 (1/molecule)/minute is the rate constant of dephosphorylation of Spo0A* by Spo0E. 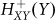and (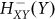) represent activation and inhibition, respectively, Hill function of gene (X) by protein (Y) (see Methods). 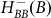is an inhibitory Hill function describing the AbrB self-inhibition. Comparison between the dynamics of the phosphorylation repressilator (Equation 1 to 4) and the classical repressilator with self-activation (See Method section) is shown in Figure 2. Inspection of the role of the AbrB self-inhibition shows that it does not have significant effects on the dynamics. Therefore, it seems that the AbrB self-inhibition is relevant to other functions of this gene. However, we kept the effect in the model for the sake of completeness. Inspection of how changes in the circuit parameters affect the dynamics is included in SI3. In particular it should be kept in mind that while the gate exhibits oscillations for a wide range of circuit parameters (Case I in SI3), for some parameters there is a decline in AbrB but oscillations are not generated (Case II and Case III in SI3). The midpoint of the Spo0A self-activation 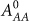, is 180, 240 and 300 proteins for Case I, II and III, respectively. The additional parameters for these cases are listed in SI6.

Figure 2. The dynamics of transcription and phosphorylation driven repressilators.

(A) and (B) are the corresponding circuits. (C) Typical dynamical properties. (a) A typical dynamical behavior - dynamics of protein levels for gene A (in red), B (in navy) and C (light blue) when signal is linearly increased at a rate of 0.125 proteins per minute. The results are for the transcription driven repressilator (circuit in (A)) when gene A is self-activation and with a Hill signal response (equation 16 in the Methods section). (b) The corresponding bifurcation diagram. Y-axis is the range of the number of protein B for different values of the signal (X-axis) computed when the signal is constant at each value. When the signal level is close to zero or larger than a threshold value (below and above the two bifurcation points marked in brown and orange), the protein level is constant and marked in black (stable fixed point). Between these bifurcation points the protein levels oscillate - the maximum and minimum levels for the oscillation states are shown in solid blue line and the average levels are shown in dotted blue line. (c) and (d) are the same but for the phosphorylation driven circuit (B), equation (1)–(4) for circuit parameters corresponding to Case I – the oscillation case. (e) and (f) are similar to (c) and (d) but for circuit parameters that do not yield oscillations – Case II.

The AbrB-Rok gating characteristics

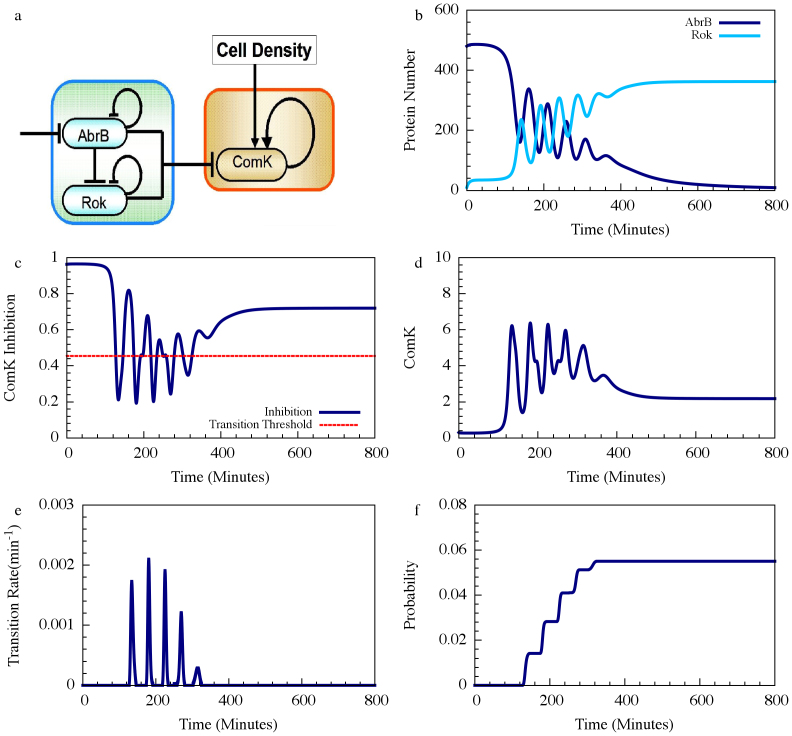
AbrB-Rok gate blocks competence transitions by transcription inhibition of ComK by both AbrB and Rok independently (Figure 3a). These effects are incorporated in the dynamical equation for ComK (denoted by K) by multiplying the production rate of K by two corresponding inhibitory Hill functions so that (see SI2 for more details):

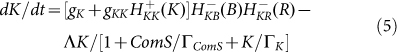R represents the concentration of Rok and the last term on the RHS of equation 5 represents the effect of ComS on the degradation of K (see Ref. 14 and SI3). Equation (5) clarifies why the gate enables competence transition only when the values of both AbrB and Rok are below a certain threshold. The AbrB inhibition of Rok is incorporated by an inhibitory Hill function , which is multiplied by another inhibitory Hill function 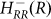representing the Rok self-inhibition. Thus, the deterministic dynamics of Rock is described by

Consequently, when AbrB oscillates it induces reciprocal oscillations in Rok with some small phase shift as is shown in Figure 3b. Therefore, at each oscillation there is a short time interval during which the values of both AbrB and RoK are sufficiently low that the inhibition of ComK is reduced as is shown in Figure 3c. Each inhibition reduction leads to a sharp increase in the concentration of ComK (Figure 3d) which in turns elevates the transition probability per unit time into competence, as is shown in Figure 3e. In other words, the AbrB-Rok competence gate opens a window of opportunity to escape into competence with the accumulated transition probability grows in steps as in shown in Figure 3f.

Figure 3. Turning oscillations into opportunity spikes for Case I.

(A) The AbrB-Rok gating of ComK. (B) The reciprocal dynamics of the AbrB and Rok. (C) The corresponding dynamic of the ComK Inhibition I defined by 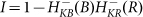. The red dash line is the threshold of 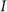, below which competence transition is possible. (D) The corresponding dynamics of ComK. (E) The transition probability per unit time illustrating the “opportunity spikes” generated at each oscillation. (F) The accumulated transition probability before commitment to sporulation.

In the example shown in Figure 3 the accumulated probability is 0.06. While the probability depends on the value of the parameters. We note that by using “realistic parameters” the probability can typically vary between 0.01 and 0.1, which is consistent with experimental observations. Also the gate function can change when the Rok transcription parameters change in a drastic manner – insufficient inhibition prevents transitions into competence, while over inhibition enhance the competence transition (SI6). This prediction can be directly tested experimentally.

Noise managment

So far, we analyzed the gate dynamics in the absence of noise. In this section we investigate, the dependence of the gate performance on its capacity to manage the effect of both external and internal noise and on its robustness with regard to changes in the circuit parameters. Our investigation are motivated by previous studies of the relationships between circuit architecture, noise behaviors and the circuit task performance¹,¹⁶,¹⁷.

External noise

Motivated by the above we investigated the AbrB-Rok gate capacity to manage external and internal noise. In SI4 we show that the cell fate determination between sporulation and competence is not sensitive to external noise. More specifically, we found that noise added to the external input signal has only weak effect on the accumulated transition probability into competence. In other words, the circuit integrates the stress signal while filtering out noise, thus guaranteeing a robust response.

Internal noise

A stochastic approach was used to investigate the AbrB-Rok gate capacity to manage internal noise. In this approach we no longer use the differential equations that describe the deterministic dynamics. Instead, we modeled the circuit considering protein synthesis, degradation, binding and unbinding as stochastic events. The different relative probabilities are set to match the corresponding rate constants in the deterministic equations and the noise level is set by the binding and unbinding rates, taken from²⁴. The circuit was then simulated with the Gillespie algorithm³⁶.

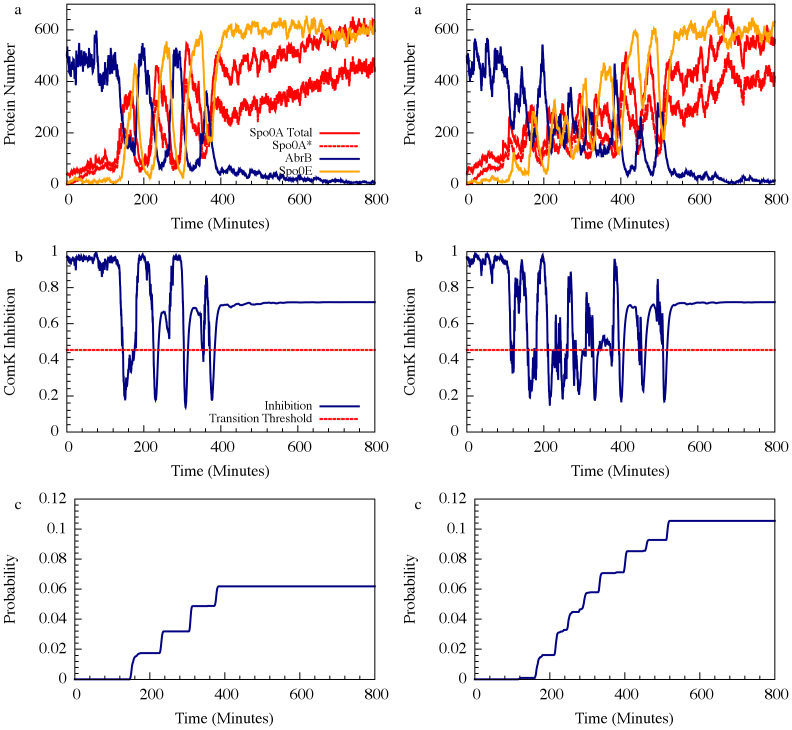
For circuit parameters which give rise to oscillatory dynamics in the deterministic case (Case I in Figure 2), the internal noise causes the oscillations to become less ordered, yet the accumulated transition probability is retained almost unchanged as is show in Figs. 4 and 5 (see SI5 for more details). For some circuit parameters which do not give raise to oscillatory dynamics in the deterministic case (Case II and Case III mentioned earlier), the internal noise has a stronger effect – it can induce oscillations in a manner similar to that of the cases where the deterministic model shows oscillatory behavior, as is shown in Figs. 4. Yet, the effect of the noise on the accumulate transition probability is also weak as is shown in Figure 5. Thus, the special architecture of the AbrB-Rok gate enables the system to manage noise in a way which leads to oscillatory dynamics even in the absence of oscillations in the deterministic limit. In addition the noise is “harnessed” to make the dynamics more robust with respect to variations in the circuit parameters.

Figure 4. The effect of internal noise for the oscillating (A) and non-oscillating (B) cases.

The simulations were performed by six versions of Gillespie algorithm, each of which with different unbinding rate of transcription factors to the promoter. The two top panels show the number of proteins for each gene for specific realization with unbinding rate 5/minute for both Case I and Case II shown in Figure 2. The two middle panels show the corresponding dynamics of I – the ComK Inhibition. The two bottom panels show the corresponding accumulated transition probabilities.

Figure 5. Noise management capabilities of the decision gate.

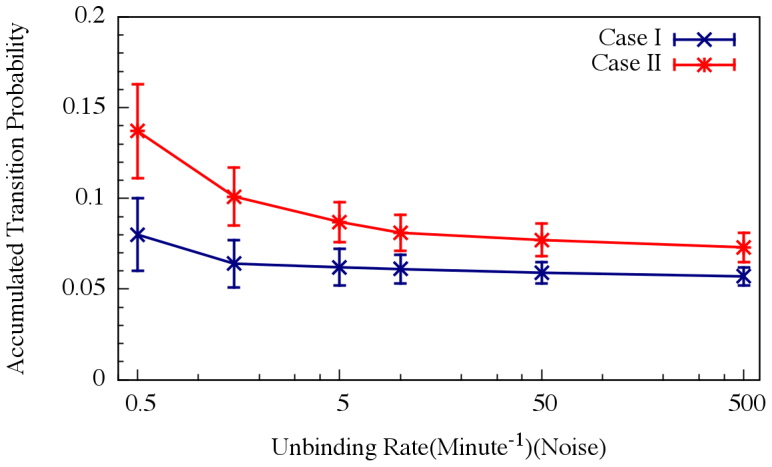
The effect of internal noise on the accumulated transition probability is shown for the oscillating and non-oscillating cases. The simulations were performed by six versions of Gillespie algorithm, each of which with different unbinding rate of transcription factors to the promoter. For each version, mean value of the accumulated transition probability and STD were computed from 100 realizations (runs). Crosses and blue line denote simulations with parameters of the oscillation Case I (shown in Figure 2); Stars and red line denote simulations with parameters of the non-oscillation Case II (shown in Figure 2).

Discussion

The current post genomic era increased information about the interactions between gene circuits to such an extent that is now possible to map the architecture of consolidative multi-module systems. This new information is paving the way to develop new classes of integrative models to comprehend the operational principles and noise management of multi-module task performing cellular networks¹⁴. A special well-studied example of such cellular system is the intricate decision-making network used by bacteria for fate determination between sporulation and competence. While each cell has the freedom to determine its own fate, the ratio between sporulation and competence is collectively regulated to fit current conditions according to the needs of the colony as a whole. This implies that the stochastic cell differentiations are carried out with special capacity of noise managements to harness the noise at different modules and different times according to the function. For example, in the adaptable timer (the Spo0A phosphorylation pathway), noise is undesirable. Stress fluctuations experienced by the individual cell should not lead to decision to sporulate at inconvenient times as it could have negative effect on the colony. Therefore the system has evolved to integrate stress signals over time, filtering out transient activations and guaranteeing a robust response¹⁴. On the other hand, the ComK stochastic switch is driven by noise that is required for the transition into competence: the ComK positive feedback loop is activated when fluctuations lead the ComK concentration to cross a certain threshold. Our studies explain how the two opposite noise requirements can be satisfied by the decision gate which regulates the opening of the stochastic switch according to the state of the timer.

Most previous studies focused on either the competence transition or the sporulation pathway. An important, yet less studied, part of the sporulation/competence decision system is the interplay between the competence switch and the sporulation timer via the AbrB-Rock decision gate studied here. The task of this gate is to regulate the opening and closing of the ComK stochastic switch according to the Spo0A timer. We demonstrated that the distinct circuit architecture of this gate leads to special dynamics and noise management characteristics. These are required for efficient task-performance of coordination between the stochastic switch and the adaptable timer - two modules with opposite noise requierments. Our studies revealed the operation-architecture principles of the gate: 1. Inhibition of inhibition – inhibition of the gate by Spo0A* and inhibition of ComK by the gate. 2. Phosporylation driven repressilator-like motif. 3. “Window of opportunity” with oscillating dynamics. We showed that the advantage of “inhibition of inhibition” is that the gate is not sensitive to noise from Spo0A* (high concentration - low noise) and at the same time adds to the noise in the regulation of ComK (low concentration – high noise)¹. The advantage of the oscillations is to increase the transition probability of each cell by steps which can improve coordination between cells as is discussed further bellow.

Thus, new principles were revealed that explain the intriguing interplay between the timer and the stochastic switch. Experimental verifications of the predicted gate oscillations require parallel monitoring of the time dynamics of the concentration of three genes within a single cell. Such measurements are feasible with current technology.

Different gene circuits can generate oscillations. As we have shown, the Spo0A*-AbrB-Spo0E repressilator motif leads to oscillations that are less sensitive to the circuit parameters and less sensitive to internal noise. For circuit parameters whose deterministic dynamics is not oscillating, the noise generates oscillating dynamics. This way the noise management of the gate renders its operation to be less sensitive to cell-cell variations in the circuit parameters. Being phosphorylation (instead of transcription) driven, the repressilator has a narrow and well-defined “window of opportunity” and is less sensitive to fluctuations in the external stress.

Since neither sporulation nor competence is advantageous to a solitary cell, it is crucial that the option to escape into competence vs. commitment to sporulation is done within a time frame, which is synchronized with the other cells. The phosphorylation driven repressilator motif facilitates narrow windows with its oscillating dynamics, which is crucial for cell-cell coordination. At each cycle the cell sends out a pheromone signal when level of Spo0A* (which regulates the Rap communication module) increases. At the same time Spo0A* has a delayed positive feedback via its activation of Spo0F and the cell also receive signals from the other cells. As we will show in details in forthcoming publication, the cell-cell communication leads to harmonization of the oscillating dynamics between the communicating cells.

Looking ahead, the new principles found in the context of sporulation vs. competence fate determination are likely to be relevant to other cases of collective cellular decisions of stressed bacteria such as cannibalism and fratricide as well as spore germination when conditions are improved. Another and less expected possible direction is cancer. Tumorigenesis involves a variety of cellular decisions such as epithelial to mesenchymal transitions, transition into dormancy (transition into quiescent state analogous to sporulation), and relapse (germination of dormant cells). Recently it has been shown that the decision of micrometastases to grow is a complex process in which several nearby micrometastases have to perform a common decision to grow together for full metastasis maturation³⁷.

Methods

Classical repressilator

To better understand the functional role of the various features of the Spo0A*-AbrB-Spo0E circuit, we first inspect the dynamics of a classical ABC repressilator that is transcription driven along a variant in which A is self-activated.

The deterministic equations of a classical ABC repressilator are given by:

The gene base production rates are g_X (X stands for A, B and C respectively) and the corresponding protein degradation rates are k_X. The transcription inhibitions are included by the inhibition Hill functions 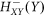represent inhibition of gene (X) by protein (Y) are given by:

Where (n) is the rank of the Hill function (nonlinearity or cooperativity) and Y₀ is the midpoint concentration. In SI1 we present the phase space analysis and the time dynamics of classical repressilator with different nonlinearity. We also show that the oscillatory behavior is retained when A is self-activated so that equation (7) is replaced by

where 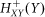is an excitatory (activation) Hill function given by:

Transcription driven repressilator

The repressilator can be driven by an input signal [I_S = S] or by another gene D (whose level is S) incorporated by replacing equation (7) with equation (13) and (14) respectively:

where I_S = S in equation (13), 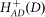is an excitatory Hill function (equation 12) and D = S in equation (14). We found, as is shown in Figure 2 and detailed in SI1, that the oscillatory behavior is retained for both cases for a wide range of signal levels. For specific choices of the circuit parameters the oscillations start above a threshold signal level S₁ and exist up to a second higher signal level S₂. When the signal is increased in time, driving the repressilator via a Hill function (equation 14) introduces nonlinearity in the production rate, which enables to reduce the range of oscillations. However, it requires taking a non-realistic high level of g_AS (orders of magnitude higher than g_A).

Inclusion of self-activation of A also enables to reduce the range of oscillations. This was shown by investigating the additional variants of the circuit in which we replaced equations (13) and (14) by equations (15) and (16) below:

Analysis of the variant described in equation (16) is detailed in SI1. We found that as long as “realistic” parameters are used (see further below), the self-activation can lead to some reduction in the oscillation range but yet does not enable to generate a narrow window to limit the oscillations to be within a limited range. The reason of this lack of flexibility has to do with the inherent coupling between the effect of the driving signal on the transcription of A and the cascade of transcription inhibitions that lead to the oscillations. This coupling is relaxed when the repressilator is phosphorylation driven as is described in the Results section.

Selection of “realistic” parameters

To meet the challenge of selecting “realistic” parameters, we began with comparison of the model of the classical repressilator with the synthetic one studied in²⁴. Based on the estimates of transcription rates of 0.5 mRNA/sec, translation rates of 0.167 mRNA/sec, mRNA half life of 2 minutes, protein half life of 10 minutes, and peak value of about 600 proteins, we chose the typical protein degradation rate as 0.1/minute, and the synthesis rate as 60 proteins/minute. Since the maximum protein levels are several hundreds, we selected the midpoint of the Hill functions to be at 100–200 proteins. Although much effort were used to determine these parameters, the features new mechanistic principles revealed by this work are robust and therefore not sensitive to precise values of these parameters.

In previous modeling of a classical repressilator, the rank of the Hill functions was taken as n = 2. We selected n = 4 to fit the rank of the Hill functions in the Spo0A-AbrB-Spo0E circuit. Consequently, the values were slightly adjusted to have the typical oscillation time of 30 minutes. The estimate of the rank of the Hill functions were based on the fact that AbrB forms a tetramer³⁸ and Spo0A forms a dimmer³⁹. Consequently, we chose the rank of the Spo0A by Spo0A* (that is mediated via σ^H) as n_AA = 3 and the rank of the inhibition of Spo0E by AbrB as n_BA = 4. We note that since there is uncertainty regarding the proper ranks of the Hill functions, we tested the behavior for other sets of ranks and found that similar results can be obtained.

The value of the production rate for AbrB is higher to account for the fact that it is unstable⁴⁰, since production rates are normalized by degradation rates. In the case of self activation of Spo0A, we selected a base production of 12 proteins per minute and the self activation rate factor as slightly higher (than 60) – 80 proteins per minute.

The relevant rate of the input signal phosphorylation of Spo0A and the Spo0E dephosphorylation of Spo0A* were estimated based on the typical phosphorylation and dephosphorylation rates discussed in⁴¹,⁴². These rates are measured in equations (1) and (2) in units of (1/molecule)/minute since they are multiply by the number of molecules (the signal S for phosphorylation and the number of Spo0E molecules for dephosphorylation). To compare the phosphorylation and dephosphorylation rates with that of proteins' synthesis and degradation we need to converted the (1/molecule)/minute units to units of (molecule/minute) and (1/minute) that are used to describe protein synthesis and degradation. Since the number of protein molecules is in the order of hundreds, the rates of phosphorylation and dephosphorylation can be several orders of magnitude higher than that of production and degradation in agreement with molecular information.

Final adjustments of the parameters were done to fit the experimental estimates of protein levels in the cells⁴ (see the parameter list in SI6). The estimations of the ComK parameters were taken from Refs ^4,6 and the estimations of the parameters related to the competence transition probability (SI2) were done to fit the experimental observations that about 5–10% of the cells make the transition (see SI6).

Author Contributions

Authors' contribution: D.S., J.O. and E.B.J. devised the model, D.S., M.L. and T.S. performed the simulations. All authors analyzed the results and wrote the article

Supplementary Material

Supplementary Information

Supporting Information