Abstract
Background
There is limited capacity to assess the comparative risks of medications after they enter the market. For rare adverse events, the pooling of data from multiple sources is necessary to have the power and sufficient population heterogeneity to detect differences in safety and effectiveness in genetic, ethnic and clinically defined subpopulations. However, combining datasets from different data custodians or jurisdictions to perform an analysis on the pooled data creates significant privacy concerns that would need to be addressed. Existing protocols for addressing these concerns can result in reduced analysis accuracy and can allow sensitive information to leak.
Objective
To develop a secure distributed multi-party computation protocol for logistic regression that provides strong privacy guarantees.
Methods
We developed a secure distributed logistic regression protocol using a single analysis center with multiple sites providing data. A theoretical security analysis demonstrates that the protocol is robust to plausible collusion attacks and does not allow the parties to gain new information from the data that are exchanged among them. The computational performance and accuracy of the protocol were evaluated on simulated datasets.
Results
The computational performance scales linearly as the dataset sizes increase. The addition of sites results in an exponential growth in computation time. However, for up to five sites, the time is still short and would not affect practical applications. The model parameters are the same as the results on pooled raw data analyzed in SAS, demonstrating high model accuracy.
Conclusion
The proposed protocol and prototype system would allow the development of logistic regression models in a secure manner without requiring the sharing of personal health information. This can alleviate one of the key barriers to the establishment of large-scale post-marketing surveillance programs. We extended the secure protocol to account for correlations among patients within sites through generalized estimating equations, and to accommodate other link functions by extending it to generalized linear models.
Keywords: Ethical study methods, privacy; enhancing the conduct of biological/clinical research and trials; assuring information system security and personal privacy; anonymization; privacy and security; health services; medical informatics; pharmacoepidemiology; medical education; advanced algorithms; personal health records and self-care systems; languages and computational methods
Introduction
Although US$500 billion is spent world wide on drugs each year,1 there is limited capacity to assess the comparative risks and effectiveness of medications after they enter the market.2–6 In Canada, 60% of people 18 years of age or older have taken at least one prescription drug in the previous 6 months, and over one-third report experiencing an adverse drug event (ADE).7 Even when safety problems are identified, there is no timely or effective method of communicating this information to physicians to inform prescribing decisions.8–10
Most countries have established a formal regulatory process for drug approval that defines the information required from the drug manufacturers to demonstrate a drug's safety and efficacy. However, drugs are typically tested in randomized controlled trials with a limited number of patients selected carefully to optimize compliance and limit comorbidity.11–13 This population of patients rarely represents the typical patient treated with the drug after approval. While pre-market studies uncover commonly occurring ADEs, they are not designed to detect rare but serious ADEs,12 nor to assess safety and effectiveness in the broader population of eventual users.14 15
The limitations of relying on safety assessments from pre-market drug approval studies were highlighted in the 1950s with the thalidomide disaster, where drugs prescribed for nausea in pregnancy produced severe congenital anomalies. In response to this problem, a voluntary system of adverse drug reaction reporting was instituted, which continues to be the cornerstone of post-market surveillance.11 However, 60 years later, there is worldwide consensus that voluntary reporting is insufficient.12 16 Only 2–10% of ADEs are reported, there are substantial delays in ADE detection, and ADE case reports lack accurate numerators and denominators to estimate incidence.11 17–19 Moreover, voluntary reporting does not allow identification of ADEs, such as myocardial infarction, which also commonly occur in the general population. For example, more than 9 million people took the now infamous weight-loss drug fen-phen before it was identified that the drug could result in cardiac valve damage, a problem that also occurs in the general population for non-drug-related causes.12 16
Traditional adverse event reporting has also been widely criticized because it substantially underestimates important patient-reported adverse effects such as nausea, fatigue, appetite loss, and diarrhea.20 21 This underestimation can have profound clinical implications because early detection and response to suboptimal patient-reported treatment outcomes can improve adherence to treatment as well as reduce the risk of adverse events.22 However, regular monitoring and follow-up is resource intensive, and difficult to incorporate into regular practice in a cash-strapped healthcare system. A number of approaches have been used for post-marketing surveillance to address these problems.
Prescription event monitoring is an active post-market surveillance method that requires physicians to respond to a follow-up questionnaire about a patients' response to new drugs.23 In one study, 94% of events detected by prescription event monitoring were not detected by spontaneous ADE reporting.19 However, response rates of physicians to follow-up questionnaires is poor, ranging from 35% to 65% and decreasing to 27.6% when information is sought for more than 30 patients from a single physician.23 24 Moreover, physicians who prescribe new drugs to more patients are generally poor responders.25 The labor-intensive nature of this method makes it unsustainable for a nation-wide undertaking.23 Even if mandatory reporting of ADEs were to be instituted, such as is the case for infectious disease reporting for public health, response rates are notoriously poor.26 27 In the public health context, authorities have addressed this limitation by increasing their reliance on computerized information sources such as data from the laboratory and medical service claims systems, as these data are more timely and reliable, and the effort to document information in a parallel reporting system is reduced.28–31
In Canada, population-level health administrative data (prescriptions, medical services, hospitalizations, mortality) can be linked to create longitudinal health histories for individual patients, which has enabled a new generation of methods to assess post-approval drug safety and effectiveness after their approval.32–41 Unfortunately, administrative data cannot be used alone for prospective surveillance because they lack important clinical variables that are needed for assessing indications for treatment, risk factors (eg, smoking), clinical (eg, blood pressure, HbA1c), and health status outcomes (eg, functional status). The increasing use of electronic health records in community- and hospital-based care may, however, provide a means of addressing both of these issues: systematic collection of important clinical variables to assess effectiveness and identification of ADEs in a timely manner.42–45
Europe, Scandinavia, Australia, and England have led the introduction of electronic health records in primary care.42–45 One byproduct of these early investments is the creation of new information sources that can be used to conduct drug safety and effectiveness evaluation. The General Practice Research Database, the first of this new genre, collects information from the electronic health records of 450 general practices in England and approximately 3.6 million active patients. It has been used to conduct over 800 studies including a sentinel study on the safety of childhood vaccines in relationship to the suspected link to the development of autism.46 Similar to paper medical records, these electronic files include information on prescribed therapy, consultations, morbidity events (diagnosis and symptoms), and lifestyle (smoking, alcohol, height, and weight).47 In the last 5 years, there has been a call to develop the potential to use these new information-rich resources for assessment of drug safety and effectiveness.2–4 6 48 Indeed, a new generation of drug safety and effectiveness studies is beginning to emerge from the electronic clinical data of large enterprise health-delivery networks.49–52
For rare adverse events, the pooling of data from multiple sources is necessary to have the statistical power and sufficient population heterogeneity to detect differences in safety and effectiveness in genetic, ethnic and clinically defined subpopulations.6 This is important because the effects of treatment may vary by sex and ethnicity,47 51–55 probably because of subpopulation differences in the prevalence of genetic polymorphisms that influence the metabolism of medication and its efficacy and toxicity.56 57
Combining data from different data custodians or jurisdictions to perform an analysis on the pooled data creates significant privacy concerns that would need to be addressed.58 It has been argued that providers would be permitted to disclose identifiable health information to certain organizations performing pharmacovigilance, such as the Food and Drug Administration in the USA.59 However, not all organizations in the USA and elsewhere that will be collecting data for the evaluation of drug, medical device, and vaccine safety will have such public health exemptions. For example, pharmaceutical companies that need to perform post-marketing surveillance on conditionally approved drugs or devices would still have to address privacy issues, as they will not have the authority to collect potentially identifiable patient information. In addition, in order to maintain public trust, even if the organization performing surveillance is permitted to collect personal health information (PHI), it may be prudent not to collect PHI on large numbers of individuals who do not experience adverse events (eg, controls).
Datasets that are distributed among multiple sites having the same fields but different records in each site are called ‘horizontally partitioned’ data. To address the privacy concerns noted above, a number of data analysis protocols for secure computation on such horizontally partitioned data have been proposed, but they all have important disadvantages. For example, the sharing of deidentified data to create a pooled dataset60–62 will result in a loss of precision of the data, meta-analytic methods will result in a loss of precision and power,63 and the accuracy of recently proposed propensity score methods were not compared with an ideal analysis on the pooled data,64 65 therefore any losses in precision and accuracy from that approach are not known. Methods for multi-site regression would retain the precision and power.66 67 However, current multi-site regression approaches are prone to inappropriate disclosure of personal information from the information matrix,68 from indicator variables, disclosures from the covariance matrix,68–71 from the iterations themselves,72 and from the information matrix across multiple models.68 Secure multi-party computation methods have been proposed for the construction of regression models on horizontally partitioned data.73–77 However, as we demonstrate in the online appendix, these methods can still leak personal information. Distributed aggregation architectures that send queries to sites and combine their responses have been proposed and deployed.78–81 These are prone to tracker queries at various levels of sophistication that can reveal personal information.82–88 A detailed review and critique of all these methods and protocols that illustrates how they can potentially still leak personal information is provided in the online appendix.
Our objective was therefore to develop a multi-site logistic regression protocol using secure multi-party computation methods, which does not disclose PHI by (1) not revealing the individual site information matrix and score vectors, (2) avoiding inference channels through multiple overlapping queries, and (3) retaining the same precision as a raw data pooled analysis. We chose logistic regression because (1) it is a commonly used analytical method for investigations of ADEs,89–93 and (2) the link function for the logistic model is more complex than for other generalized linear models (GLMs), which makes it a good one to illustrate in detail. We then show how the logistic regression protocol can be extended to generalized estimating equations (GEEs) to account for correlations among patients within a site, other GLMs such as Poisson regression and survival models.
Methods
Logistic regression
Let Y=(Y1,…,YN)′ be independent Bernoulli variables with mean E(Y)=μ=(μ1,…,μN)′. Given an intercept and a set of covariates X=[1, X.1,…,X.v], where X.j=(x1j,…,xNj)′ contains the values for covariate j, we define a logistic model with parameters β using the formula:
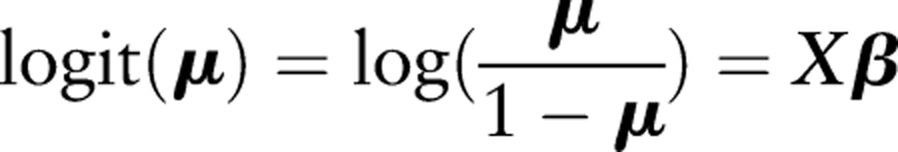 |
(we say that the logit function links the random component μ to the systematic component Xβ). The log-likelihood l (β;y) of the full model, which can be used to assess model fit (usually given as −2 log-likelihood), equals:
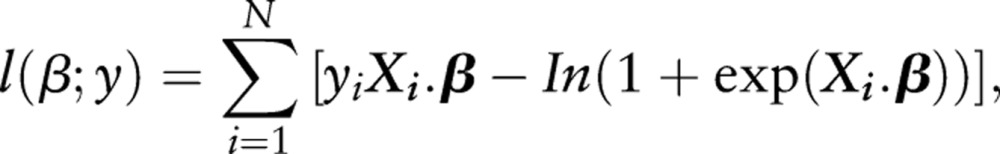 |
where Xig is row i from the design matrix X.
For a set of observations y=(y1,…,yN), we can determine parameter estimates b at which the log-likelihood l (β;y) of the model is maximized using the Newton–Raphson method (or, equivalently, the Fisher scoring method, since the estimated and observed information matrices are the same for a logistic model94). That is, we iteratively compute the estimates using b(t+1)=b(t)−[I(t)]−1u(t), at iteration t, where u(t)=X′(y−p(t)) is the estimated score vector with probability of success p(t)=logit−1(Xb(t)), and I(t)=X'W(t)X is the estimated information matrix with weight matrix W(t)=diag[pi(t)(1−pi(t))]. This fitting method can be used for any GLM (with new derivations for the score vector and information matrix),95 and has been shown to converge to a solution in fewer iterations than other optimization algorithms applied to logistic models.96
SPARK protocol
Our protocol for the secure computation of logistic regression models across horizontally partitioned data (SPARK: Secure Pooled Analysis acRoss K-sites) assumes that there are k sites providing data on the same variables for different patients, and there is a single analysis center (AC) as illustrated in figure 1 (for the case of three sites). The AC would define the model that needs to be constructed and initiate the distributed secure computation. In some instances, the sites need to communicate directly with each other. This direct communication capability that bypasses the AC is important for maintaining the security of the protocol.
Figure 1.
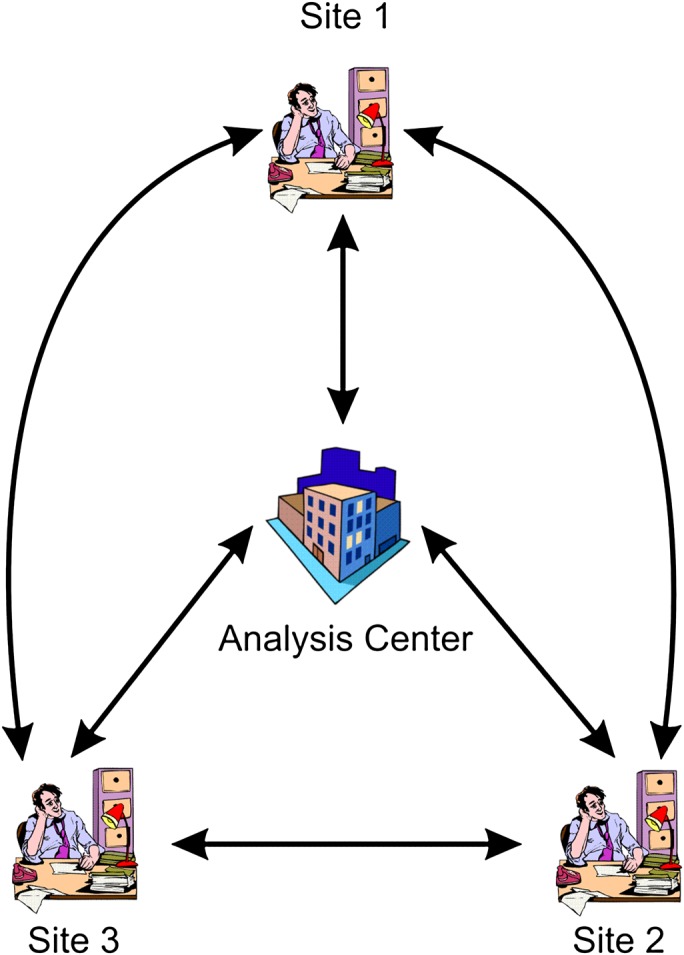
Overview of set-up for implementing the SPARK protocol when there are only three sites. This figure is only reproduced in colour in the online version.
Secure building blocks
We use the additive homomorphic encryption system proposed by Paillier.97 With the Paillier cryptosystem, it is possible to perform mathematical operations on the encrypted values themselves, such as addition and limited forms of multiplication. Formally, for any two data elements, m1 and m2, and their encrypted values, E(m1) and E(m2), the following equation is satisfied:
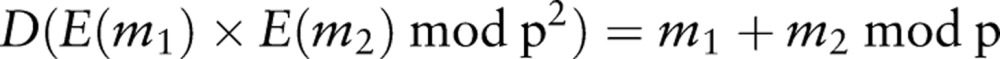 |
1 |
where p is a product of two large prime numbers, and D is the decryption function. In this type of cryptosystem, addition of the plaintext is mapped to the multiplication of the corresponding ciphertext. The Paillier cryptosystem also allows a limited form of the product of an encrypted value:
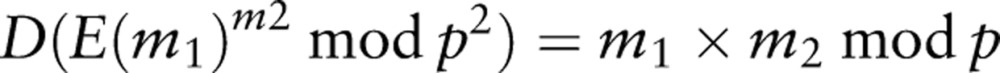 |
2 |
which allows an encrypted value to be multiplied with a plaintext value to obtain their product.
Another property of Paillier encryption is that it is probabilistic. This means that it uses randomness in its encryption algorithm so that when encrypting the same message several times it will, in general, yield different ciphertexts. This property is important to ensure that an adversary would not be able to compare an encrypted message with all possible counts from zero onwards and determine what the encrypted value is.
The SPARK protocol uses a number of secure building blocks that are needed for basic mathematical operations, such as addition, multiplication, secure dot product, matrix multiplication, and matrix inverse, which are combined to implement logistic regression. Secure dot product,98 secure multiparty multiplication,99 secure multiparty addition,99 secure matrix sum inverse for two parties,100 and secure matrix multiplication100 are existing protocols that we use in SPARK. In each of these building blocks, the final result is privately shared among the parties involved.
We extended the secure matrix sum inverse sub-protocol, which only exists for the two-party case, to the more general multi-party case. The secure computation of 2-norm distance and comparison are the other two building blocks that we use in SPARK, and these are presented in the online appendix.
Based on these secure building blocks, we describe the complete SPARK protocol in the online appendix. We also include a detailed security analysis of the protocol to illustrate that it is inherently secure and resilient to plausible collusion attacks.
Empirical evaluation
A theoretical complexity analysis of the SPARK protocol is provided in the online appendix. Our empirical evaluation of SPARK, presented here, considered the computational performance of the protocol and its accuracy compared with the results of using raw pooled datasets with SAS. For this empirical evaluation, we created some simulated datasets.
Simulation datasets
A classic simulated dataset is one formed by a set of independent normally distributed variables (eg, see Hosmer–Lemeshow101). The variables in this case could be thought of as mean-centered and scaled.95 102 Datasets of this type have been used repeatedly in the evaluation of statistical methods in medical and health research.103 104 Similarly, we use a binomial distribution to create binary variables, which could be seen as simulating binary risk factors (as in Heinze and Schemper105). Correlated variables are common, however, in health research and often used in models (see the reviews by Bagley et al106 and Mallett et al107). We therefore also created correlated data from the normally distributed variables.
A common recommendation in biostatistics is to constrain the number of covariates proportionally to the number of observations. Following Harrell,108 we therefore limited the number of observations to 40 times the number of covariates to simulate more realistic models. Harrell recommends a maximum of 10–20 ‘equivalent’ observations per covariate to avoid overfitting, where, for a logistic regression, the number of equivalent observations is the minimum number of binary outcomes at the same level (eg, the minimum number of zeros or ones). We assumed that the outcomes would be split evenly between their binary values, which meant creating twice the number of observations as the equivalent observations described by Harrell. The sizes of the resulting datasets are summarized in table 1.
Table 1.
Size of simulated datasets (excluding intercept)
| Number of covariates | 5 | 10 | 15 | 20 |
| Number of observations | 200 | 400 | 600 | 800 |
Moreover, we wished to test different variable types and therefore created datasets with independent identically distributed (iid) continuous covariates, correlated covariates, and binary indicators (thus resulting in 12 datasets when combined with table 1). The iid variables were drawn randomly from a standard normal distribution; the correlated variables were created using a Cholesky decomposition on a correlation matrix with off-diagonal entries of 0.75, applied to the iid matrix of variables (preserving their marginal distributions)109; and the binary indicators were drawn randomly from the binomial distribution, with probability of success for each variable drawn randomly from the uniform distribution (scaled so that the probability of success was restricted to values from 0.3 to 0.7 in an effort to avoid convergence problems in the estimated models).
In order to compare estimates between models with different covariate types, we needed to use the same parameter values for the 12 different logistic models. We therefore randomly drew 21 fixed values for the parameters β (for models with an intercept and up to 20 covariates) from a normal distribution with mean 0 and variance 10. The resulting draw for the first six parameters (common to each model) was the fixed column vector β'=(0.899,−5.944,1.534,−0.156,2.259,−1.868). We included an intercept, β0, hence we also included a column of ones in the design matrix X (which was otherwise exclusively populated with one of iid, correlated, or indicator variables). The outcome variable was drawn for each of the 12 models from a binomial distribution with probability of success equal to the mean response of the logistic model given by μ=logit−1(Xiβ), since μ = E (Y).110
When the outcome is rare, as would be expected with some ADEs, then the dataset would be quite unbalanced. There are two common approaches for dealing with an unbalanced dataset: (1) a down-sampling or prior correction approach reduces the number of observations so that the two classes in the logistic regression model are equal111–113; and (2) the use of weights. It has been noted that the weighting approach suffers a loss in efficiency compared with an unweighted approach when the model is exact.114 Therefore after down-sampling, the dataset would be rebalanced, which is consistent with our simulated datasets.
Having created our 12 datasets, with outcomes, we then used a simple bootstrap to generate 5000 replicates for each dataset (with the same number of observations in each replicate). In all of our evaluations, we randomly split the dataset into subsets of equal size to the different sites for each iteration of the simulation.
Computational performance evaluation
Two types of performance evaluation were performed. In the first, we assumed two sites, and the focus was to evaluate the computation time. This was calculated as the average across all replicates for each dataset. In the second evaluation we measured the computation time as the number of sites, and records in the dataset were systematically increased. We varied the number of sites from two to five, and the number of records from 100 000 to 1 million in 100 000 record increments. We did not take advantage of parallelism in these evaluations, therefore the performance should be considered a lower bound. The machine used was a commodity Windows XP platform with a dual-core Intel 2.4 GHz processor and 3 GB of RAM.
The key bit-length size for this evaluation was 1024 bits. To have a fast and accurate computation on big integer and floating point numbers, the GNU Multiple Precision Arithmetic Library was utilized inside the implementation of the protocol, and the system was developed in the C# programming language.
Accuracy evaluation
It is necessary to perform accuracy evaluations because all secure multi-party computation protocols operate only on integers. We therefore had to scale all of our real numbers into integers to perform the computations, and then scale them back when presenting the results. This scaling causes a loss of precision. The accuracy evaluation was intended to determine the extent to which the results differ from constructing models on the original pooled datasets in SAS.
We fitted logistic models to all replicates individually with SPARK and SAS using the Newton–Raphson method, without any form of ridging, and with relative parameter convergence of 1e-4. We compared the maximum difference between estimates for SPARK and SAS, including estimates for the intercept and five covariates (we exclude the additional covariates for ease of presentation).
Results
The evaluation results for performance and accuracy are shown in this section.
Computational performance
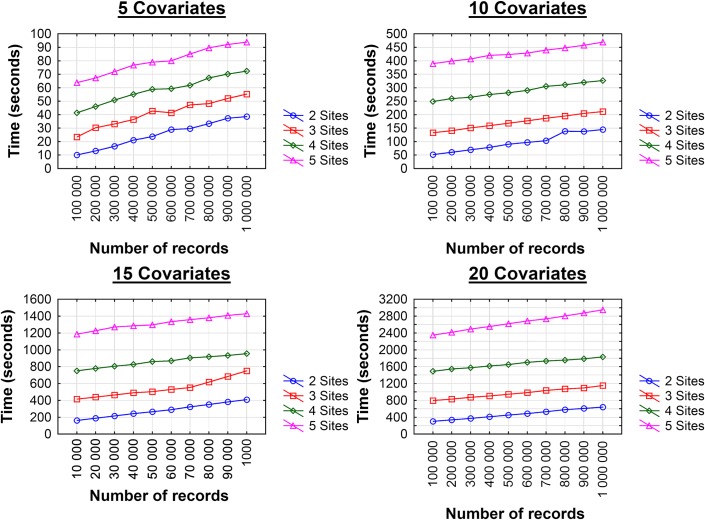
The computational performance results for the two sites are shown in table 2. These show the actual time to perform the computations at each site, and not the communication time among sites. As expected, the computation time increases with more covariates in the dataset. The variation in performance among the datasets with the same number of covariates was not dramatic. The results with large datasets and more sites are shown in figure 2. The computation time scales linearly with more records. As more sites are added, the computation time grows exponentially. However, with five sites and 1 million records, the computation is approximately 5 min, which makes the implementation practical in realistic situations.
Table 2.
Computation time for different datasets assuming two parties
| No of covariates | Type | Time (min) |
|---|---|---|
| 5 | iid | 0.0286 |
| Correlated | 0.0244 | |
| Binary | 0.0238 | |
| 10 | iid | 0.1836 |
| Correlated | 0.1395 | |
| Binary | 0.1249 | |
| 15 | iid | 0.6669 |
| Correlated | 0.4336 | |
| Binary | 0.3935 | |
| 20 | iid | 0.9804 |
| Correlated | 1.0159 | |
| Binary | 1.0026 |
Time is the average across 5000 replicates.
iid, independent identically distributed.
Figure 2.
Performance in seconds as the number of records increases from 100 000 to 1 million for two to five sites. This figure is only reproduced in colour in the online version.
Accuracy
The accuracy results are shown in table 3. Note that differences are given at a precision of 10e-6 (ie, all values in the table need to be multiplied by 10e-6), and that estimates were originally recorded at a precision of 10e-9. Mean absolute differences (not shown) were so small, with narrow CIs, that we decided it would be more meaningful to report maximum differences only.
Table 3.
Absolute difference between SPARK and SAS estimates for intercept and five covariates, based on a simple bootstrap of 5000 replicates*, with a recorded precision of 10e-9 for estimates
| No of covariates | Type | Estimate | Maximum absolute difference between estimates (×10e-6) | |||||
|---|---|---|---|---|---|---|---|---|
| Parameters | b0 | b1 | b2 | b3 | b4 | b5 | ||
| 5 | iid | 0.073 | 0.257 | 0.082 | 0.094 | 0.117 | 0.017 | |
| Correlated | 0.060 | 0.229 | 0.133 | 0.061 | 0.084 | 0.158 | ||
| Binary | 0.071 | 0.447 | 0.110 | 0.079 | 0.233 | 0.126 | ||
| 10 | iid | 0.555 | 2.050 | 0.589 | 0.162 | 0.716 | 0.740 | |
| Correlated | 0.025 | 0.089 | 0.032 | 0.017 | 0.036 | 0.059 | ||
| Binary | 0.023 | 0.072 | 0.025 | 0.024 | 0.027 | 0.027 | ||
| 15 | iid* | 0.930 | 4.340 | 0.980 | 0.807 | 1.850 | 1.510 | |
| Correlated | 0.016 | 0.075 | 0.041 | 0.028 | 0.030 | 0.027 | ||
| Binary | 0.049 | 0.120 | 0.034 | 0.034 | 0.042 | 0.028 | ||
| 20 | iid | 0.021 | 0.093 | 0.026 | 0.040 | 0.033 | 0.028 | |
| Correlated | 0.041 | 0.200 | 0.087 | 0.017 | 0.094 | 0.058 | ||
| Binary | 0.114 | 1.330 | 0.334 | 0.220 | 0.530 | 0.360 | ||
| Std errors | se0 | se1 | se2 | se3 | se4 | se5 | ||
| 5 | iid | 0.017 | 0.069 | 0.020 | 0.023 | 0.031 | 0.024 | |
| Correlated | 0.015 | 0.057 | 0.035 | 0.018 | 0.020 | 0.037 | ||
| Binary | 0.032 | 0.206 | 0.029 | 0.019 | 0.107 | 0.032 | ||
| 10 | iid | 0.376 | 1.504 | 0.429 | 0.142 | 0.524 | 0.533 | |
| Correlated | 0.006 | 0.019 | 0.007 | 0.005 | 0.007 | 0.015 | ||
| Binary | 0.004 | 0.017 | 0.004 | 0.004 | 0.005 | 0.005 | ||
| 15 | iid* | 1.548 | 8.500 | 1.960 | 1.577 | 2.860 | 1.790 | |
| Correlated | 0.002 | 0.018 | 0.005 | 0.003 | 0.005 | 0.004 | ||
| Binary | 0.005 | 0.009 | 0.003 | 0.002 | 0.004 | 0.003 | ||
| 20 | iid | 0.005 | 0.025 | 0.006 | 0.002 | 0.009 | 0.008 | |
| Correlated | 0.009 | 0.052 | 0.023 | 0.005 | 0.026 | 0.019 | ||
| Binary | 0.073 | 1.239 | 0.301 | 0.205 | 0.514 | 0.340 | ||
Replicates in which complete or quasi-complete separation was detected in SAS were excluded. This occurred in less than 2.5% of replicates for all but the dataset with 15 iid covariates, in which separation was detected in 16.6% of replicates.
iid, independent identically distributed.
Cases where complete or quasi-complete separation was detected were excluded from the results in table 3, because of potential differences in stopping criteria. Complete separation occurs when a linear combination of the data produces perfect predictions, with some observations always having a probability of one and others always having a probability of zero (ie, there exists a vector b such that Xib<0 when yi = 0, and Xib>0 when yi = 1, for all observations i); quasi-complete separation occurs when a linear combination of the data produces perfect predictions for some observations and uncertainty otherwise (ie, there exists a vector b such that Xib≤0 when yi = 0, and Xib≥0 when yi = 1, and at least one case of equality in both). Parameter estimates are infinite if the design matrix is completely or quasi-completely separable, which leads to convergence failures. Formal details are given by Albert and Anderson,115 and a more applied presentation is given by Allison.116
This type of convergence failure is common in logistic regression, and occurred in less than 2.5% of replicates for all but the dataset with 15 iid covariates, which suffered complete or quasi-complete separation in 16.6% of replicates (according to the detection criteria in SAS, as described by Allison116). We did not modify the latter replicates because variables were created and sampled using random draws, making such convergence failures difficult to eliminate in advance. Also, the original dataset was only one of our 12 test cases.
Absolute differences between SPARK and SAS estimates in table 3 that exceeded 10e-6 were most likely due to undetected quasi-complete separation. On inspection we found that replicates where this occurred had parameter estimates that were multiple times their simulated values. Therefore relative differences between SPARK and SAS were even more accurate than suggested by the absolute differences reported.
Discussion
To ensure sufficient statistical power and population heterogeneity in the detection of ADEs, data from multiple sites need to be combined. A simple pooling of such horizontally partitioned data presents serious privacy concerns. Our review of the literature found that existing architectures and methods for analyzing horizontally partitioned data would allow the disclosure of PHI under a variety of conditions. For the specific problem of detecting ADEs, we have developed a secure distributed logistic regression protocol which addresses known weaknesses of previous protocols and ensures that PHI cannot be disclosed. The detailed security analysis in the online appendix demonstrates that sites that follow the protocol cannot access raw data from other sites and presents low risk from plausible collusion scenarios. Our empirical evaluation of the protocol has demonstrated that its computational performance would be acceptable for large datasets and for multiple sites, and that its accuracy (in terms of model parameters and diagnostics) is equivalent to the values that one would obtain from an analysis using SAS on the pooled raw data.
This protocol should allow sites to contribute their patient data to multi-site analyses of ADEs with assurances that their patients' personal information will not be disclosed or inferred, but still allow the appropriate multi-site analytical models to be constructed. Because one of the key privacy concerns would be addressed, the SPARK protocol should allow analyses to commence faster and with less need for negotiating complex data-sharing agreements on PHI with each site (which can be a time-consuming process, especially if it involves data crossing jurisdictional boundaries).
Compared with other protocols that do not implement secure computation (and hence do not provide the same level of assurances), SPARK will have more communication overhead. Therefore its overall performance will also be a function of this communication overhead, which will be dependent on network latency among the sites. Details on the number of messages passed in the SPARK protocol are provided in the complexity analysis in the online appendix. In general, communications can be optimized through pipelining the data flow rather than communicating in bursts and by sending multiple messages together.
A multi-site analysis requires that all of the datasets are standardized, for example, by ensuring that coding schemes for nominal or categorical variables are consistent. This standardization effort would be required whether data are pooled for analysis or a distributed analysis is used, however.
While our primary use case has been the detection of ADEs from data distributed across multiple sites, the SPARK protocol can be used for other types of situations where the datasets are distributed, such as genetic association studies. The main drivers for using SPARK would be the need to expand the dataset that a model is built upon to increase statistical power and enhance population heterogeneity, and to deal with privacy concerns in an expeditious manner that would still ensure accurate model results.
Extensions to GEEs
In practice, one would expect that there would be stronger correlations among the patients at a particular site than other sites. For example, there may be treatment, lifestyle, or environmental factors at one site that do not exist at other sites, leading to site-specific effects on the probability of an ADE. This kind of correlation can be accounted for by constructing GEEs. In the online appendix, we provide a description of GEEs and extend the SPARK protocol to implement GEEs for logistic regression.
Extensions to other GLMs
The basic protocol we have presented here can be extended to other GLMs.94 The link functions for other GLMs are simpler than the logit function, as illustrated in table 4. Secure computation of the link functions could be applied using the building blocks in this paper. In the Poisson log function, for example, we only need to compute the exponent of the product of regression vector and design matrix, which we already have in our protocol.
Table 4.
Examples of link functions
| Name | Function |
|---|---|
| Identity | μ |
| Reciprocal | 1/μ |
| Reciprocal squared | 1/μ2 |
| Square root | 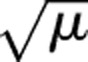 |
| Log | ln (μ) |
| Complementary log-log | ln (−ln (μ)) |
| Logit | ln (μ/(1−μ)) |
Survival models
To model adverse events, another common modeling technique is a time-to-event or Cox model. Time-to-event survival models can be used to investigate hospitalization, infection, or death. Survival analysis methods provide hazard rates and consider various types of censoring, such as withdrawal from the study, death from other causes, or loss to follow-up. Proportional hazards models, in particular, are one of the most commonly used methods in health research, and are a form of ordinal model using the complementary log-log link function on Bernoulli data.94 Therefore our extension of the secure protocol to GLMs can include this form of survival modeling.
General limitations on remote analysis systems
A full implementation of the SPARK protocol would need to address some of the concerns that exist with remote analysis systems in general. In particular, if one considers the normal equations, X'Xb=X'y, the left-hand system of equations has k(k+1)/2 unknowns, and the right-hand system of equations has k unknowns. One could therefore fit k(k+1)/2+k sub models to determine these unknowns. This does not require the exposure of the information matrix and can occur with the model results only. To address concerns from the use of sub-models, it is necessary to monitor the number of sub-models that are created and limit their use accordingly.
An adversary may attempt to circumvent limits on the number of sub-models by running multiple sub-models on highly correlated outcomes. However, the uncertainty introduced from using a different outcome may be enough to ensure the data are not recoverable. Alternatively, the protocol may instead use a different sub-sample of observations when building sub-models. This is the preferred method discussed in Sparks et al,68 although further investigation may be required to determine appropriate bounds on the desired level of uncertainty.
Other disclosure risks associated with allowing an analyst to manipulate models through a remote analysis system can be mitigated through a variety of means68 such as: variable transformations would be limited to the most common (eg, log, square root, etc), transformations of factors would not be allowed, sparse factors or interactions would not be allowed, estimates would be rounded, and samples would be used.
Supplementary Material
Footnotes
Contributors: KEE designed the study, contributed to the literature review, participated in interpreting the results, and contributed to writing the paper. SS designed the study, contributed to the literature review, participated in interpreting the results, and contributed to writing the paper. LA designed the study, contributed to the literature review, participated in interpreting the results, and contributed to writing the paper. RT defined the use case, contributed to the literature review, participated in interpreting the results, and contributed to writing the paper. CE defined the use case, participated in interpreting the results, and contributed to writing the paper. MK designed the study, participated in interpreting the results, and contributed to writing the paper.
Funding: This work was supported by the Canada Research Chairs program, the Ontario Institute for Cancer Research, the Canadian Institutes of Health Research, National Institutes of Health Grant 1R01LM009989, National Science Foundation (NSF) Grant Career-CNS-0845803, and NSF Grants CNS-0964350 and CNS-1016343.
Competing interests: None.
Provenance and peer review: Not commissioned; externally peer reviewed.
Open Access: This is an Open Access article distributed in accordance with the Creative Commons Attribution Non Commercial (CC BY-NC 3.0) license, which permits others to distribute, remix, adapt, build upon this work non-commercially, and license their derivative works on different terms, provided the original work is properly cited and the use is non-commercial. See: http://creativecommons.org/licenses/by-nc/3.0/
References
- 1.Hoffman J, Doloresco F, Vermeulen L, et al. Projecting future drug expenditures. Am J Health Syst Pharm 2010;67:919–28 [DOI] [PubMed] [Google Scholar]
- 2.Couzin J. Gaps in the safety Net. Science 2005;307:196–8 [DOI] [PubMed] [Google Scholar]
- 3.Weaver J, Willy M, Avigan M. Informatic tools and approaches in postmarketing pharmacovigilance used by FDA. AAPS J 2008;10:35–41 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gough S. Post-marketing surveillance: a UK/European perspective. Curr Med Res Opin 2005;21:565–70 [DOI] [PubMed] [Google Scholar]
- 5.Budnitz D, Pollock D, Weidenbach K, et al. National surveillance of emergency department visits for outpatient adverse drug events. JAMA 2006;296: 1858–66 [DOI] [PubMed] [Google Scholar]
- 6.Platt R, Wilson M, Chan K, et al. The new Sentinel Network–improving the evidence of medical-product safety. N Engl J Med 2009;361:645–7 [DOI] [PubMed] [Google Scholar]
- 7.Morgan S, McMahon M, Lam J, et al. The Canadian Rx Atlas. Vancouver: Centre for Health Services and Policy Research, 2005 [Google Scholar]
- 8.Lasser K, Seger D, Yu D, et al. Adherence to black box warnings for prescription medications in outpatients. Arch Intern Med 2006;166:338–44 [DOI] [PubMed] [Google Scholar]
- 9.Ray W, Stein C. Reform of drug regulation–beyond an independent drug-safety board. N Engl J Med 2006;354:194–201 [DOI] [PubMed] [Google Scholar]
- 10.Waxman H. The lessons of Vioxx–drug safety and sales. N Engl J Med 2005;352:2576–8 [DOI] [PubMed] [Google Scholar]
- 11.Wiholm B, Olsson S, Moore N, et al. Spontaneous Reporting Systems outside the US, in Pharmacoepidemiology.Strom B, ed. 3rd edn Chichester: Wiley, 2000:175–92 [Google Scholar]
- 12.Friedman MA, Woodcock J, Lumpkin MM, et al. The safety of newly approved medicines: do recent market removals mean there is a problem? JAMA 1999;281:1728–34 [DOI] [PubMed] [Google Scholar]
- 13.Rawlins M, Jefferys D. Study of United Kingdom product licence applications containing new active substances, 1987–9. BMJ 1991;302:223–5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Radley D, Finkelstein S, Stafford R. Off-label prescribing among office-based physicians. Arch Intern Med 2006;166:1021–6 [DOI] [PubMed] [Google Scholar]
- 15.Strom B, Melmon K, Miettinen O. Post-marketing studies of drug efficacy: why? Am J Med 1985;78:475–80 [DOI] [PubMed] [Google Scholar]
- 16.Blum M, Graham D, McCloskey C. Temafloxacin syndrome: review of 95 cases. Clin Infect Dis 1994;18:946–50 [DOI] [PubMed] [Google Scholar]
- 17.Carleton B. Active surveillance systems for pediatric adverse drug reactions: an idea whose time has come. Curr Ther Res 2001;62:738–42 [Google Scholar]
- 18.Kennedy D, Goldman S, Lillie R. Spontaneous Reporting Systems in the US, in Pharmacoepidemiology.Storm BL, ed. 3rd edn Chichester: Wiley, 2000: 151–74 [Google Scholar]
- 19.Fletcher A. Spontaneous adverse drug reaction reporting vs event monitoring: a comparison. J R Soc Med 1991;84:341–4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Basch E. The missing voice of patients in drug-safety reporting. N Engl J Med 2010;362:865–9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Grady D. In Reporting symptoms, Don't patients Know Best? New York times. 2010 [Google Scholar]
- 22.Tamblyn R, Abrahamowicz M, Dauphinee D, et al. Influence of physicians' management and communication ability on patients' persistence with antihypertensive medication. Arch Intern Med 2010;170:1064–72 [DOI] [PubMed] [Google Scholar]
- 23.Mann R. Prescription-event Monitoring, in Pharmacoepidemiology. In: Strom B, ed. 3rd edn Chichester: Wiley, 2000:231–46 [Google Scholar]
- 24.Key C, Layton D, Shakir S. Results of a postal survey of the reasons for non-response by doctors in a Prescription Event Monitoring study of drug safety. Pharmacoepidemiol Drug Saf 2002;11:143–8 [DOI] [PubMed] [Google Scholar]
- 25.Martin R, Biswas P, Mann R. The incidence of adverse events and risk factors for upper gastrointestinal disorders associated with meloxicam use amongst 19,087 patients in general practice in England: cohort study. Br J Clin Pharmacol 2000;50:35–42 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.MacDougall L, Majowicz S, Dore K, et al. Under-reporting of infectious gastrointestinal illness in British Columbia, Canada: who is counted in provincial communicable disease statistics? Epidemiol Infect 2008;136:248–56 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.El Emam K, Mercer J, Moreau K, et al. Physician privacy concerns when disclosing patient data for public health Purposes during a pandemic influenza Outbreak. BMC Public Health 2011;11:454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Effler P, Ching-Lee M, Bogard A, et al. Statewide system of electronic notifiable diseases reporting from clinical laboratories. JAMA 1999;282:1845–50 [DOI] [PubMed] [Google Scholar]
- 29.Mandl K, Overhage J, Wagner M, et al. Implementing syndromic surveillance: a practical guide informed by the early experience. J Am Med Inform Assoc 2004;11:141–50 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Muscatello D, Churches T, Kaldor J, et al. An automated, broad-based, near real-time public health surveillance system using presentations to hospital Emergency Departments in New South Wales, Australia. BMC Public Health 2005;5:141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Overhage J, Grannis S, McDonald C. A comparison of the completeness and timeliness of automated electronic laboratory reporting and spontaneous reporting of notifiable conditions. Am J Public Health 2008;98:344–50 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Carleton B, Foerster V, Warren L, et al. Post-marketing Pharmacosurveillance In Canada. Ottawa, ON: Health Canada, 2005 [Google Scholar]
- 33.Kozyrskyj A, Mustard C. Validation of an electronic, population-based prescription database. Ann Pharmacother 1998;32:1152–7 [DOI] [PubMed] [Google Scholar]
- 34.Levy A, O'Brien B, Sellors C, et al. Coding accuracy of administrative drug claims in the Ontario Drug Benefit database. Can J Clin Pharmacol 2003;10:67–71 [PubMed] [Google Scholar]
- 35.Tamblyn R, Lavoie G, Petrella L, et al. The use of prescription claims databases in pharmacoepidemiological research: the accuracy and comprehensiveness of the prescription claims database in Quebec. J Clin Epidemiol, 1995;48:999–1009 [DOI] [PubMed] [Google Scholar]
- 36.Wilchesky M, Tamblyn R, Huang A. Validation of diagnostic codes within medical services claims. J Clin Epidemiol 2004;57:131–41 [DOI] [PubMed] [Google Scholar]
- 37.Ray W, Griffin M, Downey W, et al. Long-term use of thiazide diuretics and risk of hip fracture. Lancet 1989;1:687–90 [DOI] [PubMed] [Google Scholar]
- 38.Guess H, West R, Strand L, et al. Fatal upper gastrointestinal hemorrhage or perforation among users and nonusers of nonsteroidal anti-inflammatory drugs in Saskatchewan, Canada 1983. J Clin Epidemiol 1988;41:35–45 [DOI] [PubMed] [Google Scholar]
- 39.Park-Wyllie L, Juurlink D, Kopp A, et al. Outpatient gatifloxacin therapy and dysglycemia in older adults. N Engl J Med 2006;354:1352–61 [DOI] [PubMed] [Google Scholar]
- 40.Spitzer WO, Suissa S, Ernst P, et al. The use of beta-agonists and the risk of death and near death from asthma. N Engl J Med 1992;326:501–6 [DOI] [PubMed] [Google Scholar]
- 41.Paterson J, Laupacis A, Bassett K, et al. Using pharmacoepidemiology to inform drug coverage policy: initial lessons from a two-province collaborative. Health Aff (Millwood) 2006;25:1436–43 [DOI] [PubMed] [Google Scholar]
- 42.Schoen C, Osborn R, Doty M, et al. A survey of primary care physicians in eleven countries, 2009: perspectives on care, costs, and experiences. Health Aff (Millwood) 2009;28:w1171–83 [DOI] [PubMed] [Google Scholar]
- 43.Jha A, Doolan D, Grandt D, et al. The use of health information technology in seven nations. Int J Med Inform 2008;77:848–54 [DOI] [PubMed] [Google Scholar]
- 44.Schoen C, Osborn R, Huynh P, et al. On the front lines of care: primary care doctors' office systems, experiences, and views in seven countries. Health Aff (Millwood) 2006;25:w555–71 [DOI] [PubMed] [Google Scholar]
- 45.Eggertson L. Canada lags US in adoption of e-prescribing. CMAJ 2009;180:E25–6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Kaye J, del Mar Melero-Montes M, Jick H. Mumps, measles, and rubella vaccine and the incidence of autism recorded by general practitioners: a time trend analysis. BMJ 2001;322:460–3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Hippisley-Cox J, Coupland C. Unintended effects of statins in men and women in England and Wales: population based cohort study using the QResearch database. BMJ 2010;340:c2197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Gottlieb S. Opening Pandora's pillbox: using modern information tools to improve drug safety. Health Aff (Millwood) 2005;24:938–48 [DOI] [PubMed] [Google Scholar]
- 49.Nichols G, Conner C, Brown J. Initial nonadherence, primary failure and therapeutic success of metformin monotherapy in clinical practice. Curr Med Res Opin 2010;26:2127–35 [DOI] [PubMed] [Google Scholar]
- 50.Hershman D, Kushi L, Shao T, et al. Early discontinuation and nonadherence to adjuvant hormonal therapy in a cohort of 8,769 early-stage breast cancer patients. J Clin Oncol 2010;28:4120–8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Kim H, Zivin K, Ganoczy D, et al. Predictors of alternative antidepressant agent initiation among U. S. veterans diagnosed with depression. Pharmacoepidemiol Drug Saf 2010;19:1049–56 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Mikuls T, Fay B, Michaud K, et al. Associations of disease activity and treatments with mortality in men with rheumatoid arthritis: results from the VARA registry. Rheumatology 2010;50:101–9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Hoffman C, Rice D, Sung H. Persons with chronic conditions. Their prevalence and costs. JAMA 1996;276:1473–9 [PubMed] [Google Scholar]
- 54.Bansard C, Lequerre T, Daveau M, et al. Can rheumatoid arthritis responsiveness to methotrexate and biologics be predicted? Rheumatology (Oxford) 2009;48:1021–8 [DOI] [PubMed] [Google Scholar]
- 55.Hippisley-Cox J, Coupland C. Individualising the risks of statins in men and women in England and Wales: population-based cohort study. Heart 2010;96:939–47 [DOI] [PubMed] [Google Scholar]
- 56.Evans W, Relling M. Pharmacogenomics: translating functional genomics into rational therapeutics. Science 1999;286:487–91 [DOI] [PubMed] [Google Scholar]
- 57.Malhotra A, Murphy GJ, Kennedy J. Pharmacogenetics of psychotropic drug response. Am J Psychiatry 2004;161:780–96 [DOI] [PubMed] [Google Scholar]
- 58.Moore K, Duddy A, Braun M, et al. Potential population-based electronic data sources for rapid pandemic influenza vaccine adverse event detection: a survey of health plans. Pharmacoepidemiol Drug Saf 2008;17:1137–41 [DOI] [PubMed] [Google Scholar]
- 59.Rosati K. Using electronic health information for pharmacovigilance: the promise and the pitfalls. J Health Life Sci Law 2009;2:171–239 [PubMed] [Google Scholar]
- 60.Coloma P, Schuemie M, Trifiro G, et al. Combining electronic healthcare databases in Europe to allow for large-scale drug safety monitoring: the EU-ADR project. Pharmacoepidemiol Drug Saf 2011;20:1–11 [DOI] [PubMed] [Google Scholar]
- 61.Velentgas P, Bohn R, Brown J, et al. A distributed research network model for post-marketing safety studies: the Meningococcal Vaccine Study. Pharmacoepidemiol Drug Saf 2008;17:1226–34 [DOI] [PubMed] [Google Scholar]
- 62.Magid D, Gurwitz J, Rumsfeld J, et al. Creating a research data network for cardiovascular disease: the CVRN. Expert Rev Cardiovasc Ther 2008;6:1043–5 [DOI] [PubMed] [Google Scholar]
- 63.Lambert PC, Sutton AJ, Abrams KR, et al. A comparison of Summary patient-level covariates in meta-regression with individual patient data meta-analysis. J Clin Epidemiol 2002;55:86–94 [DOI] [PubMed] [Google Scholar]
- 64.Rassen J, Avorn J, Schneeweiss S. Multivariate-adjusted pharmacoepidemiologic analyses of confidential information pooled from multiple health care utilization databases. Pharmacoepidemiol Drug Saf 2010;19:848–57 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Rassen J, Solomon D, Curtis J, et al. Privacy-maintaining propensity score-based pooling of multiple databases applied to a study of biologics. Med Care 2010;48(6 Suppl):S83–9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Du W, Han Y, Chen S. Privacy-Preserving Multivariate Statistical Analysis: Linear Regression and Classification. Proceedings of the Fourth SIAM International Conference on Data Mining. Philidelphia, PA: Society for Industrial and Applied Mathematics, 2004:222–33 [Google Scholar]
- 67.Wolfson M, Wallace S, Masca N, et al. DataSHIELD: resolving a conflict in contemporary bioscience—performing a pooled analysis of individual-level data without sharing the data. Int J Epidemiol 2010;39:1372–82 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Sparks R, Carter C, Donnelly J, et al. Remote access methods for exploratory data analysis and statistical modelling: privacy-preserving analytics. Comput Methods Programs Biomed 2008;91:208–22 [DOI] [PubMed] [Google Scholar]
- 69.Reiter J. New approaches to data dissemination: a glimpse into the future. Chance 2004;17:12–16 [Google Scholar]
- 70.Reiter J, Kohnen C. Categorical data regression diagnostics for remote access servers. J Stat Comput Simulation 2005;75:889–903 [Google Scholar]
- 71.O'Keefe C, Good N. Regression Output from a remote Server. Data Knowledge Eng 2009;68:1175–86 [Google Scholar]
- 72.Fienberg S, Nardi Y, Slavković A. Valid Statistical Analysis for Logistic Regression with Multiple Sources. In: Cecilia G, Kantor P, Lesk M, eds. Protecting Persons while Protecting the People. Berlin: Springer-Verlag, 2009:82–94 [Google Scholar]
- 73.Karr A, Lin X, Sanil A, et al. Analysis of integrated data without data integration. Chance 2004;17:27–30 [Google Scholar]
- 74.Karr A, Feng J, Lin X, et al. Secure analysis of distributed chemical databases without data integration. J Comput Aided Mol Des 2005;19:739–47 [DOI] [PubMed] [Google Scholar]
- 75.Fienberg SE, Fulp WJ, Slavkovic AB, et al. “Secure” Log-linear and Logistic Regression Analysis of Distributed Databases. PSD 2006.Domingo-Ferrer J, Franconi L, ed. Heidelberg: Springer, 2006:277–90 [Google Scholar]
- 76.Karr AF, Fulp WJ, Vera F, et al. Secure, privacy-preserving analysis of distributed databases. Technometrics 2007;49:335–45 [Google Scholar]
- 77.Karr AF. Secure statistical analysis of distributed databases, emphasizing what we don't know. J Privacy Confidentiality 2009;1:197–211 [Google Scholar]
- 78.Brown J, Holmes J, Shah K, et al. Distributed health networks: a practical and preferred approach to multi-institutional evaluations of comparative effectiveness, safety, and quality of care. 2010;48(6 Suppl 1):S45–51 [DOI] [PubMed] [Google Scholar]
- 79.Behrman R, Benner J, Brown J, et al. Developing the sentinel system: a national resource for evidence development. N Engl J Med 2011;364:498–9 [DOI] [PubMed] [Google Scholar]
- 80.Platt R, Wilson M, Chan K, et al. The new sentinel network: improving the evidence of medical-product safety. N Engl J Med 2009;361:645–7 [DOI] [PubMed] [Google Scholar]
- 81.Platt R, Davis R, Finkelstein J, et al. Multicenter epidemiologic and health services research on therapeutics in the HMO Research Network Center for Education and Research on Therapeutics. Pharmacoepidemiol Drug Saf 2001;10:373–7 [DOI] [PubMed] [Google Scholar]
- 82.Adam N, Wortman J. Security-control methods for statistical databases: a comparative study. ACM Comput Surv 1989;21:515–56 [Google Scholar]
- 83.Muralidhar K, Sarathy R. Privacy Violations in Accountability Data Released to the Public by State Educational Agencies. Federal Committee on Statistical Methodology Research Conference. Washington, DC: Federal Committee on Statistical Methodology, 2009 [Google Scholar]
- 84.Algranati D, Kadane J. Extracting confidential information from public documents: the 2000 department of justice report on the federal use of the death penalty in the United States. J Official Stat 2004;20:97–113 [Google Scholar]
- 85.Chin F. Security problems on inference control for SUM, MAX, and MIN queries. ACM 1986;33:451–64 [Google Scholar]
- 86.Chin FY, GZSOYO∼LU G. Auditing and inference control in statistical databases. IEEE Trans Softw Eng 1982;8:574–82 [Google Scholar]
- 87.Denning DE, Denning PJ, Schwartz MD. The tracker: a threat to statistical database security. ACM Trans on Database Syst (TODS) 1979;4:76–96 [Google Scholar]
- 88.Domingo-Ferrer J. Inference Control in Statistical Databases: From Theory to Practice. Lecture Notes in Computer Science, Vol 2316. Berlin: Springer-Verlag, 2002 [Google Scholar]
- 89.Marcum ZA, Amuan ME, Hanlon JT, et al. Prevalence of unplanned hospitalizations caused by adverse drug reactions in older veterans. J Am Geriatr Soc 2012;60:34–41 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Gibbons RD, Amatya AK, Brown CH, et al. Post-approval drug safety surveillance. Annu Rev Public Health 2010;31:419–37 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Shepherd G, Mohorn P, Yacoub K, et al. Adverse drug reaction deaths reported in United States vital statistics, 1999–2006. Ann Pharmacother 2012;46: 169–75 [DOI] [PubMed] [Google Scholar]
- 92.Seynaeve S, Verbrugghe W, Claes B, et al. Adverse drug events in intensive care units: a cross-sectional study of prevalence and risk factors. Am J Crit Care 2011;20:e131–40 [DOI] [PubMed] [Google Scholar]
- 93.Forster AJ, Murff HJ, Peterson JF, et al. Adverse drug events occurring following hospital discharge. J Gen Intern Med 2005;20:317–23 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Agresti A. Categorical Data Analysis. 2nd edn New York: Wiley, 2002 [Google Scholar]
- 95.Agresti A. Categorical Data Analysis. Wiley Series in Probability and Statistics. Hoboken, New Jersey: Wiley, 2002 [Google Scholar]
- 96.Aman Goel JJ. Comparing Various Optimization Algorithms for Binary Logistic Regression. Machine Learning Course Project Paper. Los Angeles: University of Southern California, 2010:5 [Google Scholar]
- 97.Paillier P. Public-Key Cryptosystems Based on Composite Degree Residuosity Classes. The International Conference on the Theory and Application of Cryptographic Techniques (EUROCRYPT). Prague, Czech Republic: International Association for Cryptologic Research, 1999:223–38 [Google Scholar]
- 98.Goethals B, Laur S, Lipmaa H, et al. On Private Scalar Product Computation for Privacy-Preserving Data Mining. Lecture Notes in Computer Science, Vol. 3506. Berlin: Springer-Verlag, 2004:104–20 [Google Scholar]
- 99.Samet S, Miri A. Privacy-Preserving Bayesian Network for Horizontally Partitioned Data. The 2009 IEEE International Conference on Information Privacy, Security, Risk and Trust (PASSAT2009). Los Alamitos, CA: IEEE Computer Society's Conference Publishing Services, 2009:9–16 [Google Scholar]
- 100.Han S, Ng WK, Yu PS. Privacy-preserving Linear Fisher Discriminant Analysis. The 12th Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining. Osaka, Japan: Springer-Verlag, 2008:136–47 [Google Scholar]
- 101.Hosmer DW, Lemshow S. Goodness of fit tests for the multiple logistic regression model. Comm Stat Theory Methods 1980;9:1043–69 [Google Scholar]
- 102.Geladi P, Kowalski BR. Partial least-squares regression: a tutorial. Analytica Chim Acta 1986;185:1–17 [Google Scholar]
- 103.Rosner B, Willett WC, Speigelman D. Correction of logistic regression relative risk estimates and confidence intervals for systematic within-person measurement error. Stat Med 1989;8:1051–69 [DOI] [PubMed] [Google Scholar]
- 104.Gaudart J, Giusiano B, Huiart L. Comparison of the performance of multi-layer perceptron and linear regression for epidemiological data. Comput Stat Data Anal 2004;44:547–70 [Google Scholar]
- 105.Heinze G, Schemper M. A solution to the problem of separation in logistic regression. Stat Med 2002;21:2409–19 [DOI] [PubMed] [Google Scholar]
- 106.Bagley SC, White H, Golomb BA. Logistic regression in the medical literature: standards for use and reporting, with particular attention to one medical domain. J Clin Epidemiol 2001;54:979–85 [DOI] [PubMed] [Google Scholar]
- 107.Mallett S, Royston P, Dutton S, et al. Reporting methods in studies developing prognostic models in cancer: a review. BMC Med 2010;8:1–11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Harrell F. Regression Modeling Strategies. New York: Springer, 2001 [Google Scholar]
- 109.Iman R, Conover W. A distribution-free approach to inducing rank correlation among input variables. Commun Stat Simulation Comput 1982;11: 311–34 [Google Scholar]
- 110.Kleinman K, Horton N. Using SAS for Data Management, Statistical analysis, and Graphics. Boca Raton, FL: CRC Press, 2010 [Google Scholar]
- 111.King G, Zeng L. Logistic regression in rare events data. Polit Anal 2001;9:137–63 [Google Scholar]
- 112.Lowe W. Rare Events Research, in Encyclopedia of Social Measurement.Kempf-Leonard K, ed. Cambridge: Academic Press, 2004:293–7 [Google Scholar]
- 113.Ruiz-Gazen A, Villa N. Storms prediction: logistic regression vs. random forests for unbalanced data. Case Studies in Business, Industry and Government Statistics. 2007;1:91–101 [Google Scholar]
- 114.Scott A, Wild C. Fitting logistic models under case-control or choice based sampling. J R Stat Soc 1986;48:170–82 [Google Scholar]
- 115.Albert A, Anderson J. On the existence of maximum likelihood estimates in logistic regression models. Biometrika 1984;71:1–10 [Google Scholar]
- 116.Allison P. Convergence failures in logistic regression. SAS Global Forum. 2008 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.