Energies of Low-Lying Excited States of Linear Polyenes

Abstract

Room temperature absorption and emission spectra of the all-trans isomers of decatetraene, dodecapentaene, tetradecahexaene, and hexadecaheptaene have been obtained in a series of nonpolar solvents. The resolved vibronic features in the optical spectra of these model systems allow the accurate determination of S₀ (1¹A_g^-) → S₂ (1¹B_u⁺) and S₁ (2¹A_g^–) → S₀ (1¹A_g^–) electronic origins as a function of solvent polarizability. These data can be extrapolated to predict the transition energies in the absence of solvent perturbations. The effects of the terminal methyl substituents on the transition energies also can be estimated. Franck–Condon maxima in the absorption and emission spectra were used to estimate differences between S₀ (1¹A_g^–) → S₁ (2¹A_g^–) and S₀ (1¹A_g^–) → S₂ (1¹B_u⁺) electronic origins and “vertical” transition energies. Experimental estimates of the vertical transition energies of unsubstituted, all-trans polyenes in vacuum as a function of conjugation length are compared with long-standing multireference configuration interaction (MRCI) treatments and with more recent ab initio calculations of the energies of the 2¹A_g^– (S₂) and 1¹B_u⁺ (S₂) states.

Introduction

The original report in 1972 of the discovery of a low-lying S₁ (2¹A_g^–) state in diphenyloctatetraene by Hudson and Kohler¹ was accompanied by a theoretical paper by Schulten and Karplus,² which demonstrated that extensive configuration interaction was required to account for the low energy of the S₁ (2¹A_g^–) state. Subsequent experimental efforts confirmed that E(2¹A_g^–) < E(1¹B_u⁺) for all linear polyenes with N ≥ 4, where N is the number of π-electron conjugated double bonds. A wealth of experimental data now is available on the energies and dynamics of these two low-lying states in simple polyenes, in naturally occurring carotenoids with N as high as 13,^3–12 and in synthetic carotenoids with N > 13.¹³ The presence of the low-energy 2¹A_g^– state has had a profound influence in shaping discussions of the photophysics and photochemistry of one-dimensional, π-conjugated molecules, including the role of the S₁ (2¹A_g^–) state in transferring energy from carotenoids to chlorophylls in photosynthetic systems.^3,6,14–18

Efforts to expand and improve on the original theoretical analysis of Schulten and Karplus² and the subsequent improvements by Tavan and Schulten^19–21 have been hampered by the mathematical complexity required to carry out appropriate ab initio analyses of these highly correlated, many-electron systems. The key issues involved, including the problems in developing accurate parametrizations for semiempirical approaches, have been outlined in recent publications by Nakayama et al.,²² Head-Gordon et al.,²³ Serrano-Andres et al.,²⁴ Dreuw et al.,²⁵ and Marion and Gilka,²⁶ who have calculated the S₁ (2¹A_g^–) and S₂ (1¹B_u⁺) energies of simple, unsubstituted polyenes. These calculations confirm the proper state ordering, but the quantitative details show considerable variation. A useful benchmark in comparing theory with experiment is the dependence of the E(S₂ (1¹B_u⁺)) – E(S₁ (2¹A_g^–)) energy gap on conjugation length. This not only provides an important test of theory, but also is an important parameter in understanding the photophysics of polyene systems.

One of the barriers in comparing theory with the growing body of experimental data on both short and long polyenes and carotenoids is the lack of a clear understanding of how substituents and solvent environments modify the energetics and dynamics of these systems. Another significant problem is the distinction between the electronic origins ((0–0) bands) of spectral transitions, precisely determined from the absorption and emission spectra of simple polyenes, and the “vertical” transition energies typically calculated by theory. This paper approaches these issues systematically: by using models for chromophore/solute interactions to extrapolate (0–0) transition energies to solvent-free conditions, by correcting for the modification of electronic energies by the terminal methyl substituents, and by analyzing Franck–Condon vibronic envelopes to estimate the energy differences between electronic origins and the vertical transitions obtained from theory. These corrections to the experimental data allow direct comparisons with theoretical predictions of the electronic energies of simple, unsubstituted polyenes in the absence of solvents.

We focus on the room temperature absorption and emission spectra of the all-trans dimethylpolyenes given in Figure 1. This series provides several significant advantages: these molecules are relatively easily synthesized from shorter polyene aldehydes using Wittig reactions, the terminal methyl groups impart considerable stability to these systems, which allows for purification and identification of the symmetric (C_2h) all-trans isomers, and the room temperature absorption and emission spectra have sufficient vibronic resolution to allow the accurate measurement of (0–0) transition energies in a range of nonpolar solvents. Dimethyl polyenes with N = 4–7 also have adequate fluorescence yields to allow the detection of S₁ (2¹A_g^–) → S₀ (1¹A_g^–) emission spectra in room temperature solutions. In addition, previous detailed, high-resolution investigations of the absorption and fluorescence of these systems in low-temperature mixed crystals,²⁷ in the gas phase,²⁸ and in supersonic jets²⁹ provide a substantial background of information, which facilitates the analysis and understanding of the less-resolved room solution temperature spectra presented here.

Figure 1.

Structures of all-trans-dimethylpolyenes. N = number of π-conjugated carbon–carbon double bonds.

Materials and Methods

Synthesis and Purification of All-Trans Polyenes

2,4,6,8-Decatetraene, 2,4,6,8,10-dodecapentaene, 2,4,6,8,10,12-tetradecahexaene, and 2,4,6,8,10,12,14-hexadecaheptaene were synthesized from all-trans polyene aldehydes via Wittig reactions as previously described.^30,31 These reactions tend to favor the formation of cis polyenes.³² Therefore, prior to purification by reverse-phase high-performance liquid chromatography (HPLC), the samples were photoisomerized to produce mixtures dominated by all-trans isomers. The crude reaction products initially were purified on a silica gel column (Silica Gel 60, EM Reagents) with hexane as the mobile phase. The hexane solutions were evaporated to dryness, redissolved in HPLC grade acetonitrile, and placed in a 1-cm path length cuvette. The reconstituted samples then were exposed to 311, 342, 372, and 396 nm light respectively for N = 4–7, using a 450 W xenon arc lamp directed through the double grating excitation monochromator of a Jobin-Yvon Horiba Fluorolog-3 fluorescence spectrophotometer. Samples were mixed during illumination and the progress of the photoisomerization monitored by absorption spectroscopy and HPLC. Typical illumination times were 30 min for samples with absorbances of ~1.0.

Illuminated samples were analyzed and purified with a Waters HPLC employing a Nova-Pak C18 column (3.9 × 300 mm, 60 Å pore size, and 4 μm particle size of spherical amorphous silica). A Waters 996 Photodiode Array Detector recorded the absorption spectra of the peaks emerging from the column. The all-trans isomers of decatetraene, dodecapentaene, and tetradecahexaene were isolated by using 90/5/5, acetonitrile/methanol/water (v/v/v), whereas pure acetonitrile was used as the mobile phase for hexadecaheptaene. Reinjection of samples collected from the HPLC, both before and after spectroscopic measurements, confirmed the photochemical stability of the all-trans isomers during the course of the experiments.

Absorption and Fluorescence Spectroscopy

Absorption spectra of the all-trans isomers of the polyenes in pentane, hexane, heptane, isooctane, octane, nonane, tridecane, pentadecane, hexadecane, and benzene and in EPA (5/5/2, ether/isopentane/ethanol, v/v/v) were obtained on a Cary 5000 spectrometer with 0.04 nm resolution. Fluorescence and fluorescence excitation spectra were recorded on a Jobin-Yvon Horiba Fluorolog-3 spectrometer, typically with a 1 nm bandpass. Emission spectra were corrected for the wavelength dependences of the monochromator and other optics by recording the spectrum of a standard 200 W quartz tungsten–halogen filament lamp, with irradiances traceable to NIST standard illumination sources.

Analysis of the Absorption and Fluorescence Spectra

The positions of the well-resolved S₀ (1¹A_g^–) → S₂ (1¹B_u⁺) (0–0) bands were obtained by repetitively scanning the peak positions to determine the average and estimated standard deviations of the (0–0) band in each solvent. The absorption spectrometer was calibrated by using a holmium oxide filter. The S₁ (2¹A_g^–) → S₀ (1¹A_g^–) fluorescence spectra were converted to an energy scale (cm^–1) by multiplying the experimental fluorescence intensities by the square of the wavelength.³³ The energies of the S₁ → S₀ (0–0) bands were determined by fitting the spectra to sums of Gaussian functions with use of Origin software.³⁴ Several different fits were performed on each spectrum, varying the number of Gaussians and initial guesses of position and amplitude. The results were averaged to obtain the energy and standard deviations for the S₁ (2¹A_g^–) → S₀ (1¹A_g^–) (0–0) band in each solvent.

Results and Discussion

The room temperature absorption spectra of these simple polyenes are characterized by well-resolved vibronic bands of the strongly allowed S₀ (1¹A_g^–) → S₂ (1¹B_u⁺) transitions (Figure 2). The most intense absorption features typically belong either to the “(0–0)” or the “(0–1)” vibronic band, suggesting a small displacement of the S₂ (1¹B_u⁺) state potential energy surface relative to that of the S₀ (1¹A_g^–) electronic ground state. Simple models based on semiempirical molecular orbital theory identify the strongly allowed S₀ (1¹A_g^–) → S₂ (1¹B_u⁺) transition with the promotion of an electron from the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO).^2,19,20,35 The transition energies (ΔE) exhibit an asymptotic approach to a long polyene limit following the approximation ΔE ≈ A + B/N, where N is the number of π-electron conjugated double bonds and A represents the S₀ → S₂ transition energy of the infinite polyene. For dimethyl polyenes, A is ~14 000 cm^–1, corresponding to a 1¹A_g^– → 1¹B_u⁺ (0–0) wavelength of ~700 nm in the long polyene limit.^3,36–39 Similar empirical, 1/N relationships prove useful in summarizing how the energies of other excited states depend on polyene conjugation length.⁴⁰

Figure 2.

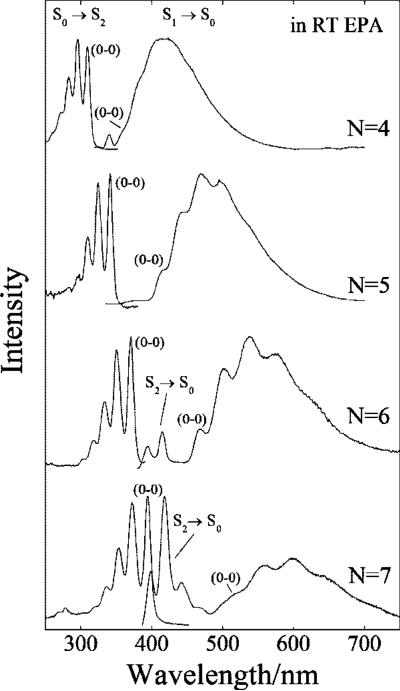
Absorption and fluorescence spectra of all-trans isomers of decatetraene, dodecapentaene, tetradecahexaene, and hexadecaheptaene in room temperature EPA (5/5/2, ether/isopentane/ethanol, v/v/v). Fluorescence spectra were obtained by exciting decatetraene and tetradecahexaene into their S₀ (1¹A_g^–) → S₂ (1¹B_u⁺) (0–0) absorption bands (decatetraene, 309 nm; tetradecahexaene, 370 nm), and dodecapentaene and hexadecaheptaene into their S₀ (1¹A_g^–) → S₂ (1¹B_u⁺) (0–1) absorption bands (dodecapentaene, 325 nm; hexadecaheptaene, 373 nm). Emission band passes were 1 nm for all spectra. Absorption and fluorescence spectra are normalized to their maximum values.

The fluorescence spectra of decatetraene (N = 4) and dodecapentaene (N = 5) are dominated by emission from the S₁ (2¹A_g^–) state. In contrast, tetradecahexaene (N = 6) and hexadecaheptaene (N = 7) show emission from both the S₁ (2¹A_g^–) and the S₂ (1¹B_u⁺) states (Figures 2 and 3). The electronic origins of the 2¹A_g^– → 1¹A_g^– emissions are significantly red-shifted relative to the origins of the 1¹A_g^– → 1¹B_u⁺ absorption bands, and the difference between the 1¹A_g^– → 1¹B_u⁺ and 2¹A_g^– → 1¹A_g^– origins provides an accurate measure of the energy separation between the 2¹A_g^– and 1¹B_u⁺ states. The S₁ (2¹A_g^–) → S₀ (1¹A_g) emission spectra exhibit vibronic progressions peaking ~3000 cm^–1 below the S₁ (2¹A_g^–) → S₀ (1¹A_g^–) origins, reflecting significant displacements in the potential energy surfaces of the 2¹A_g^– states relative to those of the 1¹A_g^– states. This is consistent with substantial rearrangements of the ground state C–C and C=C π-bond orders in the 2¹A_g^– states.

Figure 3.

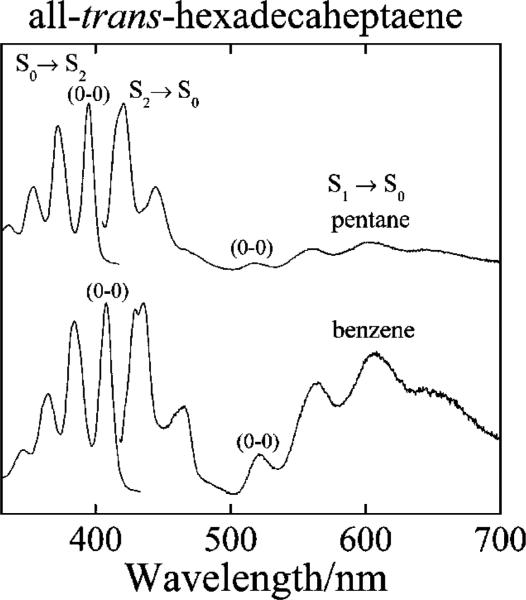
Absorption and fluorescence spectra of all-trans-hexadecaheptaene in pentane and benzene at room temperature. Fluorescence spectra were obtained by exciting into the S₀ (1¹A_g^–) → S₂ (1¹B_u⁺) (0–0) absorption band (395 nm in pentane, 408 nm in benzene). Emission band passes were 1 nm for all spectra. Absorption and fluorescence spectra are normalized to their maximum values.

To compare the experimental transition energies with those obtained from computational models, it is important to correct for the effect of the solvent environment on the polyene spectra. Figure 3 compares the absorption and emission spectra of all-trans-hexadecaheptaene (N = 7) in pentane and benzene. The (0–0) band of the 1¹A_g^– → 1¹B_u⁺ absorption spectrum in benzene is red-shifted by ~780 cm^–1 (~13 nm) relative to the (0–0) absorption band of hexadecaheptaene in pentane. However, the (0–0) band of the 2¹A_g^– → 1¹A_g^– fluorescence in benzene is shifted by only 34 cm^–1 (<1 nm) from its origin in pentane. This underscores the higher sensitivity to solvent of the strongly allowed S₀ → S₂ absorption compared to the symmetry-forbidden S₁ → S₀ transition.

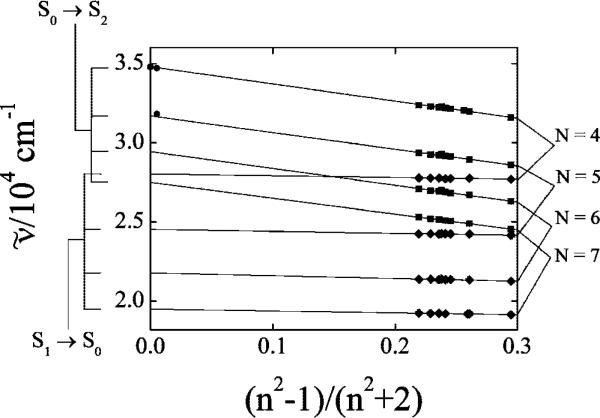
Table 1 provides a detailed summary of the 1¹A_g^– → 1¹B_u⁺ and 2¹A_g^– → 1¹A_g^– (0–0) transition energies for the four polyenes in a series of nonpolar solvents. Figure 4 presents the 1¹A_g^– → 1¹B_u⁺ and 2¹A_g^– → 1¹A_g^– transition energies as a function of the solvent polarizability, R(n) = (n² – 1)/(n² + 2), where n is the index of refraction. Linear fits to the data are summarized in Table 2. As noted in previous studies on polyenes,^4,41–43 these fits allow extrapolation to zero solvent polarizability. Decatetraene (N = 4) and dodecapentaene (N = 5) have sufficiently high vapor pressures to exhibit S₀ (1¹A_g^–) → S₂ (1¹B_u⁺) absorption spectra in room temperature, gas phase samples,^28,44–46 and the energies of the (0–0) transitions are 34 710 ± 10 cm^–1 and 31 805 ± 10 cm^–1 for the tetraene and pentaene. These gas phase (R = 0.00533) transition energies are in good agreement with those estimated by linear extrapolations of the solvent data (34 800 ± 20 cm^–1 and 31 690 ± 160 cm^–1(Table 2). High-resolution studies of decatetraene in supersonic jets (R = 0) give 34 783 ± 3 cm^–1 for the electronic origin,^28,29 in excellent agreement with the extrapolated value. The S₀ (1¹A_g^–) → S₂ (1¹B_u⁺) absorption transition energies of gaseous diphenylpolyenes with N = 1–4 also agree well with energies obtained from linear extrapolation of solution phase data.^4,41 These results and our data on the dimethylpolyenes validate the linear extrapolation of transition energies to zero solvent polarizability. This is critical given that computational studies on polyene excited state energies do not include the added complications of solvent perturbations.

TABLE 1.

Electronic Energies (in cm^–1) of the S₁ (2¹A_g^–) and S₂ (1¹B_u⁺) States of the Dimethylpolyenes^a

			S0 (11Ag–) → S2 (11Bu+)				S1 (21Ag–) → S0 (11Ag–)
solvent	n	R(n)	N = 4	N = 5	N = 6	N = 7	N = 4	N = 5	N = 6	N = 7
pentane	1.357 50	0.219 32	32 370 ± 4	29 360 ± 9	27 092 ± 4	25 320 ± 4	27 772 ± 12	24 244 ± 10	21 384 ± 21	19 183 ± 1
hexane	1.375 06	0.22895	32 287 ± 11	29 268 ± 4	26 976 ± 4	25 195 ± 2	27 770 ± 6	24 253 ± 10	21 397 ± 25	19 210 ± 2
heptane	1.387 77	0.235 85	32 233 ± 5	29 213 ± 2	26 939 ± 9	25 167 ± 6	27 775 ± 9	24 241 ± 10	21 363 ± 27	19 172 ± 2
isoctane	1.391 50	0.237 86	32 284 ± 4	29 278 ± 3	26 999 ± 4			24 259 ± 10	21 392 ± 24
octane	1.397 40	0.241 03	32 178 ± 12	29 171 ± 4	26 886 ± 5	25 102 ± 6	27 727 ± 20	24 248 ± 10	21 358 ± 31	19 218 ± 1
nonane	1.405 40	0.245 31	32 136 ± 8	29 131 ± 6	26 820 ± 2	25 063 ± 4	27 743 ± 15	24 240 ± 10	21 360 ± 28
tridecane	1.425 60	0.256 01	32 028 ± 4		26 720 ± 4				21 347 ± 23
pentadecane	1.431 50	0.259 11								19 220 ± 3
hexadecane	1.434 50	0.260 68	31 975 ± 3	28 926 ± 3		24 897 ± 7	27 759 ± 13	24 232 ± 10		19 224 ± 2
benzene	1.501 10	0.294 67	31 572 ± 5	28 599 ± 5	26 305 ± 4	24 540 ± 4	27 694 ± 9	24 161 ± 10	21 257 ± 28	19 149 ± 2
gas phase	1.008	0.005 33	34711 ± 8	31 805 ± 10
vacuum27,28	1	0	34 783 ± 3

^aN is the number of π-electron conjugated double bonds. The state energies were determined from the spectral origins (0–0) of the S₀(1¹A_g^–) → S₂ (1¹Bu⁺) absorption and S₁ (2¹Ag^–) → S₀ (1¹Ag^–) emission. R(n) = (n² – 1)/(n² + 2) is the solvent polarizability, where n is the index of refraction of the solvent. The uncertainties represent ±1σ from the mean of a set of Gaussian fits to the absorption and emission spectra.

Figure 4.

S₀ (1¹A_g^–) → S₂ (1¹B_u⁺) and S₁ (2¹A_g^–) → S₀ (1¹A_g^–) transition energies of dimethylpolyenes in nonpolar, room temperature solutions as a function of polarizability, R(n) = (n² – 1)/(n² + 2). Squares represent the (0–0) bands of the S₀ (1¹A_g^–) → S₂ (1¹B_u⁺) transitions; diamonds represent the (0–0) bands of the S₁ (2¹A_g^–) → S₀ (1¹A_g^–) transitions. S₀ → S₂ transition energies for gaseous decatetraene (in air and in vacuum) and for dodecapentaene (in air) are shown as circles. Uncertainties in the plotted values are given in Table 1 and are either comparable to or smaller than the size of the symbols in the figure. Parameters derived from linear, least-squares fits of the data are given in Table 3. Transition energies in air and vacuum were not included in the linear fits.

TABLE 2.

Parameters Used to Fit the S₀ (1¹A_g^–) → S₂ (1¹B_u⁺) and S₁ (2¹A_g^–) → S₀ (1¹A_g^–) Transition Energies of all-trans-Dimethylpolyenes to Equation 1^a

	S0 (11Ag–) → S2 (11Bu+)		S1 (21Ag–) → S0 (11Ag–)		E(11Bu+) – E(21Ag–) diff in (0–0) transition energies (cm–1)
polyene	k (cm–1)	ν0 (cm–1)	k (cm–1)	ν0 (cm–1)
decatetraene	–10 850 ± 80	34 800 ± 20	–1 090 ± 150	28 020 ± 40	6 780 ± 45
dodecapentaene	–10 490 ± 640	31 690 ± 160	–1 200 ± 240	24 530 ± 60	7 160 ± 165
tetradecahexaene	–10 630 ± 70	29 440 ± 20	–1 750 ± 430	21 790 ± 100	7 650 ± 100
hexadecaheptaene	–10 020 ± 60	27 500 ± 20	–1210 ± 600	19 500 ± 150	8 000 ± 150

^ak is the slope of the linear fit, and ν₀ is the extrapolated transition energy in the absence of solvent.

Figure 4 and Table 2 indicate that the slopes of the best-fit lines are an order of magnitude larger for the S₀ (1¹A_g^–) → S₂ (1¹B_u⁺) absorptions than for the S₁ (2¹A_g^–) → S₀ (1¹A_g^–) emissions. The greater sensitivity of the symmetry-allowed 1¹A_g^– → 1¹B_u⁺ transition to solvent polarizability can be rationalized by the perturbation theory description of solvatochromic effects. For nonpolar solutes in nonpolar solvents, e.g., dimethylpolyenes in n-alkane solvents, this leads to the following equation:^4,47,48

$$\tilde{v}\left(\text{solvent}\right)=\tilde{v}\left(\text{vacuum}\right)-a^3[M+E({\alpha }_{\mathrm{e}}-{\alpha }_{\mathrm{g}})]R\left(n\right)$$ (1)

where ν is the transition energy (in cm^–1), a is the effective solute cavity radius, M is the electric dipole transition moment for the transition, E is the average transition energy, (α_e - α_g) is the change in polarizability of the polyene upon excitation, and R(n) = (n² – 1)/(n² + 2) is the solvent polarizability. Equation 1 explains why the strongly allowed S₀ (1¹A_g^–) → S₂ (1¹B_u⁺) absorption (large M) exhibits a greater solvent effect than the symmetry-forbidden S₁ (2¹A_g^–) → S₀ (1¹A_g^–) transition (M ≈ 0). The equation also rationalizes the nonzero slopes for the symmetry-forbidden transition, confirming the larger polarizability of the S₁ (2¹A_g^–) state. Similar analyses were invoked in studies on diphenyloctatetraene¹ and decatetraene.²⁷

Calculations of polyene excited state energies have been restricted to simple, unsubstituted systems. It thus is important to understand the impact of the terminal methyl substituents on the data summarized in Tables 1 and 2. Methyl groups are known to stabilize the S₂ (1¹B_u⁺) states of polyenes.^{28,29,44–46,49,50} For example, measurements of the S₀ (1¹A_g^–) → S₂ (1¹B_u⁺) transition energy of octatetraene (no terminal methyl groups) from supersonic jet studies give a (0–0) of 35 553 ± 5 cm^–1.^44,45,51 Decatetraene isolated in a supersonic jet has a S₀ → S₂ electronic origin of 34 783 ± 3 cm^–1,^28,29 giving a 770 cm^–1 difference between the S₀ → S₂ transition energies of octatetraene and decatetraene. The S₁ (2¹A_g^–) → S₀ (1¹A_g^–) transitions energies of octatetraene and decatetraene in free jet expansions have been reported to be 28 949 and 28 963 cm^–1, respectively.⁵⁰ The 14 cm^–1 difference suggests that methyl substitution has very little influence on the 2¹A_g^– energies in these polyene systems. There are no comparable studies on the effect of terminal methyl groups on the S₀ → S₂ and S₁ → S₀ transition energies in longer polyenes. We thus assume that the ~770 cm^–1 difference between the S₀ (1¹A_g^–) → S₂ (1¹B_u⁺) transition energies of octatetraene and decatetraene also is an appropriate estimate of the net energy stabilization of S₂ (1¹B_u⁺) relative to S₀ (1¹A_g^–) for N = 5, 6, and 7. We also assume, for comparing experiment with theory, that the dimethylpolyenes and unsubstituted polyenes have identical S₁ (2¹A_g^–) energies.

One final correction, and that with the most uncertainty, must be made before comparing experimental and theoretical transition energies. Values obtained from theoretical computations typically represent “vertical” excitation energies to excited states that retain their ground state S₀ (1¹A_g^–) equilibrium geometries. On the other hand, the experimental transition energies presented in Tables 1 and 2 are associated with transitions between the well-characterized (and accurately measured) zero-point vibronic levels. Differences between vertical and (0–0) excitation energies have been discussed by Serrano-Andrés et al.,²⁴ Nakayama et al.,²² and Marian and Gilka.²⁶ Nakayama et al.²² calculated vertical excitation energies for all-trans-octatetraene (N = 4): 36 100 cm^–1 for 1¹A_g^– → 2¹A_g^– and 37 600 cm^–1 for 1¹A_g^– → 1¹B_u⁺. These energies should be compared with those calculated for the (0–0) transitions: 28 200 cm^–1 for 1¹A_g^– → 2¹A_g^– and 35 000 cm^–1 for 1¹A_g^– → 1¹B_u⁺.²² Similarly, Marian and Gilka²⁶ calculate vertical excitation energies for N = 4 of 32 420 and 34 920 cm^–1 and (0–0) transition energies of 26 210 and 33 070 cm^–1 for 1¹A_g^– → 2¹A_g^– and 1¹A_g^– → 1¹B_u⁺. The much larger predicted differences (~7900 cm^{–1 22} and 6210 cm^{–1 26}) between the vertical and (0–0) transitions for 1¹A_g^– → 2¹A_g^– relative to those for 1¹A_g^– → 1¹B_u⁺ (~2600 cm^{–1 22} and 1850 cm^{–1 26}) underscore the relatively large changes in C–C and C=C bond orders in the S₁ (2¹A_g^–) state.

Experimental estimates of the difference between the (0–0) and vertical excitation energies can be made by analyzing the Franck-Condon envelopes of the absorption and emission spectra. For example, the S₀ (1¹A_g^–) → S₂ (1¹B_u⁺) absorption spectra presented in Figure 2 exhibit a consistent pattern of maxima in the (0–0) band for N = 5, 6, and 7, whereas for N = 4, the “(0–1)” band shows the maximum absorption intensity. We thus assume the vertical S₀ → S₂ transition energy to be coincident with the (0–0) band for the longer polyenes and ~1540 cm^–1 higher than the (0–0) transition energy for the tetraene. These are rough approximations, in large part due to the rather coarse rulers provided by the ~1500 cm^–1 vibronic spacings in the Franck-Condon envelopes. Nevertheless, the vibronic structure in the room temperature absorption spectra allows a systematic estimate of the displacement of the S₂ (1¹B_u⁺) potential surface relative to that of the electronic ground state. The ~1540 cm^–1 difference between the vertical and (0–0) S₀ (1¹A_g^–) → S₂ (1¹B_u⁺) transitions in decatetraene is slightly lower than the 2600 cm^–1 difference predicted by Nakayama, et al.²² and the 1850 cm^–1 difference calculated by Marian and Gilka²⁶ for octatetraene.

We apply a similar approach to estimate the energies of the vertical transitions for the S₁ (2¹A_g^–) → S₀ (1¹A_g^–) and S₀ (1¹A_g^–) → S₀ (2¹A_g^–) transitions in the four polyenes. Fitting the room temperature emission spectra (Figures 2 and 3) to sums of Gaussians, after conversion of the spectra to energy scales, gives the following differences between the electronic origins and the Franck–Condon maxima: N = 4 (4440 cm^–1), N = 5 (2820 cm^–1), N = 6 (2710 cm^–1), and N = 6 (2650 cm^–1). For N = 5–7, the emission maxima correspond to the “(0–2)” vibronic band, whereas for N = 4, the emission maximum corresponds to the “(0–3)” vibronic band. The S₁ → S₀ emission spectrum of decatetraene points to a larger displacement of the excited state S₁ (2¹A_g^–) potential energy surface relative to that of the ground state (1¹A_g^–), consistent with electronic excitation having the largest impact on π-bonding in the smallest polyene in the series. The vibronic spacings observed in the N = 4–7 absorption and emission spectra also should be noted. The 1470, 1410, 1355, and 1325 cm^–1 vibrational progressions seen in emission systematically decrease with increasing conjugation. This is in agreement with trends seen in the ground state vibrational spectra of modes assigned to totally symmetric C–C and C=C stretches in other polyene systems.³

It is important to emphasize that the distinctive vibronic progressions observed in the room temperature spectra are due to complicated superpositions of vibrations, including combination bands involving the C–C and C=C totally symmetric (a_g) modes. For example, the low-temperature, high-resolution emission spectrum of 4-cis-hexadecaheptaene in 10 K n-pentadecane³⁰ has a maximum at 2700 cm^–1 (cf. 2650 cm^–1 calculated from the low-resolution emission spectra presented in Figure 3), which can be assigned to the combination of a C–C vibration (1148 cm^–1) and the dominant C=C vibration (1555 cm^–1). The frequencies of both of these totally symmetric (a_g) vibrations show systematic decreases with N, accounting for the vibronic trends noted in the less well-resolved room temperature spectra presented in Figures 2 and 3.

To estimate the energy difference between the (0–0) and vertical transitions for the S₀ (1¹A_g^–) → S₁ (2¹A_g^–) transition, we need to invoke the “mirror image symmetry” rule for vibronic intensities. This symmetry generally is observed between absorption and emission spectra of π-conjugated molecules for transitions connecting the same electronic states.³³ Mirror-image symmetry holds well for molecules with rigid conjugated π systems, but deviations are observed (e.g., a relatively well resolved absorption spectrum coupled with a broad emission spectrum) in cases where there are torsional degrees of freedom along the conjugated backbones.⁵² The latter is more likely the case for these flexible polyenes, which also are prone to conformational disorder. Nevertheless, the mirror image rule should provide realistic estimates of the Franck-Condon maxima expected for the S₀ → S₁ transitions. We thus estimate the difference between the S₀ (1¹A_g^–) → S₁ (2¹A_g^–) (0–0) bands and the vertical transitions to be identical with the offsets (Franck-Condon maxima) observed in the S₁ (2¹A_g^–) → S₀ (1¹A_g^–) emission spectra, i.e., 4440, 2820, 2710, and 2650 cm^–1 for N = 4, 5, 6, and 7. Note the significantly higher 7900 and ~6200 cm^–1 differences between the vertical and (0–0) S₀ → S₁ transition energies predicted by Nakayama et al.²² and Marian and Gilka²⁶ for octatetraene.

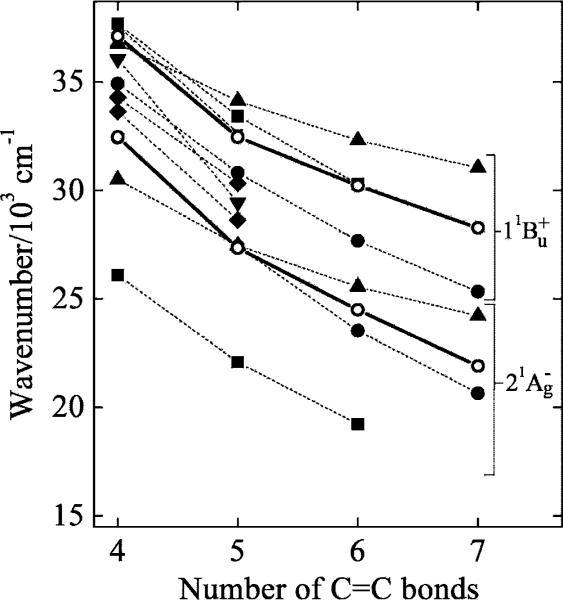
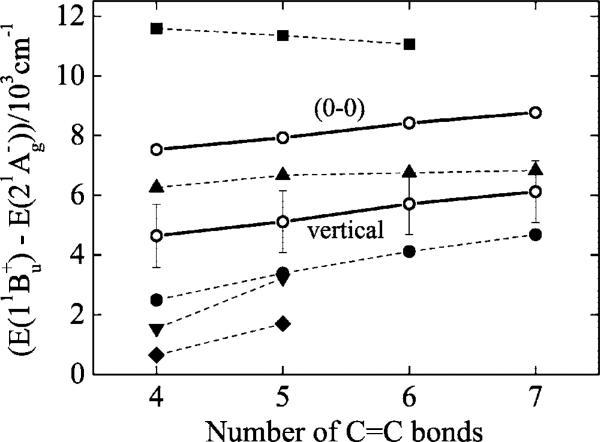
Our estimates for the vertical transition energies of the unsubstituted, simple polyenes in the absence of solvent interactions are summarized in Table 3. Figure 5 compares these energies with theoretical predictions^{20,22,23,25,26} of the vertical energies of the S₁ (2¹A_g^–) and S₂ (1¹B_u⁺) states. The computational models provide reasonable accounts of the S₂ (1¹B_u⁺) energy, including its dependence on conjugation length. On the other hand, theory provides mixed results for the S₁ (2¹A_g^–) energies. Most of the theoretical treatments calculate higher S₁ (2¹A_g^–) energies than those observed experimentally, and only Tavan and Schulten,²⁰ Dreuw et al.,²⁵ and Marian and Gilka²⁶ offer predictions beyond N = 5 (Table 4).

TABLE 3.

Estimated S₀ (1¹A_g^–) → S₂ (1¹B_u⁺) and S₀ (1¹A_g^–) → S₁ (2¹A_g^–) Transition Energies (in cm^–1) of Unsubstituted Linear Polyenes in Vacuum^a

polyene	S0 (11Ag–) → S2 (11Bu+) vertical transition	S0 (11Ag–) → S1 (21Ag–) vertical transition	E(11Bu+) – E(21Ag–) diff in vertical transition energies	E(11Bu+) – E(21Ag–) diff in (0–0) transition energies
octatetraene	37 110 ± 770	32 460 ± 735	4640 ± 1060	7550 ± 45
decapentaene	32 460 ± 760	27 350 ± 705	5110 ± 1040	7930 ± 165
dodecahexaene	30 210 ± 765	24 500 ± 680	5710 ± 1020	8420 ± 100
tetradecaheptaene	28 270 ± 770	22 150 ± 660	6120 ± 1040	8770 ± 150

^aThe estimated uncertainties in the S₀ (1¹Ag^–) → S₂ (1¹Bu⁺) and S₀ (1¹Ag^–) → S₁ (2¹Ag^–) vertical transition energies are half of the vibronic spacings observed in the absorption and emission spectra.

Figure 5.

Energies of the S₁ (2¹ A_g^–) and S₂ (1¹B_u⁺) states of unsubstituted polyenes as a function of the number of conjugated double bonds. Theoretical values (dashed lines) for vertical transitions are from Tavan and Schulten (▲),²⁰ Nakayama et al. (▲),²² Head-Gordon et al. (◆),²³ Dreuw et al. (□),²⁵ and Marian and Gilka (●).²⁶ Experimental data (○, solid lines) are from Table 3 and include corrections for solvent perturbations, the effect of methyl substitution, and the differences between (0–0) and vertical transition energies. Estimated errors for the experimental points are given in Table 3.

TABLE 4.

Different Computational Approaches to the Low-Lying Excited Electronic State Energies of Linear Polyenes^a

	N	computational method
Tavan, P.; Schulten, K.20	2–8	multireference configuration interaction method (MRCI)
Nakayama, K.; et al.22	2–5	multireference Møller–Plesset (MRMP); complete active space self-consistent field (CASSCF)
Head-Gordon, M.; et al.23	2–5	time-dependent density functional theory with Tamm–Dancoff approximation (TDDFT/TDA); BLYP functional
Dreuw, A.; et al.25	2–6	second-order algebraic diagrammatic construction ADC(2)
Marian, C.; Gilka, N.26	3 – 13	density functional theory/multireference configuration interaction method (DFT/MRCI); SV(P) with B3-LYP functional

^aN is the number of conjugated carbon–carbon double bonds in the polyenes studied.

A critical test of the applicability of the theoretical models is their ability to account for the energy gap between the S₂ (1¹B_u⁺) and S₁ (2¹A_g^–) states, an important factor in controlling the dynamics of excited state deactivation. Figure 6 compares the S₂ (1¹B_u⁺) S₁ (2¹A_g^–) “vertical” energy differences determined from quantum computations with values derived from the spectra, corrected for solvent interactions and the perturbations of the terminal methyl groups. The uncertainties in the experimental predictions of vertical transition energies are not insignificant and can be traced to the assumptions required to convert the electronic origins for the S₁ (2¹A_g^–) → S₁ (1¹A_g^–) and S₀ (1¹A_g^–) → S₂ (1¹B_u⁺) transitions into vertical excitation energies for S₀ (1¹A_g^–) → S₁ (2¹A_g^–) and S₀ (1¹A_g^–) → S₂ (1¹B_u⁺). Figure 6 also includes the considerably more precise estimates of S₂ – S₁ differences based on the energies of the S₀ → S₂ and S₁ → S₀ electronic origins. Both representations of the experimental data suggest small increases in the S₂ (1¹B_u⁺) – S₁ (2¹A_g^–) energy gap with increasing conjugation. Our experiments thus provide strong evidence for gas phase, vertical energy gaps of 4500–6500 cm^–1 for unsubstituted polyenes with N = 4–7. The data presented in Table 1 and Figure 4 indicate that these vertical energy differences decrease to ~2500–4500 cm^–1 in typical alkane solvents due the preferential stabilization of the S₂ (1¹B_u⁺) states.

Figure 6.

The S₂ (1¹B_u⁺) – S₁ (2¹A_g^–) energy gap as a function of the number of carbon–carbon double bonds. Theoretical predictions (dashed lines) on unsubstituted polyenes are from Tavan and Schulten (▲),²⁰ Nakayama et al. (▼),²² Head-Gordon et al. (◆),²³ Dreuw et al. (■),²⁵ and Marian and Gilka (●).²⁶ There are two sets of experimental data (○, solid lines). The (0–0) energy differences were obtained by extrapolating the S₀ (1¹A_g^–) → S₂ (1¹B_u⁺) and S₁ (2¹A_g^–) → S₀ (1¹A_g^–) transition energies to zero polarizability and correcting for the effects of the terminal methyl substituents. The vertical energy differences include estimates of the differences between the (0–0) and vertical S₀ → S₂ and S₀ → S₁ transition energies as described in the text (Table 3). Estimated errors for the experimental points are given in Table 3. The error bars for the experimental (0–0) energy differences are smaller than the open circle symbols.

It should be noted that the gas phase, S₂ – S₁ (0–0) energy differences presented here (6780, 7160, 7650, and 8000 cm^–1) are consistent with previously reported values (6380, 7060, 7420, and 8690 cm^–1) for the transition energies of unsubstituted polyenes with N = 4–7.^42,43 The energy values reported here are considerably more reliable due to the care taken to identify and isolate all-trans isomers by using HPLC techniques and the more careful analysis/deconvolution of the room temperature absorption and emission solvent shift data.

Appropriate estimates of the differences between (0–0) and vertical transition energies are critical for comparing the experimental results with theoretical predictions (Figure 6). The small geometry change between 1¹A_g^– and 1¹B_u⁺ leads to relatively good agreement on the difference between the vertical and (0–0) transition energies for octatetraene: cf. theory (2600 cm^–1; 1850 cm^–1)^22,26 and experiment (1540 cm^–1). However, there are large discrepancies for the 1¹A_g^– → 2¹A_g^– transition. Analysis of the Franck–Condon envelopes (Figure 2) indicates a 4440 cm^–1 difference for N = 4, considerably lower than the values (7900 cm^–1 and 6200 cm^–1) suggested by Nakayama et al.²² and by Marian and Gilka.²⁶ Marian and Gilka calculate 5000–5800 cm^–1 differences for N = 5–7, which are significantly higher than the 2700 ± 100 cm^–1 differences we estimate from the Franck–Condon envelopes. Accounting for these discrepancies offers a fertile opportunity for reconciling the vibronic intensities in polyene/cartotenoid absorption and emission spectra with more accurate descriptions of excited state geometries, especially for the 2¹A_g^– state. This also will lead to a better understanding of the theoretical and experimental data presented in Figure 6.

It is important to relate the current studies to our recent work on the symmetry control of S₁ (2¹A_g^–) → S₀ (1¹A_g^–) radiative decay in polyenes.³² This indicated that the S₁ → S₀ emissions from highly purified samples of long, symmetric all-trans polyenes most likely are due to cis isomers and/or comformationally distorted trans molecules. Less symmetric, more highly fluorescent cis species can be produced photochemically from pure all-trans samples. The fluorescence also may be due to thermal distributions of all-trans isomers that are conformationally distorted in their ground states or produced during relaxation from S₂ to S₁. Low barriers to isomerization and conformational distortion in S₁ (2¹A_g^–) are consistent with the significant rearrangement of the ground state C–C and C=C bonds in 2¹A_g^–,^3,4,22,24 and explain the unique ability of polyene S₁ states to undergo isomerization. The emission spectra and transition energies reported here thus cannot simply be associated with all-trans isomers with rigorous C_2h symmetries. The room temperature solutions described in this and all previous studies of polyene emission spectra, even for samples associated with a single peak from an HPLC collection, thus must be viewed as giving rise to a distribution of fluorescent species following excitation into either S₂ (1¹B_u⁺) or S₁ (2¹A_g^–). The relatively high resolution of the S₁ (2¹A_g^–) → S₀ (1¹A_g^–) emission spectra in room temperature solutions (Figures 2 and 3) indicates that the most highly fluorescent species have very similar excited state energies. Furthermore, previous high-resolution experiments on short polyenes point to small differences (100–200 cm^–1) between S₁ (2¹A_g^–) energies for the cis and trans isomers of simple polyenes.^53,54 It therefore is appropriate to compare the theoretical predictions of 2¹A_g^– energies of symmetric, all-trans species with energies obtained from the room temperature emission spectra described in this paper.

Conclusions

The dependence of the S₀ (1¹A_g^–) → S₂ (1¹B_u⁺) and S₁ (2¹A_g^–) → S₀ (1¹A_g^–) transition energies of decatetraene, dodecapentaene, tetradecahexaene, and hexadecaheptaene on solvent environment has been examined in detail. Room temperature solution spectra of purified, all-trans isomers have sufficient vibronic structure to allow the accurate determination of electronic origins ((0–0) bands) as a function of solvent polarizability. The shifts in transition energies of these nonpolar polyenes in nonpolar solvents are well described by perturbation theory treatments of the effect of solvation on the electronic states. Transition energies extrapolated to zero solvent polar-izability agree well with those obtained from gas phase measurements on the shorter polyenes. The extrapolated transition energies have been compared with those obtained from theory by correcting the experimental S₁ (2¹A_g^–) and S₂ (1¹B_u⁺) energies for the effect of terminal methyl group substitution and by accounting for the differences between “vertical” and (0–0) transition energies.

These data and the precise measures of the electronic origins of the S₀ (1¹A_g^–) → S₂ (1¹B_u⁺) and S₁ (2¹A_g^–) → S₀ (1¹A_g^–) transitions for the dimethylpolyenes (Tables 1 and 2) provide useful benchmarks for evaluating theoretical descriptions of the electronic states of simple polyene systems as a function of conjugation length. While current theory accounts for the correct state ordering, the ab initio predictions show significant systematic deficiencies both in predicting absolute transition energies and in accounting for differences in the 1¹B_u⁺ and 2¹A_g^– energies. Our experimental estimates of the differences between state energies based on (0–0) transitions and vertical transitionsalsowillbeusefulinunderstandingtheFranck-Condon envelopes for the dominant combinations of C–C and C=C symmetric vibrations and how the vibronic intensities relate to geometry changes in the 2¹A_g^– and 1¹B_u⁺ electronic states.