Deconvolution When Classifying Noisy Data Involving Transformations

Abstract

In the present study, we consider the problem of classifying spatial data distorted by a linear transformation or convolution and contaminated by additive random noise. In this setting, we show that classifier performance can be improved if we carefully invert the data before the classifier is applied. However, the inverse transformation is not constructed so as to recover the original signal, and in fact, we show that taking the latter approach is generally inadvisable. We introduce a fully data-driven procedure based on cross-validation, and use several classifiers to illustrate numerical properties of our approach. Theoretical arguments are given in support of our claims. Our procedure is applied to data generated by light detection and ranging (Lidar) technology, where we improve on earlier approaches to classifying aerosols. This article has supplementary materials online.

1. INTRODUCTION

In the present study, we consider signal classification problems, where the observations are d-dimensional noisy spatial functions Y_ij, for 1 ≤ i ≤ n_j, coming from population Π_j, where j = 1 or 2, and which can be modeled as Y_ij = TX_ij + δ_ij, where T is a transformation of the function of interest X_ij and δ_ij is a random error with zero mean and some correlation structure. Based on training data, the goal is to classify a new noisy data function Y whose class is unknown, as coming from one of Π₁ and Π₂.

In many instances, the function TX_ij is the result of a convolution of the function X_ij with a blurring source, that is, TX_ij = ω_T * X_ij, where * denotes the convolution operator (see Section 2.3) and ω_T is a point spread function. There, the function X_ij can be reconstructed in part by a (necessarily estimated) deconvolution operation. There is a large statistics literature on deconvolution for image data, and for data of similar type, dating from the 1980s. It includes contributions by Besag (1986), Donoho (1994), Dass and Nair (2003), Qiu (2005, 2007, 2008), and Mukherjee and Qiu (2011). Related research problems arise in spatial statistics, for example, in the contexts of remote sensing (see, e.g., Klein and Press 1992; Cressie and Kornak 2003; Crosilla, Visintini, and Sepic 2007) and statistical signal recovery (see, e.g., Johnstone 1990; Huang and Cressie 2000; Shi and Cressie 2007).

There is also a significant literature on blind deconvolution and estimation of point spread functions. This work includes contributions by Kundur and Hatzinakos (1998), Cannon (1976), Carasso (2001), Galatsanos et al. (2002), Figueiredo and Nowak (2003), Joshi and Chaudhuri (2005), Hall and Qiu (2007a, b), Qiu (2008), Huang and Qiu (2010), and Popescu and Hellicar (2010). However, the problems of deconvolution and point spread function estimation are very different from those of classification, to such an extent that, even if T were known, the methods suggested in this article would still be recommended. It should also be noted that, since neither the function X nor the noise δ is observable, it is not possible to estimate the noise and, hence, to remove it effectively from the observed data Y. In particular, in the problem treated in this article, it is not possible to compute residuals.

In our classification context, it is at least intuitively plausible that if one could recover the function X_ij, then one would use that function as the basis for classification, rather than using the noisy convolved function Y_ij. This idea has been used in the classification of different types of aerosols using long-range infrared light detection and ranging (Lidar) methods (Warren et al. 2008), where deconvolution was used to obtain estimates of the true signal, and the resulting estimates were used as the basis for classification. Our work relates to whether a signal should be deconvolved or correlated errors should be deconvolved before classification, and we shall use Lidar data to illustrate our conclusions. We shall show that there exists a transformation of the noisy convolved function Y_ij that is appropriate for classification, but that it is not necessarily related to the transformation that would be used to recover the true signal.

The real-data classification problems that motivate this work, all involve just K = 2 populations, and for this reason, and to simplify discussion, we shall confine attention to this case. However, out methodology and theoretical results extend readily to the general case K ≥ 2, using the approach suggested by Friedman (1996).

The article is organized as follows. We introduce our model and ideas in Section 2, and in Section 3, we establish theoretical properties of our procedure. In Section 4, using a variety of classifiers, we apply our approach to simulated data and to the Lidar data mentioned above. Technical arguments are deferred to the supplementary materials.

2. METHODS

2.1 Model and Classification Problem

We observe spatial data functions Y_ij (r), r ∈ , 1 ≤ i ≤ n_j, j = 1, 2, generated by the model

$$Y_{ij}(r)={TX}_{ij}(r)+{\delta }_{ij}(r),$$ (2.1)

where 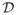denotes a d-dimensional spatial grid, or lattice; X_ij is the spatial function of interest, T is a linear transformation that blurs the signal; and δ_ij, representing noise, is a component of a correlated stochastic process with zero mean affecting the signal. In this model, the data come from two populations, Π₁ and Π₂, and, for j = 1, 2, Y_ij denotes the ith data function drawn from the jth population Π_j, where i = 1, …, n_j. To simplify notation, we define scale in such a way that 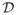⊂ ℤ^d, where ℤ is the set of all integers.

The model at Equation (2.1) is appropriate when the observations Y_ij are, for example, digitized images or Lidar signals. There, T typically represents the accumulated impact of issues such as generalized lens aberrations, atmospheric effects, motion blur, etc., and 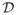is a two- or three-dimensional grid.

Remark 1

It is important to realize that Y_ij, X_ij, and δ_ij are functions defined on 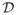, and that T (and later, the transforms R and Q, which will be defined below) is not a function; it is a functional that maps the function X_ij to the function T X_ij .

Let Y be a new data value coming from Π_k, where k = 1 or 2 is unknown. Our goal is to construct a classifier 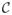(·) ≡ (·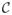|{Y_ij}_{j = 1,2; i = 1,…,nj}) from the data Y_ij that assigns Y to Π_k̂, where k̂ = 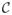(Y|{Y_{ij}j = 1,2; i = 1,…,nj}) = 1 or 2 is an estimator of k. In the applications we have in mind, where the data are images or Lidar signals, distinguishing between Π₁ and Π₂ is inherently a problem involving high-dimensional data analysis. In practice, the number of points r at which we observe data Y_ij(r) can be in the thousands, whereas the training sample sizes, n₁ and n₂, are often only limited to 20 or 30.

2.2 Deconvolution of the Data Through the Noise Transform

As we indicated in the Introduction, when the functional T is invertible, it is sometimes argued that, instead of applying standard classifiers to the data Y_ij, one should apply them to inverted data where Y and each Y_ij are replaced by T⁻¹ Y and T⁻¹ Y_ij, or rather by regularized versions of them, T̂⁻¹ Y and T̂⁻¹ Y_ij. That is, classification should be based on 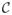(T̂⁻¹ Y|{T̂⁻¹Y_ij}_{j = 1,2; i = 1,…,nj}), instead of 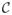(Y|{Y_ij}_{j =1,2;i=1,…,nj}). Transforming the data by T⁻¹ is a good idea when the goal is to recover the function X_ij, since we have T⁻¹ Y_ij = X_ij + T⁻¹ δ_ij, so the transformed data are no longer distorted and contain only additive noise T⁻¹ δ_ij of zero mean. This is only approximately true when using T̂⁻¹, of course; see, for example, Cannon and Hunt (1981) and Hall (1990). However, we argue that when the goal is classification, inverting T is not necessarily a good idea, and a better strategy is to transform the data in such a way that classification performance is improved.

To explore the classification problem further, let ε_ij = T X_ij − T μ_j + δ_ij, where the function μ_j is defined by μ_j = E_j(X_ij) and E_j denotes expectation, conditional on X_ij coming from population j. Then, (2.1) can be written as

$$Y_{ij}=T{\mu }_j+{\epsilon }_{ij},$$ (2.2)

where E_j(ε_ij) = E_j(δ_ij) = 0. If the processes X_ij − μ_j and δ_ij are also linear, in particular if ε_ij is stationary and Gaussian, as is often approximately the case in practice, then we can write ε_ij = R ξ_ij, where R is another linear transformation and the process ξ_ij is white noise, that is, the random variables ξ_ij(r), for r ∈ ℤ^d, are uncorrelated and have zero mean and common variance σ². In this notation, the model in Equation (2.2) can be expressed as

$$Y_{ij}=T{\mu }_j+R{\xi }_{ij},$$ (2.3)

so if R is invertible, Equation (2.3) can be written equivalently as

$$R^{-1}{Y}_{ij}=R^{-1}T{\mu }_j+{\xi }_{ij}.$$

The absence of correlation of ξ_ij, and the constant variances, suggests that, for a variety of classifiers, performance can be improved by working with the data R⁻¹ Y, rather than with Y itself. For example, this is the case when the error process ε_ij in Equation (2.2) is stationary and Gaussian and we use the centroid classifier (see Section 3.1). Indeed, there, the classifier based on such transformed data is Fisher’s linear discriminant, albeit in a much higher-dimensional setting than is usually contemplated, and so, has optimality properties. In particular, this classifier is asymptotically equivalent to applying a likelihood ratio test. More generally, we shall show in Section 3 that in non-Gaussian cases, the optimal transformation, in terms of asymptotic performance of the centroid classifier, is also R⁻¹.

These considerations suggest that, for such classifiers, far from it being a good idea to replace Y and Y_ij by their deconvolved forms T⁻¹ Y and T⁻¹ Y_ij, we should replace them by R⁻¹ Y and R⁻¹ Y_ij and base classification on 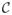(R⁻¹ Y|{R⁻¹ Y_ij}_{j = 1,2; i = 1,…,nj}). For more general classifiers too, transforming the data prior to applying a classifier can often improve performance, but not when this transform is taken to be T⁻¹. In practice, the optimal transform is unknown and is not necessarily equal to R⁻¹ for each classifier, since the best transform may depend on the particular classifier in use. Likewise, the optimal transform is not necessarily always exactly linear. However, by inverting the Y_ij’s via a carefully chosen linear transform, which we shall denote by Q⁻¹ in the next section, we can often improve classification performance significantly. We suggest such a practicable inversion technique in the next section, and we construct it from the data in such a way as to optimize classification performance.

2.3 Transforming the Data in Practice

2.3.1 Modeling the Transform

Since the best transform to apply to the data Y_ij prior to classification is generally not known, it needs to be estimated from the data. However, the sample size is usually too small for estimating this transform without imposing restrictions on it. Motivated by our discussion in the last paragraph of Section 2.2, we model the transform by the inverse Q⁻¹ of a linear transform Q = Q_θ, which depends on a low-dimensional vector of parameters θ = (θ₁, …, θ_q), as follows.

Let ω_Qθ be a nonnegative weight function defined on ℤ^d and depending on θ. Moreover, let * denote the discrete convolution operation, defined for any two absolutely square summable functions f and g by f * g(r) = Σ_s∈ℤ^df (r − s) g(s). We take Q_θ to be the linear transform that maps a function ζ to a function χ_θ = Q_θ ζ defined, for each r ∈ ℤ^d, by

$${\chi }_{\theta }(r)={\omega }_{Q_{\theta }}\ast \zeta (r).$$ (2.4)

In image analysis terminology, ω_Qθ is called the spread function of the transform Q_θ. The choice of the parameters θ will be treated in Section 2.3.3.

An example of a simple model for ω_Qθ is the two-parameter family ω_p0;θ, where θ = (ρ, ℓ) and ω_p0;θ is the ℓ-fold convolution of the probability mass function p₀, defined by

$$p_0(r)={\left(\frac{1-\rho }{1+\rho }\right)}^d{\rho }^{\mid r\mid },r\in {\mathbb{Z}}^d,$$ (2.5)

where $\mid r\mid ={\sum }_{j=1}^d\mid r_j\mid$ and |ρ| < 1 (usually, 0 < ρ < 1). This is the model we used in our numerical work in Section 4, but alternative models and more comments are given in Appendix A.2 in the supplementary materials.

2.3.2 Inverting Q

Since Q_θ is defined by a convolution, its inverse is more easily expressed in the Fourier domain. Let ζ be a function defined on ℤ^d such that Σ_r∈ℤ^d|ζ(r)|< ∞. The (discrete) Fourier transform φ_ζ(t), for t ∈ (−π, π)^d, is defined by

$${\phi }_{\zeta }(t)=\sum _{r\in {\mathbb{Z}}^d}\zeta (r)exp(i{r}^{\text{T}}t),$$ (2.6)

where, on this occasion, $i=\sqrt{-1}$. Since the Fourier transform of a convolution between two functions is equal to the product of their Fourier transforms, we deduce from Equation (2.4) that the Fourier transform of the function χ_θ is given by φ_χθ = φ_ζ φ_ωQθ.

In this notation, when φ_ωQθ (t) ≠ 0, we can write φ_ζ(t) = φ_χθ(t)/φ_ωQθ (t). If |φ_χθ|/|φ_ωQθ is integrable, then Q_θ is invertible, and the inverse transform $Q_{\theta }^{-1}$, obtained by the Fourier inversion theorem, maps the function χ_θ into the function $Q_{\theta }^{-1}{\chi }_{\theta }$ defined by (2.8), taking there 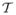= (−π, π)^d. If Q_θ is not invertible, we can typically define a generalized inverse, $Q_{\theta }^{-1}$, by truncating the integral used in Fourier inversion to a small-enough set 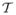⊂ (−π, π)^d, for example,

$$\mathcal{T}=\{t:|\left|t\right||\le \eta \}\text{or}\mathcal{T}=\{t:\mid t_j\mid \le \eta ,1\le j\le d\},$$ (2.7)

with η ∈ (0, π). Thus, in either case, we can write

$$Q_{\theta }^{-1}{\chi }_{\theta }(r)={(2\pi )}^{-d}{\int }_{\mathcal{T}}exp(-i{r}^{\text{T}}t)\{{\phi }_{{\chi }_{\theta }}(t)/{\phi }_{{\omega }_{Q_{\theta }}}(t)\}dt.$$ (2.8)

Remark 2

To motivate the selections of 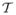in (2.7), observe that φ_ωQθ (0) equals the sum of the weights ω_Qθ (r) over r ∈ ℤ^d, and the ω_Qθ (r)’s would normally be chosen so that this sum was strictly positive, in fact equal to 1. Therefore, φ_ωQθ (0) ≠ 0, and by continuity, φ_ωQθ (t) ≠ 0 for t in a sufficiently small neighborhood of the origin. Hence, choosing 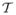as in the formulas in (2.7), for sufficiently small η, ensures that the integral at (2.8) is well defined if the function χ_θ is uniformly bounded.

For example, if we model Q_θ by taking ω_Qθ = ω_p0;θ, defined above Equation (2.5), then $Q_{\theta }^{-1}{\chi }_{\theta }$ is particularly easy to calculate. As a matter of fact, by standard calculations, we have

$${\phi }_{{\omega }_{Q_{\theta }}}(t)={\phi }_{{\omega }_{p_0;\theta }}(t)=\prod _{j=1}^d{[1+2\rho {(1-\rho )}^{-2}\{1-cos(t_j)\}]}^{-\ell },$$ (2.9)

for each t = (t₁, …, t_d)^T ∈ (−π, π)^d, so

$$Q_{\theta }^{-1}{\chi }_{\theta }(r)={(2\pi )}^{-d}\sum _{s\in {\mathbb{Z}}^d}{\chi }_{\theta }(s){\int }_{\mathcal{T}}\prod _{j=1}^d(e^{i(s_j-r_j)t_j}\times {[1+2\rho {(1-\rho )}^{-2}\{1-cos(t_j)\}]}^{\ell }{dt}_j.$$ (2.10)

The integral in Equation (2.10) is well defined if we take 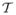= (−π, π)^d, in which case, it simplifies to

$$Q_{\theta }^{-1}{\chi }_{\theta }(r)={(2\pi )}^{-d}\sum _{s\in {\mathbb{Z}}^d}{\chi }_{\theta }(s)\prod _{j=1}^d{\int }_{-\pi }^{\pi }{e}^{i(s_j-r_j)t_j}\times {[1+2\rho {(1-\rho )}^{-2}\{1-cos(t_j)\}]}^{\ell }{dt}_j.$$ (2.11)

A very attractive aspect of this choice of Q_θ is that we do not need smoothing parameters, such as η at Equation (2.7), to regularize the integral. Further, it can be proved that each integral in Equation (2.11) is equal to a constant, depending only on |s_j − r_j|, ρ, and ℓ, and which vanishes if |s_j − r_j| > ℓ. In other words, $Q_{\theta }^{-1}{\chi }_{\theta }(r)$ is a linear combination of values of χ_θ(s), for s in a neighborhood of r (more precisely, for s such that max_{j =1,…,d} |s_j − r_j| ≤ ℓ).

2.3.3 Estimation of Unknown Parameters

Now that we have a practicable representation $Q_{\theta }^{-1}$ for the transform to apply to the data before classification, it remains to choose θ. Just as, a priori, it may seem natural to invert the data by T⁻¹, it may also seem natural to choose θ to give a good fit to the data. However, again, our goal here is to classify, and thus, θ should rather be chosen to optimize the performance of the classifier based on ${\mathcal{C}}_{\theta }(Y)\equiv \mathcal{C}(Q_{\theta }^{-1}Y\mid {\{Q_{\theta }^{-1}{Y}_{ij}\}}_{j=1,2;i=1,\dots ,n_j})$. We suggest choosing θ to minimize a cross-validation estimator of error rate.

Specifically, write π₁ for the prior probability of Π₁, which is typically taken to equal 0.5 if we have no a priori knowledge, or to n₁/(n₁ + n₂) if we believe that the proportion of observations from Π₁ in the training sample is representative of that in the population. Define

$$\widehat{e}(\theta )=\frac{{\pi }_1}{n_1}\sum _{i=1}^{n_1}I\{{\mathcal{C}}_{\theta ;-i1}(Y_{i1})=2\}+\frac{1-{\pi }_1}{n_2}\sum _{i=1}^{n_2}I\{{\mathcal{C}}_{\theta ;-i2}(Y_{i2})=1\},$$ (2.12)

where 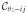denotes the version of 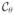constructed without using Y_ij, that is, ${\mathcal{C}}_{\theta ;-ij}(Y_{ij})=\mathcal{C}(Q_{\theta }^{-1}{Y}_{ij}\mid {\{Q_{\theta }^{-1}{Y}_{k\ell }\}}_{k=1,2;\ell =1,\dots ,n_k;(k,\ell )\ne (i,j)})$. Then, ê(θ) estimates the error rate,

$$e(\theta )={\pi }_1{P}_1\{{\mathcal{C}}_{\theta }(Y)=2\}+(1-{\pi }_1)P_2\{{\mathcal{C}}_{\theta }(Y)=1\},$$ (2.13)

where P_j denotes probability conditional on Y ∈ Π_j. We suggest choosing θ to minimize ê(θ).

Remark 3

In cases where the set 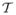cannot be taken equal to (−π, π)^d, the classifier can also depend on a small number of parameters defining 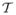, which, if they are unknown, can play the role of a smoothing parameter; see the examples in (2.7). In such cases, 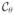, ê(θ) and e(θ) are replaced by 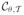, ê(θ, 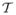) and e(θ, 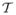), respectively, and θ and 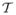re chosen to minimize ê(θ, ).

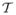3. THEORY

3.1 Centroid Classifier

There exist a variety of standard classifiers that give good performance for high-dimensional data. Here, we discuss detailed theoretical properties in the context of one of the most popular and effective methods, the centroid-based technique; for example, see James and Hastie (2001) and Shin (2008). If ${\overline{Y}}_j(r)=n_j^{-1}{\sum }_i{Y}_{ij}(r)$, the centroid method assigns a new value Y, coming from Π₁ or Π₂, to Π₁ (i.e., it puts 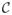(Y) = 1) if Σ_r∈ 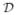[{Y(r) − Ȳ₂(r)}² − (Y(r) − Ȳ₁(r)}²] > 0, and to Π₂ (i.e., it puts 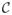(Y) = 2) otherwise. Other classifiers will be discussed in Section 4.4.

As already highlighted in Section 2.2, if the errors are stationary, then this classifier is optimized when applied to the data R⁻¹ Y_ij. Using the representation $Q_{\theta }^{-1}$ for R⁻¹, an approximation to optimal classification involves assigning a new observation Y to Π₁ (i.e., putting 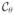(Y) = 1) if and only if S_θ(Y) > 0, where

$$S_{\theta }(Y)=\sum _{r\in \mathcal{D}}\{{\mid Z_{\theta }(r)-{\overline{Z}}_{2;\theta }(r)\mid }^2-{\mid Z_{\theta }(r)-{\overline{Z}}_{1;\theta }(r)\mid }^2\},$$ (3.1)

with ${\overline{Z}}_{j;\theta }(r)=n_j^{-1}{\sum }_i{Z}_{ij;\theta }(r)$ and where the functions Z_θ and Z_ij;θ are defined by $Z_{\theta }=Q_{\theta }^{-1}Y$ and $Z_{ij;\theta }=Q_{\theta }^{-1}{Y}_{ij}$.

In this notation, the cross-validation technique for choosing θ, described in Equation (2.12) in Section 2.3.3, can be written as

$$\widehat{e}(\theta )=\frac{{\pi }_1}{n_1}\sum _{i=1}^{n_1}I\{S_{\theta ;-i1}(Y_{i1})\le 0\}+\frac{1-{\pi }_1}{n_2}\sum _{i=1}^{n_2}I\{S_{\theta ;-i2}(Y_{i2})>0\},$$ (3.2)

where S_θ;−ij denotes the version of S_θ in (3.1) calculated with Z̄_j being replaced by ${\overline{Z}}_j^{(-i)}={(n_j-1)}^{-1}{\sum }_{k\ne i}{Z}_{kj}$. Likewise, the error rate e(θ) in Equation (2.13) can be written as

$$e(\theta )={\pi }_1{P}_1\{S_{\theta }(Y)\le 0\}+(1-{\pi }_1)P_2\{S_{\theta }(Y)>0\}.$$ (3.3)

3.2 Main Assumptions

To simplify notation, throughout Section 3, we define scale in such a way that 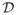, in d-variate Euclidean space, has edge width 1, for example,

$$\mathcal{D}=\{r={(r_1,\dots ,r_d)}^{\text{T}}:r_1,\dots ,r_d\in \mathbb{Z},-n\le r_1,\dots ,r_d\le n\},$$ (3.4)

where n ≥ 1. In this setting, # 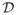≍ n^d and the training sample sizes, n₁ and n₂, are interpreted as functions of n. Let 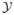denote the pair of training samples ( 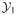, 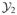), with 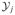= {Y_ij, 1 ≤ i ≤ n_j}, Y_ij = (Y_ij(r):r ∈ 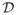). The error rate of our classifier, computed from the training dataset 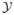, is denoted by e(θ) and defined in Equation (3.3). In this section, we give asymptotic formulas for e(θ) and ê(θ), taking 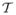to be a general subset of (−π, π)^d. For example, 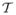might be equal to (π, π)^d, or to one of the regions defined in Equation (2.7). Theory in cases where cross-validation is used to determine 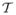, as well as θ (see Remark 3 in Section 2.3.3), can be developed at the expense of longer arguments; in the present section, we use cross-validation to optimize over θ but not 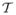, which corresponds to our practical implementation of the method; see Section 4.

We develop our theory under three main model assumptions. First, we assume that R maps a function ζ, defined on ℤ^d, into a function R ζ, defined by

$$R\zeta (r)={\omega }_R\ast \zeta (r).$$ (3.5)

Second, we assume that

$$R^{-1}T{\mu }_j,Q_{\theta }^{-1}T{\mu }_j\text{and}\xi \text{are}\text{supported}\text{on}\mathcal{D},\text{for}j=1,2.$$ (3.6)

We impose this condition only to avoid long arguments for dealing with potential edge effects. Our conclusions remain valid without it, but the proofs become considerably longer. Finally, we assume that T μ₁ − T μ₂ = T (μ₁ − μ₂) is smoother than ω_R. More precisely, we assume that T (μ₁ − μ₂) = α K * ω_R, where α is a constant and K is a function supported on 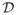. This assumption ensures that the inverse of the mean of the differences of the observed signals, R⁻¹T(μ₁ − μ₂), remains bounded. It is imposed only to make our technical arguments simpler and explicit. If it is not satisfied, then, generally speaking, the classification problem becomes simpler, in that the difference between the means of the inverted signals is even larger and, therefore, easier to detect.

We allow the distance between the two transformed means, T μ₁ and T μ₂, to vary with n, by letting α above depend on n. In particular, we assume that T(μ₁ − μ₂) = α_n K * ω_R, where α_n is a sequence of positive real numbers bounded above zero. The most important case is that where α_n (and hence the distance) decreases with increasing n, since that enables our theoretical arguments to address particularly challenging cases. We also permit the noise variance, ${\sigma }_n^2=var\{{\xi }_{ij}(r)\}$, to depend on n. We shall see that the relative sizes of n, α_n, and σ_n interact together to determine the performance of our classifier. Although this interaction is quite complex, to a large extent, it can be represented in terms of the quantity

$$u_n(\theta )=({\alpha }_n/{\sigma }_n){\int }_{\mathcal{T}}{\mid {\phi }_K\mid }^2{\mid {\phi }_{{\omega }_R}\mid }^2{\mid {\phi }_{{\omega }_{Q_{\theta }}}\mid }^{-2}/{\left\{{(2\pi )}^d{\int }_{\mathcal{T}}{\mid {\phi }_K\mid }^2{\mid {\phi }_{{\omega }_R}\mid }^4{\mid {\phi }_{{\omega }_{Q_{\theta }}}\mid }^{-4}\right\}}^{1/2},$$ (3.7)

where φ_ωR (t) = Σ_r∈ℤ^d ω_R(r) exp(i r^Tt) is the Fourier transform of ω_R and φ_K (t) = Σ_r∈ 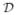K(r) exp(i r^Tt) is the Fourier transform of K; here, we used the fact that K is supported on .

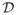To derive our theoretical results, we also need regularity conditions. These are more technical, and we shall describe them in detail in Appendix B.1 in the supplementary materials; see Equations (B.2)–(B.6).

3.3 Asymptotic Formula for Error Rate

The next theorem describes properties of e(θ) as n diverges. Let Φ denote the standard normal distribution function, and write Θ for a compact set of parameters from which θ is chosen.

Theorem 1

Assume that the data are generated by the model in (2.3), where R is of the form in Equation (3.5) and T is a linear transformation, and that (B.2)–(B.6) hold. Then,

$$\underset{\theta \in \mathrm{\Theta }}{sup}\mid e(\theta )-\mathrm{\Phi }\{-u_n(\theta )\}\mid \to 0,$$ (3.8)

where the convergence is in probability.

To elucidate the implications of Theorem 1, observe first that the asymptotic error rate, Φ(−u_n), in Equation (3.8) is a monotone decreasing function of u_n. It therefore follows from the formula in Equation (3.7) for u_n(θ) that the error rate decreases as either the distance, represented by α_n, between population means increases or the error variance, ${\sigma }_n^2$, decreases. Moreover, Hölder’s inequality implies that Φ{−u_n(θ)}, interpreted as a functional of φ_ωQθ, is minimized when φ_ωQθ = φ_ωR, that is, when the transformation Q_θ is identical to the actual transformation R.

3.4 Consistency of Cross-Validation Estimator of Error Rate

Recall the definition of ê(θ), the cross-validation estimator of error rate, in Equation (3.2). Theorem 2 shows that ê(θ) shares the same asymptotic property, Equation (3.8), as the actual error rate e(θ), and therefore, is consistent for e(θ), uniformly in θ.

Theorem 2

Assume the conditions of Theorem 1. Then,

$$\underset{\theta \in \mathrm{\Theta }}{sup}\mid \widehat{e}(\theta )-\mathrm{\Phi }\{-u_n(\theta )\}\mid \to 0,$$ (3.9)

where the convergence is in probability.

Similarly, it can be proved that if θ = θ̂ is chosen to minimize ê(θ), and used when constructing the classifier, then, under mild additional assumptions, the classifier’s actual error rate will equal min_θ∈Θ Φ{−u_n(θ)} + o(1) as n → ∞.

4. NUMERICAL WORK

4.1 Goals of Simulations

We performed simulation studies to illustrate the following properties:

1. Transforming the data by T⁻¹ prior to applying a classifier generally does not improve classification performance.

2. Transforming the data using a cross-validation-based transform ${\widehat{Q}}_{\theta }^{-1}$ generally improves classification performance even if $Q_{\theta }^{-1}$ is only a rough approximation to the best transform to apply.

   (3) The more the errors ε_ij are correlated, the larger is the improvement at (2), especially if the error variance σ² is large compared with T μ_j.

3. The performance of classifiers, applied to data transformed by ${\widehat{Q}}_{\theta }^{-1}$, improves as the training sample size and/or the fineness of the grid 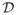increases.

4.2 Simulation Setup

4.2.1 Generation of Training Samples

We generated training samples {Y₁₁, …, Y_1n1} and {Y₂₁, …, Y_2n2}, of sizes n₁ = n₂ = 10 or n₁ = n₂ = 25, according to the model

$$Y_{ij}(r)=T{\mu }_j(r)+R{\xi }_{ij}(r),$$ (4.1)

for different curves μ_j, j = 1, 2, and transformations R and T, and with r ∈ 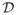⊂ ℝ or r = (r₁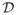, r₂) ∈ ⊂ ℝ².

We considered four pairs of mean curves μ_j, for j = 1, 2 (two univariate and two bivariate), each with several features, such as asymmetric peaks and valleys, or sinusoidal components:

1. μ_j (r) = |2r − a_j|^4/5 exp{−5 · 10⁻⁴(4r² − b_j)}, where a₁ = 5, b₁ = 100, a₂ = 4, b₂ = 80.

2. ${\mu }_j(r)=9/16·c_j^{-2}{(2r-50)}^2/{\{1.2+cos(r)\}}^2$, where, c₁ = 200, c₂ = 190.

3. ${\mu }_j(r_1,r_2)={\mid 3r_2-a_j\mid }^{2/5}exp\{-45·{10}^{-4}(r_1^2+2r_1{r}_2+r_2^2-b_j/9)\}$, with a_j and b_j as in (a).

4. μ_j(r₁, r₂) = 0.1|4 + 3r₂/50|^1/5 · exp{−(3r₁ + 20)/d_j}/{1.2 + cos(1.5r₁)} · 1_{[−20/3,∞)}(r₁),

   where d₁ = 40, d₂ = 50, and 1_{[−20/3,∞)}(r₁) = 1 if r₁ ∈ [−20/3, ∞) and 0 otherwise.

In the previous sections, the method was discussed for a grid that had edge width 1. More generally, in our simulations, we also considered examples where the grid has edge width k. In that case, the various transformations have to be rescaled by a factor k. More precisely, if a transform F has the form F ξ (r) = Σ_s∈ℤ^d ω_F(s) ξ (r − s) on a grid of edge width 1, on a grid of edge width k, it becomes $F\xi (r)=k_{\mathcal{I}}^d{\sum }_{s\in {\mathbb{Z}}_{k_{\mathcal{I}}}^d}{\omega }_F(s)\xi (r-s)$, where ℤ_k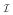 = {s/k, s ∈ ℤ}. Reflecting this discussion, we took $T{\mu }_j(r)=k_{\mathcal{I}}^d{\sum }_{s\in {\mathbb{Z}}_{k_{\mathcal{I}}}^d}{\omega }_{p_0;{\theta }_T}(s){\mu }_j(r-s)$ and

$$R\xi (r)=k_{\mathcal{I}}^d\sum _{s\in {\mathbb{Z}}_{k_{\mathcal{I}}}^d}{\omega }_{p_0;{\theta }_R}(s)\xi (r-s),$$ (4.2)

where ω_p0;θ is the function defined above (2.5), with θ = θ_T (ℓ_T, ρ_T) or θ = θ_R = (ℓ_R, ρ_R). In our bivariate models (c) and (d), we also considered

$$R\xi (r_1,r_2)=k_{\mathcal{I}}^2\sum _{s\in {\mathbb{Z}}_{k_{\mathcal{I}}}^2,\mid s_j+r_j\mid \le {\theta }_M/k_{\mathcal{I}}}{\omega }_M(\mid s_1+r_1\mid )\times {\omega }_M(\mid s_2+r_2\mid )\xi (r_1-s_1,r_2-s_2),$$ (4.3)

where, for u ∈ ℤ⁺, ω_M (u) = (θ_M + 1 − u)/Σ_u≤θM (θ_M + 1 − u), with θ_M being a positive integer.

In each case, we considered several different values of θ_R in (4.2), or θ_M in (4.3), and we took the ξ_ij (r) to be independent normal N(0, σ²). Each combination of σ and θ_R or θ_M was chosen such that good classification was possible for at least one of the versions of the centroid classifier described below; see Tables A.1–A.3 in Section A.3.1, in the supplementary materials, for all the combinations we considered in practice, and for a measure of signal-to-noise ratio in each case. Finally, we took the parameter θ_T of the transform T and the grid 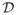where the data are observed as follows:

• Model (a): θ_T = (0.5, 3) and 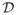= {−80, −80 + k, …, 80 − k, 80}.

• Model (b): θ_T = (0.5, 2) and 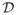= {−80, −80 + k, …, 80 − k, 80}.

• Models (c) and (d): θ_T = (0.25, 2) and 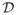= {−60, −60 + k, …, 60 − k, 60}×{−40, −40 + k, …, 40−k, 40}.

In each case, k = 2 when n₁ = n₂ = 10, and k = 1 or 2 when n₁ = n₂ = 25. In particular, when n₁ and n₂ were increased, we let the grid 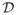become finer by decreasing k from 2 to 1 so as to illustrate point (4) in Section 4.1. We also ran simulations in the unbalanced case, where n₁ = 10 and n₂ = 25, and obtained results similar to those we shall discuss below; see Figures A.4 and A.5 in Section A.3.4 in the supplementary materials.

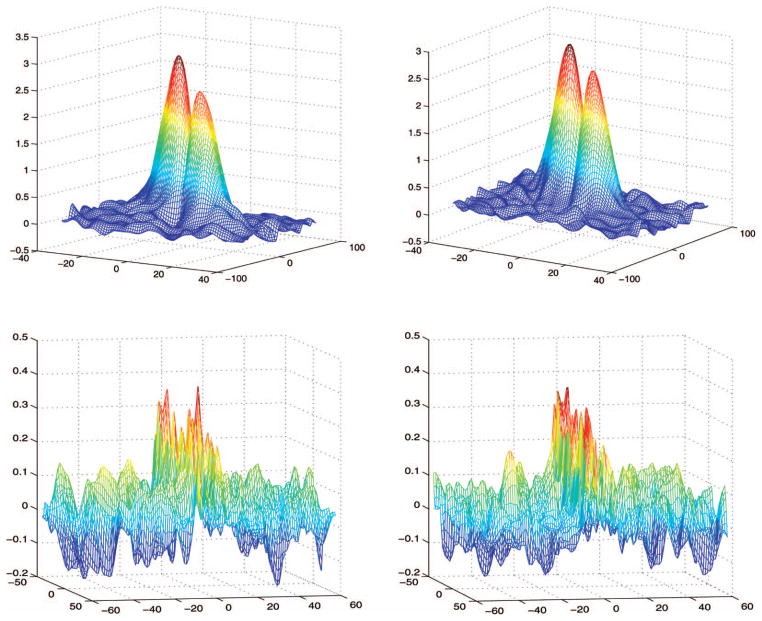
For illustration, Figure 1 shows Y₁₁ and Y₁₂ in models (c) and (d), with θ_R = (0.5, 3). Comparing with Figure 9 in Section 4.5, we can see that model (d) looks similar to our empirical example discussed in Section 4.5.

Figure 1.

Plots of Y₁₁ (left) and Y₁₂ (right), in models (c) (row 1) and (d) (row 2) with θ_R = (0.5, 3). The online version of this figure is in color.

Figure 9.

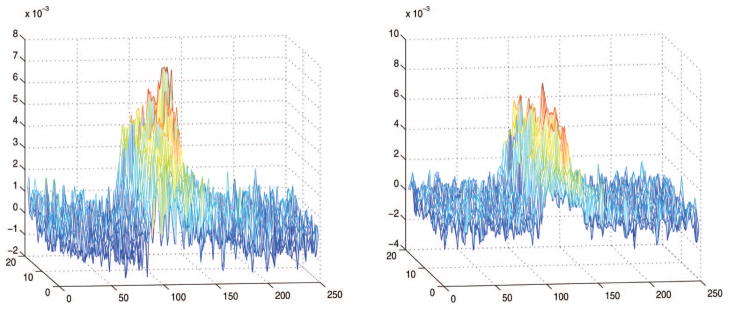
Plots of two background-corrected received data curves from population 1 (left) and population 2 (right), averaged over the 20 bursts, across wavelength and the backscatter spectral range. The online version of this figure is in color.

4.2.2 Model for Q_θ, Generation of Test Samples and Estimation of Error Rate

No matter what model we used for R, we systematically modeled Q_θ by

$$Q_{\theta }\xi (r)=k_{\mathcal{I}}^d\sum _{s\in {\mathbb{Z}}_{k_{\mathcal{I}}}^d}{\omega }_{p_0;\theta }(s)\xi (r-s),$$ (4.4)

with θ = (ℓ_Q, ρ_Q). This model is flexible, and, as discussed in detail in Section 2.3, it has attractive practical properties such as the fact that we do not need any smoothing parameters to define 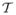in Equation (2.8), which can be taken equal to 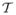= (−π, π)^d.

To test our classifier constructed from the training observations Y_ij, we generated test samples of N = 100 new data curves $Y_1^{\text{New}},\dots ,Y_{100}^{\text{New}}$, of which half came from Π1 and the other half came from Π₂, using each time the same model as the one used to generate the Y_ij’s. We applied several classifiers to three versions of the $Y_i^{\text{New}}$’s: the untransformed noisy data $Y_i^{\text{New}}$, the data $T^{-1}{Y}_i^{\text{New}}$, and the data ${\widehat{Q}}^{-1}{Y}_i^{\text{New}}$, where Q̂ denotes Q_θ̂CV, with Q_θ as in (4.4), and with θ = θ̂_CV chosen to minimize the cross-validation estimator of the classification error rate, as in Section 2.3.3, where we took π₁ = n₁/(n₁ + n₂). When R was of the form in Equation (4.2), we also applied the classifiers to the data $R^{-1}{Y}_i^{\text{New}}$.

As indicated above, we chose θ = (ρ, ℓ) to minimize the cross-validation estimator of classification error rate, where we performed the minimization over a bivariate grid of values in the range 0 ≤ ρ ≤ 0.95 and 1 ≤ ℓ ≤ 5. Here, ρ = 0 denotes the identity transform, and when ρ = 0, we do not transform the data. Observe that, in our simulations and examples, the sizes of the training datasets are small, and there is little computational cost. In larger datasets, one would use k-fold cross-validation, that is, the training data would consist of a randomly selected (1 − k⁻¹) × 100% of the data, and the test data, the remaining (100/k)%, with this procedure repeated many times to calculate an overall error rate. Wikipedia has a good description of this approach (http://en.wikipedia.org/wiki/Cross-validation_(statistics)); see also McLachlan, Do, and Ambroise (2004).

In practice, the transform T is often unknown and is not necessarily invertible. In such cases, instead of using T⁻¹, one has to use a regularized estimator T̂⁻¹ constructed from the data (see our real-data illustration). Here, for simplification, we take T as both known and invertible. While this may seem to be unfavorable to our approach, it actually does not matter since our point is to show that T⁻¹ has essentially no role to play in our classification problem, and whether T⁻¹ is known or estimated does not change our conclusions.

In each model, we generated B = 100 training samples, and for each training sample, we generated a test sample of N = 100 new data curves as described above, which we classified in one of the two populations using each of the methods described in the previous paragraph. For each training sample, we calculated the percentage of the new curves that were misclassified by each method. We obtained B = 100 misclassification percentages for each method, and the boxplots shown in Figures 2–8 were computed from these 100 percentages.

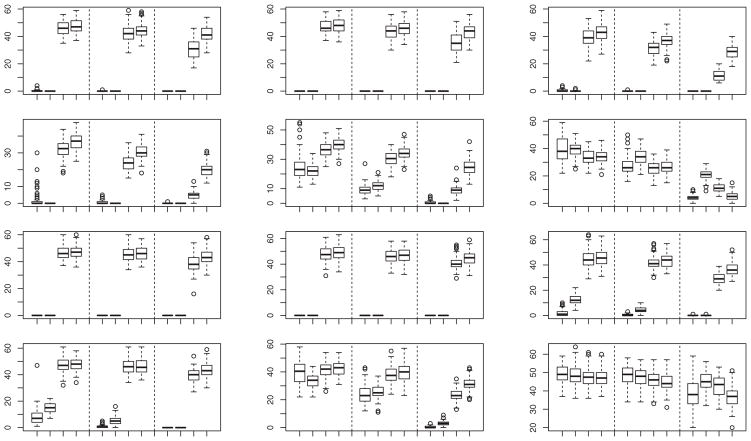
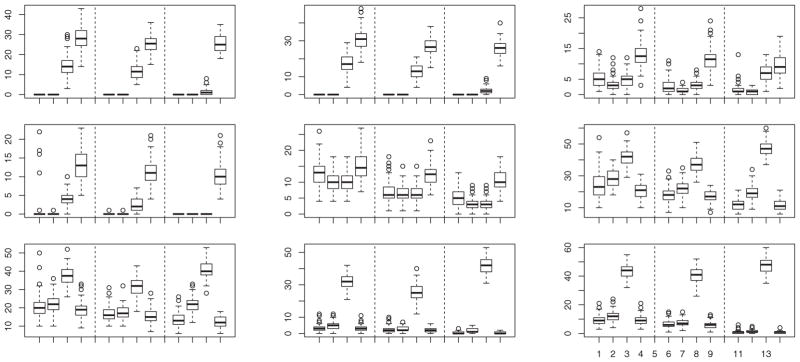
Figure 2.

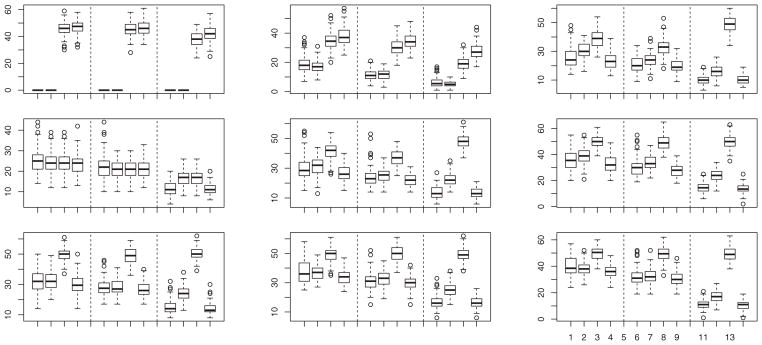
Boxplots of percentage of misclassified observations calculated from 100 simulated samples from model (a) when θ_R = (ρ_R, ℓ_R), with ρ_R = 0.75, 0.5, and 0.25 in rows 1, 2, and 3, respectively; and ℓ_R = 3, 2, and 1 in columns 1, 2, and 3, respectively. In each group of 12 boxes, the first four are for n₁ = n₂ = 10 and k = 2, the next four are for n₁ = n₂ = 25 and k= 2, and the last four are for n₁ = n₂ = 25 and k = 1. In each group of four boxes, the data are transformed by Q̂⁻¹ (first box), R⁻¹ (second box), or T⁻¹ (third box), or are untransformed (fourth box).

Figure 8.

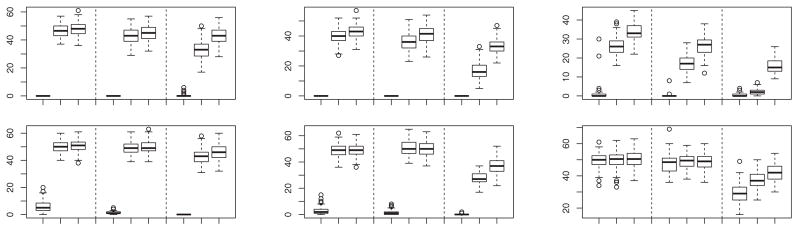
Boxplots of percentage of misclassified observations calculated from 100 simulated samples from models (c) (row 1) and (d) (rows 2) when R_r is of the form at (4.7), with θ_M,rj = θ_M + 2 · [2 cos(r_j/2)] and θ_M = 30, 20, and 10 in columns 1, 2, and 3, respectively. In each group of nine boxes, the first three are for n₁ = n₂ = 10 and k = 2, the next three are for n₁ = n₂ = 25 and k = 2, and the last three are for n₁ = n₂ = 25 and k = 1. In each group of three boxes, the data are transformed by Q̂⁻¹ (first box) or T⁻¹ (second box), or are untransformed (third box).

4.3 Simulation Results for Centroid Classifier

4.3.1 Data Coming From the Model in (4.1)

We start by reporting results obtained when applying the centroid classifier described in Section 3.1 to data generated from the model in Equation (4.1). In cases where ê achieved its minimum at several values θ, we broke the ties according to the rule described in Section A.1 in the supplementary materials. The boxplots corresponding to each of the four methods described above, for R of the form in Equation (4.2), are shown in Figures 2–4. We present the results for various values of θ_R = (ρ_R, ℓ_R), for n₁ = n₂ = 10 and k = 2, n₁ = n₂ = 25 and k = 2, and for n₁ = n₂ = 25 and k = 1, where k is the distance between two adjacent univariate components of the grid 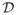. Our finite-sample results support our asymptotic theory, which implies that as n₁ and n₂ increase (i.e., as training sample size increases) and k decreases (i.e., as the grid 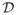becomes finer), the best results should be obtained by the centroid classifier applied to the data inverted by R⁻¹, of which $Q_{{\widehat{\theta }}_{\text{CV}}}^{-1}$ is a consistent estimator.

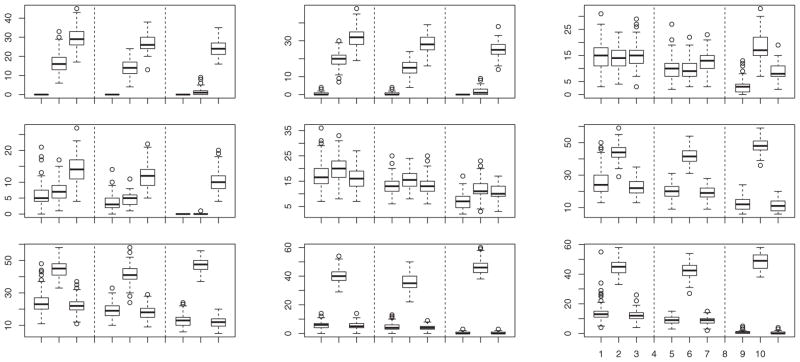
Figure 4.

Boxplots of percentage of misclassified observations calculated from 100 simulated samples from models (c) (rows 1 and 2) and (d) (rows 3 and 4) when θ_R = (ρ_R, ℓ_R), with ρ_R = 0.85 and 0.5 in rows 1, 3 and 2, 4, respectively; and ℓ_R = 3, 2, and 1 in columns 1, 2, and 3, respectively. In each group of 12 boxes, the first four are for n₁ = n₂ = 10 and k = 2, the next four are for n₁ = n₂ = 25 and k = 2, and the last four are for n₁ = n₂ = 25 and k = 1. In each group of four boxes, the data are transformed by Q̂⁻¹ (first box), R⁻¹ (second box), or T⁻¹ (third box), or are untransformed (fourth box).

Overall, our results indicate that, in finite samples, it is the latter cross-validation approach that is the most competitive. This is because this method has the ability to optimize performance based on the particular sample at hand. Unsurprisingly, transforming the data through R⁻¹ and $Q_{{\widehat{\theta }}_{\text{CV}}}^{-1}$ brings the most significant improvements when ρ_R and ℓ_R are the largest, since it is in these cases that the correlation among the ε_ij’s is the greatest. For smaller values of ρ_R and ℓ_R (e.g., ρ_R = 0.25 and ℓ_R = 1), the correlation among the ε_ij’s is relatively small, and as a result, in finite samples, the centroid method applied to the untransformed data $Y_{ij}^{\text{New}}$ is often the most competitive approach, although even in these cases, the cross-validation approach remains highly competitive. Of course, in practice, we do not know the transformation R, and our results indicate that cross-validation-based inversion is the method of choice.

4.3.2 Robustness Against Misspecification of R

Next, we illustrate the robustness of the inversion procedure by reporting the results obtained when applying the centroid classifier to the data $Q_{{\widehat{\theta }}_{\text{CV}}}^{-1}{Y}_i^{\text{New}}$, with Q as in Equation (4.4), when the true transform R was of another form, specifically the one in Equation (4.3), where we took θ_M = 10, 20, or 30. We compare this approach with the centroid-based classifier based on the data $T^{-1}{Y}_i^{\text{New}}$ and with the one based on the data $Y_i^{\text{New}}$. We show boxplots of the percentage of misclassified data curves in Figure 5, for each of the three methods and for n₁ = n₂ = 10 and k = 2, n₁ = n₂ = 25 and k = 2, and n₁ = n₂ = 25 and k = 1. Our results indicate that even if Q_θ at (4.4) is not the exact noise transformation, inverting the data through $Q_{{\widehat{\theta }}_{\text{CV}}}^{-1}$ can considerably improve on the centroid classifier based on either $T^{-1}{Y}_i^{\text{New}}$ or the untransformed data $Y_i^{\text{New}}$.

Figure 5.

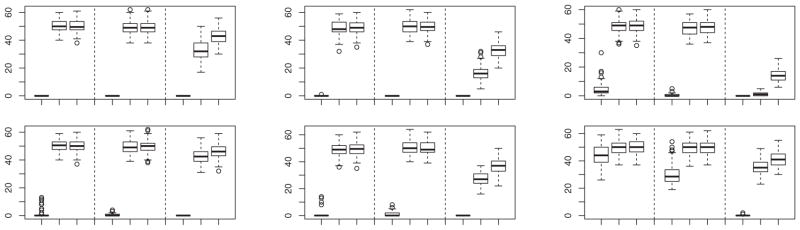
Boxplots of percentage of misclassified observations calculated from 100 simulated samples from models (c) (row 1) and (d) (rows 2) when R is of the form at (4.3), with θ_M = 30, 20, and 10 in columns 1, 2, and 3, respectively. In each group of nine boxes, the first three are for n₁ = n₂ = 10 and k = 2, the next three are for n₁ = n₂ = 25 and k = 2, and the last three are for n₁ = n₂ = 25 and k = 1. In each group of three boxes, the data are transformed by Q̂⁻¹ (first box) or T⁻¹ (second box), or are untransformed (third box).

4.3.3 Robustness Against the Stationarity Assumption

In practice, the model in Equation (4.1) is often an approximation to the model that generated the data. In this section, to investigate the effect of nonstationarity of the errors on our procedure, we report results of simulations where the data Y_ij were generated from the model

$$Y_{ij}(r)=T{\mu }_j(r)+R_r{\xi }_{ij}(r),$$ (4.5)

with the fixed transform R replaced by a transform R_r, depending on r.

In the univariate case, instead of R in Equation (4.2), we used

$$R_r\xi (r)=k_{\mathcal{I}}^d\sum _{s\in {\mathbb{Z}}_{k_{\mathcal{I}}}^d}{\omega }_{p_0;{\theta }_r}(s)\xi (r-s),$$ (4.6)

with θ_r = (ρ_r, ℓ), where ρ_r = ρ + 0.1 cos(r/α) (we considered two cases: α = 2 and α = 10) and ρ and ℓ are as in the previous section. In the bivariate case, instead of using the transform R in Equation (4.3) with constant θ_M, we used the transform

$$R_r\xi (r_1,r_2)=k_{\mathcal{I}}^2\sum _{s\in {\mathbb{Z}}_{k_{\mathcal{I}}}^2,\mid s_j+r_j\mid \le {\theta }_{M,r_j}/k_{\mathcal{I}}}{\omega }_{M,r_1}(\mid s_1+r_1\mid ){\omega }_{M,r_2}\times (\mid s_2+r_2\mid )\xi (r_1-s_1,r_2-s_2),$$ (4.7)

where, for u ∈ ℤ⁺ and j = 1, 2, ω_M,rj (u) = (θ_M,rj + 1 − u)/Σ_u≤θM,rj (θ_M,rj + 1 − u), with θ_M,rj = θ_M + 2 · [α cos(r_j/2)] (we considered two cases: α = 2 and α = 4), θ_M is as in the previous section, and, for any real number x, we use [x] to denote the integer closest to x.

Although, here, the errors R_r ξ_ij (r) were nonstationary, we inverted the data in the same way as before, using the transform $Q_{{\widehat{\theta }}_{\text{CV}}}^{-1}$. Figures 6 and 7 show boxplots of the percentage of misclassified curves for the centroid classifier constructed from the data $Q_{{\widehat{\theta }}_{\text{CV}}}^{-1}{Y}_{ij}$, Y_ij, and T⁻¹ Y_ij, where Y_ij was generated as in Equation (4.5), with μ_j from model (a) and model (b), respectively, R_r as in (4.6), and α = 2. For the case α = 10, see Figures A.1 and A.2 in the supplementary materials. Figure 8 shows similar results for the bivariate models (c) and (d), when the data were generated according to (4.5), with R_r as in Equation (4.7) and α = 2; see Figure A.3 in the supplementary materials for the case α = 4. These results indicate that our inversion method can improve classification performance significantly even when the errors are not exactly stationary; it usually does not degrade performance more than a little.

Figure 6.

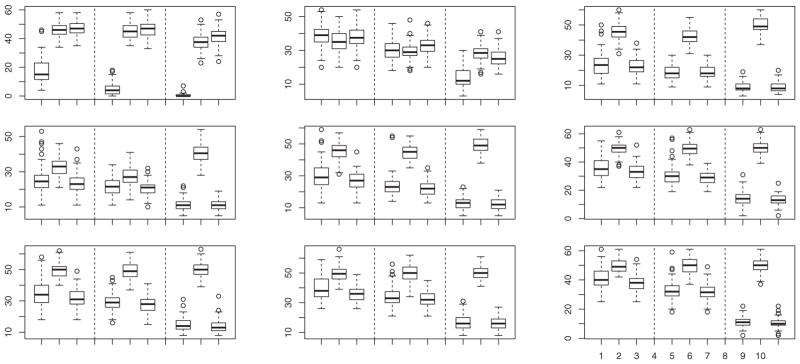
Boxplots of percentage of misclassified observations calculated from 100 simulated samples from model (a) when θ_R = (ρ_R,r, ℓ_R), with ρ_R,r = ρ_R + 0.1 cos(r/2); ρ_R = 0.75, 0.5, and 0.25 in rows 1, 2, and 3, respectively; and ℓ_R = 3, 2, and 1 in columns 1, 2, and 3, respectively. In each group of nine boxes, the first three are for n₁ = n₂ = 10 and k = 2, the next three are for n₁ = n₂ = 25 and k 2, and the last three are for n₁ = n₂ = 25 and k = 1. In each group of three boxes, the data are transformed by Q̂⁻¹ (first box) or T⁻¹ (second box), or are untransformed (third box).

Figure 7.

Boxplots of percentage of misclassified observations calculated from 100 simulated samples from model (b) when θ_R = (ρ_R,r, ℓ_R), with ρ_R,r= ρ_R + 0.1 cos(r/2); ρ_R = 0.75, 0.5, and 0.25 in rows 1, 2, and 3, respectively; and ℓ_R = 3, 2, and 1 in columns 1, 2, and 3, respectively. In each group of nine boxes, the first three are for n₁ = n₂ = 10 and k = 2, the next three are for n₁ = n₂ = 25 and k = 2, and the last three are for n₁ = n₂ = 25 and k = 1. In each group of three boxes, the data are transformed by Q̂⁻¹ (first box) or T⁻¹ (second box), or are untransformed (third box).

4.4 Other Classifiers

Although it is beyond the scope of this article to develop theory for all types of classifiers, and derive the theoretically optimal transform for each of them, we argue that our conclusions extend to other classifiers. To illustrate this, we also implemented two other classifiers often employed in high-dimensional and functional data problems, which we applied to the four versions of the data: Y_ij, T⁻¹ Y_ij, R⁻¹ Y_ij, and $Q_{{\widehat{\theta }}_{\text{CV}}}^{-1}{Y}_{ij}$, with θ̂_CV chosen to minimize the cross-validation estimate of classification error. Namely, we used the support vector machine (SVM) classifier with a linear kernel (svmtrain in MATLAB) and the logistic classifier applied to the partial least-square (PLS) projection of the data (here, data refer to any of the four versions, transformed or not, of the data); see Delaigle and Hall (2012b) and Section A.3.3 in the supplementary materials for more details on the logistic classifier, and see Delaigle and Hall (2012a) for properties of PLS in the functional context.

Boxplots summarizing the results of our simulations, in the same settings as for the centroid classifier, are shown in Figures A.6–A.11 in Section A.3.5 in the supplementary materials. From these figures, we can see that the results obtained with these two classifiers are very similar to those obtained with the centroid classifier. In other words, inverting by T⁻¹ usually did not improve the results, and, in general, inverting by the transform $Q_{{\widehat{\theta }}_{\text{CV}}}^{-1}$, chosen by cross-validation from the data, improved the results significantly (compared with using the data Y_ij or T ⁻¹ Y_ij) or, when the latter worked well, transforming the data by $Q_{{\widehat{\theta }}_{\text{CV}}}^{-1}$ did not degrade performance much.

As already noted, the best transform to apply generally depends on the particular classifier. However, an attractive aspect of our methodology is that the suggested inversion, $Q_{{\widehat{\theta }}_{\text{CV}}}^{-1}$, is chosen to minimize a cross-validation estimator of classification error. Therefore, our approach is very flexible, since in a general setting, it approximates the inverse transform that optimizes classification.

4.5 Empirical Example

We have access to data from a small experiment involving long-range infrared Lidar methods. Briefly, the idea is to discriminate between two types of aerosols that have been emitted and are to be detected by Lidar: those that are biological in nature and those that are nonbiological. There are 29 curves available to us, with n₁ = 15 nonbiological and n₂ = 14 biological signals.

The process involves a signal or waveform sent out in a series of bursts, and received Lidar data were observed. Some of the bursts were sent before the aerosol was released, and these were used to background-correct the received signal after the aerosol was released. For each sample, the data used here are the background-corrected received signals for a burst, 19 wavelengths, and 250 backscatter time points. In our illustrative analysis, we followed the procedure described below for 20 bursts collected almost simultaneously in the middle of the release period and then averaged over the bursts before classification. Thus, in our notation, Y_ij consists of the two-dimensional collection of background-corrected received signals over the wavelengths and the backscatter time points for the ith sample within the j th aerosol class. These observed data are the convolution of a true signal, the Lidar response function for a delta-pulse transmitter, with the transmitted signal. If we write 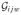(t) for this true signal for wavelength w at backscatter time point t, R_ijw(t) for the background-corrected received signal, and 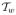(t) for the transmitted signal, then, using an integral approximation to the discrete convolution, the signal we observe is

$$R_{\mathit{ijw}}(t)={\int }_0^t{\mathcal{G}}_{\mathit{ijw}}(t-v){\mathcal{T}}_w(v)dv+{\kappa }_{\mathit{ijw}}(t),$$

where ξ_ijw(t) has mean zero. If we define 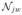(t) = E{ 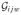(t)}, ${\mathcal{M}}_{jw}(t)={\int }_0^t{\mathcal{N}}_{jw}(t-v){\mathcal{T}}_w(v)dv$, and ${\mathcal{P}}_{\mathit{ijw}}(t)={\int }_0^t\{{\mathcal{G}}_{\mathit{ijw}}(t-v)-N_{jw}(t-v)\}{\mathcal{T}}_{\mathit{ijw}}(v)dv+{\kappa }_{\mathit{ijw}}(t)$, then we have that the observed data are given by R_ijw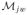(t) = (t) + 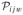(t), where 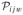(t) has mean zero. In our notation, Y_ij, μ_j, T μ_j, and ε_ij are the collection of R_ijw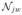(t), (t), 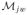(t), and 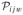(t) over the wavelengths and backscatter ranges, respectively, but averaged across 20 bursts. It is readily observed that the transformation T μ_j is linear. Two typical observed average curves for each population are given in Figure 9.

We considered three approaches. The first simply used the observed data Y_ij. The second was our method applied to the $Q_{{\widehat{\theta }}_{\text{CV}}}^{-1}{Y}_{ij}$, where Q_θ had the form as in Equation (4.4). In the third, for each burst and each wavelength, we deconvolved to estimate 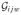(t) using the Wiener–Helstrom method described by Warren et al. (2008), and averaged over the bursts. In each case, since we could not generate new data, we estimated the misclassification error rate (i.e., misclassification percentage) by cross-validation. In other words, as in the case of the procedure described in Section 2.3.3, we built the classifier from all but one of the 29 curves, classified that curve in one of the two populations (nonbiological or biological), and averaged the results over all 29 curves.

For the centroid classifier, the cross-validation estimator of the misclassification error rate was 34.5% for the first approach based on nontransformed data, 24.1% for our cross-validation-based inversion approach, and 34.5% for the third approach based on inversion of T. For the SVM and logistic regression classifiers, the estimator of the misclassification error rate was 37.9% (SVM) or 27.6% (logistic) when the classifier was based on nontransformed data, 17.2% (SVM) or 21% (logistic) when the classifier was based on our cross-validation-based inversion method, and 58.6% (SVM) or 31% (logistic) when the classifier was based on inversion of T. For all three classifiers, the reduction in the misclassification error rate obtained by our cross-validation-based data inversion illustrates the significant improvement that can be obtained by inverting the data through a data-driven transform chosen to minimize an estimator of classification error.

Figure 3.

Boxplots of percentage of misclassified observations calculated from 100 simulated samples from model (b) when θ_R = (ρ_R, ℓ_R), with ρ_R = 0.75, 0.5, and 0.25 in rows 1, 2, and 3, respectively; and ℓ_R = 3, 2, and 1 in columns 1, 2, and 3, respectively. In each group of 12 boxes, the first four are for n₁ = n₂ = 10 and k = 2, the next four are for n₁ = n₂ = 25 and k = 2, and the last four are for n₁ = n₂ = 25 and k = 1. In each group of four boxes, the data are transformed by Q̂⁻¹ (first box), R⁻¹ (second box), or T⁻¹ (third box), or are untransformed (fourth box).