Multistate approaches in computational protein design

Abstract

Computational protein design (CPD) is a useful tool for protein engineers. It has been successfully applied towards the creation of proteins with increased thermostability, improved binding affinity, novel enzymatic activity, and altered ligand specificity. Traditionally, CPD calculations search and rank sequences using a single fixed protein backbone template in an approach referred to as single-state design (SSD). While SSD has enjoyed considerable success, certain design objectives require the explicit consideration of multiple conformational and/or chemical states. Cases where a “multistate” approach may be advantageous over the SSD approach include designing conformational changes into proteins, using native ensembles to mimic backbone flexibility, and designing ligand or oligomeric association specificities. These design objectives can be efficiently tackled using multistate design (MSD), an emerging methodology in CPD that considers any number of protein conformational or chemical states as inputs instead of a single protein backbone template, as in SSD. In this review article, recent examples of the successful design of a desired property into proteins using MSD are described. These studies employing MSD are divided into two categories—those that utilized multiple conformational states, and those that utilized multiple chemical states. In addition, the scoring of competing states during negative design is discussed as a current challenge for MSD.

Introduction

Protein engineers strive to create new proteins to serve a specific and desired function by altering the sequence of existing proteins. Because protein sequence space is astronomically vast, a major hurdle to overcome is the identification of beneficial mutations required to access the desired protein property. Computational protein design (CPD) is a useful tool for protein engineers as it allows for the in silico evaluation of amino acid sequences on a scale that is experimentally impossible to achieve.¹ CPD originated as a means to understand the forces which govern protein stability;^{2, 3} however, over the last two decades, CPD has been used to create new proteins with desired properties. For example, CPD has been successfully applied towards (i) the creation of proteins with increased stability,^{2, 4} (ii) the creation of de novo enzymes from catalytically inert protein scaffolds,^5–7 (iii) the introduction of new or altered binding specificity for metals,^8–10 small molecules,^{11, 12} peptides,¹³ proteins,^14–16 and DNA,¹⁷ (iv) the design of conformational switches,¹⁸ and (v) the creation of a novel protein fold not observed in nature.¹⁹ Thus, CPD not only tests and improves our knowledge of the forces that drive protein structure and function, but also allows us to search and harness the vastness of sequence space for the solution of real world chemical problems.²⁰

Computational protein design

CPD simulations traditionally require the following: (1) a protein backbone template, (2) a rotamer library containing a discrete set of conformations for all amino acid side chains to be tested, (3) a scoring function to rank rotamers in order of stability or desired function, and (4) an optimization algorithm to search through the combinations of rotamers to return the sequences with the best predicted scores. Backbone templates are often prepared from protein crystal structures; however solution NMR or molecular dynamics structures have also been used.^{21, 22} Generally, hydrogens are explicitly modeled in the design simulation and solvent is implicitly accounted for using a distance-dependent dielectric, a simplified surface area model,²³ or an occlusion based solvent model.^{24, 25} The preparation of template backbones can be completed with a coarse energy minimization to alleviate van der Waals clashes introduced as a result of the hydrogen addition process or those already present in the deposited crystal structure. After the backbone template has been prepared, the CPD calculation can begin by threading sets of discrete rotamers onto the template at specified positions. Following sequence optimization, the output returned by CPD algorithms is a list of ranked sequences based on their score value.

Single-state design experiments in computational protein design

Traditional CPD methodologies focus on the optimization of amino-acid sequences for coordinates from a single, fixed protein backbone template. This approach, referred to as single-state design (SSD) [Fig. 1(A)], is employed in positive design experiments whereby sequence space is searched to solve for a single desired function.²⁶ In SSD, undesired states, such as the unfolded and aggregated states, are implicitly designed against through the use of penalties added to the score of sequences expected to favor such undesired states. To date, most successful examples of CPD were achieved using the SSD approach. For instance, the application of SSD to improve protein stability has had considerable success,²⁷ leading to several hyperthermophilic variants of the well-studied β1 domain of Streptococcal protein G.^{2, 28} The SSD approach has also been used for the design of ligand binding specificity^{11, 13} as well as the design and introduction of new catalytic activity into proteins. For example, esterase,⁵ Kemp eliminase,^{6, 29} retro-aldolase,³⁰ and Diels-Alderase⁷ activities have all been successfully designed de novo using SSD.

Figure 1.

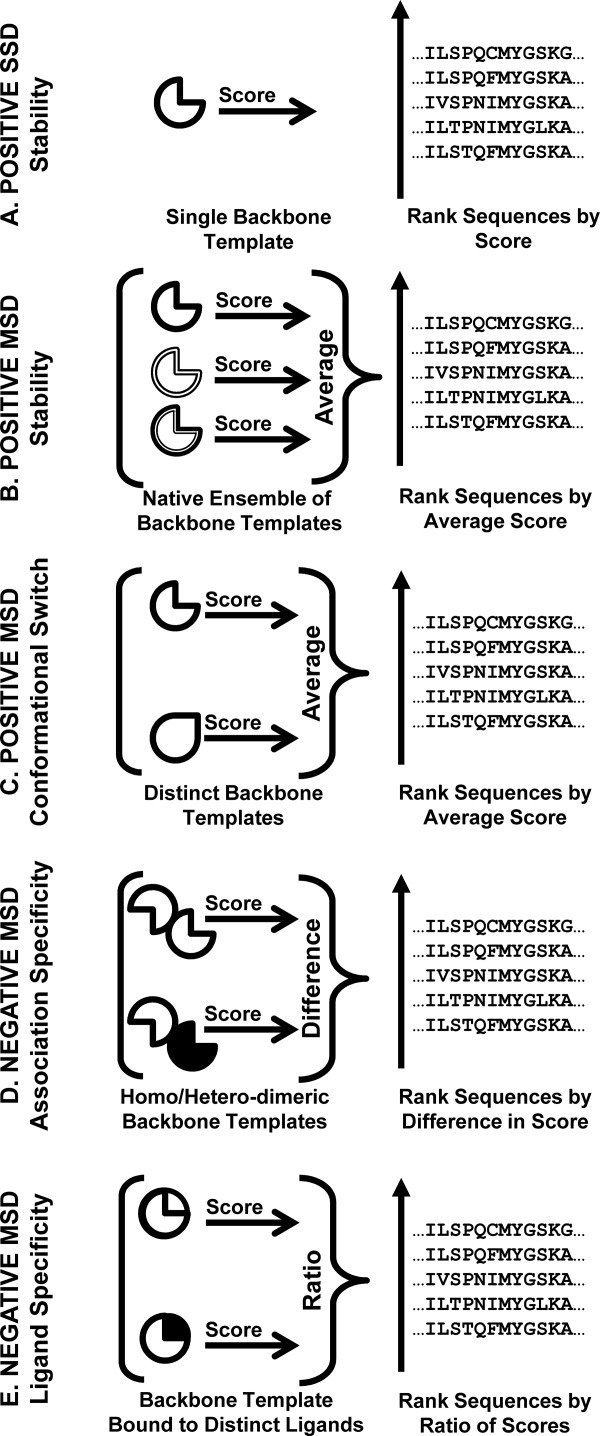
Examples of computational protein design. A: Improving the stability of a target protein fold by positive single-state design (SSD). B: Improving the stability of a target protein fold by positive multistate design (MSD). C: Designing sequences capable of adopting distinct folds by positive MSD. D: Designing oligomeric association specificity by negative MSD. E: Designing ligand binding specificity by negative MSD.

Multistate computational protein design

For the examples provided above, SSD has had success for two major reasons: the first is that the coordinates for the protein backbone template were suitable for the desired function and redesigned sequence, and the second, is that the simulation goals could be accomplished with the use of a positive design approach. However, in cases where multiple desired conformational or chemical states for a protein of interest, or cases where desired and undesired states (i.e., negative design) must be considered to design the desired property [Fig. 1(B–E)], SSD is expected to have reduced success. Cases where a “multistate” approach may be advantageous over the SSD approach include designing conformational changes into proteins, using native ensembles to mimic backbone flexibility, and designing ligand specificity or oligomeric association. All of the examples above are examples of multistate design (MSD), an emerging methodology in CPD that considers any number of protein conformational or chemical states as inputs instead of a single protein backbone template, as in SSD. MSD allows sequence selection to be driven by the energetic contributions of multiple conformational or chemical states simultaneously. In truth, all protein design problems are MSD problems because proteins are dynamic in nature since they are capable of adopting alternate local minima conformations^{31, 32} and these conformations can be further influenced and potentially stabilized by the binding of allosteric modifiers, small molecules and other proteins.³³ Additionally, proteins that bind ligands can exist in various chemical states such as the free and bound states. While SSD is well suited to positive design simulations for a single desired state, MSD is better suited to the application of simulations which require the explicit consideration of multiple adoptable states during sequence optimization.

From a computational standpoint, the major difference between MSD and SSD simulations is amino-acid sequence optimization. A multistate CPD simulation can be viewed as a collection of multiple independent single-state calculations whereby rotamers for a specific amino-acid sequence are optimized in the context of each of the conformational and/or chemical states used as input templates. This means that an amino-acid sequence will not adopt the same side-chain conformations in all states. In each of these single-state calculations, rotamer combinations are scored using typical scoring functions from SSD. In MSD, most or all single-state scores are then combined into a fitness value for each amino-acid sequence. This fitness value is a single value ranking for that amino-acid sequence across all states which reflects how well the sequence stabilizes the positive state(s), and in the context of negative design, how it also destabilizes the negative state(s) (Fig. 2). MSD optimization algorithms then attempt to optimize this fitness value as a function of amino-acid sequence. Many of the common optimization algorithms used in SSD have been adapted for MSD, including stochastic algorithms, such as Monte Carlo with simulated annealing,¹⁸ genetic algorithms,³⁴ and Fast and Accurate Side-Chain Topology and Energy Refinement (FASTER),³⁵ as well as deterministic algorithms such as dead-end-elimination.³⁶

Figure 2.

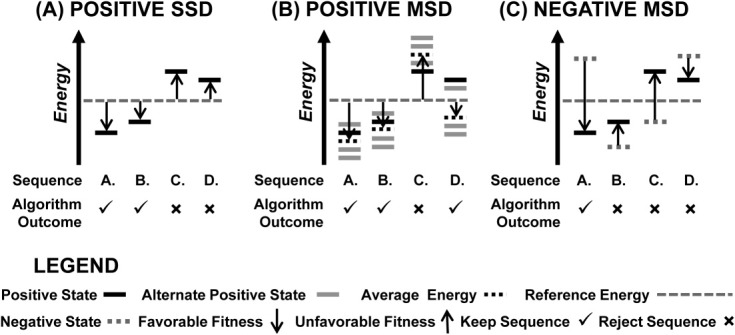
Sequence ranking and selection in single-state (SSD) and multistate (MSD) design. A: Positive SSD simulations rank a sequence using the energy from a single positive state. In this example, sequence A is kept and ranked as the best sequence because it has the largest favorable difference in energy between the single positive state and the reference energy. Sequence B is also kept although its difference in energy from the reference value ranks it lower than sequence A, while both sequences C and D are rejected as their difference in energy from the reference energy is positive and thus unfavorable. The ranking of kept sequences for this SSD example is A > B. B: Positive MSD simulations rank a sequence using the average energy over an ensemble of positive states and this average energy is used to rank the sequence relative to a reference energy. Here, sequences A and B are both kept as their average ensemble energy falls below the reference energy. Sequence C is rejected as it's ensemble average energy lies above the reference energy and sequence D is kept as its ensemble average energy is less than the reference energy, even though some of the states have an energy greater than the reference energy. The ranking of kept sequences for this MSD example is A > B > D. C: Negative MSD simulations rank a sequence by evaluating the difference in energy between the desired positive state and the competing negative state. Sequences favoring the negative state are ranked poorly. In this example, only sequence A is kept as it is the only sequence whose difference in energy between the positive and negative state is favorable and whose positive state energy falls below the reference energy. The remaining sequences (B, C and D) for this MSD example are rejected.

In this review article, recent examples of the successful design of a desired property into proteins using MSD will be described. These studies employing MSD are divided into two categories—those that utilized multiple conformational states, and those that utilized multiple chemical states. In all cases, the experimental validation of the MSD designs is described. In addition, the scoring of competing states during negative design is discussed as a current challenge for MSD.

Examples of Multistate Design

As described earlier, MSD accounts for alternate conformational and/or chemical states for all specified sequences during the CPD simulation. Alternate conformational states are included in CPD simulations by searching the same sequences on multiple different backbone templates, such as distinct folds or native ensembles [Fig. 1(B,C)]. This approach can be contrasted with the MSD of alternate chemical states which involves the simulation of the same sequences in search of alternate functions, for example, comparing sequence specificity for multiple ligands or for oligomeric association [Fig. 1(D,E)]. Both kinds of MSD simulations will be discussed below.

MSD applied to multiple conformational states

MSD can be used to design protein sequences that undergo large conformational changes depending on experimental conditions, in effect leading to protein switches whose conformation can be controlled via a desired stimulus. For example, in 2006, Ambroggio and Kuhlman engineered a conformational switch, referred to as Sw2, capable of reversibly adopting two distinct folds depending on the presence of transition metals.¹⁸ The first state, resembling a 2Cys-2His zinc finger fold, was stabilized in the presence of Zn(II) while the second state, involving assembly of the peptide into a trimeric coiled-coil fold, was favored in the absence of Zn(II) [Fig. 3(A)]. The engineering of Sw2 employed a MSD approach in which sequences were searched on two distinct protein backbones. These templates consisted of residues 13–44 of hemagglutinin from H. influenzae and residues 3–33 of the Zif268 zinc finger-DNA complex from M. musculus, corresponding to the desired coiled-coil and zinc finger conformations respectively. Rotamers were scored using the standard Rosetta energy function to which an additional scoring term based on the probability of finding specific amino acids at each position in multiple sequence alignments was added, and these scores were in turn used to compute the fitness of each sequence. The fitness of each sequence was computed as the score average for each sequence on both conformational templates. By selecting for sequences that stabilized both conformations, Ambroggio and Kuhlman performed a positive MSD simulation. The design objective for this particular example requires a MSD simulation because sequence optimization for a single conformation in a SSD approach does not guarantee the stabilization of the alternate, unconsidered, conformation.

Figure 3.

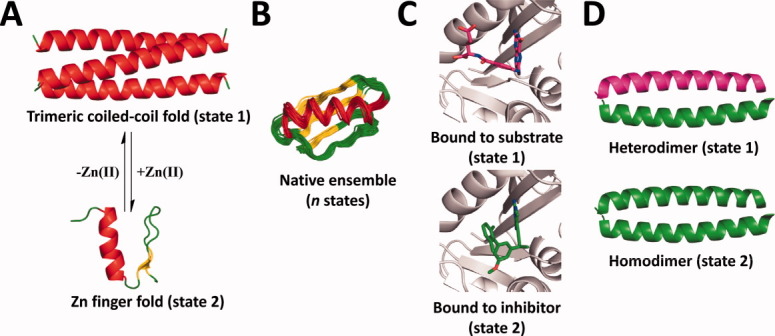
Input templates for examples of published multistate design experiments. A: Two distinct folds (a trimeric coiled-coil and a zinc finger fold) were used as inputs to design a conformational switch.¹⁸ B: Native ensembles of multiple backbone templates were used as input to design proteins with improved stability.²¹ C: Enzyme structures bound to either a substrate or an inhibitor were used as inputs to design for antibiotic resistance.⁴³ D: Coiled coil templates were used as inputs to design oligomeric association specificity.⁴⁵

To demonstrate the existence of the conformational switch, circular dichroism spectroscopy was employed to monitor the disappearance of the coiled-coil conformation in the presence of increasing concentrations of Zn(II). In corroboration with analytical ultracentrifugation data and circular dichroism (CD) spectroscopy experiments, the authors were able to support that the trimeric coiled-coil conformation of the designed Sw2 did exist in the absence of Zn(II). To conclusively demonstrate that the zinc finger conformation was achieved, cobalt absorption spectroscopy was used to show that the engineered Sw2 sequence did indeed bind Co(II) in a monomeric zinc finger fashion. Cobalt-bound Sw2 showed peaks at 310, 340, and 640 nm, consistent with what is observed for other Cys2-His2 zinc fingers. However, analytical ultracentrifugation experiments showed that Sw2 began to associate in a nonspecific manner at higher concentrations (>100 μM). This is an important observation as it demonstrates the consequence of not explicitly modeling undesired states in a negative design approach, in this case an aggregated state, during the CPD simulation. Another important consideration about this MSD example is that the sequences ability to undergo the conformational change itself was not explicitly designed for. Instead, the conformational change was expected to occur because the designed sequences were predicted to be stable in both conformational states. Despite the successful design of a conformational switch, the authors note that the current limitation of this approach lies in the ability to accurately compute the relative free energy values between the two conformations.

Another example of MSD applied to multiple conformational states was published by Allen et al.²¹ who used native backbone ensembles approximating the flexibility of proteins to design sequences that could improve the stability of a single fold belonging to the protein domain Gβ1 [Fig. 3(B)]. The overall goal was to test whether the use of native backbone ensembles in a MSD approach could predict higher quality sequences than the use of a single fixed backbone in a SSD approach. To test this, the authors used a variety of structural ensembles, including solution NMR structures as well as templates derived from constrained and unconstrained molecular dynamics (MD) simulations. These backbone ensembles were compared alongside a typical SSD simulation using a single crystallographic structure of wild type Gβ1. During the positive MSD simulation, each sequence was searched across all backbone templates and the energy of each sequence returned. To compute the fitness of each sequence across the ensemble, a Boltzmann weighted average function was used. Employing this averaging function ensured that sequences which were favored in the majority of states were not penalized by the few states which disfavored them. Stability of the sequence variants was then experimentally determined using a 96-well plate chemical denaturation assay.

It was found that significant improvement over the control SSD simulation was afforded only by the constrained MD backbone ensemble which gave sequences of similar or better stability to the wild type and returned no destabilized unfolded variants. The NMR solution structure ensemble gave 6 sequences with a stability similar or identical to that of the wild type, and 18 which were highly destabilized. The unconstrained MD ensemble performed the poorest as all 24 designed sequences failed to produce any significant fluorescence signal change during chemical denaturation, indicating that the chemical environment of the Trp fluorescence reporter is very different from that of the target structure. This observation, coupled with the low levels of protein expression for members of this library, suggests that the members of the unconstrained MD library likely assume structures that differ from the target structure. It is important to note that the backbone RMSD for the NMR ensemble, as well as the unconstrained and the constrained MD ensembles were 0.25, 0.84 and 0.12 Å, respectively.²¹ The unconstrained MD ensemble had the greatest RMSD from crystallographic structure and gave the poorest predictions of the three ensembles suggesting that larger deviations from the crystal structure may be responsible for predicting sequences that are incompatible with the target structure. There still remains a difference in the predictive capability between the NMR and the constrained MD ensembles which may be due, in part, to their respective deviation from the input crystallographic structure. These predictive differences may also arise because not all backbones included in NMR ensembles may be suitable to use as templates for CPD calculations.²² In each case, regardless of MSD ensemble or SSD template, the experimental stability and the simulation score for each sequence were not correlative. This suggests, once again, that there may be many more factors influencing the outcome and success of a MSD simulation than just the ensemble's RMSD from the input crystallographic structure. Nonetheless, this particular example demonstrates the improved predictive power that MSD can afford over SSD for the engineering of protein stability.

Backbone ensembles have also been used for the computational design of a pair of interacting proteins that is orthogonal to the wild-type proteins from which they were derived and that is capable of mediating complex biological processes within cells. In this study,¹⁶ two interacting proteins, the GTPase Cdc42 (Cdc42^WT) and its partner, the GTPase Exchange Factor named intersectin (ITSN^WT), were designed such that the new sequence variants, referred to as orthoCdc42 and orthoITSN respectively, would preferentially associate together over their wild-type parents. Following a computational alanine scan,³⁷ position 56 in Cdc42 was identified as the main candidate for affecting ITSN binding without perturbing other binding interactions that are required for the biological activity of Cdc42. Position 56 of Cdc42^WT and four positions on ITSN^WT (1369, 1373, 1376, and 1380) were then mutated in silico to introduce a specific interaction between the orthoCdc42 and its mutated binding partner, orthoITSN. Initially, the authors performed these in silico mutations using a positive SSD approach, however, Kapp et al. found that the use of a single fixed backbone template could not correctly predict mutations in ITSN that were specific to the identity of the mutated amino acid at position 56 of Cdc42. Failure to predict precisely the sidechain–sidechain interactions in a protein binding interface likely resulted from the use of a single fixed backbone, presumably by biasing the choice of rotamer during the simulation, a known artifact in CPD. To address this issue, a backbone ensemble generated using backrub motions^{38, 39} was used in design calculations where the identity but not the conformation of the mutated residue 56 was fixed while the four neighboring positions in ITSN were designed. This approach allowed for the identification of Glu at position 1373 in ITSN when an Arg residue is found at position 56 in mutated Cdc42, demonstrating that MSD yielded a specific interaction in the orthogonal binding site.

To validate the designed orthoCdc42 and orthoITSN pair, in vitro experiments were employed to examine the catalytic activity and thermal stability of the individual proteins, as well as the dissociation constant of the Cdc42^WT/ITSN^WT, Cdc42^WT/orthoITSN, orthoCdc42/ITSN^WT, and orthoCdc42/orthoITSN pairs. The first experiment monitored the catalysis of nucleotide exchange by ITSN using a fluorescently-labeled GDP analog. By measuring the loss of fluorescence as a function of time, Kapp et al. found that the mutant orthoITSN catalyzed nucleotide exchange in orthoCdc42, but not in Cdc42^WT, while ITSN^WT did not catalyze exchange in orthoCdc42, demonstrating that the designed pair maintained its activity. Thermal stability of each protein was monitored using CD spectroscopy. Thermal melts of the two wild-type and mutant proteins indicated a similar stability. The association specificity of orthoCdc42/orthoITSN was evaluated using surface plasmon resonance (SPR) spectroscopy to determine the dissociation constant (K_D) for the four possible pairs. SPR results indicated that the orthogonal pair, orthoCdc42/orthoITSN, associated specifically and preferentially (K_D = 478 ± 22 nM) while the non-cognate pairs, Cdc42^WT/orthoITSN and orthoCdc42/ITSN^WT, were not observed to associate. While specific, the designed orthogonal complex has approximately 16-fold weaker binding affinity than the wild-type Cdc42^WT/ITSN^WT complex (K_D = 29 ± 2 nM). Additional validation was done in an in vitro reconstituted system as well as in vivo in mammalian cells to demonstrate that the signal pathway's function was unimpeded when the wild-type Cdc42^WT/ITSN^WT pair was replaced with the designed orthoCdc42/orthoITSN pair.

The examples provided for MSD using multiple conformational states illustrate different ways of exploiting structural data for different design purposes. In one case, the multiple conformations were used to create a protein capable of undergoing a desired conformational change when exposed to a stimulus. In the other, the use of native backbone ensembles during a CPD simulation leads to a substantial improvement in the quality of output variants by simulation. In this latter example, improvements likely result from decreasing the number of false negatives, which occur because many rotamers, which could be compatible with slight changes in the backbone, would be considered sterically incompatible and be discarded because the protein backbone is not allowed to relax after rotamer placement.⁴⁰ Although researchers have focused on remodeling the backbone during the CPD simulation,⁴¹ in effect creating a flexible backbone that would be capable of tolerating rotamers that cause slight steric clashes, MSD with native ensembles that mimic backbone flexibility can be used as an alternative. For example, native backbone ensembles derived from molecular dynamics simulations, backrub motions, and kinematic closure refinement protocols have been used as inputs in MSD to recapitulate antibody–antigen interface amino acid residues that were experimentally observed by phage display.⁴² In the future, MSD with native ensembles could be combined with the design of desired properties such as ligand binding and oligomeric association to improve the quality of designs.

MSD applied to multiple chemical states

Multiple chemical states, such as protein/ligand complexes or oligomeric association of subunits, can be used in MSD to explicitly design for specificity using a negative design approach. One example of the application of MSD to modify ligand binding specificity is a study by Frey et al. who examined the effect of mutations to the antibiotic target dihydrofolate reductase of the methicillin resistant S. aureus on both inhibitor binding and catalytic activity.⁴³ In this article, Frey et al. sought to investigate whether or not mutations that conferred antibiotic resistance while maintaining catalytic activity could be predicted in an attempt to assist the drug design process. In this manner, MSD was applied to screen for sequences which preferentially bound the natural substrate dihydrofolate (chemical state 1) over a propargyl-linked antifolate inhibitor (chemical state 2) using a single backbone template [Fig. 3(C)]. Even though a single protein backbone was used, this is an example of MSD as two templates with different ligands were considered during sequence optimization. The fitness of each sequence, describing the binding preference, was calculated by taking the ratio of the score describing the binding affinity for the substrate over the score of the binding affinity for the inhibitor. Thus, the authors sought to identify sequences that scored highly for dihydrofolate and poorly for the inhibitor. Their MSD simulation returned 105 mutants with a score ratio of infinity. Four double mutant sequences, which exhibited a significantly better dihydrofolate score than the other sequences, were experimentally tested. Three of the experimentally tested double mutants (V31Y/F92I, V31Y/F92S, V31F/F92L) conferred antibiotic resistance (resulting in 18, 8.7, and 13 fold increases to the original K_i of 10 nM, respectively) while maintaining sufficient catalytic activity to maintain cell viability (36-, 107-, and 306-fold decreases to the original k_cat/K_M of 2.14 μM⁻¹ s⁻¹, respectively). It is important to note that the MSD design procedure required the X-ray crystallographic structures of dihydrofolate reductase bound separately to both the substrate and inhibitor. Having both templates eliminated the need for translation and rotation of either substrate or inhibitor in the active site of the protein for each sequence solution to be scored.

MSD can also be used for the design of oligomeric association of protein subunits. As many biological processes are mediated and controlled by protein–protein interactions, the ability to design for protein–protein binding specificity is of paramount importance. A recent review by Chen and Keating⁴⁴ describes an integrated approach to the design of protein–protein interaction specificity using computational design and experimental library screening methodologies. Here, we focus on publications employing a MSD approach to tackle the design of oligomeric association specificity and the challenge associated with the simultaneous design of specificity and stability.

In a pioneering example of MSD, Havranek and Harbury developed and experimentally validated this approach for the redesign of GCN4 dimeric coiled-coil association specificity.⁴⁵ By considering both the homo and heterodimer form of each coiled-coil sequence pair in the MSD simulation [Fig. 3(D)], Havranek and Harbury could direct formation to prefer one specific oligomeric association (homodimer) in positive design fashion while searching the same sequences against formation of the other oligomeric association (heterodimer) in a negative design fashion and vice versa. Two additional states, the unfolded and aggregated states, were also explicitly designed against. The score for each sequence in each state was the computed free energy. The fitness of each sequence was evaluated by the difference in free energy for the target state from the ensemble of competing states. Havranek and Harbury used the S. cerevisiae GCN4 homodimeric coiled-coil structure as their design scaffold for both the target dimeric positive state(s) and the competing dimeric negative state(s). The unfolded state was modeled using AGADIR parameters⁴⁶ and the aggregated state was determined by re-evaluating the stability of the target dimer with an adjusted dielectric constant to reflect the environment of an aggregated protein. Experimental validation of the association specificity and stability predicted from MSD simulation was carried out using a disulfide-exchange assay and a urea denaturation assay, respectively. Havranek and Harbury were able to produce 8 new individual sequence variants which preferentially associated as homodimers and 4 new sequence pairs which preferentially associated as heterodimers. However, most of the designed sequences were destabilized when compared to the wild-type. Furthermore, Havranek and Harbury's results demonstrated that omission of any structures from the ensemble of negative states (i.e. the competing homo/hetero-dimer, unfolded or aggregated states) was detrimental to the performance and outcome of their simulation. For example, omission of the unfolded and aggregated states during the MSD simulation gave 2 sequence pairs which were predicted to associate specifically but also to be unstable, while omission of either the competing homo/hetero-dimer state resulted in a total loss of predicted association specificity.

Another example of MSD using chemical states was the redesign of the H. influenzae SspB adaptor protein. In this study, Bolon et al. designed the wild-type sequence, which associates as a homodimer, into mutant variants that preferentially associate as heterodimers.⁴⁷ The authors employed and compared both a SSD and MSD approach to their CPD objective. The first approach (SSD) involved stabilization of the heterodimer in a positive design fashion without explicit consideration of the homodimer, while the second approach (MSD) explicitly included the competing homodimer state. Two pairs of sequence variants at positions 12, 15, 16 and 101, found at the dimer interface, were produced. The first pair, containing Phe12/Ala15/Phe16/Ile101 (FAFI) in one subunit and Leu12/Ala15/Leu16/Ile101 (LALI) in the other subunit, was found after SSD while the second pair, containing Leu12/Ser15/Leu16/Ala101 (LSLA) in one subunit and Tyr12/Gly15/Phe16/Met101 (YGFM) in the other subunit, was found using the MSD approach. For both the SSD and MSD approaches, the score for each dimer sequence pair was computed using the standard DREIDING force field⁴⁸ terms. In the case of SSD, the lowest energy sequence was selected while in the case of MSD, the fitness for oligomeric association specificity was computed by taking the difference in energy between the target heterodimer state and the competing homodimer states (fitness = 2 × E_AB − E_AA − E_BB, where E is the energy and A and B are different monomeric subunits). To experimentally validate their designs, Bolon et al. employed ion-exchange chromatography to isolate homodimer and heterodimer species and a urea denaturation assay to examine stability. These experiments allowed the authors to calculate the free energy of dissociation/unfolding at 30°C which demonstrated that their SSD approach could not produce sequences (sequence pair 1 variants (A) FAFI and (B) LALI) which favored either the homo or heterodimer state (ΔG_AA = 24.3, ΔG_BB = 25.6, ΔG_AB = 25.6 [kcal/mol]) while the MSD approach allowed for the design of sequences (sequence pair 2 variants (A) LSLA and (B) YGFM) that favorably formed heterodimers over homodimers (ΔG_AA = 14.5, ΔG_BB = 17.5, ΔG_AB = 20.1 [kcal/mol])). While the MSD approach allowed for the successful design of specificity, the stability of the heterodimer relative to the wild-type sequence (WT) was reduced (WT: LAYV, ΔG_WT-WT = 23.6 kcal/mol vs. 20.1 kcal/mol for the LSLA/YGFM heterodimer).

The computational redesign of oligomeric association using MSD has also been successfully accomplished by Ali et al. who redesigned a previously engineered homotetramer, comprised of four ββα motif peptides referred to as BBAT2, to prefer association in a heterotetrameric fashion.⁴⁹ In this MSD example, the positive state consisted of the heterotetrameric assembly (ABAB, where A and B are different monomeric subunits) of two previously designed mutants of BBAT2, which was generated using symmetry operations on their crystal structures (PDB codes 1SNA and 1SNE). In addition, four negative states consisting of the two homotetramers (AAAA and BBBB, where A and B are different monomeric subunits) and the unfolded state for each peptide (A_Unfolded and B_Unfolded) were included. The unfolded state energy was evaluated by the sum of the energy of all amino acids, belonging to the designed sequence, in the context of a Gly-Gly-Xaa-Gly-Gly pentapeptide model. All energies were computed using a modified CHARMM19 force field.⁵⁰ Stability of the tetramer was computed as the difference between the unfolded state energy and the heterotetramer energy (E_Unfolded – E_ABAB) while the specificity of the complex was calculated as the energy difference between two heterotetramers and the respective homotetramers (E_AAAA + E_BBBB − 2 × E_ABAB). Sequences were ranked using both stability and specificity fitnesses. Those that possessed high fitness values for both stability and specificity were further minimized and rescored. It was found after MSD that monomers having Glu and/or Asp mutations at positions 11, 13, and 18, and monomers having Arg and/or Lys at opposing sites on adjacent subunits (positions 11 and 13 from one monomer interact with positions 18 and 13 on the other monomer, respectively) conferred the best fitness values for directing specificity of the complex to the heterotetramer. Two heterotetramers were thus designed—BBAhetT1 and BBAhetT2, composed of 2 subunits each of individual peptides A-Ala and B-Phe, or A-Abu and B-Phe, respectively. Each of the designed monomers (A-Ala, A-Abu, and B-Phe) displayed very weak CD signal between 200 and 300 nm when tested individually, indicating that they have very little secondary structure. However, equimolar mixtures of A-Ala/B-Phe (BBAhetT1) and A-Abu/B-Phe (BBAhetT2) gave rise to a significant increase in ellipticity indicative of interhelical association. The heterotetrameric association specificity of BBAhetT1 and BBAhetT2 was also demonstrated by fluorescence quenching experiments (the A-Ala and A-Abu monomers were synthesized with a quencher while the B-Phe monomer was synthesized with a fluorophore) and analytical ultracentrifugation. Finally, the crystal structure of BBAhetT1 was solved and confirmed the designed C₂-symmetric heterotetramer assembly. Thermal denaturation experiments of the two designed heterotetramers demonstrated that they are less stable than the parent BBAT2 homotetramer. These results again demonstrate that the sequences identified by MSD, although displaying a different oligomeric association specificity, also display decreased stability, similar to what Bolon et al.⁴⁷ observed in their design of the SspB adaptor protein.

This trade-off between increased specificity and decreased stability arises from the fact that sequence optimization for the design of oligomeric association specificity in the previous examples involved a negative design approach which did not explicitly attempt to increase the stability of the positive state. To address this issue, Grigoryan et al. developed a landmark computational framework, referred to as cluster expansion and linear programming-based analysis of specificity and stability (CLASSY).⁵¹ The CLASSY framework is initiated by designing for stability of the positive state, i.e. the design–target heterodimer, without consideration of specificity. This first positive design calculation yields a sequence with maximum affinity for the target but does not necessarily confer specificity over competing states (off-targets) or itself (design). This is followed by a negative design calculation whereby sequences are optimized by computing the difference in energy between the positive state (design–target) and the best ranking competing state (design–design or design–off-target). By sequentially introducing a larger specificity constraint defined as the energy difference between the lowest energy undesired state and the desired target state, specificity can be gradually increased. This procedure, referred to as a specificity sweep, allows for the optimization of sequences maximizing the specificity of the desired interaction while minimizing the resulting decreased stability of the target state.

To validate their CLASSY framework, Grigoryan et al. designed and tested 48 peptides to bind representative members across the 20 families of the human basic-region leucine zipper (bZIP) transcription factors, known to associate as homo- and/or heterodimeric parallel coiled-coils. Experimental screening of their designs was completed using a micro array assay where the target bZIPs were immobilized onto the surface of the array and the plate was washed with designed peptides bearing a fluorescent dye.⁵² The authors showed that of the 48 designed peptides, 40 bound to their intended target bZIP. The seven designed peptides that showed the highest specificity were further characterized by thermal denaturation monitored with CD spectroscopy. Each of the seven designed peptides were denatured in the presence of either their intended target bZIP, the next-best interaction partner reported by the array experiment, a protein closely related by sequence identity to the target bZIP, or the design peptide itself, giving a total of 28 peptide mixtures. Thermal melts from 18 of the 21 mixtures containing undesired design-off-target or design–design complexes showed no increase in temperature of denaturation compared with that of the average of the individual components, indicating that the designed specificity was achieved. Thus, Grigoryan et al. showed that the problem involving the sacrifice of stability to achieve enhanced specificity could be in part circumvented by their CLASSY framework.

In the design examples described above, MSD was used to design for ligand binding or oligomeric association specificity. Since the design of specificity requires the evaluation of alternate competing states, it is not surprising that MSD in a negative design approach was required to achieve the design goal. Indeed, the optimization of sequences for one state using SSD does not guarantee that the same sequence will be detrimental to the other state(s). In the future, it will be interesting to see if positive MSD using multiple chemical states could be used to design for desired small molecule binding specificity. For example, enzyme/substrate complexes could be used as inputs for MSD to explicitly design for broad specificity or multisubstrate enzymes.

Current Challenge for Multistate Design

The examples described above illustrate how MSD can improve the quality of designs, either by identifying sequences that are compatible with desired states and incompatible with undesired ones or by keeping sequences that would have been discarded in the context of a single fixed backbone template. Although MSD can provide an improved and successful avenue over SSD for CPD, there remains a challenge to overcome in order to improve its usefulness for the design of any desired protein property. This challenge is the accurate modeling of energetic effects arising from destabilizing mutations in competing states during negative design.

In negative design calculations, the selection of relevant sequences for the negative state can be difficult. This difficulty arises from the fact that the score values for the negative state may not be meaningful. Consider the example shown in Figure 4, where the same hypothetical five amino acid sequence (Tyr-Ser-Trp-Ala-Ala) was scored in the context of two negative state backbones. Using negative state backbone A, a severe steric clash between the sidechains of Tyr and Trp leads to an overinflated energy for the negative state. As a result, this sequence would be preferred during a negative MSD calculation as its fitness, that is the difference in energy between the positive and negative states, would be very high. However, although steric clashes are likely destabilizing in the context of a real protein, backbone motions can alleviate them through conformational rearrangements. Thus, negative states that contain multiple steric clashes should be preferred in negative MSD since they are likely to destabilize proteins more efficiently. Bolon et al. recognized this observation and came up with a workaround to select sequences exhibiting many steric clashes in the negative state. To do this, Bolon et al. restricted the pairwise interaction energy between two rotamers exhibiting unfavorable steric clashes at a maximum value to approximate conformational relaxation, thereby giving preference to sequences having multiple smaller steric clashes, considering them to be more acceptable than sequences having a few major steric clashes.⁴⁷ For the hypothetical example in Figure 4, negative state backbone B contains two smaller steric clashes between the sidechain of Trp and the sidechains of Tyr and Ala. Although the fitness of the sequence is lower because the difference in energy between the negative state and the positive state is lower, the sequence can now be selected even in the presence of sequences that contain major steric clashes. Although this strategy helps to address the issue of conformational relaxation in the negative state, it is still unknown whether the modeling of the negative state in this fashion is physically relevant. Another approach to address the issue of relevant scoring of the negative state is the use of more rigorous statistical mechanics methods to score the negative states.⁵³ For this approach to be successful, accurate atomic models of the negative states are required. However, methods to generate accurate atomistic models for aggregated and unfolded states have not yet been developed and validated, limiting the use of this approach in negative design.

Figure 4.

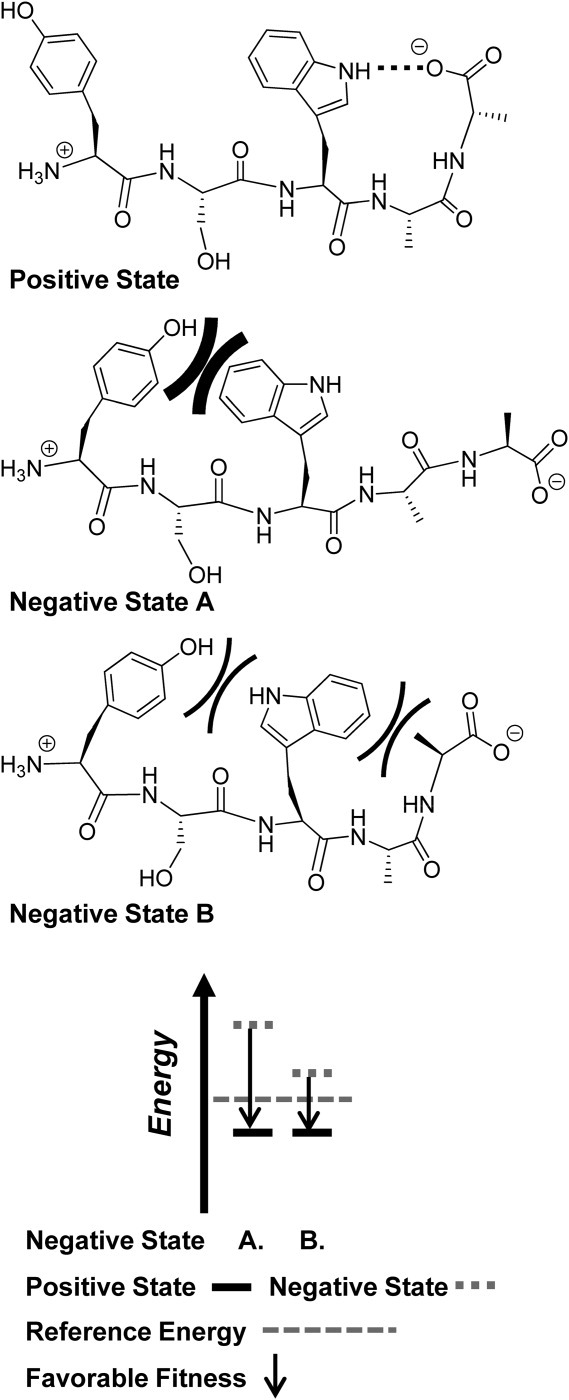
Negative state selection and its impact on scoring in multistate design. A sequence of a hypothetical pentapeptide (Tyr-Ser-Trp-Ala-Ala) is modeled and scored in the context of a single desired positive state and one of two competing negative states. Negative state A has a major unfavorable interaction (thick curved lines) between the sidechains of Tyr and Trp while negative state B has two minor unfavorable interactions (thin curved lines) between the sidechain of Trp and the sidechains of Tyr and Ala. Meanwhile, the positive state has the best energy due to a favorable electrostatic interaction between the sidechain of Trp and the terminal carboxylate group (dotted line). The positive state also lacks unfavorable steric interactions. Although negative state A is physically less relevant than negative state B, it results in a more favorable ranking of the sequence due to a large difference in energy with the positive state.

Conclusions

The ability of MSD to use multiple conformational or chemical states as inputs for protein sequence optimization can potentially yield higher quality designed sequences for a number of different applications. Protein properties that can benefit the most from MSD are those that are dynamic in nature such as ligand binding specificity, oligomeric association, and conformational switching. MSD can also lead to improved sequences for the design of protein stability by explicitly taking into account negative states such as the unfolded and aggregated states. With the development of search algorithms that can handle large numbers of states during MSD,³⁵ and the development of a generic program for MSD⁵⁴ that allows users to rapidly tailor the fitness function to be optimized in order to achieve the desired design goal, more complex protein design problems requiring the consideration of hundreds of positive and negative, chemical and conformational states will likely be achievable in the future.

Glossary

Abbreviations

BBAT2

beta-beta-alpha tetramer 2

Cdc42

cell division control protein 42 homolog

CD

circular dichroism

CPD

computational protein design

FASTER

fast and accurate side-chain topology and energy refinement

ITSN

GTPase exchange factor named intersectin

MD

molecular dynamics

MSD

multistate design

RMSD

root mean square deviation

SSD

single-state design

SPR

surface plasmon resonance