Identifiability and Estimation of Causal Effects in Randomized Trials with Noncompliance and Completely Nonignorable Missing Data

Summary

In this article, we first study parameter identifiability in randomized clinical trials with noncompliance and missing outcomes. We show that under certain conditions the parameters of interest are identifiable even under different types of completely nonignorable missing data: that is, the missing mechanism depends on the outcome. We then derive their maximum likelihood and moment estimators and evaluate their finite-sample properties in simulation studies in terms of bias, efficiency, and robustness. Our sensitivity analysis shows that the assumed nonignorable missing-data model has an important impact on the estimated complier average causal effect (CACE) parameter. Our new method provides some new and useful alternative nonignorable missing-data models over the existing latent ignorable model, which guarantees parameter identifiability, for estimating the CACE in a randomized clinical trial with noncompliance and missing data.

1. Introduction

Two common problems in clinical trials are noncompliance and missing outcome data. Noncompliance occurs when some subjects fail to follow their assigned treatments; missing outcome data occurs when study investigators cannot collect outcome information on some subjects. Ignoring noncompliance or missing outcome data may result in biased estimates of causal effects. Moreover, the assumed mechanism of missing data also has an impact on the estimated causal effects. Many methods have been developed for handling either missing data or noncompliance, but researchers have only recently started to develop methods for handling both missing outcome data and noncompliance in the same study (Frangakis and Rubin, 1999; Yau and Little, 2001; O’Malley and Normand, 2005; Zhou and Li, 2006).

Frangakis and Rubin (1999) proposed a moment estimator for the complier average causal effect (CACE) parameter under binary compliance status and a latent ignorable (LI) missing outcome assumption. The LI assumption means that the missing-data mechanism has no residual dependence on the outcome, given the observed data and latent compliance class. Under the same LI assumption, Zhou and Li (2006) derived maximum likelihood (ML) estimates as well as moment estimates of the CACE when the compliance status is a discrete variable with three categories and when the outcome variable is binary. O’Malley and Normand (2005) gave the moment and ML estimators of the CACE for a continuous outcome variable.

The above-mentioned methods may yield biased estimators of the CACE if the missing-data mechanism is of a different type of nonignorable missing mechanism from latent ignorability. The mechanism of missing outcome Y may depend on missing values of Y. For example, some subjects may drop out of a study because of a patient’s declining health, which is related to Y given the observed data and latent compliance class. As a motivating example, consider a study on the effectiveness of influenza vaccine in reducing morbidity in high-risk adults (McDonald, Hui, and Tierney, 1992). This study began in 1978 and lasted for 3 years. There were about 2000 patients enrolled in the study. Physicians were randomly assigned to the treatment group and the control group at the beginning of the study. The physicians assigned to the treatment group would encourage their eligible patients to get a flu shot. But the patients themselves decided whether or not to take flu shots. One of the main outcomes in the study was flu-related hospitalization. Some patients’ outcomes were not observed, and the reason for missing outcomes may depend on the missing values. For example, some subjects were missing their outcomes because they had the flu but went to different hospitals than the study hospital, and as a result their outcomes were not recorded. Or, some patients were missing their outcomes because the reason for their hospitalization was unknown. When the missing-data mechanism depends on the outcome, we define this situation as completely nonignorable (CN). The LI missing-data mechanism assumes that subjects drop out only because of subjects’ latent compliance status.

Analysis of CN missing data is more difficult than analysis of LI data. One major difficulty under the CN missing-data mechanism is the issue of parameter identifiability. Here we say that a parameter vector θ is identifiable by observation of Y if distinct values for θ yield distinct distributions for Y, that is, if F (y; θ) = F (y; θ′), then θ = θ′, where F is the distribution of Y (Bickel and Doksum, 1977). When the missing-data mechanism is nonignorable, some of the parameters may not be identifiable even if the data provide enough degrees of freedom (Little and Rubin, 2004). Several authors have proposed methods for dealing with CN. For example, Brown (1990) developed an estimation method for missing normal outcome variables in longitudinal studies under the CN missing mechanism. Robins and Rotnitzky (2004) discussed parameter identifiability in randomized trials with noncompliance. Vansteelandt and Goetghebeur (2005) discussed parameter identifiability in randomized trials with noncompliance and missing data. However, no methods are available for dealing with the CN missing-data mechanism and noncompliance in the same study.

In this article, we fill the gap by first studying identifiability of the model parameters under the CN assumption. We show that the parameters are identifiable under two different conditions. The first condition assumes that the missing-data mechanism depends only on the missing outcome variable. If this assumption does not hold, the parameters are not identifiable. However, we can show that the parameters are also identifiable if we can find an observed discrete covariate X before the treatment assignment, which is associated with Y in each subpopulation of the compliance and treatment level. Then we derive both moment and ML estimators.

The article is organized as follows. We describe notation and assumptions in Section 2. In Section 3, we give the theoretical results on identifiability of the parameters. In Section 4, we conduct simulation studies to assess the finite-sample properties of the derived estimators and sensitivity of the proposed estimators to depart from the assumed conditions. Then we illustrate application of the proposed methods in a real study. We give some concluding remarks in Section 5. The proofs of theorems are presented in the Web Appendix.

2. Notation and Assumptions

For the ith patient, we let Z_i represent the randomized treatment assignment (1 = new, 0 = control) with ξ = P (Z _i = 1), and let D _i (z) be the potential binary treatment variable, indicating which treatment the ith patient would receive (1 = new treatment received, 0 = control received) if the patient is assigned to treatment z. We also let Y _i (z) denote the potential binary outcome variable if the ith patient is assigned to treatment z; Y _i (z) = 0 if the patient goes to the hospital due to the flu and Y _i (z) = 1 otherwise. Finally, we let R_i (z) be the binary response indicator of Y _i (z), that is, R_i (z) = 1 if Y _i (z) is observed and R_i (z) = 0 if Y _i (z) is missing. In our notation, D _i (z), Y _i (z), and R_i (z) are potential outcomes of a patient. Finally, we use Z _i to denote the observed treatment assignment of the patient, and D _i = D _i (Z _i), Y _i = Y _i (Z _i), and R_i = R_i (Z _i) denote observed treatment actually received, the observed outcome, and the observed response indicator of the patient.

Following Imbens and Rubin (1997), we let U _i be the compliance status of the ith patient, defined as follows:

$$U_i=\{\begin{array}{lllll}c,\hfill & \text{if}\hfill & D_i(0)=0\hfill & \text{and}\hfill & D_i(1)=1\hfill \\ n,\hfill & \text{if}\hfill & D_i(0)=0\hfill & \text{and}\hfill & D_i(1)=0\hfill \\ a,\hfill & \text{if}\hfill & D_i(0)=1\hfill & \text{and}\hfill & D_i(1)=1\hfill \\ d,\hfill & \text{if}\hfill & D_i(0)=1\hfill & \text{and}\hfill & D_i(1)=0,\hfill \end{array}$$

where c, n, a, and d represent complier, never-taker, always-taker, and defier, respectively. Here U _i is an unobserved variable, representing the compliance behavior pattern of the patient. Let ω _u = P (U _i = u). We assume P (ω_c) > 0 throughout this manuscript. For simplicity, we also denote ρ_yzu = P (R_i = 1 | Y _i = y, Z _i = z, U _i = u) and θ_yzu = P (Y _i = y | Z _i = z, U _i = u). As in Imbens and Rubin (1997) and Frangakis and Rubin (1999), in this article we consider CACE as the parameter of interest, defined as CACE = E{Y _i (1) − Y _i (0) | U _i = c}.

Because the joint distribution of the potential outcomes Y _i (z), R_i (z), and U _i conditional on Z = z can be expressed as a function of the parameters ω_u, ρ_yzu, and θ_yzu, the causal effects are identifiable if we can show that these parameters are identifiable. Next, we give the necessary assumptions to make these parameters identifiable under the CN missing mechanism.

• Assumption 1

  Stable unit treatment value assumption (SUTVA) (Angrist, Imbens, and Rubin, 1996; Imbens and Rubin, 1997).

SUTVA implies that potential outcomes do not depend on the treatment status of other individuals.

• Assumption 2

  Randomization: Z is randomized.

We can express the CACE as CACE = θ_11c− θ_10c under the randomization assumption.

• Assumption 3

  Monotonicity: D _i (1) ≥ D _i (0) for all subjects, which implies there are no defiers.

• Assumption 4

  Exclusion restrictions among never-takers and always-takers (Angrist et al., 1996): P {Y _i (1) | U _i = n} = P {Y _i (0) | U _i = n}, and P {Y _i (1) | U _i = a} = P {Y _i (0) | U _i = a}.

Under randomization, the exclusion restriction implies that P (Y _i | Z _i = 1, U _i = n) = P (Y _i | Z _i = 0, U _i = n), and P (Y _i | Z _i = 1, U _i = a) = P (Y _i | Z _i = 0, U _i = a); that is, θ_11n = θ_10n and θ_11a = θ_10a. In some studies, such as those with double blinding, exclusion restrictions are reasonable.

• Assumption 5

  Compound exclusion restrictions among never-takers and always-takers (Frangakis and Rubin, 1999): P {Y _i (1), R_i (1) | U _i = n} = P {Y _i (0), R_i (0) | U _i = n}, and P {Y _i (1), R_i (1) | U _i = a} = P {Y _i (0), R_i (0) | U _i = a}.

Assumption 5 is stronger than Assumption 4. Besides having the same implications as Assumption 4, Assumption 5 also implies P (R | Z = 1, U = n) = P (R | Z = 0, U = n) and P (R | Z = 1, U = a) = P (R | Z = 0, U = a). Assumption 4 instead of Assumption 5 is required in our Theorems 1 and 2, where the missing-data mechanism does not depend on latent compliance status variable U (Assumptions 6 and 7). However, Assumption 5 is required in Theorem 3 where the missing-data mechanism depends on both missing outcomes and U (Assumption 8).

3. Identifiability and Estimation

In this section, we discuss additional conditions needed to identify the causal parameters under the CN assumption and then propose moment and ML estimators of the causal effects. Intuition behind how identification of parameters is achieved is related to the idea of instrumental variables. As we know, if there are no missing outcomes, causal parameters are identifiable under the standard Assumptions 1 to 4 of an instrumental variable, as shown in Angrist et al. (1996). When the missing-data mechanism depends only on outcomes, under Assumptions 1 to 4 and the additional Assumption 6, U and Z can be considered as instrumental variables, and the causal parameters are still identifiable. In Section 3.1, we consider a missing-data mechanism model in which the mechanism of missing outcome Y depends only on the outcome Y itself; that is, only the outcome Y has an effect on R. Under this assumption we provide a sufficient condition on parameter identifiability in Theorem 1. Without any other assumptions on the missing-data mechanism, only this model and LI model can be identified.

When the missing-data mechanism depends on more variables, an additional instrumental variable is required to identify parameters. If the missing-data mechanism depends on not only Y but also the treatment assignment Z, we can still identify the parameters in this model when we have one additional covariate X that can affect the outcome Y but does not depend on the other variables D and Z in the study. This model is more general than the first missing-data model. Here X and U are used as instrumental variables for finding the effect of Y on R. In Section 3.2, we present the results under this more general model. In Section 3.3, we extend our identifiability results to a discrete outcome with more than two categories.

3.1 Identifiability without Covariate

We consider a CN mechanism that satisfies the following assumption:

• Assumption 6

  P {R_i (z) | Y _i (z), D _i (z), U = u} = P {R_i (z) | Y _i (z)} for z = 0 and 1, and P {R_i (1) | Y _i (1) = y} = P {R_i (0) | Y _i (0) = y}.

When Z is randomized, the first equality implies P (R | Y, D, U = u, Z) = P (R | Y, Z), and the second equality implies P (R | Y, Z = 1) = P (R | Y, Z = 0), so Assumption 6 implies ρ_{y z u} = ρ_{y z′ u′} for any z ≠ z′ or u ≠ u′, which means that R is independent of (Z, U, D), given Y.

Before studying parameter identifiability, we compare Assumption 6 with the LI assumption. The LI assumption requires that potential outcomes and associated potential non-response indicators are independent within each level of the latent compliance covariate (Frangakis and Rubin, 1999), that is, P {R(1) | U, Y (1)} = P {R(1) | U } and P {R(0) | U, Y (0)} = P {R(0) | U }. The LI assumption means that patients drop out because of their latent compliance class. Yet Assumption 6 means that patients may drop out because of worsening disease, which is related to the outcome. For example, they may drop out when they feel worse after taking the assigned drugs. In our study, Y measures the hospitalization status of a subject, and the reason for missing Y of a subject may be due only to her/his hospitalization status. So whether patients drop out of the trial is determined by their outcomes, not by other inherent and invariable subject characteristics. These two assumptions are so different that a wrong assumption will have a serious impact on estimation of CACE. We will see this point in our simulations.

The next theorem shows that the parameters are all identifiable under Assumption 6. For simplicity, we denote ρ_y = ρ_yzu and δ_yzu = P (Y _i = y, R_i = 1 | Z _i = z, U _i = u). Under Assumption 6, the vector of parameters is θ = (ξ, ω_a, ω_n, θ_10a, θ_11n, θ_11c, θ_10c, ρ₀, ρ₁).

Theorem 1

If Y is not independent of Z given U or if Y is not independent of U given Z, then under Assumptions 1–4 and Assumption 6, the vector of parameters, θ, is identifiable.

We give a detailed proof of this theorem in the Web Appendix. It is worthwhile to note that if Y is independent of Z given U and is also independent of U given Z, we cannot identify all of the parameters. However, from θ_10a = θ_11n = θ_11c = θ_10c, we can get CACE = θ_11c − θ_10c = 0, which means that the treatment has no causal effect on the outcome.

After we have shown identifiability of θ, we can derive the moment and ML estimators of θ. Let N _yrzd be the observed number of patients with Y = y, R = r, Z = z, D = d. The observed data, N _{y 1z d} (for y, z, d = 0, 1) and N _{+0z d} (for z, d = 0, 1), can be considered as arising from a multinomial distribution with corresponding cell probabilities, ν _{y 1z d} and ν_{+0z d}, where N_{+0z d} = Σ_y N_{y 0z d} denotes an observed frequency with y’s value missing, ν_{y 1z d} = P (Y = y, R = 1, Z = z, D = d), and ν_{+0z d} = P (R = 0, Z = z, D = d). Then the moment estimator of CACE is ${\widehat{\text{CACE}}}_{\text{nocova}}=\frac{{\widehat{\delta }}_{11c}-{\widehat{\delta }}_{10c}}{\widehat{{\rho }_1}}$. In addition, we can show that ${\widehat{\text{CACE}}}_{\text{nocova}}$ has an asymptotically normal distribution using the central limit theorem and the multivariate delta method. Because the moment estimates may be outside of the parameter space in practice (Zhou and Li, 2006), we propose the expectation–maximization algorithm to find ML estimates in this article. In Theorem 1 the complete-data likelihood function is given as $L_c(\theta )={\mathrm{\Pi }}_{i=1}^{N}P(Z_i)P(U_i)P(D_i\mid Z_i,U_i)P(Y_i\mid Z_i,U_i)P(R_i\mid Y_i)$ the E-step, we take the expectation of the complete data, given the observed data and the previous parameter estimate θ = θ^(k), that is $n_{\mathit{yrzu}}^{(k+1)}=E\{n_{\mathit{yrzu}}\mid \text{observed}-\text{data},{\underset{\_}{\mathit{\theta }}}^{(k)}\}$. In the M-step, we can get the ML estimates θ^{(k +1)} from $n_{\mathit{yrzu}}^{(k+1)}$. More details of our expectation–maximization algorithm are given in the Web Appendix.

3.2 Identifiability with a Covariate

In some clinical trials, there are good reasons to believe that the missing-data mechanism is also affected by the treatment assignment, not just the outcome, because the occurrence of side effects differs between treatment arms. In some clinical trials, a direct effect of the treatment assignment on the missing-data mechanism is essentially implied by the study design. For example, when patients in the treatment group experience severe side effects, they are removed from further study. Therefore, the response indicator of the outcome, R, depends not only on the outcome Y itself but also on other variables. The parameter vector θ is not identifiable under only Assumptions 3, 4, and 6 without further assumptions. In this case, we can introduce an additional covariate X so that Z is independent of X and U. Suppose that X is associated with Y in each subpopulation of U = u and Z = z (that is, P (y | x, z, u) ≠ P (y | z, u) for some x and for all u and z) such that the parameter vector θ becomes identifiable. For example, in some clinical trials it may be reasonable to assume that patient age is associated with Y in each subpopulation. Here we assume that x is discrete. Then the following theorem shows that the parameters are identifiable. Let α_xu = P (X = x, U = u), ρ_yzux = P (R = 1 | Y = y, Z = z, U = u, X = x), and θ_yzux = P (Y = y | Z = z, U = u, X = x). To emphasize the dependence of the causal effect parameter on covariates, we write CACE as CACE_cova, which is defined as follows:

$$\begin{array}{l}{\text{CACE}}_{\text{cova}}=\sum _{x}E\{Y(1)-Y(0)\mid U=c,X=x\}P(X=x\mid U=c)\\ =\sum _x({\theta }_{11cx}-{\theta }_{10cx}){\alpha }_{xc}/{\omega }_c.\end{array}$$

With the availability of this covariate X, we can replace Assumption 6 by the following assumption.

• Assumption 7

  For z = 0 and 1,

$$P\{R_i(z)\mid Y_i(z),D_i(z),U=u,X=x\}=P\{R_i(z)\mid Y_i(z)\}.$$ (1)

Assumption 7 means that the missing-data mechanism depends on both the outcome Y and the assigned treatment Z. To identify the parameters under Assumption 7, we introduce an observed covariate X as an additional instrumental variable in Theorem 2.

When the treatment assignment Z is randomized, we have from equation (1) that ρ_{y z u x} = ρ_{y z u′ x′} for any u ≠ u′ or x ≠ x′, and thus we can simply denote ρ_yzux as ρ_{y z}. The vector of parameters, θ, is denoted as θ = (ξ, ω_a, ω_n, α_{x a}, α_{x n}, α_{x c}, θ_{10a x}, θ_{11n x}, θ_{11c x}, θ_{10c x}, ρ₀₀, ρ₀₁, ρ₁₀, ρ₁₁).

Theorem 2

Suppose that X is an observed discrete covariate that depends on Y in each subpopulation of U = u and Z = z. Then under Assumptions 1–4 and Assumption 7, the vector of parameters, θ, is identifiable.

We give a proof of Theorem 2 in the Web Appendix. Under the model in Theorem 2, we can obtain the estimate of CACE as ${\widehat{\text{CACE}}}_{\text{cova}1}={\sum }_x({\widehat{\delta }}_{11cx}/{\widehat{\rho }}_{11}-{\widehat{\delta }}_{10cx}/{\widehat{\rho }}_{10}){\widehat{\alpha }}_{xc}/{\widehat{\omega }}_c$.

Note that in Theorems 1 and 2 we make only the exclusion restriction assumption, which is weaker than the compound exclusion restriction assumption made in Frangakis and Rubin (1999). If we also make the stronger compound exclusion assumption, we can further relax Assumption 7 to allow the missing-data mechanism to depend on both the missing outcomes and latent compliance status variable.

• Assumption 8

  For z = 0 and 1,

$$P\{R_i(z)\mid Y_i(z),D_i(z),U=u,X=x\}=P\{R_i(z)\mid Y_i(z),U=u\}.$$ (2)

This assumption assumes that the missing-data mechanism depends on Y, Z, and U. When the treatment assignment Z is randomized, using equation (2) we obtain that ρ_{y z u x} = ρ_{y z u x′} for any x ≠ x′, and thus we can simply denote ρ_yzux as ρ_yzu. Because the compound exclusion assumption (Assumption 5) holds, we have that ρ_{y 0n} = ρ_{y 1n} and ρ_{y 0a} = ρ_{y 1a}. Hence, the vector of parameters, θ, is

$$\begin{array}{l}\underset{\_}{\mathit{\theta }}=(\xi ,{\omega }_a,{\omega }_n,{\alpha }_{xa},{\alpha }_{xn},{\alpha }_{xc},{\theta }_{10ax},{\theta }_{11nx},{\theta }_{11cx},{\theta }_{10cx},{\rho }_{11n},\\ {\rho }_{01n},{\rho }_{00a},{\rho }_{10a},{\rho }_{11c},{\rho }_{01c},{\rho }_{00c},{\rho }_{10c}).\end{array}$$

Theorem 3

Suppose that X is an observed discrete covariate that depends on Y in each subpopulation of U = u and Z = z. Then under Assumptions 1–3, 5, and 8, the parameters in θ are identifiable.

The difference between the models in Theorems 2 and 3 is in their missing-data mechanisms. For the model in Theorem 3, R depends on Y(Z), Z, and U, whereas R depends only on Y(Z) and Z in the model of Theorem 2. For the model of Theorem 3, we can obtain the estimate of CACE as ${\widehat{\text{CACE}}}_{\text{cova}2}={\sum }_x({\widehat{\delta }}_{11cx}/{\widehat{\rho }}_{11c}-{\widehat{\delta }}_{10cx}/{\widehat{\rho }}_{10c}){\widehat{\alpha }}_{xc}/{\widehat{\omega }}_c$.

3.3 Extension to Multilevel Outcomes

In this subsection we generalize Theorems 1, 2, and 3 to a multilevel outcome. Let Y be a K-level discrete variable, where Y = 0, …, K − 1, and let the covariate X be a J− valued variable, i.e., X ∈ {0, 1, …, J − 1}. Because the proofs of the corollaries are similar to Theorems 1–3 below, we omit the proofs for simplicity.

Corollary 1

If Y has fewer levels than five, that is K < 5, and the rank of the 4 × K matrix,

$$\left(\begin{array}{cccc}{\delta }_{01n}& {\delta }_{11n}& \dots & {\delta }_{K-1,1n}\\ {\delta }_{00a}& {\delta }_{10a}& \dots & {\delta }_{K-1,0a}\\ {\delta }_{01c}& {\delta }_{11c}& \dots & {\delta }_{K-1,1c}\\ {\delta }_{00c}& {\delta }_{10c}& \dots & {\delta }_{K-1,0c}\end{array}\right),$$

is equal to K, then the result of Theorem 1 holds.

Note if K > 4, the model of Theorem 1 cannot be identified without additional assumptions, because the number of degrees of freedom in the observed data is 4K + 3, which is smaller than the number of parameters 5K −1.

Corollary 2

Let us define the following J × K matrices:

$${\underset{\_}{\mathbf{\Delta }}}_{zu}^{\text{Multi}}=\left(\begin{array}{cccc}{\delta }_{0zu0}& {\delta }_{1zu0}& \dots & {\delta }_{K-1,zu0}\\ {\delta }_{0zu1}& {\delta }_{1zu1}& \dots & {\delta }_{K-1,zu1}\\ ⋮& ⋮& \dots & ⋮\\ {\delta }_{0zu,J-1}& {\delta }_{1zu,J-1}& \dots & {\delta }_{K-1,zu,J-1,}\end{array}\right)$$ (3)

where u = n, a, c, and z = 0, 1.

1. When J ≥ K, if the ranks of the two J × K matrices, ${\underset{\_}{\mathbf{\Delta }}}_{1n}^{\text{Multi}}$ and ${\underset{\_}{\mathbf{\Delta }}}_{0a}^{\text{Multi}}$, are equal to K, then the result of Theorem 2 holds.

2. When J ≥ K, if the ranks of the four J × K matrices, ${\underset{\_}{\mathbf{\Delta }}}_{1n}^{\text{Multi}},{\underset{\_}{\mathbf{\Delta }}}_{1c}^{\text{Multi}},{\mathbf{\Delta }}_{0a}^{\text{Multi}}$, and ${\underset{\_}{\mathbf{\Delta }}}_{0c}^{\text{Multi}}$, are all equal to K, then the result of Theorem 3 holds.

4. Simulation Studies and Application

In our simulation studies, we first assessed the relative performance of the moment and ML estimators in finite-sample sizes when the assumptions were correct. We then assessed the sensitivity of the derived moment and ML estimators when some of the assumptions were violated.

In the first simulation study, we generated 1000 samples, each of which had a sample size of N = 500, under the model with a covariate as specified in Theorem 2. The percentage of missing data was 0.5445. We computed the moment and ML estimates of the parameters for every sample, their means, standard deviations, and actual coverage percentages of 95% confidence intervals. The results are reported in Table 1. We used the bootstrap to estimate the standard deviation. Because the moment and ML estimators have an asymptotically normal distribution, we computed the confidence intervals based on the normal assumption. We also generated data under the missing-data models given in Theorems 1 and 3. Because the results were similar to those for Theorem 2, we report only the results on the missing-data model with a covariate in Theorem 2 for simplicity. From Table 1, we saw that except for ξ, ω_n, and ω_a, the ML estimators performed better than the moment estimators. In addition, for half of the samples the moment estimates were not proper (meaning that at least one of the estimates for the sample was outside of the corresponding parameter’s range). Hence we would recommend the ML estimates over the moment estimates.

Table 1.

Simulation results of comparison between moment method and ML method with covariate in Theorem 2, including mean, standard deviation, and actual 95% coverage probability. The level of covariate is 2, and N = 500.

	Moment method			ML method
Real parameters	Mean	Std. dev.	95% Cover	Mean	Std. dev.	95% Cover
ξ = 0.5	0.4998	0.0225	0.950	0.4998	0.0225	0.950
P (U = n | X = 0) = 0.3	0.3003	0.0451	0.949	0.2993	0.0448	0.948
P (U = a | X = 0) = 0.2	0.2020	0.0422	0.954	0.2008	0.0419	0.947
P (U = n | X = 1) = 0.1	0.1007	0.0240	0.949	0.1001	0.0239	0.950
P (U = a | X = 1) = 0.5	0.5009	0.0397	0.949	0.4997	0.0393	0.949
P (X = 0) = 0.4	0.3997	0.0229	0.956	0.3997	0.0229	0.956
θ 10a 0 = 0.6	0.7124	0.3501	1.000	0.6201	0.2387	0.995
θ 11n 0 = 0.3	0.5013	0.3681	1.000	0.2967	0.1169	0.961
θ 11c 0 = 0.8	0.6835	0.4362	1.000	0.7673	0.1727	0.953
θ 10c 0 = 0.2	0.3617	0.3806	0.832	0.2398	0.1981	0.941
θ 10a 1 = 0.5	0.6372	0.3430	1.000	0.5236	0.1690	0.966
θ 11n 1 = 0.2	0.4067	0.3863	0.804	0.2014	0.1301	0.959
θ 11c 1 = 0.7	0.6224	0.4610	1.000	0.6429	0.2745	0.936
θ 10c 1 = 0.1	0.2005	0.2614	0.911	0.1194	0.1052	0.956
ρ00 = 0.2	0.2331	0.2756	0.916	0.2111	0.0507	0.950
ρ01 = 0.3	0.3357	0.2883	0.912	0.3062	0.0793	0.952
ρ10 = 0.6	0.4103	0.2760	0.876	0.6271	0.2145	0.999
ρ11 = 0.8	0.3515	0.3154	0.639	0.8288	0.1237	0.997
CACE=0.6	0.3823	0.6703	0.922	0.5254	0.2928	0.933

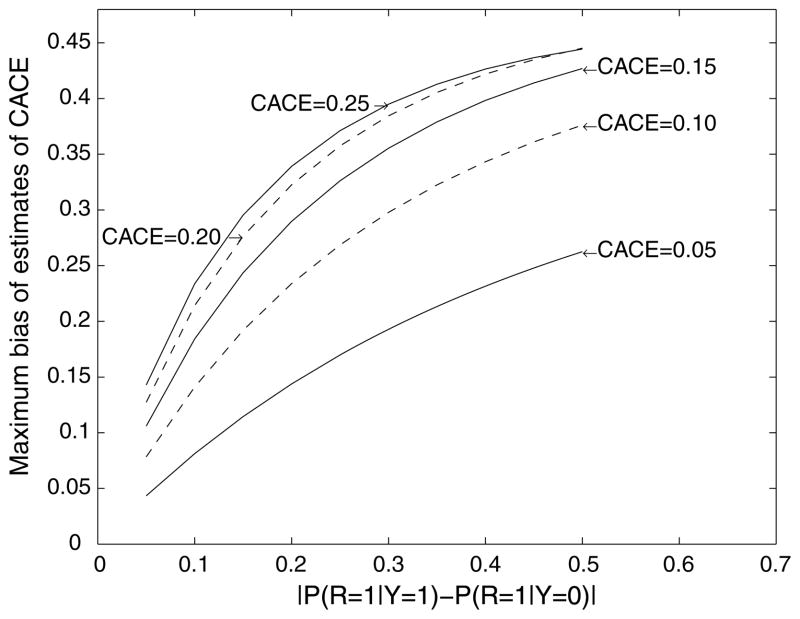
Next we conducted a sensitivity analysis of the proposed estimators between the LI assumption and CN assumption. We assumed that the true model satisfied the CN assumption described in Theorem 1, but we estimated the CACE under the incorrect LI assumption. Thus, the true CACE_true was θ_11c− θ_10c, and the estimated CACE_estimated was $\frac{{\theta }_{11c}{\rho }_1}{{\theta }_{11c}{\rho }_1+(1-{\theta }_{11c}){\rho }_0}-\frac{{\theta }_{10c}{\rho }_1}{{\theta }_{10c}{\rho }_1+(1-{\theta }_{10c}){\rho }_0}$. Let bias = |CACE_estimated – CACE_true|. We maximized bias over all values from 0.0 to 1.0 by step 0.01 of θ _11c, θ _10c, ρ ₁, and ρ ₀. The results are reported in Figure 1. Each curve in Figure 1 represents a fixed CACE value, which was set to be 0.05, 0.1, 0.15, 0.2, and 0.25, respectively. For each of the five true CACE_true values, we plotted a curve to represent the relationship between the maximum bias of CACE estimates and a real parameter | P (R = 1 | Y = 1) − P (R = 1 | Y = 0) | in Figure 1. Here, | P (R = 1 | Y = 1) − P (R = 1 | Y = 0) | could be interpreted as a measure of the departure of the assumed LI model from the true CN model. The larger | P (R = 1 | Y = 1) − P (R = 1 | Y = 0) | was, the further away the assumed LI model was from the true CN model. From Figure 1, we saw that the further away the assumed LI model was from the true CN model, the bigger the bias of the CACE estimates obtained under the wrong LI model. From Figure 1, we also saw that the bias of the estimated CACE would depend on the value of the true CACE. In general, the larger the true CACE, the bigger the bias of the estimated CACE. As the true CACE decreased, the bias of the estimated CACE also decreased, and as the CACE value tended to zero, the difference between the estimates of the CACE under the CN and LI models also tended to zero.

Figure 1.

Real model: CN; supposed model: LI.

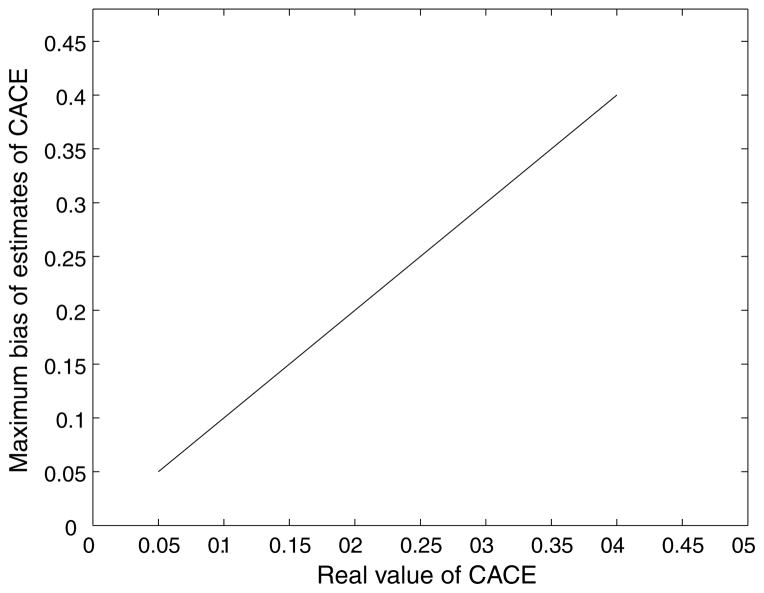
In Figure 2, we assumed that the true missing-data mechanism model was the LI model, but we used the incorrect CN model to estimate the CACE. Thus the true CACE_true was θ_11c− θ_10c and the estimated CACE_estimated was $\frac{(1-{\theta }_{11n}){\gamma }_{1n}-(1-{\theta }_{10a}){\gamma }_{0a}}{{\gamma }_{1n}{\gamma }_{0a}({\theta }_{10a}-{\theta }_{11n})}({\theta }_{11c}{\gamma }_{1c}-{\theta }_{10c}{\gamma }_{0c})$, where γ_{z u} = P(R = 1 | Z = z, U = u). The bias was still denoted as bias = |CACE_estimated – CACE_true|. We maximized bias over all values from 0.0 to 1.0 (in steps of 0.01) of θ_11c, θ_10c, θ_11n, θ_10a, ρ_1n, ρ_0a, ρ_1c, and ρ_0c. We also found that the maximum bias of the estimated CACE increased as the value of the true CACE increased. Thus, the estimator of CACE was sensitive to the model for the missing-data mechanism. The estimator of the CACE obtained from the LI model was biased if the true missing-data mechanism was the CN model, and vice versa. On the other hand, if the value of CACE tended to zero, the maximum bias tended to zero regardless of whether the true missing-data mechanism model was the CN model or the LI model. Here the estimate of CACE under the LI assumption was given by Zhou and Li (2006), and the estimate of CACE under the CN assumption was given by Theorem 1 in this article.

Figure 2.

Real model: LI; supposed model: CN.

We also compared our method with the method in which subjects with missing data were discarded. We generated 1000 samples with sample size N = 3000 under the model of Theorem 1. In Table 2, we reported means and standard errors of estimates of CACE, derived using our method and the method of discarding subjects with missing data. We fixed ρ ₀ = 0.1 and let ρ₁ vary from 0.2 to 0.9 whereas the other parameters were fixed at ξ = 0.5, ω_n = 0.2, ω_a = 0.3, θ_10a = 0.6, θ_11n = 0.3, θ_11c = 0.8, and θ_10c = 0.2. From Table 2, we saw that the bias of CACE estimates obtained by discarding subjects with missing data increased as |ρ₁ − ρ₀| increased, whereas the estimates obtained by our method were very close to the true CACE regardless of the value of |ρ₁ − ρ₀|.

Table 2.

Sensitivity analysis of CN and the method of ignoring incompletely observed subjects. Covariate X is binary and N = 3000. The true value of CACE is 0.6.

	CACE		CACEignor
Value of ρ1	Mean	Std. dev.	Mean	Std. dev.
ρ1 = 0.2	0.5923	0.0891	0.5621	0.0867
ρ1 = 0.3	0.5992	0.0795	0.5018	0.0715
ρ1 = 0.4	0.5977	0.0754	0.4474	0.0611
ρ1 = 0.5	0.6001	0.0695	0.3983	0.0547
ρ1 = 0.6	0.5987	0.0663	0.3595	0.0490
ρ1 = 0.7	0.5947	0.0636	0.3239	0.0455
ρ1 = 0.8	0.5965	0.0631	0.2998	0.0410
ρ1 = 0.9	0.6017	0.0545	0.2757	0.0376

We applied our method to the flu shot data in Zhou and Li (2006). We assumed that the CN missing-data mechanism satisfied Assumption 6. The observed data and the results are reported in Table 3. Because the moment estimates might not be proper, we only summarize the ML method. From the table, ρ̂₀ = 1 and the estimated standard deviation was equal to zero. This result means that all patients who were hospitalized must be observed.

Table 3.

Application to the flu shot data

Flu shot data (Zhou and Li, 2006)
	Z = 0, D = 0	Z = 0, D = 1	Z = 1, D = 0	Z = 1, D = 1
R = 1 Y = 0	573	143	499	256
R = 1 Y = 1	49	16	47	20
R = 0 Y = ?	492	17	497	9

ML estimates of flu shot data
Parameters	MLE	Std dev. (bootstrap)	95% CI
ξ	0.5065	0.0097	(0.4874, 0.5255)
ωn	0.7839	0.0108	(0.7627, 0.8051)
ωa	0.1348	0.0091	(0.1170, 0.1525)
θ10a	0.1757	0.0234	(0.1300, 0.2215)
θ11n	0.5216	0.0143	(0.4936, 0.5495)
θ11c	1.379e-016	0.0268	(0.0000, 0.0526)
θ10c	0.1393	0.1722	(0.0000, 0.4768)
ρ0	1.0000	0.0000	(1.0000, 1.0000)
ρ1	0.1151	0.0095	(0.0965, 0.1337)
CACE	−0.1393	0.1743	(−0.4808, 0.2022)

The estimated CACE and its 95% confidence interval were −0.1393 and (−0.4808, 0.2022), respectively. For comparison purposes, we listed the estimated CACE and its 95% confidence interval from Zhou and Li (2006) under the LI assumption. Under latent ignorability, the estimated CACE was −0.009, and the associated 95% confidence interval of CACE was (−0.211, 0.229). Both methods reached the same conclusion that influenza vaccination was not associated with reduced risk of hospitalization for respiratory illness.

There were several limitations related to these results. First, we ignored clustering effects in the data, which might lead to violation of the SUTVA assumption. Second, because the study was not double blind, the exclusion restriction assumption might be questionable, particularly among the always-takers, who were probably at high risk for flu and, as a result, might receive other interventions besides flu shots when their physicians received a reminder about flu shots.

5. Conclusions

Under an ignorable missing-data mechanism, we could derive valid ML estimates without modeling the missing-data mechanism. Hence, if enough information is available about the missing-data mechanism, the ignorability assumption can be made to hold. However, in many studies, such as our flu shot study, not enough information about the missing-data mechanism was available to make the ignorable assumption hold. Moreover, our simulation results showed that the estimates of the CACE were biased when the assumed ignorable missing mechanism was wrong. So, it is worthwhile to explore estimation methods under the nonignorable missing mechanism assumption.

In this article, we discussed the problem of noncompliance and nonignorable missing outcome mechanism. One major problem in dealing with nonignorable missing data is the issue of parameter identifiability. We gave sufficient conditions for identifying causal effect parameters under the CN missing-data mechanism, which was one type of nonignorable missing-data mechanism and was different from the existing LI assumption. Under the CN missing-data mechanism, we gave a theorem on parameter identification when the missing-data mechanism depended only on outcomes. With the availability of a certain type of covariate, we allowed the missing-data mechanism to depend on not only the missing outcome variable but also the treatment assignment Z and the latent compliance status variable U. From the simulation results, we concluded that the estimate of CACE was sensitive to the missing-data mechanism assumption. Thus, we should pay attention to the missing-data mechanism operating in a given research context. It is still an open problem as to how to test which of the two nonignorable missing-data mechanisms, CN or LI, holds. However, when the true CACE value was zero, from the simulation results, we concluded that the CACE estimate was not sensitive to which of the two nonignorable missing-data mechanism assumptions was true.

It is worth pointing out that the validity of our method requires finding a discrete covariate X that satisfies the assumptions in our models. It may not be easy to find such covariates in practice. Arguably, this is a problem that needs to be answered on a case-by-case basis.

Another problem in practice is whether it is of interest to explicitly ignore information on the missingness process when such information is available, because we do not need other covariates apart from X under our models. We suggest collecting this information, except when we know the missingness process and such a covariate X before we collect the data.