Predicting climate effects on Pacific sardine

Abstract

For many marine species and habitats, climate change and overfishing present a double threat. To manage marine resources effectively, it is necessary to adapt management to changes in the physical environment. Simple relationships between environmental conditions and fish abundance have long been used in both fisheries and fishery management. In many cases, however, physical, biological, and human variables feed back on each other. For these systems, associations between variables can change as the system evolves in time. This can obscure relationships between population dynamics and environmental variability, undermining our ability to forecast changes in populations tied to physical processes. Here we present a methodology for identifying physical forcing variables based on nonlinear forecasting and show how the method provides a predictive understanding of the influence of physical forcing on Pacific sardine.

Ecosystem-based management (EBM) is an essential challenge that places strong demands on our understanding of coupled social–ecological systems. EBM requires an understanding of how human activities such as fishing influence and are influenced by other parts of the ecosystem. This includes accounting for the effects of the physical environment on exploited populations. However, the interactions between ecosystem components can be complex, and unraveling physical–biological interactions remains a challenge. For instance, a retrospective study of 35 exploited and unexploited species in the California Current shows that fishing pressure can amplify the influence of environmental forcing on populations by truncating the age structure (1). This study and others (2–4) demonstrate that the effect of environmental forcing on populations can be contingent on fishing effort, current abundance, and age structure. This raises an important issue: Ecosystem variables are not separate, decomposable forces. Instead, their interactions are state-dependent, meaning that the impact of one variable on another depends on the state of the variables.

State-dependent behavior can confound many traditional statistical methods. Witness that valid correlations between physical and biological variables can be difficult to find (5) and can appear and disappear with time (6). In fact, nonlinear systems (systems with state-dependent interactions) can produce mirage correlations: variables that seem positively correlated over one period in time may seem negatively correlated or unrelated over another period (7). A meta-analysis of environment–recruitment relationships in marine populations shows that these correlations hold up poorly when retested with new data (6). Consequently, EBM requires more robust methods for identifying driving variables and understanding their influence on population and community dynamics. Here, we show that methods based on multivariate state space reconstruction (SSR) (8) offer an alternative method for studying physical–biological interactions from observational time series. It is a robust framework for studying ecosystems empirically. For those unfamiliar with state space reconstruction, we recommend two short animations (http://simplex.ucsd.edu/Movie_s1.mov and http://simplex.ucsd.edu/Movie_s2.mov). These techniques have been successful in identifying state-dependent physical–biological interactions in larval reef fish populations (9) and in models with simple periodic forcing (10). To demonstrate the utility of multivariate SSR for ecosystem-based management, we investigate the current conundrum over the management of Pacific sardine (Sardinops sagax). The Pacific sardine fishery in the California Current ecosystem (CCE) is a rare example of a fishery that has been managed with explicit consideration for the environment. However, conflicting evidence concerning the effect of temperature on sardine productivity (11) led to removal of this pioneering environmental control rule in 2012.

The policy was informed by a rich history of research. Sardine populations around the world have undergone boom–bust cycles. Crashes in California have coincided with crashes in other areas of the world (12), and boom–bust dynamics appear in sedimentary records well before human exploitation began (13). These facts have led to the hypothesis that changing environmental conditions drive sardine crashes and/or shifts in distribution, although fishing pressure has likely exacerbated global crashes in the recent past (3, 14). In the CCE, sardine recruitment seems to peak when and where upwelling is intermediate (15). In the CCE, intermediate upwelling is associated with low (14–15 °C) and high (>20 °C) temperatures. The association between high sardine recruitment and warm episodes is puzzling, because warm episodes are associated with low productivity. This sparked a search for potential mechanisms linking water temperature and sardine abundance. One possible mechanism is that release from larval predation during warm periods outweighs the scarcity of food (16). Alternatively, sardine may respond to offshore upwelling driven by wind-stress curl, as opposed to coastal upwelling (17).

Motivated by these studies, Jacobson and MacCall (18) sought a quantitative relationship between sardine and temperature. They found a statistical correlation between log reproductive success (one way of quantifying recruitment) and the 3-y average of the Scripps Institution of Oceanography (SIO) pier sea surface temperature (SST). They then verified the relationship using a modeling approach based on generalized additive models and formulated a best-management strategy for sardine that incorporated the influence of sea temperature. In light of these findings, the Pacific Fishery Management Council modified the sardine management plan to explicitly account for SST (19). Recently, McClatchie et al. (11) repeated the correlation analysis of Jacobson and MacCall (but not the modeling approach) with the addition of 17 y of new data. They found that the statistical correlation between recruitment and SST is no longer significant when the newer data are included. They concluded that the SIO pier temperature does not influence sardine dynamics, and the temperature-based control rule was subsequently rescinded.

Another explanation for these new findings is that temperature does influence sardine, but in a state-dependent way, causing mirage correlation between temperature and sardine. Indeed, we can directly test for state dependence in sardine population dynamics using S-maps (20). With S-maps, a family of models that range from linear (θ = 0) to highly nonlinear (θ ≥ 1) is used to forecast the target time series. For the sardine ichthyoplankton time series, nonlinear (state-dependent) models produce better forecasts than linear models, suggesting that sardine have state-dependent dynamics (Figs. S1 and S2). Furthermore, Sugihara et al. (7) analyzed historical landings of sardine and SIO pier SST with convergent cross-mapping (an alternative to correlation that detects state-dependent interactions) and found that the SIO pier temperature does affect sardine.

Consequently, the failure of the sardine–temperature correlation to hold up to retesting does not mean that the SIO pier temperature is irrelevant to sardine. Rather, the problem requires an analytical framework specifically suited to ecological systems with interdependent parts. To this end, the recent work (7) with convergent cross-mapping detected a cause–effect relationship between temperature and sardine. However, it is not sufficient for management to know whether a physical variable is affecting a population. It is also necessary to predict how environmental conditions will affect population dynamics. Multivariate SSR can address this need.

Thus, we seek to demonstrate multivariate SSR as a practical tool for understanding the influence of temperature on Pacific sardine population dynamics. First, we present a conceptual overview of multivariate SSR and use simple models to demonstrate the methods. We then apply the method to ichthyoplankton time series of Pacific sardine. We show that when the population dynamics of sardine are treated nonlinearly, the SIO SST and other broad-scale indicators can improve forecasts of year-to-year changes in abundance. We illustrate how multivariate SSR can predict the effect of changes in SIO SST on sardine and is thereby a useful tool for exploring possible temperature scenarios. Finally, models show how these methods can predict the outcomes of harvest targets under different climate regimes.

Primer on Multivariate State Space Reconstruction.

SSR is based on the theory of dynamic systems. If a time series variable X(t) is part of a dynamic system, a set of rules (e.g., a system of difference or differential equations) dictates how X changes in time based on the current value of X and the variables that interact with X. As an example, consider three species, X, Y, and Z, modeled with coupled logistic equations that represent a three-species food chain (21) (SI Text gives a full description). The differential equations dictate how the abundance of each species changes in time given the current state of each population.

A typical way to view the system is as separate time series of each species, as shown for species X in Fig. 1D. However, we can also view the system in a multidimensional space, taking the abundances of species X, Y, and Z as the coordinate axes. This defines the state space of this simple ecosystem. Viewed in the state space, each time point corresponds to a vector and the changes in the ecosystem over time (abundances of the three populations) form a trajectory (Fig. 1A). Two time points nearby in the state space represent two similar states of the ecosystem and the populations will follow similar trajectories as time progresses.

Fig. 1.

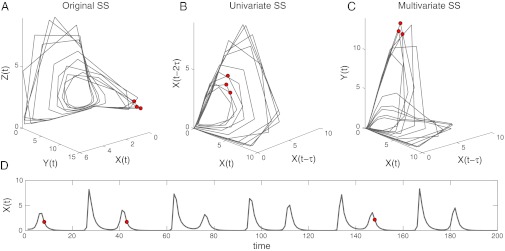
State space reconstruction demonstrated with a three-species logistic model. (A) The trajectory of the model ecosystem is plotted in three dimensions using the abundances X(t), Y(t), and Z(t) as coordinates. (B) The trajectory is shown in the univariate SSR coordinates, [X(t), X(t−1), X(t−2)], where lags of X take the place of the other variables. (C) The trajectory is shown in multivariate SSR coordinates, [X(t), X(t−1), Y(t)]. The system is in a similar state (nearby in state space) at times t₁, t₂, and t₃ (red) based on all three representations. Hence, any of these state spaces (original or reconstructed) can be used for nearest-neighbor forecasting. (D) The abundance of species X is shown as a time series.

Often in ecology only one or a few variables are actually measured. In these cases, Takens’s theorem and its multivariate generalization (8, 22, 23) show that it is still possible to represent the system dynamics in a state space by substituting time lags of the measured variables [e.g., X(t−1)] for the unknown variables as coordinates. In effect, the information in the unobserved variables is encoded in the observed time series, and so a single time series can be used to reconstruct the state space. This gives a time-delayed coordinate representation (or embedding) of the system trajectories. Fig. 1 B and C illustrate univariate (using lags of only one variable) and multivariate (using lags of two or more variables) embeddings for the three-species model. Importantly, the trajectories in the reconstructed state space are uniquely matched to trajectories in the original state space, and states (vectors) that are neighboring in one space are also neighboring in the others. Observe that at time t₁, t₂, and t₃ (shown in red) the ecosystem is in a similar state based on all three pictures.

One basic application of SSR embeddings is forecasting. Because vectors nearby in state space evolve similarly in time, the future abundance at one time point can be predicted based on the behavior of its nearest neighbors in the reconstructed state space. In this paper, we use two different types of forecasts. The first is simplex projection, where a weighted average is taken over the E + 1 nearest neighbor vectors in the reconstructed state space (24) (E is the dimension of the state space). The second is S-maps (20, 25), where a linear model is fit for each observed vector in the reconstructed state space using all of the remaining vectors (cross-validation). However, the vectors nearby the target in state space are given greater weight, controlled by the nonlinearity parameter θ, and so S-maps can give either linear (θ = 0) or nonlinear (θ > 0) forecasts. By comparing the performance of locally weighted (nonlinear) forecasts to the global linear forecasts (θ = 0), S-maps can be used to test for nonlinear dynamics. A significant increase in forecast skill for the locally weighted model is taken as evidence of nonlinear dynamics (state dependence). Note that simplex projection can be the better tool for exploratory analysis (less possibility for overfitting), but S-maps can ultimately give better forecasts. A detailed mathematical description of these techniques with summary code is given in SI Text. Interested parties are encouraged to contact the authors regarding software and guidance for analysis.

Validating Multivariate Embeddings.

Multivariate embeddings that use two variables X and Y should make good forecasts only if Y and X are interacting parts of the same system. This suggests that SSR forecasting can be used to check for interactions between variables (7). Each SSR embedding is a different representation of the same fundamental system. A priori it is not possible to know whether one particular choice of lagged variables will give better forecasts than another (8). Stochastically forced systems, however, are a special case. For a purely stochastic forcing variable Y, the current state cannot be inferred from past values of the forced variable. The only way to include this environmental information in SSR forecasts of X is to have Y(t) as a coordinate variable, and nearest neighbor forecasts based only on lags of X(t) will necessarily have greater uncertainty. By this logic, if a stochastic variable Y has an effect on X, then adding Y (with the appropriate lag) should always improve univariate forecasts of X. In this way, comparing multivariate to univariate SSR forecasts can identify stochastic driving variables.

Scenario Exploration with Multivariate SSR.

In ecology we are interested not only in knowing whether two variables interact, but also how they interact. Consider a Ricker model for a population S (Eq. 1). In this case, the model is exactly known, and we can simply calculate S(t+1) for different hypothetical past temperatures T₁, T₂, and so on, to understand the effect temperature has on the population. When studying real populations, however, the true model is not known. Scenario exploration with multivariate SSR is a way to explore climate effects in real systems without assuming a particular model structure. Scenario exploration involves constructing a multivariate embedding to predict S(t+1) using different values of T to explore the effect of temperature on the stock.

To demonstrate scenario exploration, we begin with toy models, which allow us to compare predictions based on multivariate SSR to calculations with the exact model. The temperature-driven Ricker model given by Eq. 1 in Materials and Methods is a simple model of a population that has nonlinear dynamics and is driven by temperature. We explore the effect of temperature, T, on the stock, S, using the multivariate embedding [S(t), S(t−1), S(t−2), S(t−3), T(t)]. For each t, we predict the effect that an increase in past temperature ΔT = 0.1σ_T (10% of the SD of the temperature time series) would have on the population abundance the following year. That is, we use simplex projection to make a nearest-neighbor forecast of S(t+1) for the state space vector [S(t), S(t−1), S(t−2), S(t−3), T(t) + ΔT]. Fig. 2A shows the predictions of SSR scenario exploration plotted against the true values calculated from the model for 10 time series of 50 y each with different initial conditions and realizations of T and ε_proc. The result is robust to a wide range of growth rates (Fig. S3).

Fig. 2.

Scenario exploration illustrated for a short (50-y) time series generated with known models that are forced by temperature. For each time series point t, the effect of warming on S(t+1) is predicted with multivariate SSR for warming of ΔT = 0.1σ (10% of the SD of T). SSR predictions are compared with calculations with the known model for (A) a single-species Ricker model (Eq. 1) and (B) species 1 in a multispecies Ricker model (Eq. 2) for 10 model realizations.

Importantly, SSR methods can be applied in both single- and multispecies contexts, even when there are no records of the other interacting species. As a demonstration we repeat the analysis above on the three-species extension of the basic Ricker model defined in Eq. 2. However, we only use the time series of the target species S₁ and the temperature T to do scenario exploration. Fig. 2B shows that scenario exploration can still predict the effect of temperature on a population in a multispecies complex, even if the other species are unobserved. For both the single- and multispecies models, the correlation between SSR predictions and model calculations is high: ρ = 0.75 and 0.86, respectively.

Results

We use multivariate SSR methods to determine whether and how sardine are affected by their environment. We first apply multivariate SSR to sardine data to verify that the SIO pier SST influences sardine dynamics and determine whether it is the best single environmental indicator variable. Table 1 displays the improvement in forecast skill ΔF of multivariate embeddings using the SIO pier SST and other environmental indicators. Including SIO pier SST in embeddings improves forecasts with simplex projection, indicating that SIO SST influences sardine, and ΔF is significantly greater than can be explained by the null model (P < 0.05). Several other variables show positive ΔF, including the Pacific Decadal Oscillation (PDO), North Pacific Gyre Oscillation (NPGO), and the Southern California Bight (SCB) satellite SST, suggesting these are also relevant to Pacific sardine population dynamics. Of these, only the PDO is significant (P < 0.05). The PDO and SIO SST are highly correlated, so this is not surprising. The method suggests three variables that are least likely important to sardine dynamics: Newport Pier SST, North Pacific Index (NPI), and Southern Oscillation Index (SOI); each of these has a strong negative effect on forecasting.

Table 1.

Relevance of environmental indicators to sardine dynamics

Variable	ρmulti	ΔF	P
SIO Pier temperature (surface)	0.4085	0.0872	0.04
PDO	0.3968	0.0755	0.04
SCB satellite SST	0.3652	0.0439	0.12
NPGO	0.3452	0.0239	0.19
SIO Pier temperature (bottom)	0.3128	−0.0085	—
MEI	0.3034	−0.0179	—
SOI	0.2434	−0.0779	—
NPI	0.2152	−0.1061	—
Newport Pier temperature (surface)	0.2117	−0.1096	—

Forecasts of sardine ichthyoplankton are compared between the multivariate embedding [X(t), X(t−1), X(t−2), Y(t)] and the univariate embedding [X(t), X(t−1), X(t−2)] for each candidate environmental indicator variable, Y. The forecast skill (correlation ρ between observations and predictions) of multivariate embeddings using each of the candidate variables are shown; the univariate forecast skill is ρ_uni = 0.3213. ΔF = ρ_multi − ρ_uni > 0 indicates that the environmental variable influences sardine, whereas large negative ΔF indicates the variable is irrelevant. Significance of ΔF > 0 is tested using phase-randomized surrogate time series of the environmental variables. MEI, Multivariate El Niño Index.

To explicitly test the notion that the influence of environment (SST) on sardine depends on population state, we compare the out-of-sample forecasts of Pacific sardine ichthyoplankton with a univariate linear forecasting model (using only lags of sardine) to both linear and nonlinear multivariate forecasting models that also account for temperature. For simplicity, all models use S-maps, which can be made linear or nonlinear by adjusting the nonlinear tuning parameter, θ. The base univariate linear (θ = 0) model is equivalent to an order-E autoregressive (AR) model, whereas the multivariate linear (θ = 0) model has an added linear term for the SIO pier SST. The nonlinear S-map model uses the same dimensions as the multivariate linear model, but the nonlinear parameter θ > 0 is fit in-sample. Fig. 3 shows the percentage reduction in error of the multivariate models over the univariate linear base model. Error is quantified as mean absolute error (Fig. 3 Left) or root-mean-squared error (Right). Using either measurement, the nonlinear model that incorporates temperature does best. Furthermore, linearly including temperature increases forecasting error (percentage improvement in error is negative in both plots). Thus, accounting for temperature only improves forecasts when the model is state-dependent (nonlinear).

Fig. 3.

Linear and nonlinear forecasting models for Pacific sardine icthyoplankton that include SIO pier SST are compared with a base univariate linear model. The left plot shows the percent improvement in mean absolute error (MAE) of the out-of-sample forecasts for each model over the base model, (MAE_base − MAE_model)/MAE_base. The right plot shows the same, but using RMSE. The base model errors are MAE = 0.99, RMSE = 1.47 (normalized to the SD).

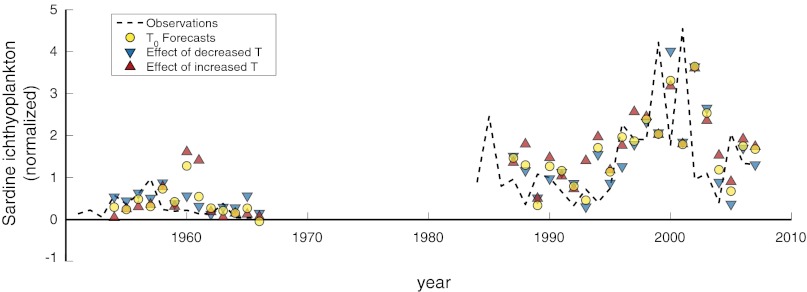
Because multivariate attractor reconstructions using either SIO SST or PDO give good predictions of sardine abundance, these embeddings can be used for scenario exploration to understand how past conditions affected sardine and to predict the response of sardine to future environmental scenarios. As an illustration, we do scenario exploration using the multivariate embedding that includes SIO pier SST, [X(t), X(t−1), X(t−2), SST(t)]. For each historical observation, X(t), we explore how X(t+1) would have differed if temperatures were warmer or cooler by half the SD σ_SST of the historical pier temperature. That is, we predict X(t+1) for the state [X(t), X(t−1), X(t−2), SST(t) ± ΔT], where ΔT = 0.5σ_SST. Fig. 4 shows the multivariate SSR prediction for sardine with the historic temperature (yellow circles), increase in temperature (red triangles), and decrease in temperature (blue triangles), along with the observed time series (dashed black line). Note that SSR predictions were made of first differences and converted back into raw ichthyoplankton abundance.

Fig. 4.

Effect of warming and cooling on sardine population calculated using scenario exploration. Using the multivariate embedding based on lags of sardine abundance and SIO pier SST (Table 1), we explore the effect of perturbing the historical temperatures (averaged over 3 y) by ΔT = ± 0.5σ_SST on sardine abundance in the following year. The historical time series is shown as a black dashed line. Multivariate SSR forecasts based on historical temperatures (yellow circles), warming by ΔT = +0.5σ_SST (red triangles), and cooling by ΔT = −0.5σ_SST (blue triangles) are shown.

Discussion

We demonstrated the application of multivariate SSR to studying physical–biological interactions. The predictions obtained do not assume a particular functional form for the environmental interaction; they rely only on the choice of the embedding dimension and environmental variable(s). This multivariate embedding can then be used in place of model equations to understand and predict the effect of changes in a driving variable on population dynamics.

Scenario exploration with multivariate embeddings motivates the development of new adaptive management schemes based on short-term forecasting. If time series of a human control variable (e.g., fishing effort or mortality) are available, management could be based on scenario exploration with multivariate embeddings that include abundance, temperature, and the control variable. Simultaneously exploring different temperature and harvesting scenarios could then reveal how temperature affects the relationship between fishing and future biomass. As an ad hoc illustration of this idea, take the Ricker model described by Eq. 3, which explicitly includes temperature and fishing mortality. Fig. 5 shows the results of using scenario exploration at a single time point to assess the relationship between fishing mortality and next year’s abundance when the temperature increases by ΔT = 0.5σ_T (half the SD of T) from the previous year (red), remains constant (green), or decreases by ΔT = 0.5σ_T (blue). The results of scenario exploration (filled squares) closely match the calculations made with the exact model (dotted lines). This type of scenario exploration would tell managers the permissible level of fishing given a target biomass and recent ocean conditions. This approach is analogous to the greedy heuristic strategies that are used in high-dimensional approximate optimization problems (26). Of course, considerable work remains to be done to develop and evaluate management plans based on these methods.

Fig. 5.

Model illustration of how simultaneous scenario exploration over temperature and fishing mortality might hypothetically be used in management. The effect of fishing mortality F on future biomass S(t+1) is plotted for three temperature scenarios: T increases by 0.5σ_T (red), remains constant (green), or decreases by 0.5σ_T (blue). Even with just a 50-y time series, multivariate SSR predictions (filled squares) closely match the model calculations (dotted lines).

More immediately, these methods offer a data-motivated perspective on the dynamic relationship between sardine and environmental conditions in the CCE. We find that including either SIO SST or the PDO in the multivariate embedding improves forecast skill (ρ) by ∼30%. These indicators reflect environmental forcing of sardine population dynamics that is not captured by more traditional methods. We conclude that environmental considerations should in fact play an important role in Pacific sardine management. Additional analyses demonstrating the influence of SIO SST on Pacific sardine landings using related SSR methods (7) support this assertion.

Our results further suggest that good management must reflect the complexity underlying the interaction between environmental changes and population dynamics (Fig. 3). Exploring the effect of SIO pier SST on sardine using multivariate SSR (shown in Fig. 4) suggests that, on average, increasing temperature results in higher forecasts of abundance than decreasing temperature. This corroborates the previous results used in the management plan that warm water is better for sardine. However, our empirical analysis shows that the effect of temperature depends on the specific state of the population. For example, changes in temperature seem to have little or opposite effect in the early years of the time series, when the population is at a much lower abundance, and in later years with very large abundance (e.g., 1999–2001). This suggests any temperature-sensitive control rule for sardine should be different at low, intermediate, and high sardine abundances.

Like other nonparametric methods, SSR benefits from greater time series length. Although there is no absolute rule regarding length, forecast skill improves with time series length (7); for fisheries it is usually difficult to get significant predictability with time series shorter than 30 points. Therefore, management applications of SSR will be best suited to fisheries with longer time series. Even when time series are short, however, good predictability is possible by combining data from similar fisheries (27). For practical application to management, it is also important to acknowledge measurement error. State space forecasting is robust to measurement error (28, 29). Furthermore, we can consider extending the deterministic simplex projection (or S-map) to incorporate an estimated distribution for measurement error for each time series point. This would be extended to spatial distributions for the state vectors in the attractor reconstruction and ultimately give distributions for the forecast.

Note that we expect greater error in scenario exploration when temperature scenarios exceed the bounds of historic data. In these cases, there are no appropriate historical observations of the dynamics on which to base forecasts. The more extreme the scenario, the greater the chance of encountering dynamics never previously recorded. Parameterized methods have a potential advantage over nonparametric methods in extrapolating beyond observed behavior. However, there is uncertainty in extrapolation with any method. The grim reality of anthropogenic climate change and overfishing is that as we continue stressing ecosystems, we catalyze ecological outcomes that are increasingly surprising but less and less predictable from historical observations. Regardless of the analytical approach, the precautionary principal is critical.

Moving forward, scenario exploration with multivariate SSR can be applied to understand relationships between two (or more) dynamically interacting variables. Here, we focused on the case of abundance and temperature. It would also be possible to use catch or abundance of another species as the second variable and explore the ecological impact of harvesting one stock on another. Demonstrating the feasibility of using SSR in a multispecies context for a particular fishery is an important potential capability of these methods that remains to be shown.

Given that climate change and overfishing are dual threats to many marine species, it is critical to consider environmental conditions when formulating management strategies. Our analysis with multivariate SSR illustrates the value of explicitly considering complex dynamics in population responses to environmental forcing. For Pacific sardine, there is a clear dependence on the physical environment that can be captured using available, broad-scale indicators of conditions in the CCE. These general methods can offer immediate insight into environmental forcing of species with long time series and suggest a promising avenue of research into operational schemes for implementing ecosystem-based management.

Materials and Methods

Variable Identification.

We compare the forecasting skill of the univariate state space [X(t), X(t−1), …, X(t−(E−1))] and the multivariate state space [X(t), X(t−1)_, …, X(t−(E−1)), Y(t−d)], where E is the optimal univariate embedding dimension (SI Text) and d is the lag of the environmental forcing. We then evaluate the forecast skill using the correlation coefficient ρ between observed and predicted values, and the relevant quantity for identifying variables is ΔF = ρ_multi − ρ_uni. A physical variable is considered relevant if ΔF is significantly greater than 0. To test significance, we use the Ebisuzaki randomization procedure to shuffle the environmental time series values while preserving the spectrum (30); this destroys any temporal relationship with the biological time series. For our analysis of Pacific sardine, we compute ρ_multi for 500 randomizations of each environmental variable to produce null distributions for ΔF. Note that each environmental variable thus has its own null distribution.

Forecast Comparison.

To explicitly investigate state dependence in the influence of temperature on sardine, we compare three S-map forecasts of the Pacific sardine ichthyoplankton. S-maps requires two parameters: the embedding dimensions, E (number of lags to use for forecasts), and the nonlinear tuning parameter, θ. For simplicity, we restrict all three models to use the same number of univariate lags (lags of sardine), but the multivariate models also includes SIO pier SST (averaged over the previous 3 y) as an additional dimension. As is typically done for S-map analysis (20), we use simplex projection to determine E (the optimal number of univariate lags) over the range 1–8. For the linear models, θ = 0. For the nonlinear model, we must also fit 0 < θ < 10.

All forecasts were made out-of-sample. We restricted our forecasts to the 22 points in the time series that have eight consecutive lags. So for each target point, we find the E that minimizes the mean absolute error (MAE) of forecasts using univariate simplex projection on the remaining 21 points. We then find θ over the range [0, 10] that minimizes the MAE of multivariate S-map forecasts using cross-validation over the remaining 21 points. Finally, we use these parameters to forecast the target point out-of-sample.

Model Examples.

The most basic Ricker model only shows nonlinear dynamics (as demonstrated for Pacific sardine in Figs. S1 and S2) at values of the growth parameter, r, that are considerably higher than those usually fit in management models. However, when the species dynamics are influenced by process error, nonlinear dynamics arise at considerably lower values of r (31). Here, we include process error as additive with the growth rate, giving

where ε(t) is a normally distributed random variable with mean(ε) = 0 and SD(ε) = 0.2. The temperature T(t) was modeled as red noise by applying a 10-y averaging window to white noise. For Fig. 2A, we set r = 2 and ψ = 0.3.

Nonlinear dynamics can also arise in the Ricker model when the interactions between multiple species are considered. Thus, we also used the following three-species extension of the Ricker model:

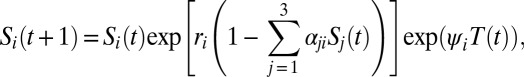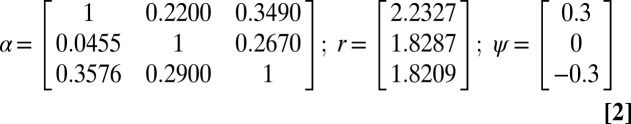for i = (1,2,3). Note that the growth rates r_i were drawn randomly from the interval [1.5, 2.5] and the nondiagonal elements of the interaction matrix α were drawn randomly from [0, 0.5].

For Fig. 5 we include a term for fishing mortality, F, in Eq. 1 as follows:

where F(t) is modeled as a uniformly distributed random variable over the range [0, 0.3]. As in Fig. 2A, we set r = 2 and ψ = 0.3. To explore how temperature conditions change the effect of harvesting on the population, we did scenario exploration with the multivariate embedding [S(t), S(t−1), S(t−2), S(t−3), T(t), F(t)]. The three temperature scenarios we illustrate are T(t) = T(t−1) + 0.5σ_T, T(t) = T(t−1), and T(t) = T(t−1) − 0.5σ_T (σ_T is the SD of the modeled temperature). The figure was made using a 50-y time series to predict the behavior at time t = 50. To get the best forecasts, we use a strongly nonlinear S-map rather than simplex projection. For simplicity, we specified θ = 5 rather than explicitly fitting θ for this model example.

Data.

We used five climate indices that have been linked to biological changes in the California Current: the SOI (32), NPI (33), PDO (34), NPGO (35), and Multivariate El Niño/Southern Oscillation Index (36). We also used daily temperature data from the SIO Pier in La Jolla, CA and the City of Newport Beach Pier in Newport Beach, CA (http://shorestation.ucsd.edu/data/index_data.html). For the SIO Pier, we used both surface (0 m) and bottom (5 m) temperatures. Finally, we used an index for SST in the Southern California Bight based on National Oceanic and Atmospheric Administration Extended Reconstructed Sea Surface Temperature v3 analysis (www.esrl.noaa.gov/psd/) averaged over four contiguous 2° × 2° areas, following McClatchie et al. (11). All environmental indicators were averaged over a 3-y window and normalized to match the original analysis (18), but not first-differenced. For time series with daily resolution, this meant a straight daily average. For the other time series, the average was taken over monthly values.

Time series for S. sagax were derived from the CalCOFI ichthyoplankton surveys as in Hsieh (5) from 1950 to 2007. CalCOFI ichthyoplankton abundance provides an index of adult spawning stock biomass (37). For the normalized first differences of the sardine ichthyoplankton data, we determined the best embedding dimension to be E = 3 (SI Text).