A Shock Tube and Chemical Kinetic Modeling Study of the Oxidation of 2,5-Dimethylfuran

Abstract

A detailed kinetic model describing the oxidation of 2,5-dimethylfuran (DMF), a potential second-generation biofuel, is proposed. The kinetic model is based upon quantum chemical calculations for the initial DMF consumption reactions and important reactions of intermediates. The model is validated by comparison to new DMF shock tube ignition delay time measurements (over the temperature range 1300 – 1831 K and at nominal pressures of 1 and 4 bar) and the DMF pyrolysis speciation measurements of Lifshitz et al. [J. Phys. Chem. A 102 (52) (1998) 10655-10670] Globally, modeling predictions are in good agreement with the considered experimental targets. In particular, ignition delay times are predicted well by the new model, with model experiment deviations of at most a factor of two, and DMF pyrolysis conversion is predicted well, to within experimental scatter of the Lifshitz et al. data. Additionally, comparisons of measured and model predicted pyrolysis speciation provides validation of theoretically calculated channels for the oxidation of DMF. Sensitivity and reaction flux analyses highlight important reactions as well as the primary reaction pathways responsible for the decomposition of DMF and formation and destruction of key intermediate and product species.

1. Introduction

Furans have attracted recent interest as second-generation biofuels due to the potential for their large scale production from fructose and glucose^1-2 and complex biomass such as cellulose³. 2,5-Dimethylfuran (DMF) has received specific attention following the demonstration by Román-Leshkov et al.¹ of its synthesis through the acid-catalyzed dehydration of fructose (C₆H₁₂O₆) to produce a 5-hydroxymethylfurfural (HMF, C₆H₆O₃) intermediate that can be converted to DMF (C₆H₈O) by copper-ruthenium catalyzed hydrogenolysis. DMF has several advantages over ethanol, the liquid biofuel currently produced in the largest quantities worldwide, as a fuel for spark-ignition (SI) automotive engines. DMF has greater volumetric energy density, higher research octane number (RON), and lower water solubility than ethanol. A comparison of relevant properties for gasoline and gasoline alternatives, including ethanol, 1-butanol, another potential second-generation biofuel ^4-6, and DMF is given in Table 1.

Table 1.

Fuel properties.

Fuel	gasoline	ethanol	1-butanol	DMF
Structure
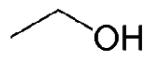
Lower heating value [MJ kg−1]	~42.5	28.9	33.1	33.3
Volumetric energy density [MJ L−1]	~32	20	29	30
Research Octane Number, RON	92-98	109	96	119
Autoignition temperature [K]	520-550	635	616	559
Boiling point [K]	315-480	352	390	366
Water solubility [g L−1]	insoluble	fully miscible	63.2	2.3

Due to DMF’s favorable properties and the potential for its synthesis from carbohydrate feedstocks, DMF has recently been studied as a potential alternative to petroleum-derived gasoline for SI engines. Zhong et al.⁷, Daniel et al.⁸, and Wu et al.⁹ showed in a series of SI engine studies that DMF gave very similar performances and emissions to commercial gasoline with slightly greater combustion efficiency and no apparent adverse effects to engine hardware. Rothamer and Jennings¹⁰ also have studied DMF/gasoline blends in a direct-injection SI engine, showing reduced propensity for knocking with the addition of DMF. Additionally, there have been a number of studies focused on measurement of laminar flame speeds and Markstein lengths for DMF and DMF mixtures ^11-14 and DMF flame instability ¹⁵. Notable observations from these studies include the measurement of laminar flame speeds for DMF that are within 10% of those for gasoline for φ = 0.9-1.1 ¹² and within 15% of those for iso-octane, a primary reference fuel with RON = 100, for φ = 0.9-1.5 ¹⁴. Recently Somers et al.¹⁶ have investigated the combustion behavior of 2-methylfuran, closely related to DMF, reporting laminar flame speeds, shock tube ignition delay times, and a comprehensive kinetic model for the description of the high-temperature oxidation of 2-methylfuran.

In work related to the thermochemistry and elementary reaction kinetics of DMF and related compounds, Simmie and Curran¹⁷ have recently performed quantum chemical (QC) calculations for the enthalpies of formation and bond dissociation energies of DMF, related furans, and related radical species (potential products of DMF dissociation). Their results show that the lowest energy bond in DMF is the C-H bond of the methyl groups (85.5 kcal mol⁻¹). In contrast, the ring-carbon-H bonds (120 kcal mol⁻¹) and the ring-carbon-CH₃ bonds (115 kcal mol⁻¹) are very strong due to the electronic structure of DMF and the geometrical stiffness of the five-membered ring which comprises DMF. These strong bonds make DMF fairly unreactive at high temperatures relative to other fuels and a good knock-inhibitor, as indicated by its high RON given in Table 1 and the experimentally observed reduced knocking propensity of DMF/gasoline blends¹⁰. Following the Simmie and Curran¹⁷ QC thermochemistry calculations, Simmie and Metcalfe¹⁸ investigated the unimolecular decomposition of DMF using QC methods and found channels involving the opening of the aromatic ring to be most important.

Studies focused on the kinetics of DMF thermal decomposition include a very low-pressure (~0.1 Pa) flow reactor study of DMF by Grela et al.¹⁹ who measured products, including carbon monoxide (CO), pentadiene isomers (C₅H₈), water (H₂O) and benzene (C₆H₆), and proposed a mechanism for DMF thermal decomposition. Lifshitz et al.²⁰ studied the thermal decomposition of DMF behind reflected shock waves in a single-pulse shock tube over the temperature range 1070-1370 K and at overall densities of ~3×10⁻⁵ mol cm⁻³, corresponding to pressures from 2 to 3.7 bar. A large number of products resulting from unimolecular cleavage of the ring and consecutive free radical reactions were obtained under shock heating, including CO, vinylacetylene (C₄H₄), acetylene (C₂H₂), methane (CH₄), ethylene (C₂H₄), and ethane (C₂H₆), among others. To model the observed product distribution, Lifshitz et al. developed a DMF decomposition reaction scheme containing 50 species and 181 reactions.

In recent work Djokic et al.²¹ studied the decomposition of DMF in a flow tube at temperatures from 873 to 1098 K providing speciation data describing both the fragmentation and molecular growth kinetics for DMF. In other recent work Friese et al.^22-23 have measured the formation of H atoms using atomic resonance absorption following shock heating of DMF and the H-atom precursor, ethyl iodide. Friese et al.²² recommended rate coefficients for the fission of C-H bonds in the DMF methyl groups and the reaction of H atoms with DMF. Sirjean and Fournet have also recently investigated the potential energy surface for the reaction of H atoms with DMF²⁴ as well as the thermal decomposition of the 5-methyl-2-furanylmethyl radical²⁵, via theoretical calculations and master equation/RRKM modeling.

Wu et al.²⁶ recently identified combustion intermediates formed during DMF oxidation in a low-pressure (4.0 kPa) premixed laminar DMF/O₂/Ar flame at an equivalence ratio of 2.0 using tunable vacuum ultraviolet (VUV) synchrotron radiation photoionization with molecular-beam mass spectrometry. More than 70 species were detected, including furan and its derivatives, aromatics, and free radicals. Possible reaction pathways of DMF, 2-methylfuran, and furan were proposed based on the intermediates identified. In following work, Tian et al.²⁷ performed speciation measurements, also using synchrotron radiation photoionization mass spectrometry, for low-pressure premixed furan/O₂/Ar flames. They identified 40 intermediate species and developed a detailed kinetic model for furan oxidation.

To assess the potential of DMF as a gasoline replacement or additive, a validated detailed kinetic model for the oxidation of DMF is required. Such a model, when incorporated into computational fluid dynamics (CFD) simulations, will allow for predictive assessment of DMF influence on engine performance (e.g., efficiency, emissions, knocking propensity, etc.)²⁸. However, despite the research efforts focused on DMF synthesis, flame propagation and speciation, thermochemistry, and thermal decomposition reaction kinetics, to our knowledge, a detailed kinetic model for the oxidation of DMF has yet to be proposed in the literature. Additionally, limited kinetic measurements exist in the literature for the quantitative assessment and validation of a DMF oxidation model and no measurements have been previously reported for DMF ignition delay times, an important kinetic model validation target describing fuel reactivity.

Here, for the first time, a detailed kinetic model describing the oxidation of DMF is proposed. The kinetic model is based upon quantum chemistry calculations for the initial DMF consumption reactions and important reactions of intermediates. The model is validated by comparison to new shock tube ignition delay time measurements for DMF, the first such measurements reported to our knowledge, and the thermal decomposition speciation measurements of Lifshitz et al.²⁰, which represent good targets to study the first decomposition steps of DMF.

2. Experimental Method

Ignition delay time measurements were carried out in a 12.3 cm inner diameter, high-purity, low-pressure (< 10 bar), stainless steel shock tube previously described by Moss et al.²⁹. Measurements were made in the reflected shock region for seven DMF/O₂/Ar reactant mixtures specified in Table 2 for temperatures from 1300 to 1831 K and at nominal pressures of 1 and 4 bar. Reactant mixtures were made by introducing DMF vapor (99% purity from Sigma Aldrich) into the evacuated mixing vessel and then adding O₂ (99.995% purity from Noble Gases) and Ar (99.999% purity from Noble Gases) from high-pressure cylinders at appropriate proportions as determined using partial pressures; all gases were introduced through a stainless steel manifold and the DMF was stored in air free glassware. Pressures were measured using a high-accuracy Baratron manometer and a Setra diaphragm pressure gauge and the manifold and mixing vessel were evacuated using a mechanical rotary vacuum pump (ultimate pressure of 2×10⁻³ Torr). Once synthesized, the mixtures were mechanical mixed using a vane stirrer located inside the mixing vessel for at least 30 minutes prior to experiments. Prior to experiments the shock tube driven section was evacuated using a Varian V70 turbomolecular pump (ultimate pressure of 1×10⁻⁶ Torr with a leak rate of 3×10⁻⁶ Torr min⁻¹). Following driven section evacuation, the reactant mixtures were loaded into the driven section and shock waves were generated by filling the evacuated driver section with pure He and bursting single polycarbonate diaphragms; diaphragm rupture was achieved using a fixed mechanical cutter.

Table 2.

DMF/O₂/Ar mixtures studied.

Φ	mol% DMF	mol% O2	mol% Ar	Pressure [bar]
1	1.0	7.5	91.5	1 and 4
1	0.5	3.75	95.75	1
1	0.25	1.875	97.875	1
0.5	1.0	15	84	1
0.5	0.5	7.5	92	1
1.5	1.0	5	94	1
1.5	0.5	2.5	97	1

The incident shock velocity was measured using four time of traversal measurements made with five fast response (rise time ≤1 μs) piezoelectric pressure transducers spaced (PCB model 113A) over the last 1.24 m of the driven section. The time intervals for passage of the shock wave were determined by sending the signals from the five transducers to four Phillips PM6666 timer counters (0.1 Us resolution). The four incident shock velocity measurements were linearly extrapolated to the end wall of the driven section for determination of the incident shock velocity at the test location. The final pressure transducer, located 2 cm from the end wall, was also used for quantitative pressure measurements in the incident and reflected shock regimes. The incident shock velocity extrapolated to the end wall test location were used to determine incident and reflected shock conditions using the normal shock equations with the known initial reactant mixture composition, temperature, and pressure and the known thermochemical properties for the reactant mixture. The initial pressure was measured using a high-accuracy Baratron manometer and the initial room temperature was measured using a mercury thermometer. The thermochemical properties for O₂ and Ar were taken from the Goos et al. database ³⁰ and those for DMF were taken from quantum chemical calculations performed at the CBSQB3 level as part of the present study. The estimated uncertainty in the reflected shock temperature and pressure are 1% and 1.5% respectively. These uncertainties result from a consideration of uncertainties in initial conditions (temperature, pressure, and mixtures composition) and measured incident shock velocity, by far the largest contributor to uncertainty in the post shock conditions.

Following passage of the reflected shock wave, the pressure rises slowly at the test location over the course of the test time due to viscous gas dynamics. In the present experiments the pressure gradient is measured to be (dP/dt)(1/P₀) = +2% ms⁻¹ to +3% ms⁻¹ and has been included in the homogenous reactor kinetic modeling described in later sections for a more accurate description of the shock tube test environment than provided by the traditional adiabatic constant volume model.

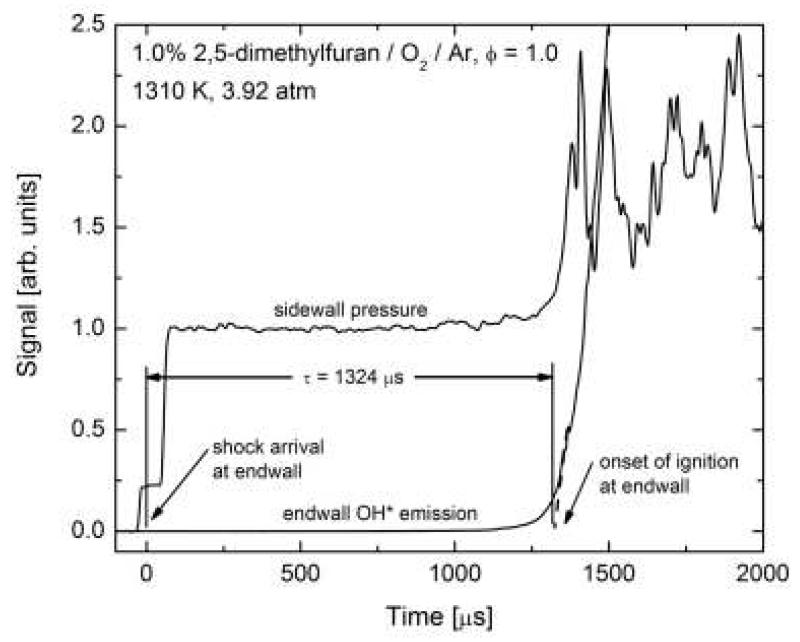
Ignition times were measured using chemiluminescence from electronically-excited OH radicals (OH*), measured through the driven section end wall, and pressure measured at a side wall location 2 cm from the end wall. A UV fused silica optic flush mounted in the shock tube end wall provided optical access and OH* chemiluminescence was observed using a UG-5 colored glass filter and high-speed silicon photodetector. Figure 1 illustrates an example ignition delay time measurement. The ignition delay time is defined as the time interval between the arrival and reflection of the shock at the end wall and the onset of ignition at the end wall. The incident shock velocity measurement and measurement of the time of passage at the last pressure transducer, 2 cm from the end wall, allow for determination of the shock arrival at the end wall. The onset of ignition at the end wall is defined by extrapolating the maximum slope in the end wall OH* chemiluminescence to the baseline pre ignition value. All signals were recorded using a National Instruments PCI-6133 data acquisition card (3 MHz, 14-bit and eight analog input channels) interfaced to a desktop computer with LabVIEW software. Reported ignition delay times have estimated uncertainties of at most ±20% (2-σ confidence interval) based on contributions from uncertainties in reflected shock conditions and uncertainties in interpreting measured signals.

Figure 1.

Example ignition delay time measurement for a 1.0/7.5/91.5 mol% DMF/O₂/Ar mixture (φ = 1.0) at reflected shock conditions of 1310 K and 3.92 atm. Ignition delay time measured was 1324 μs.

3. Experimental results

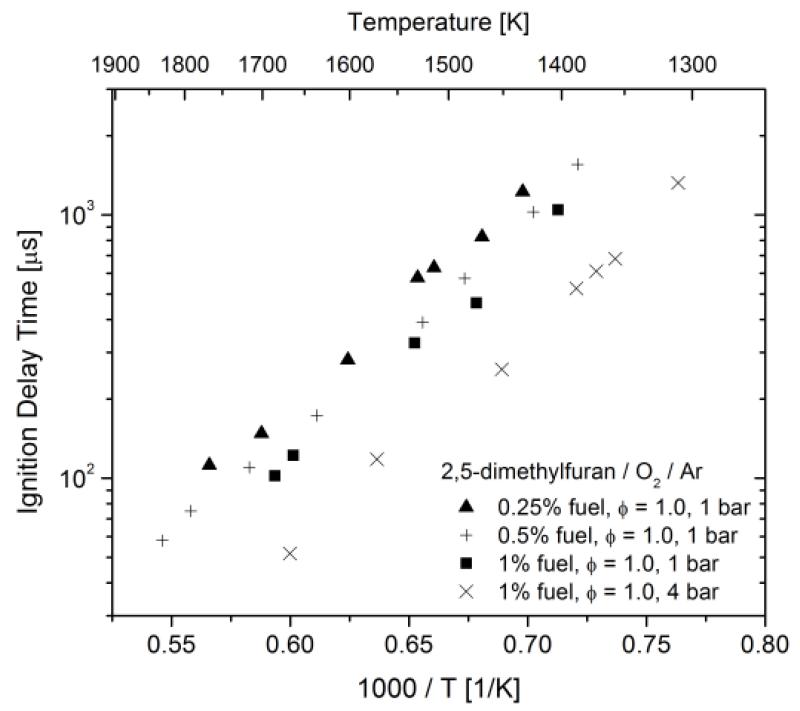
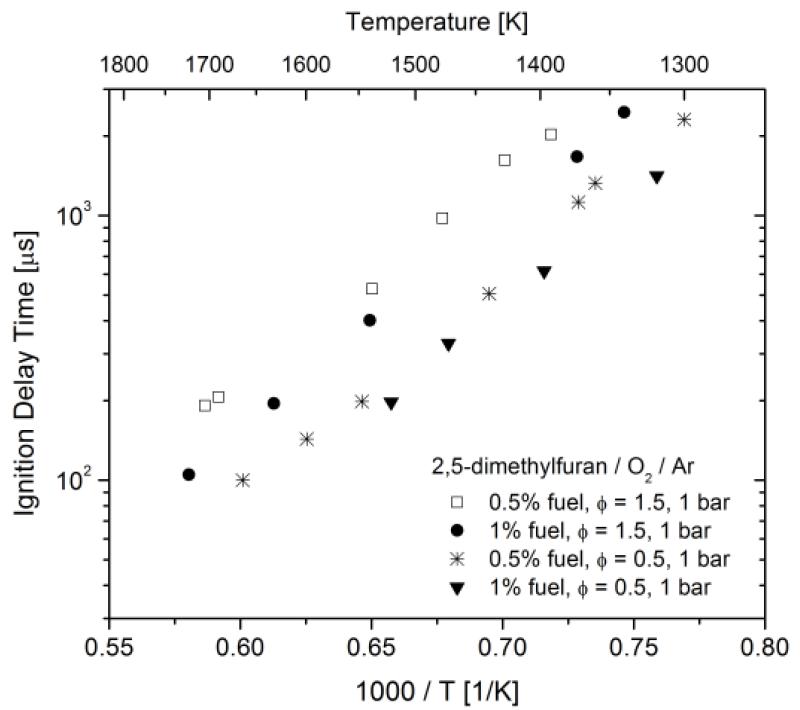
Measured ignition delay times are shown in Figures 2 and 3 and tabulated in the appended Supplementary Material. The data shows Arrhenius exponential dependence on inverse temperature, typical of high-temperature ignition, with apparent activation energy for all data sets near 40 kcal mol⁻¹. Ignition delay times are observed to decrease with increasing fuel concentration, at fixed pressure and equivalence ratio, and decrease with increasing pressure, for fixed reactant mixture composition. Ignition delay times are observed to increase with increasing equivalence ratio (decreasing O₂ fraction), for fixed pressure and DMF fraction. The ignition delay time dependencies on mixture composition and pressure can be described using power-laws in the concentrations of the three reactant gas constituents. Based on linear least squares regression analysis for all the data, the following correlation was formulated to describe ignition delay time:

$$\tau =1.8\times {10}^{-8}{\left[\mathrm{DMF}\right]}^{0.34(\pm 0.04)}{\left[{\mathrm{O}}_2\right]}^{-0.79(\pm 0.03)}{\left[\mathrm{Ar}\right]}^{-0.37(\pm 0.05)}\exp \left(21000\right(\pm 300\left)\right[\mathrm{K}]∕\mathrm{T})\left[\mu \text{s}\right]$$

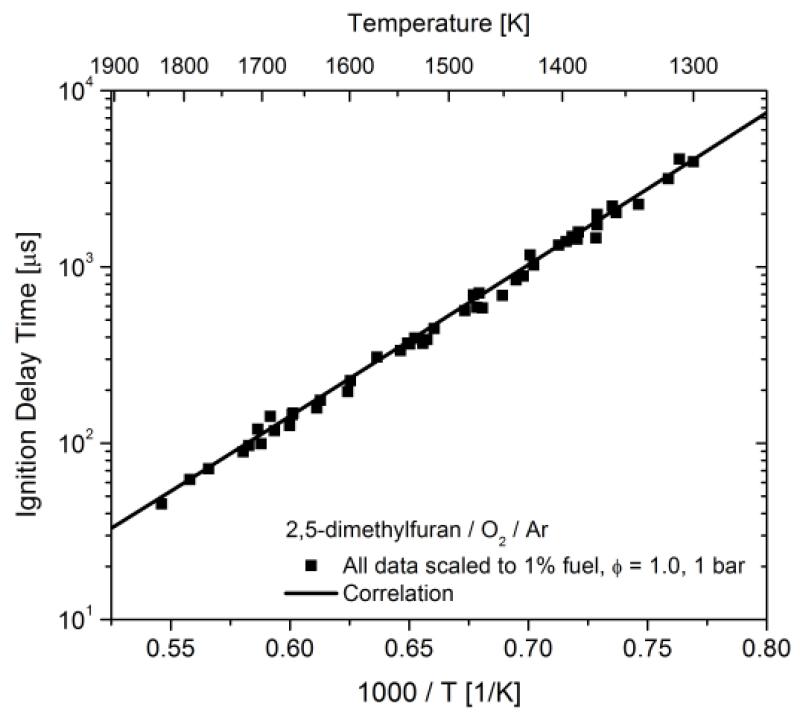
where concentrations [X_i] are in units of mol cm⁻³ and the temperature T is in Kelvins. The uncertainties in correlation parameters given are the 1-σ uncertainties in the regression analysis which result from the scatter in the experimental data. In Figure 4 the experimental data has been correlated to a common condition (1% DMF, Φ = 1.0, and 1 bar) to demonstrate the suitability of the correlation; the correlation provides a high R² value of 99.5%. The correlation should not be extrapolated far from the conditions of the reported experiments due to the complicated and non-linear dependencies of oxidation chemistry on reactant mixture composition, temperature, and pressure. It is also worth noting that the correlation given above results in ignition time dependence on pressure of τ ~ P^−0.81.

Figure 2.

Ignition delay time measurements for DMF/O₂/Ar mixtures at φ = 1.0 and 1 and 4 bars.

Figure 3.

Ignition delay time measurements for DMF/O₂/Ar mixtures at φ = 0.5 and 1.5 and 1 bar.

Figure 4.

All measured ignition delay times correlated to 1% DMF, φ = 1.0, and 1 bar using the correlation given in the text.

4. Detailed Chemical Kinetic Model

A new model has been developed to describe the pyrolysis and oxidation kinetics of DMF at high temperatures following the chain reaction theory used in EXGAS^31-32, a software for the automatic generation of kinetic models. The organizational structure of the model is as follows. Newly developed high-temperature DMF kinetics were integrated with a base mechanism comprised of the toluene reaction kinetics proposed by Bounaceur et al.³³ and recently revisited by Husson et al.³⁴. The base mechanism describes the oxidation of toluene and benzene as well as the high-temperature chemistry of C₃-C₄ hydrocarbons³⁵. In this work, the recently updated reaction base for C₀-C₂ hydrocarbons proposed by Curran and co-workers was also adopted³⁶. The base mechanism is appended with a set of reactions describing the high-temperature pyrolysis and oxidation of DMF, i.e., the primary mechanism. The high-temperature chemistry of molecular products formed in the primary mechanism and not reacting in the base model are then described in a secondary mechanism. In this section, the key elements of the primary and secondary mechanisms, given in Table 3, are discussed in detail. Emphasis is also given to the reactions of some major products that were not adequately described in the base model.

Table 3.

Primary and secondary mechanism of the high-temperature pyrolysis and oxidation of DMF. Units are cm³, s, kcal, mol.

Reaction	A	n	Ea	Footnote	No.
Unimolecular reactions of 2,5-dimethylfuran
Unimolecular initiations by breaking of a C-C or C-H bond
DMF = M5F-2yl + CH3	2.60 × 1016	0.000	110.532	a	(1)
R1C6H7O + H (+M) = DMF (+M)  LOW/3.03 × 10136 −33.350 55.560/  TROE/0.163 714 728 5112/	6.55 × 1013	0.070	−0.051	a a	(2)
DMF-3yl + H (+M) = DMF (+M)  LOW/1.0 × 1094 −21.840 13.900/  TROE/0.043 304 60000 5896/  O2/0.4/B2CO/0.75/CO2/1.5/H2O/6.5/Ar/0.35/	1.0 × 1014	0.000	0.000	b c	(3)
Unimolecular initiations by H transfer
DMF = M4C6H8O (P = 1 bar)	8.62 × 1072	−16.850	108.602	a	(4)
DMF = M4C6H8O (P = 10 bar)	6.02 × 1044	−8.758	90.804	a	(5)
DMF = M4C6H8O (high pressure limit)	2.47 × 1011	0.659	68.712	a	(6)
Unimolecular initiations by CH3 transfer
DMF = CA1	6.54 × 1010	0.815	81.420	a	(7)
CA1 = CH3CHCO + PC3H4	8.52 × 1013	0.321	31.670	a	(8)
CA1 = M2C6H8O + PC3H4	1.02 × 1012	0.272	7.795	a	(9)
CA1 = B1	4.69 × 1013	0.015	30.862	a	(10)
B1 = CH3CHCO + PC3H4	1.67 × 1013	0.115	10.853	a	(11)
B1 = B3 + CO	3.61 × 1013	0.155	10.537	a	(12)
B3 = C5H8 Duplicate	3.65 × 1005	1.803	7.927	a	(13)
B3 = C5H8 Duplicate	7.25 × 1006	1.643	7.530	a	(14)
B3 = C5H8-12	7.48 × 1004	2.001	22.542	a	(15)
Unimolecular initiations by ring opening
DMF = B2	4.85 × 1013	0.489	82.727	a	(16)
B2 = M3C6H8O	1.41 × 1012	0.049	1.610	a	(17)
B2 = M5C6H8O	1.60 × 1009	1.006	9.294	a	(18)
B2 = M6C6H8O	6.74 × 1008	0.892	1.230	a	(19)
M6C6H8O = C6H6-12 + H2O	1.20 × 1008	1.523	75.786	a	(20)
M6C6H8O => C6H6-l2 + OH + H	3.61 × 1014	0.000	81.632	a	(21)
M3C6H8O = M2C6H8O	9.60 × 1008	1.157	41.665	a	(22)
M5C6H8O = M7C6H8O	2.27 × 1011	−0.135	20.545	a	(23)
M5C6H8O =CH3CO + nC4H5	7.44 × 1016	0.000	86.910	a	(24)
Bimolecular initiations
DMF + O2 = R1C6H7O + HO2	4.20 × 1012	0.000	36.800	d	(25)
DMF + O2 = DMF-3yl + HO2	2.00 × 1013	0.000	71.600	d	(26)
DMF + DMF = R1C6H7O + RI6CH9O	5.00 × 1014	0.000	54.200	d	(27)
Decomposition of important products formed by unimolecular initiations of DMF
M4C6H8O decomposition sub-mechanism
Unimolecular initiations by breaking of a C-C bond
CH3CO+C4H5-1s(+M)=M4C6H8O(+M)  LOW/6.75 × 1083 −19.22 14.980/  TROE/0.735 60000 513 100000/	2.00 × 1013	0.000	0.000	a	(28)
Pericyclic reactions
M4C6H8O = CH2CO + C4H6-12	9.25 × 1008	1.218	77.070	a	(29)
M4C6H8O = C5H8-23 + CO	3.05 × 1010	0.785	89.076	a	(30)
M4C6H8O = CH3CH3CHCCH + CO	6.63 × 1009	0.762	77.547	a	(31)
M4C6H8O = CH2CO + C4H6-1	5.42 × 1007	1.772	65.550	a	(32)
M2C6H8O decomposition sub-mechanism
Unimolecular initiations by CH3 transfer
M2C6H8O = CA4	7.89 × 1010	0.794	82.894	a	(33)
CA4 = CH3CHCO+PC3H4	1.87 × 1014	0.156	32.181	a	(34)
CA4 = M11C6H8O	1.04 × 1012	0.254	7.553	a	(35)
Unimolecular initiations by H transfer
M2C6H8O = CA3	3.82 × 1011	0.613	69.588	a	(36)
CA3 = M9C6H8O	7.69 × 1012	0.014	0.323	a	(37)
M9C6H8O = C5H8-2 + CO	4.44 × 1008	1.229	37.544	a	(38)
M9C6H8O = C5H7-2s + HCO	6.19 × 1016	0.000	68.633	a	(39)
Unimolecular initiations by breaking of a C-H bond
M2C6H8O = M2-R1 + H	2.41 × 1015	0.070	86.099	a	(40)
M2C6H8O = M2-R2 + H	1.49 × 1015	0.070	90.063	a	(41)
Unimolecular initiations by ring opening
M2C6H8O = M10C6H8O	9.74 × 1013	0.304	82.685	a	(42)
M2C6H8O = M8C6H8O	1.10 × 1011	1.261	90.364	a	(43)
MIOC6H8O = M11C6H8O	9.60 × 1008	1.157	41.665	a	(44)
Propagation reactions of DMF
H-abstractions on the allylic H atom
DMF + H = R1C6H7O + H2	3.10 × 1005	2.700	3.434	e, f	(45)
DMF + O = R1C6H7O + OH	3.50 × 1011	0.700	5.900	g	(46)
DMF + OH = R1C6H7O + H2O	1.01 × 1004	3.133	2.156	h	(47)
DMF + C2H3 = R1C6H7O + C2H4	4.42	3.500	4.690	i	(48)
DMF + HO2 = R1C6H7O + H2O2	1.90 × 1004	2.600	13.900	j	(49)
DMF + CH3 = R1C6H7O + CH4	6.99 × 1001	3.365	7.084	k	(50)
DMF + C3H5 = R1C6H7O + C3H6	1.37	3.852	14.370	l	(51)
DMF + iC4H3 = R1C6H7O + C4H4	1.37	3.852	14.370	l	(52)
DMF + iC4H5 = R1C6H7O + 1,3-C4H6	1.37	3.852	14.370	l	(53)
DMF + C5H5# = R1C6H7O + C5H6#	1.37	3.852	14.370	l	(54)
DMF + C-C5H7 = RIC6H7O + C-C5H8	1.37	3.852	14.370	l	(55)
DMF + R4C6H7O = RIC6H7O + c-C6H8O	1.37	3.852	14.370	l	(56)
H-abstractions on the vinylic H atom
DMF + H = DMF-3yl + H2	8.20 × 1005	2.500	12.280	l	(57)
DMF + OH = DMF-3yl + H2O	3.93 × 1004	2.668	7.692	h	(58)
DMF + CH3 = DMF-3yl + CH4	1.36	3.500	12.900	l	(59)
Decomposition of R1C6H7O (P=1 bar)
RIC6H7O = R2C6H7O	2.26 × 1070	−16.301	72.605	m	(60)
R2C6H7O = R3C6H7O	1.32 × 1039	−8.059	33.755	m	(61)
R3C6H7O = R4C6H7O	5.46 × 1024	−3.896	15.278	m	(62)
R3C6H7O = R5C6H7O	6.90 × 1037	−7.501	29.831	m	(63)
R4C6H7O = M2C6H6O + H	2.92 × 1085	−20.593	90.371	m	(64)
R4C6H7O = R6C6H7O	4.93 × 1079	−19.232	84.873	m	(65)
R4C6H7O = R9C6H7O	7.47 × 1084	−20.558	90.140	m	(66)
R5C6H7O = aC5H7 + CO	3.31 × 1018	−2.001	8.335	m	(67)
R6C6H7O = M2C6H6O + H	6.52 × 1048	−10.466	51.890	m	(68)
R6C6H7O = M3C6H6O + H	1.62 × 1045	−9.440	47.815	m	(69)
R6C6H7O = R7C6H7O	2.02 × 1035	−6.601	35.635	m	(70)
R7C6H7O = C5H7-1s + CO	5.82 × 1029	−5.129	29.918	m	(71)
R9C6H7O = c-C5H7 + CO	2.13 × 1024	−3.987	16.361	m	(72)
Decomposition of R1C6H7O (P=10 bar)
R1C6H7O = R2C6H7O	2.22 × 1064	−14.352	71.907	m	(73)
R2C6H7O = R3C6H7O	3.83 × 1043	−9.056	40.265	m	(74)
R3C6H7O = R4C6H7O	6.03 × 1026	−4.384	18.074	m	(75)
R3C6H7O = R5C6H7O	8.84 × 1044	−9.263	38.103	m	(76)
R4C6H7O = M2C6H6O + H	8.03 × 1080	−18.952	92.217	m	(77)
R4C6H7O = R6C6H7O	2.50 × 1073	−17.156	84.765	m	(78)
R4C6H7O = R9C6H7O	1.72 × 1080	−18.903	91.827	m	(79)
R5C6H7O = aC5H7 + CO	1.50 × 1022	−2.921	12.232	m	(80)
R6C6H7O = M2C6H6O + H	1.58 × 1057	−12.472	61.774	m	(81)
R6C6H7O = M3C6H6O + H	6.96 × 1052	−11.311	57.134	m	(82)
R6C6H7O = R7C6H7O	1.35 × 1041	−7.976	42.911	m	(83)
R7C6H7O = C5H7-1s + CO	1.18 × 1025	−3.554	28.780	m	(84)
R9C6H7O = c-C5H7 + CO	3.56 × 1027	−4.752	20.577	m	(85)
Decomposition of R1C6H7O (high pressure limit)
RIC6H7O = R2C6H7O	7.70 × 1013	0.157	40.185	m	(86)
R2C6H7O = R3C6H7O	3.76 × 1006	1.743	19.124	m	(87)
R3C6H7O = R4C6H7O	9.65 × 1011	−0.112	9.074	m	(88)
R3C6H7O = R5C6H7O	8.56 × 1013	−0.216	21.332	m	(89)
R4C6H7O = M2C6H6O + H	2.82 × 1011	1.020	48.755	m	(90)
R4C6H7O = R6C6H7O	8.17 × 1008	1.360	43.750	m	(91)
R4C6H7O = R9C6H7O	1.47 × 1013	0.402	49.868	m	(92)
R5C6H7O = R8C6H7O	5.31 × 1011	0.208	7.761	m	(93)
R6C6H7O = M2C6H6O + H	1.38 × 1011	0.833	32.670	m	(94)
R6C6H7O = M3C6H6O + H	8.98 × 1010	0.793	30.741	m	(95)
R6C6H7O = R7C6H7O	8.00 × 1012	0.200	25.451	m	(96)
R7C6H7O = C5H7-1s + CO	1.36 × 1014	0.150	25.979	m	(97)
R8C6H7O = aC5H7 + CO	7.84 × 1010	0.619	1.623	m	(98)
R9C6H7O = RIOC6H7O	9.80 × 1008	0.757	9.697	m	(99)
R10C6H7O = c-C5H7 + CO	1.24 × 1013	0.239	6.901	m	(100)
Decomposition of DMF-3yl
DMF-3yl = CH3COCHCCCH3	1.10 × 1013	0.306	31.200	n	(101)
CH3COCHCCCH3 = CH3CCCHCO + CH3	1.14 × 1014	− 0.085	58.228	o	(102)
CH3CCCHCO + H = CH2CCCHCO + H2	1.74 × 1005	2.500	2.510	p	(103)
CH3CCCHCO + OH = CH2CCCHCO + H2O	3.00 × 1006	2.000	−0.298	q	(104)
CH3CCCHCO + CH3 = CH2CCCHCO + CH4	2.20	3.500	5.670	r	(105)
CH2CCCHCO = CO + iC4H3	1.36 × 1014	0.150	25.979	k	(106)
CH2CCCHCO + H = CH3CCCHCO	5.80 × 1013	0.180	−0.130	s	(107)
CH3CCCHCO + H = CH3CCCH2CO	1.32 × 1013	0.000	3.260	l	(108)
CH3CCCH2CO = CO + C4H5-2	2.00 × 1013	0.000	13.800	t	(109)
CH3CCCH2CO + O2 = CH3CCCHCO + HO2	2.60 × 1011	0.000	2.500	l	(110)
H-addition on DMF (P=1bar)
DMF + H = MF + CH3	5.86× 1025	−3.180	16.721	e	(111)
DMF + H = CH3CO + C4H6-1,3	2.85× 1067	−14.870	49.399	e	(112)
H-addition on DMF (P=10bar)
DMF + H = MF + CH3	2.32× 1022	−2.270	13.215	e	(113)
DMF + H = CH3CO + C4H6-1,3	1.72× 1053	−11.040	35.043	e	(114)
H-addition on DMF (high pressure limit)
R1C6H9O = DMF + H	1.69× 1012	0.459	32.886	e	(115)
DMF + H = MF + CH3	1.38× 1014	0.059	31.433	e	(116)
R1C6H9O = R3C6H9O	8.90× 1012	0.087	22.724	e	(117)
R3C6H9O = R7C6H9O	2.18× 1009	1.211	32.006	e	(118)
R7C6H9O = CH3CO + C4H6-1,3	1.72× 1013	0.293	31.199	e	(119)
OH-addition on DMF (high pressure limit)
DMF + OH = CH3CO + CH3CHO + C2H2	7.95× 1012	0.000	−0.665	u	(120)
Terminations for R4C6H7O with H atoms
R4C6H7O + H = M2C6H6O + H2	1.00× 1013	0.000	0.000	b	(121)
R4C6H7O + H = c-C6H8O	1.00× 1014	0.000	0.000	b	(122)
Decomposition of primary products formed by propagation reactions of DMF
M2C6H6O and M3C6H6O decomposition sub-mechanisms
Unimolecular initiations
C6H5O# + H (+M) = M2C6H6O (+M)	1.00× 1014	0.000	0.000	b	(123)
LOW/1.00 × 1094 −21.840 13.900/				v
TROE/0.043 304 60000 5896/
O2/0.4/B2CO/0.75/CO2/1.5/H2O/6.5/Ar/0.35/
C6H5O# + H (+M) = M3C6H6O (+M)	1.00× 1014	0.000	0.000	b	(124)
LOW/1.00 × 1094 −21.840 13.900/				v
TROE/0.043 304 60000 5896/
O2/0.4/B2CO/0.75/CO2/1.5/H2O/6.5/Ar/0.35/
H-abstractions
M2C6H6O + H = C6H5O# + H2	1.20× 1008	1.738	2.540	k	(125)
M2C6H6O + OH = C6H5O# + H2O	3.00× 1006	2.000	−1.520	l	(126)
M2C6H6O + O = C6H5O# + OH	8.80× 1010	0.700	3.250	l	(127)
M2C6H6O + CH3 = C6H5O# + CH4	1.00× 1011	0.000	7.300	l	(128)
M2C6H6O + C2H3 = C6H5O# + C2H4	2.21	3.500	4.690	l	(129)
M2C6H6O + C3H5 = C6H5O# + C3H6	4.90× 1011	0.000	9.400	w	(130)
M2C6H6O + C3H3 = C6H5O# + PC3H4	4.90× 1011	0.000	9.400	w	(131)
M2C6H6O + C3H3 = C6H5O# + aC3H4	4.90× 1011	0.000	9.400	w	(132)
M2C6H6O + iC4H5 = C6H5O# + C4H4	4.90× 1011	0.000	9.400	w	(133)
M2C6H6O + iC4H5 = C6H5O# + 1,3-C4H6	4.90× 1011	0.000	9.400	w	(134)
M2C6H6O + C5H5# = C6H5O# + C5H6#	4.90× 1011	0.000	9.400	w	(135)
M2C6H6O + R4C6H7O = C6H5O# + c-C6H8O	4.90× 1011	0.000	9.400	w	(136)
M3C6H6O + H = C6H5O# + H2	2.40× 1008	1.738	2.540	x	(137)
M3C6H6O + OH = C6H5O# + H2O	3.00× 1006	2.000	−1.520	l	(138)
M3C6H6O + O = C6H5O# + OH	8.80× 1010	0.700	3.250	l	(139)
M3C6H6O + CH3 = C6H5O# + CH4	1.00× 1011	0.000	7.300	l	(140)
M3C6H6O + C2H3 = C6H5O# + C2H4	2.21	3.500	4.690	l	(141)
M3C6H6O + C3H5 = C6H5O# + C3H6	4.90× 1011	0.000	9.400	w	(142)
M3C6H6O + C3H3 = C6H5O# + PC3H4	4.90× 1011	0.000	9.400	w	(143)
M3C6H6O + C3H3 = C6H5O# + aC3H4	4.90× 1011	0.000	9.400	w	(144)
M3C6H6O + iC4H5 = C6H5O# + C4H4	4.90× 1011	0.000	9.400	w	(145)
M3C6H6O + iC4H5 = C6H5O# + 1,3-C4H6	4.90× 1011	0.000	9.400	w	(146)
M3C6H6O + C5H5# = C6H5O# + C5H6#	4.90× 1011	0.000	9.400	w	(147)
M3C6H6O + R4C6H7O = C6H5O# + c-C6H8O	4.90× 1011	0.000	9.400	w	(148)
Pericyclic reactions (P=1bar)
M2C6H6O = B1C6H6O	8.11× 1063	−14.452	75.948	m	(149)
M3C6H6O = B1C6H6O	6.92× 1064	−14.517	77.116	m	(150)
M2C6H6O = C6H5OH#	7.46× 1074	−17.738	90.359	m	(151)
M2C6H6O = M5C6H6O	4.06× 1057	−12.576	67.450	m	(152)
M3C6H6O = C2H2 + C4H4O	2.06× 10105	−26.174	127.274	m	(153)
B1C6H6O = M4C6H6O	1.50× 1019	−1.926	8.585	m	(154)
M4C6H6O = C5H6# + CO	3.39× 1053	−11.662	51.575	m	(155)
M5C6H6O = C5H6# + CO	7.99× 1065	−15.948	70.413	m	(156)
Pericyclic reactions (P=10bar)
M2C6H6O = B1C6H6O	9.89× 1045	−9.230	65.683	m	(157)
M3C6H6O = B1C6H6O	4.88× 1046	−9.231	66.645	m	(158)
M2C6H6O = C6H5OH#	2.76× 1055	−12.012	80.069	m	(159)
M2C6H6O = M5C6H6O	1.60× 1041	−7.815	57.745	m	(160)
M3C6H6O = C2H2 + C4H4O	5.05× 1089	−21.220	123.476	m	(161)
B1C6H6O = M4C6H6O	6.74× 1017	−1.511	8.112	m	(162)
M4C6H6O = C5H6# + CO	2.60× 1048	−9.957	51.544	m	(163)
M5C6H6O = C5H6# + CO	1.83× 1062	−14.493	73.465	m	(164)
Pericyclic reactions (P=high pressure limit)
M2C6H6O = B1C6H6O	1.26× 1012	0.442	43.034	m	(165)
M3C6H6O = B1C6H6O	4.26× 1012	0.485	43.873	m	(166)
M2C6H6O = C6H5OH#	1.62× 1011	0.633	50.879	m	(167)
M2C6H6O = M5C6H6O	5.16× 1012	0.314	38.597	m	(168)
M3C6H6O = C2H2 + C4H4O	8.36× 1014	0.313	76.646	m	(169)
BlC6H6O = M4C6H6O	5.78× 1012	−0.056	4.606	m	(170)
M4C6H6O = C5H6# + CO	1.14× 1013	0.221	29.390	m	(171)
M5C6H6O = C5H6# + CO	2.15× 1011	0.231	42.201	m	(172)
c-C6H8O decomposition
Decomposition of c-C6H8O
c-C6H8O + H = H2 + R4C6H7O	5.00× 1004	2.500	−1.900	l	(173)
c-C6H8O + OH = H2O + R4C6H7O	3.00× 1006	2.000	−1.520	l	(174)
c-C6H8O + CH3 = CH4 + R4C6H7O	1.00× 1011	0.000	7.300	l	(175)
c-C6H8O = C2H4 + C4H4O	8.36× 1014	0.313	76.646	y	(176)
Methylfuran decomposition
Unimolecular initiations of MF
MF = CH3COCHCCH2	2.29× 1012	0.416	70.891	n	(177)
MF = CH3CHCCHCHO	2.46× 1011	0.659	68.712	z	(178)
Decomposition of CH3COCHCH2 and CH3COCHCH2
CH3CO + C3H3 = CH3COCHCCH2	4.04× 1015	−0.800	0.0	aa	(179)
CH3CHCCHCHO = C4H6-1 + CO	7.90× 1014	0.000	69.880	n	(180)
CH3CHCCHCHO = C4H5-1s + CHO	7.90× 1014	0.000	69.880	bb	(181)
CH3CHCCHCHO + H = CH3CHCCHCO + H2	4.00× 1013	0.000	4.200	cc	(182)
CH3chcchcho + OH = CH3CHCCHCO + H2O	4.00× 1013	0.000	4.200	cc	(183)
CH3CHCCHCHO + CH3 = CH3CHCCHCO + CH4	2.00× 10−06	5.600	2.500	cc	(184)
CH3CHCCHCO = C4H5-1s + CO	6.00× 1012	0.340	12.300	k	(185)
H-abstractions
MF + H = furylCH2 + H2	0.70× 1005	2.700	3.434	dd	(186)
MF + O = furylCH2 + OH	1.75× 1011	0.700	5.900	g	(187)
MF + OH = furylCH2 + H2O	5.10× 1003	3.133	2.156	h	(188)
MF + HO2 = furylCH2 + H2O2	9.50× 1003	2.600	13.900	j	(189)
MF + CH3 = furylCH2 + CH4	7.00× 1001	3.364	7.084	dd	(190)
MF + C3H5 = furylCH2 + C3H6	6.86× 10−01	3.852	14.370	k	(191)
MF + C5H5# = furylCH2 + C5H6#	6.86× 10−01	3.852	14.370	ee	(192)
MF + c-C5H7 = furylCH2 + c-C5H8	6.86× 10−01	3.852	14.370	ee	(193)
MF + H = M5F-2yl + H2	4.20× 1005	2.500	12.280	n	(194)
MF + O = M5F-2yl + OH	6.00× 1010	0.700	8.960	n	(195)
MF + OH = M5F-2yl + H2O	1.10× 1006	2.000	2.780	n	(196)
MF + CH3 = M5F-2yl + CH4	0.68	3.500	12.900	n	(197)
Reactions of furylCH2
furylCH2= OCHCHCHCCH2	2.05× 1013	0.238	40.156	dd	(198)
OCHCHCHCCH2=OCCHCHCHCH2	5.70× 1010	1.000	28.700	l	(199)
OCHCHCHCCH2 = CO + n-C4H5	1.30× 1014	0.000	22.390	ff	(200)
furylCH2 + H = MF	1.00× 1014	0.000	0.000	b	(201)
Reactions of M5F-2yl
M5F-2yl = CH3CCHCHCO	1.80× 1013	0.341	34.510	n	(202)
CH3CCHCHCO = PC3H4+CHCO	5.30× 1015	−0.234	34.234	n	(203)
M5F-2yl + H = MF	1.00× 1014	0.000	0.000	b	(204)
H-additions
MF + H = MFH	1.11× 1045	−11.170	6.205	dd	(205)
MF + H = furan + CH3	2.32× 1022	−2.270	13.215	dd	(206)
MFH = CH3CHCHCHCHO	5.37× 1012	0.151	24.172	k	(207)
CH3CHCHCHCHO = CH3CH2CHCHCO	1.95× 1011	0.529	23.465	k	(208)
CH3CH2CHCHCO = C4H7-V + CO	1.30× 1014	0.000	22.390	ff	(209)

^aFrom Sirjean and Fournet³⁷

^bEstimated rate coefficients from Allara and Shaw⁵⁵.

^cAdapted from Wang and Frenklach ⁵⁶.

^dCalculated as proposed by Ingham et al. ³⁸.

^eFrom Sirjean and Fournet²⁴.

^fUpper limit of the reported rate coefficient (within its uncertainty range).

^gAnalogy with the reaction C₃H₆ + O ⁵⁷.

^hFrom Simmie and Metcalfe ¹⁸.

ⁱAnalogy with the reaction C₃H₆ + C₂H₃ ⁵⁷.

^jAnalogy with the reaction C₃H₆ + HO₂ ⁵⁷.

^kThis work, CBS-QB3, following the computational method described in³⁷

^lCalculated using reaction rate rules proposed by Heyberger et al. ⁵⁸.

^mFrom Sirjean and Fournet ²⁵

ⁿEstimated from analogy with furan ²⁷.

^oThis work, CBS-QB3//MP2/6-31G(d), following the computational method described in ²⁵.

^pAnalogy with the reaction C₃H₆ + H ⁵⁷.

^qAnalogy with the reaction C₃H₆ + OH ⁵⁷.

^rAnalogy with the reaction C₃H₆ + CH₃ ⁵⁷.

^sAnalogy with the reaction C₃H₅ + H⁵⁹.

^tBased on the correlation proposed by Sirjean et al. ⁶⁰.

^uEstimated, rate coefficient based on furan + OH from Atkinson ⁴¹.

^vAnalogy with phenoxy + H ⁶¹.

^wAnalogy with phenol + cyclopentadienyl radical from Tian et al. ²⁷.

^xAnalogy with reaction (125).

^yAnalogy with the reaction (169).

^zAnalogy with reaction (6).

^aaAnalogy with the reaction CH₃ + CH₃CO from Tsang and Hampson ⁶²

^bbAnalogy with the furan mechanism from Sendt et al. ⁶³.

^ccAnalogy with the reactions of CH₃CHO from Tian et al. ²⁷.

^ddAnalogy with the reactions of DMF.

^eeAnalogy with reaction (190).

^ffAnalogy with the reaction C₂H₃CO = C₂H₃ + CO from Mereau et al. ⁶⁴.

4.1 Unimolecular and bimolecular initiation of DMF

An important characteristic of the DMF unimolecular decomposition sub-mechanism within the proposed kinetic model is that rate coefficients for a majority of the crucial reactions are based on the conclusions of theoretical quantum calculations performed in a recent study³⁷.

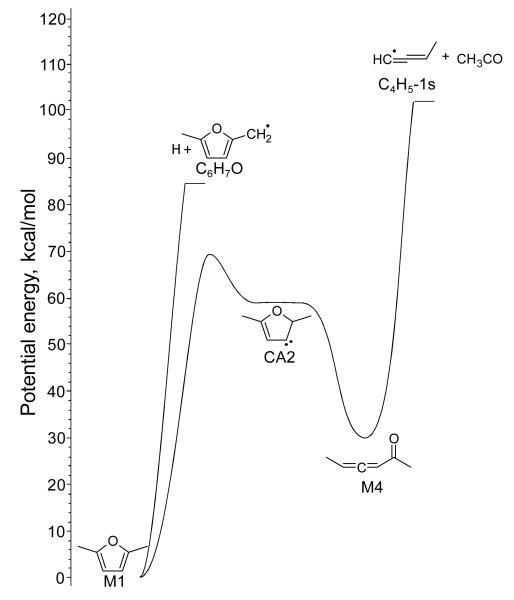
The most important features of this study are briefly recalled here. Three types of initiation reaction were envisaged for DMF: (a) initial C-C or C-H bond fissions in the lateral methyl groups, (b) furan ring opening by C-O bond fission producing a diradical, and (c) internal hydrogen atom or methyl group transfer involving the formation of carbenic intermediates than can further decompose into molecular products. All these pathways were explored in detail. Based on the computed potential energy surfaces (PES), thermochemical data and high-pressure limit rate coefficients were determined and included in a sub-mechanism for DMF unimolecular decomposition. The theoretical study³⁷ showed that the unimolecular decomposition of DMF is dominated by two product channels: CH₃CO radical + C₄H₅-1s (buta-1,2-dien-1-yl) and R1C₆H₇O (5-methyl-2-furanylmethyl) radical + H atom. The PES computed for these two decomposition pathways is presented in Figure 5. The C₆H₇O + H exit channel is directly reached by initial C-H bond cleavage in DMF. CH₃CO and C₄H₅-1s are produced via a carbenic initiated rearrangement of DMF into hexa-3,4-dien-2-one (M4) which in turn decomposes into these products through C-C bond cleavage. It was shown that under combustion conditions, CH₃CO and C₄H₅-1s solely decompose into CH₃ + CO and C₄H₄ (1-buten-3-yne) + H atom, respectively.

Figure 5.

Potential energy of the unimolecular decomposition of DMF, adapted from Sirjean and Fournet³⁷. Energy at 0 K computed using the CBS-QB3 method.

In the present kinetic model, all unimolecular decomposition pathways computed in reference³⁷ were included, along with computed thermochemical data and high-pressure limit rate coefficients (reactions 1-24 and 28-44 in Table 3); detailed structures of the species can be found in reference³⁷ and have been reported in the supplementary materials. As most of the target experimental data were obtained near atmospheric pressure, pressure dependencies of rate parameters for the most important unimolecular and chemically activated reactions were systematically considered when available. Pressure-dependent kinetic parameters for the two preponderant pathways in DMF unimolecular decomposition (Figure 5) were taken from reference³⁷ (reactions 1, 4 or 5, and 28). Note that a detailed chemical kinetic model is available in the supplementary material and contains high-pressure limit and atmospheric pressure (1 bar) rate coefficients for all the unimolecular decompositions considered, except for minor channels (reactions 7-24 and 29-44) for which only high-pressure limit rate parameters have been calculated. Using high-pressure limit rate parameters for these minor thermal decomposition routes set an upper limit for the production of minor DMF fragments via these reactions.

The bimolecular initiations of DMF with O₂ leading to stabilized R1C₆H₇O radicals and vinylic 2,5-dimethylfuran-3-yl radicals (named DMF-3-yl, reactions 25 and 26) were considered with kinetic parameters proposed by Ingham et al.³⁸. The self bimolecular initiation of DMF leading to R1C₆H₇O and R1C₆H₉O was also taken into account (reaction 27) with estimated kinetic parameters.

4.2 Propagation reactions of DMF

Because of the symmetry of DMF, only two types of hydrogen atoms can be considered in the H-abstraction reaction class: H-abstractions from the methyl groups of DMF (producing the resonantly stabilized R1C₆H₇O radical) and from the furan ring leading to the vinylic radical (DMF-3yl). As mentioned earlier, we aim to test the detailed chemical kinetic model against pyrolysis species profiles obtained by Lifshitz et al.²⁰ in single-pulse shock tube experiments. For this reason, H-abstraction from DMF by C₂H₃, C₃H₅, iC₄H₃, iC₄H₅, C₅H₅#, c-C₅H₇, and R4C₆H₇O radicals were considered in addition to those by H and O atoms and OH, CH₃ and HO₂ radicals because the former hydrocarbon radicals were found to be present in non-negligible concentrations under pyrolysis conditions. Given the difference of stability between R1C₆H₇O (Δ_fH° = 2.7 kcal mol⁻¹) and DMF-3yl radicals (Δ_fH° = 37.5 kcal mol⁻¹), only the most important H-abstractions by H, OH, and CH₃ were taken into account for the formation of the vinylic DMF-3-yl radical.

The kinetic parameters for H-abstraction reactions by OH radicals from DMF (reactions (47) and (58)) were taken from the ab initio study of Simmie and Metcalfe¹⁸. Rate coefficients for H-abstractions by H atoms from DMF producing the stabilized R1C₆H₇O radical was taken from the theoretical study of Sirjean and Fournet²⁴. In their study, the PES of this reaction was studied at the CBS-QB3 and G4 level of theories and compared to G3 results of Simmie and Metcalfe ¹⁸. It was shown that the computed energy barriers for the H-abstraction by H atoms ranged between 4.9 (G4 level of theory) and 7.1 kcal mol⁻¹ (G3 method). The computed CBS-QB3 energy barrier of 5.9 kcal mol⁻¹ was ultimately adopted in reference²⁴ with a quoted uncertainty of ±1.5 kcal mol⁻¹. Therefore, a factor of two in uncertainty was reported in the computed rate coefficient between 1000 and 2000 K²⁴, i.e., the lower and upper bound for the value of rate parameter k are defined by k/2 and k*2, respectively. In this work, preliminary sensitivity analyses showed that this reaction is crucial in both pyrolysis and oxidation simulations. The sensitivity of DMF conversion under pyrolysis conditions and the sensitivity of shock tube ignition delay times to this reaction (H-abstraction from DMF by H atoms producing the stabilized R1C₆H₇O radical) motivated an increase in the initial rate coefficient towards the upper limit of its uncertainty range. Consequently, the upper limit of the rate coefficient recommended in reference²⁴ was adopted for reaction (45). Kinetic parameters for all other H-abstraction reactions were obtained by analogies and reaction rate rules from the literature, except for H-abstraction from DMF by methyl radicals yielding R1C₆H₇O + CH₄. This rate coefficient was calculated in the present work at the CBS-QB3 level of theory using the same computational approach as presented in reference²⁴.

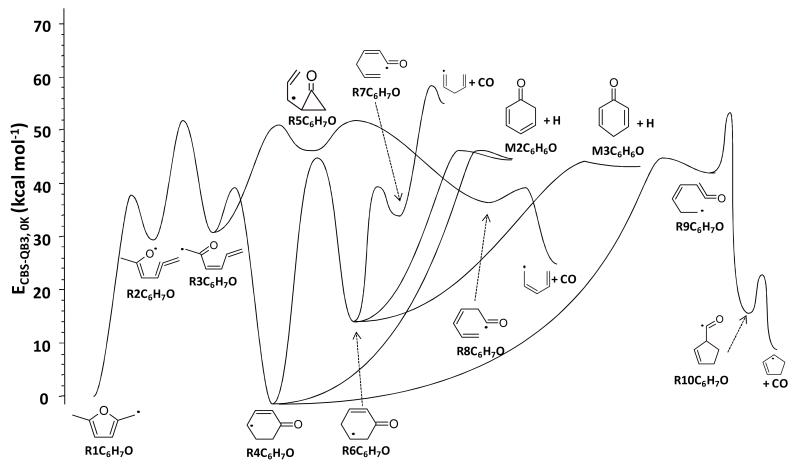
The decomposition of resonantly stabilized R1C₆H₇O radical is central to the high-temperature chemistry of DMF. In the present kinetic model, description of its unimolecular decomposition are solely based on conclusions of theoretical calculations performed by Sirjean and Fournet²⁵. Briefly, the PES of the thermal decomposition of R1C₆H₇O was investigated thoroughly, for the first time, using CBS-QB3 calculations. Among all pathways examined, only those kinetically important were retained in the Master Equation (ME)/RRKM simulations. Note that the C-H bond scission from R₁C₆H₇O was not considered in the final mechanism since preliminary simulations showed that this reaction had no kinetic influence in our conditions. This result is consistent with previous theoretical study²⁵. The final PES proposed in this recent work is depicted in Figure 6. ME/RRKM modeling showed that the main decomposition pathway of R1C₆H₇O involves a ring enlargement, in three steps, leading to the formation of R4C₆H₇O followed by a C-H bond beta scission yielding 2,4-cyclohexadienone (M2C₆H₆O). Other decomposition channels ultimately produce linear and cyclic unsaturated C₅H₇ species and CO via the formation of R5C₆H₇O, R6C₆H₇O, and R9C₆H₇O radicals. Three sets of reactions are presented in Table 3 for the pressure dependence of R1C₆H₇O: at 1 bar (reactions 60-72), 10 bar (reactions 73-85) and high-pressure limit (reactions 86-100). All thermochemical data for C₆H₇O radicals were taken from CBS-QB3 calculations of reference²⁴.

Figure 6.

Potential energy of the unimolecular decomposition of R1C₆H₇O, adapted from Sirjean and Fournet ²⁵. Energy at 0 K computed using the CBS-QB3 method.

As H-abstraction reactions leading to the vinylic DMF-3-yl radical were shown to be negligible, the decomposition of DMF-3-yl was described only by the most important reactions (reactions 101-110). The ring opening of the vinylic DMF-3yl radical by β-scission was written based on an analogy with furan-3-yl radical²⁷. The resulting linear 5-oxohex-2-yn-4-yl radical (CH₃COCHCCCH₃) cannot easily eliminate CO, as in the case of furan, because of the presence of the methyl groups. For this reason, its decomposition was assumed to proceed mainly by a C-C bond β-scission yielding CH₃ radicals and pent-1-en-3-yn-1 one (CH₃CCCHCO). Reactions consuming the latter species were also included: (a) H-abstraction by H atoms, CH₃, and OH radicals leading to the formation of the stabilized pent-1-en-3-yn-5-anoyl radical (•CH₂CCCHCO) and its subsequent C-C bond α-scission into CO and C₄H₃ radicals; (b) Initial C-H bond fission yielding pent-1-en-3-yn-5-anoyl radicals and H atoms; (c) Hydrogen addition on the carbon atom located in α position of the C=O group and the subsequent C-C bond α-scission of the adduct into CO and but-2-yn-1-yl radical (C₄H₅-2). Thermochemical data of all species contained in the DMF-3yl decomposition sub-mechanism were calculated with THERGAS software³⁹, based on group additivity methods⁴⁰, except for ketones where CBS-QB3 calculations were performed. Kinetic parameters for these processes were estimated from analogies with the literature and are detailed in the footnotes of Table 3.

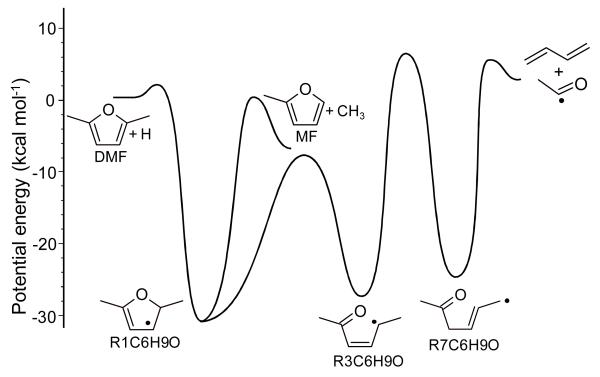
The description of addition reactions of H atoms to DMF (reactions 111-119) are also based on the recent theoretical chemical kinetic study²⁴. All possible decomposition routes of the initial adducts of the DFM + H reaction were thoroughly studied using CBS-QB3 calculations and ME/RRKM simulations. It was shown that two exit channels need to be considered to properly describe this process: (a) the classical ipso substitution DMF + H → 2-methylfuran (MF) + CH₃ (reaction 111), and (b) rearrangements of the initial stabilized adduct ultimately yielding 1,3-butadiene and the acetyl radical (CH₃CO) (reaction 112). The detailed reaction pathways for the H-atom addition to DMF are described in Figure 7. The ring opening of the stabilized R1C₆H₉O adduct produces R3C₆H₉O radical that can undergo an internal H-atom transfer via a 5 membered cyclic transition state yielding R7C₆H₉O radical. The C-C bond β-scission of the latter radical ultimately yields 1,3-butadiene and CH₃CO radical. At the high-pressure limit, all intermediates are included in the reaction sub-mechanism (reactions 115-119). For lower pressures, an adequate description of this reaction sequence requires it to be treated as a chemically-activated system, as it was in reference²⁴ where it was shown that all C₆H₉O intermediates are not stabilized at high temperatures and atmospheric pressure. Therefore, at 1 bar the H-atom addition to DMF can be described by reactions 111 and 112. All thermochemical and kinetic data were taken from the theoretical study presented in reference²⁴.

Figure 7.

Potential energy for the addition an H-atom to DMF, adapted from Sirjean and Fournet ²⁴. Energy at 0 K computed using the CBS-QB3 method.

OH-addition to DMF (reaction 120) is an important process for the description of DMF combustion chemistry. However, no information on this elementary reaction is available in the literature. For this reason, this reaction was considered in the proposed kinetic model assuming that this process will ultimately lead to the formation of CH₃CO, acetaldehyde, and acetylene. The formation of these products was postulated solely based on a mechanistic investigation of the addition reaction using thermochemical kinetics principles. The rate coefficient for this process was assumed similar to that of furan + OH measured by Atkinson⁴¹.

Termination reactions of the resonantly stabilized R4C₆H₇O radical with H atoms were also included because this radical can be found in non-negligible quantity under pyrolysis conditions (reactions 121-122). These reactions lead to the formation of cycloheaxa-2,4-dien-1-one (M2C₆H₆O), one of the most important primary products of DMF combustion, and cyclohex-2-en-1-one (cC₆H₈O). The decomposition reactions of these products are detailed in the secondary mechanism.

4.3 Secondary mechanism

The description of the secondary mechanism focuses on the consumption routes of the main primary products that were not described in the base models. The oxidation and thermal decomposition chemistry of 2,4- and 2,5-cyclohexadienone (M2C₆H₆O and M3C₆H₆O) as well as 2-methylfuran (MF) were comprehensively detailed in the secondary mechanism because of the crucial role played by these products in the combustion of DMF.

The decomposition reactions of cyclohexadienone molecules considered in the secondary mechanism involves several reaction classes:

• -Initial C-H bond fission leading to phenoxy radicals and H atoms (reactions 123 and 124). The reverse combination reactions were written with pressure dependent kinetic parameters similar to that of the phenoxy combination with H atoms to produce phenol.
• -H-abstractions from M2C₆H₆O and M3C₆H₆O by H and O atoms and OH, CH₃ and HO₂ radicals, and by larger hydrocarbon radicals: C₂H₃, C₃H₅, iC₄H₃, iC₄H₅, C₅H₅#, c-C₅H₇, and R4C₆H₇O. All these reactions lead to the formation of phenoxy radicals whose combustion chemistry is described in the base model.
• -The unimolecular decomposition routes of these two cyclohexadienones have been theoretically studied in detail by several groups within the framework of phenol thermal decomposition^42-44. Thermochemical and kinetic data were taken from the recent theoretical study²⁵ of the thermal decomposition of 5-methyl-2-furanylmethyl (R1C₆H₇O). These reactions were re-investigated at the CBS-QB3 level of theory with a focus on the determination of pressure-dependent kinetic parameters specific to these molecules. Three sets of pressure-dependent reactions can be selected in our DMF combustion kinetic model: for atmospheric pressure conditions (reactions 149-156), at 10 bar (reactions 157-164), and in the high-pressure limit (reactions 165-172).

The 2-methylfuran (MF) decomposition sub-mechanism is mostly based on analogies with DMF and furan reactions. It includes unimolecular initiations, H-atom abstractions and additions, and the subsequent decomposition of the created radicals. Most thermochemical data were computed using the CBS-QB3 method. This sub-mechanism is not intended to be a comprehensive combustion kinetic model for MF. It was developed only to describe in a simplified and effective way the principle decomposition routes of MF.

Three unimolecular initiation reactions were included:

• -The initial C-H bond fission leading to stabilized furan-2-ylmethyl radicals (reaction 201).
• -α-Carbene formation (on the MF moiety with a methyl group) followed by CO elimination from penta-2,3-dienal (CH₃CHCCHCHO). This sequence (reactions 178 and 180) is based on the main unimolecular decomposition pathway for furan. In addition, H-abstraction by H, OH, and CH₃ from the aldehydic hydrogen atom of penta-2,3-dienal (considered because of a low C-H bond dissociation energy) and the subsequent CO elimination from the formed radical were added (reactions 182 185).
• -α-Carbene formation (on the methyl-free moiety of MF) leading to the formation of penta-3,4-dien-2-one (CH₃COCHCCH₂) which in turn mainly decomposes by initial C-C bond fission yielding acetyl (CH₃CO) and propargyl (C₃H₃) radicals. This carbenic initiated thermal decomposition route (reactions 177 and 179) is based on analogy with the main unimolecular decomposition pathway for DMF.

H-abstractions from MF by H, O, OH, CH₃, HO₂, C₅H₅#, C₃H₅, and c-C₅H₇ radicals (reactions 186-197) and the decomposition of the radicals produced are based on analogies with furan and DMF. It is expected that the preponderant reaction flux from H-abstraction will lead to the formation of resonantly stabilized furan-2-ylmethyl radicals (named furylCH2). The main decomposition path of this radical should follow the trends observed in the decomposition furanyl radicals: a ring opening, followed by an internal H-atom transfer via a 5-membered ring transition state structure, and the elimination of CO (reactions 198-200).

H-addition to MF was also considered in the MF sub-mechanism (reactions 205 – 209). A simplified reaction scheme was adopted. It consists of the addition of a hydrogen atom to MF leading to the formation of the resonantly stabilized 2-methyl-2,3-dihydrofuran-3-yl radical (reaction 205). Based on analogies with hydrogen atom addition to DMF and furan, two decomposition routes for the initial adduct were included: the ipso substitution leading to furan and CH₃ treated here as a chemically activated reaction with a similar rate coefficient as that determined at 1 bar for DMF, and the characteristic reaction sequence found for furan: ring opening, internal transfer of the aldehydic H atom, and elimination of CO (reactions 207-209). The latter reactions are not treated as chemically activated, but, as a first approximation, high-pressure limit rate coefficients determined in the case furan are used.

Only the most important features of high-temperature DMF thermal decomposition and oxidation chemistry included in the kinetic model have been discussed here. Complete high-pressure limit and atmospheric pressure kinetic models can be found in the supplemental material. Care was taken to provide a reference for each DMF- and MF-specific reaction. In this work, only the atmospheric pressure rate coefficients were used for validation as all experimental data were obtained near atmospheric pressure. The complete atmospheric pressure model features 294 species and 1459 reactions.

5. Model validation

The proposed kinetic model is assessed and validated at high-temperature conditions through comparisons with new ignition delay times, measured behind reflected shock waves, and pyrolysis product speciation measurements made in single-pulse shock tube experiments by Lifshitz et al.²⁰.

5.1 Shock tube (ST) ignition delay times

Simulations were performed with the SENKIN code from the CHEMKIN-II program suite⁴⁵. For the simulation of the new DMF ignition delay times (described in §2 and §3), a pressure gradient consistent with that observed experimentally in the post-reflected shock-heated gases was included in the simulations (3% ms⁻¹) through the prescription of a volume history as described by Chaos and Dryer⁴⁶. Simulations were performed for each individual experimental condition. The onset of ignition was determined from simulations using the maximum slope of the exited OH* radical profiles, which corresponds to the experimental definition of ignition delay. Chemistry to describe the formation of electronically-excited OH radicals (OH*) from Hall and Petersen⁴⁷ was included in the kinetic model.

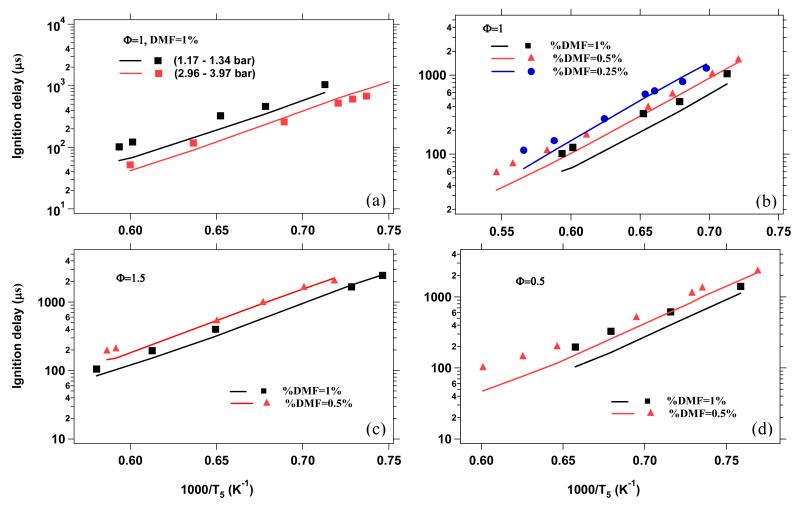
Figure 8 presents a comparison between experimental and simulated ignition delay times. The model predicts well the decrease in ignition delay time with increasing pressure as exhibited in Figure 8a. At higher pressures (~4 bar) the agreement with experiments is slightly better (maximum deviation of a factor 1.3) than near atmospheric pressures (maximum deviation of a factor 1.8 at high temperatures). Figures 8b, 8c, and 8d show that the decrease of ignition delay times (near 1 bar) with increasing DMF concentration is well reproduced at Φ = 1.0, 1.5, and 0.5, respectively. The overall agreement of model predictions and experimental data is good to satisfactory with similar predicted and measured overall activation energy (slopes in Figure 8) and a maximum deviation in ignition delay times of around a factor of two. For all equivalence ratios, it can be noted that the model-experiment agreement is excellent at lower concentrations (0.25% and 0.5% of DMF in O₂/Ar) and slightly deteriorates towards higher concentrations (1% of DMF in O₂/Ar). It is also observed that the model predictions are in somewhat better accord with experiment at rich conditions, where deviations are at most a factor of 1.4, than at lean conditions, where deviations of up to a factor of two exist.

Figure 8.

Comparison of experimental (points) and model predicted (solid lines) ignition delay times. (a) 1% DMF in O₂/Ar at φ = 1 and ~1 and ~4 bar; (b) 1%, 0.5%, and 0.25% DMF in O₂/Ar at φ = 1 and ~1 bar; (c) 1% and 0.5% DMF in O₂/Ar at φ = 1.5 and ~1 bar; (d) 1% and 0.5% DMF in O₂/Ar at φ = 0.5 and ~1 bar.

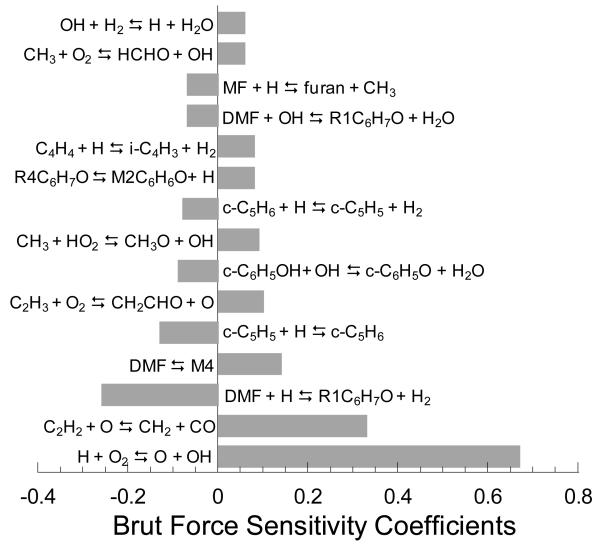
Figure 9 presents sensitivity coefficients obtained through a brute force sensitivity analysis for ignition delay at a representative experimental condition (1% DMF/7.5% O₂/Ar, φ = 1.0, 1474 K, and 1.35 bar). Rate coefficients were increased and decreased by a factor of two and sensitivity coefficients were calculated using:

$$\ln S_i=\frac{\ln \left(\frac{{\tau }_{-}}{{\tau }_{+}}\right)}{\ln \left(\frac{2k_i}{0.5k_i}\right)}$$

where τ₋ and τ₊ are the computed ignition delay times corresponding to, respectively, a decrease and an increase by a factor two of a rate coefficient k_i.

Figure 9.

Logarithmic sensitivity coefficients (see text) for ignition delay time with respect to reaction rate parameters, computed for 1% DMF/7.5 % O₂ in Ar at φ = 1.0, T₅ = 1474 K, and P₅ = 1.35 bar.

It can be seen in Figure 9 that the most sensitive reaction promoting overall DMF reactivity is, as expected at high-temperatures, the branching reaction H + O₂ ⇄ OH + O. Aside from reactions of methyl radicals with HO₂ and O₂ leading respectively to CH₃O + OH and HCHO + OH, which slightly promote the reactivity by creating reactive OH radicals from less reactive methyl radicals, all other sensitive reactions pertain to the oxidation chemistry of DMF itself or of its most important decomposition products (acetylene, cyclopentadiene, vinylacetylene, and phenol). Among acetylene reactions within the C₀–C₂ reaction base, the addition of O atoms to C₂H₂ producing CH₂ and CO was found to strongly promote reactivity. Once CH₂ is formed, it mainly reacts with O₂ yielding OH + CHO. The latter radical predominantly decomposes into H atoms and CO. Consequently, the consumption of one reactive O atom by addition to acetylene, ultimately leads to the formation of two very reactive radicals (an H-atom and OH). The reaction C₂H₃ + O₂ ⇄ CH₂CHO + O within the C₀–C₂ chemistry also appears in the sensitivity analysis as promoting overall reactivity. In addition to the production of a reactive O atom, this pathway leads ultimately to the generation of an H-atom or a methyl radical through the unimolecular decomposition of the CH₂CHO radical, all starting from the vinyl radical.

Two of the most sensitive reactions with regards to ignition delay are directly related to the primary mechanism of DMF. H-abstraction by H atoms from DMF, leading to the formation of R1C₆H₇O + H₂, is the most sensitive inhibitive reaction. This result is not surprising since H-abstraction competes with the branching reaction H + O₂ ⇆ OH + O and yields a stabilized free radical (R1C₆H₇O). However, it is worth noting that this reaction has a promoting effect at pyrolysis conditions. The second sensitive reaction is related to the unimolecular initiation of DMF, described in the potential energy surface given in Figure 5. As shown in Figure 5, M4C₆H₈O subsequently decomposes to CH₃CO and buta-1,2-dien-1-yl (C₄H₅-1s) which in turn can react by C-H bond scission to form vinylacetylene and an H atom. Thus, the promoting effect of DMF ⇄ M4C₆H₈O is due to the formation of H atoms.

Among all the reactions involving primary species, some processes involving cyclopentadiene and phenol have a significant sensitivity. H-abstraction by H atoms from cyclopentadiene or the combination of H atoms and cylcopentadienyl radicals are largely inhibiting since these two reactions consume H atoms and form stable species (auto-catalytic cycle producing H₂ from two H-atoms). The H-abstraction by OH radicals from phenol also has an inhibiting effect on the conversion of DMF. In fact, this reaction leads to the formation of phenoxy radicals (C₆H₅O) which mainly decomposes to CO and cyclopentadienyl radicals.

5.2 Pyrolysis product profiles

Lifshitz et al.²⁰ studied the pyrolysis of DMF in a single-pulse shock tube for temperatures ranging from 1080 to 1350 K and pressures between 2 and 3 bar. They performed chromatographic analyses of the quenched post-shock pyrolysis product gases and detected and quantified twenty products from methane to benzene. In order to compare the DMF model proposed here to the Lifshitz et al. pyrolysis speciation measurements, simulations were carried out using the atmospheric pressure model and SENKIN⁴⁵. Not all data from the Lifshitz et al. study were considered but instead simulations were carried out for twenty experimental conditions uniformly distributed in temperature, residence time, and pressure-space. The results of these twenty simulations were then curve fit to highlight the global trends.

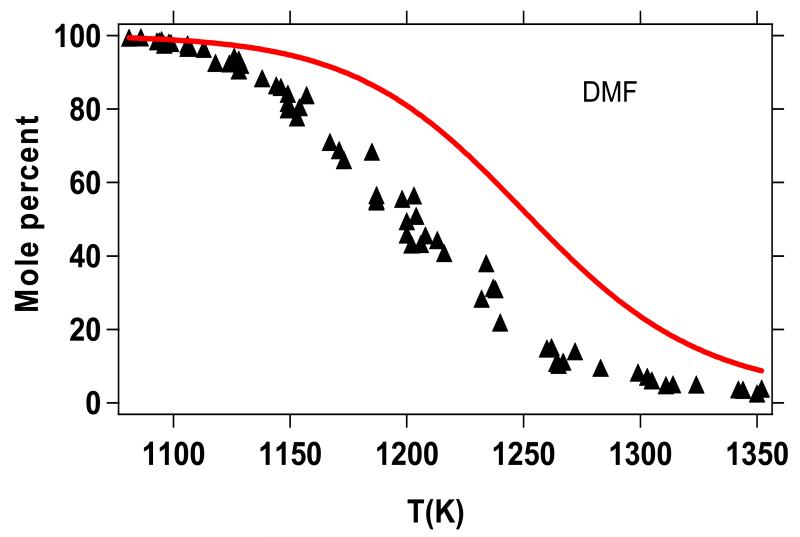
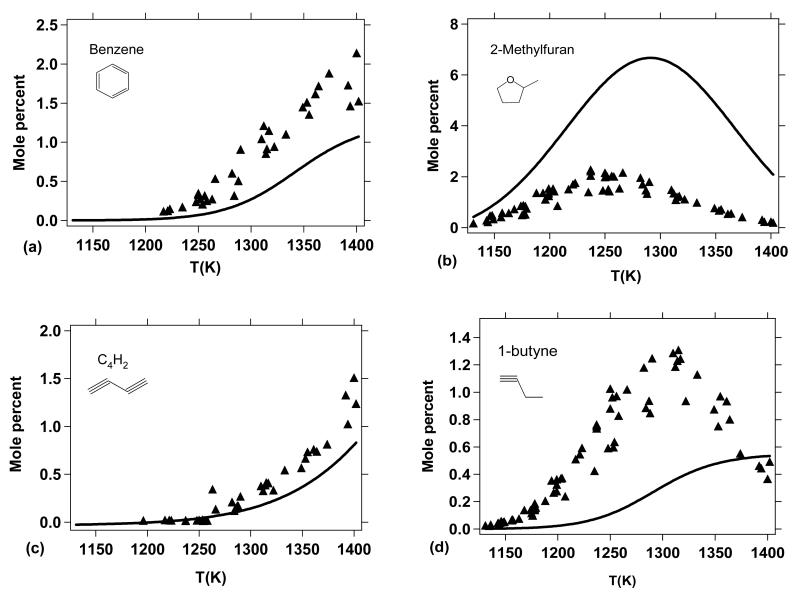
Figure 10 shows a comparison between the simulated consumption of DMF and the experimental results obtained by Lifshitz et al.²⁰. In all figures, the points correspond to experimental data while the simulated results are represented by curves and are expressed in mole percent. The mole percent of a given species is calculated as the ratio of its mole fraction over the sum of the species mole fractions. Note that only species quantified experimentally by Lifshitz et al. were considered in the sum of the simulated species mole fractions. As shown in Figure 10, a very low conversion of DMF is predicted by the kinetic model with respect to the experimental results. Given the extreme changes that the model would require in order to increase the DMF conversion to the levels seen in Figure 10, it is difficult or impossible to explain the lack of conversion/reactivity as simply a failure of the model. Moreover, in the previous section (§5.1), the agreement between measured ignition delay times and model predictions was rather good. This contradiction led us to investigate further the experimental reflected shock temperatures estimated by Lifshitz et al.²⁰, in their single-pulse shock tube experiments.

Figure 10.

Lifshitz et al.²⁰ single-pulse shock tube pyrolysis measurements for DMF conversion, reported in terms of mole percent DMF in the product gases (see text), with comparison to predictions from the present kinetic model. The post shock temperatures given (x-axis) are those predicted by Lifshitz et al.²⁰.

In the Lifshitz et al. study²⁰ the reflected shock temperatures (T₅) were calculated from the extent of the decomposition of 1,1,1-trifluoroethane which served as an internal chemical thermometer standard. Its decomposition, according to reaction (1):

$${\mathrm{CH}}_3-{\mathrm{CF}}_3={\mathrm{CH}}_2={\mathrm{CF}}_2+\mathrm{HF},$$ (1)

is a first-order unimolecular reaction and was assigned a rate coefficient of k = 10^14.8 exp(−74115 (cal mol⁻¹)/RT) s⁻¹ in the Lifshitz et al. study²⁰. The temperature behind the reflected shock was then estimated by Lishitz et al. using:

$$T=-(E∕R)\left[\ln \right(-\frac{1}{At}\ln (1-\chi )\left]\right(K)$$ (2)

where t is the residence time, A and E are the kinetic parameters involved in the previous expression of k and χ is the extent of decomposition defined as:

$$\chi ={[\mathrm{CH}2=\mathrm{CF}2]}_t∕({[\mathrm{CH}2=\mathrm{CF}2]}_t+{[\mathrm{CH}3-\mathrm{CF}3]}_t)$$ (3)

The rate coefficient k given above for reaction (1) was measured by Tsang and Lifshitz in a previous shock tube study, related to the kinetic stability of 1,1,1-trifluoroethane⁴⁸. In this work⁴⁸, two reactions were used again as internal standards to measure T₅: (1) the elimination of water from tert-butanol and (2) the unimolecular decomposition of perfluorocyclobutane yielding two C₂F₄. For each reaction, uncertainty of a factor of three in the rate coefficient at 1200 K was considered by the authors, which in turn implies a similar uncertainty for their measurement of the rate coefficient for reaction (1).

These results led us to calculate, from quantum chemistry methods, the rate coefficient for the decomposition of 1,1,1-trifluoroethane. The CBS-QB3 level of theory was applied to compute energies by using the Gaussian09 software⁴⁹; we refer readers to reference²⁵ for more information on the methodology used. The derivation of the rate coefficients was performed using the Chemrate software⁵⁰. A high-pressure limit rate coefficient was obtained from canonical transition state theory (equation 4):

$$k_{\infty }\left(T\right)=\kappa \left(T\right)L\frac{k_{B}T}{h}\frac{Q_{TS}\left(T\right)}{Q_R\left(T\right)}exp[-\frac{V^{\#}}{RT}],$$ (4)

where V^# is the classical barrier height. Q_TS(T) and Q_R(T) represent the partition functions calculated, respectively, for the transition state (TS) and the reactant (R); κ(T) is the transmission coefficient; and L is the statistical factor defined as:

$$L=\frac{{\sigma }_R\times n_{TS}}{{\sigma }_{TS}\times n_R}$$ (5)

In equation (5), σ_R and σ_TS are the external symmetry of, respectively, the reactant and the transition state, while n_R and n_TS correspond to the number of optical isomers for reactant and transition state, respectively. In the calculation of k_∞(T), σ_R and σ_TS were removed beforehand from the rotational partition function to avoid counting them twice. For equation (4), the value of L is equal to 3 in accordance with the work of Barker et al.⁵¹. The internal rotation around the C-F bond in CF₃-CH₃ was treated as an hindered rotor with a barrier height of 3.1 kcal mol⁻¹ (calculated at the B3LYP-6-311G(d,p) level of theory) and with an internal symmetry of 3.

Tunneling was taken into account for hydrogen transfer with Eckart transmission coefficients. The characteristic length of the Eckart function is obtained from forward and reverse barrier heights (E₁ and E₋₁) at 0 K along with the imaginary frequency (ν_i) of the transition state using the equations reported by Johnston and Heicklen⁵².

It is noted that the RRKM or non-RRKM character of this reaction is still debated ^53-54, an issue beyond the scope of the present study. In the present work the pressure dependence was taken into account using Chemrate⁵⁰ to calculate the rate coefficient at 2.5 bar, corresponding to the mean pressure of the Lifshitz et al. experiments ²⁰. Table 4 summaries the results of the theoretical calculations and provides some comparisons with literature data for HF elimination from 1,1,1-trifluoroethane.

Table 4.

Rate coefficients calculated in this work for the HF elimination from CF₃CH₃ compared with literature data.

Reference	A (s−1)	n	E (kcal mol−1)	k(1200K) s−1	k(1800K) s−1
Tsang and Lifshitz20 (k2.5bar)a	6.31×1014	0	74.00	21.0
This workb (k2.5bar)	6.17×1013	0	71.66	5.5
Kiefer et al.53 (k∞)c	1.58 ×1015	0	75.03		1.2 ×106
This work (k∞)	2.70×1014	0	74.83	6.3
Giri and Tranter54 (k1bar)d	3.24 ×1044	−9.34	78.50		3.8×104
This worke (k1bar)	3.10×1055	−11.905	99.31		4.8×104

^aExperimental study performed over the temperature range 1070-1370 K and pressures between 2 and 4 atm

^bObtained from RRKM calculations between 1000 and 1500 K using Ar as buffer gas (σ=3.54Å and ε/k_Β= 39.95 K) and <ΔE>_down=750cm⁻¹ as proposed in reference (54)

^cExperimental study performed at very high temperatures (1600-2400K) and pressures between 15-550 Torr

^dExperimental study performed over the temperature range 1500 and 1840 K and for pressures between 600 and 1200 Torr.

^eCalculated from RRKM calculations between 1000 and 2000K using neon as buffer gas (σ= 2.82 Å and ε/k_Β=32.8 K) and <ΔE>_down=750cm⁻¹ as proposed in reference (54).

The rate coefficient for reaction (1) calculated at the CBS-QB3 level of theory is 3.8 times smaller than the experimental value measured by Tsang and Lifshitz⁴⁸ at 2.5 bar and 1200 K, a difference that is slightly beyond the uncertainty given by Tsang and Lifshitz. It is worth noting that pressure falloff cannot account for the temperature disparity. Indeed, at 1200K, the calculated high-pressure limit rate constant is close to 6.3 s⁻¹, compared with a calculated rate of 5.5 s⁻¹ at 2.5 bar (Table 4). The small degree of pressure falloff calculated for this reaction at 1200 K and 2.5 bar is consistent with the RRKM calculations reported by Tsang and Lifshitz. Before computing the corresponding temperatures with the new rate coefficient for reaction (1), we compared to other data available in the literature. To our knowledge, no recent experimental data have been published for reaction (1) in the same temperature range but experimental and theoretical studies were performed at higher temperatures by Kiefer et al.⁵³ and Giri and Tranter ⁵⁴. In the former study, Kiefer et al.⁵³ reported a high-pressure rate coefficient calculated theoretically at the G3 level of theory (Table 4). The activation energy found by Kiefer et al.⁵³ is in a very good agreement with our CBS-QB3 value but their A-factor is much greater (factor of 5.8). This difference may partly be explained by the treatment of the internal rotation around the C-C bond (they considered a harmonic oscillator rather than a hindered rotor) but mostly by the use of an overestimated reaction path degeneracy (rpd). Indeed, the value used for the rpd by Kiefer et al.⁵³ (rpd = 9) seems questionable, as discussed by Barker et al.⁵¹. Indeed, Kiefer et al. considered a vibrational model for the torsion and using this approach in equation (5) should lead to a value of three for the rpd. Using a rpd of three in Kiefer et al. study would lead to correct agreement with the rate coefficient for reaction (1) calculated here (a deviation of a factor of 1.8 at 1800 K, after correction of the Kiefer et al. rate coefficient for rpd). In the second study of reaction (1), Giri and Tranter⁵⁴ investigated the dissociation of 1,1,1-trifluoroethane behind reflected shock waves using shock tube time-of-flight mass spectrometry. They proposed a rate coefficient for high temperatures (1500-1840 K) and for pressures ranging from 600 to 1200 Torr (Table 4). We estimated the rate coefficient for reaction (1) from RRKM calculations using the same Lennard Jones parameters and < ΔE>_down as proposed by Giri and Tranter⁵⁴ and obtained very good agreement with their experimental rate coefficient (deviation of a factor of 1.3 at 1800 K). These results suggest that our CBS-QB3 rate coefficient is consistent and can be used to re-calculate the “experimental temperatures” of the Lifshitz et al. single-pulse shock tube study²⁰. Using relations (2) and (3) and the new rate coefficient for reaction (1) given in Table 4 for 2.5 bar, we computed new temperatures for the Lifshitz et al.²⁰. DMF pyrolysis experiments (Table 5). It is worth noting that the residence times in the experimental study of Lifshitz et al., vary from 1.8 to 2.3 ms. In the present calculations, a mean residence time for experiments was used (t = 2.12 ms).

Table 5.

Reflected shock temperatures (T₅) calculated with the rate coefficients proposed by Tsang et al. ⁴⁸ (used in the study of Lifshitz et al. ²⁰) and rate coefficients from this work for the decomposition of 1,1,1-trifluoroethane.

χ	Residence time t (s)	Texp (K) From Lifshitz et al.20	Tcorr(K) This work	ΔT (K) =Tcorr-Texp
0.99	0.00212	1411	1498	87
0.9	0.00212	1375	1456	82
0.8	0.00212	1357	1436	79
0.7	0.00212	1343	1419	77
0.6	0.00212	1330	1404	75
0.5	0.00212	1317	1389	73
0.4	0.00212	1302	1373	70
0.3	0.00212	1286	1354	68
0.2	0.00212	1266	1331	65
0.1	0.00212	1234	1295	61
0.001	0.00212	1069	1110	40

As shown in Table 5, we systematically estimated higher temperatures for the “experimental” temperatures of the Lifshitz et al.²⁰ study, with differences ranging from 40 to 87 K. We derived, from the Table 5 data, a linear correlation (equation 6) between the experimental temperatures (T_exp) obtained by Lifshitz et al. and the modified temperature (T_corr) calculated here:

$$T_{corr}\left(K\right)=1.14\times T_{exp}\left(K\right)-110$$ (6)

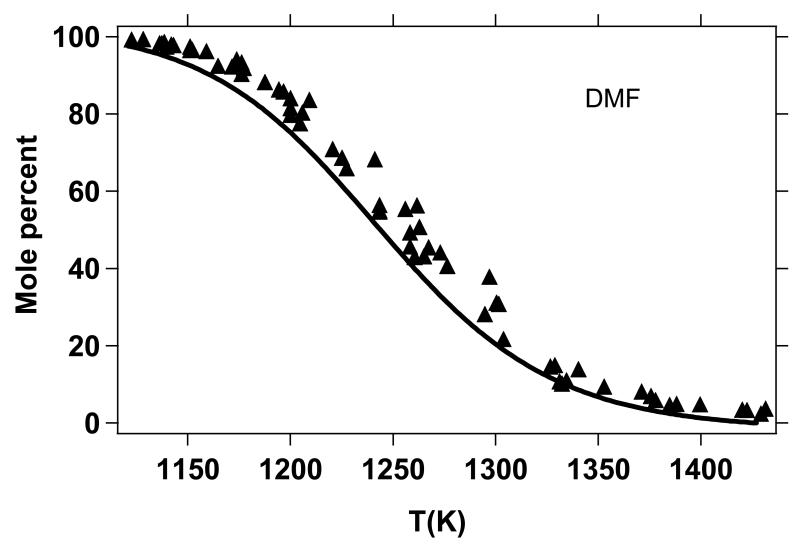
Figure 11 shows a comparison of the Lifshitz et al. measurement for DMF conversion with model prediction after the temperature correction; significant improvement in model performance relative to that shown in Figure 10 is observed.

Figure 11.

Lifshitz et al.²⁰ single-pulse shock tube pyrolysis measurements for DMF conversion, reported in terms of mole percent DMF (see text) in the product gases, with comparison to predictions from the present kinetic model. The post shock temperatures given (x-axis) for the Lifshitz et al. experiments are those predicted in the present study using refined rate coefficients described in Table 4.

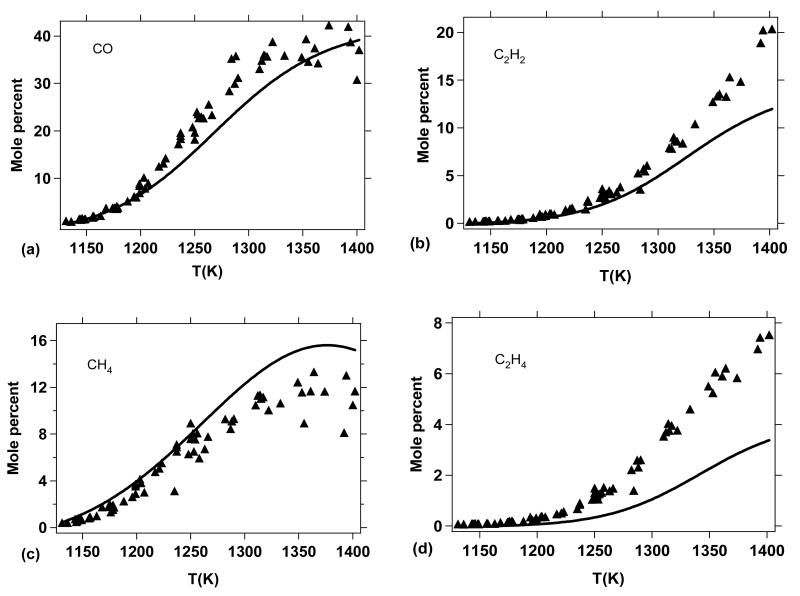
Since the computed pyrolysis conversion of DMF is in good agreement with the experimental results of Lifshitz et al.²⁰, we decided to further compare the distribution of predicted pyrolysis products with those measured. Figure 12 shows model predictions compared to measurements for the major products observed by Lifshitz et al. Globally, the agreement is rather satisfactory. To analyze the kinetics respsonsible for the predicted pyrolysis product distribution, in Figures 13, 14, and 15, reaction flux analyses are given for DMF (Figure 13) and the primary products: cylohexa-2,4-dien-1-one (M2C₆H₆O) and cylohexa-2,5-dien-1-one (M3C₆H₆O) (Figure 14) and 2-methylfuran (Figure 15).

Figure 12.

Measured pyrolysis products from the Lifshitz et al.²⁰ study with comparison to predictions from the present kinetic model (see text for mole percent definition).

Figure 13.

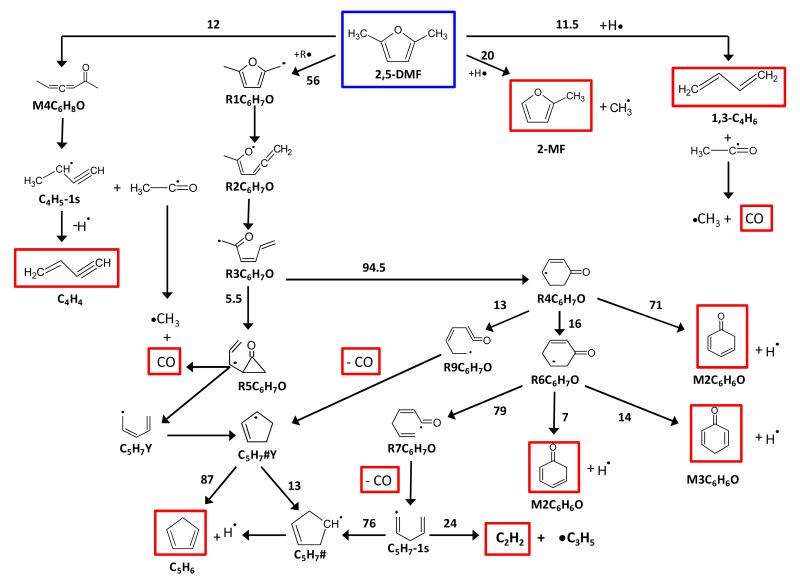
Reaction flux analysis for DMF pyrolysis; conditions: 1300 K, 2 bar, residence time of 1 ms corresponding to 47% DMF conversion. Given reaction fluxes (numbers associated with arrows) are relative to the consumption of a given species and are expressed in percent.

Figure 14.

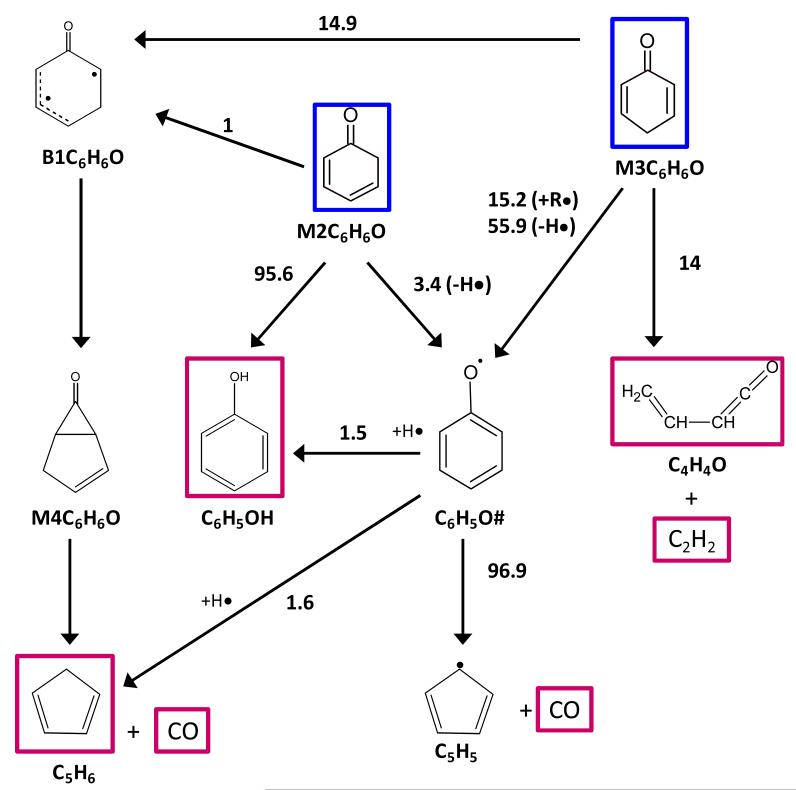
Reaction flux analysis for cyclohexadienone (M2C₆H₆O and M3C₆H₆O) during DMF pyrolysis; conditions: 1300 K, 2 bar, residence time of 1 ms corresponding to 47% DMF conversion. Given reaction fluxes (numbers associated with arrows) are relative to the consumption of a given species and are expressed in percent.

Figure 15.

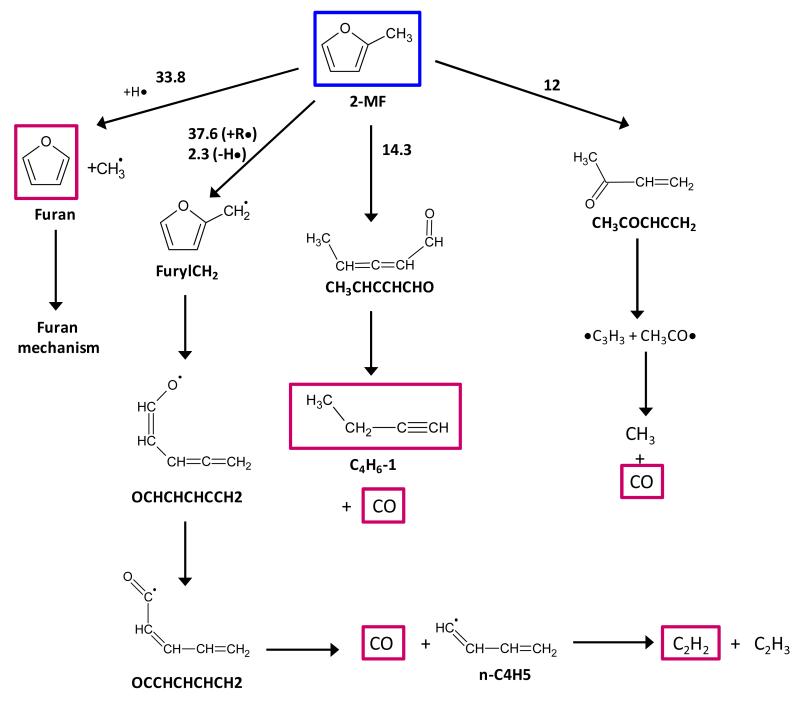
Reaction flux analysis for 2-methylfuran during DMF pyrolysis; conditions: 1300 K, 2 bar, residence time of 1 ms corresponding to 47% DMF conversion. Given reaction fluxes (numbers associated with arrows) are relative to the consumption of a given species and are expressed in percent.

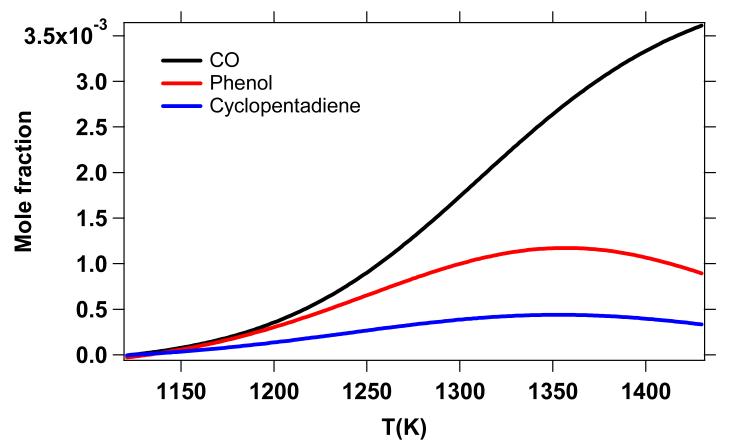
As shown in Figure 12a, the formation of carbon monoxide is very well reproduced by the model, consistent with the conversion of DMF observed in Figure 11 as many of the channels involved in DMF thermal decomposition lead to the formation of carbon monoxide (Figures 13, 14, and 15). From this point of view, CO can be considered a good indicator of the thermal conversion of DMF. The formation of acetylene (Figure 12b) is also satisfactorily represented; however, the ethylene yields (Figure 12d) are somewhat underpredicted by the model, especially for temperatures above 1300 K.

Reaction flux analysis (Figure 13) shows that the formation of C₂H₄ does not occur from the direct decomposition of DMF or important primary species (Figures 14 and 15). In fact, ethylene is mainly formed from secondary reactions involving C₂H₆ and 1,3-C₄H₆ according to:

$${\mathrm{H}}_3\mathrm{C}-{\mathrm{CH}}_3\stackrel{+\mathrm{H},{\mathrm{CH}}_3}{\to }{\mathrm{H}}_2{\mathrm{C}}^{•}-{\mathrm{CH}}_3\stackrel{+\mathrm{M}}{\to }{\mathrm{H}}_2\mathrm{C}={\mathrm{CH}}_2+{\mathrm{H}}^{•}$$

$${\mathrm{H}}_2\mathrm{C}=\mathrm{CH}-\mathrm{CH}={\mathrm{CH}}_2\stackrel{+\mathrm{H}}{\to }{\mathrm{H}}_2\mathrm{C}=\mathrm{CH}-{\mathrm{CH}}_2-{\mathrm{CH}}_2^{•}\to {\mathrm{H}}_2\mathrm{C}={\mathrm{CH}}_2+{\mathrm{H}}_2\mathrm{C}={\mathrm{CH}}^{•}$$

Both C₂H₆ (Figure 12d) and 1,3-C₄H₆ (Figure 12f) are slightly over predicted by the model (especially C₂H₆) which could be due to a lack of conversion towards the formation of C₂H₄ within the model.

The methane profile, another important product, is correctly reproduced by the model (Figure 12c). The slight over prediction of methane yields is consistent with the slight over prediction of C₂H₆, since these two products are both formed from methyl radicals. It is possible that an excessive production of CH₃ within the model could be responsible for the over prediction of both CH₄ and C₂H₆.

Vinylacetylene (C₄H₄) is a key species in DMF decomposition and its yield is very well predicted by the model (Figure 12e). In recent work, Sirjean and Fournet²⁴ studied, via quantum chemistry calculations, the unimolecular initiation of DMF and they showed that the main decomposition channel leads to the formation of C₄H₄. The reaction flux analysis for DMF (Figure 13) reveals that this channel, under the present model, is the only way to form vinylacetylene; hence, the good model-experiment agreement for vinylacetylene yields shown in Figure 12e are a partial validation of the previous theoretical calculation. Another key compound is the buta-1,3-diene (1,3-C₄H₆). As discussed previously the shape of the experimental and predicted profiles for 1,3-C₄H₆ (Figure 12f) are in agreement but the model slightly over predicts the yield of buta-1,3-diene. This result is interesting because buta-1,3-diene is mainly formed from primary reactions involving H addition to DMF, as showed in Figure 13. This route has been recently proposed by Sirjean and Fournet²⁴ and competes with the well-known ipso-addition, leading to 2-methylfuran and CH₃. The good agreement observed between the experimental and predicted 1,3-C₄H₆ profiles, suggests that the proposed channel is pertinent and explains buta 1,3-diene formation under pyrolysis conditions.

The last important species quantified by Lifshitz et al.²⁰ is cyclopentadiene (Figure 12g). The model over predicts the formation of this species at all temperatures but the shape of the model-predicted profile is in agreement with the measurements. Several channels are involved in the formation of C₅H₆ but all are related to the thermal decomposition of R1C₆H₇O, initially produced by H-abstraction from DMF. For each channel, the first reactions involve the ring opening of R1C₆H₇O, followed by an internal H-atom transfer to form R3C₆H₇O (Figure 13). From R3C₆H₇O, three routes can explain the formation of cyclopentadiene:

• -A C₃ ring closure leading to R5C₆H₆O. The ring formed can be opened again by β-scission to give a new radical (not shown in Figure 13) which reacts, in turn, by fast CO elimination to produce the stabilized free radical C₅H₇Y. C₅H₇Y reacts mainly by ring closure to form cyclopent-2-en-1yl (C₅H₇#) which leads to cyclopentadiene by C-H bond fission. Even though this channel represents a minor consumption flux for R3C₆H₇O, its contribution to the formation of C₅H₆ cannot be neglected.
• -Figure 13 shows that R3C₆H₇O reacts mainly by C₆ ring enlargement to form R4C₆H₇O (more than 90% of R3C₆H₇O reacts via this channel under the pyrolysis conditions of the Lifshitz et al.²⁰ study). C-H bond scission represents the most important decomposition channel for R4C₆H₇O and leads to the formation of cyclohexa-2,4-dien-1-one (M2C₆H₆O). Additionally, two other pathways can contribute to the production of C₅H₆ from R4C₆H₇O. One channel is a ring opening, leading to R9C₆H₇O which in turn reacts by CO elimination to form the cyclopent-2-en-1-yl-radical (C₅H₇#Y). The C₅H₇#Y radical mostly undergoes C-H bond fission to form cyclopentadiene. The second channel involves an internal H-atom shift into the ring structure of R4C₆H₇O and leads to the production of R6C₆H₇O. The ring opening of R6C₆H₇O followed by a fast CO elimination (Figure 13), yields to the formation of penta-1,4-dien-1-yl (C₅H₇ 1s). This radical can react by β-scission to form acetylene and the allyl radical (C₃H₅) but most of the consumption flux of C₅H₇-1s goes towards the cyclopent-3-en-1-yl (C₅H₇#) radical, which in turn decomposes into cyclopentadiene and an H atom.
• -The last channels in which cyclopentadiene is formed involves the thermal decomposition of cyclohexa-2,4-dien-1-one (M2C₆H₆O) and cyclohexa-2,5-dien-1-one (M3C₆H₆O). A reaction flux analysis for these two primary products is presented in Figure 14. The majority of M2C₆H₆O decomposes, via a concerted reaction, into phenol; C₅H₆ formation via M2C₆H₆O decomposition represents only a minor pathway. By contrast, the multi step decomposition of cyclohexa-2,5-dien-1-one leads to the formation of C₅ species (cyclopentadiene and cyclopentadienyl radicals). The first step involves the formation of a biradical (B1C₆H₆O) which reacts by internal addition to form a bicyclic species (M4C₆H₆O). A concerted elimination of CO from M4C₆H₆O leads to the formation of cyclopentadiene. Another production channel for cyclopentadiene is related to the unimolecular initiation of M3C₆H₆O to form phenoxy (C₆H₅O#) and an H atom. The phenoxy radical decomposes mainly into CO and cyclopentadienyl (C₅H₅) which can react by combination with H atoms to form cyclopentadiene. However under the pyrolysis conditions explored here, this last channel is of little importance.

Above we report that phenol is the major product of cyclohexa-2,4-dien-1-one decomposition (M2C₆H₆O) and accumulates to high concentrations under the pyrolysis conditions considered by Lifshitz et al.²⁰. Even though Lifshitz et al. expected ketenes as pyrolysis products and tried to detect them, they did not mention phenol formation. However, Djokic et al. ²¹ recently observed phenol formation during DMF pyrolysis. Figure 16 shows the mole fractions for CO, cyclopentadiene, and phenol obtained from modeling predictions at the pyrolysis conditions encountered in the Lifshitz et al. study²⁰. The model-predicted phenol yield is a factor of two greater than the predicted cyclopentadiene yield C₅H₆; hence, phenol is a primary product of the thermal decomposition of DMF under the proposed kinetic model, consistent with the recent results of Djokic et al.²¹.

Figure 16.

Predicted phenol, CO, and cyclopentadiene mole fractions under batch reactor conditions (2 bar, 0.5% DMF dilute in argon, residence time of 2 ms).

Several less important minor species were also quantified in the Lifshitz et al. DMF pyrolysis study²⁰ and some comparisons between experimental and model predicted results for minor species are shown in Figure 17. The formation of benzene (Figure 17a) is well predicted by the model as is the formation of diacetylene C₄H₂ (Figure 17c). This latter result is not surprising since C₄H₂ is produced directly from vinylacetylene (C₄H₄) which is also well described by the model. Under the pyrolysis conditions considered, the formation of benzene comes mostly (~70%) from the ipso addition of H atoms to phenol (reaction 7):

(7)

The good agreement between experimental and predicted benzene profiles further supports the formation of phenol during the pyrolysis of DMF.

Figure 17.

Experimental (points) and model predicted (lines) minor species yields (in mole percent) observed and quantified in the single-pulse shock tube study of Lifshitz et al.²⁰.

In contrast to other results, the simulations largely over predict the formation of 2-methylfuran (by a factor of three) even though the maximum of the curve is well located in temperature space. Figures 14 and 15 describe the main pathways involved in the formation and consumption of 2-methylfuran. The formation of 2-methylfuran species only occurs by the following ipso reaction:

(8)

A previous theoretical study²⁴ provides a calculation of the high-pressure rate coefficient for reaction 8 which is consistent with literature data ¹⁸. As described in reference²⁴, reaction 8 competes with other channels, mostly the formation of buta-1,3-diene (Figure 13), and is chemically activated. The pressure dependence of the reaction 8 rate coefficient was taken into account in the kinetic simulations of DMF pyrolysis presented here. Uncertainties in the theoretical calculation of the reaction 8 rate coefficient could induce the over prediction of 2-dimethylfuran yields. However, it is worth noting that the formation of C₄H₆, which mainly comes from DMF + H, is well predicted by the model. Slow consumption of 2-methylfuran could partially explain the over predicted 2-methylfuran yields relative to experiment. Figure 15 shows the main consumption pathways for 2-methylfuran. A significant proportion of 2-methylfuran (34%) reacts by ipso addition, similar to reaction 8, to form furan and a methyl radical. Unfortunately, furan was not quantified in the experimental study of Lifshitz et al. ²⁰. Another important channel, accounting for 40% of 2-methylfuran consumption under the Figure 15 conditions, involves the formation of the furan-2-ylmethyl radical (furylCH₂ in Figure 15) which in turn reacts to form intermediates which decompose into CO and n-C₄H₅. The n-C₄H₅ radical entirely reacts by β-scission to form C₂H₂ and vinyl radicals. For the Figure 15 conditions, this channel accounts for about 80% of the n-C₄H₅ formation and 30% of the acetylene formation. We previously showed that C₂H₂ is under predicted, in particular at the higher temperatures of the Lifshitz et al. study²¹, a result that could be consistent with an under prediction of 2-methylfuran conversion to acetylene.

The last interesting channel involved in the consumption of 2-methylfuran is its unimolecular initiations. Figure 15 shows that two unimolecular initiation channels must be considered for 2-methylfuran and that one of them leads to the formation of 1-butyne. In the present model, 1-butyne is only produced by this channel. A comparison of experimental and kinetic model predictions for 1-butyne yields from DMF pyrolysis is given in Figure 17d and clearly shows an under prediction of 1-butyne formation by the model. However, in this case, it is seems difficult to connect the under prediction of 1 C₄H₆ with the conversion of 2-methylfuran. The yield of 1-butyne is well represented at the highest pyrolysis temperatures (~1400 K) while that of 2-methylfuran is largely over predicted by the model at these conditions. Moreover, the shape of the theoretical curve is not consistent with experimental results, indicating that formation pathways for 1-butyne may be missing from the model. In fact, the thermal decomposition of 2-methylfuran within the model is mostly described based on analogies with the detailed mechanism of DMF developed in this work and the furan mechanism proposed in reference²⁷. Several rate coefficients for reactions involving 2-methylfuran have been deduced from structure reactivity relationships. A more thorough study of 2-methylfuran decomposition is necessary in order to improve prediction of its pyrolysis yields in the present kinetic model.

6. Conclusion

A detailed kinetic model describing the oxidation and pyrolysis of 2,5-dimethylfuran (DMF) was developed in a comprehensive and consistent way, based on previous theoretical calculations involving the unimolecular initiations of DMF, reactions of DMF + H, as well as the thermal decomposition of 5-methyl-2-furanylmethyl radical, the most important radical produced from DMF. Specifically, the model includes the decomposition channels of important primary and secondary products such as cyclohexadienones, 2-methylfuran, furan, phenol, cyclopentadiene, vinylacetylene, and others. In addition, shock tube ignition delay time measurements for DMF are reported for the first time. These experimental results were used to validate the model at high-temperature combustion conditions. The model predicted ignition delay times are in generally good agreement with the experimental findings, with model-experiment deviations of at most a factor of two. The modeling predictions are particularly good at stoichiometric and rich conditions with maximum deviation with experiment of a factor of 1.8 and 1.4, respectively. Sensitivity analysis indicates that, among all reactions having an influence on the conversion of DMF, reactions in the primary mechanism such as H-abstraction from DMF by H atoms (and to a lesser extent by OH radicals) and the unimolecular initiation resulting in ring opening (DMF→M4C₆H₈O) are very sensitive and influence to a large degree the global reactivity at shock tube conditions. Sensitivity analysis also reveals that reactions involving important primary DMF fragments such as cyclopentadiene and phenol can have a substantially influence on the conversion of DMF.

Finally, a comparison between the pyrolysis speciation measurements of Lifshitz et al. ²⁰ and those predicted by the proposed model provided a validation of several theoretical predictions for rate parameters included in the model. However, prior to comparison of model predictions with the Lifshitz et al. speciation measurements, the rate coefficient used to compute the experimental temperatures in the Lifshitz et al. study, via the chemical thermometer technique, was reevaluated using quantum chemistry calculations. Following reevaluation of the Lifshitz et al. experimental temperatures, good agreement between the experimental and predicted conversion of DMF is observed and the predicted distribution of pyrolysis products is satisfactory for most products. A reaction flux analysis carried out at pyrolysis conditions, illustrates the important routes for the formation of specific products. For example, within the context of the proposed model C₄H₄ can only produced by unimolecular initiation (i.e., DMF ring opening, DMF→M4C₆H₈O) and the formation of buta-1,3-diene mostly occurs by H addition to DMF. Reaction flux analysis shows that the primary pyrolysis consumption pathway for DMF begins with an H-abstraction followed by a ring opening and then an H-atom transfer. At this stage of the primary pyrolysis pathway, a ring enlargement process occurs resulting in the formation of a C₆ ring which, in turn, decomposes into cyclohexadienone or to a lesser extent into the cyclopentadienyl radical. This primary pathway finally leads to the formation of cyclopentadiene, a major product of the Lifshitz et al. study, but more so to the formation of phenol. While phenol was not detected by Lifshitz et al.²⁰, the very recent pyrolysis study of Djokic et al.²¹ clearly shows the formation of phenol at similar pyrolysis conditions.

Given that the model reported here is the first comprehensive kinetic model for the oxidation of DMF and that the high-temperature kinetics of DMF are rather complicated due its unique furanic structure, there are surely improvements to be made in the future to the proposed model. However, the model does predict well the global reactivity of DMF at high-temperature combustion conditions, as illustrated by the good agreement with new shock tube ignition delay time measurements, and predicts well the conversion of DMF at pyrolysis conditions and predicts satisfactorily the pyrolysis product distribution. Importantly, the channels proposed in the thermal decomposition of this unsaturated cyclic ether, based mostly on theoretical quantum chemistry calculations, appear to be consistent with experimental observations.