Reconstructing regulatory networks from the dynamic plasticity of gene expression by mutual information

Abstract

The capacity of an organism to respond to its environment is facilitated by the environmentally induced alteration of gene and protein expression, i.e. expression plasticity. The reconstruction of gene regulatory networks based on expression plasticity can gain not only new insights into the causality of transcriptional and cellular processes but also the complex regulatory mechanisms that underlie biological function and adaptation. We describe an approach for network inference by integrating expression plasticity into Shannon’s mutual information. Beyond Pearson correlation, mutual information can capture non-linear dependencies and topology sparseness. The approach measures the network of dependencies of genes expressed in different environments, allowing the environment-induced plasticity of gene dependencies to be tested in unprecedented details. The approach is also able to characterize the extent to which the same genes trigger different amounts of expression in response to environmental changes. We demonstrated the usefulness of this approach through analysing gene expression data from a rabbit vein graft study that includes two distinct blood flow environments. The proposed approach provides a powerful tool for the modelling and analysis of dynamic regulatory networks using gene expression data from distinct environments.

INTRODUCTION

Network analysis using gene expression data has been widely applied as an approach to studying the regulatory causality of transcriptional processes involved in cell survival and proliferation (1–4). In responding to changes in environmental conditions, a functional cell would modify the expression of particular genes through signalling regulation to make it possible to preserve the robustness of cellular processes (5). A comprehensive characterization of regulatory networks behind such an environment-induced response becomes essential in studying how cells adapt and survive under non-ideal conditions. However, current strategies for network construction from gene expression data in a single environment are inadequate for our understanding of the complex regulatory mechanisms that underlie biological adaptation and function. Furthermore, the static feature of these strategies assumes that genes are expressed in a steady state, making it infeasible to describe the dynamic patterns of an evolving process (6).

The purpose of this article is to develop a computational model for constructing regulatory networks of dynamic gene expression in response to environmental changes. The difference of expression for the same gene between different environments is called expression plasticity (7,8). As a new concept, expression plasticity has emerged to be useful for studying the constraints for the evolution of gene expression in fluctuating environments (9–11). Our model for network construction capitalizes on gene expression plasticity, aimed at gleaning a better insight into the regulatory mechanisms for an organism’s adaptation to environmental changes. The model is founded on mutual information, a quantity that measures the mutual dependence of the two random variables, particularly in terms of positive, negative and non-linear correlations (12).

The approach for gene expression analysis with mutual information is not entirely new. Michaels et al. (13) attempted to cluster dynamic gene expression profiles according to information theory. Butte and Kohane (14) computed pair-wise mutual information for the expression of all genes using a method of discretizating variable domains. Steuer et al. (1) described the basic theory of mutual information and pioneered its usage to detect dependencies of different genes. Priness et al. (15) compared the properties of different methods for clustering gene expression profiles based on mutual information and classic Euclidean distance and Pearson correlation measures. A path consistency algorithm has been developed to reconstruct gene regulatory networks based on conditional mutual information (16). There are several applications of information-theoretic approaches for network reconstruction in a mammalian cellular context (17) and Escherichia coli transcriptional studies (18). Meyer et al. (19) packed mutual information into an R package minet for inferring transcriptional networks from microarray data. Rajapakse et al. (20,21) used information theory to reconstructing gene regulatory networks during the differentiation of a multipotential haematopoietic progenitor.

Despite these developments, the use of mutual information to reconstruct regulatory networks based on the environment-induced plasticity of time-series expression profiles has not been explored. The model presented in this article will take advantage of mutual information in measuring the non-linear dependency of different variables to unravel the dynamic changes of network architecture in a response to the environment. The model was used to analyse experimental gene expression data obtained from rabbit vein grafts exposed to two different wall shear conditions, where these different environments resulted in two distinct adaptation phenotypes (22,23). The model has been validated through a simulation study. By extending the model to reconstruct a web of mutual relationships among genes and the target phenotype, it provides a useful tool for inferring the causality of gene regulation.

MUTUAL INFORMATION

Shannon (24) provided a mathematical theory of measuring the amount of uncertainty and quantifying the theoretical maximum capacity of information by a communication system to eliminate such uncertainty. This theory, called information theory, has been widely applied in a variety of fields. In what follows, we implement Shannon’s information theory to reconstruct a regulatory network with gene expression plasticity data.

Expression plasticity entropy

In mutual information, we view gene expression profiles as a discrete random variable. Suppose that expression profiles of genome-wide transcriptional genes are measured at the same series of time points for the same organism that receives two different treatments. For a particular gene, the difference of its time-dependent expression curve between the two treatments describes the pattern of how this gene responds to the change in the treatment’s environment. Wang et al. (23) have developed a dynamic model for clustering genes into distinct groups based on the temporal patterns of their expression profiles in a relation to specific biological functions.

Our model being developed here is to construct a regulatory network of these genes in terms of their dynamic relationships formed in response to environmental change. Mutual information allows the non-linear dependence among different genes to be characterized. We define the difference of the expression value of the same gene at the same time point between the two environments as the expression plasticity of this gene (7,8). Let ΔX denote the time-dependent expression plasticity variable of a gene at time points {1,…, T}, expressed as ΔX = {Δx₁,…, Δx_T}.

Suppose that D is the value range of ΔX, and the subinterval set {D_j}, j = 1, 2, … , M, is a partition of D, satisfying that _j{D_j} = D, and D_j∩D_k = φ if j ≠ k. Note that M is the number of subsections partitioned from the domain D. For convenience, we denote the partition {D_j} simply as D. Define the delta function as follows,

where i = 1, 2, … , T, and j = 1, 2, … , M. Then the probability of D_j according to the expression plasticity variable ΔX is defined as,

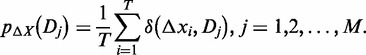Based on the probability defined above, in accordance with Shannon (24), the entropy of ΔX with a given partition D is defined as

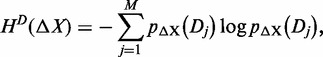(1)

where the bottom of the logarithmic function, usually 2 or e, could be any positive number without changing the properties of entropy. In this article, we will use 2, in accordance with the definition based on bits by Shannon. If p_ΔX (D_j) = 0 in Equation (1), the expression p_ΔX(D_j)logp_ΔX(D_j) is mathematically undefined. But it can be redefined to be its limit 0 when p_ΔX(D_j) goes to 0 from the right side of 0.

According to Faser and Swinney (25), when the measurement is expressed as ΔX, we can describe the expression plasticity entropy H^D(ΔX) as the degree of surprise, i.e. the elimination of uncertainty about ΔX. Information entropy has many properties, several of which are listed as follows:

1. The entropy H^D(ΔX) reaches its minimum 0 if the expression plasticity ΔX as a variable is determined, i.e. ΔX is no longer random. In this case, the probability of one element in {D₁, … , D_M} is 1 and that of each of the other elements is 0.

2. If {D₁, … , D_M} are equiprobable, then entropy H^D(ΔX) is maximized to the value logM. In this case, the entropy H^D(ΔX) is the most uncertain; i.e. H^D(ΔX) is the hardest to predict.

Conditional entropy of expression plasticity

Analogously to the delta function defined earlier in the text, we can also define joint-delta function as follows.

where i = 1, 2,…, T, and j, k = 1, 2,…, M. Then the joint probability and the conditional probability of {D_j, D_k} according to the expression plasticity variable ΔX and ΔY are defined as follows, respectively.

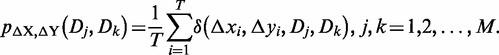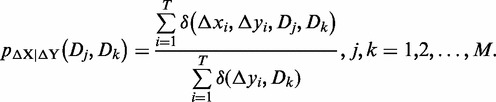According to information theory (24), we can calculate the conditional entropy of the expression plasticity of one gene ΔX, given the expression plasticity of another gene ΔY with time-series values {Δy₁,…,Δy_T}, which is defined as

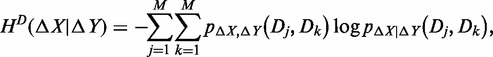(2)

where H_D(ΔX|ΔY) is the conditional entropy measuring the remaining uncertainty of ΔX if ΔY vis determined, which has the following property,

(3)

If ΔX and ΔY are statistically independent of each other, we have

(4)

Joint entropy of expression plasticity

The joint entropy of expression plasticity for the two genes, H^D(ΔX, ΔY), is defined, analogously to H_D(ΔX), as

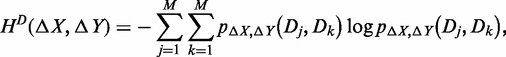(5)

where p_ΔX,ΔY(D_j, D_k) is defined based on the expression plasticity variables Δx and Δy for the two genes. The joint entropy is not greater than the sum of the entropies of two expression plasticity variables, i.e.

(6)

IfΔX and ΔY are statistically independent, we have

(7)

The relationship among the entropy, conditional entropy and joint entropy is expressed as

(8)

Equation (8) implies that the uncertainty of the joint system (ΔX, ΔY) is the uncertainty of ΔY, plus the conditional uncertainty of ΔX given ΔY.

Mutual information

The mutual information between two variables of expression plasticity ΔX and ΔY according to a domain partition D is defined as

(9)

From Equation (6), we have

(10)

Furthermore, from Equation (7), we obtain the conclusion that, if ΔX and ΔY are statistically independent, their mutual information is 0.

Mutual information is symmetrical, i.e.

(11)

In sum, mutual information shown by Equation (9) measures the dependency between the expression plasticity of two arbitrary genes, no matter the dependency is linear or non-linear.

DISCRETIZATION

To apply mutual information of expression plasticity, the random variable domain must first be partitioned into discrete bins. Butte and Kohane (14) used a straightforward method of evenly dividing a domain interval into a certain number of sub-intervals and then approximating the probabilities by the corresponding relative frequencies of occurrence. The mutual information by this approach depends much on the distribution type of the expression plasticity variables and the distribution parameters. Schreiber and Schmitz (26) proposed an adaptive partitioning method. Per this method, each resultant sub-interval for a random variable contains approximately equal number of occurrences. This method is more precise than the straightforward one in finding the mutual information. In Supplementary Text S1, we illustrate the procedure of bin characterization by these two methods.

The two methods described earlier in the text may not produce ideal results when the variable distribution types are the same but the distribution parameters are different. This is common, especially for gene expression data. To improve the calculation of mutual information by Schreiber and Schmitz’s (26) method, we partition the domains of the two random variables of expression plasticity under consideration according to a common standard, while simultaneously making the intervals adaptive to the respective data. We call this process ‘common adaptive partitioning’. Let Δx_t and Δy_t′ denote two random variables of expression plasticity measured at time t and t′, respectively, expressed as

(12)

whose means are denoted as (µ_X, µ_Y) and standard deviations denoted as (σ_X,σ_Y). Suppose is a sequence of real numbers, q₀ = –∞, q_τ+1 = ∞ and 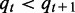for 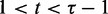. Except for the two infinities, the other τ parameters are to be determined later, which are denoted as

(13)

The domains of ΔX and ΔY are partitioned by a transformation of the sequence into the following intervals, expressed, respectively, as

(14)

Let 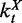, 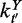and 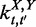denote the numbers of time-dependent expression plasticity values from Equation (12) located in the tth interval of X, in the t′th interval of Y and in the tth interval of X while simultaneously in the t′th interval of Y, respectively.

Our purpose is to select an optimal parameter set described in Equation (13) that makes the time-dependent expression plasticity profiles divided as evenly as possible for both ΔX and ΔY domains. This criterion is determined by a statistic

(15)

Several optimization techniques, such as simulated annealing and genetic algorithms, have been available to solve the optimization task described in Equation (15). Supplementary Text S2 gives a procedure for uniformly dividing time-dependent expression plasticity for the two genes. After the time-dependent expression plasticity profiles are divided per Equation (15), we calculate three kinds of probabilities as follows:

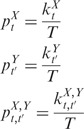(16)

where T is the total number of time points as defined in Equation (12). These probabilities are then used to calculate the mutual information between the expression plasticity variables ΔX and ΔY by Equations (1), (5) and (9). The partition determined by C in Equation (15) is called the common partition of expression plasticity variables ΔX and ΔY.

MUTUAL INFORMATION BETWEEN GROUPS AND ENVIRONMENTS

In gene expression analysis, clustering is a first step towards studying gene function by subdividing the genes into a smaller number of categories and then comparing dissimilarities among the categories (23,27). In each category or group, there are a set of functionally similar genes. From the perspective of mutual information, we want to know whether the grouping result is reasonable and how the groups are related with each other. To solve these problems, the mutual information between and within groups should first be defined.

For any two groups, G₁ and G₂, there are a number of genes with a similar dynamic expression plasticity trajectory. Let X and Y denote an arbitrary gene from groups G₁ and G₂, respectively. According to a common partition D for G₁ and G₂, the mutual information of expression plasticity ΔX and ΔY between the two groups according to a common partition D is defined as

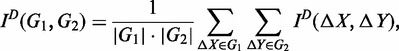(17)

where |G₁| and |G₂| are the numbers of genes in G₁ and G₂, respectively.

The calculation of the dependence of gene expression in response to different environments is based on the mutual information of environmentally induced expression plasticity. There is an alternative to calculating such dependence, which is based on the mutual information of gene expression between two environments. Let X denote an arbitrary gene from a group G. In this group, this across-environment mutual information according to a common partition D is defined as

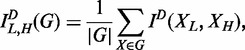(18)

where |G| is the number of genes in G; X_L and X_H are the expression profiles of a gene in environment L and H, respectively.

Equation (17) provides a procedure for calculating the mutual information of dynamic expression plasticity between different groups of genes. The reconstruction of regulatory networks from dynamic expression plasticity trajectories can shed light on the mechanistic pattern of how genes respond differently to environmental change according to their biological function. Equation (18) can be used to study the dependence of the expression of individual genes between different environments. By accumulating all genes within groups, different groups can be compared for the extent of such dependence.

RESULTS

Working example

In previous work by Wang et al. (23), a dynamic model was developed and used to identify unique groups of genes based on their differential response to the local environment. Specifically, vein bypass grafts, exposed to either high or low flow, were harvested at 2 h, 1 day, 7 days or 28 days after implantation (20). Microarray analysis of 14 958 genes was used to define and cluster the temporal response of the transcriptional profile induced by the local flow environment. Wang et al.’s model identified eight groups, symbolized by A (0.0116), B (0.0123), C (0.3354), D (0.3831), E (0.1134), F (0.0359), G (0.0100) and H (0.0083), where the numbers in parentheses are the proportions of genes belonging to a particular group. These groups display different patterns of environment-induced changes in gene expression trajectories. Our mutual information approach was applied to reconstruct a regulatory network that encompassed the dynamics of gene expression. Our analysis was based on three scenarios: (i) reconstructing an overall network by jointly using time-series gene expression data from the two flow environments; (ii) reconstructing a network by using the expression plasticity between high and low flows; and (iii) reconstructing two networks by using time-series gene expression data separately for two flows.

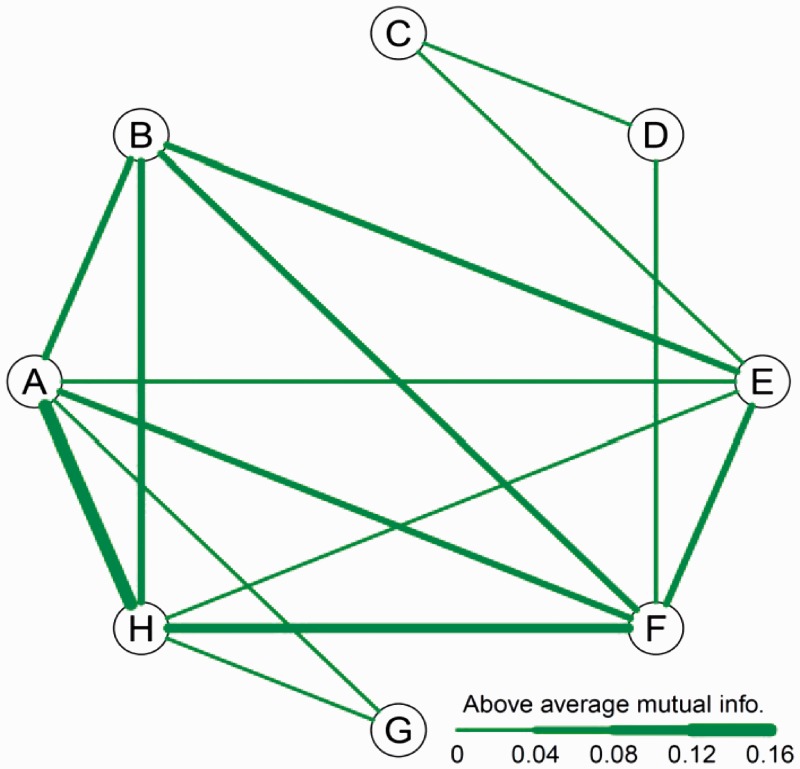
According to scenario (i), a sparse network of gene expression was obtained (Figure 1), in which a few pairs of gene groups have regulatory connections. Of all pair-wise relationships, group A shares the highest level of mutual information with group H, followed by the level of mutual information between groups H and F, groups B and E, groups A and F, groups B and F and so forth. Several pairs of groups share very low mutual information. It appears that groups C, D and G are substantially dissimilar to the rest of the groups, with each of these groups only weakly connected with two other clusters.

Figure 1.

An overall regulatory network of eight groups of rabbit genes constructed by jointly using expression data from high and low flows.

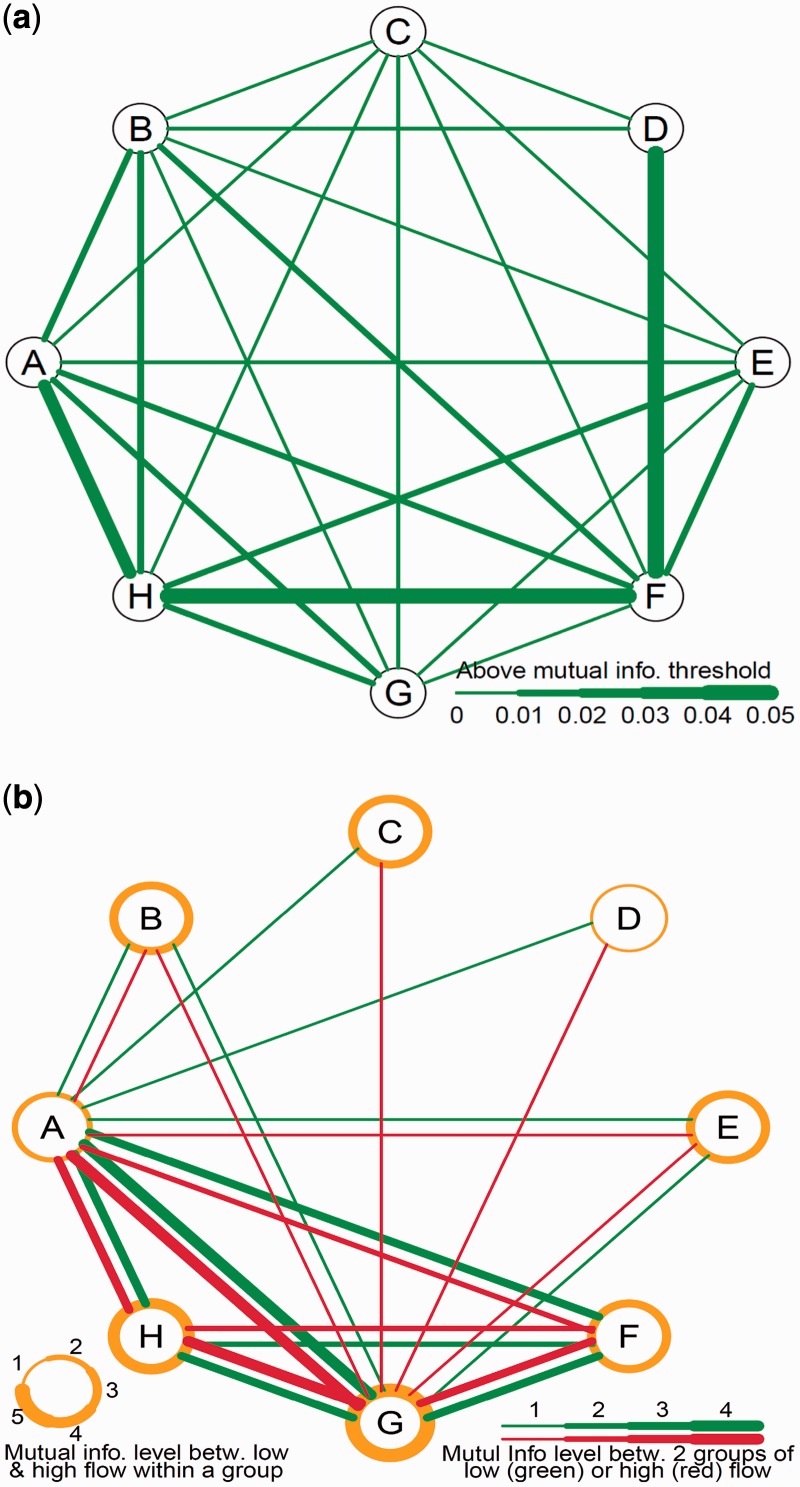
Scenario (ii) emphasizes the similarities of gene groups in terms of their pattern of differential expression over two different flows. Figure 2a provides a quantitative description of the level of regulatory connections among eight gene groups identified by Wang et al.’s (23) dynamic model. Although many connections are observed, the levels of mutual information are highly variable. To respond to environmental changes from one flow to next, groups A and H, groups H and F, and groups F and D would adjust their expression profiles in a highly similar way. As such, we conclude that groups A, H, F and D share substantial overlapping information, compared with other clusters in the network. The significant overlap and network autonomy among these four groups is further underscored by the configuration of group D, which, except for weak connections with groups C and B, only demonstrates the dominant connection to group F.

Figure 2.

Regulatory network of eight groups of rabbit genes expressed in high and low flows. (a) Between-group network reconstruction based on average value of expression between the two treatments. (b) Within- and between-group network reconstruction based on gene expression separately in low and high flows. The thickness of a circle represents the level of mutual information between two treatments within a group, whereas the thickness of lines represents the level of mutual information between two groups in low (green) and high flows (red). The lines representing mutual information below the average level are omitted.

To reconstruct the networks per scenario (iii), we calculated with the common partition D the mutual information of expression dynamics of genes X_j and Y_j from two groups G₁ and G₂, respectively, in a particular environment j using

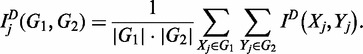This equation was used to calculate group-wise dependence separately for each different environment. It is interesting to see that the degree of dependence between groups is not identical for low and high flows (Figure 2b). For example, groups A is associated with groups C and D in the low flow, but this association does not occur in the high flow. Figure 2b provides a quantitative measure of the difference in the level of group-wise mutual information of gene expression between the two treatments. In addition, the amount of mutual information of the two treatments for the same group varies, depending on group type. Group G is most highly associated between low and high flows, followed by groups H, E and F. Within group D, the two flows are weakly associated. The results given in Figure 2 provide a comprehensive characterization of regulatory networks of genes related to vein graft remodeling, which are expressed differently in response to low and high flow environments.

Computer simulation

The basic idea of using mutual information to reconstruct networks for genes expressed in a single environment has been available in the literature. Some studies critically analysed the advantages of information-based approaches over those based on classic Euclidean distance and Pearson correlation measures (1,15). Thus, we will not focus on methodological comparisons in this article, rather than on the investigation of the advantage of our information-based approach in studying gene expression plasticity.

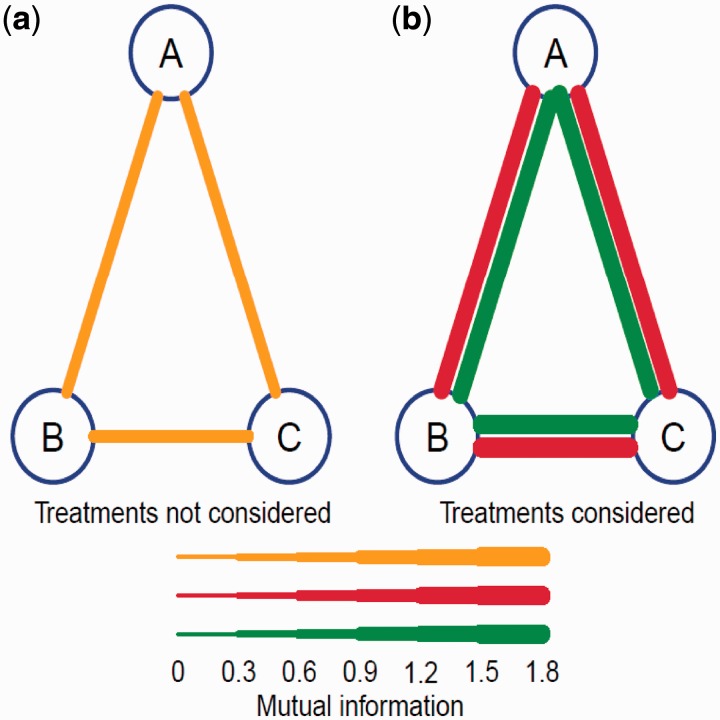
We simulated two data sets each of three equally sized groups of genes expressed in a time course. In the first data set, genes are measured in a single environment, whereas the second data set contains genes measured in two different treatments. Our model was used to analyse these two sets of data, having results to be in a good agreement with the actual case of each data set (Figure 3). However, it is impossible that a good result can be obtained for gene expression in two environments using a traditional single-environment approach.

Figure 3.

Regulatory network constructed from simulated data sets of genes expressed in a single environment (a) and two different environments (b).

DISCUSSION

Many biological processes including plant and animal development are coordinated by cell-to-cell communication regulated by genes (5). High-throughput measurement techniques have now led to the identification of tens of thousands of genes involved in sensing external cues. However, the dynamic interplay between genes is highly complex and cannot be understood by a simple approach (28). The reconstruction of gene regulatory networks can be a valuable tool for identifying the key mechanisms that shape the dynamics of cellular and transcriptional processes (6,29).

External stimuli or agents can alter the speed and direction of cellular processes through differential expression of the gene set. There exist specific mechanisms that shepherd the signal into the nucleus, where signal integration occurs by complex transcription factor networks. In this article, we describe a procedure for quantitative modelling of biological regulatory networks regulated by gene expression using mutual information. Beyond classic correlation parameters, mutual information can measure and evaluate the non-linear dependencies of random variables (12,14,24). We extended this information-based approach to assess and detect the non-linear dependencies of genes both between and within different gene groups of a particular function.

Our model has combined two complexities of network reconstruction. First, although much previous work focuses on static (steady-state) gene regulation, improved biotechnologies have allowed the measures of dynamic gene expression data during a biological process. The availability of dynamic data enables geneticists to better study the regulatory machineries underlying cellular processes (2) but, meanwhile, brings about a difficulty in analysing and interpreting expression data. Second, as gene expression is environment dependent (5), the reconstruction of regulatory networks by integrating environmental impact is crucial. By taking into account dynamic and environment-dependent complexities of gene expression, our model allows the reconstruction of more mechanistic and, therefore, more powerful regulatory networks.

The new model based on mutual information can effectively handle any dynamic relationships of genes, linear or non-linear, a characteristic better than classic Euclidean distance and Pearson correlation measures (15), and thereby should be able to find its broader application in computational biology. The model was used to analyse a time-series data set of gene expression measured for vein bypass grafts subjected to two distinct conditions, high and low blood flow, leading to the construction of genetic network that connects different groups of genes with different response trajectories to the local environment (23). The model can quantify the mutual dynamic relationships of different genes in terms of their differential expression to environmental change. The model was validated through computer simulation, showing its practical usefulness. In practice, when the number of genes is large, some inference procedure for selecting important groups, such as some permutation procedure, may be helpful and can be implemented.

There is much room for the model to be improved. First, our model assumes a normal distribution of gene expression, which is reasonable for microarray data. However, an increasing body of expression data is being collected by high throughput cDNA sequencing (RNA-Seq). The current model will need to be modified to accommodate the feature of Poisson distribution, which characterizes the data obtain from RNA-Seq (30). Second, the ultimate goal of network construction is to identify key genes or elements that can determine or alter the behaviour of an outcome, such as the critical stenosis that leads to vein bypass graft failure. Thus, the incorporation of outcome variables into the network and the estimation of direct or indirect effects of each gene on the outcome are essential for mechanistic characterization. Third, it is likely that the regulation of gene elements is under global genetic control (31). The integration of mutual information into genetic mapping will provide a powerful means of identifying expression quantitative trait loci that control regulatory networks. The characterization of expression quantitative trait loci will enable geneticists to gain a better understanding of the aetiology underlying complex traits or diseases.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online: Supplementary Texts 1 and 2.

FUNDING

Funding for open access charge: [NSF/IOS-0923975, UL1 TR000127] from the National Center for Advancing Translational Sciences (NCATS) and NIH [R01-HL095508].

Conflict of interest statement. None declared.