Clinical Decision Support and Closed-Loop Control for Cardiopulmonary Management and Intensive Care Unit Sedation Using Expert Systems

Abstract

Patients in the intensive care unit (ICU) who require mechanical ventilation due to acute respiratory failure also frequently require the administration of sedative agents. The need for sedation arises both from patient anxiety due to the loss of personal control and the unfamiliar and intrusive environment of the ICU, and also due to pain or other variants of noxious stimuli. While physicians select the agent(s) used for sedation and cardiovascular function, the actual administration of these agents is the responsibility of the nursing staff. If clinical decision support systems and closed-loop control systems could be developed for critical care monitoring and lifesaving interventions as well as the administration of sedation and cardiopulmonary management, the ICU nurse could be released from the intense monitoring of sedation, allowing her/him to focus on other critical tasks. One particularly attractive strategy is to utilize the knowledge and experience of skilled clinicians, capturing explicitly the rules expert clinicians use to decide on how to titrate drug doses depending on the level of sedation. In this paper, we extend the deterministic rule-based expert system for cardiopulmonary management and ICU sedation framework presented in [1] to a stochastic setting by using probability theory to quantify uncertainty and hence deal with more realistic clinical situations.

I. Introduction

Modern control technology is having a revolutionary impact in modern medicine through medical robotics (stereotactical brain surgery, implant fitting, and coronary procedures), electrophysiological systems (pacemakers and automatic implantable defibrillators), life support (ventilators and artificial hearts), and medical imaging (image-guided surgery and therapy). An additional area of medicine that can benefit enormously from systems and control oriented ideas is clinical pharmacology, in which mathematical modeling plays a prominent role [2]–[8]. This is particularly true when dealing with critically ill patients in the intensive care unit (ICU) or in the operating room. These patients often require administration of drugs to regulate key physiological variables, such as level of consciousness, heart rate, blood pressure, ventilatory drive, etc., within desired targets. The rate of administration of these drugs is critical, requiring constant monitoring and frequent adjustments. Open-loop control by clinical personnel can be tedious, imprecise, time-consuming, and sometimes of poor quality. Hence, the need for closed-loop control (active control) in medical drug delivery systems is significant, with the potential for improving the quality of medical care as well as curtailing the increasing cost of health care.

One of the main drawbacks in developing active control-based drug delivery systems is the lack of accurate mathematical models for characterizing the dynamic behavior of drugs on physiological variables. System nonlinearities, model parameter variations from patient to patient, as well as parameter variations within the same patient under different conditions make it very challenging to develop models and effective control law architectures for active drug delivery systems. Standard data-driven system identification techniques may not be applicable to complex biological system modeling involving in situ diagnostics. This challenge is even more pronounced in ICU sedation modeling, where sensors may not give reliable measures of sedation levels. As an example, there have been a number of investigations of processed electroencephalogram (EEG) monitoring (all using the bispectral index (BIS) monitor) of ICU patients and the results have been inconsistent [7], [9], [10].

Patients in the ICU who require mechanical ventilation due to acute respiratory failure also frequently require the administration of sedative agents. The need for sedation arises from patient anxiety due to the loss of personal control and the unfamiliar and intrusive environment of the ICU. In addition, pain or other variants of noxious stimuli frequently require administration of anxiolytic and analgesic drugs for patient comfort. In particular, the interface between the patient and the ventilator is typically an endotracheal tube passing through the oropharynx and into the trachea. Due to the powerful gag reflex, this tube is very noxious. Without sedation patients can become dangerously agitated, risking dislodgement of life support devices in the worst case and, in any case, resulting in stress that is ethically unacceptable and also physiologically unacceptable due to deleterious increases in heart rate, blood pressure, and work of breathing.

Sedation of mechanically ventilated patients in the ICU is an important and challenging problem with ethical, clinical, and financial implications. At the ethical level, we have a self-evident moral imperative to provide adequate anxiolysis and analgesia for patients in the ICU. From the clinical perspective, it is important that this be done without either overdosage or under-dosage as either may have undesirable clinical effects. At the financial level, sedation of patients in the ICU requires large investments of health care provider time, with a commensurate financial cost, while inefficient titration of sedation and analgesia may prolong ICU length of stay.

While physicians select the agent(s) used for sedation, the actual administration of these agents is the responsibility of the nursing staff. The ICU nurse has one of the most task-laden jobs in medicine and titration of the sedative drug dose to achieve the optimal levels of sedation can be a difficult and time consuming task. If clinical decision support systems and closed-loop control systems could be developed for critical care monitoring and the administration of sedation, the ICU nurse could be released from the intense monitoring of sedation, allowing her/him to focus on other critical tasks.

In clinical practice the dose of sedative agent is varied, or titrated, to achieve the desired level of sedation. The level of sedation is currently based on clinical scoring systems. One example is the Motor Activity Assessment Score (MAAS) [11] in which patients are given an integer score of 0–6 as follows: 0) unresponsive; 1) responsive only to noxious stimuli; 2) responsive to touch or name; 3) calm and cooperative; 4) restless and cooperative; 5) agitated; and 6) dangerously agitated.

To implement closed-loop control in an acute environment, control of cardiovascular function also needs to be addressed along with sedation since hemodynamic management and control of consciousness are interrelated. For example, a major side effect of cardiac surgery is that patients can become hypertensive [12], requiring treatment to prevent cardiac dysfunction, pulmonary edema, myocardial ischemia, stroke, and bleeding from fragile sutures. Although drugs are available for treating postoperative hypertension, titration of these drugs to regulate blood pressure is often difficult. Underdosing leaves the patient hypertensive, whereas overdosing can reduce the blood pressure to levels associated with shock.

Although blood pressure control is important, cardiovascular function involves several other important variables, all of which are interrelated [12]. The ICU clinician must ensure not only that blood pressure is within appropriate limits but also that cardiac output (i.e., the amount of blood pumped by the heart per minute) is acceptable and that the heart rate is within reasonable limits. Closed-loop control of blood pressure has been investigated in clinical studies [13]. However, the fact that this framework has not been widely adopted by clinicians is not surprising when one considers the complex interrelationships among hemodynamic variables [6].

Since cardiovascular and central nervous system functions are critical in the acute care environment, technologies have evolved for their measurements. The challenge for extending feedback control technology to the problem of sedation of critically ill patients, however, is finding the appropriate performance variable for control. Hence, the first step in the development of closed-loop control of sedation is the discovery of an objective, continuously-measurable parameter that correlates with clinician assessment of the level of sedation. Once such a parameter is discovered and validated, it then becomes necessary to use the measure of sedation for the titration of drug dose. One particularly attractive strategy is to utilize the knowledge and experience of skilled clinicians, capturing explicitly the rules expert clinicians use to decide on how to titrate drug doses depending on the level of sedation [1]. In this paper, we extend the rule-based expert system approach for cardiopulmonary management and ICU sedation presented in [1] to a stochastic setting by using probability theory to quantify system uncertainty and hence deal with more realistic clinical situations.

II. Closed-Loop Sedation Control Architecture

In this section, we present a closed-loop feedback expert system architecture for ICU sedation control. The closed-loop system is composed of the controller, the plant (patient), and the plant output measurement block (i.e., sedation assessment block). Within our sedation control framework, the plant (patient) is a dynamical system with unknown dynamics, where the input is the sedative drug dose and the output is the patient behavior. Patient behavior refers to patient's level of sedation and analgesia, manifested through facial expression, gross motor movement, pain, agitation, blood pressure, and heart rate. The goal of the sedation assessment feedback block is to monitor the patient's behavior, and objectively assess the sedation level based on one of the clinical scoring systems (e.g., MAAS). The input to the controller is the desired level of sedation, and the objective assessment of sedation provided by the sedation assessment block. The closed-loop system is shown in Fig. 1. The current clinical practice in the ICU involves human expert assessment of patient's level of sedation (corresponding to the sedation assessment block), and titration of the correct dose of sedatives (corresponding to the controller).

Fig. 1.

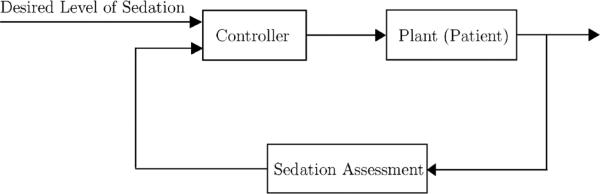
Closed-loop sedation control architecture.

Closed-loop control of ICU sedation is virtually nonexistent in the literature. However, control algorithms have been developed, simulated, and implemented for the related problem of closed-loop control of general anesthesia. The first of these have focused on the control of inhalation anesthesia and several adaptive control algorithms have been proposed; see [14]–[21] and the references therein. These algorithms have been shown to provide superior control of general inhalation anesthesia in simulations and animal studies. However, they are not directly relevant to the specific problem of ICU sedation since the controlled variable is the end-tidal anesthetic concentration. It is not possible with current technology to rapidly measure the plasma concentration of the intravenously administered drugs commonly used for ICU sedation. Thus, drug concentration is not a viable control variable. Furthermore, drug concentration, even if it could be measured rapidly, is not the best control variable. We are far more interested in drug effect than concentration.

One approach to closed-loop control of sedation is to design a system that processes the information currently used by the medical staff and mimics the human process of decision making for ICU sedation. Such a system can be equipped with various sensors, including the bispectral index (a derivative of the EEG signal) monitor [22], [23], actigraph (accelerometer for measuring hand and leg movement) [24], [25], and digital imaging (for measuring facial expression and gross motor movement) [7], [26], [27]. In a recent study, machine learning methods have been used to assess the level of pain in patients using facial expressions and analyze the correlation between computer and human expert pain intensity assessments [28], [29]. With measurements provided by different viable sensors, an expert system can be designed which mimics expert human actions and follows a similar decision making process.

Finally, it is important to note that temporal variability in the pharmacological response of individual patients and limitations in the reliable and reproducible effect of the medications used pose a significant challenge for the problem of ICU sedation control. In point of fact, this is exactly why “fixed” sedation dosing schemes do not work, and ongoing assessment of the depth of sedation and, then, titration to desired effect is necessary. We postulate that clinical outcomes will be improved if a systematic probabilistic expert system framework for sedation management is developed.

III. Instrumentation for Clinical Pharmacology

The sensors used in the ICU to monitor patient status include those that measure hemodynamic status, respiratory status, renal function, and central nervous function. Hemodynamic status is most typically assessed by continuous monitoring of heart rate and electrocardiograph (ECG). The ECG measures the electrical potential difference between skin electrodes placed at various sites on the torso and limbs, and can be analyzed to provide continuous heart rate measurement as well as identify signs of cardiac dysfunction. Hemodynamic function is also assessed using blood pressure measurements. While this may be done using noninvasive methods, it is most typically done by placing a small plastic catheter directly into an artery (most often the radial artery as it passes through the underside of the wrist) and then using a pressure transducer to convert the pulse pressure wave into an electrical signal. In a similar fashion, catheters are also often placed into large central veins (such as the internal jugular vein) so that their tips are situated close to the entry of the main veins (superior vena cava or inferior vena cava) returning blood to the heart. Pressure waves in these veins are then transduced into electrical signals to provide the central venous pressure. This gives an indirect measure of the volume of blood in the heart which is a major determinant of cardiac output, the volume of blood pumped by the heart per minute.

In some situations in which there is more profound cardiac dysfunction, a pulmonary artery catheter is placed. This is a catheter that runs through the heart into the pulmonary artery (i.e., the artery going from the heart to the lungs) and can measure pressures in the pulmonary artery (another indirect measure of volume in the heart) as well as directly measure cardiac output. Finally, it is important to monitor the adequacy of blood flow to the various tissues of the body. One common technique is to measure the amount of oxygen in venous blood. If the delivery of oxygen to tissue decreases, then there will be a greater relative extraction of oxygen from the delivered blood by the tissue, and hence, the venous blood returning to the heart will have less oxygen in it. This is most typically measured as the percentage of hemoglobin molecules (the primary carrier of oxygen in the blood) that are bound to oxygen (referred to as the venous saturation).

The purpose of respiration is to eliminate carbon dioxide from and deliver oxygen to the blood. Hence, the most important monitors of respiratory function are measures of carbon dioxide and oxygen in the blood. With the most commonly used sensor technologies these are not directly measurable; however, it is possible to continuously measure hemoglobin oxygen saturation, the percentage of hemoglobin in arterial blood that is bound to oxygen, using absorbance spectroscopy and light emitting diode technology. In addition, many ICUs use continuous analysis of gas exhaled from the lungs to measure end-tidal carbon dioxide concentration, an indirect and approximate measure of blood carbon dioxide concentrations. Furthermore, modern mechanical ventilators are equipped to measure the pressure used to expand the lungs when the patient is undergoing mechanical ventilation, as well as respiratory rate.

Assessment of renal function is not as sophisticated as either hemodynamic or respiratory monitoring. Currently renal function is most typically assessed by the continuous measurement of urine output. Sensors for assessment of central nervous system function are currently in their infancy, at least as far as routine clinical use is concerned.

IV. Probabilistic Expert System for Cardiopulmonary Management and ICU Sedation Control

In this section, we introduce a probabilistic expert system for cardiopulmonary management and ICU sedation control. A knowledge-based system, and, in particular, an expert system, is a computer program that is capable of making deductions based on the information provided by the user and the information stored in its knowledge base. In other words, a knowledge-based system is a system which applies a “rules of thumb” approach to a symbolic representation of knowledge [30]. The main characteristic that distinguishes a knowledge-based system from a conventional computer program is its structure [31]. Expert systems are a subclass of knowledge-based systems, where their objective is to emulate the human expert behavior [31], [32].

Expert systems in general deal with two different types of problems: deterministic versus stochastic. As a result, expert systems belong to one of the two general classes of: 1) deterministic expert systems and 2) stochastic expert systems. Deterministic expert systems are also referred to as rule-based expert systems due to the fact that in such systems the deduction process is based on a series of rules [32]. A more challenging set of problems is that involving uncertainty in knowledge and in the problem variables. Stochastic expert systems specifically deal with such problems and different frameworks exist to address uncertainty including certainty factors [33], fuzzy logic [34], theory of evidence [35], and, more recently, probability theory [32]. In the probabilistic approach, a joint probability distribution function over the set of variables is defined and the inference is based on probability rules. Such expert systems are referred to as probabilistic expert systems.

In [1], a rule-based expert system is introduced for cardiopulmonary management and ICU sedation. One of the limitations of the rule-based expert system proposed in [1] is its inability to deal with uncertainty. More specifically, it assumes perfect accuracy in the measurement of present and previous MAAS scores, blood pressure, and heart rate. While current technology allows for high accuracy measurements of blood pressure and heart rate, the MAAS score, which quantifies the level of sedation and agitation of the patient, is subjective and can result in inconsistencies and variability in sedation administration. Moreover, in a rule-based expert system there is no uncertainty associated with the rules. A more general approach would allow for rules with multiple conclusions, where a different level of uncertainty is associated with each conclusion. In this section, we use probability theory to quantify uncertainty to extend the rule-based expert system given in [1] to deal with more realistic situations.

In the Bayesian interpretation of probability, as opposed to the classical interpretation, the probability of an event is an indication of the uncertainty associated with the event rather than its frequency [36]. In the probabilistic approach to expert systems, the system variables are regarded as random variables and, in contrast to rule-based expert systems, probabilistic expert systems do not possess “if-then” rules but rather the relationship between the variables is defined using a joint probability distribution [32]. If the joint probability distribution of a probabilistic model is known, probabilities associated with different situations can be computed using marginalization and probability conditioning [37].

A drawback of the probabilistic approach to expert systems is computational complexity. The computational complexity increases with the increase in the number of random variables and the number of possible values they can take. This increase is exponential in the number of random variables. Bayesian networks [38] (also known as belief networks) is a graphical framework in machine learning which exploits the conditional independence between variables to reduce the computational complexity of the probabilistic model.

Before stating the main results of this section, we need the following definitions.

Definition 4.1 [39], [40]: A directed graph $\mathcal{G}$ is a pair $(\mathcal{V},\mathcal{E})$, where $\mathcal{V}=\{v_1,v_2,\dots ,v_N\}$ is the set of vertices and $\mathcal{E}=\{e_1,e_2,\dots ,e_M\}\subseteq \mathcal{V}\times \mathcal{V}$ is the set of edges. Every edge $e_l\in \mathcal{E},l\in \{1,\dots ,M\}$, corresponds to an ordered pair of vertices $(v_i,v_j)\in \mathcal{V}\times \mathcal{V}$, where v_i and v_j are the initial and terminal vertices of the edge e_l. In this case, e_l is incident into v_j and incident out of v_i; v_i is the parent of v_j and v_j is the child of v_i. Moreover, ${\Pi }_w\triangleq \{v\in \mathcal{V}:(v,w)\in \mathcal{E}\}$ is the set of all parents of $w\in \mathcal{V}$. A directed path from v_i1 to v_ik is a set of distinct vertices {v_i1, v_i2,..., v_ik} such that $(v_{i_j},v_{i_{j+1}})\in \mathcal{E}$, j = 1,..., k – 1. A directed path is closed if v_i1 = v_ik. A cycle is a nontrivial closed path where all the vertices (except for the first and last) are distinct. A directed acyclic graph is a directed graph containing no cycles.

For the next definition, p(·) and p(·|·) denote the probability density function and the conditional probability density function operators, respectively.

Definition 4.2 [38]: Let $\mathcal{V}=\{X_1,X_2,\dots ,X_n\}$, where X_i, i = 1,..., n, is a random variable and takes on values from a set ${\mathcal{X}}_i\subset \mathbb{R},i=1,\dots ,n$. A Bayesian network $\mathcal{B}$ is an ordered pair $(\mathcal{G},ϴ)$, where $\mathcal{G}=(\mathcal{V},\mathcal{E})$ is a directed acyclic graph, $\mathcal{E}\subseteq \mathcal{V}\times \mathcal{V}$ is the set of edges, and Θ is the set characterizing the probabilistic relationship between the vertices (random variables) and is defined by

$$ϴ\triangleq \{p(x_i\mid X_{i_1}=x_{i_1},\dots ,X_{i_M}=x_{i_M}):x_i\in {\mathcal{X}}_i,i=1,\dots ,n,i_1,\dots ,i_M\in {\mathcal{I}}_{X_i}\}$$ (1)

where ${\mathcal{I}}_{X_i}\triangleq \{j:X_j\in {\Pi }_{X_i}\}$ is the parent index set of X_i, M = card(II_Xi, and card (·) is the cardinality operator.

Note that a Bayesian network $\mathcal{B}=(\mathcal{G},ϴ)$ defines a unique joint probability distribution over $\mathcal{V}$ given by

$$p(x_1,x_2,\dots ,x_n)=\prod _{i=1}^{n}p(x_i\mid x_{i_1},\dots ,x_{i_M})$$ (2)

where $i_1,\dots ,i_M\in {\mathcal{I}}_{X_i}$, and where, for simplicity of exposition, we denote the conditional probability density function p(x_i | X_i1 = x_i1,..., X_iM = x_iM) by p(x_i | x_i1,..., x_im). Moreover, a Bayesian network represents the causal relationships between different random variables. More specifically, if X_j ∈ II_Xi, i, j ∈ {1,..., n}, then X_j directly influences (causes) X_i. This interpretation of an edge between two vertices is crucial in the construction of the Bayesian network. Each random variable is either observed (i.e., its value is known), or hidden (i.e., its value is unknown). In the graphical representation of a Bayesian network, the vertices corresponding to the observed random variables are shaded. Given a Bayesian network and the set of observed random variables, the inference involves finding the posterior probability distribution of any set of random variables given the observed random variables by marginalizing the joint probability distribution. An advantage of Bayesian networks is that they reduce the computational complexity of the inference stage. For a more comprehensive discussion on Bayesian networks, see [36]–[38].

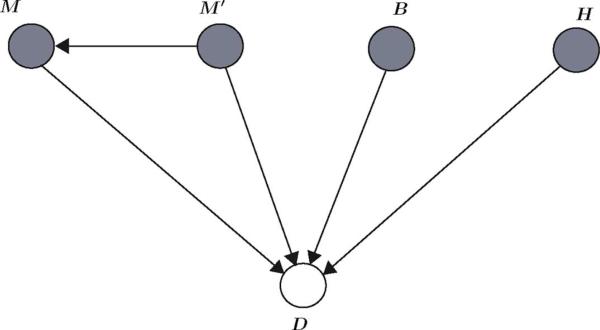
In this section, we use a Bayesian network framework to design a probabilistic expert system for cardiopulmonary management and ICU sedation control. We first start by constructing a Bayesian network for ICU sedation control. Next, we extend the Bayesian network to control patient hemodynamics. Let $\mathcal{B}=(\mathcal{G},ϴ)$ represent the Bayesian network and let the patient's current MAAS score, previous MAAS score, blood pressure, heart rate, and required drug dose for sedation be given by the random variables M, M’, B, H, and D, respectively, where range(M) = range(M’) = {0, 1,..., 6}, range(D) = {1, 2,..., 12}, $\text{range}\left(B\right)=\text{range}\left(H\right)={\mathbb{R}}_{+}$, where ${\mathbb{R}}_{+}$ denotes the set of positive scalars, and, for a given function $f:\mathcal{X}\to \mathcal{Y}$, $\text{range}\left(f\right)\triangleq \mathcal{Y}$. Note that there are 12 distinct actions (primary action) given in the first part of the conclusion of each rule in Table I in [1], and hence, we have assigned a unique number to each distinct action. The graph $\mathcal{G}$ for this Bayesian network is given in Fig. 2. The current and previous MAAS scores, blood pressure, and heart rate, which constitute the inputs to the expert system and directly influence the required drug dose, are observed and their corresponding vertices are shaded in Fig. 2.

TABLE I.

Comparison of the Human-Assessed Patient Agitation With the Predicted Agitation State Given by the Alarm Algorithm

	Patient Not Agitated	Patient Agitated
Alarm On	48	206
Alarm Off	2628	125

Fig. 2.

Graph of a Bayesian network capturing the relationships between the current MAAS score (M), previous MAAS score (M’), blood pressure (B), heart rate (H), and required drug dose (D).

A potential problem associated with the Bayesian network given in Fig. 2 is its inability to capture the uncertainty associated with the measurement of the MAAS scores. In particular, in order to perform a meaningful inference, the exact values of the current and previous MAAS scores should be known (observed). However, as discussed earlier, the assessment process is highly subjective, and the assessed scores can involve a high degree of uncertainty. A closer examination of the current and previous MAAS scores reveals that these random variables are essentially hidden variables, that is, they are “driven” by other factors. The MAAS score reflects the patient's agitation and sedation level, which can be observed through facial expressions, gross motor movement, guarding (i.e., a response in which the patient withdraws from a potentially noxious stimulus), heart rate and blood pressure stability, noncardiac sympathetic stability, and nonverbal pain scale. These observed factors can be regarded as random variables taking on values from appropriate sets. For example, machine learning techniques can be used to classify photographs based on the patient's facial expressions into pain and non-pain classes, which in turn can be used to assess pain intensity on a scale from 0 to 100 [28], [29]. Hence, a more complete model for the probabilistic expert system should include these observed random variables as well.

Let the random variables U₁,..., U₆ represent the current objective assessment of the facial expression, gross motor movement, guarding, heart rate and blood pressure stability, noncardiac sympathetic stability, and nonverbal pain scale, respectively, and let $U_1^{\prime },\dots ,U_6^{\prime }$ represent the previous objective assessment of these variables. Moreover, let $\text{range}\left(U_1\right)=\text{range}\left(U_1^{\prime }\right)=\{0,1,2\}$, where 0, 1, and 2 denote, respectively, a relaxed face, grimacing and moaning face, and grimacing and crying face; $\text{range}\left(U_2\right)=\text{range}\left(U_2^{\prime }\right)=\{0,1,2\}$, where 0, 1, and 2 denote, respectively, lying quietly, cautious movement, and restless withdrawal; $\text{range}\left(U_3\right)=\text{range}\left(U_3^{\prime }\right)=\{0,1,2\}$, where 0, 1, and 2 denote, respectively, lying quietly, splinting and tense, and rigid and stiff; $\text{range}\left(U_4\right)=\text{range}\left(U_4^{\prime }\right)=\{0,1,2\}$, where 0, 1, and 2 denote, respectively, stable, moderate change, and marked change; $\text{range}\left(U_5\right)=\text{range}\left(U_5^{\prime }\right)=\{0,1,2\}$, where 0, 1, and 2 denote, respectively, warm and dry skin, flushed and sweaty, and pale and sweaty; and $\text{range}\left(U_6\right)=\text{range}\left(U_6^{\prime }\right)=\{0,\dots ,10\}$, where 0 and 10 denote, respectively, no pain and extreme pain.

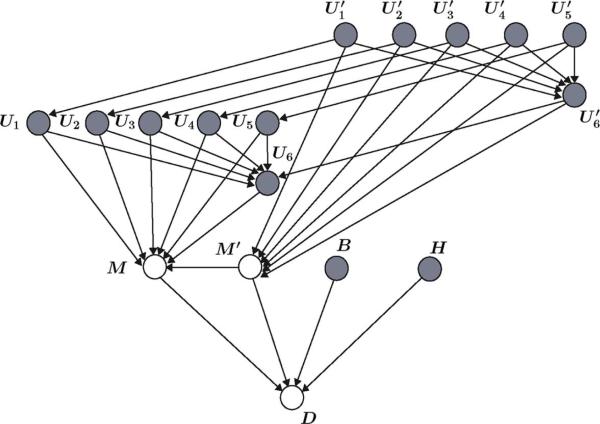
The graph of the Bayesian network which includes these new random variables is given in Fig. 3. Note that the current and previous MAAS scores are no longer observed, and hence, are not shaded. It is worth noting here that the graph represented in Fig. 3 corresponds to a Bayesian network of a probabilistic expert system and it is not aimed at modeling the interactions between the variables involved in ICU sedation. The Bayesian network capturing the actual interaction of these variables has a different dependency structure, and hence, its corresponding graph would be different from the graph given in Fig. 3.

Fig. 3.

More general graph of a Bayesian network capturing the relationship between the MAAS score and other observable factors; namely, current and previous objective assessments of facial expression $U_1,U_1^{\prime }$, gross motor movement $U_2,U_2^{\prime }$, guarding $U_3,U_3^{\prime }$, heart rate and blood pressure stability $U_4,U_4^{\prime }$, non-cardiac sympathetic stability $U_5,U_5^{\prime }$, and non-verbal pain scale $U_6,U_6^{\prime }$.

The Bayesian network corresponding to the graph given in Fig. 3 can be used to determine the proper drug dose for ICU sedation. Specifically, the joint probability distribution $p(u_1,\dots ,u_6,u_1^{\prime },\dots ,u_6^{\prime },m,m^{\prime },b,h,d)$, where $u_1,\dots ,u_5,u_1^{\prime },\dots ,u_5^{\prime }\in \{0,1,2\}$, $u_6,u_6^{\prime }\in \{0,\dots ,10\}$, $m,m^{\prime }\in \{0,1,\dots ,6\},b,h\in {\mathbb{R}}_{+}$, and d ∈ {1, 2,..., 12}, can be computed using the relationship given in (2); namely

$$p(u_1,\dots ,u_6,u_1^{\prime },\dots ,u_6^{\prime },m,m^{\prime },b,h,d)=\left(\prod _{i=1}^{5}p\left(u_i^{\prime }\right)\right)p\left(b\right)p\left(h\right)p(u_6^{\prime }\mid u_1^{\prime },\dots ,u_5^{\prime })\cdot \left(\prod _{i=1}^{5}p(u_i\mid u_i^{\prime })\right)p(u_6\mid u_1,\dots ,u_5,u_6^{\prime })\cdot p(m\mid u_1,\dots ,u_6,m^{\prime })p(m^{\prime }\mid u_1^{\prime },\dots ,u_6^{\prime })\cdot p(d\mid m,m^{\prime },b,h).$$ (3)

The probability distribution of the drug dose suggested by the Bayesian network is given by

$$\begin{array}{cc}\hfill p(d\mid u_1,\dots ,u_6,u_1^{\prime },\dots ,u_6^{\prime },b,h)& =\frac{p(u_1,\dots ,u_6,u_1^{\prime },\dots ,u_6^{\prime },b,h,d)}{p(u_1,\dots ,u_6,u_1^{\prime },\dots ,u_6^{\prime },b,h)}\hfill \\ \hfill & =\frac{{\sum }_{m=0}^6\sum _{m^{\prime }=0}^{6}p(u_1,\dots ,u_6,u_1^{\prime },\dots ,u_6^{\prime },m,m^{\prime },b,h,d)}{{\sum }_{m=0}^6\sum _{m^{\prime }=0}^6{\sum }_{d=1}^{12}p(u_1,\dots ,u_6,u_1^{\prime },\dots ,u_6^{\prime },m,m^{\prime },b,h,d)}\hfill \end{array}$$ (4)

where we use marginalization to eliminate m and m’, and m, m’, and d from the probability density functions in the numerator and denominator of (4), respectively. Note that p(d | m, m’, b, h), which captures the drug dosing pattern of the medical staff, can be determined through statistical techniques (e.g., maximum likelihood estimates [37]) and clinical data collection. In addition, the probability distributions p(m | u₁,..., u₆, m’) and $p(m^{\prime }\mid u_1^{\prime },\dots ,u_6^{\prime })$ capture the relationship between the facial expression, gross motor movement, guarding, heart rate and blood pressure stability, noncardiac sympathetic stability, and nonverbal pain scale and the MAAS score, which also requires clinical data collection. The prior probability distributions over $U_1^{\prime },\dots ,U_5^{\prime }$, B, and H denoted by $p\left(u_i^{\prime }\right),i=1,\dots ,5,p\left(b\right)$, and p(h), respectively, as well as the conditional probability distributions $p(u_i\mid u_i^{\prime }),i=1,\dots ,6,p(u_6^{\prime }\mid u_1^{\prime },\dots ,u_5^{\prime })$, and $p(u_6\mid u_1,\dots ,u_5,u_6^{\prime })$ can also be determined by statistical techniques.

Given the probability distribution of the drug dose suggested by the Bayesian network $p(d\mid u_1,\dots ,u_6,u_1^{\prime },\dots ,u_6^{\prime },b,h)$, different strategies for choosing the drug dose can be used. One such strategy involves selecting the drug dose corresponding to the mode of the distribution given by

$$D_{\text{suggested}}={\text{argmax}}_{d\in \{1,\dots ,12\}}p(d\mid u_1,\dots ,u_6,u_1^{\prime },\dots ,u_6^{\prime },b,h)$$ (5)

where D_suggested denotes the drug dose suggested by the Bayesian network.

Finally, note that the Bayesian network can also be used to compute the probability distribution of the drug dose (and hence, the suggested drug dose) when only partial observations are available. In particular, the posterior probability distribution on the drug dose can be computed when the observed variables are a subset of the observed variables in Fig. 3. Partial observation can result from sensor failure, where a particular state of the patient is unavailable at the time of a decision. For example, if only the blood pressure, heart rate, facial expression, and gross motor movement data is available, $p(d\mid u_1,u_2,u_1^{\prime },u_2^{\prime },b,h)$ gives the probability distribution for the drug dose based on these partial observations.

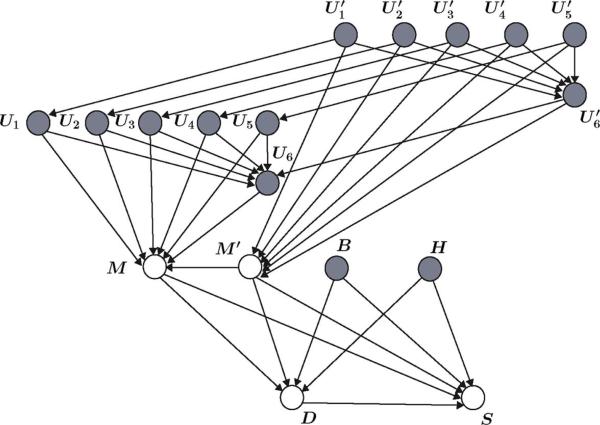
The same probabilistic methodology can be used to account for a secondary action (see Table I in [1]) in the Bayesian network. In this case, appropriate random variables have to be defined and the graph given in Fig. 3 should be modified accordingly. Alternatively, a hybrid probabilistic-deterministic expert system can be defined, where the primary actions given by the first part of the conclusions in Table I in [1] are described by a Bayesian network and the secondary action is given by Table II in [1]. Specifically, define the switching random variable S, where range(S) = {0, 1}. The random variable S acts as a switch, where S = 0 denotes that the hemodynamic control expert system (HDCES) (see Tables I and II of [1]) is off-line and S = 1 denotes that the HDCES is activated. The activation could be probability-based where the HDCES is activated if $P(S=1\mid u_1,\dots ,u_6,u_1^{\prime },\dots ,u_6^{\prime },b,h)>T$, where 0 < T < 1, P(· | ·) is the conditional probability operator, and T is a threshold value. Note that based on Table I in [1], the activation of the HDCES depends on the current and previous MAAS scores, blood pressure, heart rate, and the required drug dose for ICU sedation. The graph of the hybrid Bayesian network is shown in Fig. 4.

Fig. 4.

Gsraph of a hybrid probabilistic-deterministic Bayesian network where the random variable S controls the activation of the hemodynamic control expert system.

V. Probabilistic Alarm Algorithm for Critical Care Monitoring

A potentially key application of the probabilistic expert system developed in Section IV is its applicability to clinical decision support, critical care monitoring, and lifesaving interventions. A clinical decision support system is a computer program that can directly provide the medical staff with assessments and recommendations in the clinical decision making process [41]. A clinical decision support system can be coupled to a closed-loop control system to provide a hierarchical hybrid control architecture characterized by continuous-time control algorithms at the lower-level units and logical decision-making units at the higher-level of the hierarchy. In particular, a hybrid controller would involve the clinician evaluating the patient through a decision support system and an autonomous closed-loop controller adjusting the desired regimen to maintain sedation at a desired level. This controller architecture allows for the expert system to directly aid in clinical decision making as well as critical care monitoring and lifesaving interventions.

In this section, we use the framework presented in Section IV to design an alarm algorithm for agitation detection in ICU patients. An alarm system refers to an automatic warning system that constantly monitors a specific state of the patient and notifies the medical staff in case of an abnormality [42]. An agitation detection alarm system can reduce the medical staff's workload as well as safeguard against life-threatening situations in the ICU.

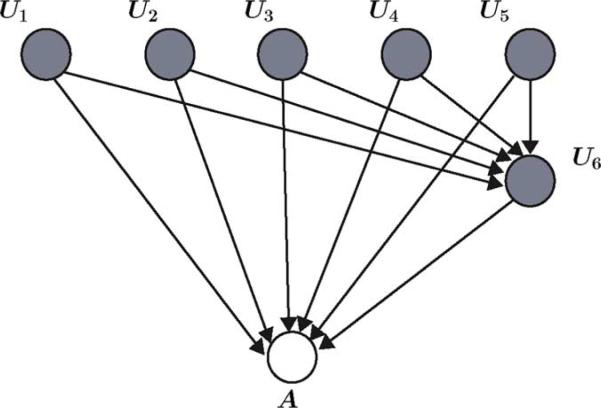
To design an alarm algorithm for agitation detection, let the patients's facial expression, gross motor movement, guarding, heart rate and blood pressure stability, noncardiac sympathetic stability, nonverbal pain scale, and patient agitation be given by the random variables U₁,..., U₆ and A, respectively, where range(U_i = {0, 1, 2}, i = 1,..., 5, range(U₆) = {0,..., 10}, and range(A) = {0, 1}. Here, A = 0 and A = 1 denote, respectively, absence of agitation corresponding to an MAAS score of 0–3 and presence of restlessness and agitation corresponding to an MAAS score of 4–6. The graph of the Bayesian network for the alarm algorithm is given by Fig. 5. Note that the random variables U₁,..., U₆ are considered as observed variables, and hence, are shaded.

Fig. 5.

Graph of a Bayesian network of an alarm algorithm for critical care monitoring.

The joint probability distribution for this network is given by

$$p(u_1,\dots ,u_6,a)=p\left(u_1\right)\cdots p\left(u_5\right)p(u_6\mid u_1,\dots ,u_5)\cdot p(a\mid u_1,\dots ,u_6)$$ (6)

where u_i ∈ {0, 1, 2}, i = 1,... 5, u₆ ∈ {0,..., 10}, and a ∈ {0, 1}. In addition, the posterior probability of the patient's agitated state is given by

$$\begin{array}{cc}\hfill p(a\mid u_1,\dots ,u_6)& =\frac{p(u_1,\dots ,u_6,a)}{p(u_1,\dots ,u_6)}\hfill \\ \hfill & =\frac{p(u_1,\dots ,u_6,a)}{{\sum }_{a=0}^{1}p(u_1,\dots ,u_6,a)}.\hfill \end{array}$$ (7)

The patient's agitation state is based on the observation of facial expression, gross motor movement, guarding, heart rate and blood pressure stability, noncardiac sympathetic stability, and nonverbal pain scale and is given by

$$A_{\text{predicted}}={\text{argmax}}_{a\in \{0,1\}}p(a\mid u_1,\dots ,u_6)$$ (8)

where we select the agitation state with the highest probability.

To elucidate the efficacy of our proposed approach we apply our framework to a retrospective study involving recorded sedation and agitation data for 366 patients admitted to the ICU in Northeast Georgia Medical Center, Gainesville, GA, over the period of May 6, 2009 to April 27, 2010. The patient's age ranged from 18 to 90 years. The length of stay in the ICU ranged from 1 to 93 days. In addition, the available data set included 15 052 measurements of facial expressions, gross motor movement, guarding, heart rate and blood pressure stability, noncardiac sympathetic stability, nonverbal pain scale, and agitation state. We used the hold-out method [36] for validation of the alarm algorithm, where 12 000 measurements of the random variables U₁,..., U₆ and A were used to train the Bayesian network. The algorithm was tested on the remaining 3052 measurements of U₁,..., U₆.

We used the MATLAB version R2008a and the Bayesian Network MATLAB Toolbox [43] to compute the posterior probability distributions of the patient's agitation state. In the training stage, we used the maximum likelihood estimates approach to estimate the probability distributions in (6) and used a uniform Dirichlet prior to avoid zero conditional probabilities for cases not present in the training data set [37]. In addition, in the testing stage, we used the junction-tree inference algorithm [36]. Table I gives the predicted agitation state A_predicted given by (8) as compared to the human-assessed patient agitation. Based on the results, when the algorithm predicted the presence of patient agitation, in 18.9% of the test cases the patient was not agitated (false positive rate of 18.9% with a 95% confidence interval of 14.4% to 24.4%). In addition, when no agitation was reported by the algorithm in 4.5% of the test cases the patient was experiencing agitation (false negative rate of 4.5% with a 95% confidence interval of 3.8% to 5.4%). The confidence interval is calculated based on the framework presented in [44]. In 45 cases out of a total of 3 052 cases the algorithm was undecided; that is, the posterior probability of the patient's agitation state was uniform.

VI. Conclusion

In this paper, we presented an approach for designing clinical decision support and closed-loop control systems for cardiopulmonary management and sedation control in an ICU using expert systems. It is important to note that expert systems are already in widespread use in other branches of medicine, more prominently in disease diagnosis, where the system inputs are the patient's details and symptoms, and the system outputs are probable diagnoses, recommended treatments or drugs which may be prescribed. Such systems are typically open-loop and may be regarded as rule-based search engines to help the clinician in his/her mapping of a given set of symptoms to a possible cause (disease).

Here, we are proposing to close the loop in a very specific sedation and cardiovascular function scenario using a set of heuristics in combination with Bayesian networks. A major challenge is the system identification aspect of the problem, that is, identifying a reasonable system model in case the plant is the patient. In contrast to more conventional identification techniques (e.g., sine sweeps), here the result must be more subjective but still very useful. Nevertheless, putting problems in drug administration in a closed-loop control framework has the strong potential for making the therapies more robust and thus much less amenable to human error.

The framework proposed here is just the first step in such a program. Future work will involve the development of objective assessments for ICU sedation using gross motor movement, facial expression, and responsiveness to stimuli. In particular, we will explore the relationship between gross motor movement, facial expression, and responsiveness to stimuli, and the MAAS score in the form of probability distributions which are best determined by clinical data collection. In addition, the drug dosage suggested by the expert system will be compared to the drug dose prescribed by various experienced clinicians.