Abstract
Microbes produce many molecules that are important for their growth and development, and the consumption of these secretions by nonproducers has recently become an important paradigm in microbial social evolution. Though the production of these public goods molecules has been studied intensely, little is known of how the benefits accrued and costs incurred depend on the quantity of public good molecules produced. We focus here on the relationship between the shape of the benefit curve and cellular density with a model assuming three types of benefit functions: diminishing, accelerating, and sigmoidal (accelerating then diminishing). We classify the latter two as being synergistic and argue that sigmoidal curves are common in microbial systems. Synergistic benefit curves interact with group sizes to give very different expected evolutionary dynamics. In particular, we show that whether or not and to what extent microbes evolve to produce public goods depends strongly on group size. We show that synergy can create an “evolutionary trap” which can stymie the establishment and maintenance of cooperation. By allowing density dependent regulation of production (quorum sensing), we show how this trap may be avoided. We discuss the implications of our results for experimental design.
Introduction
Cooperative behaviour is a ubiquitous feature of interactions at all levels of biology, and a large body of theory has been developed to explain the apparent paradox of its evolution and maintenance in the face of noncooperative social cheats (e.g. Smith and Szathmáry 1995; Keller 1999; West et al. 2006). Over the past decade, microbes have proven effective in testing this theoretical work. They reproduce very quickly and are relatively easy to control and genetically manipulate. They have been used to elucidate major parts of social evolution theory like the evolution of altruism and spite and to support related evolutionary hypotheses (Griffin et al. 2004; Gardner et al. 2004; West et al. 2006). Additionally, microorganisms are fascinating in their own right and understanding their sociality carries major health consequences (Brown et al. 2009).
In microbes, among the social traits most studied is production of secreted compounds, for example compounds that scavenge for iron when iron is limited (Griffin et al. 2004) or those that convert sucrose to glucose when glucose is limited (MacLean and Gudelj 2006; Gore et al. 2009). Investigation in the past decade has only scratched the surface of these public goods, and the list of known public goods products is quickly growing (West et al. 2006). Most of this work focuses on Hamilton’s rule (rb > c) as the condition that favors the evolution of social traits. There has been a primary focus on population structuring (shaping Hamilton’s r), though all three quantities are essential in social evolution (West et al. 2006).
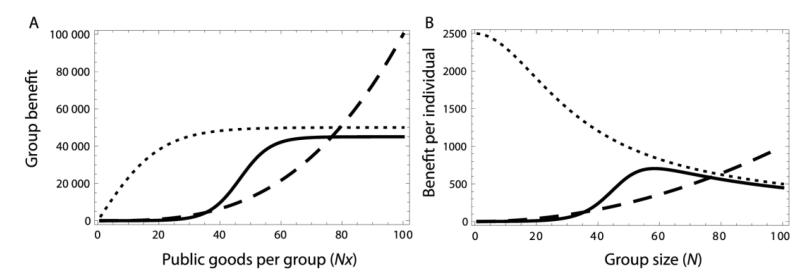
In this paper, we primarily focus on fitness effects (shaping Hamilton’s b and c) and specifically the group-beneficial traits of public goods production. Figure 1A shows three plausible benefit functions: one decelerating, one accelerating, and one sigmoidal (first accelerating then decelerating). We use “synergy” to refer to acceleration in benefit functions, which corresponds to the first part of the sigmoidal function and all of the accelerating function in figure 1A. This synergy allows per-capita fitness benefits to increase with group size as shown in figure 1B, sometimes termed “group augmentation” (Kokko et al. 2000). Synergy is abundant in biology, from ant pheromone trails to human architecture (Clutton-Brock 2002; Sumpter and Brännström 2008; Sumpter 2010). The mechanisms causing this synergy vary widely (Sumpter and Brännström 2008). Despite the abundance of synergy in other cooperative organisms, the phenomenon is not well-investigated in microbes. Though recent work has uncovered benefit nonlinearities in Myxococcus and an engineered E. coli system (Smith et al. 2010; Chuang et al. 2010), it is generally ruled out in mathematical models (West and Buckling 2003; Foster 2004; Ross-Gillespie et al. 2009), and the scope and impact of these nonlinearities has not been well investigated. Here we argue that although its sources and abundance are still not well understood, synergy is likely to be a key factor in microbe evolution.
fig 1.
Accelerating, decelerating, and sigmoidal benefit functions. A) Total benefit as a function of total public goods investment Nx, expressed as the product of the group size N and the cooperative investment per individual, x. The solid and dashed lines represent synergistic (accelerating) benefits as they have positive concavity for some intervals, whereas the dotted line always represents diminishing returns. B) Corresponding per-capita benefit B(Nx)/N as a function of group size, N, assuming that every individual cooperates at some fixed amount (here, x = 1, meaning full cooperation). The benefit functions used are B(x) = α(β + deκ–bx)−1 − α(β + deκ)−1 with α = 105, d = 1, β = 1, κ = 0, and b = 0.1 (decelerating benefits; dotted line), B(x) = bxa with b = 0.1 and α = 3 (accelerating benefits; dashed line), and α(β +deκ–bx)−1 − α(β + deκ)−1 where α = 90000, d = 1, β = 2, κ = 10, b = 0.2. (sigmoidal benefits; solid line).
Synergy occurs any time each additional public goods molecule produced gives a greater fitness benefit than the previous. Many biological molecules themselves can provide benefits in a sigmoidal fashion due to ‘positively cooperative reactions” (Hill 1910). Aside from basic molecular properties, sigmoidal benefits are often expected due to ecological interactions. For instance, the normal lifecycle of many invading parasites requires production of threshold quantities of toxins to function and/or to be able to overwhelm the immune system (Williams et al. 2000). Synergy may also arise from less apparent and more complex ecological interactions. For example, an adversarial molecule which, up to some point neutralizes produced public goods, could lead to synergy. For example, plants that produce “quorum quenching” molecules which neutralize quorum sensing molecules (whose production is, itself, cooperative (Diggle et al. 2007)). Synergy could even be caused by the consumption of others’ public goods, as in, for example, the siderophore pyoverdine secreted by Pseudomonas aeruginosa (Brown and Kümmerli 2010).
Most theoretical studies of co-operative microbial interactions typically preclude synergy (Brown and Johnstone 2001; Foster 2004; West and Buckling 2003; Ross-Gillespie et al. 2009). It has previously been concluded that high density is disfavorable for public goods cooperation because a producing cell enjoys a growth benefit proportional to the average production of its neighbors, allowing nonproducers more opportunities to exploit high-producing cells (Ross-Gillespie et al. 2009). As we shall see here, the opposite conclusion is possible when synergy exists. Synergy has been studied previously theoretically in other contexts where an individual is classified as either a cooperator or defector (Queller 1985; Archetti 2009a,b) and more recently in a continuous-trait model (Deng and Chu 2011); see Archetti 2009b for a review on nonlinear public goods games in biology. Here, we extend these studies to continuously variable traits to understand aspects of evolution not examined in previous frameworks. We show that synergy often permits an evolutionary repellor near non-production which can have important consequences and demonstrate the role quorum sensing may play in its avoidance.
If the fitness effects of public goods production depend on density, then this should provide evolutionary pressure for microbes to regulate their production accordingly. By releasing autoinducer molecules, a cell can assess how many other cells surround it, a proxy for cellular density, and can up-regulate or down-regulate various genes in response (Fuqua et al. 1996; Robson et al. 1997). This mechanism, known as quorum sensing, regulates the expression of many genes for the secretion of extracellular molecules. In this paper, we also investigate the co-evolution of quorum sensing and a synergistic trait.
Model
We adopt a standard setting for studying games with continuous cooperative investments (Doebeli et al. 2004). We consider an infinite population, in which each individual i has a strategy or trait value xi which represents the individual’s level of cooperative investment. For simplicity, we will assume that individual cooperative investments are constrained between 0 and 1, i.e. 0 ≤ xi ≤ 1. The demographic dynamics unfold in discrete generations. At each generation, groups of size N are randomly formed. Assuming that the players in one of these groups have the respective strategies x1,…,xN, the payoff for an individual i in the group, 1 ≤ i ≤ N, is given by:
| (1) |
Here, B(x1 + … + xN) is the collective benefit of the group’s cooperative investment (fig. 1A). The collective benefit is divided equally among the N individuals in the group to give the per-capita benefit (fig. 1B), and C(xi) is the cost of the investment. Both the benefit and cost functions are assumed strictly increasing.
The selection gradient
| (2) |
indicates the direction of gradual evolutionary change in a monomorphic population of individuals all having the same trait value x, where primes denote first derivatives. For details on how the selection gradient is derived from the demographic model and how it relates to gradual evolutionary change, see Geritz et al. (1997); Sumpter and Brännström (2008); Doebeli et al. (2004); Dieckmann and Law (1996). With small mutational steps, the evolutionary dynamics will proceed in the direction indicated by the selection gradient and will cease only at a boundary strategy or at an interior strategy x* at which the selection gradient vanishes, D(x*) = 0. Such strategies are said to be evolutionarily singular. If nearby monomorphic populations evolve towards the singular strategy, it is said to be convergence stable. A convergence stable singular strategy can either be evolutionarily stable (then called continuously stable), effectively an endpoint of evolution, or it can be an evolutionary branching point at which a monomorphic population may gradually diverge to become dimorphic (Geritz et al. 1997). Mathematically, the requirement that a singular strategy is convergence stable but not evolutionarily stable can be written:
| (3) |
where double primes denote second derivatives. We refer to Doebeli et al. (2004); Geritz et al. (1997) for details. In words, this condition implies that both the benefit function B and the cost function C need to be decelerating in the vicinity of the singular strategy x*.
Group size has been considered previously as the number of founders initiating a microbe colony (see Brännström and Dieckmann 2005; Brännström et al. 2010), but our analysis takes N to be the size of the group of interacting cells or neighboring bacteria within a public good molecule’s radius of diffusion, which will often be a proxy for cellular density. To consider impacts of genetic assortment, we suppose that when a focal individual joins a group at the beginning of a generation, some positive fraction of the other individuals in the group may be identical to it by descent. This fraction is a random variable ρ. We show in Online Appendix A1 that, with these assumptions, the selection gradient takes the form:
| (4) |
where brackets indicate the expectation. The condition for convergence stability is:
| (5) |
and the criterion for evolutionary stability is:
| (6) |
Again, both the benefit function B and the cost function C need to be decelerating in the vicinity of the singular strategy x* for evolutionary branching to occur. Interestingly, we see that the mean of ρ (which is simply others-only relatedness, see Online Appendix) is sufficient to define convergence stability, but both its mean and variance are required for evolutionary stability. Higher variance in ρ makes conditions for evolutionary branching more restrictive.
We also consider the effects of group size-dependent regulation (quorum sensing) on the maintenance of cooperation. Here an individual can alter its behavior, dependent on the size of its group. At sufficiently low group sizes, the public good is not produced, or produced in very little quantity, whereas at sufficiently high group sizes, production is simply the productive investment x. The payoff to individual i with trait values (x, s) in this model variant is simply:
| (7) |
where Q(si,N) = 1/(1 + eSi–N). Here si determines the group size threshold above which individual i produces public goods and below which does not (see Appendix for further details).
Results
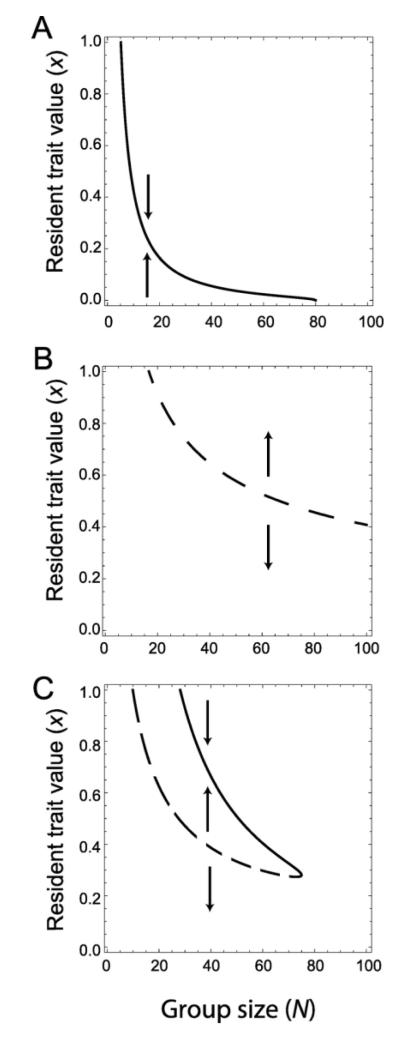
We begin by assuming that groups are formed entirely randomly among the whole population, so that there is no correlation among phenotypes of group members. Figure 2A shows the evolutionary dynamics under small mutational steps when the benefit is a decelerating function of the group’s total cooperative investment (dotted line in fig. 1; diminishing returns, see also Foster 2004). Here per-capita benefits decrease with group size. Assuming that the cost is proportional to the investment C(x) = cx, it follows that the selection gradient D(x) = B′(Nx)/N – c is strictly decreasing with x, so there is exactly one continuously stable strategy (both convergence stable and evolutionarily stable) which is either full defection, an intermediate level of cooperation, or full cooperation (fig. 2A). This CSS, once reached, is resistant to invasions by mutants with phenotypes sufficiently close on either side. This is very much the standard picture of evolutionary games involving costs and benefits to cooperation; the evolutionarily stable cooperative investment decreases with group size N (Ross-Gillespie et al. 2009).
fig 2.
Bifurcation plots illustrating the evolutionary dynamics with decelerating, accelerating, and sigmoidal benefit functions. The solid lines indicate the location of interior singular strategies for different group size N. Arrows indicate the direction of gradual evolution of a monomorphic population. A) Decelerating benefits. There is a unique evolutionarily stable strategy which decreases with group size. When group sizes are greater than approximately 80, cooperation is entirely disfavored. (B(x) = α(β + deκ–bx)−1) − α(β + deκ)−1 with α = 2000, d = 1, β = 1, κ = 0, and b = 0.8) B) Accelerating benefits. For small group sizes there is a unique evolutionarily stable strategy corresponding to full defection. As the group size increases, full cooperation also becomes an evolutionarily stable strategy. Any interior singular strategy is repelling and decreases with group size, but never reaches zero. (B(x) = bxa with b = 0.1 and α = 3) C) Sigmoidal benefits. Up to two interior singular strategies are possible, one repelling and the other attracting. (B(x) = α(β + deκ–bx)−1 − α(β + deκ)−1 where α = 10000, d = 1, β = 2, κ = 7, and b = 0.3). Each convergent stable attractor could potentially be an evolutionary branching point. The cost function used is C(x) = cx with c = 5.
Whereas figure 2A illustrates the implications for the most common assumptions on benefit functions, it is not necessarily the case that increasing total producers leads to decreasing per-capita benefits. The alternative scenario is where the per-capita benefit derived from cooperative interactions increases with group investment (fig. 2B). Here, for linear cost functions, the selection gradient D(x) is strictly increasing and there is either one or two convergence stable strategies, corresponding to no cooperative investment or full cooperative investment. Typically, for small groups, no investment is the only evolutionarily stable strategy, but at some critical group size full investment also becomes stable (fig. 2B).
In a biologically realistic setting, synergistic interactions cannot continue indefinitely and there is a critical level at which the per-capita benefit of additional cooperative investment begins to decrease. This leads to a sigmoidal form of the benefit function B. In this situation, the evolutionary dynamics can incorporate elements of both cases discussed above. This can be seen in figure 2C where we have two branches of singular strategies; the lower is repelling (since it comes from the synergistic lower part of the benefit function), and the upper branch is attracting (due to decelerating portion of the benefit function at higher cooperative investments). In this example, cooperation first becomes possible at intermediate sizes, and then suddenly shifts to no cooperation at high group sizes.
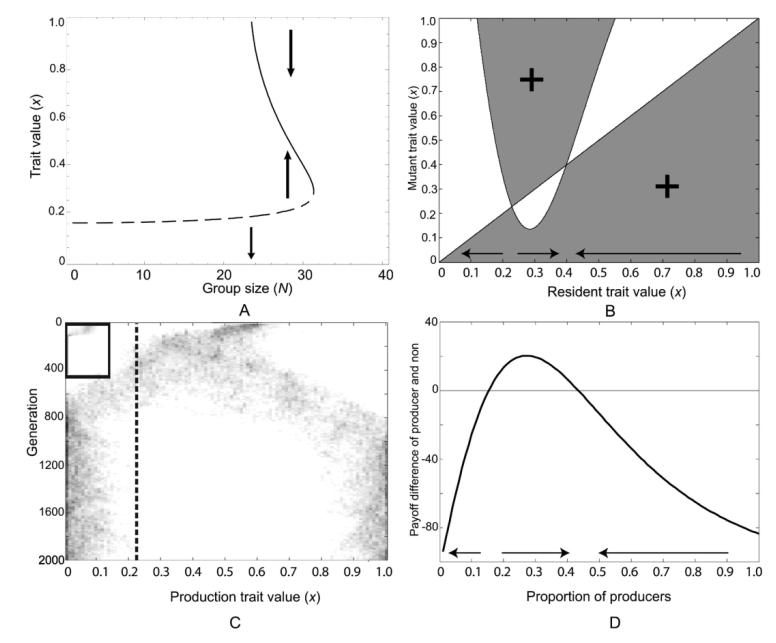
Thus far, we have assumed that costs are proportional to the amount invested, leading to a linear cost function. When costs are non-linear, the population can sometimes become dimorphic in the vicinity of a singular strategy. In this case, the two evolutionary branches diverge and may eventually end up on opposite sides of the convergence stable solution in a process is known as evolutionary branching (Geritz et al. 1997). In this case, the branches may end on opposite sides of the evolutionary repellor caused by the synergistic part of the benefit curve as well. Figure 3 A-C demonstrates (assuming no assortment) that not only is coexistence possible when the benefits are synergistic, but the coexisting community can emerge from an initially monomorphic community in small evolutionary steps. Figure 3B and 3C show the evolutionary dynamics with group size fixed (N = 30). If the population starts with a trait value below approximately x = 0.2, evolution proceeds toward zero investment. If, instead, the trait value is initially above this threshold, evolutionary branching occurs and a stable coexistence between full producers and nonproducers is eventually achieved.
fig 3.
Evolutionary branching and the emergence of two coexisting strategies of full defection and full cooperation in a setting with sigmoidal benefits and non-linear costs. A) Bifurcation plot illustrating the effects of group size on directional selection for the function used in the other diagrams in the figure. B) A pairwise invasibility plot (PIP) illustrating the monomorphic evolutionary dynamics. There are two singular strategies at approximately x = 0.2 and x = 0.4 of which only the latter is convergence stable. Monomorphic populations with trait values above the first singular strategy will evolve towards the second singular to the singular strategy where they undergo disruptive selection and subsequently evolutionary branching. C) Individual-based simulation demonstrating evolutionary branching at approximately x = 0.4, thus corroborating the predictions from the PIP. The inserted panel shows the evolutionary dynamics for populations which initially have trait values lower than the first singular strategy at approximately x = 0.2; here investment decreases to zero. D) Population dynamics of the resultant coexisting strategies of full defection (x = 0) and full cooperation (x = 1). If the fraction of cooperators is initially below approximately 18%, the cooperators will be eliminated altogether. Otherwise, the population dynamics will result in a stable coexistence with approximately 45% cooperators. The sigmoidal benefit function used is the same as in figure 1, B(x) = b(x3 + βx2)(x2 + α)−1, but with different parameters b = 200, β = 450, α = 180. The non-linear cost function used is C(x) = c1x – c2x2 with c1 = 170, c2 = 50. The assumed group size in B-D is N = 30.
Figure 3D, which depicts population dynamics between two strategies, shows that the coexistence is maintained by frequency-dependent population dynamics. If, however, a high enough frequency of nonproducers would for any reason accumulate in the population, the producers will be eliminated leaving only nonproducers. We have a wide range of outcomes for a single benefit and cost function: full investment by all; full investment by some proportion of the population and zero investment by all others; and zero investment by all – dependent only on initial conditions and group size. In this example, all singular strategies are evolutionarily unstable, but as equation 3 shows, group size can also determine whether a population evolves toward an intermediate evolutionarily stable investment level or whether a dimorphic population emerges.
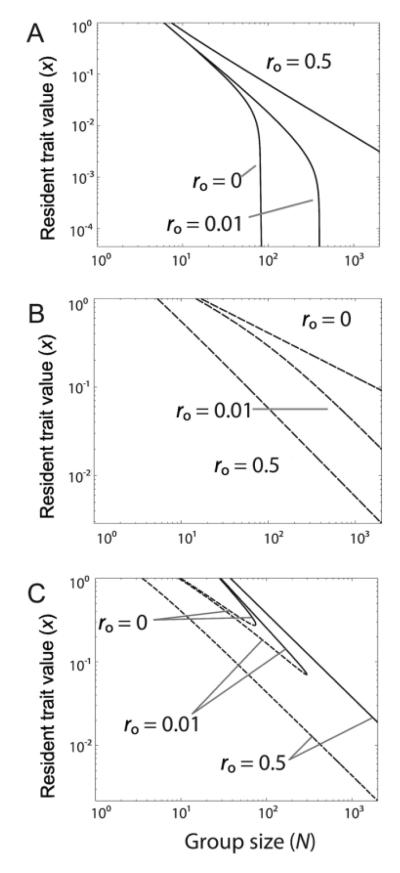
We have until now assumed random assortment among all individuals in the population (ρ = 0). This may be acceptable in situations where the individuals are interpreted as founders which may have dispersed from afar, but in many other biological contexts, the groups will not be well-mixed. As shown in figure 4, high assortment makes cooperation more likely to evolve; compared to plots in figure 2 in the bifurcation plots of singular strategies, the repelling branches (convergence unstable) are lowered and the attracting (convergence stable) branches are raised. This is because the benefits grow but there is no longer the need to split the spoils among many genotypes. This relates to previous work with discrete types demonstrating that assortment decreases the critical cost for a mixed equilibrium between cooperators and defectors Archetti 2009a,b. Assortment is especially important in large groups where direct benefits are not alone sufficient to maintain cooperation. Sufficiently high relatedness values may allow cooperation to be maintained at some positive level for arbitrarily high group sizes, even when the benefit function is diminishing or sigmoidal (in contrast to fig. 2). From equation 4, with linear costs, cooperation is stable at arbitrarily high group sizes when the maximum value of B′(x) exceeds c/rw (see Appendix). If cooperation is convergence stable at some group size with no assortment (ro = 0), then in a clonal population (ro = 1) a positive level of cooperation is also convergence stable at arbitrarily high group sizes. Equations 5 and 6 make clear that the conditions for evolutionary branching are very dependent on both the mean and variance of ρ. We give an example in the Online Appendix where changing Var(ρ) can alter evolutionary stability without affecting convergence stability, thus determining whether evolutionary branching occurs.
fig 4.
Effect of assortment (positive relatedness) on the evolutionary dynamics of decelerating, accelerating, and sigmoidal benefit functions. The different curves on each plot correspond to different degrees of others-only relatedness (which are equal to the values of 〈ρ〉): ro = 0, ro = 0.01, and ro = 0.5. Solid lines indicate attracting (convergence-stable) singular strategies, while dashed lines indicate singular strategies which are repelling (not convergence stable). Panels A, B, and C have use all the same benefit and cost functions as in figure 2.
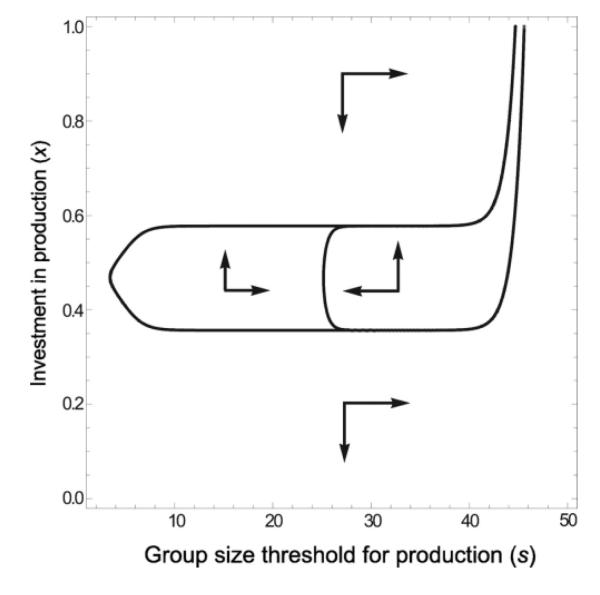
In figure 5, we show the joint evolution of the trait for public goods production and the quorum sensing threshold group size above which the trait is expressed (see equation 7). In this case, costs and benefits of expression correspond to those in figure 2C. At each generation, a group is formed of size 5 or size 45 with equal probability. When the public good is constitutively produced, the population always ends at nonproduction, then unstable even at large group sizes. In contrast when group size dependent regulation of the trait is allowed to evolve, the cooperation can be maintained. The threshold (s) can evolve such that the cooperative trait is not expressed at the low group size (5) but is expressed at other group sizes, when it is advantageous (see Online Appendix for an example). Figure 5 also reveals that when the investment value x is sufficiently low, the threshold s is expected to increase which can make investment less likely to subsequently increase.
fig 5.
Joint evolution of the public goods production trait x and the group-size threshold s, above which the production is expressed. Benefits and costs are as in figure 2C. At each generation, a group is formed of size 5 or size 45 with equal probability. For very low quorum sensing thresholds, production is not affected by changes in group size and evolution inevitably brings the production down to zero. However, for an intermediate range of the quorum sensing threshold s, public goods production can be stably maintained. This is true even if the threshold and production is allowed to co-evolve, provided that initial state is a population with an intermediate quorum sensing threshold and a sufficiently high production. For other initial conditions, co-evolution will bring the production down to zero and increase the threshold to arbitrarily large values.
Discussion
Our results underline several important caveats for experiments on microbes. In pairwise invasibility experiments, it is important to realize that just because a producer may be unable to invade cheats when at low frequencies, this does not necessarily mean it cannot be very stably maintained at higher frequencies. So even if cheats invade cooperators but not the reverse, coexistence at intermediate levels may still be possible. After the demonstration that a producer is exploited by a cheat one should also test how producers fare at different starting frequencies. It is possible above some starting frequencies, producers will achieve intermediate abundances, but below this threshold will be lost.
Our analysis also points to the potential complexities of varying density in microbe experiments. If laboratory results using well-mixed cultures do not accord with natural settings, differences in density in addition to relatedness should be explored. For instance, figures 3 and 4 show that density in addition to relatedness can be crucial to the qualitative evolutionary dynamics. In figure 4, in the simplest case with no assortment, group size and initial conditions determine whether all nonproducers, all cheats, or some combination of the two will be reached; as equation 3 shows, group size can also determine whether a uniform level of intermediate investment is the evolutionary endpoint or whether the population splits into a dimorphism. Microbe experiments are characterized by bacterial populations in high densities in nutrient-rich and enemy-free environments, which can be vastly different from many natural environments, and these differences must be carefully considered.
In this paper we have focused primarily on the shapes of benefit functions in social evolution, and a significant part of our consideration was the repellor that can arise from sigmoidal functions. When we considered nonlinear cost functions, it was only to understand their effect on evolutionary branching. However, diminishing cost functions in addition to synergy can possibly lead to evolutionary repellors (see Online Appendix A1). Additionally, evolutionary repellors exist in other, noncooperative contexts as well. For instance, dynamics qualitatively similar to the sigmoidal case have been demonstrated in epidemiological contexts, dependent on tradeoffs in parasite transmission strategies (Ferdy and Godelle 2005).
Whenever synergy exists, the benefit curve will most likely be sigmoidal, since benefits cannot accelerate indefinitely. The most significant qualitative difference between the diminishing functions that are typically assumed and sigmoidal functions is that the latter often permits an evolutionary repellor, making non-production locally stable (figure 2C). Once above this repellor, public goods production is stable, and we have shown that gradual evolution in addition to loss of function mutations can lead to a coexistence between producer and nonproducer. But how does the population cross the repellor initially from below, allowing cooperation to be established? Kin selection theory offers one explanation. As figure 3 shows, in assorted populations for high group sizes, the repellor becomes arbitrarily close to zero, lowering the hurdle to production. With sufficiently high relatedness, cells in high densities do not need to share the spoils among many genotypes, and thus cooperation can be maintained at arbitrarily high densities. This assortment, along with a jump in phenotype space by mutation or acquisition of mobile genetic elements may allow this repellor to be overcome (Smith 2001; Nogueira et al. 2009; Rankin et al. 2011). Even after this crossover, the evolutionary trap is always present, and if long enough spans of time are spent in low density populations as is common in many bacteria at some point in their lifecycles, the cooperative trait value can drop below the repellor and be lost forever.
One mechanism to avoid the evolutionary trap created by synergy is density-dependent gene regulation or quorum sensing. The evolutionary advantage of quorum sensing is usually phrased as limiting expression of particular genes to certain cellular densities. Cells which express genes only at high densities, when they receive a benefit, gain a fitness advantage over a nonregulated counterpart. We have shown that quorum sensing can prevent non-producers from invading when density is too low, limiting the cheat load that could otherwise sink cooperation. The density-dependent increase in fitness may be nonsynergistic (Brookfield 1998; Brown and Johnstone 2001; Czárán and Hoekstra 2009) due to, for instance, reduced loss of secretions into the environment at high cellular densities. In contrast, figure 5 shows that when the regulated trait is synergistic, this effect can prevent the trait from falling below the evolutionary repellor. In either scenario, quorum sensing may help maintain public goods production in the population by upregulating it only when favored by natural selection. However in the synergistic case, quorum sensing also helps prevent the collapse of cooperation while cells grow in low-density environments (figure 5).
Many bacteria spend much of their time in low densities until their environment changes upon, for example, entering a host. By restricting expression to high density, cooperation is not diminished when at low numbers for relatively long periods of time. Though low densities can cause declines in production regardless of the cause of group augmentation, in the synergistic cases (2B and 2C), the situation is especially dire. Restricting expression to high population sizes effectively bypasses the synergistic portion of the benefit function, and consequently, the cooperative trap (below which cooperation may not recover) is avoided (figure 5). There are several adaptive explanations for autoinduction sensing, including to sense density, to sense diffusion properties, and even to sense the presence of other strains of bacteria (Brookfield 1998; Redfield 2002). Whatever this mix of adaptive functions selecting for quorum sensing, the prevention of widespread cooperative collapse may be an important consequence. However, we also see in figure 5 that quorum sensing does little to help cooperation initially overcome the repellor. In fact, at very low levels of production (under the evolutionary repellor), the quorum sensing threshold may actually increase and make stable cooperation even more difficult to achieve. So quorum sensing is unhelpful in crossing the repellor initially but may be crucial for the maintenance of cooperation by preventing a population from slipping into the trap after cooperation has already been established.
It would be interesting to integrate our work into a more demographically sophisticated model. As a result of groups being reformed at each generation in our model, successful individuals replace other individuals drawn from the entire population, rather than more realistic models with limited dispersal in viscous populations (Wright 1949; Hamilton and May 1977; Rousset 2004). This limited dispersal causes competition among patchmates which can have major effects on evolution (Hamilton and May 1977; Taylor 1992). Equation 6 indicates that higher variance of the degree of assortment among groups in a population can make the conditions for evolutionary branching more narrow; this would be interesting to study further in the context of the effects on evolutionary branching of various dispersal regimes (Ajar 2003). Another possible consideration for future work is that in our model, the individual traits did not affect relatedness. However a feedback between the trait and relatedness is possible, as in the classic example of the evolution of dispersal rates (Hamilton and May 1977; Rousset and Ronce 2004) where dispersal rate affects relatedness and vice versa (Lion and van Baalen 2008; Lehmann and Rousset 2010). This could also occur when the patch size increases with public goods production; if a patch has a higher carrying capacity dependent on cooperation within it, synergistic functions may lead to interesting dynamics.
On a more biological note, we reiterate that a particular microbe may best be represented by different functional forms from what we use here. For instance, we did not consider the possibility that in high densities, fewer molecules are lost into the environment which would also increase group benefits at higher densities. In addition to this, some microbes have preferential access to their own public goods products even when in a well-mixed environment (Gore et al. 2009). For example, we could allow producers to get a benefit greater than the equal share of production we give them in the model studied here. However, even in microbes with properties different than those specified here, synergy will likely play a prominent role. Lastly, the interplay between the production and regulation in our model made simplifying assumptions about the evolution of autoinduction thresholds, and in reality a particular quorum sensing network can regulate many traits, rather than only one. With many traits, the quorum sensing trait will be likely be more stable. The evolvability of various features of quorum sensing (in this case, the group size at which autoinduction occurs) has not received significant attention in the literature, however there is evidence that various aspects of the quorum sensing are evolveable (Ansaldi and Dubnau 2004; Ichihara et al. 2006; Sandoz et al. 2007). Future work integrating molecular details into the evolution of these thresholds could be very interesting.
Supplementary Material
References
- Ajar É. Analysis of disruptive selection in subdivided populations. BMC Evolutionary Biology. 2003;3(1):22. doi: 10.1186/1471-2148-3-22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ansaldi M, Dubnau D. Diversifying selection at the bacillus quorum-sensing locus and determinants of modification specificity during synthesis of the comx pheromone. Journal of bacteriology. 2004;186(1):15. doi: 10.1128/JB.186.1.15-21.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Archetti M. Cooperation as a volunteer’s dilemma and the strategy of conflict in public goods games. Journal of Evolutionary Biology. 2009a;22(11):2192–2200. doi: 10.1111/j.1420-9101.2009.01835.x. ISSN 1420-9101. [DOI] [PubMed] [Google Scholar]
- Archetti Marco. The volunteer’s dilemma and the optimal size of a social group. Journal of Theoretical Biology. 2009b;261(3):475–480. doi: 10.1016/j.jtbi.2009.08.018. ISSN 1095-8541. [DOI] [PubMed] [Google Scholar]
- Brännström Å, Dieckmann U. Evolutionary dynamics of altruism and cheating among social amoebas. Proceedings: Biological Sciences. 2005;272:1609–1616. doi: 10.1098/rspb.2005.3116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brännström Å, Gross T, Blasius B, Dieckmann U. Consequences of fluctuating group size for the evolution of cooperation. J Math Biol. 2010 doi: 10.1007/s00285-010-0367-3. [DOI] [PubMed] [Google Scholar]
- Brookfield JFY. Quorum sensing and group selection. Evolution. 1998;52:1263–1269. doi: 10.1111/j.1558-5646.1998.tb02007.x. [DOI] [PubMed] [Google Scholar]
- Brown SP, Johnstone RA. Cooperation in the dark: Signalling and collective action in quorum-sensing bacteria. Proceedings: Biological Sciences. 2001;268:961–965. doi: 10.1098/rspb.2001.1609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown SP, West SA, Diggle SP, Griffin AS. Social evolution in micro-organisms and a trojan horse approach to medical intervention strategies. Philosophical Transactions of the Royal Society B. 2009;364:3157–3168. doi: 10.1098/rstb.2009.0055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown SP, Kümmerli R. Molecular and regulatory properties of a public good shape the evolution of cooperation. Proceedings of the National Academy of Sciences. 2010 doi: 10.1073/pnas.1011154107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chuang JS, Rivoire O, Leibler S. Cooperation and hamilton’s rule in a simple synthetic microbial system. Molecular systems biology. 2010;6(1) doi: 10.1038/msb.2010.57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clutton-Brock T. Breeding together: kin selection and mutualism in cooperative vertebrates. Science. 2002;296(5565):69. doi: 10.1126/science.296.5565.69. [DOI] [PubMed] [Google Scholar]
- Czárán T, Hoekstra RF. Microbial communication, cooperation and cheating: Quorum sensing drives the evolution of cooperation in bacteria. PLoS ONE. 2009;4:1–10. doi: 10.1371/journal.pone.0006655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deng Kuiying, Chu Tianguang. Adaptive evolution of cooperation through darwinian dynamics in public goods games. PLoS ONE. 2011;6(10):e25496. doi: 10.1371/journal.pone.0025496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dieckmann U, Law R. The dynamical theory of coevolution: a derivation from stochastic ecological processes. Journal of Mathematical Biology. 1996;34(5):579–612. doi: 10.1007/BF02409751. [DOI] [PubMed] [Google Scholar]
- Diggle SP, Griffin AS, Campbell GS, West SA. Cooperation and conflict in quorum-sensing bacterial populations. Nature. 2007;450:411–414. doi: 10.1038/nature06279. [DOI] [PubMed] [Google Scholar]
- Doebeli M, Hauert C, Killingback T. The evolutionary origin of cooperators and defectors. Science. 2004;306:859–862. doi: 10.1126/science.1101456. [DOI] [PubMed] [Google Scholar]
- Ferdy JB, Godelle B. Diversification of transmission modes and the evolution of mutualism. The American Naturalist. 2005;166(5):613–627. doi: 10.1086/491799. [DOI] [PubMed] [Google Scholar]
- Foster KR. Diminishing returns in social evolution: the not-so-tragic commons. Journal of Evolutionary Biology. 2004;17:1058–1072. doi: 10.1111/j.1420-9101.2004.00747.x. [DOI] [PubMed] [Google Scholar]
- Fuqua WC, Winans SC, Greenberg PE. Census and consensus in bacterial ecosystems: the luxr-luxi family of cell quorum-sensing regulators. Annual Review of Micriobiology. 1996;50:727–751. doi: 10.1146/annurev.micro.50.1.727. [DOI] [PubMed] [Google Scholar]
- Gardner A, West SA, Buckling A. Bacteriocins, spite and virulence. Proceedings of the Royal Society of London B. 2004:1529–1535. doi: 10.1098/rspb.2004.2756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geritz SAH, Kisdi E, Meszéna G, Metz JAJ. Evolutionarily singular strategies and the adaptive growth and branching of the evolutionary tree. Evolutionary Ecology. 1997;12(1):35–57. ISSN 0269-7653. [Google Scholar]
- Gore J, Youk H, Oudenaarden A. Snowdrift game dynamics and facultative cheatingin yeast. Nature. 2009;459:253–256. doi: 10.1038/nature07921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griffin AS, West SA, Buckling A. Cooperation and competition in pathogenic bacteria. Nature. 2004;430:1024–1027. doi: 10.1038/nature02744. [DOI] [PubMed] [Google Scholar]
- Hamilton WD, May RM. Dispersal in stable habitats. Nature. 1977 [Google Scholar]
- Hill AV. The possible effects of the aggregation of the molecules of haemoglobin on its dissociation curves. J Physiol. 1910;40(4) [Google Scholar]
- Ichihara H, Kuma K, Toh H. Positive selection in the comc-comd system of streptococcal species. Journal of bacteriology. 2006;188(17):6429. doi: 10.1128/JB.00484-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keller L. Levels of Selection in Evolution. Princeton University Press; 1999. [Google Scholar]
- Kokko H, Johnstone RA, Clutton-Brock TH. The evolution of cooperative breeding through group augmentation. Proceedings of the Royal Society of London B. 2000:187–196. doi: 10.1098/rspb.2000.1349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehmann L, Rousset F. How life history and demography promote or inhibit the evolution of helping behaviours. Philosophical Transactions of the Royal Society B: Biological Sciences. 2010;365(1553):2599. doi: 10.1098/rstb.2010.0138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lion Sebastien, van Baalen Minus. Self-structuring in spatial evolutionary ecology. Ecology Letters. 2008;11(3):277–295. doi: 10.1111/j.1461-0248.2007.01132.x. [DOI] [PubMed] [Google Scholar]
- MacLean RC, Gudelj I. Resource competition and social conflict in experimental populations of yeast. Nature. 2006;441(7092):498–501. doi: 10.1038/nature04624. ISSN 0028-0836. [DOI] [PubMed] [Google Scholar]
- Nogueira T, Rankin DJ, Touchon M, Taddei F, Brown SP, Rocha EPC. Horizontal gene transfer of the secretome drives the evolution of bacterial cooperation and virulence. Current Biology. 2009;19(20):1683–1691. doi: 10.1016/j.cub.2009.08.056. ISSN 0960-9822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Queller DC. Kinship, reciprocity and synergism in the evolution of social behaviour. Nature. 1985;318(6044):366–367. ISSN 0028-0836. [Google Scholar]
- Rankin DJ, Rocha EPC, Brown SP. What traits are carried on mobile genetic elements, and why? Heredity. 2011;106:1–10. doi: 10.1038/hdy.2010.24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Redfield RJ. Is quorum sensing a side effect of diffusion sensing? TRENDS in Microbiology. 2002;10(8):365–370. doi: 10.1016/s0966-842x(02)02400-9. ISSN 0966-842X. [DOI] [PubMed] [Google Scholar]
- Robson ND, Cox ARJ, McGowan SJ, Bycroft BW, Salmond GPC. Bacterial n-homoserine-lactone-dependent signalling and its potential biotechnological applications. Trends in Biotechnology. 1997;15:258–264. doi: 10.1016/S0167-7799(97)01102-5. [DOI] [PubMed] [Google Scholar]
- Ross-Gillespie A, Gardner A, Buckling A, West SA, Griffin AS. Density dependence and cooperation: Theory and a test with bacteria. Evolution. 2009;63:2315–2325. doi: 10.1111/j.1558-5646.2009.00723.x. [DOI] [PubMed] [Google Scholar]
- Rousset F. Genetic structure and selection in subdivided populations. The Princeton University Press; 2004. [Google Scholar]
- Rousset F, Ronce O. Inclusive fitness for traits affecting metapopulation demography. Theoretical population biology. 2004;65(2):127–141. doi: 10.1016/j.tpb.2003.09.003. [DOI] [PubMed] [Google Scholar]
- Sandoz KM, Mitzimberg SM, Schuster M. Social cheating in pseudomonas aeruginosa quorum sensing. Proceedings of the National Academy of Sciences. 2007;104(40):15876. doi: 10.1073/pnas.0705653104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith J. The social evolution of bacterial pathogenesis. Proceedings of the Royal Society of London. Series B: Biological Sciences. 2001;268(1462):61. doi: 10.1098/rspb.2000.1330. ISSN 0962-8452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith J, Van Dyken JD, Zee PC. A generalization of hamilton’s rule for the evolution of microbial cooperation. Science (New York, NY) 2010;328(5986):1700. doi: 10.1126/science.1189675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith J. Maynard, Szathmáry E. The Major Trnasitions in Evolution. Oxford University Press; 1995. [Google Scholar]
- Sumpter DJT. Collective Animal Behavior. Princeton University Press; 2010. [Google Scholar]
- Sumpter DJT, Brännström Åke. Synergy in Social Communication. Oxford University Press; 2008. [Google Scholar]
- Taylor PD. Inclusive fitness in a homogeneous environment. Proceedings of the Royal Society of London. Series B: Biological Sciences. 1992;249(1326):299–302. [Google Scholar]
- West SA, Griffin AS, Gardner A, Diggle SP. Social evolution theory for microorganisms. Nature. 2006;4:597–604. doi: 10.1038/nrmicro1461. [DOI] [PubMed] [Google Scholar]
- West SA, Buckling A. Cooperation, virulence and siderophore production in bacterial parasites. Proceedings of the Royal Society of London. Series B: Biological Sciences. 2003;270(1510):37. doi: 10.1098/rspb.2002.2209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams P, Camara M, Hardman A, Swift S, Milton D, Hope VJ, Winzer K, Middleton B, Pritchard DI, Bycroft BW. Quorum sensing and the population-dependent control of virulence. Philosophical Transactions of the Royal Society of London. Series B: Biological Sciences. 2000;355(1397):667. doi: 10.1098/rstb.2000.0607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S. The genetical structure of populations. Annals of Human Genetics. 1949;15(1):323–354. doi: 10.1111/j.1469-1809.1949.tb02451.x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.