The equilibria of vesicles adhered to substrates by short-ranged potentials

Abstract

In equilibrium, a vesicle that is adhered to a horizontal substrate by a long-range attractive, short-range repulsive force traps a thin layer of fluid beneath it. In the asymptotic limit that this layer is very thin, there are quasi-two-dimensional boundary-layer structures near the edges of the vesicle, where the membrane's shape is governed by a balance between bending and adhesive stresses. These boundary layers are analysed to obtain corrections to simpler models that instead represent the adhesive interaction by a contact potential, thereby resolving apparent discontinuities that arise when such models are used. Composite expansions of the shapes of two-dimensional vesicles are derived. When, in addition, the adhesive interaction is very strong, there is a nested boundary-layer structure for which the adhesive boundary layers match towards sharp corners where bending stresses remain important but adhesive stresses are negligible. Outside these corners, bending stresses are negligible and the vesicle's shape is given approximately by the arc of a circle. Simple composite expansions of the vesicle's shape are derived that account for the shape of the membrane inside these corners.

1. Introduction

Vesicles are closed bilayers of lipid molecules, have numerous biological and biomedical applications, and have been studied in the context of many experimental situations. Recent laboratory experiments [1] have demonstrated how chemical patterning of a substrate, in such a way that a vesicle is preferentially adhered to specific regions, allows the vesicle's spreading to be controlled. Phase separation of a multi-component bilipid membrane has been observed to occur, both experimentally [2] and in numerical simulations [3], in response to an adhesive interaction either with another membrane or with a substrate. Smith et al. [4] computed the equilibrium shapes of vesicles as they are pulled from flat adhesive substrates by an applied force, and similar computations were subsequently performed for curved adhesive substrates [5]. Although the equilibrium configurations of such systems are well studied, the dynamic evolution of a vesicle during adhesive processes has received much less theoretical attention. We will analyse the physical balances that govern the shapes of vesicles in equilibrium, with an emphasis on the small-scale regions near the substrate, which control the dynamics owing to the viscous dissipation occurring primarily inside these regions.

An important theoretical insight was made by Seifert & Lipowsky [6], who treated the adhesive interaction as a contact potential, and gave a novel boundary condition for the meridional curvature of an axisymmetric vesicle at its contact line using a balance between adhesive and bending stresses. Seifert [7] gave a detailed derivation of this condition for two-dimensional vesicles, and described the variety of shapes that are possible depending on the relative importance of the adhesive strength and the membrane's bending stiffness. The representation of the adhesive interaction using a contact potential is an approximation that omits the presence of any fluid that is trapped beneath the vesicle. Nonetheless, it has yielded good agreement with experiments such as the forced deformation by magnetic tweezers of a vesicle that is adhered to a substrate [8]. One significant drawback of using a contact-potential model is that any translation or spreading of the vesicle along the substrate would cause the no-slip condition at the stationary substrate to be incompatible with the no-slip condition at the membrane. This incompatibility arises in the form of a non-integrable singularity in the viscous stresses at the contact point and is analogous to the ‘contact-line singularity’ encountered in the context of spreading viscous droplets [9]. One of our primary aims in analysing the effects of the wetting layer of fluid beneath the vesicle is to provide an avenue by which this singularity may be resolved.

Several workers have analysed the dynamics of vesicles in a finite-ranged potential rather than a contact potential. Cantat & Misbah [10] and Cantat et al. [11] computed numerically, and derived scalings for, the constant-speed translation of a vesicle along a substrate in response to a prescribed gradient in the adhesive attraction of the substrate for the vesicle's membrane. Cantat & Misbah [12] derived scalings for the lift force experienced by adhered vesicles under shear flow. Numerical computations must resolve the membrane near the substrate on a length scale comparable with that of the adhesive force and are, therefore, expensive when this length scale is small. An asymptotic analysis of this region, developed herein, could be incorporated into such computations to bypass this difficulty. The numerical convergence of equilibrium solutions for a finite-ranged potential towards those of a contact potential has been discussed qualitatively by Seifert [7], and more recently shown by Zhang et al. [13] by way of a phase-field model. The first part of this paper performs an asymptotic analysis of these shapes, in the limit that the length scale of the adhesive interaction is very small, thereby quantifying the above conclusions and placing them on a firmer footing.

If the vesicle is very strongly adhered to a substrate, then it spreads out in order to maximize its contact area. This causes the vesicle's membrane to have large tension and its shape to be approximately a spherical cap [6], whose curvature and contact angle are determined at leading order by global area and volume constraints. The membrane's tension is then related to the adhesion strength and to the contact angle by a Young–Dupré equation. The relatively small aspect ratio of such shapes has motivated their analysis, in two dimensions, using a long-wave approximation [14]. However, such an approximation breaks down near the edges of the vesicle owing to the membrane having to turn back under itself so that it lies flat on the substrate, giving sharp corners at the edges of the vesicle. This causes there to be an apparent discontinuity in the membrane's slope and is a consequence of the omission of bending stresses. Similar discontinuities have been observed and resolved asymptotically, for three-dimensional axisymmetric vesicles, by previous workers [15,16], in the context of budding phenomena exhibited by multi-phase vesicles. This analysis was applied by Das & Du [17] to strongly adhered axisymmetric vesicles, and we adapt their analysis to describe two-dimensional vesicles and to investigate the parameter ranges for which such asymptotic expansions are accurate. Our motivation is to understand the parameter regimes for which it is appropriate to use a long-wave approximation to describe the shape of an adhered vesicle.

The analysis in this paper derives new quantitative corrections to simpler models that represent the adhesive interaction by a contact potential rather than by a finite-ranged potential. New scaling laws are derived that describe the boundary-layer regions which correspond to the ‘contact lines’ predicted by contact-potential models, and the corrections to such models owing to the thin wetting layer of fluid beneath the vesicle are quantified by means of a composite expansion for the vesicle's shape. The regime where the adhesive interaction is very strong is also analysed, and we explain how a composite expansion for the vesicle's shape may be constructed while avoiding the use of higher-order terms as in [16]. We compare this expansion with numerically obtained solutions for the vesicle's shape, and thus describe the regimes in which our expansion is valid.

In §2, we describe the problem and explain the equations that govern the equilibrium shapes of the vesicle. In §3, we obtain equilibrium shapes through numerical solution of these equations, and review the possible regimes of equilibrium solutions obtained by Seifert [7]. In §4, we analyse these solutions in the asymptotic limit that the range of the adhesive interaction is very small, and describe the leading-order corrections to results that are obtained using a contact-potential model, and in §5, we describe the vesicle shapes in the limit that the adhesive potential is very large, thereby causing the vesicle to spread so that it has a small aspect ratio. We summarize and discuss our results in §6.

2. Formulation of problem

For ease of exposition, we focus on two-dimensional vesicles throughout the main text, but in appendix A, we describe how our results can be generalized to three dimensions. Throughout the analysis, dimensional quantities are denoted using asterisks and dimensionless quantities using undecorated variables. Lengths are non-dimensionalized with the radius of a circular cylinder of equal surface area, which we denote L* and which is given by P*/2π, where P* is the vesicle's surface area per unit dimensional width. Areas are then scaled with L^*2 and volumes with L^*3. The vesicle is modelled as a closed, inextensible and impermeable bilipid membrane of bending stiffness κ*. Energies are non-dimensionalized with κ* and pressures with the corresponding scale κ*/L^*3.

The vesicle's volume, which corresponds to its cross-sectional area A in a two-dimensional formalism, is constant owing to the membrane's impermeability. The vesicle's surface area, which corresponds to its perimeter in a two-dimensional formalism, is also constant owing to the membrane's inextensibility. We parametrize the vesicle's shape using the arclength (given by s=s*/L*) measured anti-clockwise from the centre of the underside of the vesicle, as shown in figure 1a, so that it is given by x(s)=(x,y) for two-dimensional vesicles and by x(s)=(r,y) for axisymmetric vesicles. The vesicle is attracted towards the substrate by a long-range attractive, short-range repulsive interaction so that, in the absence of any other effects, the membrane would overlie a thin wetting layer on the substrate. In the analysis that follows, we represent this interaction by the potential [11]

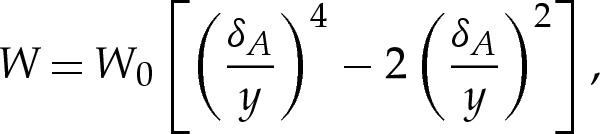2.1

which is independent of the position x along the substrate, and thereby assumes that the physical properties of both the substrate and the vesicle's membrane are homogeneous. After non-dimensionalizing, the vesicle's equilibrium shape is governed by three dimensionless parameters, which are

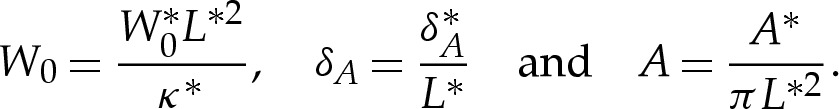2.2a–c

The parameter A represents the vesicle's reduced cross-sectional area, and the numerical prefactor has been chosen so that A=1 for a vesicle of circular cross section. The parameter δ_A is the dimensionless height at which W(y) is minimized and, therefore, represents the preferred thickness of the wetting layer beneath the vesicle. The parameter W₀ represents the energetic advantage in the membrane's moving from the far field to height δ_A above the substrate. We shall see that the equilibrium shape of the vesicle depends on W(y) primarily through the values of W₀ and δ_A, and that altering the quantitative form of the potential (2.1) leaves the results qualitatively unchanged.

Figure 1.

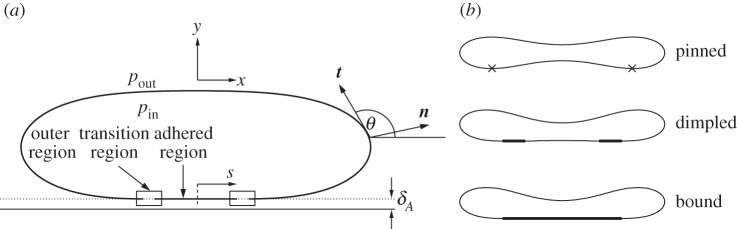
(a) Diagram of a vesicle adhered to a substrate by a short-ranged potential. The length scale of the potential is δ_A, and in the regime where this length scale is small, the vesicle's membrane has three asymptotic regions that are labelled. (b) The three types of equilibria considered in this paper. Bold lines represent the regions of the membrane that are in contact with the substrate in the limiting case δ_A=0 of a contact potential, and crosses represent the isolated points where pinned shapes touch the substrate.

The membrane exerts a traction on the surrounding fluid owing to its bending stress, its tension and its adhesive interaction with the substrate, which results in there being a discontinuity across the membrane in the stress tensor of the fluid. In equilibrium, there is no fluid flow and, therefore, no deviatoric stress component. Hence, the stress tensor is given by σ=−pI. After non-dimensionalizing, the difference between the tractions exerted on the outside and the inside of the membrane is given by [11],

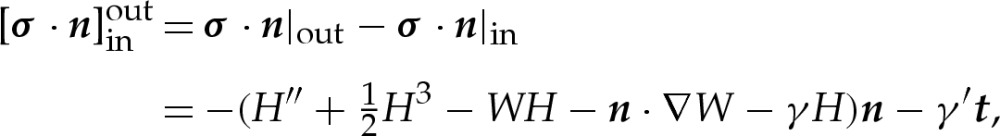2.3

where primes here denote differentiation with respect to s and the vector t is the unit tangent vector to the membrane (and equal to x′), which is inclined at an angle θ upwards from horizontal. The vector n is the outward-pointing unit normal to the membrane and H is twice the membrane's dimensionless mean curvature, defined by the equation t′=−Hn. The first two terms on the right-hand side of (2.3) represent the bending stress of the membrane and are derived from the Helfrich energy [18]. The next two terms represent the stresses that arise owing to the adhesive interaction between the membrane and the substrate, and the final terms are Lagrange-multiplier terms that enforce the membrane's inextensibility. We note that γ differs from the membrane's tension, which we denote by T, according to the relation T=γ+W [11]. Substitution of this relation into (2.3) yields

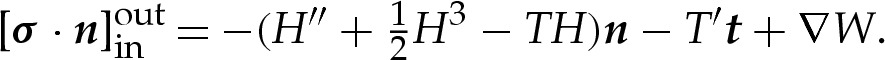The advantage of using γ in preference to T is that in equilibrium, γ is constant, whereas the tension T must vary spatially to balance the tangential gradient in the adhesive potential. We note that, in contrast to problems associated with viscous droplets where the surface energy is known but the surface area is unknown, the inextensibility of the membrane means that the variable γ is not an intrinsic property of the interface, but must be determined as part of the problem.

In equilibrium, the pressures p_in and p_out inside and outside the vesicle, respectively, are spatially constant, and their difference across the membrane is balanced by the normal component of the traction exerted by the membrane. Hence, n⋅[σ⋅n]^out_in=(p_in−p_out). Because the fluid is at rest, there is no deviatoric stress component and so t⋅[σ⋅n]^out_in=0. Hence, the stress balance (2.3) implies that

2.4a,b

The membrane's bending stiffness is typically around 10⁻¹⁹ J [18], whereas values for the adhesive energy per unit area have been found experimentally to range between 5×10⁻¹⁰ and 10⁻⁶ J m⁻² [19], depending on the physical properties of the substrate and of the membrane. If we assume that the radius of the vesicle is about 5 μm, then W₀ may range between 10⁻¹ and 2.5×10². The wetting-layer thickness has values that range between 30 and 100 nm [20], from which it follows that δ_A ranges between 6×10⁻³ and 2×10⁻². This motivates our analysing the vesicle in the asymptotic limit that δ_A≪1 and also in the secondary asymptotic regime 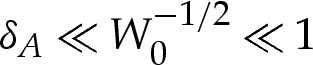, for which the adhesive interaction is strong.

3. Equilibrium membrane shapes

For ease of exposition, we focus for the moment on two-dimensional vesicles, and postpone further discussion of three-dimensional vesicles to appendix A. Because the adhesive potential W is independent of x, we replace ∇W by (dW/dy)e_y from now on, which means that equilibrium shapes satisfy

3.1a

where p is equal to p_in−p_out and must be determined as part of the solution, together with the geometric equations

3.1b–d

Equations (3.1) comprise a fifth-order system of differential equations, with unknown parameters p and γ. Seven boundary conditions and integral constraints are therefore required. We assume that the vesicle is symmetric about x=0, and compute only the shape of the right-hand half of the vesicle. The appropriate boundary conditions, applied on the centreline of the vesicle, are then

3.2a–c

on the underside of the vesicle, and

3.2d–f

on the upper side of the vesicle. The vesicle's area is enforced by the integral constraint

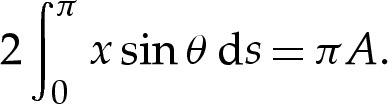3.2g

The conditions (3.2) fully determine the solution to (3.1).

The system (3.1)–(3.2) depends on the three parameters in (2.2), namely the adhesive amplitude W₀, the adhesive length scale δ_A and the reduced area A of the vesicle. To facilitate the description of the variety of shapes that are possible, we show in figure 2 how the free energy E of the vesicle, given in the dimensionless variables by [7]

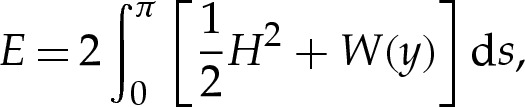3.3

varies with W₀ for different reduced areas A and adhesion length scales δ_A. As δ_A decreases, the vesicle shapes approach a limit (shown in figure 2b by solid lines) that corresponds to there being a contact potential, for which the free energy is given by

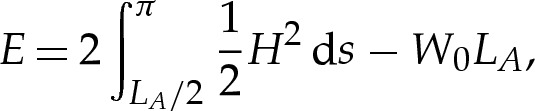3.4

instead of (3.3), where L_A is the length of membrane in contact with the substrate. In this limit, Seifert [7] gave a detailed description of the effects of varying A and W₀ on the vesicle's shape. We briefly summarize Seifert's conclusions before building on them in §4, where we analyse the vesicle's shape when δ_A is very small but non-zero. In particular, we resolve the apparent discontinuity in the membrane's curvature at the contact point, which would otherwise imply a singular-valued traction owing to the bending-stress term in (2.3).

Figure 2.

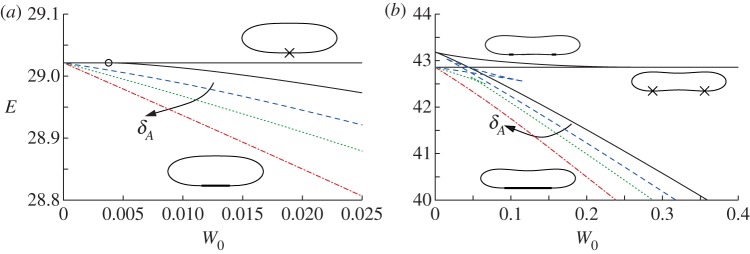
The free energy E of equilibrium membrane shapes versus the adhesive amplitude W₀, for reduced areas (a) A=0.85 and (b) A=0.65, and for values of the adhesive length scale δ_A given by 2.5×10⁻³ (dashed line), 10⁻² (dotted line) and 4×10⁻² (dashed-dotted line). The solid lines show the dependence of E on W₀ for the contact potential (3.4), which represents the limit δ_A=0. Representative vesicle shapes in this limit are shown with the parts of the membrane that are in contact with the substrate represented by bold lines or crosses for isolated points. In (a), the continuous transition between bound and pinned solution branches is marked by a circle. (Online version in colour.)

When δ_A=0 and the adhesive amplitude W₀ is small, the vesicle has a ‘pinned’ shape that touches the substrate only at isolated points (figure 1b). The adhesive stress is not large enough to otherwise modify the vesicle's shape from the shape it would have if the adhesive potential was absent. The free energy, therefore, does not depend on W₀, and the pinned solutions are represented in figure 2 by the lines for which E is constant. The pinned shapes are convex when 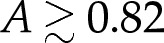, and therefore touch the substrate only at a single point, and we denote the membrane's curvature there by H_bot. There is a continuous transition (circled in figure 2a) from pinned shapes to ‘bound’ shapes that occurs as W₀ is increased through 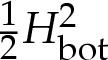. Above this value, the adhesive stress is sufficient to deform the underside of the vesicle by pulling it down to form a flat, adhered region on the underside of the vesicle. As W₀ is increased further, the length of the adhered region for these bound shapes increases, further lowering the free energy of the vesicle. The bound shapes are represented in figure 2a by the solution branch for which E decreases as W₀ increases, and in figure 2b by the lower of the two solution branches for which E decreases as W₀ increases.

Figure 2b shows the dependence of E on W₀ when the reduced area is given by A=0.65, for which the pinned shape is not convex, but instead has dimples on its upper and lower sides. The dimpled underside means that there is now a discontinuous transition from pinned states to bound states, owing to the finite energy loss associated with flattening out the membrane within the dimple and bringing it into contact with the substrate. (The crossing of the pinned and bound solution branches in figure 2b is only apparent as a consequence of their projection onto the (W₀,E) plane.) There is an intermediate solution branch, not mentioned by Seifert [7], but later observed by Smith et al. [4] in the context of axisymmetric vesicle shapes, which is unstable. Figure 2b shows how this solution branch has higher free energy than both the pinned and the bound shapes, and how it terminates onto the pinned and bound solution branches. Along this dimpled-solution branch, there is a region on the underside of the vesicle that is not adhered to the substrate. We expect that there are similar unstable equilibria that have multiple dimples, which would have an even larger free energy, but we have not pursued finding these equilibria here.

Figure 2 shows how the solution branches for a finite-ranged potential converge towards those of a contact potential as 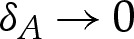. An important qualitative difference is that there is a loss of existence of the pinned solution branch above a critical value of W₀. The reason is that a finite-ranged potential affects a finite length of the membrane rather than only an isolated point. If the adhesive stress is large enough, then this region of the membrane would be pulled towards the substrate, deforming the vesicle away from its pinned shape. Hence, there are no equilibria with pinned vesicle shapes for large values of W₀. Another difference between the solution branches for a finite-ranged potential and those of a contact potential is that the dimpled-solution branch exists only for sufficiently small values of δ_A, as can be seen in figure 2b for δ_A=4×10⁻². In this case, the pinned shape has a dimple whose height is about 5×10⁻², and there is not a sufficient scale separation between the dimple's height and δ_A. Instead, the dimple is absorbed into the adhered region of the vesicle.

In the following sections, we analyse the equilibria of the vesicle in the asymptotic limit δ_A≪1 with the aim of quantifying the differences from the limiting case δ_A=0 of a contact potential. In this limiting case, for bound vesicle shapes, the membrane approaches the substrate with a curvature that is determined by a balance between bending stresses and adhesion [6,7]. Because the adhered part of the membrane lies flat on the substrate, its curvature there is zero, causing there to be an apparent discontinuity in the curvature across the contact point. Our analysis in §4 shows that when the range of the adhesive interaction is finite but small, there is a boundary layer (figure 3c) across which the curvature varies rapidly between zero, towards the substrate, and the finite value away from the substrate. From now on, we refer to this boundary layer as the ‘transition region’, the flat part of the membrane as the ‘adhered’ region and the remainder of the membrane (for which y≫δ_A) as the ‘outer region’ (figure 1a). Our analysis of the transition region recovers the curvature boundary condition that was derived using a macroscopic energy argument by Seifert [7]. We derive composite expansions to describe the vesicle's shape and obtain the 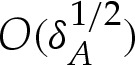corrections to the vesicle's free energy. We follow a similar procedure for pinned vesicle shapes, quantifying the deformation of the pinned shape near the substrate where adhesive stresses are significant. In §5, we consider cases where the adhesive energy is also strong, so that there is further separation of scales in the outer region. In these cases, the majority of the outer solution may be approximated as a ‘tension-dominated’ region [17], in which bending stresses are negligible. This introduces sharp corners where the membrane meets the substrate, and we show how there are boundary layers there across which the membrane's inclination and curvature change rapidly (figure 3b) so that bending stresses are dominant. We adapt the analysis of [17] to derive a composite expansion for the membrane's shape, and thereby obtain asymptotic corrections to estimates of the vesicle's shape obtained by neglecting bending stresses completely.

Figure 3.

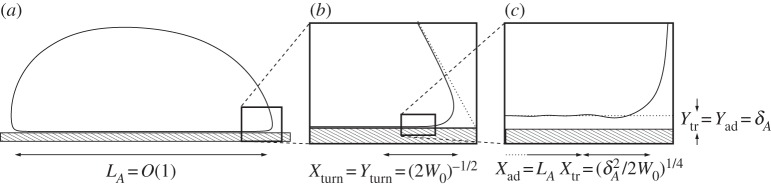
Diagram showing the nested boundary-layer structure that arises in the regime, where the wetting-layer thickness is small and the adhesion strength is large. A derivation of the scalings is given in the text.

4. Asymptotic analysis for adhesive potentials of very small length scale and arbitrary strength

The asymptotic corrections to the limiting case δ_A=0 are qualitatively different depending on whether, in this limit, the vesicle is in contact with the substrate in ‘adhered regions’ of finite length (bound and dimpled shapes) or only at isolated points (pinned shapes). We, therefore, consider these cases separately in the following subsections. We rescale variables throughout with respect to characteristic horizontal and vertical scales given, respectively, by X_* and Y _*, and use carets to denote rescaled quantities.

(a). Bound and dimpled vesicles

In the asymptotic limit 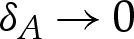, the vesicle shapes approach the shape that corresponds to there being a contact potential, with an adhered and outer region that meet at the contact points (figure 1a). The outer region, therefore, has O(1) length scale, and we use the scalings X_out=Y _out=1. Similarly, for the adhered region, we use X_ad=1 but, because the wetting layer has thickness δ_A, we use Y _ad=δ_A. In the transition region, adhesive stresses are again important, and we use Y _tr=δ_A. Because the curvature there scales like (2W₀)^1/2 [7], we derive a scaling for X_tr using the balance 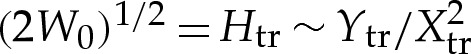. It follows that scalings for the transition region are given by

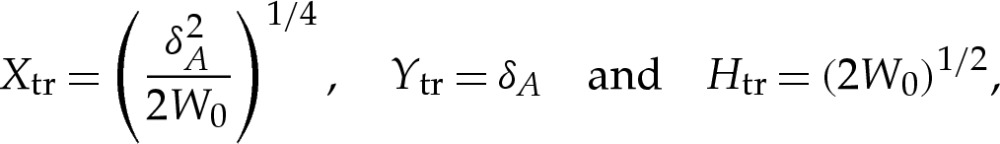4.1a–c

where the numerical factors of 2 have been retained for convenience. The boundary-layer structure is depicted in figure 3, in the case that the adhesive amplitude W₀ is large. The analysis in this section applies to arbitrary values of W₀. The ‘turn-around’ boundary layer, depicted in figure 3b, is present in the outer region only if W₀ is large. We discuss this special case further in §5, but here state that if W₀ is not large, then the adhesive boundary layer in figure 3c simply matches directly onto the outer region in figure 3a. In §4a(i), we show how a detailed analysis of the transition region recovers the curvature boundary condition H=(2W₀)^1/2, which after rescaling corresponds to .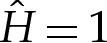

(i). Transitional region

To analyse the transitional region, we first rescale variables using (4.1a–c) to give

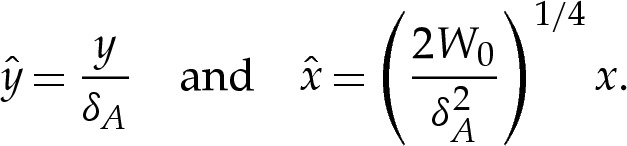4.2

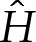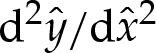We then substitute for the potential W(y) in (3.1a) using (2.1) and for using to obtain, at leading order for δ_A≪1,

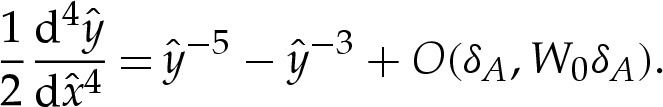4.3

Three matching conditions are sufficient to determine the solution up to translations in .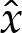

Because the scalings for the adhered region are given by Y _ad=δ_A and X_ad=1, the membrane's curvature there scales like δ_A and from (3.1a), its shape satisfies (in unscaled variables)

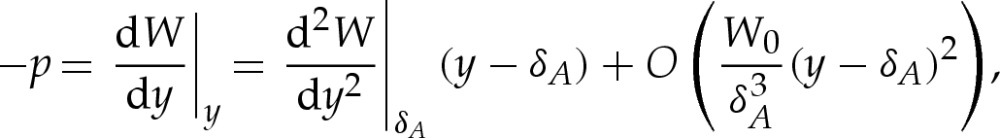which relates the pressure difference across the membrane to the adhesive stress exerted on it. Because the pressure difference is determined by the outer region, it follows that p=O(1) as 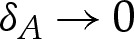and, hence, that

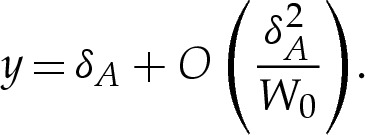We take the leading-order approximation y=δ_A throughout the adhered region. In the scaled variables for the transition region, the membrane's height must, therefore, approach unity towards the adhered region. We linearize about this height to obtain

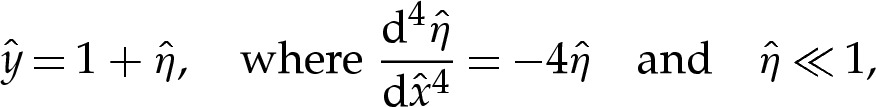the solutions to which have the form . If the adhered region is to the left of the transition region, then we must suppress the two modes that grow exponentially as 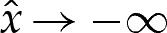by prescribing the conditions

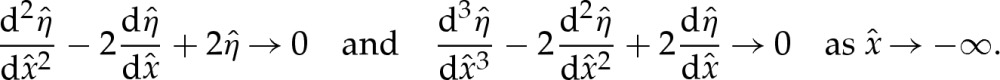4.4a,b

We compute the appropriate solution of (4.3) using a shooting method, where the membrane height is prescribed to have the form

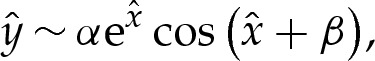near 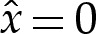, to ensure that (4.3) and (4.4) are satisfied. We set the amplitude α to some small value, which has the effect of prescribing the origin's position. The phase β remains to be determined, and we will use it as a shooting parameter. Towards the outer region, the bending moment H′ is O(1) in the original unscaled variables, which implies that 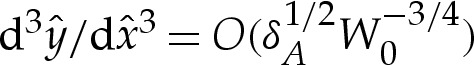as 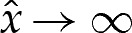. We approximate this constraint using the matching condition that

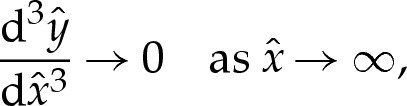4.4c

which, together with (4.4a,b), determines the solution in the transition region up to a translation.

Figure 4a shows the shape of the membrane in the transition region. Also shown is the displacement of the shape from the limiting case that there is a contact potential, which we use in §4a(ii) to obtain a composite expansion for bound membrane shapes. This limiting case is flat to the left of the contact point and, on the very short length scale of the adhesive boundary layer, has constant curvature to the right of the contact point. The position of the contact point is determined through extrapolation of the far-field behaviour of the transition region leftwards to the point where the membrane's slope is given by .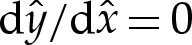

Figure 4.

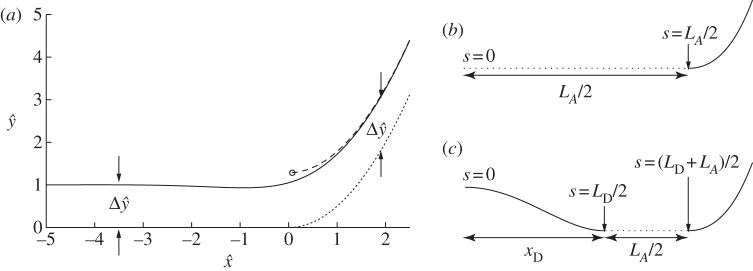
(a) Asymptotic solution for the membrane's shape inside the transition region (solid line), the extrapolation of its quadratic behaviour in the far field (dashed line) to where the slope is zero, thereby estimating the position of the contact point (circled), and the membrane's shape in the contact-potential limit that δ_A=0 (dotted). Also shown is the vertical displacement 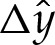of the asymptotic solution from the limiting case of a contact potential. (b,c) Schematic of the boundary conditions (4.8) and (4.9) for (b) bound vesicles, for which x_D=L_D=0, and (c) dimpled vesicles.

We note that (4.3) has a first integral, given by

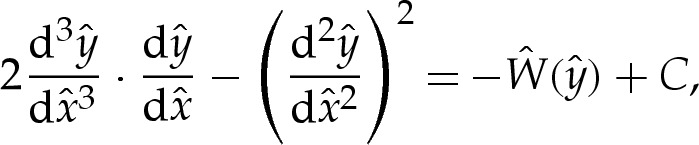4.5

and, because 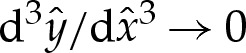both towards the adhered region and towards the outer region, it follows that

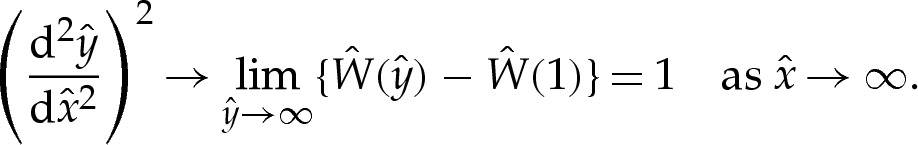4.6

This result holds regardless of the quantitative form of 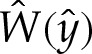. In dimensional variables, this means that the curvature approaches 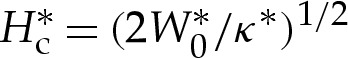, thereby recovering the boundary condition presented by Seifert [7] for the limiting case of a contact potential.

(ii). Outer region

Because the outer region has y≫δ_A, the adhesive potential there is O(1) as 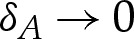, and we take the leading-order approximation that W=0, so that the membrane's equilibrium shape is governed by (3.1), with (3.1a) replaced by

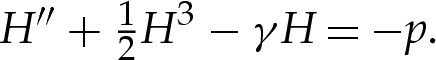4.7

The length L_A of the membrane in contact with the substrate (figure 3a) is unknown and represents an additional variable that must be determined, together with p and γ, as part of the solution. If the outer solution is a bound shape, then eight constraints are required to close the problem. If the outer solution has a dimpled shape, then the membrane inside the dimple must be treated separately by solving (4.7) in a second domain. This gives a tenth-order system of differential equations, with unknown parameters p, γ, L_A, the length L_D of the membrane inside the dimple and the contact-point position x_D at the edge of the dimple to be determined. Hence, 15 constraints are required to close the problem for dimpled shapes. On the upper side of the vesicle, we again prescribe the conditions (3.2d–f) at the centre, but on the lower side, we replace (3.2a–c) by conditions that match towards the transition region, which are

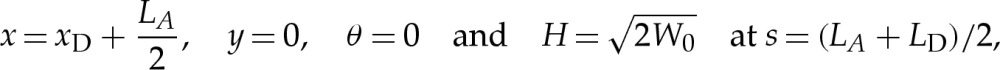4.8a–d

where x_D=L_D=0 for bound vesicle shapes, and we replace the area constraint (3.2g) by

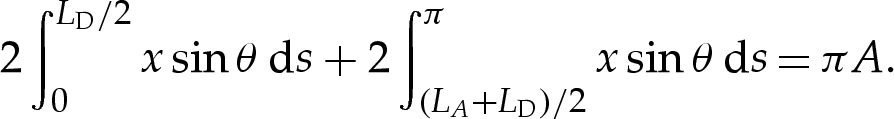4.8e

Dimpled shapes require, in addition, the boundary conditions

4.9a–c

4.9d–g

where (4.9a–c) represent the vesicle's symmetry about the centreline x=0. The constraints (4.8a,b) and (4.9d,e) represent the position of the contact points, and omit the small translation of the outer solution by an O(Y _tr) amount in the y-direction. The transition boundary layer has inclination from horizontal given by 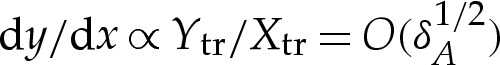and curvature given by 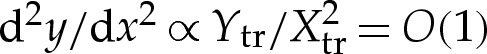. The boundary conditions (4.8c) and (4.9f) make the leading-order approximation that the inclination of the membrane in the outer solution is zero, and (4.8d) and (4.9g) ensure that the membrane's curvature matches smoothly to the value obtained in §4a(i). A schematic of the boundary conditions on the outer region for adhered and dimpled vesicles is given in figure 4b,c.

Figure 5a compares composite expansions of the membrane's bound shape near the substrate to the corresponding shapes obtained through direct numerical solution of (3.1)–(3.2), for parameter values W₀=2.5, A=0.65 and δ_A=6×10⁻³ and 2.4×10⁻². The composite expansions incorporate the corrections 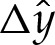to the membrane's shape, as shown in figure 4a. We describe their construction in greater detail in appendix B. The composite expansions yield very good agreement with the direct numerical solutions, and the errors that remain are O(W₀δ_A,δ_A). These errors are caused in part by the omission of higher-order terms in the governing equation (4.3) for the transitional region.

Figure 5.

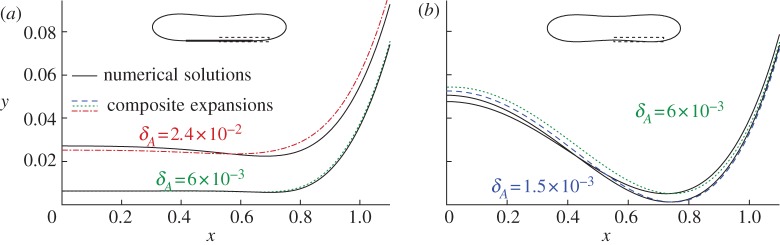
Comparison of composite expansions for the membrane shape to the shapes obtained through numerical solution of (3.1)–(3.2), for A=0.65 and (a) W₀=2.5×10⁻¹ and (b) W₀=6×10⁻². In (b) near x=0, the plots for δ_A=6×10⁻³ are the higher of the two composite expansions and the lower of the two numerical solutions. (Online version in colour.)

We show in appendix B that the transition regions modify the free energy by 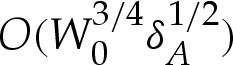, so that it is given, to 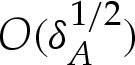, by

4.10a

and

4.10b

where E₀ is the free energy (3.4) of the vesicle in the limit of a contact potential.

Our analysis of bound and dimpled vesicles has given an improved resolution of the membrane's shape near the contact line. We have shown how the membrane in the outer region matches smoothly onto the adhered region via a transition region that is governed by a balance between bending and adhesive stresses. This transition region resolves the apparent discontinuity in curvature between the outer and adhered regions, and gives rise to a slight decrease (figure 2) in the free energy compared with the value predicted by contact-potential models.

(b). Pinned vesicles

We now consider the deformation of pinned vesicles by a finite-ranged potential. In the limiting case of a contact potential, the shape of the outer region is given, near the substrate, by

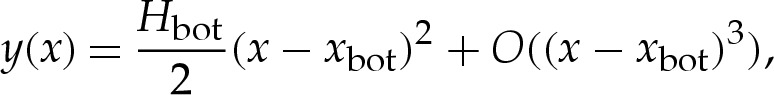4.11

where H_bot and x_bot are the values of the membrane's curvature and the x-coordinate at the lowest point of the vesicle. A finite-ranged adhesive potential deforms the membrane in the region where y=O(δ_A), which has an 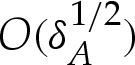horizontal length scale. We, again, use the rescaled variables

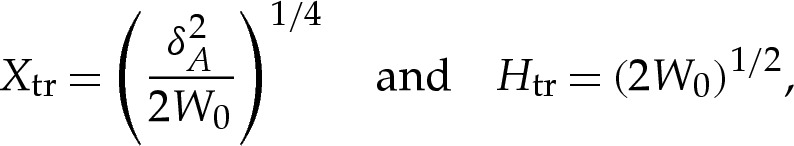in order to facilitate comparison of the results of this section with those of the analysis of bound vesicles in §4a. Hence, from (4.3), the rescaled height is governed by

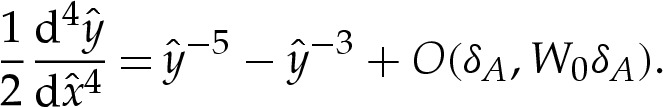4.12a

Because the shape (4.11) of the membrane is symmetric at leading order, we prescribe the conditions

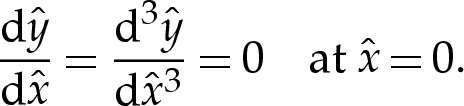4.12b

As for the transition region, one of the matching conditions matches the bending moment towards the outer region. Another condition is needed to enforce the approach of the membrane's curvature towards 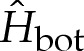away from the substrate. We, therefore, prescribe

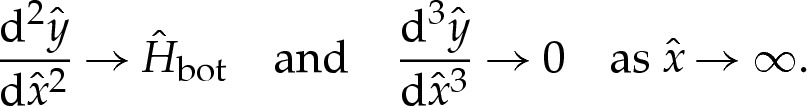4.12c

The solutions to (4.8) comprise a one-parameter family of solutions that depend on the rescaled curvature 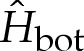of the membrane near the substrate. Figure 6a shows the variation of the membrane's curvature for a range of values of 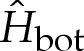, and implies that the main effect of the finite-ranged potential is to slightly flatten the bottom of the vesicle so that the curvature there is decreased. As the solution branch is traversed with 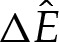decreasing, the bottom of the membrane flattens out until its shape is given by two symmetrically located transition-boundary-layer solutions. As the membrane flattens out, its free energy decreases, as implied by figure 6b, which plots the scaled correction of the free energy from the pinned shape owing to the finite-ranged potential given by

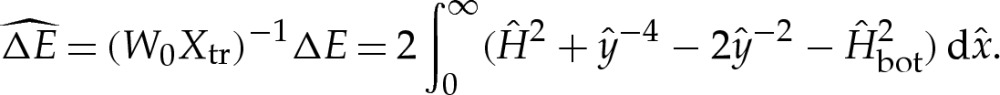4.13

Figure 6.

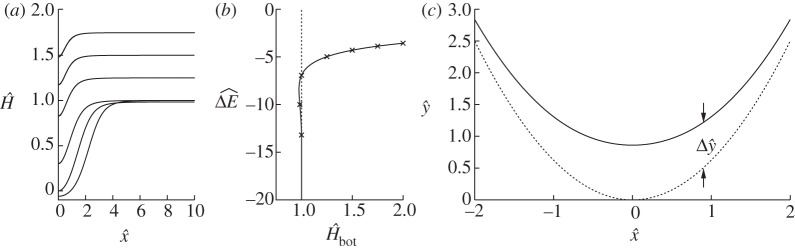
Perturbation of the membrane's shape by adhesive stresses. (a) Solutions for the membrane's curvature, for values of 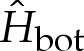that range from approximately unity to 1.75 and which are marked in (b) by crosses. (b) The change in free energy as a function of the membrane's curvature 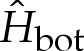towards the outer region. (c) The correction to the membrane's shape near the substrate owing to the adhesive interaction, for 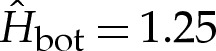. The solid line is the solution to (4.8) and the dotted line is the leading-order solution of constant curvature given by the pinned solution. The pinned shape is translated upwards by 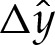to obtain the composite expansions shown in figure 5b.

We note that solutions exist for which 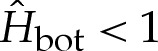, which corresponds to W₀>H²_bot/2 in the unscaled dimensionless variables.

Figure 6c shows the correction to the membrane's shape owing to the adhesive interaction, which is used in the construction of the composite expansions shown in figure 5b.

5. Asymptotic behaviour of strongly adhered two-dimensional vesicles

We now consider the regime W₀≫1, for which the vesicle is strongly adhered to the substrate. If, in addition, the wetting-layer thickness satisfies 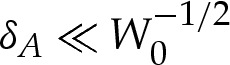, then the shape of the vesicle has a nested-boundary-layer structure, as depicted in figure 3. In the outer region, bending stresses are then important only in boundary layers at the edges of the vesicle that have 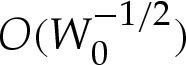length scale ([6]; also implied by the curvature boundary condition (4.8d)). Similar boundary layers have been analysed in the context of three-dimensional axisymmetric vesicles [17], for which the pressure difference across the membrane is prescribed. In the present problem, the vesicle is two dimensional, and its cross-sectional area is prescribed, whereas the pressure difference must be determined as part of the solution. In this section, we will show how earlier boundary-layer analyses may be applied to such vesicles. The role of the boundary layers is to resolve apparent discontinuities in the membrane's slope at the edge of the vesicle. Because the slope must vary rapidly so that θ=0 (or 2π) at the substrate, we refer to these boundary layers as ‘turn-around’ boundary layers. In the regime 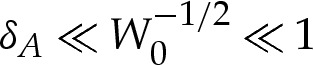, the nested boundary-layer structure means that adhesive stresses are negligible throughout both the turn-around boundary layer and the outer region. Hence, there is no contribution of adhesive stresses to γ and we refer to γ as the tension for the remainder of this section.

(a). Tension-dominated region

If bending stresses are negligible away from the edges of the vesicle, then (4.7) implies that the membrane's shape there is governed by a balance between the tension in the membrane and the pressure jump across it, so that the curvature of the membrane in this region is given by H_out∼p/γ. Hence, for two-dimensional vesicles, the shape of the membrane is given by the arc of a circle of curvature H_out that meets the substrate at a contact angle θ_out (figure 7a). The values of H_out and θ_out are determined by constraints on the vesicle's perimeter and cross-sectional area. At leading order, the contact angle depends only on the vesicle's reduced area, with a small modification caused by the difference in arclength of the turn-around boundary layer from that of the sharp corner that it corrects. It is straightforward to show that

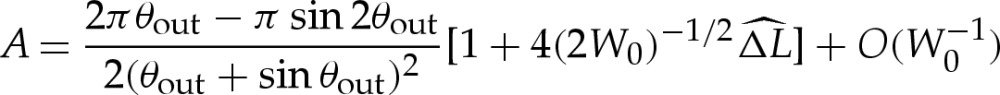5.1a

and

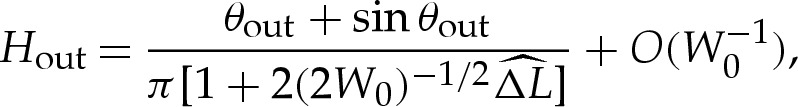5.1b

where the quantity 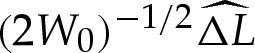will be determined and represents the arclength correction from each of the turn-around boundary layers at the edges of the vesicle. The higher-order correction terms are, in part, owing to the correction to the vesicle's cross-sectional area, and we omit them from now on.

Figure 7.

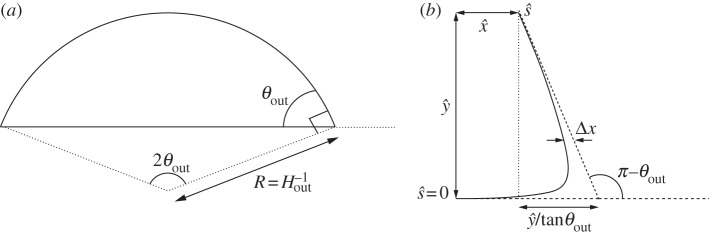
Diagrams defining (a) the curvature H_out of the tension-dominated region and the angle θ_out that it subtends and (b) the geometry of the turn-around boundary layer.

In the analysis that follows, we use the leading-order value of θ_out that is obtained by omitting the 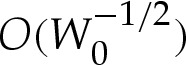terms in (5.1); we denote this angle by θ⁰_out.

(b). Turn-around boundary layer

To understand the turn-around boundary layer, we adapt an earlier asymptotic analysis [17] for strongly adhered vesicles for which the pressure difference across the membrane is prescribed and assumed to be large. In that problem, the leading-order shape of the vesicle is unknown a priori, and either the curvature or the apparent contact angle of the tension-dominated region must be determined by matching towards the boundary layer. Furthermore, Das & Du [17] state that it is necessary to apply a matching procedure at one order higher, as detailed by Das & Jenkins [16] and which is equivalent to 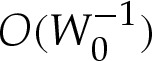in our notation, to resolve the vesicle's shape inside the boundary layer. Our analysis differs because the geometric equations (5.1) are sufficient to determine the leading-order shape of the tension-dominated region independently of the boundary-layer regions at the edges. Furthermore, we will show that, by constructing a composite expansion using a different method from that in [17], it is possible to resolve the membrane's shape correct to 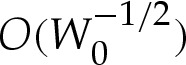everywhere, while avoiding the analysis of higher-order terms.

We use rescaled variables to describe the shape of the membrane in the turn-around boundary layer. Because the curvature is given by H=(2W₀)^1/2 at the contact point, and the membrane's slope θ varies by an O(1) amount across the boundary layer, we scale lengths with (2W₀)^−1/2. For two-dimensional vesicles, the stress balance (4.7) is then given by

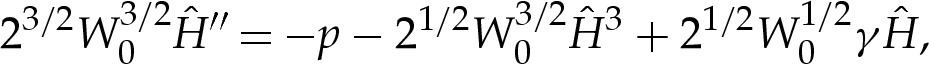5.2

where primes denote differentiation with respect to .

In equilibrium, the tension-dominated region is governed by p=γH and, because H_out=O(1) from (5.1b), the pressure is asymptotically negligible in the turn-around boundary layer from (5.2). (When p is used as a control parameter, as in [17], it is therefore necessary to expand to higher orders to perform a direct matching between the inner and outer regions.) We define a rescaled tension 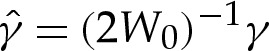so that (5.2) simplifies to

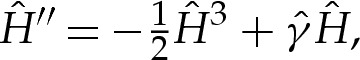5.3

the leading-order solution to which is given by [16],

5.4

where S is a constant to be determined by matching towards the tension-dominated region. This can be integrated using 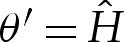to obtain

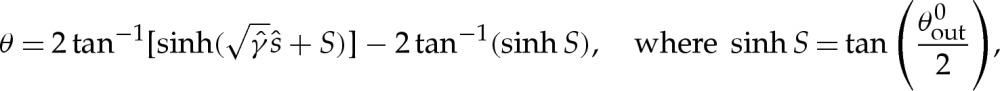5.5a,b

and where the origin of has been selected to coincide with the contact point where θ=0, and S enforces (at leading order) the approach of θ towards the value π−θ_out needed to match towards the tension-dominated region (figure 7b). The membrane's inclination (5.5) may be integrated using 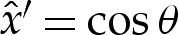and 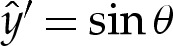to obtain

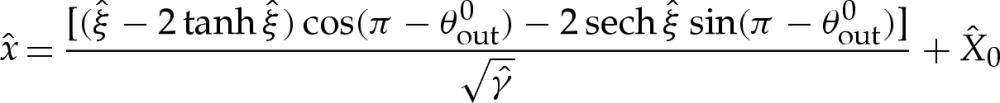5.6a

and

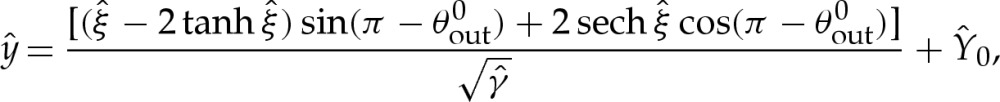5.6b

where 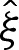is given by

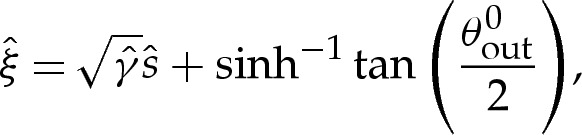5.6c

and where and are constants to enforce the boundary condition 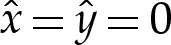at the contact point, where 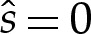or, equivalently, where 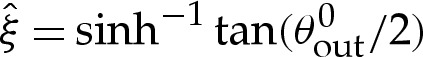. (Das & Jenkins [16] obtained an expression equivalent to (5.5a) for three-dimensional axisymmetric vesicles; we shall show that by also deriving , it is possible to obtain a composite expansion at 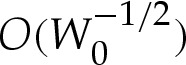without computing higher-order 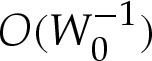terms in the turn-around boundary layer.)

Finally, the tension 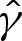is determined by the curvature condition 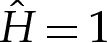at the contact point, where (from (4.8d)). From (5.4), this implies that 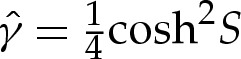, which yields, after some manipulation,

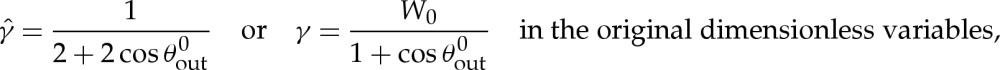5.7

thereby recovering the expression that was obtained in [6] by appeal to a macroscopic force balance between the outward spreading adhesive force and the inward force of the membrane's tension.

To derive the composite expansion, (5.1) and (A 4) require the arclength correction to be obtained. The geometry depicted in figure 7b implies that this correction is given by

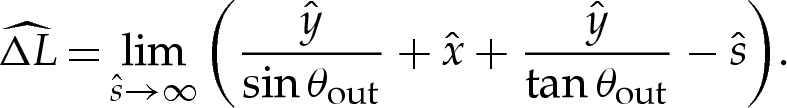5.8

Substitution for , , 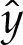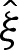and 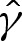into (5.8) using ((5.5) and (5.7) then gives, after rearrangement,

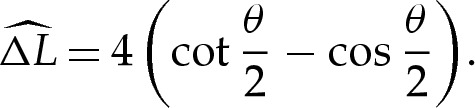5.9

We note that this diverges as 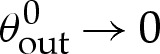, as might be expected on the grounds that the larger change in angle from 0 to π−θ⁰_out requires a larger adjustment to be made by bending stresses across the turn-around boundary layer.

Across the turn-around boundary layer, the membrane's inclination θ monotonically approaches the value π−θ_out required by the tension-dominated region. Hence, the horizontal distance 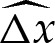of the membrane from the extrapolated shape of the tension-dominated region, given by

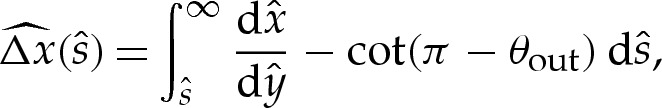5.10

(figure 7) decreases monotonically with arclength. Furthermore, 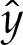increases monotonically with arclength and, hence, 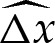may be expressed as an implicit function of 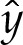. We compute 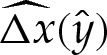numerically using (5.5) and (5.10), and then construct the composite expansion using, in the unscaled dimensionless variables,

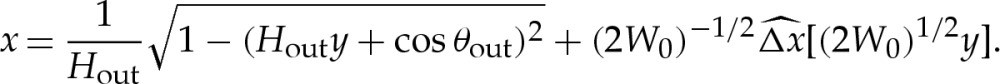5.11

The first term is the leading-order circular-arc shape. For an expansion that is consistent at 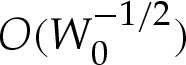, the values of H_out and θ_out must be obtained using (5.1) or (A 4) with the arclength correction given by (5.8). Because we have constructed our expansion using 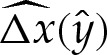rather than performing a direct composite expansion of x(s), our omission of 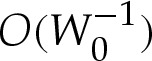terms is of no consequence. Although the apparent contact angle θ_out differs from the leading-order value θ⁰_out used in (5.9), this difference is only 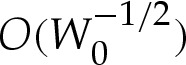, and corresponds to an 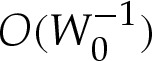error in the unscaled variables. Hence, our expansion is consistent at .

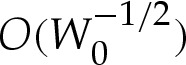Figure 8 compares composite expansions of the shape of a two-dimensional vesicle to those obtained through numerical solution of (4.7)–(4.8), for reduced areas given by A=0.5 and A=0.25 and adhesive amplitudes W₀ of 10² and 4×10². The agreement is generally very good, but there is a noticeable discrepancy when A is small. The probable reason is that the apparent contact angle decreases with A, and that small contact angles require larger corrections to be made across the turn-around boundary layer (cf. (5.9)). It follows that the corrections to the tension-dominated region are large enough that the omission of the 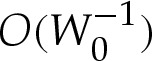(or higher-order) terms in the composite expansion are no longer valid. We conclude that a tension-dominated solution provides a good approximation to the vesicle's shape, provided both that the reduced area is large enough that the apparent contact angle 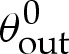is significant, and that the adhesive strength is large enough that the 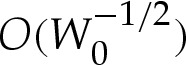corrections to the leading-order contact angle are small. (We note that although close agreement was demonstrated [17] between their asymptotic and numerical solutions for axisymmetric vesicles, the apparent contact angles of the vesicles used were large enough for the asymptotic solution to be accurate.)

Figure 8.

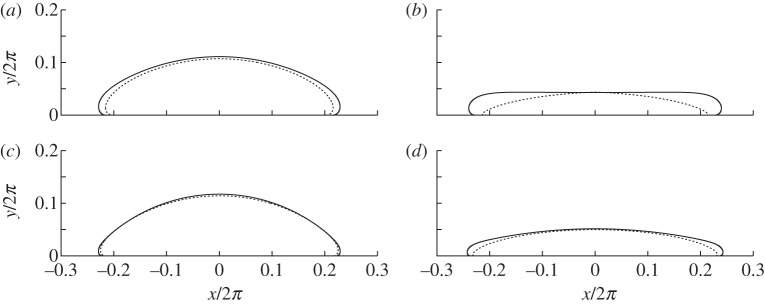
Comparison of the full numerical solution (solid lines) to (4.7)–(4.8) with composite expansions (dotted lines) for vesicles of area (a,c) 0.5 and (b,d) 0.25. The values of W₀ used are (a,b) 10² and (c,d) 4×10².

6. Discussion

We have analysed the effects of thin wetting layers that are beneath adhered vesicles, and thereby derived asymptotic corrections to contact-potential models that omit these effects completely. The classical boundary condition obtained by Seifert & Lipowsky [6] and Seifert [7] for the membrane's curvature at the contact point has been recovered using a novel approach of resolving the membrane's shape near the substrate. This approach yields, in addition, the leading-order corrections to the vesicle's shape and free energy. Incorporation of these corrections through a composite expansion of the vesicle's shape gives close agreement with shapes obtained through solution of a more complicated system (3.1)–(3.2) of equations. Our analysis has focused on two-dimensional vesicles, but in appendix A, we describe how our results may easily be generalized to describe three-dimensional vesicles provided the adhesive length scale is much smaller than the azimuthal radius of curvature of the membrane near the substrate. In this regime, the transitional boundary layer is quasi-two-dimensional and is described, at leading order, by our analysis in §4a(i). The scalings that were obtained in §4 for the region near the contact line will allow the time scales of dynamic phenomena to be estimated. To demonstrate this, we briefly describe the spreading of a vesicle along an adhesive substrate, which is driven by the adhesive stresses pulling the membrane down and impeded, primarily, by the viscous dissipation beneath the membrane in the transitional boundary layer. Because the horizontal length scale X_tr of this region is much longer than the vertical length scale Y _tr, the dissipation is due to lubrication flow [21]. The horizontal momentum balance thus implies that μ∂²u/∂y²∼∂p/∂x, where the pressure is given by (∂W/∂y)|_h. Hence, the horizontal velocity scale is given by

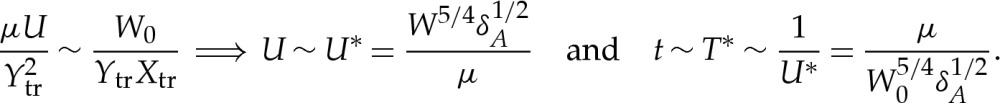6.1a,b

Figure 9 shows how the spreading speed, which we define by 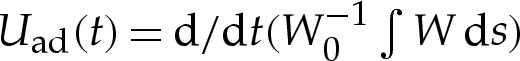, varies during the spreading of a two-dimensional vesicle of reduced area 0.85. The adhesive amplitude is given by W₀=0.25, and the adhesive length scales are given by δ_A=2.5×10⁻², 5×10⁻² and 10⁻¹. The dynamic viscosity is set to unity. The simulations use a boundary-integral technique based on the method described by Veerapaneni et al. [22], and are initialized with the shape of a free vesicle that is positioned so that its lowest point lies at y=δ_A. After scaling the velocities and times according to (6.1a,b), there is a collapse of the spreading speed for early times. This suggests that our scaling analysis is an important step towards understanding the physical processes that govern the time it takes for a vesicle to adhere to a substrate. We anticipate also that our work would be applicable to understand other dynamic processes, such as the motion of an adhered vesicle in response to an external force such as an external shear flow [12,23], a gradient in the adhesive potential across the substrate [10,11], or aspiration through suction by a micro-pipette [8]. Recently, a series of works [24–26] analysed the role of a wetting layer on the adhesion and motion of viscous droplets along substrates in a variety of configurations, and demonstrated that even the simple process of a viscous droplet adhering to a substrate involves several distinct phases of motion. We are currently attempting to understand how the inclusion of the membrane's bending stiffness in their model might broaden the range of observed phenomena.

Figure 9.

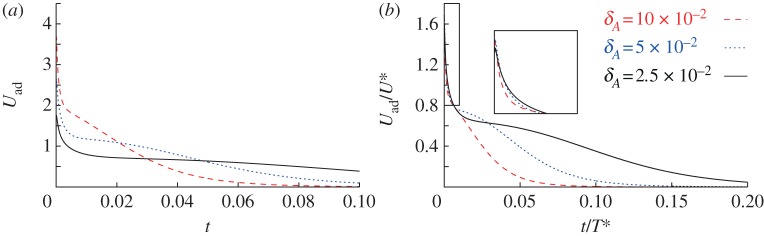
The variation of spreading speed with time. (a) Unscaled time and speed. (b) Times and speeds have been rescaled with the scalings (6.1a,b) obtained using a lubrication approximation. (Online version in colour.)

Section 5 revisited the approximation that a two-dimensional vesicle's shape is given by a circular cap when the adhesive interaction is very strong. The Young–Dupré equation (5.7) described by Seifert & Lipowsky [6] (for three-dimensional axisymmetric vesicles) for the apparent contact angle of a two-dimensional vesicle has been recovered by adapting an earlier analysis [17] of the shape of the vesicle within the turn-around boundary layers. (In appendix A, we describe how our analysis of two-dimensional vesicles may readily be applied also to three-dimensional axisymmetric vesicles.) We showed how composite expansions may be constructed for the vesicle's shape, which generally give good agreement with numerical solutions to (4.7)–(4.8). Our construction avoids the detailed matching procedure detailed in [16] (and used by [17]), which requires the computation of terms at 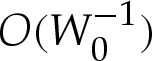rather than only the simpler 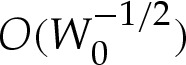terms needed by our expansion. We showed also that the approximation of the vesicle's shape by a tension-dominated circular cap is valid only if both the adhesive stress and the vesicle's reduced area are large enough that the apparent contact angle is large. Because the corrections to the tension-dominated region become large as the apparent contact angle decreases, we expect that the higher-order analysis in [17] would also break down if the apparent contact angle were small. It is likely that their expansion would yield better agreement for moderately small apparent contact angles, but we have not pursued a quantitative comparison here. We conclude that care should be taken when approximating the shape of a vesicle of small reduced cross-sectional area by a circular cap, even if the adhesive amplitude W₀ is large. Our analysis provides a means of quantifying the parameter ranges, in particular the ranges of the reduced volume, for which such an approximation is appropriate.

The boundary-layer analysis in §5 may be used to improve previous models that have analysed the dynamics of adhered vesicles using a long-wave approximation [14]. Because the vesicle's membrane must lie flat on the substrate, such an approximation breaks down near the edges of the vesicle. An understanding of the dynamic behaviour of the turn-around boundary layers at the edges of the vesicle could, therefore, be used to derive more rigorous boundary conditions that represent them in the context of a long-wave model. However, more work is needed to analyse vesicle shapes for which the membrane is not tension dominated but, instead, under compression (as arises, for example, during the drying of adhered vesicles [14]). The compression of the membrane means that it permits bending modes, so that the upper surface of the membrane can be dimpled. An apparent contradiction is that the Young–Dupré equation (5.7) implies that a boundary-layer solution exists only if the rescaled tension satisfies 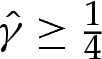. However, this equation rests on the assumption that the pressure difference across the membrane is determined solely by the tension-dominated region, so that the pressure difference is negligible on the short boundary-layer length scale of the edges of the vesicle. In the case where the pressure difference is, instead, forced externally, the omission of the pressure term in (5.3) may no longer be valid, and boundary-layer solutions that match towards compressed membranes could be permissible for sufficiently large pressure differences across the membrane. The existence, and resolution, of analogous boundary layers for adhered vesicles with compressed membranes therefore remains an open question. We note that although the analysis of Das & Jenkins [17] and Das & Du [16] concerns vesicles for which the osmotic pressure is prescribed, their non-dimensionalization assumes implicitly that the pressure inside the vesicle is higher than outside and, hence, that the membrane is under tension.

Figure 9b suggests that although the scaling (6.1a,b) gives a good collapse early in the adhesive process, there is a noticeable discrepancy at later times. We believe that this is caused by the trapping of a finite-amplitude dimple [27,28] beneath the vesicle, a process that is not described by the lubrication theory used to obtain (6.1a,b). Work towards understanding how such dimples affect the adhesion of vesicles is currently underway.

Appendix A. Three-dimensional vesicles

We briefly describe how the results in the main text may be generalized to three-dimensional vesicles. We non-dimensionalize lengths with the length scale given by L*=(S*/4π)^1/2, where S* is the vesicle's dimensional surface area. The three-dimensional analogue of the reduced cross-sectional area is the reduced volume, given by

A1

where V * is the vesicle's dimensional volume.

The different geometry of three-dimensional axisymmetric vesicles compared with two-dimensional ones slightly modifies the equation that governs their equilibrium shapes; the analogue to (2.4) is given by [17],

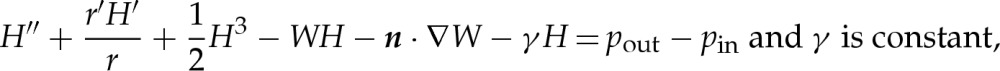A2a,b

where primes denote differentiation with respect to arclength measured azimuthally, and r denotes the horizontal distance from the axis of rotation. Equation (A 2) differs from (2.4) through the presence of the r′H′/r term on the left-hand side. Although the presence of this term modifies the shape in the outer region, it is negligible at leading order in the transition region. To see this, observe that in the transition region, the leading-order bending-stress terms are given by 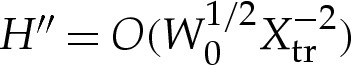and 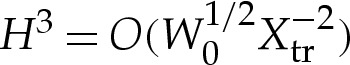in the original dimensionless variables, whereas r′H′/r is asymptotically negligible because r′/r=O(1) and 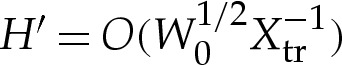. It follows that the solution obtained in §4a(i) for two-dimensional vesicles is also the leading-order solution for axisymmetric vesicles. The underlying reason is that in the regime δ_A≪1, the length scale of the transitional region is much smaller than the radius of curvature of the contact line, which means that the transitional region may be treated as if it were two-dimensional. It follows that our analysis applies also to three-dimensional vesicles that are not axisymmetric, provided the length scale X_tr of the transitional boundary layer is much smaller than the azimuthal radius of curvature of the membrane near the substrate. Such a regime always holds, provided δ_A is sufficiently small.

The turn-around boundary layer analysed in §5 is also exhibited by strongly adhered, three-dimensional axisymmetric vesicles. The membrane's inclination, measured meridionally, is governed by

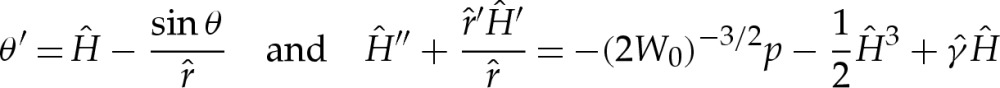A3a,b

(cf. and (5.3) for two-dimensional vesicles), where primes here denote differentiation with respect to the rescaled arclength , which is given by (2W₀)^1/2s. Because and 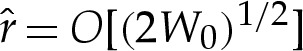in the scaled variables, it follows that (A 3) is identical to 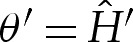and (5.3) at leading order. Hence, the solutions in §5 for the turn-around boundary layer may be applied directly to three-dimensional axisymmetric vesicles in the regime 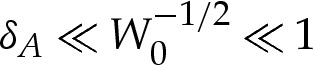. The tension-dominated region is modified slightly owing to the different geometry, and at leading order, it is given by a spherical cap of radius 2/H_out. The presence of the turn-around boundary layer modifies the dimensional surface area S* by 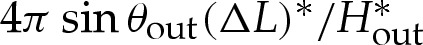, which modifies in turn the length scale L*. It can be shown that the reduced volume and curvature are given to 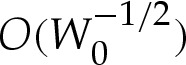by

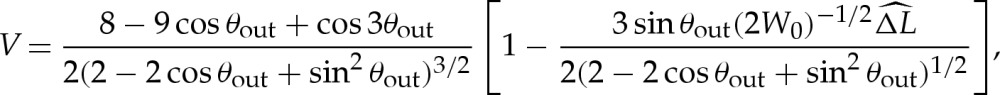A4a

and

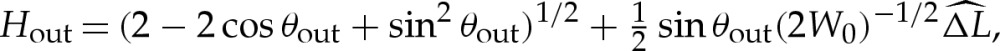A4b

and we note that the leading-order terms have previously been given by Seifert [29]. After determining the values of H_out and θ_out to 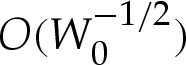, the composite expansion for the vesicle's shape is given by

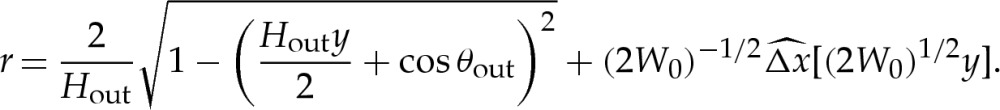A5

Appendix B. Construction of composite expansions for the shapes of bound and dimpled vesicles

In the limiting case that δ_A=0, the membrane has one (for bound vesicles) or two (for dimpled vesicles) adhered regions that are flat. To derive the corrections owing to the presence of the wetting layer, we rescale coordinates using the scales X_tr and Y _tr and position the origin at the point where the membrane would touch the substrate in the case that δ_A=0, as shown in figure 4a. The solution to the asymptotic equation (4.3) is then calculated. The curvature approaches unity as 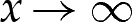, and the membrane's shape, therefore, approaches a parabola. Extrapolation of this parabola to the left to the point where its slope is zero yields an estimate for the position of the contact point. The transitional solution is translated in the x-direction so that this estimate is located at 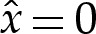, as shown in figure 4a. After translating the transitional solution in this way, the composite expansion for the membrane's shape is given by

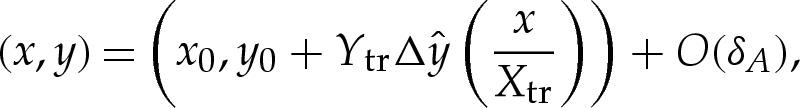B1

where the dependence of 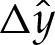on 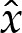is depicted in figure 4a, and (x₀,y₀) denote the membrane's shape in the limiting case δ_A=0.

The correction to the free energy from each transitional boundary layer is computed using the integral

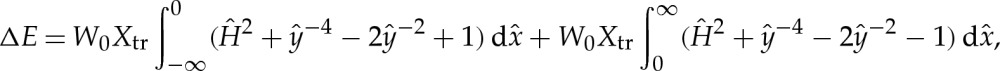B2

which has the numerical value

B3

(There are other contributions from corrections made to the adhered and outer regions, but these are asymptotically negligible as .)

Bound vesicles have two transitional boundary layers, one for each side of the adhered region, and dimpled vesicles have four. The correction (B3) is, therefore, multiplied by the appropriate amount to give the estimates (4.10) quoted in the main text.