Anisotropic particles align perpendicular to the flow direction in narrow microchannels

Abstract

The flow orientation of anisotropic particles through narrow channels is of importance in many fields, ranging from the spinning and molding of fibers to the flow of cells and proteins through thin capillaries. It is commonly assumed that anisotropic particles align parallel to the flow direction. When flowing through narrowed channel sections, one expects the increased flow rate to improve the parallel alignment. Here, we show by microfocus synchrotron X-ray scattering and polarized optical microscopy that anisotropic colloidal particles align perpendicular to the flow direction after passing a narrow channel section. We find this to be a general behavior of anisotropic colloids, which is also observed for disk-like particles. This perpendicular particle alignment is stable, extending downstream throughout the remaining part of the channel. We show by microparticle image velocimetry that the particle reorientation in the expansion zone after a narrow channel section occurs in a region with considerable extensional flow. This extensional flow is promoted by shear thinning, a typical property of complex fluids. Our discovery has important consequences when considering the flow orientation of polymers, micelles, fibers, proteins, or cells through narrow channels, pipes, or capillary sections. An immediate consequence for the production of fibers is the necessity for realignment by extension in the flow direction. For fibrous proteins, reorientation and stable plug flow are likely mechanisms for protein coagulation.

The flow orientation of anisotropic particles in narrow channels is relevant in many fields, ranging from the spinning and molding of fibers to the flow of cells or proteins through thin capillaries (1–4). It is commonly assumed that anisotropic particles align parallel to the flow direction (5). When flowing through thin channel sections, one expects the increased flow rate to improve the alignment. We investigated the alignment of anisotropic colloids (i.e., cylindrical micelles) flowing through thin sections of microchannels using synchrotron microfocus small-angle X-ray diffraction and polarized optical microscopy. Surprisingly, we find that anisotropic colloids orient perpendicular to the flow direction after passing through narrow channel sections. The perpendicular alignment is surprisingly stable, extending throughout the remaining part downstream of the channel. Ongoing experimental studies indicate that this observation holds for other anisotropic cylindrical or disk-like colloids as well. We show by microparticle image velocimetry and finite element fluid dynamics simulations that the perpendicular flow orientation is induced by perpendicular extensional flow in the expansion zone after the narrow section. Only close to the channel walls does shear flow dominate, leading to parallel flow orientation of anisotropic particles.

In situ investigations of the flow orientation of colloids in solution under very well-defined flow conditions have recently become possible with the development of X-ray transparent microfluidic devices and high-brilliance microfocused X-ray beams at dedicated synchrotron beamlines (6–9). Due to the small channel dimensions, fluid flow in microchannels is mostly laminar even for high flow rates. Under laminar flow conditions, there is a well-defined flow velocity profile within the channels. Such conditions are ideal to perform detailed investigations of the flow orientation of anisotropic colloids in various channel geometries.

There are many different types of anisotropic particles that are of high relevance for such studies, including semiflexible polymer chains, carbon nanotubes, fibrous proteins, rod-like nanoparticles, and DNA (10–14). For our first experiments, we chose cylindrical polymer micelles, a particularly well-suited model system for investigating the shear orientation of anisotropic particles (15). They possess large axial ratios, and their thickness can be adjusted over a wide range from 5 to 50 nm by tailoring the polymer molecular weight. In addition, their bending modulus can be varied and their contour lengths can range from nano- to micrometers. Their orientational distribution can be determined in situ using small-angle X-ray scattering (SAXS) or small-angle neutron scattering (SANS), and it has been correlated to their rheological properties measured simultaneously using rheo-SANS experiments (16–18). All these studies have been performed under Couette flow. In most cases of technological relevance, however, anisotropic particles are transported using pressure-driven flow (19, 20).

Results

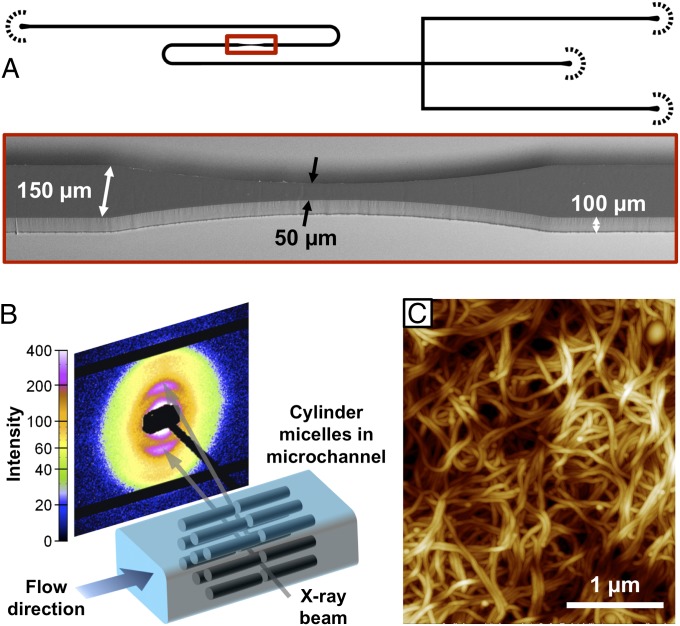
In the present study, we investigate the shear orientation of aqueous solutions of cylindrical block copolymer micelles under pressure-driven flow using specially designed Kapton- and polydimethylsiloxane (PDMS)-based X-ray transparent microfluidic devices. We use cylindrical micelles of different types of amphiphilic block copolymers, polyisoprene-b-ethylene oxide (PI-PEO) and polyethylenebutylene-b-ethylene oxide (PEB-PEO), in water at concentrations from 5–30% wt/wt in the nematic phase. In this concentration range, the flow orientation of the cylindrical micelles within the channels can be investigated using polarized optical microscopy and microfocus synchrotron SAXS as shown in Fig. 1. The microfluidic chip design comprises a flow-focusing cross-junction as well as narrow and curved channel sections. The cylindrical micelles have diameters of 25 nm and contour lengths of several micrometers, as shown by the atomic force microscopy image in Fig. 1C.

Fig. 1.

Schematic experimental setup for studying the orientation of cylindrical micelles in microchannels using SAXS. (A) Inverse black and white image of the microfluidic device drawn in AutoCAD 2011, together with a SEM image showing the actual dimensions of the narrow microchannel section. (B) X-ray beam alignment and SAXS pattern measured for a flowing stream of cylindrical micelles in a microchannel. (C) Atomic force microscopy image of an isotropic assembly of the cylindrical micelles used in the present study.

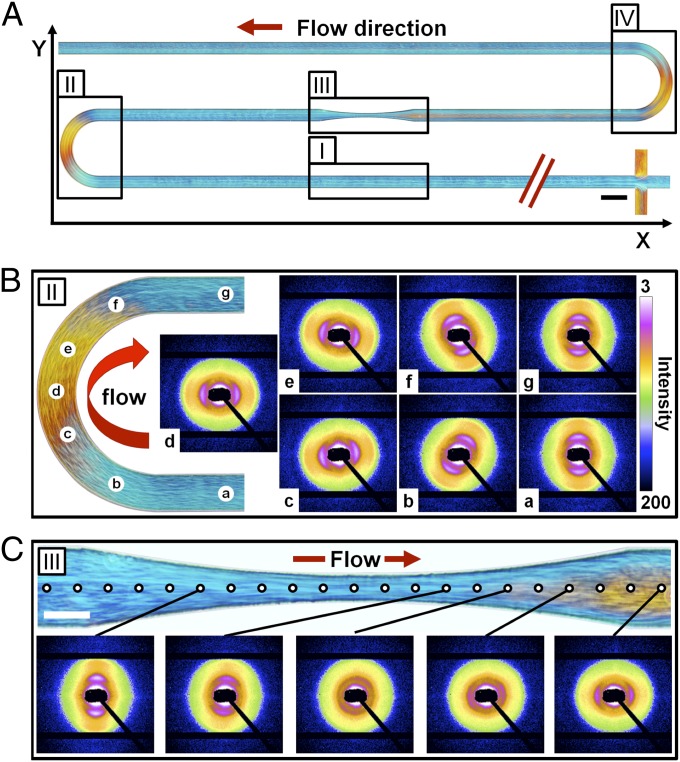
In our studies, we were interested in the orientation behavior of the cylindrical micelles when flowing through channel cross-junctions and narrow as well as curved sections. Fig. 2A shows a polarized optical microscopy image of a flowing solution of cylindrical micelles giving an overview of their observed orientational behavior along the channel. Using a quarter wave plate allows us to distinguish between cylindrical micelles oriented horizontally (Fig. 2A, blue) and vertically oriented micelles (Fig. 2A, orange). The orientational distribution of the micelles when passing the T-junction at the beginning of the channel indicates that the development length for complete reorientation is very small, being less than 10 μm. Fig. 2 B and C show the X-ray scattering patterns measured in the curved and narrow sections of the channel. For all scattering patterns, we observe pronounced first-order reflections together with weak second-order reflections corresponding to mutual parallel alignment of the micelles, typical for nematic or hexagonal order. From the radial position of the reflections, the average center-to-center distance between adjacent micelles is determined to be 58 nm.

Fig. 2.

Orientation of cylindrical micelles in curved and narrow sections of a microfluidic device. (A) Alignment of an aqueous solution of PI-PEO cylindrical micelles (20% wt/wt) at a flow rate of 32.4 μm⋅h⁻¹ visualized using polarization microscopy. Blue areas indicate orientation of cylindrical micelles parallel to the x axis, and orange areas indicate orientation parallel to the y axis. (B) Curved microchannel section with measured SAXS patterns at different channel positions. (C) Narrowed microchannel section with measured SAXS patterns along the center line, showing the surprising perpendicular orientation of the cylindrical micelles after passing through the channel tapering. (Scale bars: 100 μm.)

In the first straight section I of the microchannel, shown in Fig. 2A, we observe the expected parallel alignment of the cylindrical micelles with respect to the flow direction. When flowing through the curved section II, the micelles remain oriented parallel to the flow direction. This results in a blue → orange → blue change of the birefringence interference color and a 180° rotation of the azimuthal angle of the first-order Bragg peak, as shown in Fig. 2B. When flowing further into the contraction zone of the narrow section III, the micelles remain aligned in flow direction as indicated by the blue birefringence interference color and the azimuthal positions of the Bragg peaks, which appear on the meridian of the detector. As expected, the azimuthal peak widths become smaller, indicating improved alignment of the micelles in the flow direction.

When scanning with the X-ray beam further downstream into the channel expansion zone, we observe a surprising behavior. First, in a region directly behind the exit of the microchannel narrowing, there is no preferred orientation, as is apparent from the observed Debye–Scherrer rings (Fig. 2C). Further downstream, the micelles become oriented perpendicular to the flow direction. We observe an interference color change from blue to orange in the polarized microscopy image (Fig. 2C), and the Bragg reflections now appear on the equator of the detector. This orientation is stable along the remaining part of the channel and does not even change in the subsequent curved section IV. Only close to the channel walls are the wormlike micelles are aligned parallel to the flow direction, as indicated by the blue interference color close to the channel walls (Fig. 2C). There is a stable, relatively sharp interface between parallel- and perpendicular-aligned micelles in the remaining part of the channel further downstream. When the wormlike micelles are subjected to planar extensional flow in the x-direction in a subsequent narrow channel section, they again become aligned in the flow direction in the contraction zone and perpendicularly aligned in the subsequent expansion zone (see Supporting Information).

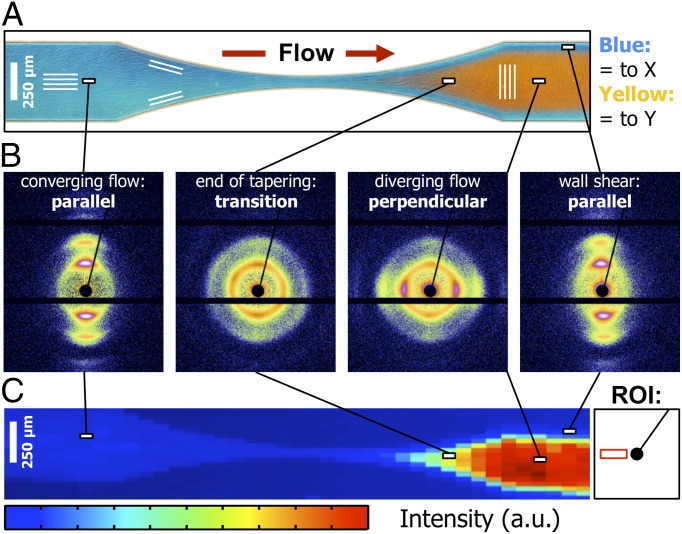
We performed additional synchrotron X-ray measurements to scan the complete contraction/expansion zone of the narrow section to map the orientation of the cylindrical micelles. The results are shown in Fig. 3, together with a polarized optical micrograph of the channel section. We indeed find the cylindrical micelles to be oriented parallel to the flow orientation in the expansion zone close to the channel walls (Fig. 3B). Here, the azimuthal position of the Bragg reflections is located on the meridian of the diffraction pattern, whereas in the central part of the expansion zone, the Bragg reflections are located on the equator. To compare the results of the microfocus X-ray diffraction scanning experiments with the polarized optical micrographs, we mapped the diffracted intensity on the equatorial region of the diffraction patterns onto the corresponding position of the X-ray beam (Fig. 3C). Regions with high equatorial intensity correspond to regions where the micelles are oriented perpendicular to the flow direction. The intensity map corresponds very well to the birefringence interference colors, as shown in Fig. 3A.

Fig. 3.

Orientation of PEB-PEO cylindrical micelles determined by scanning microfocus X-ray diffraction. (A) Alignment of cylindrical micelles in the narrow section visualized by polarized optical microscopy. (B) X-ray diffraction patterns measured at the positions indicated in A and B. (C) Pixel map of the equatorial intensity of the diffraction patterns at different positions in the channel tapering. The high intensity in the expansion zone corresponds to micelles with an orientation perpendicular to the flow direction. a.u., arbitrary unit; ROI, region of interest.

We have reproduced this behavior for wormlike polymer micelles of different block copolymers, different concentrations (5–30%, wt/wt) and width ratios of the main channel, and narrow section diameter (10:1–2.5:1), and we always found the same behavior, as described above. Ongoing experiments on cylindrical micelles with much higher bending rigidity, on disk-like micelles, and on very flexible surfactant wormlike micelles show that this phenomenon is generally occurring. We have searched the literature for similar observations to find that Barrett et al. (9) have recently observed similar behavior for sodium dodecyl sulfate (SDS)/cetyltrimethylammonium chloride (CTAC) lamellae in a microfluidic test experiment at the Diamond synchrotron light source (United Kingdom).

Discussion

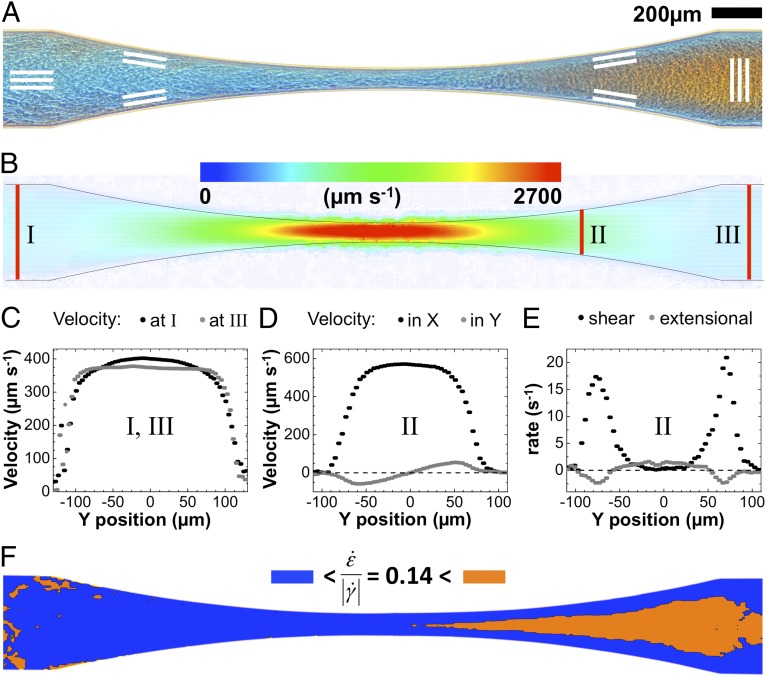
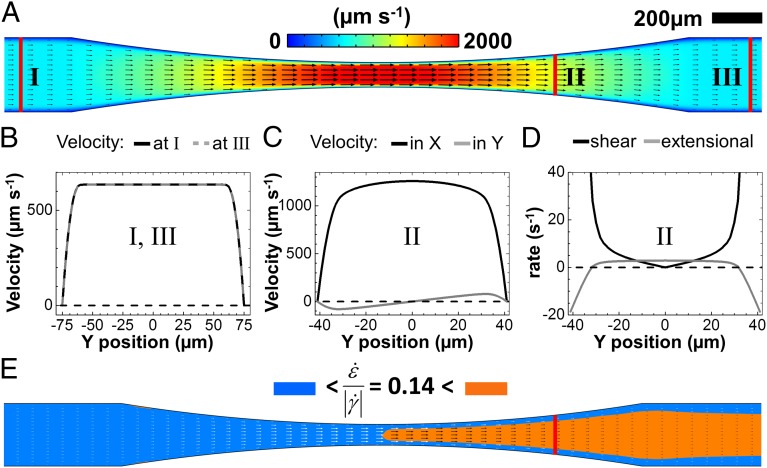
If reorientation in a perpendicular direction in a channel expansion zone is a general property of anisotropic colloids, it should have its cause in the flow pattern. Using microparticle image velocimetry with added tracer particles, we determined the velocity profiles [i.e., v_x(x,y), v_y(x,y)] in the narrow section, as shown in Fig. 4. Entering the channel, a contraction zone with planar extensional flow in the flow (x-) direction is followed by an expansion zone with planar extensional flow along the perpendicular (y-) direction. Fig. 4A shows the polarized optical micrograph of this channel section, indicating zones with parallel (blue) and perpendicular (orange) flow orientation. Fig. 4B shows the measured flow velocity, obtained from velocimetry measurements of added tracer particles. As expected, the flow velocity v_x(x,y) is largest in the narrow section of the channel. Fig. 4C shows the measured velocity profiles across the channel at position I before entering the contraction zone and at position III after the expansion zone. The velocity profiles are both nonparabolic, a consequence of the shear-thinning, non-Newtonian flow behavior of the micellar solution. The velocity profiles differ, yet both correspond to hydrodynamically stable states. The velocity profile ahead of the tapering at position I has a broad but clearly noticeable maximum, whereas the velocity profile behind the tapering at position III is nearly flat, similar to plug flow. The orientational order and velocity profile observed at position III are also obtained beyond an extensional zone when the narrow and extending zones are periodically repeated in a microfluidic device, as shown in Supporting Information.

Fig. 4.

Velocity field 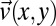of cylindrical micelles measured by microparticle image velocimetry. (A) Alignment of cylindrical micelles in the narrow section visualized by polarized optical microscopy. (B) Modulus of the measured particle velocity in the wide and narrow channel sections. (C) Velocity profile 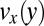in the pretapering zone I (black circles) and posttapering zone III (gray circles). (D) Velocity profiles 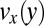(black circles) and 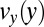(gray circles) in the expansion zone II. (E) Shear rate 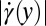(black circles) and extensional rate 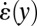(gray circles) in the expansion zone II. (F) Map of the ratio 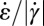in the wide and narrow channel sections. In the orange regions, 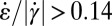, whereas in the blue regions, . The resulting color map shows good agreement with the polarized optical micrograph in A and the X-ray intensity map in Fig. 3C.

Fig. 4D shows the measured velocity components v_x and v_y across the channel at position II in the expansion zone. From the velocity components, the shear rates 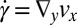and the extensional rates 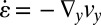can be calculated, as displayed in Fig. 4E. We observe that in the middle part of the cross-sectional view, the extensional rate 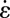is either larger or at least of comparable magnitude relative to the shear rate 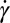. In Fig. 4F, we color regions with 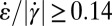orange and regions with blue for comparison with the flow birefringence pattern in Fig. 4A. We note that the near-zero values of 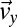in the regions before the contraction zone and after the expansion zone of the channel lead to some scattering of the data. However, we observe that by choosing a threshold of 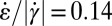, regions of high extensional rates in Fig. 4F agree well with regions of perpendicular orientation in Figs. 3C and 4A. At the channel walls, shear flow dominates, such that and micelles remain oriented in the flow direction as observed experimentally. The beginning of the sharp rise of the shear rate 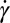close to the channel wall (Fig. 4E) defines a relatively sharp transition with a stable interface between zones of perpendicular and parallel cylinder orientation.

We thus have two important experimental findings: (i) In the expansion zone, the extensional rate 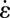is comparatively high (Fig. 4E), and (ii) in regions where it is high (i.e., 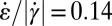), micelles reorient (Fig. 4 A and F). To obtain more insight into the first effect, we performed computational fluid dynamics (CFD) simulations to calculate shear rates and extensional rates in the contraction/expansion zone. The calculations are performed for Newtonian liquids, as well as for isotropic non-Newtonian, shear-thinning liquids. Solutions of cylindrical micelles are known to be strongly shear-thinning (16). The shear rate-dependent viscosity used in our simulations was measured by using a cone-plate rheometer and fitting the measured flow curve to the Cross equation (see Supporting Information). This equation describes the measured data well and serves to parameterize the flow curve in terms of its high- and low-shear viscosity, the relaxation time, and a power-law exponent. Details of the simulations and the experiment are described in Supporting Information. The calculated velocity field 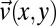for an isotropic shear-thinning solution in the contraction/expansion zone for a typical channel geometry and flow rate used in the experiments is presented in Fig. 5A.

Fig. 5.

Velocity field 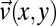for cylindrical micelles calculated by CFD simulations. (A) Calculated velocity in the wide and narrow channel sections. (B) Calculated velocity profiles 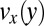in the pretapering zone I (solid black line) and posttapering zone III (dashed gray line). (C) Velocity profiles 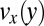(solid black line) and 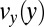(solid gray line) in the expansion zone indicated in A. (D) Shear rate 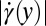(solid black line) and extensional rate 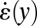(solid gray line) in the expansion zone. (E) Map of the ratio 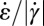in the wide and narrow channel sections. In the orange regions, 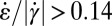, whereas in the blue regions, . The resulting color map shows good agreement with the polarized optical micrographs in Fig. 3A, the X-ray intensity map in Fig. 3C, and the measured velocity map in Fig. 4F.

Fig. 5B shows the calculated velocity profiles across the channel at position I before entering the contraction zone and at position III after the expansion zone. The velocity profiles are both nonparabolic as expected for shear-thinning fluids (21), with an almost constant flow velocity in the central part of the channel and a strongly decreasing flow velocity close to the channel walls. Fig. 5C shows the calculated velocity components 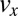and 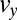, and Fig. 5D shows the corresponding shear rate 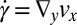and the extensional rate 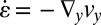along the line across the expansion zone indicated in Fig. 5A. We observe, similar to the experimental data shown in Fig. 4, that over the major center part of the cross-section in the expansion zone, the extensional rate 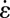is larger or at least of the same order of magnitude as the shear rate 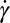. Fig. 5E shows the calculated ratio 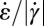over the contraction/expansion zone with a color scale adjusted such that orange indicates areas with 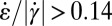, whereas blue indicates the zone with . A comparison with Fig. 4F shows good agreement with the experimentally determined flow profile. In addition, we show experimentally and numerically that the range with 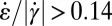is larger for non-Newtonian fluids than for Newtonian fluids, as can be seen by comparing Figs. 4E and 5E with the corresponding figures in Supporting Information. This shows that shear thinning leads to the observed large regions with high extensional rates perpendicular to the flow direction.

A comparison of the measured (Fig. 4F) and calculated (Fig. 5E) perpendicular extensional rates with the measured micellar orientational distributions (Figs. 3 A and C and 4A) shows that by choosing a threshold of 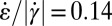, the orange zones with perpendicular alignment and the blue zones with parallel alignment are nearly quantitatively reproduced. This is a strong indication that the observed perpendicular orientation is caused by the large perpendicular extensional rates in the expansion zone. To establish the detailed relation between extensional rates and orientational distribution requires taking into account the mutual interrelation between cylinder orientation and fluid flow, which is involved and cannot currently be captured in a simple continuum fluid model, such as the one used above. The CFD simulations have their strength, because they also show that with decreasing flow rate and diameter of the tapered cross-section in the microchannel, the zone with perpendicular-oriented micelles increases, which is in good agreement with our experimental observations (see Supporting Information). However, they do not reproduce the differences observed in the two stable velocity profiles ahead of and behind the microchannel tapering, as shown in Fig. 4C, because these differences are caused by the different viscosities parallel and perpendicular to the local mean orientation of the micelles (i.e., their orientational distribution), similar to nematic liquid crystals (22, 23). What is generally known is that extensional flow is much more effective in orienting and aligning anisotropic particles compared with shear flow (24, 25). Extensional flow leads to reorientation if the extension rates become comparable to the shear rates. With an internal relaxation time of the cylindrical micelles of 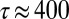s, as determined from the rheological measurements and extensional rates of 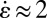s⁻¹ (Fig. 4E), values of the Deborah number De are 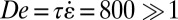. Under these conditions, the micelles are highly susceptible to flow-induced alignment.

In conclusion, we have found two types of stable flow profiles of micellar solutions with either parallel or perpendicular micelle orientation in the center of a microchannel. Experiments with solutions of cylindrical micelles of different types and recent literature indicate that the reorientation in a perpendicular direction relative to the flow after passing through a narrow channel section is generally occurring for anisotropic cylindrical and disk-like suspensions. This perpendicular orientation is caused by strong extensional fluid flow in which the extensional contribution is amplified by shear thinning. This phenomenon has important implications when considering the flow orientation of polymers, fibers, proteins, or cells through narrow sections, such as dies, molds, or tapered capillaries. An immediate consequence for the production of fibers is the necessity of subsequently applying extensional forces to realign polymers or fibrils in the flow direction for optimal fiber mechanical properties. For fibrous proteins, reorientation and stable plug flow are mechanisms for protein or cell coagulation with potential relations to thrombosis (26). Current experiments indicate that perpendicular flow orientation can be used to orient cylindrical micelles perpendicular to the surface if the channel widens perpendicular to it, which is of relevance for applications involving electrical or thermal transport perpendicular to a surface, such as in hybrid solar cells.

Materials and Methods

Fabrication of Microfluidic Devices.

The microchannel master of the microfluidic device is fabricated using optical lithography (27). The microchannel network is designed in AutoCAD 2011 (Autodesk) and printed on a mask foil with a UV-absorbent ink (Zitzmann GmbH). An inverse black and white image of the device design is shown in Fig. 1A. To pump fluids into the device, inlet ports are interfaced with tubing. Their punch location is surrounded by polygons that scatter light, making it easy to see and accurately punch the corresponding PDMS replicas that are fabricated using soft lithography, as described in detail in Supporting Information (28, 29). Stable tubing interfaces are an important prerequisite for long-term in situ scanning experiments at the synchrotron beamline.

Preparation of Cylindrical Micelle Solution.

PI₁₁₀-PEO₁₉₈ [weight-averaged molecular weight (M_w) = 16,200 g⋅mol⁻¹] is prepared by sequential living anionic polymerization, yielding a block copolymer with narrow polydispersity M_w/M_n = 1.02, where M_w and M_n are the weight- and number-averaged molecular weights, respectively. The synthesis and characterization of PI-PEO is described in detail elsewhere (30). PEB₃₉-PEO₁₀₂ (mean M_w = 7,700 g⋅mol⁻¹, M_w/M_n = 1.06) was obtained from Evonik and lyophilized before use. The dry polymers are dissolved in Millipore-quality water with a resistivity of 18.1 MΩ⋅cm⁻¹ before use. The solutions are homogenized using an UltraTurrax T8 (IKA Werke GmbH) and stored to allow the copolymer to swell in the water for 3 wk at room temperature. Before the microfluidic experiments, the solutions are filtered through a polytetrafluorethylene filter with 5-μm pore size.

Device Operation at the Beamline.

The experiments are performed at the beamlines BW4 (31) and P03 (32) at HASYLAB/DESY. The microfluidic device is connected to high-precision syringe pumps (Nemesys system; Cetoni GmbH) and positioned in the X-ray beam. After collecting the necessary background data of an empty microchannel, the syringe pumps are set to typical flow rates of 32.4 μL⋅h⁻¹, corresponding to a mean stream velocity of 360 μm⋅s⁻¹. After 15 min of equilibration time, measurements along the flow direction are performed with a microfocused X-ray beam at a wavelength of λ = 0.1381 nm. At both beamlines, the beam is 20 µm in width and 30 µm in height. X-ray scattering patterns are recorded with step sizes of 70 µm at a distance of 3.128 m behind the microfluidic device using a Pilatus 300K detector (Dectris Ltd.) with a pixel size of 172 µm by 172 µm. The integration time is 240 s.