Abstract
Detecting topological order in cold-atom experiments is an ongoing challenge, the resolution of which offers novel perspectives on topological matter. In material systems, unambiguous signatures of topological order exist for topological insulators and quantum Hall devices. In quantum Hall systems, the quantized conductivity and the associated robust propagating edge modes—guaranteed by the existence of nontrivial topological invariants—have been observed through transport and spectroscopy measurements. Here, we show that optical-lattice-based experiments can be tailored to directly visualize the propagation of topological edge modes. Our method is rooted in the unique capability for initially shaping the atomic gas and imaging its time evolution after suddenly removing the shaping potentials. Our scheme, applicable to an assortment of atomic topological phases, provides a method for imaging the dynamics of topological edge modes, directly revealing their angular velocity and spin structure.
Keywords: optical lattices, degenerate atomic gases, quantum Hall effects, chiral edge states
The integer quantum Hall (QH) effect revolutionized our understanding of quantum matter, revealing the existence of exotic phases not described by the standard theory of phase transitions (1, 2). In this phenomenon, the Hall conductivity is quantized,  —where e is the electron charge, h is Planck’s constant and ν is an integer—whenever the Fermi energy resides in an energy gap. The integers ν are related to topological invariants—Chern numbers—that are associated with the bulk energy bands (1, 3, 4). Their topological origin guarantees that the Chern numbers are constant as long as the bulk gaps remain open, explaining the signature plateaus in the Hall resistivity, present when external parameters, such as magnetic fields, are varied. Moreover, a holographic principle stipulates that a topologically ordered bulk gap, with topological invariant ν, necessarily hosts ν propagating modes localized on the sample’s edge (5). These topological edge states are chiral—their motion has a well-defined orientation—inhibiting scattering processes in the presence of disorder.
—where e is the electron charge, h is Planck’s constant and ν is an integer—whenever the Fermi energy resides in an energy gap. The integers ν are related to topological invariants—Chern numbers—that are associated with the bulk energy bands (1, 3, 4). Their topological origin guarantees that the Chern numbers are constant as long as the bulk gaps remain open, explaining the signature plateaus in the Hall resistivity, present when external parameters, such as magnetic fields, are varied. Moreover, a holographic principle stipulates that a topologically ordered bulk gap, with topological invariant ν, necessarily hosts ν propagating modes localized on the sample’s edge (5). These topological edge states are chiral—their motion has a well-defined orientation—inhibiting scattering processes in the presence of disorder.
In condensed matter physics, direct observations of edge states remain relatively rare. A first signature was obtained from magnetoplasmons created by pulsed voltages (6). Other evidence arises from edge transport in engineered Aharonov–Bohm interferometers with QH systems (7, 8). By contrast, the “routinely used” spectroscopic reconstruction of mid-gap states (1) is consistent with the expected topological band structure but does not prove their chiral nature.
Cold atoms trapped in optical lattices and subjected to synthetic gauge fields (9, 10) are an ideal platform for realizing topological insulating phases. Making topology manifest in experiments, however, is a fundamental challenge. In this context, transport experiments are conceivable (11) but technically demanding. Existing proposals for measuring topological invariants (12–16) have experimental drawbacks and can only be applied to very specific configurations. Likewise, detecting topological edge states (17–22), for example through light-scattering methods (23), requires complicated manipulations to separate the small edge-state signal from the bulk background (20, 24).
Here, we introduce a simple method to directly visualize the propagation of topological edge modes, by studying the time evolution of an atomic QH system after suddenly releasing constraining walls (Fig. 1). We show that the movement of the chiral edge states, encircling the initially vacant regions, is directly visible in the atomic density. This reveals the edge states' angular velocity and provides an unambiguous signature of chiral edge modes in the atomic system (Fig. 1). Our method is straightforward and insensitive to experimental imperfections: It only relies on a large initial occupancy of edge states. Crucially, our method requires that the edge states contribution to the density remains spatially separated from the bulk, which can be realized by populating a dispersionless bulk band with a nonzero Chern number. We present several detection techniques, applicable to both flat and dispersive bands, that demonstrate the universal applicability to atomic systems with propagating edge modes.
Fig. 1.
Experimental scheme and general strategy. (A) Trapped cold atomic fermions move on a square optical lattice in the presence of a synthetic uniform magnetic flux 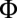 . Two repulsive potentials, initially forming holes in the atomic cloud, are suddenly removed at time
. Two repulsive potentials, initially forming holes in the atomic cloud, are suddenly removed at time 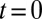 . At all times, atoms are confined by an additional circular potential. We generally assume that the confining barriers are perfectly sharp but eventually discuss the case of smoother potentials. (B) The system is initially prepared in a quantum Hall phase: Chiral edge states propagate along the edges determined by the repulsive walls and the external confinement. After releasing the walls, the edge states tend to propagate along the Fermi radius determined by the circular confinement: They encircle the initially vacant regions.
. At all times, atoms are confined by an additional circular potential. We generally assume that the confining barriers are perfectly sharp but eventually discuss the case of smoother potentials. (B) The system is initially prepared in a quantum Hall phase: Chiral edge states propagate along the edges determined by the repulsive walls and the external confinement. After releasing the walls, the edge states tend to propagate along the Fermi radius determined by the circular confinement: They encircle the initially vacant regions.
We consider a two-dimensional optical lattice filled with noninteracting fermions, subjected to a uniform synthetic magnetic flux  (25, 26), and confined by a circular potential,
(25, 26), and confined by a circular potential, 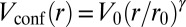 . In the experiment,
. In the experiment, 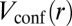 can be made nearly arbitrarily sharp
can be made nearly arbitrarily sharp 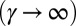 (27, 28); this configuration is of particular interest for our scheme, as demonstrated below. The resulting system realizes the Hofstadter model (29) with second-quantized Hamiltonian
(27, 28); this configuration is of particular interest for our scheme, as demonstrated below. The resulting system realizes the Hofstadter model (29) with second-quantized Hamiltonian
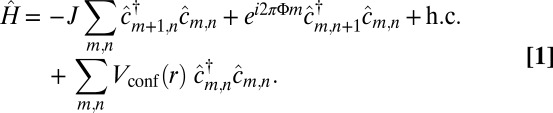 |
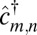 describes the creation of a fermion at lattice site
describes the creation of a fermion at lattice site 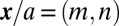 , where
, where 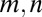 are integers; J is the tunneling amplitude; and we take the lattice period a as our unit of length. This model has a topological band structure (1, 4): When
are integers; J is the tunneling amplitude; and we take the lattice period a as our unit of length. This model has a topological band structure (1, 4): When 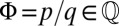 , the bulk energy spectrum splits into q subbands (29), each associated with a nonzero Chern number (4). This guarantees the existence of robust edge states in the bulk energy gaps (5). These edge states are chiral in the sense that they propagate along the Fermi radius
, the bulk energy spectrum splits into q subbands (29), each associated with a nonzero Chern number (4). This guarantees the existence of robust edge states in the bulk energy gaps (5). These edge states are chiral in the sense that they propagate along the Fermi radius 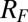 (i.e., the edge of the atomic cloud delimited by the confining potential
(i.e., the edge of the atomic cloud delimited by the confining potential 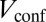 ) with a definite orientation of propagation. It is convenient to represent such nontrivial spectra by diagonalizing the Hamiltonian Eq. 1 on a cylindrical geometry (5) (Fig. 2). This picture shows a clear separation of the bulk and edge states dispersions that survive in the experimental circular geometry produced by
) with a definite orientation of propagation. It is convenient to represent such nontrivial spectra by diagonalizing the Hamiltonian Eq. 1 on a cylindrical geometry (5) (Fig. 2). This picture shows a clear separation of the bulk and edge states dispersions that survive in the experimental circular geometry produced by 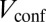 (20, 24, 30). In the following, we specifically study the configurations
(20, 24, 30). In the following, we specifically study the configurations 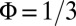 and
and 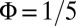 and set the Fermi energy
and set the Fermi energy 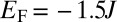 inside the lowest bulk energy gap (Fig. 2). In both these situations, the lowest energy band is associated with the Chern number
inside the lowest bulk energy gap (Fig. 2). In both these situations, the lowest energy band is associated with the Chern number 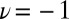 , which guarantees the occupancy of a single edge mode with same chirality
, which guarantees the occupancy of a single edge mode with same chirality 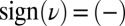 . These two configurations differ significantly in that the occupied bulk band is nearly flat (dispersionless) in the case
. These two configurations differ significantly in that the occupied bulk band is nearly flat (dispersionless) in the case 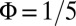 , while it is dispersive for
, while it is dispersive for 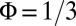 (Fig. 2).
(Fig. 2).
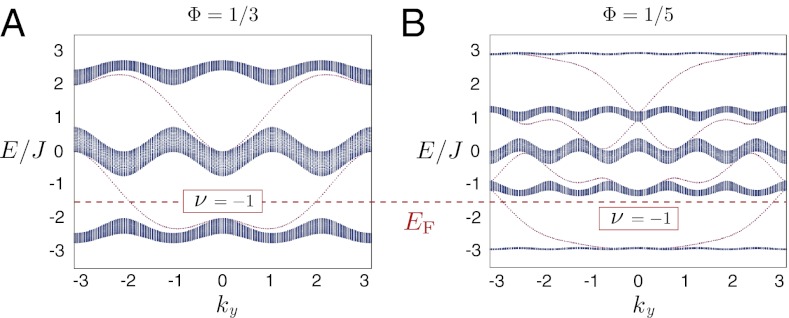
Fig. 2.
Bulk and edge states spectrum: dispersive vs. flat bands. Energy spectrum 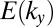 as a function of the quasi-momentum
as a function of the quasi-momentum 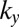 for (A)
for (A) 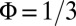 and (B)
and (B) 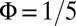 , obtained by diagonalizing the Hamiltonian Eq. 1 on a finite cylinder directed along the x direction, with
, obtained by diagonalizing the Hamiltonian Eq. 1 on a finite cylinder directed along the x direction, with 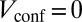 . The projected bulk bands
. The projected bulk bands 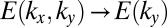 , shown in blue, are separated by large gaps of order
, shown in blue, are separated by large gaps of order 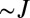 . The red dispersion branches that are visible within the bulk gaps correspond to propagating modes that are localized on the opposite edges of the cylinder. When the Fermi energy is set within the first bulk gap, a single edge mode is populated on each edge of the cylinder (the lowest bulk band corresponds to the Chern number
. The red dispersion branches that are visible within the bulk gaps correspond to propagating modes that are localized on the opposite edges of the cylinder. When the Fermi energy is set within the first bulk gap, a single edge mode is populated on each edge of the cylinder (the lowest bulk band corresponds to the Chern number 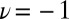 for
for 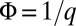 ). When considering the circular geometry realized in an experiment
). When considering the circular geometry realized in an experiment 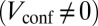 and setting
and setting 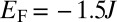 , one is guaranteed that a single edge mode will be populated because the Chern number ν does not rely on the specific geometry used (20, 24, 30). When
, one is guaranteed that a single edge mode will be populated because the Chern number ν does not rely on the specific geometry used (20, 24, 30). When 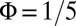 , the lowest energy band is characterized by the tiny flatness ratio,
, the lowest energy band is characterized by the tiny flatness ratio, 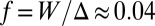 , where
, where 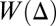 denotes the first band (gap) width; in this topological quasi-flat band configuration, the populated edge states are expected to propagate more rapidly than the bulk.
denotes the first band (gap) width; in this topological quasi-flat band configuration, the populated edge states are expected to propagate more rapidly than the bulk.
Our scheme (i) demonstrates the existence of propagating modes that are localized close to the Fermi radius and (ii) identifies their chirality and angular velocity  . To achieve this goal, we consider a geometry that constrains the QH system within two regions of the trap, as sketched in Fig. 1, resembling a bat in flight. This initial “bat” geometry is shaped by a pair of sharp potential walls
. To achieve this goal, we consider a geometry that constrains the QH system within two regions of the trap, as sketched in Fig. 1, resembling a bat in flight. This initial “bat” geometry is shaped by a pair of sharp potential walls  defined by
defined by 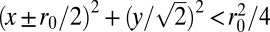 , creating holes in the density distribution (SI Appendix). In the bat geometry, we set the Fermi energy within the lowest bulk gap
, creating holes in the density distribution (SI Appendix). In the bat geometry, we set the Fermi energy within the lowest bulk gap 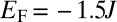 and suddenly remove
and suddenly remove 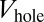 at time
at time 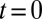 . We then study the dynamics of the atomic density with all other parameters unchanged. The bat shape is optimized for visualizing the time-evolving chiral edge states in the density
. We then study the dynamics of the atomic density with all other parameters unchanged. The bat shape is optimized for visualizing the time-evolving chiral edge states in the density 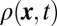 for
for 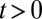 (Fig. 1B). In the following, we discuss how this “wall-removal” strategy can be exploited to reveal the edge states properties, as they progressively encircle the initially empty regions in a chiral manner.
(Fig. 1B). In the following, we discuss how this “wall-removal” strategy can be exploited to reveal the edge states properties, as they progressively encircle the initially empty regions in a chiral manner.
Results
Time-Evolving Density for Dispersive Systems.
Fig. 3A shows the time-evolving density distribution 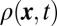 for
for 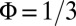 . This example highlights the importance of the bulk band structure, because it demonstrates the drawbacks encountered when preparing a system with dispersive bulk bands (Fig. 2A). The time evolution in Fig. 3A illustrates two main effects: (i) the progressive encircling of the holes by particles at the system’s radial-edge (with localization length
. This example highlights the importance of the bulk band structure, because it demonstrates the drawbacks encountered when preparing a system with dispersive bulk bands (Fig. 2A). The time evolution in Fig. 3A illustrates two main effects: (i) the progressive encircling of the holes by particles at the system’s radial-edge (with localization length 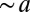 ) and (ii) the undesired and rapid filling of the holes by bulk states (Fig. 1B). Once
) and (ii) the undesired and rapid filling of the holes by bulk states (Fig. 1B). Once 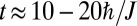 , the atomic cloud’s initial bat shape has become cyclonic, already indicating the presence of chiral edge states. To provide further insight, we separately calculated the contribution stemming from the initially populated edge states,
, the atomic cloud’s initial bat shape has become cyclonic, already indicating the presence of chiral edge states. To provide further insight, we separately calculated the contribution stemming from the initially populated edge states, 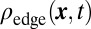 (Materials and Methods). In the corresponding Fig. 3B, we observe that the edge states, which propagated along the edges delimited by the bat potential at
(Materials and Methods). In the corresponding Fig. 3B, we observe that the edge states, which propagated along the edges delimited by the bat potential at 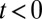 , become localized along the circular edge at
, become localized along the circular edge at 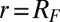 , and that they follow a “chiral” motion. These edge states remain localized on the edge for very long times and only slightly disperse into the bulk of the system, as can be anticipated from the small wavefunction overlap between edge and bulk states. Fig. 3A emphasizes the problematic (nonchiral) filling of the holes by the many dispersive bulk states, which strongly inhibits the detection of the edge states in experiments. The speed at which this filling occurs is to be compared with the circular motion of the edge states, which can be estimated from the group velocities
, and that they follow a “chiral” motion. These edge states remain localized on the edge for very long times and only slightly disperse into the bulk of the system, as can be anticipated from the small wavefunction overlap between edge and bulk states. Fig. 3A emphasizes the problematic (nonchiral) filling of the holes by the many dispersive bulk states, which strongly inhibits the detection of the edge states in experiments. The speed at which this filling occurs is to be compared with the circular motion of the edge states, which can be estimated from the group velocities 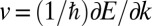 associated with the bulk and edge states (Fig. 2A). Additional interference takes place within the system, leading to small but visible patterns in the density. Fig. 3B shows that these patterns mainly originate from interferences between bulk states.
associated with the bulk and edge states (Fig. 2A). Additional interference takes place within the system, leading to small but visible patterns in the density. Fig. 3B shows that these patterns mainly originate from interferences between bulk states.
Fig. 3.
Evolution of the spatial densities after releasing the walls. (A) The spatial density 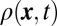 , and (B) the contribution of the initially populated edge states
, and (B) the contribution of the initially populated edge states 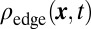 . The chiral motion is a signature of the nontrivial Chern number
. The chiral motion is a signature of the nontrivial Chern number 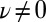 . In all the figures,
. In all the figures, 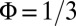 ,
, 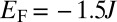 , and we considered infinitely sharp circular confinement
, and we considered infinitely sharp circular confinement 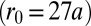 and ellipsoidal walls
and ellipsoidal walls 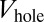 . The total number of particles is
. The total number of particles is  , whereas the number of initially populated edge states is
, whereas the number of initially populated edge states is 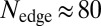 .
.
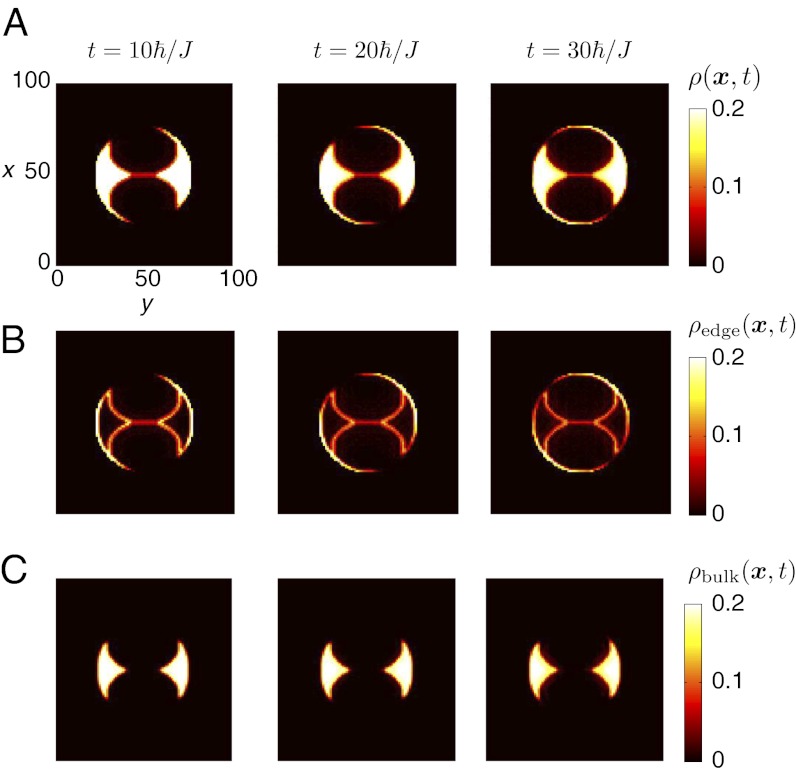
Flat Topological Bulk Bands.
For 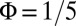 and
and 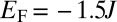 , the dispersionless (flat) bulk band represented in Fig. 2B is totally filled, and most of the edge states lying in the first bulk gap are populated. The corresponding time-evolving density
, the dispersionless (flat) bulk band represented in Fig. 2B is totally filled, and most of the edge states lying in the first bulk gap are populated. The corresponding time-evolving density 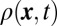 , depicted in Fig. 4A, is radically different than for
, depicted in Fig. 4A, is radically different than for 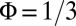 (Fig. 3A). For
(Fig. 3A). For 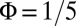 , the edge states encircle the initially forbidden regions in a chiral manner, largely unperturbed by the now motionless bulk, making them directly visible in in situ images of the cloud. The dispersionless nature of the bulk states is further illustrated in Fig. 4C, which shows the evolution of
, the edge states encircle the initially forbidden regions in a chiral manner, largely unperturbed by the now motionless bulk, making them directly visible in in situ images of the cloud. The dispersionless nature of the bulk states is further illustrated in Fig. 4C, which shows the evolution of 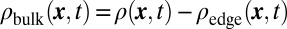 . The initial bulk states are immobile for times
. The initial bulk states are immobile for times 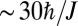 . In Fig. 4B, the evolution of the initially populated edge states
. In Fig. 4B, the evolution of the initially populated edge states 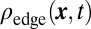 shows an interesting behavior: Some edge states with energies close to the flat bulk band are almost dispersionless and remain localized on the edges delimited by the bat potential. In contrast, the many edge states at higher energies are dispersive, encircling the holes in a clear and chiral manner. The instructive dynamics of the density
shows an interesting behavior: Some edge states with energies close to the flat bulk band are almost dispersionless and remain localized on the edges delimited by the bat potential. In contrast, the many edge states at higher energies are dispersive, encircling the holes in a clear and chiral manner. The instructive dynamics of the density 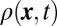 , which is due to the clear separation of the edge and bulk states during the evolution, can also be understood by studying the population of the single-particle eigenstates (SI Appendix). Moreover, our method is highly robust against perturbations in the density (or equivalently in the Fermi energy,
, which is due to the clear separation of the edge and bulk states during the evolution, can also be understood by studying the population of the single-particle eigenstates (SI Appendix). Moreover, our method is highly robust against perturbations in the density (or equivalently in the Fermi energy,  ), because it only relies on the occupation of dispersionless bulk states and sufficiently many edge states. We verified that the edge-state signal is unambiguous when a high energy (dispersive) band is initially filled (SI Appendix). Thanks to the topological quasi-flat band configuration, the edge states propagation can be visualized on long time scales, without being affected by the bulk dispersion. For
), because it only relies on the occupation of dispersionless bulk states and sufficiently many edge states. We verified that the edge-state signal is unambiguous when a high energy (dispersive) band is initially filled (SI Appendix). Thanks to the topological quasi-flat band configuration, the edge states propagation can be visualized on long time scales, without being affected by the bulk dispersion. For 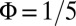 and a typical system size
and a typical system size 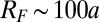 , we find
, we find 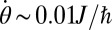 , which would require a realistic time
, which would require a realistic time 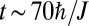 to observe the
to observe the 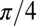 -rotation undergone by the edge states. We verified that our results are stable when the spacious ellipsoidal walls are replaced by small perturbative potentials (SI Appendix). Finally, the edge/bulk ratio can be further improved by initially confining the entire atomic cloud to a small region located in the vicinity of the circular edge (SI Appendix).
-rotation undergone by the edge states. We verified that our results are stable when the spacious ellipsoidal walls are replaced by small perturbative potentials (SI Appendix). Finally, the edge/bulk ratio can be further improved by initially confining the entire atomic cloud to a small region located in the vicinity of the circular edge (SI Appendix).
Fig. 4.
The topological quasi-flat band configuration. (A) The spatial density 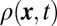 , (B) the contribution of the initially populated edge states
, (B) the contribution of the initially populated edge states 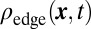 , and (C) the contribution of the initially populated bulk states
, and (C) the contribution of the initially populated bulk states 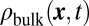 . In all the figures,
. In all the figures, 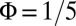 and
and 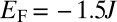 . The total number of particles is
. The total number of particles is 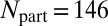 , whereas the number of initially populated edge states is
, whereas the number of initially populated edge states is 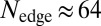 . Note the dispersionless nature of the occupied bulk states, which highly improves the detection of the edge-state signal.
. Note the dispersionless nature of the occupied bulk states, which highly improves the detection of the edge-state signal.
Revealing Topological Edge States in Dispersive Systems.
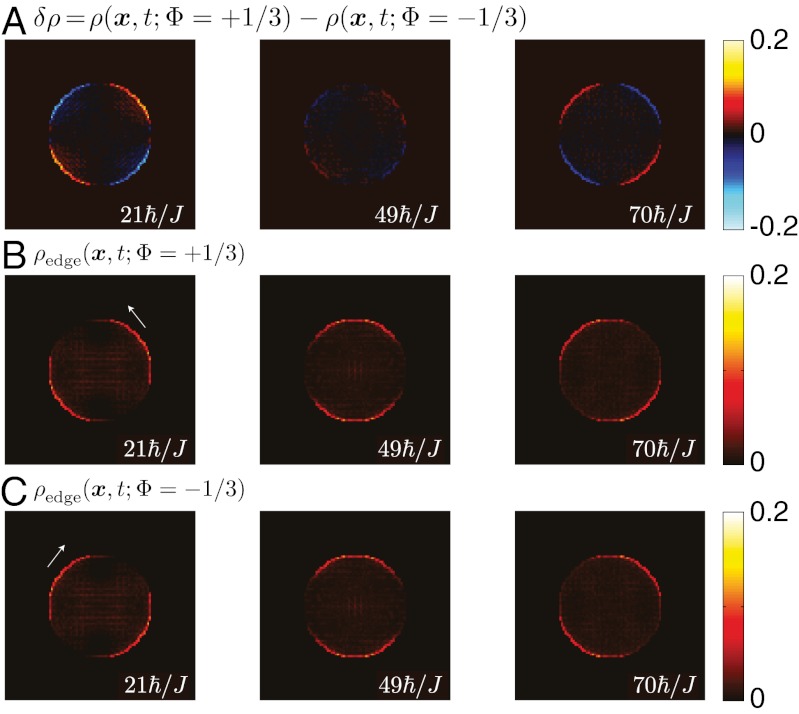
We now describe two methods for isolating the edge-states contribution 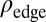 from that of the bulk states, useful for systems with dispersive bulk bands. The first method consists in performing two successive experiments, using the same apparatus and parameters, but with opposite fluxes
from that of the bulk states, useful for systems with dispersive bulk bands. The first method consists in performing two successive experiments, using the same apparatus and parameters, but with opposite fluxes 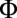 and
and 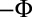 . The difference between the two images
. The difference between the two images 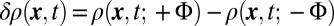 lacks the nonchiral contribution of the bulk states and is simply given by
lacks the nonchiral contribution of the bulk states and is simply given by 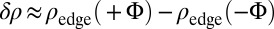 (Fig. 5). For our bat geometry,
(Fig. 5). For our bat geometry, 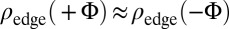 when the edge states have undergone a rotation of
when the edge states have undergone a rotation of 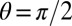 . This determines the time
. This determines the time 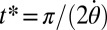 when the signal
when the signal 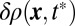 disappears, giving the angular velocity of the edge states. This situation is illustrated in Fig. 5 for the
disappears, giving the angular velocity of the edge states. This situation is illustrated in Fig. 5 for the 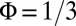 “dispersive” case, where we find
“dispersive” case, where we find 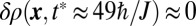 , in good agreement with the angular velocity
, in good agreement with the angular velocity 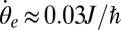 of the populated edge states (20, 24). We verified that slight differences in the filling [e.g.,
of the populated edge states (20, 24). We verified that slight differences in the filling [e.g., 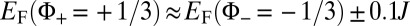 ], for example due to finite temperature effects between the two successive experiments, or variations in the flux (e.g.,
], for example due to finite temperature effects between the two successive experiments, or variations in the flux (e.g., 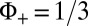 and
and 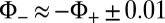 ), do not significantly affect the signal
), do not significantly affect the signal 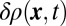 , highlighting the robustness of this method against experimental imperfections.
, highlighting the robustness of this method against experimental imperfections.
Fig. 5.
The opposite-flux method for dispersive systems. (A) Evolution of the difference 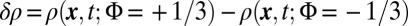 , for the same configuration as in Fig. 3. This method yields a clear manifestation of the edge states,
, for the same configuration as in Fig. 3. This method yields a clear manifestation of the edge states, 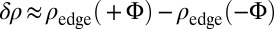 , by eliminating the undesired contribution of the many bulk states. The edge states chirality is deduced from the evolution of the red and blue patterns. (B) The edge-states contribution
, by eliminating the undesired contribution of the many bulk states. The edge states chirality is deduced from the evolution of the red and blue patterns. (B) The edge-states contribution 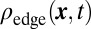 for
for 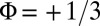 and (C) for
and (C) for 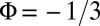 . In the central column, we note the vanishing of the signal
. In the central column, we note the vanishing of the signal 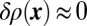 that occurs at time
that occurs at time 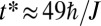 , indicating that the edge states angular velocity is
, indicating that the edge states angular velocity is 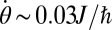 for
for 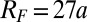 and
and 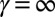 (SI Appendix).
(SI Appendix).
The second method aims to efficiently reduce the bulk dispersion by suddenly lowering the potential walls 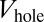 at
at  , instead of removing them completely. This operation can be achieved in such a way that only the edge states with sufficiently high energies are allowed to propagate, while leaving the bulk states away from the holes. This “edge-filter method” can be realized by setting the Fermi energy within the first bulk gap and then suddenly lowering the potential
, instead of removing them completely. This operation can be achieved in such a way that only the edge states with sufficiently high energies are allowed to propagate, while leaving the bulk states away from the holes. This “edge-filter method” can be realized by setting the Fermi energy within the first bulk gap and then suddenly lowering the potential 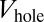 to the value
to the value 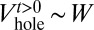 at
at 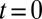 , where W is the width of the lowest bulk band. The great efficiency of this method is presented in SI Appendix for the case
, where W is the width of the lowest bulk band. The great efficiency of this method is presented in SI Appendix for the case 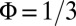 .
.
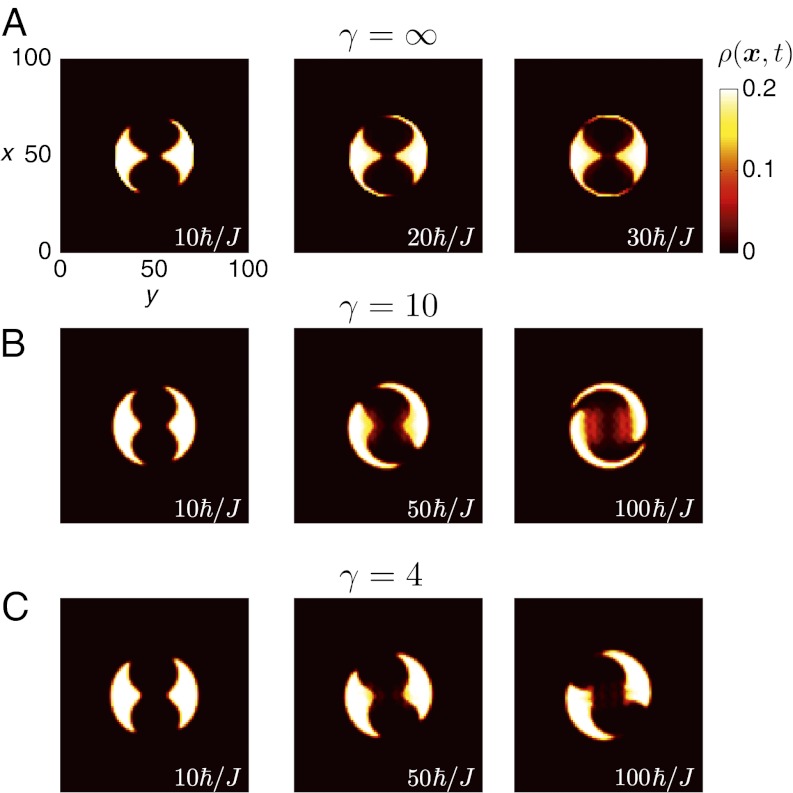
Robustness of the Edge States Against Disorder.
We now investigate the robustness of the edge states motion in the presence of disorder. This perturbation, which plays a fundamental role in solid-state systems, can be engineered in optical-lattice setups, for instance using speckle potentials (31). We study the effects of disorder by considering a random potential 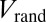 , with energies uniformly distributed within the range
, with energies uniformly distributed within the range  . The results are presented in Fig. 6 for the case
. The results are presented in Fig. 6 for the case 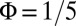 . We find that the chiral edge states signal remains robust for disorder strengths
. We find that the chiral edge states signal remains robust for disorder strengths 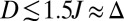 , where
, where  is the size of the bulk gap. Interestingly, we can still distinguish a cyclonic cloud—a signature of the edge states chirality—for values up to
is the size of the bulk gap. Interestingly, we can still distinguish a cyclonic cloud—a signature of the edge states chirality—for values up to 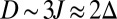 . The immunity of the chiral edge states against disorder, a hallmark of the QH effect, could thus be demonstrated using our cold-atom setup.
. The immunity of the chiral edge states against disorder, a hallmark of the QH effect, could thus be demonstrated using our cold-atom setup.
Fig. 6.
Effects of disorder. The spatial density 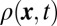 for
for 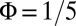 ,
, 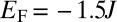 ,
, 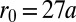 , and
, and 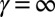 . The disorder strength is (A)
. The disorder strength is (A) 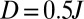 , (B)
, (B)  , and (C)
, and (C) 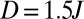 .
.
Gaussian Walls and Smooth Circular Confinements.
In the absence of walls 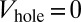 , the edge states lying in the first bulk gap are radially localized, with a radius determined by their energy and the circular confinement. Writing the circular confinement as
, the edge states lying in the first bulk gap are radially localized, with a radius determined by their energy and the circular confinement. Writing the circular confinement as 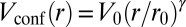 , we find that an edge state
, we find that an edge state 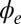 with energy
with energy 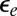 is characterized by a localization radius
is characterized by a localization radius
where 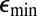 is the minimum of the bulk band. This result is illustrated in Fig. 7, for
is the minimum of the bulk band. This result is illustrated in Fig. 7, for 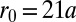 ,
, 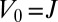 , and
, and 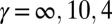 , where the wavefunctions amplitudes
, where the wavefunctions amplitudes 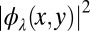 are plotted as a function of the x coordinate, and their corresponding energies
are plotted as a function of the x coordinate, and their corresponding energies 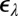 . For an infinitely abrupt trap (27),
. For an infinitely abrupt trap (27), 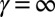 , all the edge states are located at the constant Fermi radius
, all the edge states are located at the constant Fermi radius 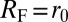 . Therefore, the edge states contribution to the density
. Therefore, the edge states contribution to the density 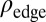 yields a clear circular signal, with localization length of the order of the lattice spacing a. In contrast, for finite γ, the populated edge states are localized on different radii
yields a clear circular signal, with localization length of the order of the lattice spacing a. In contrast, for finite γ, the populated edge states are localized on different radii  , leading to a broadening of the edge-state signal
, leading to a broadening of the edge-state signal 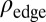 . For the situation illustrated in Fig. 7, this broadening is of the order
. For the situation illustrated in Fig. 7, this broadening is of the order 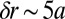 for
for 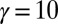 and
and 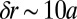 for
for 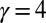 . Let us stress another crucial aspect of these smoothly confined QH systems, which is the fact that the angular velocity
. Let us stress another crucial aspect of these smoothly confined QH systems, which is the fact that the angular velocity 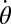 of the chiral edge states, as well as the number
of the chiral edge states, as well as the number 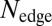 of available edge states within a bulk gap, highly depend on the potential’s smoothness γ: The angular velocity is maximized for highly abrupt confinements
of available edge states within a bulk gap, highly depend on the potential’s smoothness γ: The angular velocity is maximized for highly abrupt confinements 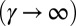 , whereas the number
, whereas the number 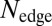 is larger for smooth potentials (19, 20, 24, 30). We numerically evaluated the angular velocity of the edge states (20, 24) for
is larger for smooth potentials (19, 20, 24, 30). We numerically evaluated the angular velocity of the edge states (20, 24) for  and
and 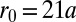 , and we found
, and we found 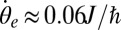 for
for 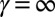 ,
, 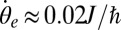 for
for 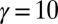 , and
, and 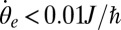 for
for 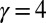 (and we note that the angular velocity
(and we note that the angular velocity 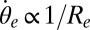 ). Scaling to a more realistic radius
). Scaling to a more realistic radius 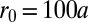 , we find that the edge states, which are populated below
, we find that the edge states, which are populated below 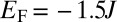 , undergo a rotation of
, undergo a rotation of 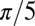 after a time
after a time
Fig. 7.
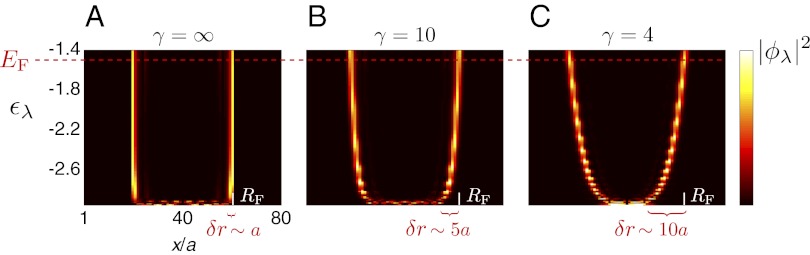
Smooth confinements and edge states. The amplitudes 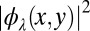 of the single-particle wavefunctions as a function of the x coordinate and their corresponding energy
of the single-particle wavefunctions as a function of the x coordinate and their corresponding energy  , and setting y at the center of the trap. Here,
, and setting y at the center of the trap. Here, 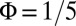 , and the external potential is given by
, and the external potential is given by 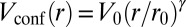 , with
, with 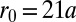 and
and 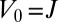 . (A)
. (A) 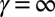 , (B)
, (B) 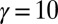 , and (C)
, and (C) 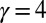 . The Fermi radius
. The Fermi radius 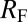 is shown for
is shown for 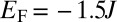 . The populated edge states
. The populated edge states 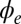 are localized on the radii
are localized on the radii 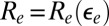 (Eq. 2), leading to a broadening
(Eq. 2), leading to a broadening 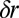 of their contribution to the spatial density
of their contribution to the spatial density 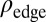 for finite γ.
for finite γ.
indicating that it is highly desirable to design a sharp circular confining trap 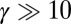 (27), to clearly observe the edge states rotating motion during reasonable experimental times
(27), to clearly observe the edge states rotating motion during reasonable experimental times 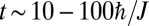 .
.
We now investigate the density evolution 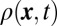 for smooth confining traps and initial Gaussian walls
for smooth confining traps and initial Gaussian walls 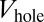 . First of all, we note that the presence of Gaussian walls does not destroy the edge states lying within the first bulk gap. In this bat geometry, the edge states are localized on the outer edge delimited by
. First of all, we note that the presence of Gaussian walls does not destroy the edge states lying within the first bulk gap. In this bat geometry, the edge states are localized on the outer edge delimited by 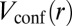 , but also on the smooth boundary delimited by the Gaussian potentials. Therefore, when
, but also on the smooth boundary delimited by the Gaussian potentials. Therefore, when 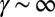 , the edge states behave as in Fig. 7A in the vicinity of the outer circular edge
, the edge states behave as in Fig. 7A in the vicinity of the outer circular edge  , whereas they behave similarly as in Fig. 7C in the vicinity of the Gaussian walls. We point out that, in our scheme, it is the behavior of the edge states near the outer circular edge that plays an important role. Indeed, as shown in Fig. 8A, replacing the infinitely abrupt walls
, whereas they behave similarly as in Fig. 7C in the vicinity of the Gaussian walls. We point out that, in our scheme, it is the behavior of the edge states near the outer circular edge that plays an important role. Indeed, as shown in Fig. 8A, replacing the infinitely abrupt walls 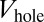 by Gaussian potentials does not qualitatively affect the evolution of the density
by Gaussian potentials does not qualitatively affect the evolution of the density 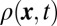 presented in Fig. 4A.
presented in Fig. 4A.
Fig. 8.
Smooth confinements and the density evolution. Evolution of the spatial density for 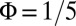 and
and 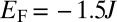 . The walls
. The walls 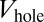 are produced by asymmetric Gaussian potentials, with standard deviations
are produced by asymmetric Gaussian potentials, with standard deviations 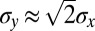 . The external confining potential is
. The external confining potential is 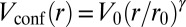 , with
, with 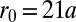 and
and  . (A)
. (A) 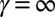 , (B)
, (B) 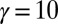 , and (C)
, and (C) 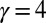 . Note the broadening
. Note the broadening 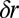 of the edge-state signal (Fig. 7) and also the deceleration of the motion as the confinement becomes smoother
of the edge-state signal (Fig. 7) and also the deceleration of the motion as the confinement becomes smoother 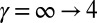 .
.
However, as can be anticipated from the discussion above, replacing the perfectly sharp potential 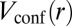 by smoother confinements,
by smoother confinements, 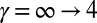 , has dramatic consequences on the dynamics. In Fig. 8B, which shows the evolution of the density for
, has dramatic consequences on the dynamics. In Fig. 8B, which shows the evolution of the density for 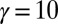 , we clearly observe the broadening
, we clearly observe the broadening  of the edge-state contribution
of the edge-state contribution  , as they progressively encircle the holes. We also note the slower motion undergone by the edge states, which have a reduced angular velocity
, as they progressively encircle the holes. We also note the slower motion undergone by the edge states, which have a reduced angular velocity 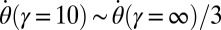 , as seen above. An even more dramatic situation is illustrated for the case
, as seen above. An even more dramatic situation is illustrated for the case  in Fig. 8C. These results demonstrate the robustness of the edge-state motion in the presence of smooth confining traps and Gaussian walls, but they greatly emphasize the importance of designing sharp external confinements to improve the experimental detectability of the topological edge states.
in Fig. 8C. These results demonstrate the robustness of the edge-state motion in the presence of smooth confining traps and Gaussian walls, but they greatly emphasize the importance of designing sharp external confinements to improve the experimental detectability of the topological edge states.
Conclusions
In this article, we introduced a simple, yet powerful, method to image the dynamics of topological edge states in atomic systems. Our scheme shapes an atomic gas, initially prepared in a topological phase, and directly images its time evolution. By explicitly revealing the presence of propagating chiral edge modes, this method provides an unambiguous signature of topological order in the context of cold atomic gases. Importantly, we have discussed the applicability of our method under realistic experimental conditions, emphasizing the importance of using sharp confining potentials to improve the detection of the edge-states signal. The schemes introduced in this work to reduce, or even eliminate, the irrelevant contribution of dispersive bulk states can be applied to a wide family of topological atomic systems, such as the promising Haldane-like optical lattice (12, 14) and fractional QH atomic gases (32–34). Finally, our method can be directly extended to visualize the propagation of  topological (spin-polarized) edge states, both in 2D (18, 35) and 3D (36), by using standard spin-dependent imaging methods (28).
topological (spin-polarized) edge states, both in 2D (18, 35) and 3D (36), by using standard spin-dependent imaging methods (28).
Materials and Methods
The system is prepared in the ground-state of the initial Hamiltonian,
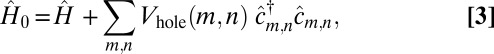 |
where the potential 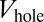 describes the walls initially present in the trap and where
describes the walls initially present in the trap and where 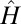 is given by Eq. 1. We denote the number of available sites before and after removing the walls by
is given by Eq. 1. We denote the number of available sites before and after removing the walls by 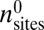 and
and 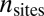 , respectively, and we define the ratio
, respectively, and we define the ratio 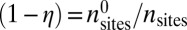 . When
. When 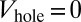 , the total number of sites within the trap is approximatively given by the area
, the total number of sites within the trap is approximatively given by the area 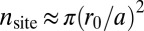 , while the outer circular edge contains about
, while the outer circular edge contains about 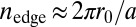 lattice sites. The holes in the density created by
lattice sites. The holes in the density created by 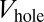 correspond to
correspond to 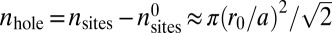 vacant sites, leading to the large ratio
vacant sites, leading to the large ratio 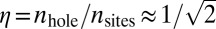 . For
. For 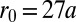 , the system initially contains
, the system initially contains 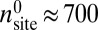 sites and the number of sites delimiting the edge of the bat is
sites and the number of sites delimiting the edge of the bat is 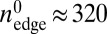 sites. Thus, the spacious holes used in our calculations lead to a large edge/bulk ratio. For
sites. Thus, the spacious holes used in our calculations lead to a large edge/bulk ratio. For  , and initially setting the Fermi energy in the lowest bulk gap, leads to the filling factor
, and initially setting the Fermi energy in the lowest bulk gap, leads to the filling factor 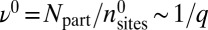 . After removing the walls
. After removing the walls  , the filling factor is reduced to the smaller value
, the filling factor is reduced to the smaller value 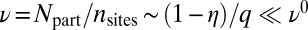 .
.
The groundstate of Hamiltonian Eq. 3 is written as
 |
where the operator 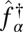 creates a particle in the single-particle state
creates a particle in the single-particle state 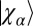 , with energy
, with energy  located below the Fermi energy
located below the Fermi energy 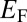 . Here
. Here 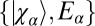 represents the complete set of single-particle eigenstates and eigenvalues satisfying the stationary Schrödinger equation
represents the complete set of single-particle eigenstates and eigenvalues satisfying the stationary Schrödinger equation
We are interested in the time evolution of the spatial density  after removing the walls
after removing the walls 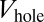 at
at 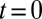 . The evolution of the single-particle states
. The evolution of the single-particle states 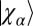 is then entirely governed by the Hamiltonian
is then entirely governed by the Hamiltonian 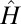 . It is therefore convenient to introduce the eigenstates and eigenvalues
. It is therefore convenient to introduce the eigenstates and eigenvalues  corresponding to the Hamiltonian
corresponding to the Hamiltonian 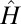 ,
,
We then define 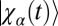 as the time evolution of the initial state
as the time evolution of the initial state 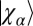 according to the Hamiltonian
according to the Hamiltonian  ,
,
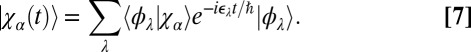 |
The spatial density 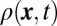 at time t is given by
at time t is given by
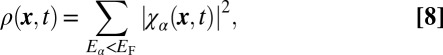 |
namely, the particle density 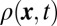 is entirely governed by the time-evolution of the initially occupied single-particle states. The time evolution of the atomic cloud, after releasing the walls
is entirely governed by the time-evolution of the initially occupied single-particle states. The time evolution of the atomic cloud, after releasing the walls  at
at 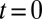 , can therefore be numerically evaluated through a direct diagonalization of the Hamiltonians
, can therefore be numerically evaluated through a direct diagonalization of the Hamiltonians 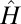 and
and 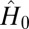 . In our study, a crucial aspect consists in identifying the regimes for which the edge states propagating around the initially forbidden regions provide a clear signal, which is not perturbed by the many bulk states. It is therefore desirable to separately evaluate the contributions of the initially populated bulk and edge states. We introduce the corresponding quantities
. In our study, a crucial aspect consists in identifying the regimes for which the edge states propagating around the initially forbidden regions provide a clear signal, which is not perturbed by the many bulk states. It is therefore desirable to separately evaluate the contributions of the initially populated bulk and edge states. We introduce the corresponding quantities
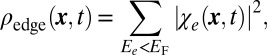 |
where the sum 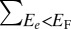 is restrained to the populated edge states with energies
is restrained to the populated edge states with energies 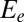 located within the bulk gap.
located within the bulk gap.
Supplementary Material
Acknowledgments
We thank J. Beugnon, I. Bloch, G. Bulnes Cuetara, M. Müller, and S. Nascimbène for discussions. This work was supported by the Fonds de la Recherche Scientifique (FNRS Belgium), Agence Nationale de la Recherche (ANR) via the project AGAFON (Artificial gauge fields on neutral atoms), European Research Council (ERC) project Quantum Gauge Theories and Ultracold Atoms (QUAGATUA), the Emergences program (Ville de Paris and Université Pierre et Marie Curie), and ERC Many-Body physics in gauge fields with ultracold Yb atoms in optical lattices (ManyBo) Starting Grant. Work at Innsbruck is supported by the integrated project AQUTE, the Austrian Science Fund through Spezialforschungsbereich (SFB) F40 FOQUS, and by the Defense Advanced Research Projects Agency (DARPA) Optical Lattice Emulator (OLE) program. I.B.S. acknowledges the financial support of the National Science Foundation (NSF) through the Physics Frontier Center at Joint Quantum Institute (JQI) and the Army Research Office (ARO) with funds from both the Atomtronics Multidisciplinary University Research Initiative (MURI) and DARPA OLE Program.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1300170110/-/DCSupplemental.
References
- 1.Hasan MZ, Kane CL. Colloquium: Topological insulators. Rev Mod Phys. 2010;82:3045–3067. [Google Scholar]
- 2.Qi XL, Zhang SC. Topological insulators and superconductors. Rev Mod Phys. 2011;83:1057–1110. [Google Scholar]
- 3.Thouless DJ, Kohmoto M, Nightingale MP, den Nijs M. Quantized Hall conductance in a two-dimensional periodic potential. Phys Rev Lett. 1982;49:405–408. [Google Scholar]
- 4.Kohmoto M. Zero modes and the quantized Hall conductance of the two-dimensional lattice in a magnetic field. Phys Rev B Condens Matter. 1989;39(16):11943–11949. doi: 10.1103/physrevb.39.11943. [DOI] [PubMed] [Google Scholar]
- 5.Hatsugai Y. Chern number and edge states in the integer quantum Hall effect. Phys Rev Lett. 1993;71(22):3697–3700. doi: 10.1103/PhysRevLett.71.3697. [DOI] [PubMed] [Google Scholar]
- 6.Ashoori RC, Stormer HL, Pfeiffer LN, Baldwin KW, West K. Edge magnetoplasmons in the time domain. Phys Rev B Condens Matter. 1992;45(7):3894–3897. doi: 10.1103/physrevb.45.3894. [DOI] [PubMed] [Google Scholar]
- 7.Ji Y, et al. An electronic Mach-Zehnder interferometer. Nature. 2003;422(6930):415–418. doi: 10.1038/nature01503. [DOI] [PubMed] [Google Scholar]
- 8.Zhang Y, et al. Distinct signatures for Coulomb blockade and Aharonov-Bohm interference in electronic Fabry-Perot interferometers. Phys Rev B. 2009;79:241304–241308. [Google Scholar]
- 9.Aidelsburger M, et al. Experimental realization of strong effective magnetic fields in an optical lattice. Phys Rev Lett. 2011;107(25):255301–255305. doi: 10.1103/PhysRevLett.107.255301. [DOI] [PubMed] [Google Scholar]
- 10.Dalibard J, Gerbier F, Juzeliūnas G, Öhberg P. Colloquium: Artificial gauge potentials for neutral atoms. Rev Mod Phys. 2011;83:1523–1543. [Google Scholar]
- 11.Brantut JP, Meineke J, Stadler D, Krinner S, Esslinger T. Conduction of ultracold fermions through a mesoscopic channel. Science. 2012;337(6098):1069–1071. doi: 10.1126/science.1223175. [DOI] [PubMed] [Google Scholar]
- 12.Alba E, Fernandez-Gonzalvo X, Mur-Petit J, Pachos JK, Garcia-Ripoll JJ. Seeing topological order in time-of-flight measurements. Phys Rev Lett. 2011;107(23):235301–235305. doi: 10.1103/PhysRevLett.107.235301. [DOI] [PubMed] [Google Scholar]
- 13.Zhao E, Bray-Ali N, Williams C, Spielman IB, Satija I. Chern numbers hiding in time-of-flight images. Phys Rev A. 2011;84:063629–063633. [Google Scholar]
- 14.Goldman N, et al. Measuring topology in a laser-coupled honeycomb lattice: From Chern insulators to topological semi-metals. New J Phys. 2013 15:013025. [Google Scholar]
- 15.Price HM, Cooper NR. Mapping the Berry curvature from semiclassical dynamics in optical lattices. Phys Rev A. 2012;85:033620. [Google Scholar]
- 16.Umucalilar RO, Zhai H, Oktel MÖ. Trapped Fermi gases in rotating optical lattices: Realization and detection of the topological hofstadter insulator. Phys Rev Lett. 2008;100(7):070402–070405. doi: 10.1103/PhysRevLett.100.070402. [DOI] [PubMed] [Google Scholar]
- 17.Scarola VW, Das Sarma S. Edge transport in 2D cold atom optical lattices. Phys Rev Lett. 2007;98(21):210403–210406. doi: 10.1103/PhysRevLett.98.210403. [DOI] [PubMed] [Google Scholar]
- 18.Goldman N, et al. Realistic time-reversal invariant topological insulators with neutral atoms. Phys Rev Lett. 2010;105(25):255302. doi: 10.1103/PhysRevLett.105.255302. [DOI] [PubMed] [Google Scholar]
- 19.Stanescu TD, Galitski V, Das Sarma S. Topological states in two-dimensional optical lattices. Phys Rev A. 2010;82:013608. [Google Scholar]
- 20.Goldman N, Beugnon J, Gerbier F. Detecting chiral edge states in the Hofstadter optical lattice. Phys Rev Lett. 2012;108(25):255303–255305. doi: 10.1103/PhysRevLett.108.255303. [DOI] [PubMed] [Google Scholar]
- 21.Kraus CV, Diehl S, Zoller P, Baranov MA. Preparing and probing atomic Majorana fermions and topological order in optical lattices. New J Phys. 2012;14:113036–113052. [Google Scholar]
- 22.Killi M, Paramekanti A. Use of quantum quenches to probe the equilibrium current patterns of ultracold atoms in an optical lattice. Phys Rev A. 2012;85:061606–061610. [Google Scholar]
- 23.Papp SB, et al. Bragg spectroscopy of a strongly interacting 85Rb Bose-Einstein condensate. Phys Rev Lett. 2008;101(13):135301–135304. doi: 10.1103/PhysRevLett.101.135301. [DOI] [PubMed] [Google Scholar]
- 24.Goldman N, Beugnon J, Gerbier F. Identifying topological edge states in 2D optical lattices using light scattering. Eur Phys J Special Topics. 2013;217:135–152. [Google Scholar]
- 25.Jaksch D, Zoller P. Creation of effective magnetic fields in optical lattices: The Hofstadter butterfly for cold neutral atoms. New J Phys. 2003;5:56. [Google Scholar]
- 26.Gerbier F, Dalibard J. Gauge fields for ultracold atoms in optical superlattices. New J Phys. 2010;12:033007. [Google Scholar]
- 27.Meyrath TP, Schreck F, Hanssen JL, Chuu CS, Raizen MG. Bose-Einstein condensate in a box. Phys Rev A. 2005;71:041604–041607. [Google Scholar]
- 28.Weitenberg C, et al. Single-spin addressing in an atomic Mott insulator. Nature. 2011;471(7338):319–324. doi: 10.1038/nature09827. [DOI] [PubMed] [Google Scholar]
- 29.Hofstadter DR. Energy levels and wave functions of Bloch electrons in rational and irrational magnetic fields. Phys Rev B. 1976;14:2239–2249. [Google Scholar]
- 30.Buchhold M, Cocks D, Hofstetter W. Effects of smooth boundaries on topological edge modes in optical lattices. Phys Rev A. 2012;85:63614–63625. [Google Scholar]
- 31.Sanchez-Palencia L, Lewenstein M. Disordered quantum gases under control. Nat Phys. 2010;6:87–95. [Google Scholar]
- 32.Sørensen AS, Demler E, Lukin MD. Fractional quantum Hall states of atoms in optical lattices. Phys Rev Lett. 2005;94(8):086803–086806. doi: 10.1103/PhysRevLett.94.086803. [DOI] [PubMed] [Google Scholar]
- 33.Cooper NR. Rapidly rotating atomic gases. Adv Phys. 2008;57:539–616. [Google Scholar]
- 34.Graß T, Juliá-Díaz B, Lewenstein M. Quasihole dynamics as a detection tool for quantum Hall phases. Phys Rev A. 2012;86:053629–053635. [Google Scholar]
- 35.Béri B, Cooper NR. Z(2) topological insulators in ultracold atomic gases. Phys Rev Lett. 2011;107(14):145301–145305. doi: 10.1103/PhysRevLett.107.145301. [DOI] [PubMed] [Google Scholar]
- 36.Bermudez A, et al. Wilson fermions and axion electrodynamics in optical lattices. Phys Rev Lett. 2010;105(19):190404–190407. doi: 10.1103/PhysRevLett.105.190404. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.