Capture and quality control mechanisms for ATP binding

Abstract

The catalytic events in members of the nucleotidylyl transferase superfamily are initiated by a millisecond binding of ATP in the active site. Through metadynamics simulations on a class I aminoacyl-tRNA synthetase (aaRSs), the largest group in the superfamily, we calculate the free energy landscape of ATP selection and binding. Mutagenesis studies and fluorescence spectroscopy validated the identification of the most populated intermediate states. The rapid first binding step involves formation of encounter complexes captured through a fly-casting mechanism that acts up on the triphosphate moiety of ATP. In the slower nucleoside binding step, a conserved histidine in the HxxH motif orients the incoming ATP through base-stacking interactions resulting in a deep minimum in the free energy surface. Mutation of this histidine significantly decreases the binding affinity measured experimentally and computationally. The metadynamics simulations further reveal an intermediate quality control state that the synthetases and most likely other members of the superfamily use to select ATP over other nucleoside triphosphates.

Introduction

Extensive NMR and molecular dynamics (MD) simulation studies emphasize that enzymatic catalysis is tightly coupled to enzyme conformational changes,^1–3 which can be theoretically described by a walk on the protein free energy landscape. Yet, a quantitative understanding is missing for how the substrate binds to the often deeply buried active site. Recently, brute-force MD simulations have been performed to investigate the dynamics of substrate binding^4,5 on the microsecond timescale. These studies revealed an ensemble of transition pathways at the atomic level, and greatly expanded our understanding of substrate binding.⁴ However, many substrates require milliseconds or even longer to bind. Sufficient sampling of these rare events has been computationally too expensive to be performed.

Metadynamics techniques developed by Parrinello, Laio and co-workers^6,7 enhance sampling to successfully quantify substrate binding by calculating the underlying free energy landscapes.^8–11 In metadynamics, sampling is accelerated by adding a biasing potential based on pre-defined “collective variables” (CVs) to overcome the free energy barrier. While not unique, this set of CVs should discriminate between the states of interest and approximately describe the true “reaction coordinate”. For an appropriately chosen set of variables, the biasing potential in metadynamics can be used to estimate the underlying free energy surface (FES),^7,12 from which the main binding pathway and interactions with the protein can be determined.

Adenosine-5′-triphosphate (ATP) is a ubiquitous coenzyme that provides free energy for numerous enzymatic reactions. These ATP-driven reactions typically involve ATP and substrate binding, followed by subsequent chemistry and product release. Although several studies have compared the protein dynamics of the bound state with the unbound state,^13–16 the dynamic process of ATP binding per se, its associated enzyme conformational changes, and importantly the selection of ATP over other nucleoside triphosphates have remained elusive. Herein, we addressed these questions by combining metadynamics, steered molecular dynamics (SMD),^17,18 unbiased molecular dynamics (MD) simulations, mutagenesis as well as fluorescence spectroscopy to calculate and examine the free energy landscape of ATP binding to glutamyl-tRNA synthetase (GluRS), a member of the class-I aminoacyl-tRNA synthetase (aaRS) family.¹⁹

The class I aaRSs are quintessential members of the nucleotidylyl transferase (NT) superfamily that also includes several key enzymes for biosynthesis of NAD and coenzyme A (http://scop.berkeley.edu/). These superfamily members catalyze closely-related chemical reactions (Figure S1), in which the nucleophilic attack of the α-phosphate of ATP results in an activated adenylate intermediate with a concomitant release of pyrophosphate. The ATP binding domain in this superfamily has a classical Rossmann fold—an alternating α/β topology present in nucleotide-binding proteins such as kinases and dehydrogenases. Across the superfamily, a conserved “HxxH” motif is located in the loop connecting the first β-strand to the following α helix.²⁰ In aaRS, mutation of the “HxxH” motif significantly reduces the k_cat by 10⁵-fold and K_M by 4-fold.²¹ The class I aaRSs also contain a signature “KMSKS” motif that is remotely related to the “Walker” sequence found in other nucleotide binding proteins,^22,23 including myosin and ATP synthase.

We chose GluRS as an optimal model to investigate ATP binding for not only the class I aaRSs but also the NT superfamily. Class I aaRSs represent the largest family of NT and bind ATP as a prerequisite for the universal aminoacylation reactions that is critical in setting the genetic code.²⁴ In GluRS, ATP binds to an inactive conformation, which switches to an active state upon tRNA binding.²⁵ This effectively removes the interference of the ensuing chemical reactions from the experimental measurement of ATP binding. Furthermore, high-resolution X-ray crystal structures of GluRS in various ligand states^26–28 enabled us to explore the dynamics of ATP binding at atomic resolution using MD simulations.

Our metadynamics simulations demonstrated that the most stable conformation in the FES corresponds to the crystal structure. Moreover, the calculated binding free energy is within the error of experimental measurement. The string method²⁹ was used to identify the dominant ATP binding pathway. From the pathway, we identified an intermediate state in which ATP forms base-stacking interaction with the second histidine in the critical signature “HIGH” motif. Mutation of this histidine results in a substantial decrease of ATP binding affinity. We observed intermediate conformational states that GluRS uses to select ATP over other nucleoside triphosphates. This observation was further verified by unbiased MD simulations. Taken together, our simulations provide a complete, quantitative picture of ATP binding at atomic resolution and yield predictions that have been verified experimentally. The detailed binding mechanism may provide insights for other enzymes in the nucleotidylyl transferase superfamily that share a similar ATP binding site.

Materials and Methods

Simulation systems

The bound GluRS:Glu:ATP complex and the unbound GluRS:Glu complex were modeled based on two crystal structures of Thermus thermophilus GluRS: the 1.80 Å structure of GluRS:Glu:ATP ternary complex (PDB entry 1J09)²⁷ and 1.98 Å structure of GluRS:Glu binary complex (PDB entry 2CUZ),²⁸ respectively. The program PROPKA³⁰ was used to perform pK_a calculations to aid the assignment of side-chain protonation states. In the crystal structure, ATP forms a stable complex with Mg²⁺and three water molecules in GluRS active site. This [ATP·Mg·3H₂O]²⁻ complex is stable in our MD simulations (Figure S3). Further validation of this assignment is provided in the supporting information. Both systems were then solvated in ~80×135×72 ų water boxes with TIP3P water molecules to ensure the minimum distance between any protein/ATP atom and the side of the box is 12 Å and neutralized with 5 (3) K⁺ ions for the bound (unbound) complex in VMD.³¹ The final systems contain ~7.1×10⁴ atoms.

In the unbiased simulation of ATP binding to GluRS:Glu, the water box was enlarged to allow five [ATP·Mg·3H₂O]²⁻ molecules to be placed in the bulk with randomized orientations and sufficient separation. The minimum distance between ATP and GluRS was larger than 15 Å and the minimum distance between each ATP molecule was larger than 14 Å, such that motion of each ATP can be considered as independent during the early phase of the simulation. Four different sets of ATP configurations were simulated (ATP binding I to ATP binding IV in Table S1). To further enhance the sampling, for each ATP configuration, four distinct GluRS:Glu complexes were used based on the conformational diversity of the KMSKS loop (see below). Each system was solvated and neutralized using the same protocol as described above. The additional ATP and water molecules increases the size of the system to ~100 ×100 ×160 ų with the final systems contain ~1.4×10⁵ atoms.

To perform SMD simulations of pulling ATP in water solvent, the [ATP·Mg·3H₂O]²⁻ complex was solvated in a 48×36×30 ų water box. The system was then neutralized using the protocol described above. The final system contains ~4.1×10³ atoms.

Additional SMD simulations have been performed to pull ATP away from the unbound state. These simulations require an enlarged water box such that the ATP molecule is at least 12 Å away from the GluRS or its mirror images throughout the trajectory. The unbound state sampled by metadynamics (see below) was solvated in a water box whose x axis was extended by 10 Å. The resulting system (~9.4×10⁴ atoms) was minimized and equilibrated using the protocol described above with the phosphorus atom of ATP being fixed and constrained, respectively. Six conformations in 100 ps intervals were chosen from the final stage of equilibration and used as the initial conformations for subsequent SMD simulations.

Unbiased MD simulations

A total of ~250 ns unbiased MD simulations were performed (Table S1), using the program NAMD 2.7³² with CHARMM 27 parameter set.³³ All unbiased simulations were done with periodic boundary conditions using the NPT ensemble. Langevin dynamics was used to keep the temperature at 298 K with a damping constant of 5 ps⁻¹, and a Langevin piston³⁴ was applied to maintain the pressure at 1 atm. The bonded, nonbonded, and electrostatic interactions were calculated at time steps of 1, 2, and 4 fs, respectively. For nonbonded interaction, the switching (cutoff) distance was set at 10 (12) Å. The Particle Mesh Ewald (PME) method³⁵ with a grid density of at least 1 Å⁻³ was used for computing long-range electrostatic interactions. The minimization and thermalization of the bound (for the metadynamics) and unbound systems (for sampling of the conformational diversity of the KMSKS loop) were performed as described previously.³⁶ Both systems were equilibrated for 3 ns followed by 22 ns production run.

In order to generate representative structural ensembles for the unbiased ATP binding simulations, root-mean-square deviation (RMSD) conformational clustering was performed. Structures were extracted in 200 ps intervals over the simulation trajectory of the unbound state. The resulting 110 structures were superimposed using all C_α atoms to remove overall rotation and translation. The RMSD of all heavy atoms in the KMSKS loop (residue 241 to 250) was chosen as the distance metric and the clustering was performed using the cluster program in VMD.³¹ Four main clusters were selected with a cutoff of 1 Å; from each cluster, one snapshot was chosen for ATP binding simulations.

To elucidate the quality control mechanism of GluRS over the incoming nucleoside triphosphate, a 1.2-ns simulation was performed for GluRS:Glu:ATP or GluRS:Glu:GTP with the adenine distance and ribose distance (see below) restrained to 4.34 and 6.31 Å, respectively. This restraint corresponds to the high free energy state we identified from the metadynamics calculations (see below) and is hypothesized to be the starting point of the quality control step. The first 0.2 ns is considered as equilibration, and 50 distinctive configurations were extracted in 20 ps intervals over the rest 1 ns simulation. Each configuration is used as the initial configuration for twenty 10-ps trajectories, whose initial velocities were drawn randomly from a Maxwell-Boltzmann distribution. Therefore, for each GluRS:Glu:ATP and GluRS:Glu:GTP system, 1,000 10-ps simulations have been performed to simulate the binding of nucleosides (Table S1).

Metadynamics simulations

Metadynamics is a powerful algorithm to rapidly explore and accurately determine the free energy landscape of a system.^6,7,37 We applied a new variant of metadynamics, well-tempered metadynamics,⁷ using program NAMD 2.7³² in conjunction with the PLUMED plugin.³⁸ In the well-tempered metadynamics formalism,⁷ the FES at time t, F(s,t), as a function of the collective variable, s, is calculated by

$$F(s,t)=-\frac{T+\mathrm{\Delta }T}{\mathrm{\Delta }T}V(s,t),$$ (1)

where V(s,t) is the biasing potential added to the system, T + ΔT is the enhanced temperature of CV and T is the simulation temperature (298 K). Based on previous studies,^7,9 an 11-fold reduction in the barrier is achieved by assigning ΔT = 2980 K. At long time, F(s,t) converges to true FES of the system, F(s). The history-dependent biasing potential V(s,t) is constructed by summing the Gaussians deposited along the trajectory:

$$V(s,t)=\sum _{t^{\prime }=\tau ,2\tau ,\cdots }^t\omega {\text{e}}^{V(s,t^{\prime })/\mathrm{\Delta }T}exp\left(-\frac{{(s-s(t^{\prime }))}^2}{2{\sigma }^2}\right).$$ (2)

Each term in the summation is a Gaussian of width σ, height ωe^{V(s,t′)/ΔT} and is deposited at time t′ = nτ on the value of s(t′). Unlike standard metadynamics, at each deposition time t′, the initial height of the Gaussians, ω, is scaled down by the exponential of the concurrent biasing potential V(s,t′) over ΔT, a parameter tuning the height of Gaussians. This new feature accelerates the convergence of FES and avoids the sampling of physically-irrelevant high free energy states caused by over-filling. The definition of CVs for different simulations and the corresponding parameters are detailed in the following subsections. In all metadynamics simulations, the starting point is taken from the equilibrated bound GluRS:Glu:ATP complex. The results were analyzed and visualized by a combination of homemade Python, MATLAB programs and VMD.³¹

Metadynamics simulation of KMSKS loop’s conformation in ATP binding

Two CVs were used to investigate the conformational change of KMSKS loop in the ATP binding process. Both CVs had the same initial deposition rate of 1.0 kcal/(mol · ps), which gradually decreased in the simulation according to the well-tempered metadynamics formalism. The first CV characterized the distance between ATP and its binding site in GluRS. It was calculated as the center-of-mass (CoM) distance between heavy atoms in ATP and a list of atoms of the ATP binding site in GluRS (Table S2). The width of the Gaussian was 0.5 Å. To enhance the sampling of the relevant CV space, a quartic wall was applied to this CV to prohibit the distance exceeding 20 Å, which is sufficient for ATP to completely dissociate from GluRS. To capture the flexibility of the KMSKS loop, the second CV was the mean square deviation (MSD) of the C_α atoms in the KMSKS loop (residues 241 to 250) as well as the following side chain atoms: NZ atoms for Lys243, Lys246 and CZ atom for Arg247. The same set of atoms were used for alignment and the crystal structure was used as the reference. The width of this CV was 0.07 Ų. The metadynamics simulation has been run for the equivalent of 60 ns in classical MD “time”. During the course of the simulation, all of the relevant low free energy CV space was explored, and at the end of the simulation, the weighted hill height was almost zero (< 0.002 kcal/mol).

Metadynamics simulation of nucleoside binding

To gain a more detailed picture of ATP binding after the docking of its triphosphate group, two additional CVs were chosen to monitor the interaction between GluRS and the nucleoside part of ATP. The initial deposition rate for both CVs was 0.4 kcal/(mol · ps). The first CV, adenine distance, was the CoM distance between N1, N6 atoms of ATP and backbone N and O atoms of Leu236. These atoms form two hydrogen bonds and are responsible for the recognition of the adenine base. Similarly, the second CV, ribose distance, was the CoM distance between two oxygen atoms on the backbone carboxyl group of glutamate substrate and O3′ of the ribose. The hydrogen bond between these atoms anchors the ribose of ATP in the crystal structure. For both CVs, the width was 0.2 Å and a quartic wall was applied to prohibit the distance from exceeding 11 Å. The metadynamics simulation has been run for the equivalent of 60 ns in classical MD “time”. During the course of the simulation, all of the relevant low free energy CV space was explored, and at the end of the simulation, the weighted hill height was almost zero (< 0.002 kcal/mol).

To assess the accuracy and reproducibility of the metadynamics calculation, we performed another round of metadynamics simulation starting from an intermediate state (Figure 4C) rather than the bound state. The same set of CVs was used, but we restrained the distance within 6 Å to focus on the nucleoside selection step. We varied the width of the Gaussian to be 0.3 Å, and the initial deposition rate was lowered to 0.2 kcal/(mol · ps). The simulation has been run for 20 ns in classical MD “time”, and at the end of the simulation, the weighted hill height was almost zero (< 0.002 kcal/mol).

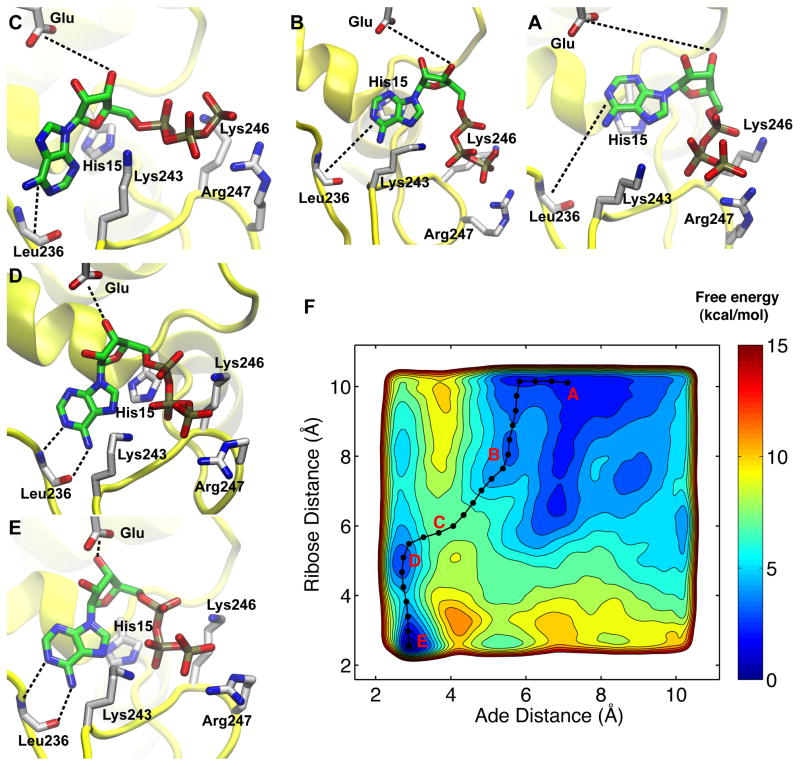
Figure 4. Free energy surface of adenine and ribose binding as a function of two distance CVs.

The contours were drawn every 1 kcal/mol. The four PMF basins (A, B, D, E) and the putative transition state (C) along the main binding pathway (black line and dots) are highlighted in the free-energy surface (F). The five snapshots surrounding the FES represented the following configurations: A, the starting configuration in which adenine forms base-stacking interaction with His15; B, the sliding of adenine along the surface of His15 side chain; C, the putative transition state; D, an intermediate state in which the adenine has docked but the ribose has not; E, the fully bound state. The ATP and its interacting residues were shown in licorice, while the protein was shown in yellow cartoon. The hydrogen atoms were not displayed for clarity.

SMD simulation of ATP pulling

To test if there is a residual free energy change of ATP unbinding after it is 20 Å away from its binding site, additional SMD simulations were performed to irreversibly pull ATP along the x axis for 10 Å (Figure S4) and the resulting force-extension profile was used to reconstruct the free energy change using the Jarzynski identity.³⁹ The center of mass of the heavy atoms in the [ATP:Mg]²⁻ complex was pulled at a constant velocity of 10 Å/ns. To ensure the validity of stiff-spring approximation,¹⁸ the force constant was chosen to be 1,000 pN/Å. For the SMD simulations in a water box, fifty 1-ns SMD runs were performed with different initial velocities. For the SMD pulling runs of the unbound state, twenty 1-ns SMD pulling runs with randomized initial velocities were performed from each of the six distinctive initial conformations Table S1. The free energy of the unbiased system was reconstructed from the SMD simulations following previously described method,¹⁸ and is summarized in the supporting information.

Cloning and in vitro transcription of the T. thermophilus tRNA^Glu gene

To reconstitute the T. thermophilus GluRS aminoacylation complex in vitro, the gene for T. thermophilus ${\text{tRNA}}_{\text{GAG}}^{\text{Glu}}$ was amplified via PCR from 50 ng T. thermophilus genomic DNA (American Type Culture Collection, Manassas, VA) and was cloned into pUC18 vector using BamHI and HindIII restriction sites to yield pUC18LiTttRNAGlu. The plasmid (450 μg) was digested overnight with 25 units of SacII and then used as a template for in vitro runoff transcription.⁴⁰ The SacII digestion cleaves the tRNA template after the penultimate nucleotide at the 3′ end to generate tRNA^Glu without the terminal ${\text{A}}_{76}({\text{tRNA}}_{\mathrm{\Delta }{A}_{\text{76}}}^{\text{Glu}})$. The ${\text{tRNA}}_{\mathrm{\Delta }{A}_{76}}^{\text{Glu}}$ transcript was purified by electrophoresis on a 10% polyacrylamide gel that contained 8 M urea, and the terminal A₇₆ was added enzymatically with nucleotidylyl transferase as described previously.⁴¹

Preparation of wild-type T. thermophilus GluRS

The T. thermophilus GluRS gene was amplified via PCR from 50 ng T. thermophilus genomic DNA and cloned into pET15b vector using NdeI and BamHI sites. The resulting plasmid p15LiTtGluRS was used to transform E. coli BL21 (DE3) strain to express GluRS via IPTG induction. The GluRS was purified via HIS-Select HF nickel affinity resin (Sigma, St. Louis, MO) followed by HiTrap 16/60 size-exclusion Superdex 75 purification column (GE Healthcare, Piscataway, NJ). The activity of GluRS was tested by in vitro aminoacylation assays containing 60 mM tris(hydroxymethyl)aminomethane (Tris) pH 7.5, 10 mM MgCl₂, 1 mM dithiothreitol (DTT), 40 μM [¹⁴C]-glutamate (GE Healthcare), 2 mM ATP, 5 μM tRNA^Glu and 100 nM GluRS. The assays were performed at 37 °C as described previously in detail.⁴²

Preparation of T. thermophilus GluRS mutants

The plasmid p15LiTtGluRS containing the wild-type T. thermophilus GluRS gene was used as a template to introduce alanine mutations of His15 (H15A), Lys246 (K246A) and Arg247 (R247A) for subsequent overexpression and purification of each protein. The site-directed mutagenesis was introduced via plasmid mutagenesis. A 25-μL thermocycling reaction containing 25 ng of plasmid DNA template, 50 ng of each forward and reverse primer (sequences are provided in Table S3), 50 μM dNTPs, and 1.25 unit of Pfu DNA polymerase in commercial buffer was heated at 95 °C for 1 min. The DNA was then amplified for 20 cycles under the following conditions: 95 °C for 1 min, 53 °C for 1 min (60 °C for H15A), and 68 °C for 10 min. The DNA was subsequently digested with 20 units of DpnI for 3 hours at 37 °C to eliminate the template DNA and used for transformation of E. coli DH5α strain. The DNA sequence of the mutant GluRS genes were confirmed by UIUC core sequencing facility. The mutant GluRS proteins were purified in the same protocol as the wild-type enzyme.

Fluorescence Measurements of ATP binding constant

Fluorescence measurements of both wild-type and mutant GluRS were performed at 25 °C using a Cary Eclipse fluorescence spectrophotometer (Varian, Inc.). To measure the intrinsic fluorescence of T. thermophilus GluRS, the protein was excited at 295 nm, and its emission was detected at 340 nm. To measure the binding constant of ATP, titrations were carried out at 25 °C following the protocol by Pugh et al.⁴³ The reaction buffer contained 60 mM Tris-HCl pH 7.5, 10 mM MgCl₂, 1 mM DTT and 1 mM glutamate. After equilibrating at 25 °C for 2 min, the base-line fluorescence was recorded before addition of 0.25 μM GluRS. Increases in the fluorescence were recorded over 1 min and attributed to the fluorescence of GluRS:Glu complex. Upon addition of each aliquot of ATP, the fluorescence signal was allowed to equilibrate, recorded over 1 min and averaged. To correct the inner filter effect of ATP,⁴⁴ the corrected fluorescence intensity F_corr was calculated using the observed fluorescence intensity F_obs with the following equation:⁴⁵

$$\frac{F_{\mathit{corr}}}{F_{\mathit{obs}}}=\frac{2.3{dA}_{ex}}{1-{10}^{-{dA}_{ex}}}\times {10}^{{gA}_{em}}\times \frac{2.3{sA}_{em}}{1-{10}^{-s{A}_{em}}},$$ (3)

where A_ex is the absorbance/cm of the solution at the excitation wavelength, A_em is the absorbance/cm of the solution at the emission wavelength, and d, g, and s are cuvette dimensions defined in Figure 2 by Puchalski et al.⁴⁵ The K_d value was determined by fitting the experimental data to the following binding equation with 1:1 binding stoichiometry:

$$\frac{{[\mathit{ATP}]}_{\mathit{bound}}}{{[E]}_{\mathit{total}}}=\frac{{[\mathit{ATP}]}_{\mathit{free}}}{K_d+{[\mathit{ATP}]}_{\mathit{free}}}.$$ (4)

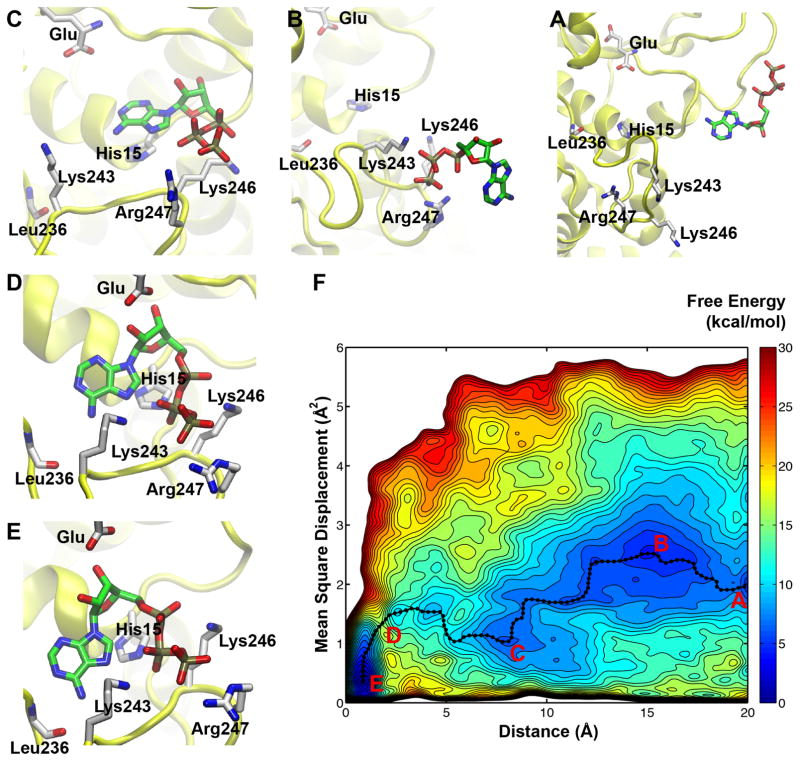
Figure 2. Free energy surface of ATP binding to GluRS:Glu as a function of the distance and mean square displacement CVs.

The contours are drawn every 1 kcal/mol. The four main free energy basins (A–C, E) and the putative transition state (D) are highlighted on the free-energy surface (F). The five snapshots displayed in the surrounding panels represent the following configurations: A, unbound state; B, “encounter complex”; C, an intermediate state features base-stacking interaction between His15 and adenine; D, relative high energy state; E, fully bound state. The ATP and its interacting residues are shown in licorice, while the protein is shown in yellow. The hydrogen atoms are not displayed for clarity.

All the analysis were performed using homemade Python scripts.

Results and discussion

Dynamics of the ATP-bound state

GluRS is one of the three aaRSs that catalyze the amino acid activation step only in the presence the cognate tRNA.²⁵ In GluRS:Glu:ATP ternary complex, ATP adopts an inactive conformation: the α-phosphate of ATP is more than 6.2 Å away from the carboxyl group in glutamate backbone.²⁷ This distance is reduced to 2.7 Å in TrpRS, where ATP adopts an active conformation.⁴⁶ As indicated in Figure S2, ATP remains inactive throughout our unbiased MD simulation of the ternary complex. Therefore, our simulation faithfully represents the inactive ATP conformation.

X-ray crystallographic study further revealed that in the active site of GluRS, ATP forms an [ATP·Mg·3H₂O]²⁻ complex,²⁷ where Mg²⁺ has an ideal octahedral coordination with one non-bridging oxygen from each of the three phosphate groups and oxygen from each of the three surrounding water molecules, as in Figure 1A. Theoretical studies showed that this coordination state is one of the two most stable configurations of ATP:Mg²⁺ complex in aqueous solution.⁴⁷ Significantly, this coordination state is also conserved in the nucleotidylyl transferase superfamily,^48,49 and remains stable in our 22-ns unbiased MD simulation, as shown in Figure S3.

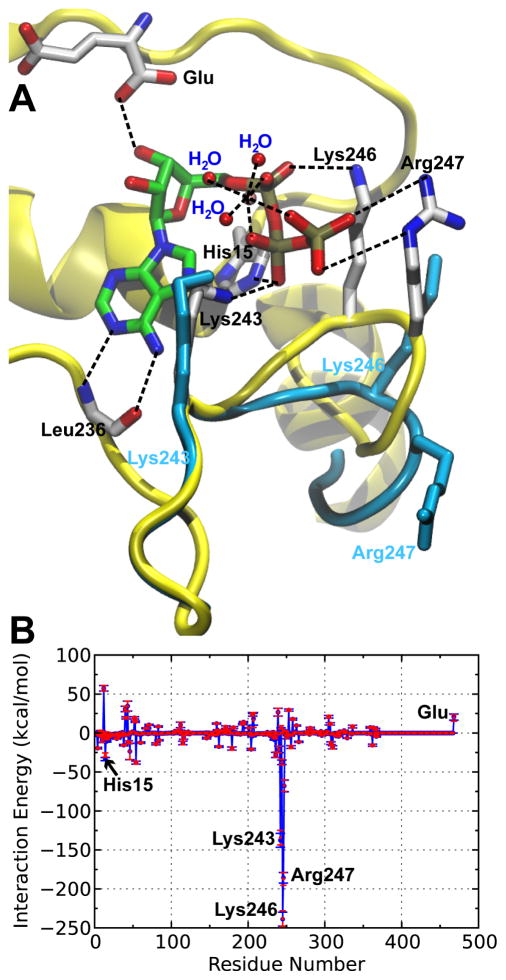
Figure 1. Three-dimensional structure and energetics of GluRS:Glu:ATP ternary complex.

A. Crystal structure of the GluRS:Glu:ATP ternary complex (PDB: 1J09). The ATP adopts a configuration which all three phosphate groups are coordinated with the Mg²⁺ (pink), together with three extra water molecules to form a stable octahedral structure. The hydrogen bonds and salt bridges were indicated by dashed lines and the key residues interacting with ATP were annotated. The positions of the three positively-charged residues and KMSKS loop (cyan) in the absence of ATP is also shown (PDB: 2CUZ). The significant rearrangement of Lys246, Arg247 together with the latter half of the KMSKS loop is a result of ATP binding. B. Mean local nonbonded interaction energies (blue) and electrostatic interactions (red) of GluRS:Glu with [MgATP·3H₂O]²⁻. The results were based on a 22-ns MD simulation of the ternary complex and the error bars represented standard deviations calculated from 2,200 frames.

To elucidate the energetic basis of ATP binding, the local nonbonded interaction energies between each residue in GluRS and ATP were averaged over simulation of the bound state and plotted in Figure 1B. The stabilization is mainly attributed to the electrostatic interaction with three positively charged residues in the KMSKS loop,⁵⁰ where Lys246 displays the highest stabilization energy, consistent with affinity labeling experiments.⁵¹ The pivotal role of the KMSKS loop in ATP binding is further demonstrated by the structural alignment of the bound and unbound states, as indicated in Figure 1A. ATP binding leads to a large conformational change of the KMSKS loop, which shifts the GluRS active site from an “open” conformation (unbound state) to a “closed” conformation (bound state). Similar conformational changes have also been observed in other class I aaRSs^46,52,53 as well as other members of the nucleotidylyl transferase superfamily,⁴⁹ and have been considered to support an “induced-fit” mechanism of binding.^49,52

Metadynamics reveals the main pathway for ATP binding

The free energy surface of ATP binding—shown in Figure 2—is constructed from 60-ns metadynamics simulations, using the mean-square-displacement (MSD) of the KMSKS loop along with the distance between ATP and GluRS binding site as the CVs of metadynamics simulations. The accuracy of the free energy calculation is demonstrated by a perfect overlap between the global minimum and the crystallographic state, with an average MSD around 0.4 Ų. Furthermore, the free energy difference between the bound (state E in Figure 2) and unbound states (state A in Figure 2) is 7 kcal/mol. This prediction is consistent with the experimental results (see below). Further SMD simulations justified the assignment of the unbound state, and lowered the free energy to 6.6 kcal/mol (Figure S4 and supporting text).

The free energy surface reveals the atomic details of the ATP binding at an unprecedented level. The main binding pathway of ATP is identified by using the zero-temperature string method²⁹ to calculate the minimum free energy pathway between the bound and unbound states. Representative conformations corresponding to the free energy minima along the path are depicted in Figure 2. By inspecting these conformations, we delineated the binding of ATP into the following five states that characterize the two main stages.

The first stage includes the binding of triphosphate group and the formation of encounter complexes. Figure 2A corresponds to the unbound state, in which ATP does not interact directly with GluRS and the KMSKS loop of GluRS adopts an “open” conformation. The ensemble of encounter complexes are represented by a wide basin in the free energy landscape, and Figure 2B depicts one representative snapshot. In these encounter complexes, ATP binds to GluRS exclusively via the interaction between its triphosphate group and at least one of the three positively charged residues in KMSKS loop. The free energy map predicts that binding of triphosphate is a fast, downhill process, without any significant free energy barrier. Additional unbiased MD simulations have been performed to confirm this prediction and further strengthen the free energy calculations (see below).

In the second stage, nucleoside binding follows the encounter complex and involves an intermediate state, as shown in Figure 2C. With the triphosphate group anchored in a conformation similar to the crystal structure, the adenine base flips inward and forms a base-stacking interaction with His15 in the active site. As Figure 2D shows, further binding of ATP abolishes this base-stacking interaction to allow the binding of ribose, which results a relative high energy state. Figure 2E shows the structure of the bound state, which corresponds to the global minimum of the free energy surface.

Free energy calculations suggest a significant barrier (11 kcal/mol) for the second stage. Hence, the binding of the nucleoside moiety is the rate-limiting step of ATP binding. The MSD of the KMSKS loop gradually decreases with the binding of ATP, in agreement with the “induced-fit” model.

Experimental verification of metadynamics simulation

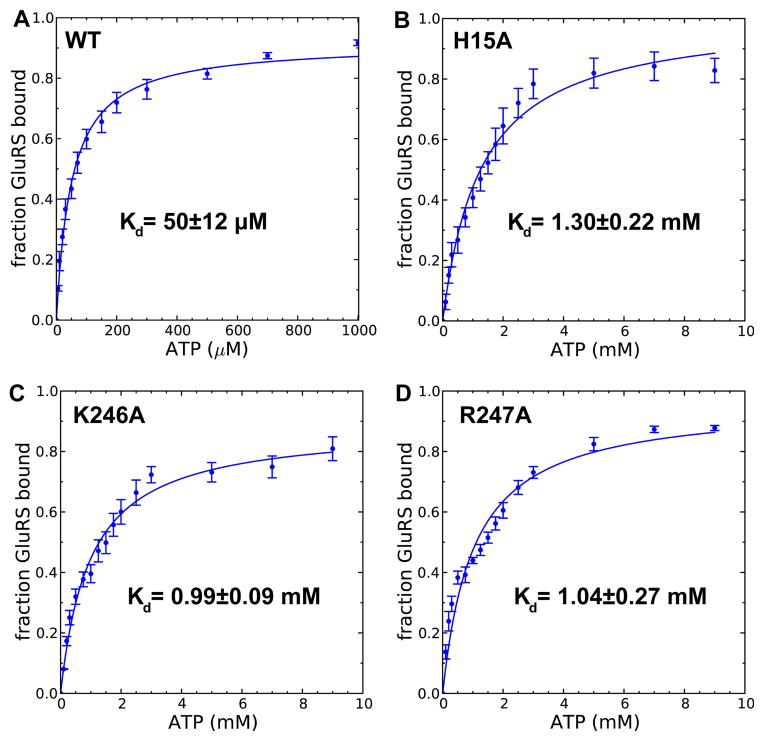
One key prediction of the metadynamics simulation is that the binding free energy of ATP is 7 kcal/mol. To validate this result, an in vitro system of T. thermophilus GluRS was set up. Figure S5 shows the purified recombinant GluRS was active as it robustly aminoacylated in vitro transcribed T. thermophilus tRNA^Glu. The ATP binding to GluRS:Glu decreases protein’s intrinsic fluorescence by ~15% (Figure S6), and this decrease enables us to measure the K_d of ATP by fluorescence titration (Figure S7). The inner filter effect of ATP, a main obstacle in a previous study,⁴⁴ was corrected using Equation 3. Figure 3A shows the K_d is 50±12 μM, comparable to the K_d of other class I aaRS obtained by stopped-flow fluorescence experiments (70±10 μM).⁵⁴ The measured K_d corresponds to a binding free energy of 5.9±0.2 kcal/mol, which is in excellent agreement with our calculated result.

Figure 3. Determination ofK_d between ATP and GluRS:Glu complex.

The fraction of ATP-bound wild-type GluRS (A), H15A (B) as well as K246A (C) and R247A (D) GluRS mutant are plotted as a function of ATP concentration. Error bars represented standard deviations from triplicated measurements.

Metadynamics simulations suggest KMSKS loop and His15 stabilize encounter complexes (Figure 2B) and the base-stacking intermediate (Figure 2C), respectively. To test these predictions, we introduced three single mutations: an alanine mutation of His15 (H15A), and alanine mutations of Lys246 Arg247 in the KMSK loop (K246A, R247A). Significantly, we observed a 26-fold decrease of ATP binding affinity in the H15A mutant (Figure 3B) as well as ≈20-fold decrease in K246A and R247A (Figure 3C,D). While the function of KMSKS loop can be understood by electrostatic interactions and is evident from the energetic calculation of the bound state (Figure 1B), the importance of His15 is only revealed with a dynamic picture of ATP binding calculated with metadynamics simulation. Furthermore, our computational and experimental results provide a thermodynamic explanation of the conservation of this histidine among class I aaRSs,⁵⁵ and may be further extended to the whole nucleotidylyl transferase superfamily.

Sampling triphosphate group binding with unbiased MD simulations

Metadynamics simulation further predicts the formation of the encounter complexes is a downhill process. Since this hypothesis is difficult to test experimentally, we refer to unbiased MD simulations for a computational verification. Five ATP molecules were placed distantly from the enzyme and sixteen independent unbiased MD simulations, each for 10 ns, were performed. Even though the ratio of ATP:GluRS (5:1) in the simulations is much lower compared to the experimental ratio (4,000~10,000:1), this already enhances the sampling and allows a direct observation for the encounter complexes formation.

The unbiased simulations reveal diverse possible conformations of the encounter complex, consistent with the corresponding broad basin in the free energy surface. Figure S8 summarizes the nine distinct encounter complexes observed from sixteen 10-ns simulations. In these encounter complexes, the triphosphate group of ATP binds to GluRS with one of the three positively charged residues in the KMSKS loop, suggesting a critical role of electrostatic interactions in forming encounter complexes.⁵⁶ This is corroborated by the observation that the 1 k_BT electrostatic isosurface forms a funnel around the KMSKS loop to attract the negatively charged [ATP·Mg·3H₂O]²⁻ (Figure S9). Figure S10 shows that other members of the NT superfamily also contain similar electrostatic funnels. A similar electrostatic-funneling mechanism has been proposed to guide the initial binding of ADP to its membrane transporter.⁵⁷

In one trajectory, the triphosphate group of ATP serendipitously bound to GluRS in a way similar to the crystal structure, albeit with the nucleoside oriented outside of the binding pocket. Figure S11 illustrates several intermediates of the binding—in the early stage of binding, Arg247 adopts an extended conformation and gradually folds back, bringing ATP closer to its binding site. This is reminiscent of the “fly-casting” mechanism for DNA-protein binding.⁵⁸ A complete binding was not observed even though this simulation was extended for another 30 ns. This is also consistent with the prediction from metadynamics simulation that the binding of nucleoside has a much higher free energy barrier.

Identifying nucleotide selection mechanism through metadynamics

To gain a more detailed understanding of the nucleoside binding, the rate-limiting step of ATP binding, we applied a new set of collective variables that directly monitor the binding of ribose and adenine, respectively. Figure 4F shows the resulting free energy surface from 60-ns meta-dynamics simulations. Figure 4E illustrates the structure corresponding to the global minimum, and it is essentially the crystallographic state with a heavy-atom MSD of merely 0.3 Ų. Another minimum is the base-stacking intermediate, as shown in Figure 4A. A minimum free energy path that connects these two states was calculated using the zero-temperature string method²⁹ and it is shown in Figure 4. Detailed analysis of the trajectory revealed that His15 serves as the platform for adenine to slide into the pocket via base stacking interaction (Figure 4A–B). This is consistent with our previous metadynamics simulation and mutagenesis results.

Further movement of the adenine requires the disruption of the base stacking interactions and leads to a high free energy state, as in Figure 4C. The free energy starts to decrease when adenine binds to Leu236 backbone via two hydrogen bonds, as shown in Figure 4D. This recognition mechanism is conserved through the NT superfamily and is even utilized by in vitro selected proteins that bind ATP.⁵⁹ We hypothesize that GluRS selects incoming ATP between the high free energy state (Figure 4C) and the base-bound state (Figure 4D). A similar-sized GTP will be blocked since it loses both hydrogen bonds with Leu236 backbone and is electrostatically repulsive (Figure S12). Significantly, the selection of the correct nucleoside (Figure 4D) precedes ribose binding and formation of the fully bound state as shown in Figure 4E. In addition, given the importance of this transition, an independent metadynamics run from different initial conformation has been performed and yields almost identical results, as shown in Figure S13. This demonstrates that the choice of the CVs here captures the most important degrees of freedom for nucleoside binding.

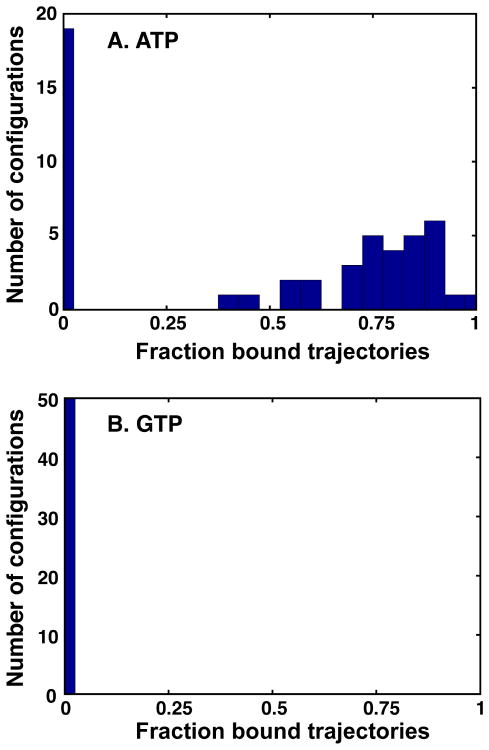
The hypothesis that nucleoside selection occurs during the transition from the high free energy state to the base-bound state is further supported by unbiased MD simulations. Fifty different configurations obtained from restrained dynamics at the high free energy state were used as the initial configuration, from which twenty 10 ps trajectories were run with velocities drawn randomly from a Maxwell-Boltzmann distribution Table S1. The base is considered bound when the distance is less than 3.5 Å. During the 10 ps simulation, the cognate substrate ATP reaches the bound state with a probability larger than 0.5 in 30 out of the 50 starting configurations (472 out of 1,000 simulations in total, Figure 5A). In sharp contrast, for the control GTP simulations, binding did not occur in any of the 1,000 simulations (Figure 5B).

Figure 5. Distribution of fraction bound trajectories for unbiased MD simulations of ATP or GTP binding.

Fifty different initial configurations were chosen for nucleoside binding simulations. For each starting configurations, twenty 10 ps trajectories were run with velocities drawn randomly from a Maxwell-Boltzmann distribution. The fraction of bound trajectories is calculated and its distribution is plotted for both ATP (A) and GTP (B).

Conclusion

ATP is a key molecule providing energy for many cellular processes. The binding of ATP has been studied here by all-atom MD simulations and fluorescence measurement, using GluRS, a quintessential enzyme in nucleotidylyl transferase superfamily as an example. The metadynamics simulations indicate that ATP binding is a two-step process. In the first step, the triphosphate group of ATP is attracted to active site of GluRS via three flexible positively-charged residues in the KMSKS loop. This result is also confirmed by long-time unbiased MD simulations, which further revealed formation of several putative encounter complexes within 10 ns. In the second step, the adenine slides into the binding pocket using His15 as its platform followed by the binding of ribose to the carboxyl group of the reactive Glu. The underlying free energy landscape of this process was calculated by metadynamics and further confirmed by fluorescence measurement. The importance of His15 and the KMSKS loop in ATP binding was confirmed by mutagenesis studies, in which the mutants displayed at least 20-fold reduction in ATP binding affinity. Furthermore, our simulation suggests that the nucleotide selection precedes the binding of ribose, underscoring the insight dynamics brings to understanding the ligand recognition process.

To our knowledge, this study reports the first comprehensive atomic level investigations of an ATP binding process that takes place on a milli-second timescale. Remarkably, even though such kinds of processes are still out of the range of conventional MD simulations, we were able to gain much insight from a judicious combination of advanced sampling techniques and experiments. The detailed mechanism presented in this study may apply to other members of the nucleotidylyl transferase superfamily, and it will be interesting to compare with other protein families with distinct ATP binding site.