Abstract
Background
Left ventricular (LV) systolic strain provides additional prognostic value to LV ejection fraction (LVEF) and wall motion analysis. However, the relationship between myocardial multidirectional strain and LVEF, and the effect of LV hypertrophy on this relationship, are not completely understood especially in unselected populations.
Methods
LV global longitudinal (εL) and circumferential (εC) systolic strain analysis was performed by two-dimensional speckle-tracking echocardiography in 215 participants from a community-based study. LV radial wall thickening was measured as global radial strain (εR), and LVEF was assessed by biplane Simpson’s method.
Results
εR was significantly associated with εC (β=−0.56, p<0.01) and with εL (β= −0.18, p<0.01). The contribution of εL to εR was especially evident in subjects with lower εC and in presence of LV hypertrophy (β= −0.30, p<0.01). εL and εC were significantly associated with LVEF (β= −0.36 and β=−0.49, both p<0.01) independent of LV mass and other confounders, and their interaction significantly improved the prediction of LVEF (R-square change=0.14) but not of εR (R-square change=0.002).
Conclusions
εR is mainly related to εC with a smaller contribution of εL, which becomes especially evident in subjects with lower εC and in presence of LV hypertrophy. Therefore, radial thickening may not detect subclinical LV longitudinal function reduction in normal ventricles and when εC is preserved. While a reduction in εL has a limited impact on εR, it exerts a greater effect on global LVEF, therefore for a more accurate LVEF prediction both εL and εC need to be considered.
Keywords: Left ventricle, Systolic function, Strain, Ejection fraction, Speckle-tracking, Echocardiography
In clinical practice, left ventricular (LV) systolic function is commonly measured at the endocardial level (LV chamber function), and is usually assessed by echocardiographically determined ejection fraction (LVEF). The analysis of LV wall motion, which is often performed by visual estimation of systolic myocardial thickening, is also a widely used method for assessing LV systolic function.1,2 More recently, speckle-tracking echocardiography has made possible the non-invasive assessment of myocardial deformation (strain) over different spatial axes.3,4 Myocardial strain analysis has provided new insights in the understanding of LV mechanics far beyond the information provided by LVEF. Past studies showed that, even in the presence of a normal LVEF, LV strain may be selectively affected in the longitudinal or circumferential direction depending on the pathophysiology and the extension of the damage to the myocardial wall.5–7 Furthermore, the analysis of LV myocardial strain appears to carry prognostic value that is greater than, and additional to, the traditional LV systolic function evaluation by LVEF and wall motion analysis.8
In previous studies including a wide range of LV conditions, from normal to ischemic heart disease and heart failure, good correlations were found between LVEF and LV longitudinal strain,1,9 to the point that the latter has been proposed as an alternative method to quantify global LVEF.10 However, theoretical considerations and the evidence of the additional prognostic value of longitudinal strain over LVEF, along with its ability to uncover systolic dysfunction when LVEF is still normal, are reasons to believe that these two parameters express different aspects of LV function and should not be considered as equivalent.11,12 LVEF and LV wall thickening are, in fact, the final result of the contraction of a complex system of fibers in the myocardial wall,13 in which the subendocardial and subepicardial fibers have prevalent longitudinal direction and are arranged in counter-directional helical loops, and the midwall fibers have prevalent circumferential orientation.14 This architectural structure determines the systolic longitudinal shortening and torsion of the LV, and the thickening of the myocardium in the radial direction, which in turn causes the shift of the endocardium towards the LV cavity.15,16
Since the relationships of longitudinal and circumferential LV wall systolic components with radial thickening and LVEF have not been completely characterized especially in unselected populations without overt cardiac disease, we aimed at analyzing the association of the longitudinal and circumferential components of LV wall systolic function with LV radial thickening and global LVEF in participants from a community-based cohort study. Furthermore, we evaluated the impact of LV hypertrophy on these associations. The study of these relationships would provide a better understanding of LV mechanics and potentially clarify the basis for the additional prognostic information provided by the multidirectional assessment of myocardial deformation over the assessment of wall motion and global LVEF.
METHODS
Study population
The present study was performed in participants from the Cardiac Abnormalities and Brain Lesions (CABL) study, a community-based cohort study whose primary aim was to investigate cardiovascular predictors of subclinical cerebrovascular disease. CABL parent study is the Northern Manhattan study (NOMAS). NOMAS and CABL study design and methodological details have been described previously.17,18 Subjects were contacted by using random digit dialing of both published and unpublished telephone numbers. Briefly, patients were enrolled if they: 1) were at least 50 years of age; 2) lived in a pre-defined geographic area of northern Manhattan for at least 3 months in a household with a telephone; and 3) did not have a prior diagnosis of stroke. Study participants for whom speckle-tracking strain analysis over the three dimensional axes was available constitute the sample of the present study. The study was performed in accordance with the ethical standards of the Declaration of Helsinki and was approved by the Institutional Review Board of Columbia University Medical Center. Written informed consent was obtained from all study participants.
Cardiovascular risk factors were ascertained through direct examination and interview by trained research assistants. Hypertension was defined as systolic blood pressure ≥140 mm Hg or diastolic blood pressure ≥90 mm Hg at the time of the visit (mean of two readings), or history of hypertension or use of anti-hypertensive medications. Diabetes mellitus was defined as fasting blood glucose ≥126 mg/dL or history of diabetes or of use diabetes medications. Hypercholesterolemia was defined as total serum cholesterol >240 mg/dL, history of hypercholesterolemia or of use of lipid-lowering treatment. Coronary artery disease (CAD) was defined as prior myocardial infarction, coronary artery bypass grafting, or percutaneous coronary intervention.
Echocardiographic Assessment
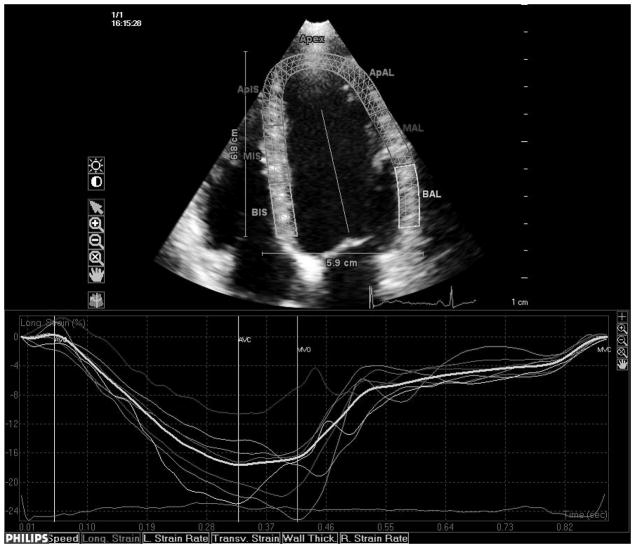
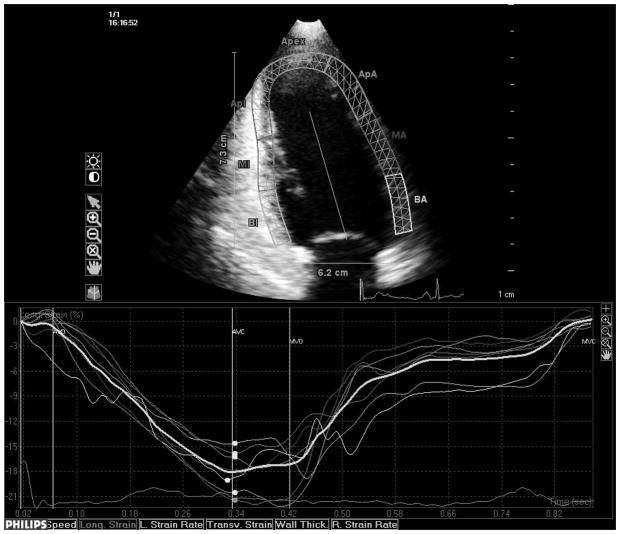
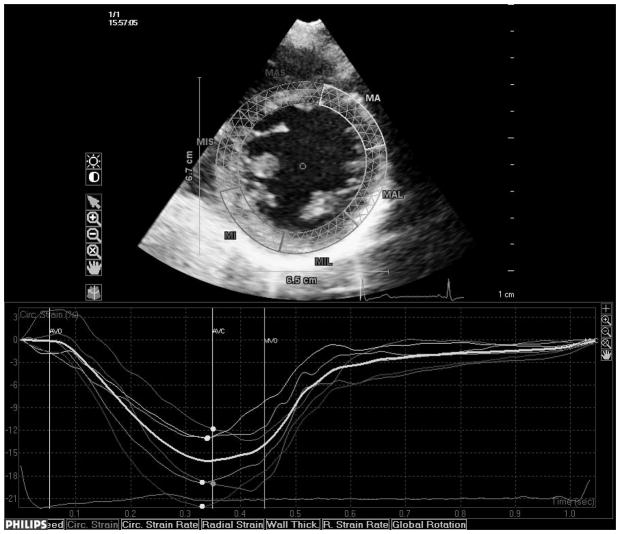
Transthoracic echocardiography evaluation was performed using a commercially available system (iE 33, Philips, Andover, MA) by a trained registered cardiac sonographer. LV diameters and wall thickness were measured from a parasternal long-axis view according to the recommendations of the American Society of Echocardiography (ASE).19 LV mass was calculated with a validated formula20 and indexed by body surface area (LV mass index). LV hypertrophy was defined using the ASE guidelines sex-specific cutoffs.19 Left ventricular relative wall thickness, an index of LV geometry, was calculated with the formula: (2×posterior wall thickness)/end-diastolic diameter.21 LV ejection fraction (LVEF) was calculated using the biplane modified Simpson’s rule. Speckle-tracking analysis of LV systolic function was performed offline (QLAB Advanced Quantification Software version 8.1, Philips) as previously described.22 The software utilizes an image-processing algorithm that analyzes myocardial motion by frame-to-frame tracking of stable patterns of pixels (“speckles”) in two-dimensional gray-scale image loops. Global longitudinal peak systolic strain (εL) was calculated averaging longitudinal strain over 12 segments from the apical four and two-chamber views (Fig. 1, panels a and b). From manually selected landmark points in apical views, endocardial borders are automatically detected by the software, and each wall is divided in to three segments (basal, mid and apical). Manual correction was performed when LV wall was not correctly sampled. Subsequently, automatic tracking of myocardial speckles was performed throughout the cardiac cycle. Strain curves were visualized for each segment, and the average peak systolic strain was calculated. LV circumferential and radial functions were assessed from a parasternal short axis view at the papillary muscle level (Fig. 1, panels c and d). From manually selected anatomical landmark points (circumference delimiting the outer LV myocardial border, center of the circumference, limit of the inferior and anterior interventricular septum), the software identifies LV endocardial and epicardial borders and divides the LV in six segments. Then, tracking of myocardial speckles is performed throughout the entire cardiac cycle. Manual adjustments were performed when border recognition was not optimal. Peak systolic circumferential strain (εC) and peak systolic radial strain (εR) were calculated averaging the peak systolic strain values from the analyzed ventricular segments. Segments with poor tracking quality (either visually estimated or based on internal software algorithms) were excluded from the calculation of the average global strains. Three cycles were recorded at a frame rate > 45 fps, and were averaged for strain analysis. Aortic and mitral valve opening and closing times were measured from the LV outflow Doppler profile and were incorporated in the speckle-tracking strain profile in order to measure systolic strain and to exclude post-systolic components.
Fig. 1.
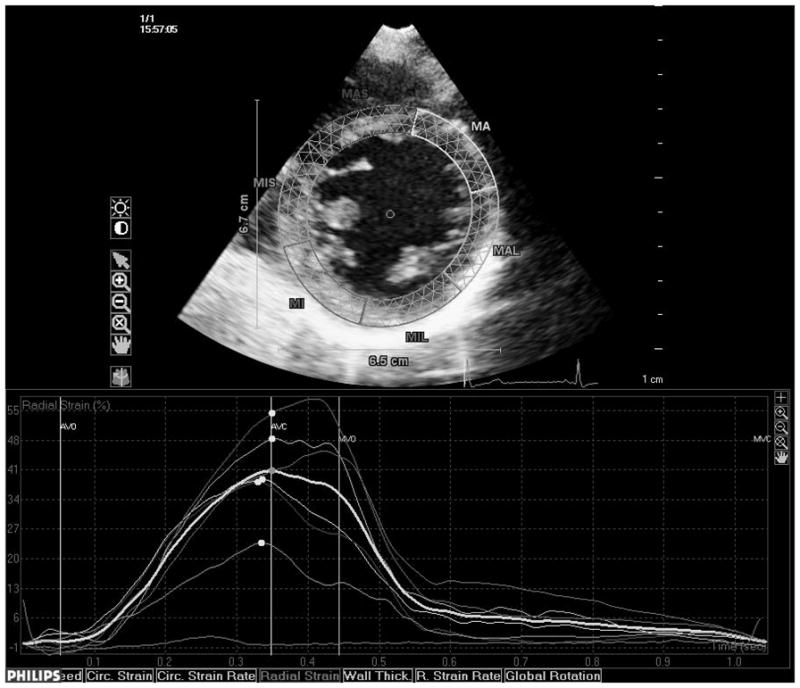
Speckle-tracking analysis of LV strain. Measurement of longitudinal systolic strain from the apical views (a and b). Measurement of systolic circumferential (c) and radial strain (d) from the parasternal mid-ventricular short-axis view.
Reproducibility of speckle-tracking measurements
Intra-and inter-observer reproducibility of speckle-tracking measurements were assessed in a random sample of 20 study participants. Intra-observer intraclass correlation coefficients (ICC) were: 0.82 for εL (95% CI: 0.60–0.93, p<0.01), 0.89 for εC (95% CI: 0.74–0.95, p<0.01), 0.92 for εR (95% CI: 0.82–0.97). Mean difference between measurements was 0.07±2.3% for εL, 0.37±2.2% for εC, and 0.47±3.8%for εR (p values non-significant for all comparisons); coefficients of variation (standard deviation/mean) were 8.4% for εL, 8.0% for εC, and 9.6% for εR. Inter-observer ICCs were 0.85, 0.82 and 0.83 respectively for εL, εC and εR. Mean difference between measurements was 0.08±2.4% for εL, 0.88±2.6% for εC, 1.15±5.2% for εR (p values non-significant for all comparisons); coefficients of variation were 9.2% for εL, 9.7% for εC, and 11.2% for εR.
Statistical Analysis
Data are presented as mean ± standard deviation for continuous variables and as proportions for categorical variables. One-way ANOVA was performed to test differences in εR and LVEF between tertiles of εL and εC. Univariate linear regressions were used to assess the correlates of εL and εC. Multivariate linear regressions were performed to assess the independent association of LV deformation parameters and LVEF. Predictors and outcome variables were standardized with corresponding standard deviations and parameter estimates (β) and relative standard errors were reported. A stepwise selection of the covariates was utilized, with entry and removal criteria set at a probability level of 0.1 and 0.2 respectively. For all statistical analyses, a two-tailed p<0.05 was considered significant. Statistical analyses were performed using SPSS software version 17.0 (SPSS Inc., Chicago, IL).
RESULTS
Clinical, demographic, and echocardiographic characteristics of the 215 study participants are shown in Table 1. Mean LVEF was 61.5±9.0%. 33 subjects (15.3%) had LVEF <55%, of these 24 had LVEF between 45–54%, 4 had LVEF between 30–44% and 5 had LVEF <30%.
Table 1.
Clinical and echocardiographic characteristics of the study sample
| Clinical/demographics | N=215 |
| Age, years | 68.6 ± 10.3 |
| Body mass index, kg/m2 | 27.3 ± 4.4 |
| Women, n (%) | 123 (57.2) |
| Hypertension, n (%) | 150 (69.8) |
| Diabetes, n (%) | 55 (25.6) |
| Hypercholesterolemia, n (%) | 129 (60.0) |
| CAD, n (%) | 5 (2.3) |
| Echocardiographic data | |
| LV end-diastolic diameter, mm/m2 | 26.1 ± 3.3 |
| LV mass index, g/m2 | 104.6 ± 26.6 |
| LV hypertrophy, n (%) | 87 (40.5) |
| Relative wall thickness | 0.48 ± 0.08 |
| LVEF, % | 62.5 ± 8.6 |
| LVEF < 55%, n (%) | 33 (15.3) |
| Speckle-tracking data | |
| εL, % | −17.2 ± 3.6 |
| εC, % | −18.6 ± 4.4 |
| εR, % | 27.5 ± 8.1 |
LVEF: Left ventricular ejection fraction. CAD: Coronary artery disease εL: Global systolic longitudinal strain. εC: Global systolic circumferential strain. εR: Global systolic radial strain.
Correlates of εL and εC
Univariate correlates of longitudinal and circumferential function were assessed in linear regression analyses. εL was significantly correlated with age (β=0.15, p<0.05), LV mass (β =0.24, p<0.01), male sex (β=0.14, P<0.05), hypertension (β=0.24, p<0.01), and diabetes (β =0.15, p<0.05). εC was significantly correlated with LV mass (β=0.33, p<0.01) and hypertension (β=0.14, p<0.05).
Relation of εL and εC with radial thickening and LVEF
To analyze the relationship of εL and εC with εR and LVEF, the study population was divided into tertiles of εL and εC. Subsequently, two matrix tables were built crossing εL and εC tertiles in order to obtain nine groups of subjects with different εL and εC combinations. In Table 2, εR was calculated for each group. The group in the lowest tertile of εL and εC had the lowest εR (19.7±6.9%), whereas the group with highest εL and εC had the highest εR (34.4±6.7%, p<0.01). εR significantly increased with increasing values of εC in every tertile of εL (all p<0.01). On the other hand, εR significantly increased with increasing εL only in the group with lowest εC (p<0.01). A similar analysis was then performed with LVEF (Table 3). The lowest LVEF was found in the group with lowest εL and εC (51.3±14.9%), and the highest LVEF was found in the highest εL/εC tertile combination (67.6±3.6%, p<0.01). LVEF increased with increasing εC in all εL tertiles (all p<0.01). LVEF, however, followed a different pattern than εR, also increasing significantly with increasing εL in all εC tertiles (all p<0.05). The frequency of a LVEF < 55% in each group also followed this pattern.
Table 2.
εR values in εL and εC tertiles
| εL | |||||
|---|---|---|---|---|---|
| 1st tertile N=69 |
2nd tertile N=73 |
3rd tertile N=73 |
P value* | ||
| εC | 1st tertile N=78 |
19.7 ± 6.9 | 23.6 ± 5.3 | 25.1 ± 5.7 | <0.01 |
| 2nd tertile N=64 |
25.9 ± 4.6 | 27.6 ± 6.5 | 28.8 ± 4.1 | 0.30 | |
| 3rd tertile N=73 |
32.6 ± 10.2 | 31.5 ±6.7 | 34.4 ± 6.7 | 0.35 | |
| P value* | <0.01 | <0.01 | <0.01 | ||
Values in table are mean εR (%)± standard deviation. εL: Global systolic longitudinal strain. εC: Global systolic circumferential strain. εR: Global systolic radial strain.
One-way ANOVA between tertiles.
Table 3.
LVEF in εL and εC tertiles
| εL | |||||
|---|---|---|---|---|---|
| 1st tertile N=69 |
2nd tertile N=73 |
3rd tertile N=73 |
P value* | ||
| εC | 1st tertile N=78 |
51.3 ± 14.9 (55.6%) | 60.6 ± 4.2 (16.0%) | 61.1 ± 5.3 (5.9%) | <0.01 |
| 2nd tertile N=64 |
59.1 ± 6.3 (22.2%) | 62.9 ± 5.1 (10.0%) | 64.1± 4.1 (0%) | <0.05 | |
| 3rd tertile N=73 |
64.5 ± 5.4 (6.7%) | 65.3 ± 3.2 (0%) | 67.6 ± 3.6 (0%) | <0.05 | |
| P value* | <0.01 | <0.01 | <0.01 | ||
Values in table are mean LVEF (%)± standard deviation. Values in parentheses indicate the % of subjects with a LVEF <55% in each group. εL: Global systolic longitudinal strain. εC: Global systolic circumferential strain.
One-way ANOVA between tertiles.
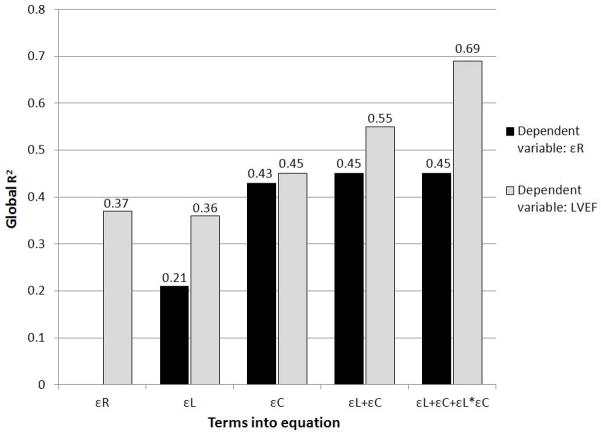
The different impact of strain components on radial thickening and LVEF was further assessed by linear regression models (Table 4). In unadjusted analyses, both εL and εC were significantly associated with εR and with LVEF; however, the relative contribution of εL toward LVEF (β= −0.36) was higher than that toward εR (β= −0.18), whereas the parameter estimate of εC towards LVEF was slightly lower than that towards εR (β= −0.49 and −0.56, respectively). These results were confirmed also after adjusting for age, sex, body mass index, hypertension, diabetes and relative wall thickness. Subsequently, we tested whether an interaction was present between εL and εC in the relationship with εR and LVEF (Table 4, model 3). No interaction was found between εL and εC in relation to εR, whereas a significant interaction was found towards LVEF (β for the interaction term=−0.41, p<0.01). The analysis was performed separately in participants with and without LV hypertrophy to assess differences in LV mechanics due to LV mass increase (Table 4). Interestingly, εL was significantly associated with εR only in participants with LV hypertrophy, whereas εC was significantly and strongly associated with εR in both groups (all p<0.01). The significant association of εL and εC with LVEF was confirmed in both groups (all p<0.01); parameters estimates, however, were higher for εC than for εL in participants without LV hypertrophy, and were of similar magnitude in those with LV hypertrophy. R-square values of linear models predicting εR and LVEF (Figure 2) showed how the model including εL and εC predicted LVEF better than either term alone, and also better than εR; the inclusion of the interaction between εL and εC significantly improved the global fit of the model in predicting LVEF (R2-change=0.14) but not εR (R2-change=0.002).
Table 4.
Relationship of εL and εC with εR and LVEF in all participants and in those with and without LV hypertrophy
| All
|
LVH −
|
LVH +
|
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| εR
|
LVEF
|
εR
|
LVEF
|
εR
|
LVEF
|
|||||||
| β | P value | β | P value | β | P value | β | P value | β | P value | β | P value | |
|
|
|
|
|
|
|
|||||||
| Model 1 | ||||||||||||
| εL | −0.18 | <0.01 | −0.36 | <0.01 | −0.10 | 0.16 | −0.26 | <0.01 | −0.30 | <0.01 | −0.44 | <0.01 |
| εC | −0.56 | <0.01 | −0.49 | <0.01 | −0.57 | <0.01 | −0.46 | <0.01 | −0.50 | <0.01 | −0.49 | <0.01 |
|
|
|
|
|
|
|
|||||||
| Model 2* | ||||||||||||
| εL | −0.20 | <0.01 | −0.36 | <0.01 | −0.14 | 0.07 | −0.30 | <0.01 | −0.34 | <0.01 | −0.40 | <0.01 |
| εC | −0.56 | <0.01 | −0.48 | <0.01 | −0.58 | <0.01 | −0.49 | <0.01 | −0.46 | <0.01 | −0.44 | <0.01 |
|
|
|
|
|
|
|
|||||||
| Model 3 | ||||||||||||
| εL − εC interaction | −0.05 | 0.34 | −0.41 | <0.01 | −0.06 | 0.38 | −0.36 | <0.01 | −0.04 | 0.68 | −0.39 | <0.01 |
Values in table are standardized correlation coefficients (β).εL: Peak systolic longitudinal strain. εC: Peak systolic circumferential strain. εR: Peak systolic radial strain. LVH: Left ventricular hypertrophy. LVEF: Left ventricular ejection fraction.
Adjusted for age, sex, body mass index, hypertension, diabetes, and relative wall thickness.
Fig. 2.
R-square values for linear models predicting εR and LVEF. On the x-axis are shown the independent variables included in each model: εR in the first model, εL in the second model, εC in the third model, εL and εC in the fourth model, εL and εC plus their interaction (εL*εC) in the fifth model.
DISCUSSION
In this study, we analyzed the LV systolic function measuring myocardial deformation by two-dimensional speckle-tracking echocardiography, in the attempt to elucidate the relationship between the multidirectional components of LV deformation and global LV function (LVEF). The main findings of our study are: (1) εC is the strongest contributor to LV radial thickening, with a smaller but also significant contribution from εL which becomes especially evident when εC is reduced and in hypertrophic ventricles; (2) εL and εC are significantly associated with LVEF and show significant interaction in their effect; and (3) a reduction in εL may not significantly affect radial thickening if εC is preserved, but it has a greater impact on LVEF. Because LVEF is correlated to both εL and εC, an important consequence of our findings is that, given a specific value of strain over one axis, LVEF distribution can vary significantly depending on the value of the orthogonally oriented strain. Those findings were confirmed after controlling for factors such as age, sex, body mass index, hypertension, diabetes, and LV relative wall thickness.
Relation of LV longitudinal and circumferential strain with radial thickening
As a result of a force applied in a given direction, an elastic body experiences two opposite deformations: one on the same direction of the force (linear or principal strain) and one on the perpendicular direction (lateral strain).23 In the contracting heart, the shortening of longitudinal and circumferential fibers causes a deformation of LV segments both in the longitudinal and circumferential direction (negative principal strains), therefore concentrating all the lateral (positive) strain in the radial direction, resulting in wall thickening. This “cross-fiber shortening”, allows the heart to efficiently maximize LV fiber contraction in order to obtain high radial thickening values from the relatively limited shortening (10–15%) at the level of the sarcomere.15,24,25 Consistently with this model, our study showed how both εL and εC are significant contributors to radial thickening. This contribution, however, is not equal. εC showed to be a greater contributor to εR than εL especially when LV hypertrophy is absent. This finding may be due at least partly to the fact that the circumferentially-oriented fibers constitute the majority of fibers in the normal LV wall,26 and that in hypertrophic ventricles the relative contribution of longitudinal fibers increases thus giving a greater contribution to wall thickening. Also, we found that the contribution of εL to wall thickening was significant only in the lowest εC tertile group, when the LV circumferential function is reduced.
Relation of LV deformation with LVEF
While radial function is determined by LV wall fiber contraction and thickening, LVEF is influenced by the radial wall thickening and by the reduction of the LV long and short axes.27,28 LV longitudinal strain by speckle-tracking provides a good estimate of the LV long axis reduction and of the systolic motion of the mitral annulus,29 and this is likely the reason of the greater impact of εL on LVEF than on εR (the longitudinally oriented fibers are less represented in the LV wall, thus impacting less radial thickening, however the long axis reduction will translate in a greater effecton LVEF). We demonstrated that, besides their significant main effect on LVEF, a significant statistical interaction was present between εL and εC in determining LVEF. A possible explanation of this interaction may be found in the duplex action of longitudinal and circumferential shortening, which on one hand cause the LV long-axis shortening and the short axis radius reduction and on the other hand contribute to the radial thickening. It is known, in fact, that LV long and short axes reduction have greater impact than radial wall thickening on LVEF, as elegantly demonstrated in a pioneer study by Bogaert and Rademakers.30 In that study, the authors showed how in the normal human left ventricle, regions with higher wall thickening did not necessarily produce a higher regional EF, whereas regions with higher longitudinal and circumferential shortening were associated with higher regional EF. Our data suggest that this may be particularly true for εL, which showed limited impact on radial thickening (probably due to the lesser representation of longitudinal fibers in the LV wall) but had a more significant effect on LVEF. Finally, the longitudinal fibers are also major determinants of the LV systolic twist, further contributing to LV ejection.31
Clinical implications
Our study showed that the measurement of only one strain component, either longitudinal or circumferential, does not provide an accurate estimate of LVEF or radial thickening in an unselected population with mostly normal LVEF. We showed that the best LVEF prediction was reached when both εL and εC, and their interaction, were taken into account. Previous studies that showed stronger correlations between LVEF and εL were performed in small selected populations often including both normal subjects and patients with very depressed LVEF due to ischemic heart disease, dilated cardiomyopathy and heart failure.1,10,11 However, when LVEF is severely depressed, εL will also be very likely depressed, and their overall correlation may result excellent especially if normal or supernormal LVEFs are included in the distribution. We are the first to show that in an unselected population, which in large part included participants with normal LVEF but with a wide range of risk factors, global systolic function depends on the interaction of both εL and εC, and that this interaction is very heterogeneous. In fact, we showed that LVEF, even when in the normal range, may be associated to a heterogeneous array of wall mechanics. This heterogeneity is at least in part associated with some cardiovascular risk factors and cardiac structure features. Hypertension, diabetes, CAD and a higher LV mass were associated with a reduced longitudinal function, whereas an increased LV mass and hypertension were associated with a reduced circumferential function. In this respect, we confirm findings from other studies in hypertensive patients that reported a reduction in absolute values of LV longitudinal, circumferential or radial function.32–37 Another consequence of our findings is that traditional wall motion analysis may not reveal subclinical LV dysfunction in presence of a reduction of longitudinal systolic function if the circumferential function is normal or increased. This is also in line with previous studies showing that myocardial wall deformation provides prognostic information additional to the traditional wall motion assessment.8
Study limitations
Although the main three-dimensional axes were explored, other components of the LV wall that contribute to determine LV systolic function, such as LV torsion, were not available for all subjects in our study. The interaction between differently oriented fibers inside the LV wall generates complex secondary strain patterns (shear strain) that could not be taken into account in our study. Also, the interaction between the three principal strains is a complex three-dimensional phenomenon, therefore the use of two-dimensional speckle-tracking might not fully describe all the components of this interactions. These additional components may have improved the prediction of LVEF allowed by the individual myocardial deformation components. Finally, our population was an unselected sample from the community, mostly including subjects with significant representation of cardiovascular risk factors; therefore our data may not apply to subjects with LV structure and function significantly affected by disease processes not represented in our cohort (acute ischemia, cardiomyopathies, post-ischemic remodeling, etc.).
Conclusions
In an unselected population from the community, neither εL nor εC, when considered alone, provide a good estimate of LVEF; therefore, for an accurate LVEF prediction, both εL and εC need to be considered. εR is mostly influenced by εC and less by εL; thus, radial thickening, often used to visually estimate LV systolic function, may not be sensitive enough to detect subclinical reductions in LV longitudinal function especially when circumferential function is preserved and in absence of LV hypertrophy. These observations may at least in part explain the additional prognostic value of εL over traditional parameters of LV systolic function observed in previous studies.
Acknowledgments
Grants: The study was supported by grants from the National Institute of Neurological Disorders and Stroke (NINDS) R01 NS36286 (P.I.: Dr. Marco R. Di Tullio) and R01 NS29993 (P.I.: Drs. Ralph L. Sacco/Mitchell S.V. Elkind)
The Authors wish to thank Michele Alegre, R.D.C.S., Rui Liu, M.D., Janet DeRosa, M.P.H., and Rafi Cabral, M.D., for their help in the collection and management of the data.
Footnotes
Conflicts of interest: None.
References
- 1.Palmieri V, Russo C, Buonomo A, et al. Novel wall motion score-based method for estimating global left ventricular ejection fraction: validation by real-time 3D echocardiography and global longitudinal strain. Eur J Echocardiogr. 2010;11:125–130. doi: 10.1093/ejechocard/jep177. [DOI] [PubMed] [Google Scholar]
- 2.Lebeau R, Di LM, Amyot R, et al. A new tool for estimating left ventricular ejection fraction derived from wall motion score index. Can J Cardiol. 2003;19:397–404. [PubMed] [Google Scholar]
- 3.Amundsen BH, Helle-Valle T, Edvardsen T, et al. Noninvasive myocardial strain measurement by speckle tracking echocardiography: validation against sonomicrometry and tagged magnetic resonance imaging. J Am Coll Cardiol. 2006;47:789–793. doi: 10.1016/j.jacc.2005.10.040. [DOI] [PubMed] [Google Scholar]
- 4.Geyer H, Caracciolo G, Abe H, et al. Assessment of myocardial mechanics using speckle tracking echocardiography: fundamentals and clinical applications. J Am Soc Echocardiogr. 2010;23:351–369. doi: 10.1016/j.echo.2010.02.015. [DOI] [PubMed] [Google Scholar]
- 5.Chan J, Hanekom L, Wong C, et al. Differentiation of subendocardial and transmural infarction using two-dimensional strain rate imaging to assess short-axis and long-axis myocardial function. J Am Coll Cardiol. 2006;48:2026–2033. doi: 10.1016/j.jacc.2006.07.050. [DOI] [PubMed] [Google Scholar]
- 6.Fang ZY, Leano R, Marwick TH. Relationship between longitudinal and radial contractility in subclinical diabetic heart disease. Clin Sci (Lond) 2004;106:53–60. doi: 10.1042/CS20030153. [DOI] [PubMed] [Google Scholar]
- 7.Sengupta PP, Narula J. Reclassifying heart failure: predominantly subendocardial, subepicardial, and transmural. Heart Fail Clin. 2008;4:379–382. doi: 10.1016/j.hfc.2008.03.013. [DOI] [PubMed] [Google Scholar]
- 8.Stanton T, Leano R, Marwick TH. Prediction of all-cause mortality from global longitudinal speckle strain: comparison with ejection fraction and wall motion scoring. Circ Cardiovasc Imaging. 2009;2:356–364. doi: 10.1161/CIRCIMAGING.109.862334. [DOI] [PubMed] [Google Scholar]
- 9.Reant P, Barbot L, Touche C, et al. Evaluation of global left ventricular systolic function using three-dimensional echocardiography speckle-tracking strain parameters. J Am Soc Echocardiogr. 2012;25:68–79. doi: 10.1016/j.echo.2011.10.009. [DOI] [PubMed] [Google Scholar]
- 10.Brown J, Jenkins C, Marwick TH. Use of myocardial strain to assess global left ventricular function: a comparison with cardiac magnetic resonance and 3-dimensional echocardiography. Am Heart J. 2009;157:102–105. doi: 10.1016/j.ahj.2008.08.032. [DOI] [PubMed] [Google Scholar]
- 11.Delgado V, Mollema SA, Ypenburg C, et al. Relation between global left ventricular longitudinal strain assessed with novel automated function imaging and biplane left ventricular ejection fraction in patients with coronary artery disease. J Am Soc Echocardiogr. 2008;21:1244–1250. doi: 10.1016/j.echo.2008.08.010. [DOI] [PubMed] [Google Scholar]
- 12.Ahmed MI, Desai RV, Gaddam KK, et al. Relation of torsion and myocardial strains to LV ejection fraction in hypertension. JACC Cardiovasc Imaging. 2012;5:273–281. doi: 10.1016/j.jcmg.2011.11.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.LeGrice IJ, Smaill BH, Chai LZ, et al. Laminar structure of the heart: ventricular myocyte arrangement and connective tissue architecture in the dog. Am J Physiol. 1995;269:H571–H582. doi: 10.1152/ajpheart.1995.269.2.H571. [DOI] [PubMed] [Google Scholar]
- 14.Greenbaum RA, Ho SY, Gibson DG, et al. Left ventricular fibre architecture in man. Br Heart J. 1981;45:248–263. doi: 10.1136/hrt.45.3.248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rademakers FE, Rogers WJ, Guier WH, et al. Relation of regional cross-fiber shortening to wall thickening in the intact heart. Three-dimensional strain analysis by NMR tagging. Circulation. 1994;89:1174–1182. doi: 10.1161/01.cir.89.3.1174. [DOI] [PubMed] [Google Scholar]
- 16.Sengupta PP, Krishnamoorthy VK, Korinek J, et al. Left ventricular form and function revisited: applied translational science to cardiovascular ultrasound imaging. J Am Soc Echocardiogr. 2007;20:539–551. doi: 10.1016/j.echo.2006.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sacco RL, Khatri M, Rundek T, et al. Improving Global Vascular Risk Prediction With Behavioral and Anthropometric Factors The Multiethnic NOMAS (Northern Manhattan Cohort Study) J Am Coll Cardiol. 2009;54:2303–2311. doi: 10.1016/j.jacc.2009.07.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Russo C, Jin Z, Homma S, et al. Effect of obesity and overweight on left ventricular diastolic function: a community-based study in an elderly cohort. J Am Coll Cardiol. 2011;57:1368–1374. doi: 10.1016/j.jacc.2010.10.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lang RM, Bierig M, Devereux RB, et al. Recommendations for chamber quantification: a report from the American Society of Echocardiography’s Guidelines and Standards Committee and the Chamber Quantification Writing Group, developed in conjunction with the European Association of Echocardiography, a branch of the European Society of Cardiology. J Am Soc Echocardiogr. 2005;18:1440–1463. doi: 10.1016/j.echo.2005.10.005. [DOI] [PubMed] [Google Scholar]
- 20.Devereux RB, Alonso DR, Lutas EM, et al. Echocardiographic assessment of left ventricular hypertrophy: comparison to necropsy findings. Am J Cardiol. 1986;57:450–458. doi: 10.1016/0002-9149(86)90771-x. [DOI] [PubMed] [Google Scholar]
- 21.Ganau A, Devereux RB, Roman MJ, et al. Patterns of left ventricular hypertrophy and geometric remodeling in essential hypertension. J Am Coll Cardiol. 1992;19:1550–1558. doi: 10.1016/0735-1097(92)90617-v. [DOI] [PubMed] [Google Scholar]
- 22.Russo C, Jin Z, Homma S, et al. Left atrial minimum volume and reservoir function as correlates of left ventricular diastolic function: impactof left ventricular systolic function. Heart. 2012;98:813–820. doi: 10.1136/heartjnl-2011-301388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Shaw MC, Sata T. The plastic behavior of cellular materials. Int J Mech Sci. 1966;8:469–473. [Google Scholar]
- 24.Dumesnil JG, Shoucri RM, Laurenceau JL, et al. A mathematical model of the dynamic geometry of the intact left ventricle and its application to clinical data. Circulation. 1979;59:1024–1034. doi: 10.1161/01.cir.59.5.1024. [DOI] [PubMed] [Google Scholar]
- 25.Sonnenblick EH, Ross J, Jr, Covell JW, et al. The ultrastructure of the heart in systole and diastole. Changes in sarcomere length. Circ Res. 1967;21:423–431. doi: 10.1161/01.res.21.4.423. [DOI] [PubMed] [Google Scholar]
- 26.Streeter DD, Jr, Spotnitz HM, Patel DP, et al. Fiber orientation in the canine left ventricle during diastole and systole. Circ Res. 1969;24:339–347. doi: 10.1161/01.res.24.3.339. [DOI] [PubMed] [Google Scholar]
- 27.Jones CJ, Raposo L, Gibson DG. Functional importance of the long axis dynamics of the human left ventricle. Br Heart J. 1990;63:215–220. doi: 10.1136/hrt.63.4.215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.de Simone G, Ganau A, Roman MJ, et al. Relation of left ventricular longitudinal and circumferential shortening to ejection fraction in the presence or in the absence of mild hypertension. J Hypertens. 1997;15:1011–1017. doi: 10.1097/00004872-199715090-00012. [DOI] [PubMed] [Google Scholar]
- 29.Hayashi SY, Lind BI, Seeberger A, et al. Analysis of mitral annulus motion measurements derived from M-mode, anatomic M-mode, tissue Doppler displacement, and 2-dimensional strain imaging. J Am Soc Echocardiogr. 2006;19:1092–1101. doi: 10.1016/j.echo.2006.04.014. [DOI] [PubMed] [Google Scholar]
- 30.Bogaert J, Rademakers FE. Regional nonuniformity of normal adult human left ventricle. Am J Physiol Heart Circ Physiol. 2001;280:H610–H620. doi: 10.1152/ajpheart.2001.280.2.H610. [DOI] [PubMed] [Google Scholar]
- 31.Sengupta PP, Tajik AJ, Chandrasekaran K, et al. Twist mechanics of the left ventricle: principles and application. JACC Cardiovasc Imaging. 2008;1:366–376. doi: 10.1016/j.jcmg.2008.02.006. [DOI] [PubMed] [Google Scholar]
- 32.Palmon LC, Reichek N, Yeon SB, et al. Intramural myocardial shortening in hypertensive left ventricular hypertrophy with normal pump function. Circulation. 1994;89:122–131. doi: 10.1161/01.cir.89.1.122. [DOI] [PubMed] [Google Scholar]
- 33.Rosen BD, Edvardsen T, Lai S, et al. Left ventricular concentric remodeling is associated with decreased global and regional systolic function: the Multi-Ethnic Study of Atherosclerosis. Circulation. 2005;112:984–991. doi: 10.1161/CIRCULATIONAHA104.500488. [DOI] [PubMed] [Google Scholar]
- 34.Hare JL, Brown JK, Marwick TH. Association of myocardial strain with left ventricular geometry and progression of hypertensive heart disease. Am J Cardiol. 2008;102:87–91. doi: 10.1016/j.amjcard.2008.02.101. [DOI] [PubMed] [Google Scholar]
- 35.Kang SJ, Lim HS, Choi BJ, et al. Longitudinal strain and torsion assessed by two-dimensional speckle tracking correlate with the serum level of tissue inhibitor of matrix metalloproteinase-1, a marker of myocardial fibrosis, in patients with hypertension. J Am Soc Echocardiogr. 2008;21:907–911. doi: 10.1016/j.echo.2008.01.015. [DOI] [PubMed] [Google Scholar]
- 36.Kouzu H, Yuda S, Muranaka A, et al. Left ventricular hypertrophy causes different changes in longitudinal, radial, and circumferential mechanics in patients with hypertension: a two-dimensional speckle tracking study. J Am Soc Echocardiogr. 2011;24:192–199. doi: 10.1016/j.echo.2010.10.020. [DOI] [PubMed] [Google Scholar]
- 37.Narayanan A, Aurigemma GP, Chinali M, et al. Cardiac mechanics in mild hypertensive heart disease: a speckle-strain imaging study. Circ Cardiovasc Imaging. 2009;2:382–390. doi: 10.1161/CIRCIMAGING.108.811620. [DOI] [PubMed] [Google Scholar]