Abstract
Membrane proteins exist in distinctly different environments than do soluble proteins, resulting in differences between their respective biophysical and evolutionary properties. In comparison with soluble proteins, relatively little is known about how the unique biophysical properties of membrane proteins affect their evolutionary properties at the residue level. In particular, transmembrane (TM) regions of membrane proteins tend to be more conserved than regions outside of the membrane (extramembrane [EM] regions), but the mechanisms underlying this phenomenon are not well understood. Here, we combine homology-based high-resolution three-dimensional protein models with rigorous evolutionary rate calculations to quantitatively assess residue-level structure–evolution relationships in the yeast membrane proteome. We find that residue evolutionary rate increases linearly with decreasing residue burial, regardless of the hydrophobic or hydrophilic nature of the solvent environment. This finding supports a direct relationship between a residue’s selective constraint and the extent of its packing interactions with neighboring residues, independent of hydrophobic effects. Most importantly, for a fixed degree of burial, residues from TM regions tend to evolve more slowly than residues from EM regions. We attribute this difference to the increased importance of packing constraints and the decreased importance of hydrophobic effects in TM regions. This additional selective constraint on TM residues plays a dominant role in explaining why TM regions evolve more slowly than EM regions. In addition to revealing the universality of the linear relationship between residue burial and selective constraint across solvent environments, our work highlights the distinct residue-level evolutionary consequences imposed by the unique biophysical properties of the membrane environment.
Keywords: membrane protein, protein structure, solvent accessibility, dN/dS, S. cerevisiae
Introduction
Membrane proteins account for more than 20% of the predicted proteins in sequenced genomes (Wallin and von Heijne 1998). Unlike soluble proteins, which are surrounded by the aqueous environment, membrane proteins are composed of transmembrane (TM) regions residing in the hydrophobic membrane interior and extramembrane (EM) regions residing in the aqueous environment exterior to the membrane (fig. 1). As a result of this distinction, physical principles governing the folding and stability of membrane proteins differ significantly from those governing soluble proteins (White and Wimley 1999; Popot and Engelman 2000; Bowie 2005). The evolutionary properties of TM residues are also distinct from those of soluble protein residues (Jones et al. 1994; Goldman et al. 1998; Tourasse and Li 2000; Eyre et al. 2004; Oberai et al. 2009), yet the manner in which biophysical and structural properties of membrane proteins quantitatively affect their evolutionary properties at the residue level is not well understood.
Fig. 1.—
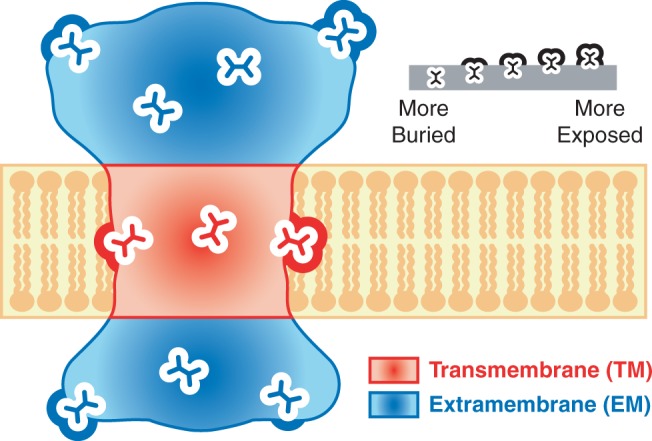
Residue environments within membrane proteins. A cartoon diagram of a membrane protein in cross section. Residues from membrane proteins fall into two distinct types of regions: TM regions (red), which lie within the membrane in which the protein is embedded, and EM regions (blue), which lie outside of the membrane. In both TM and EM regions, residues experience different degrees of burial within the protein, ranging from completely buried to highly exposed.
In contrast to membrane proteins, a great deal is known regarding the biophysical and structural determinants of residue evolution for soluble proteins. For soluble protein residues, it is now known that degree of burial is a major predictor of evolutionary rate and that buried residues evolve more slowly than exposed residues (Perutz et al. 1965; Overington et al. 1992; Goldman et al. 1998; Bustamante et al. 2000; Choi et al. 2006; Conant and Stadler 2009; Franzosa and Xia 2009; Ramsey et al. 2011). Recently, we constructed a large-scale, quantitative model relating residue evolutionary rate to degree of burial for yeast soluble proteins (Franzosa and Xia 2009). Our method features accurate estimates of structural and evolutionary properties at the residue level: Residue burial is directly calculated from high-quality, homology-based three-dimensional (3D) structural models of yeast proteins, and evolutionary rate is rigorously calculated based on sequence alignments of orthologs from closely related yeast species. Our analysis revealed that residue evolutionary rate scales linearly with relative solvent accessibility (RSA). In other words, as residues become progressively more exposed (less buried), selective constraint relaxes at a constant rate.
The linear trend between residue instantaneous evolutionary rate and RSA that we observed previously was based on soluble proteins only (Franzosa and Xia 2009). It is not known if this linear trend holds for the TM and EM regions of membrane proteins, and more importantly, to what extent such a trend can explain the global difference in evolutionary properties of TM regions versus EM regions. Earlier studies have shown that rates and patterns of amino acid substitutions for TM regions of membrane proteins are very different from those for soluble proteins (Jones et al. 1994), that TM regions evolve more slowly than EM regions of membrane proteins (Tourasse and Li 2000), that buried residues are more conserved than surface residues in TM regions (Goldman et al. 1998; Eyre et al. 2004; Kauko et al. 2008; Mokrab et al. 2010), and that buried, polar or coil residues are highly conserved in TM regions (Kauko et al. 2008; Mokrab et al. 2010; Illergard et al. 2011). However, solvent exposure was usually treated as a binary variable in previous studies, where residue sites were classified into buried versus surface sites, even though solvent exposure is a continuous property that varies from complete burial to complete exposure (fig. 1).
Three recent studies (Kauko et al. 2008; Oberai et al. 2009; Illergard et al. 2010) pioneered the use of a continuous measure of solvent exposure for studying membrane protein evolution. Illergard et al. (2010) found that residue substitution rate increases linearly with RSA when averaged over all membrane proteins, but they did not carry out separate calculations for TM regions and EM regions of membrane proteins. Kauko et al. (2008) and Oberai et al. (2009) found that residue conservation increases monotonically with increasing residue burial for both TM and EM regions. However, both studies binned degree of residue burial into intervals with unequal range, preventing a quantitative assessment of the effect of burial on residue evolution. After controlling for solvent accessibility, Kauko et al. (2008) found that TM sites have lower indel rates than EM sites for both helical and coil residues and that TM sites have lower amino acid substitution rates than EM sites for coil residues, which comprises only 7% of all sites within the deep membrane core. However, when controlling for solvent accessibility, this difference in amino acid substitution rates between TM and EM sites is diminished for helical residues, which comprises the majority of TM sites for α-helical TM proteins (Kauko et al. 2008). Similarly, Oberai et al. (2009) failed to find any difference in residue conservation between TM and EM sites after controlling for solvent accessibility.
These negative results seem to indicate that TM and EM sites with similar solvent exposure evolve at similar rates. However, it is possible that these negative results are caused by the methodological disadvantages of previous analyses that prevented the quantitative and sensitive detection of important evolutionary differences between TM and EM regions. Instead of calculating instantaneous rate of evolution over a fixed species tree, all three aforementioned studies (Kauko et al. 2008; Oberai et al. 2009; Illergard et al. 2010) used residue conservation scores or amino acid substitution rates based on sequence alignments of homologous proteins from diverse species, without directly taking into account differences in species divergence time and without explicitly separating orthologs from homologs, thus preventing a rigorous and sensitive characterization of selective constraint. So far, there has been no proteome-wide study on the quantitative relationship between residue burial and instantaneous evolutionary rate for the TM and EM regions of membrane proteins, and hence the role of this relationship in explaining the global evolutionary rate difference between TM and EM regions remains unexplored.
In this work, we apply the rigorous and quantitative framework that we developed previously for soluble proteins (Franzosa and Xia 2009) to the study of residue-level structure–evolution relationships for membrane proteins in yeast, using high-quality homology-based 3D structural annotations of 59 membrane proteins encoded in the yeast nuclear genome, and evolutionary rates calculated from sequence alignments of orthologs from four closely related yeast species. Because membrane proteins that do not have well-defined orthologs in these yeast species are excluded from subsequent analysis, we choose to focus on four closely related yeast species as an optimal balance between robust evolutionary statistics and coverage of a large number of yeast membrane proteins. We find that in spite of the vast difference in the solvent environment for TM and EM regions of membrane proteins, the quantitative relationships between residue evolutionary rate and degree of solvent exposure are very similar: For both TM and EM regions of membrane proteins, the trends are strong, positive, and linear. More importantly, for a given degree of residue burial, TM residues are consistently more slowly evolving than EM residues and must therefore be subject to consistently stronger selective pressure. Although previous studies have attributed the heightened conservation of TM regions to their increased fraction of buried residues (Oberai et al. 2009), we demonstrate here that the newly observed systematic increase in selective constraint across all TM residues is the dominant determinant of the reduced evolutionary rate of TM regions relative to EM regions.
In addition, our study highlights the universality of the linear relationship between residue evolutionary rate and solvent exposure across diverse environments (soluble proteins, EM regions, and TM regions of membrane proteins), supporting residue packing constraint as the major driving force behind these linear trends. Because of the decreased importance of hydrophobic effects in the membrane interior, residue packing takes on increased importance in TM regions, thus providing a natural explanation for the systematic increase in selective constraint across all TM residues. Our study reveals distinct principles governing the structure–evolution relationships of membrane proteins at the residue level and highlights the manner in which residue-level biophysical properties drive the global evolutionary behavior of membrane proteins.
We focus on the budding yeast Saccharomyces cerevisiae because it is an ideal model system for genomic analysis. The yeast proteome has been extensively annotated. In addition to the budding yeast, several closely related yeast taxa have also been sequenced. The ortholog relationships among the yeast genes have been accurately determined, a prerequisite for calculating evolutionary rate. Focusing on yeast also allows for a direct comparison with our previous work on proteome-wide structure–evolution relationships in yeast soluble proteins (Franzosa and Xia 2009). The fundamental difference in biophysical properties between membrane and aqueous environments and its effects on protein evolution are expected to be largely species independent. Thus, we expect that our results are broadly applicable to a wide range of membrane proteomes from bacteria to higher eukaryotes.
Materials and Methods
We constructed a data set of homology-based 3D structural annotations of nuclear-encoded yeast membrane proteins in the following way. We first assembled two data sets: 1) the set of yeast open reading frames (ORFs) annotated as “integral to membrane” in the Saccharomyces Genome Database (Cherry et al. 1998) and 2) the set of membrane proteins of known 3D structure from the Protein Data Bank (Berman et al. 2000) that are divided into TM and EM regions based on annotations from the MPtopo database (Jayasinghe et al. 2001). We then identified the most significant sequence alignment between each yeast ORF and a membrane protein of known 3D structure based on alignment E value, as determined using the gapped Basic Local Alignment Search Tool (BLAST) software program (Altschul et al. 1997). We saved optimal yeast ORF-to-structure mappings with E value < 10−5 as homology-based 3D structural annotations of yeast membrane proteins. Our final data set consists of 59 structurally annotated yeast membrane proteins, which contribute a total of 7,090 TM residues and 6,844 EM residues for subsequent analysis (supplementary table S1, Supplementary Material online).
For ungapped positions in the yeast ORF-to-structure alignments, we assigned physical properties determined for residue sites in the membrane proteins of known 3D structure to the corresponding aligned yeast protein residues. In addition to assigning residues to TM and EM regions based on the annotations from the MPtopo database, we calculated the solvent-accessible surface area (SASA) for residues in the membrane proteins of known 3D structure using MSMS (Sanner et al. 1996), excluding hydrogen atoms. We used a 1.4 Å sphere (representing a water molecule) as a solvent probe for all residues. Notably, residues in TM regions are normally solvated by lipids, not water. However, for our purposes, a residue’s SASA is used merely as a proxy for its degree of burial within the protein. Our degree-of-burial calculations are relatively insensitive to the precise nature of the solvent probe, provided that the same probe is used consistently for all residues. We normalized raw SASA values to the 99th percentile within each residue type as determined from distributions of large numbers of residues generated during our previous work (Franzosa and Xia 2009). This procedure accounts for differences in the sizes and empirical SASA distributions of the 20 different amino acid residue types. The resulting normalized SASA values take the form of RSA, a quantity which varies between 0 (for completely buried residues) and 1 (for maximally exposed residues); we set outlier residues to RSA = 1 during the normalization procedure.
Each structurally annotated yeast membrane protein in our final data set is associated with its most significantly aligned orthologs in the three closely related yeasts S. paradoxus, S. mikatae, and S. bayanus, as determined from orthology and sequence annotations in the Fungal Orthogroups Repository (Wapinski et al. 2007). We aligned codons from the four total yeast species to their corresponding residue sites in the 3D models of yeast membrane proteins using the original ORF-to-structure alignments as templates. We then concatenated columns from these codon alignments that correspond to residues with similar physical properties (e.g., EM vs. TM environment, and degree of burial). We calculated a single dN/dS value over the yeast tree for each group of concatenated codon columns using the codeml software program within the Phylogenetic Analysis by Maximum Likelihood (PAML) package (Yang 1997). dN/dS compares the rate of nonsynonymous amino acid changing substitutions (dN) to the rate of synonymous substitutions (dS) at the DNA level, with the latter acting as a normalizing factor. We estimated the error in our measurements of dN/dS using 100 rounds of bootstrap resampling, following our previous work (Franzosa and Xia 2012). We fit lines to dN/dS versus RSA relationships using a standard procedure that accounts for variation in the error in dN/dS estimation between RSA bins (Press et al. 2007).
Results and Discussion
TM Regions Evolve More Slowly than EM Regions
To evaluate the effects of the membrane environment on residue-level protein structure–evolution relationships in yeast (S. cerevisiae), we annotated 59 yeast membrane proteins and their orthologs in three closely related yeast species with 3D structures based on sequence homology. Because of the distinctly different selective forces acting upon nuclear- versus mitochondrial-encoded proteins, we focused on nuclear-encoded membrane proteins for this work. Residues from membrane proteins can be divided into two types based on the region of the membrane protein in which they lie: TM residues, which lie in the membrane-embedded TM regions, and EM residues, which lie outside of the membrane in EM regions (fig. 1). It was previously observed that TM regions tend to evolve more slowly (i.e., experience greater selective constraint) than EM regions (Tourasse and Li 2000; Oberai et al. 2009). Consistent with this observation, we find that the value of dN/dS is approximately 42% smaller among the 7,090 TM residues in our data set relative to the 6,844 EM residues (dN/dS = 0.036 vs. 0.062; fig. 2). dN/dS compares the rate of nonsynonymous amino acid changing substitutions (dN) to the rate of synonymous substitutions (dS) in protein coding sequences, and it is often used as a measure of selective constraint. Because the comparison between TM and EM residues is carried out within the same membrane proteins, this difference in dN/dS between TM and EM regions cannot be attributed to protein-level properties of membrane proteins such as expression level and essentiality.
Fig. 2.—
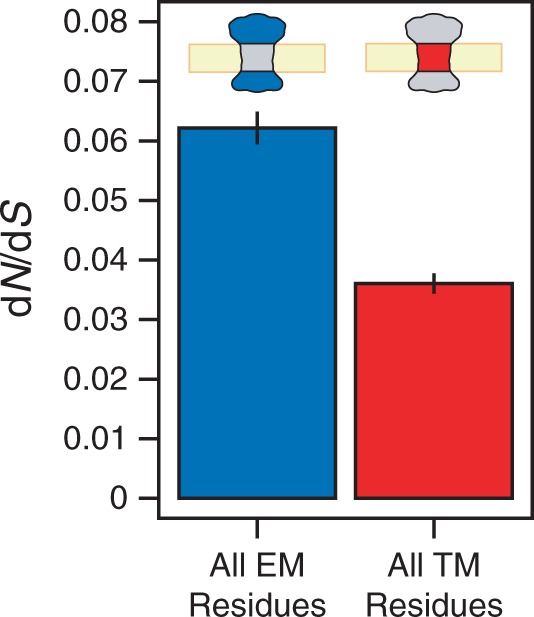
TM regions evolve more slowly than EM regions. When residues from membrane proteins are binned broadly according to the type of region in which they lie (EM vs. TM), we observe that residues from TM regions (red) tend to evolve much more slowly than their counterparts in EM regions (blue), as measured by dN/dS. Error bars reflect estimates of the standard error from 100 rounds of bootstrap resampling.
Average Burial and Hydrophobicity in TM and EM Regions
Oberai et al. (2009) carried out an analysis of residue-level conservation of membrane protein structures not restricted to any particular genome. They attributed the higher residue conservation of TM regions relative to EM regions entirely to the observation that TM regions tend to contain a greater proportion of buried residues than EM regions. Because buried residues tend to be more conserved than exposed residues in both aqueous environments (Perutz et al. 1965; Overington et al. 1992; Goldman et al. 1998; Bustamante et al. 2000; Choi et al. 2006; Conant and Stadler 2009; Franzosa and Xia 2009; Ramsey et al. 2011) and membrane environments (Goldman et al. 1998; Eyre et al. 2004; Kauko et al. 2008; Oberai et al. 2009), an enrichment for buried residues in TM regions could explain the observed decrease in the average evolutionary rate in TM regions.
We quantified the degree of residue burial in our data set using RSA, as outlined in the Materials and Methods section. We define degree of solvent exposure to be the same as RSA, and we consider both water molecules in the aqueous environment and lipid molecules in the membrane environment as possible solvents for proteins. RSA = 0 implies that the residue is completely buried, RSA = 1 implies that the residue is maximally exposed relative to other residues of the same type, and RSA values between 0 and 1 correspond to intermediate degrees of burial. Our RSA distributions calculated from structurally annotated yeast membrane proteins agree with the findings of Oberai et al., namely that TM regions tend to contain a greater proportion of “highly buried” (RSA ≤ 0.2) residues than EM regions (51% of TM residues have RSA ≤ 0.2, compared with 37% of EM residues; fig. 3A).
Fig. 3.—
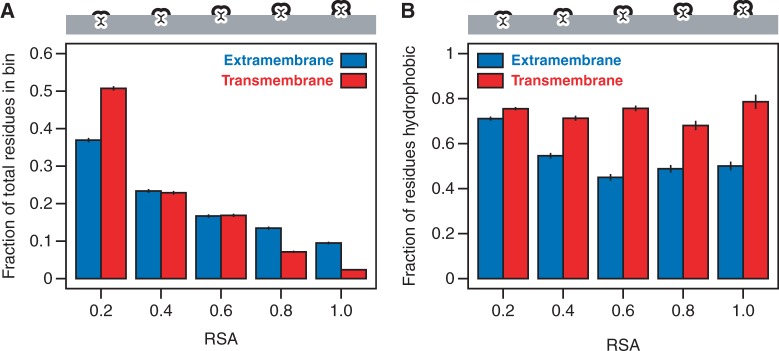
Physical properties of residues from TM and EM regions. (A) Relative to EM regions, TM regions contain a larger proportion of highly buried residues (RSA ≤ 0.2). (B) Residues from TM regions tend to be strongly hydrophobic independent of their degree of burial, whereas only the most buried EM residues reach this level of hydrophobicity. Error bars reflect the standard error.
A second major difference between TM and EM regions that could potentially contribute to their difference in evolutionary rate is hydrophobicity distribution. Although buried residues in both TM and EM regions tend to be biased toward hydrophobic residues, exposed TM residues also tend to be hydrophobic as a result of their exposure to the lipid environment. Indeed, if we divide residues evenly into “hydrophobic” and “hydrophilic” classes (Kyte and Doolittle 1982), we observe that highly buried TM and EM residues with RSA ≤ 0.2 are both strongly enriched for hydrophobic residues in S. cerevisiae (76% of TM residues with RSA ≤ 0.2 are classified as hydrophobic, compared with 71% of EM residues; fig. 3B). However, as RSA increases, enrichment for hydrophobic residues drops in the EM regions, but remains roughly constant throughout the TM regions (fig. 3B), consistent with previous observations (Stevens and Arkin 1999). Thus, in addition to their difference in RSA distributions, EM and TM regions differ markedly in their amino acid composition, and this could also potentially contribute to the decrease in overall evolutionary rate in TM regions (Graur 1985).
Residue Evolutionary Rate Scales Linearly with Solvent Accessibility in Both TM and EM Regions
To investigate whether the difference in selective constraint between TM and EM regions (fig. 2) could be entirely attributed to differences in their RSA or hydrophobicity distributions, we further subdivided residues into smaller RSA bins and calculated RSA-specific dN/dS values for residues from TM and EM regions. Previously, using a large data set of 3D homology models of yeast proteins, we showed that dN/dS increases in a strong, positive, linear manner with increasing RSA for soluble proteins (Franzosa and Xia 2009). Here, we calculated the trend between dN/dS and RSA for residues from membrane proteins according to the environment in which they lie (within or outside of the membrane). By excluding soluble proteins and only comparing residues within membrane proteins in this analysis, we control for any inherent biases within membrane proteins.
Consistent with our previous findings based on soluble proteins (Franzosa and Xia 2009), we observe a strong, positive, linear trend between dN/dS and RSA for residues in EM regions of membrane proteins (r = 0.98, P < 10−6; fig. 4). Despite the functional differences between membrane and soluble proteins, the EM regions of membrane proteins are similar to soluble proteins in that they are surrounded by the aqueous environment. As a result, it is not surprising that soluble proteins and EM regions of membrane proteins exhibit similar linear relationships between residue-level dN/dS and RSA. On the other hand, we also observe a strong, positive, linear trend between dN/dS and RSA for TM residues (r = 0.93, P < 10−4; fig. 4), in spite of the vast difference in biophysical environment between TM and EM regions. The linear model is justified by the statistical significance associated with the fit. Furthermore, fitting the dN/dS versus RSA data with a more complex quadratic model does not significantly improve the goodness-of-fit compared with the linear model (P = 0.27 for EM; P = 0.92 for TM). In addition to being very simple and providing a better fit to data than more complex models, the linear model is also conceptually justified by the residue packing argument that we put forward. Supplementary figure S1, Supplementary Material online, compares the EM and TM trends to a trend calculated over 795 soluble proteins in our previous work (Franzosa and Xia 2012); the soluble protein trend is qualitatively more similar to the EM trend than to the TM trend.
Fig. 4.—
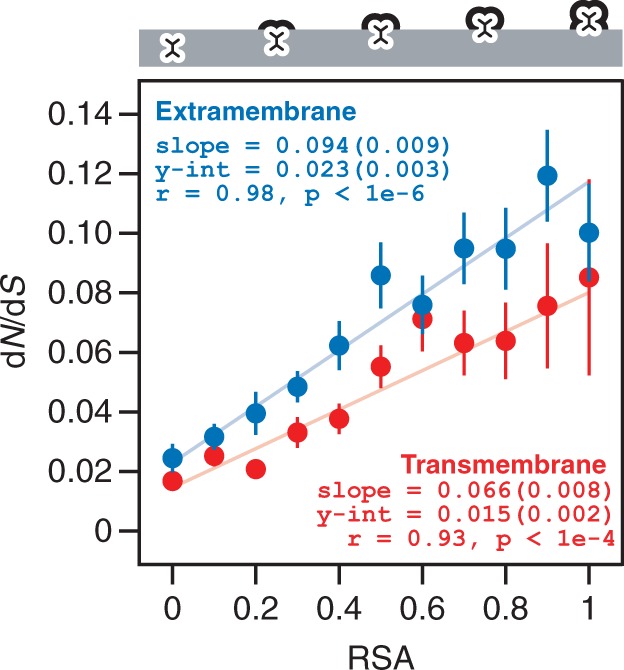
dN/dS scales linearly with exposure for TM and EM residues. When binning residues from TM and EM regions according to degree of exposure (as measured by RSA), we find that dN/dS tends to increase linearly with RSA in both regions. Notably, for a given degree of exposure (RSA bin), residues from TM regions are always evolving more slowly than similarly buried residues from EM regions. The slope and intercept of each trend are provided for reference; values in parentheses reflect the standard error.
TM Residues Evolve More Slowly than EM Residues with the Same Degree of Burial
Although the overall dN/dS versus RSA trends are similar, dN/dS values for TM residues are consistently lower than dN/dS values for EM residues for any given degree of residue burial (RSA bin) (fig. 4). The slope and intercept of the TM trend are both significantly lower than those of the EM trend (t-statistic-based two-tailed P = 0.025 and P = 0.043). Our observations are different from those of Oberai et al. (2009) and Kauko et al. (2008), who found that the trends between residue conservation and degree of burial were not significantly different between the EM and TM regions for most residue sites. Notably, our analysis of residue-level structure–evolution relationships is more quantitative than the analyses by Oberai et al. and Kauko et al. in two critical ways: 1) we calculate evolutionary rates by comparing orthologs from a fixed set of closely related species to control for divergence time, as opposed to measuring conservation across homologous proteins from diverse species without directly controlling for divergence time and 2) we divide residues into RSA bins with equal range, rather than dividing into intervals with unequal range.
Our observed similarities and differences between the TM and EM trends are due entirely to selection at the amino acid sequence level. Using un-normalized dN as a proxy for selection at the amino acid sequence level, we find that the trends between dN and RSA for TM versus EM residues are qualitatively similar to the trends observed between dN/dS and RSA (fig. 5A). However, the trends between dS and RSA for TM versus EM residues are identical and essentially flat (fig. 5B). Because dS measures the rate of synonymous substitutions, this result implies that there is comparatively little variation in the degree of selection at the level of synonymous codons among residues from membrane proteins, independent of solvent environment or degree of burial.
Fig. 5.—
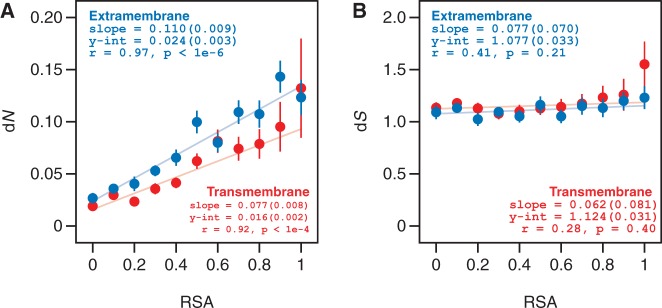
The relationship between dN/dS and RSA for TM and EM residues is driven by selection at the amino acid sequence level. We investigated the relationship between residue burial and selection at (A) the amino acid sequence level (as measured by dN) and (B) the synonymous codon level (as measured by dS). The dN versus RSA trends for TM and EM residues are qualitatively similar to the dN/dS versus RSA trends from figure 4. Conversely, there is very little variation in rates of synonymous selection between TM and EM residues and across RSA bins.
Why Do TM Regions Evolve More Slowly than EM Regions?
The results illustrated in figure 4 have important implications regarding the nature of selective constraint in TM versus EM regions. It was previously proposed that TM regions tend to evolve more slowly than EM regions due entirely to the fact that TM regions contain a larger fraction of buried residues (Oberai et al. 2009). Although it is true that TM regions contain a larger fraction of buried residues than EM regions (fig. 3A), TM residues also evolve consistently more slowly than EM residues with similar degrees of burial (fig. 4). Indeed, the dN/dS value for completely buried EM residues is more than 50% larger than the value for completely buried TM residues (0.023 vs. 0.015; t-statistic-based two-tailed P = 0.043; fig. 4). This suggests that the 42% lower overall evolutionary rate of TM regions relative to EM regions (fig. 2) is due to a combination of two effects: 1) a general enrichment for buried, slowly evolving residues in TM regions (fig. 3A) and 2) a systematic decrease in the evolutionary rates of all TM residues, independent of degree of burial (fig. 4).
How important is the increased fraction of buried residues in TM regions in explaining the 42% lower overall evolutionary rate of TM regions? We answer this question in the following way. We assume that TM residues follow the same dN/dS versus RSA trend as EM residues (i.e., ignoring the systematic difference between the TM and EM trends) and then predict overall dN/dS for EM and TM regions based on average RSA only. EM regions have average RSA of 0.35, yielding a predicted overall dN/dS of 0.056. On the other hand, TM regions have average RSA of 0.25, yielding a predicted overall dN/dS of 0.047. Hence, on the basis of difference in average degree of burial alone, we predict that TM residues should evolve only 16% more slowly than EM residues, a much smaller effect than the observed difference of 42% (fig. 2).
How important is the systematic decrease in evolutionary rates of all TM residues independent of degree of burial (fig. 4) in explaining the lower overall evolutionary rate of TM regions? To answer this question, we assume that TM residues follow the same RSA distribution as EM residues (i.e., ignoring the systematic difference in RSA distribution between TM and EM regions) and then predict overall dN/dS for EM and TM regions based on expected dN/dS versus RSA trends only (fig. 4). The average RSA over all EM residues is 0.35. The predicted overall dN/dS for EM regions is therefore 0.056 (as above), whereas the predicted overall dN/dS for TM regions is 0.038. Thus, considering only the difference between the EM and TM trends, we predict that TM residues should evolve 33% more slowly than EM residues. This is larger than the 16% difference predicted above based on the difference in average burial only and closer to the observed difference of 42% (fig. 2). We therefore conclude that the systematic increase in selective pressure for TM residues relative to EM residues with similar degree of burial (fig. 4) is the dominant determinant of the difference in overall evolutionary rate of TM versus EM regions (fig. 2).
Although not the dominant determinant, the difference in RSA distribution does contribute independently to the overall evolutionary rate difference between TM and EM regions. Indeed, if we predict TM dN/dS based on a combination of TM-specific RSA distribution and dN/dS versus RSA trend, the resulting prediction is 44% smaller than the predicted EM dN/dS based on a combination of EM-specific RSA distribution and dN/dS versus RSA trend. This is in very good agreement with the observed difference of 42%. These predictions are illustrated in supplementary figure S2, Supplementary Material online.
It was previously observed that soluble proteins with small average RSA tend to evolve more quickly than soluble proteins with large average RSA (Bloom et al. 2006). If we assume that this observation also holds for the TM and EM regions of membrane proteins, then because TM regions have smaller average RSA than EM regions, TM regions are expected to evolve more quickly than EM regions. Thus, the observation that TM regions evolve more slowly than EM regions further confirms out conclusion that there is a systematic increase in selective constraints for TM sites relative to EM sites imposed by the special properties of the membrane environment, and it is this systematic increase in selective constraints rather than the difference in RSA distribution that is the dominant determinant of the slower overall evolutionary rate of TM regions relative to EM regions.
Residue Packing as a Dominant Driving Force behind the Linear dN/dS versus RSA Trends
There are three possible candidate driving forces behind the linear residue dN/dS versus RSA trends observed for both soluble and membrane proteins: 1) backbone hydrogen bonding, which is responsible for the formation of secondary structures; 2) hydrophobic interaction, which is the dominant driving force in the folding of soluble proteins; and 3) residue packing, which is important in the formation of a tightly packed protein interior.
Backbone hydrogen bonding cannot be a dominant driving force, as it is generally well conserved between closely related proteins and does not directly depend on the protein sequence. Side chain hydrogen bonding does, however, depend on sequence, and its effect on protein evolution is similar to packing, which we will discuss in detail later. Hydrophobic interactions cannot be a dominant driving force either for three reasons. First, our earlier work demonstrated that in soluble proteins, buried residues evolve more slowly than exposed residues independent of hydrophobicity (Franzosa and Xia 2009). Second, the expected dN/dS values for TM residues increase more than 5-fold across the RSA range (from dN/dS = 0.015 to 0.081; fig. 4), whereas degree of hydrophobicity remains roughly constant with increasing RSA (fig. 3B). This suggests that the positive slope of the dN/dS versus RSA trend for TM regions is not driven by hydrophobicity. Third, for the most buried residues in the TM and EM regions (RSA ≤ 0.2), the fractions of TM and EM residues that are hydrophobic are very similar (76% vs. 71%; fig. 3B), yet EM residues are evolving more than 50% faster (fig. 4). This means that the systematic differences in evolutionary rates observed between TM and EM residues with similar degrees of burial are largely not driven by hydrophobicity. Hence, although increased hydrophobicity is a hallmark of TM regions, it is not a driving force behind 1) the overall similarity in the linear trends between dN/dS and RSA for membrane and soluble proteins (fig. 4) (Franzosa and Xia 2009), 2) the overall evolutionary rate difference between TM and EM regions of membrane proteins (fig. 2), or 3) the difference in the dN/dS versus RSA trends for residues from TM versus EM regions (fig. 4).
Instead, we argue that residue packing is a dominant driving force behind the linear dN/dS versus RSA trends for both soluble and membrane proteins. In our earlier work, we demonstrated that although solvent accessibility is a convenient measure of residue burial, there was evidence to indicate that residue–residue packing was in fact the true agent of selective constraint for soluble proteins (Franzosa and Xia 2009). More buried residues (with lower average RSA) will also tend to make more contacts with neighboring residues, and these contacts help to stabilize the native structure of the protein. Indeed, the packing of residues is so precise that we may think of proteins as solutions to 3D “jigsaw puzzles,” wherein the outside pieces make fewer contacts with other pieces and are therefore more free to change, whereas the buried inside pieces are heavily constrained by their densely packed environment (Richards 1974). This would explain why we observe a positive relationship between dN/dS and RSA for both EM and TM regions: Despite the vast difference in solvent environment between EM and TM regions, buried residues in both EM and TM regions make more residue–residue contacts and therefore make greater contributions to protein stability than exposed residues. Given this additional structural and functional importance, it is not surprising that buried residues in both EM and TM regions experience heightened selective constraint compared with exposed residues.
In a soluble protein, the folding process is driven in large part by the hydrophobic effect, that is, the tendency for hydrophobic residues to bury themselves, such that unfavorable contacts with the surrounding solvent (water) are minimized (Dill 1990). On the other hand, TM residues in membrane proteins are highly hydrophobic regardless of degree of burial (as seen in fig. 3B), consistent with previous observations that membrane proteins are not “inside-out” soluble proteins (Rees et al. 1989; Stevens and Arkin 1999). In the absence of the hydrophobic effect, it was proposed that residue–residue packing effects must dominate the stability of TM regions of membrane proteins (Stevens and Arkin 1999). The fact that dN/dS among TM residues is always lower than dN/dS among EM residues for a given degree of burial may reflect the fact that, although EM regions are stabilized both by the hydrophobic effect and residue–residue packing, in TM regions packing is a more dominant force, and hence must be more intensely selected. Indeed, TM residues are known to be packed more tightly than soluble protein residues (Eilers et al. 2000; Adamian and Liang 2001; Lehnert et al. 2004). This additional constraint on residue–residue packing throughout the TM regions of membrane proteins has a major effect on the overall evolution of these regions and contributes to an explanation of why TM residues in general are more conserved than their EM counterparts, independently of their elevated average burial and hydrophobicity.
Observed TM and EM Differences Cannot Be Explained by Overall Evolutionary Rate Variation between Proteins
Our observations that TM residues tend to be more conserved than EM residues both globally (fig. 2) and across the range of residue burial (fig. 4) are based on averages over 59 yeast membrane proteins. To ensure that our findings cannot be attributed to variation in the background evolutionary rates of these proteins, it is important to show that TM residues also tend to be more conserved than EM residues on a per-protein basis, both throughout each protein and within specific burial regimes. The importance of comparing EM residues with TM residues on a per-protein basis was elegantly demonstrated in a recent study (Spielman and Wilke 2013). However, per-protein analyses involve much smaller numbers of residues than we have considered up to this point. To ensure meaningful statistical analysis, we classified residue burial on a per-protein basis using three broad RSA bins (RSA < 1/3, 1/3 < RSA < 2/3, and RSA > 2/3) and required a minimum of 25 residues in any single bin for dN/dS estimation.
Among the 55 yeast membrane proteins in our data set containing at least 25 EM residues and 25 TM residues, the TM residues have lower dN/dS than the EM residues in 73% of cases, a strong and statistically significant tendency (Wilcoxon signed-rank test, two-tailed P < 10−4; fig. 6). This suggests that the tendency of TM residues to evolve more slowly than EM residues across our data set (fig. 2) cannot be explained by the overall evolutionary rate variation between yeast membrane proteins.
Fig. 6.—
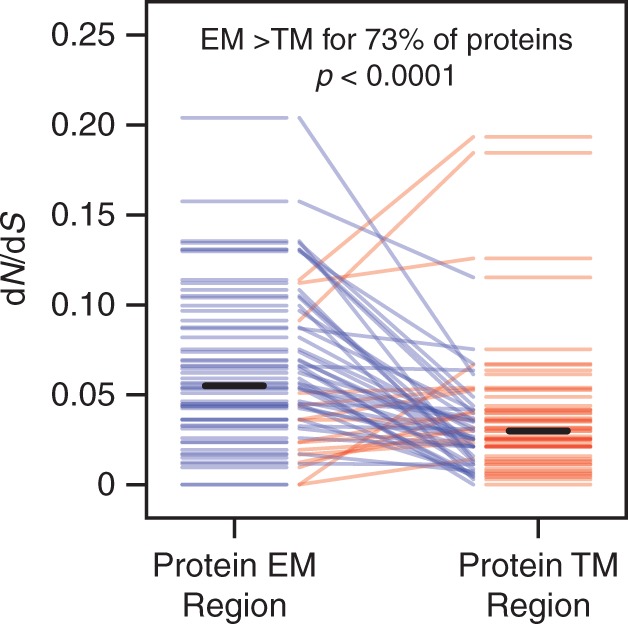
TM residues evolve more slowly than EM residues for most proteins. We divided the 59 yeast membrane proteins in our data set into protein-specific EM and TM regions and calculated dN/dS for any region containing at least 25 residues. EM and TM regions from the same protein are connected by lines, which are colored blue if the EM region has a higher dN/dS value and red if the TM region has a higher dN/dS value. EM regions tend to have higher dN/dS values than TM regions within the same protein. Solid black bars indicate the average dN/dS over all EM or TM protein regions.
Moreover, per-protein analysis supports our more general conclusion that TM residues tend to be more conserved than EM residues of the same degree of burial (fig. 4). Among the 39 yeast membrane proteins contributing at least 25 EM residues and 25 TM residues of high burial (RSA < 1/3), the TM residues have lower dN/dS than the EM residues in 67% of cases (P = 0.0013; fig. 7A). In addition, among the 24 proteins contributing sufficient EM and TM residues of intermediate burial (1/3 < RSA < 2/3), the TM residues have lower dN/dS than the EM residues in 71% of cases (P = 0.0089; fig. 7B). There are too few TM residues with low burial (RSA > 2/3) to perform meaningful statistical comparison with EM residues on a per-protein basis: The average protein in our data set contains only eight TM residues with RSA > 2/3, and no protein contains the minimum 25 residues we deemed necessary for dN/dS estimation (fig. 7C). In conclusion, in regimes of both high and intermediate residue burial where sufficient data exist for proper statistical comparison, per-protein analysis suggests that the difference between the TM and EM trends observed in figure 4 cannot be explained by the overall evolutionary rate variation between membrane proteins.
Fig. 7.—
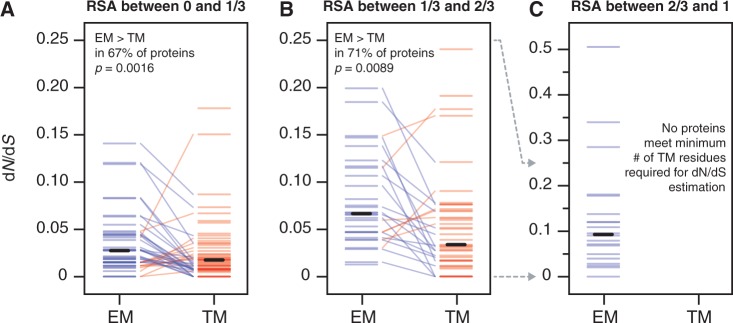
TM residues evolve more slowly than similarly buried EM residues for most proteins. We divided the 59 yeast membrane proteins in our data set into protein-specific EM and TM regions and then binned residues in these regions according to broad burial regime (high burial, RSA < 1/3; intermediate burial, 1/3 < RSA < 2/3; and low burial, RSA > 2/3). We calculated dN/dS for any bin containing at least 25 residues. EM and TM bins from the same protein are connected by lines, which are colored blue if the EM bin has a higher dN/dS value and red if the TM bin has a higher dN/dS value. Solid black bars indicate the average dN/dS over all bins of a particular type. In the (A) high burial and (B) intermediate burial regimes, EM residues tend to have higher dN/dS values than TM residues within the same protein. In the (C) low burial (high exposure) regime, TM residues are too rare within individual membrane proteins to conduct a statistically meaningful comparison with EM residues.
Conclusions
We have presented the first quantitative model of the relationships between biophysical and evolutionary properties of yeast membrane proteins at the residue level. In spite of the vast differences in solvent environment between membrane proteins and soluble proteins, we find that residues in each environment follow the same striking trend: As solvent accessibility increases, the rate of amino acid sequence evolution increases proportionally. This evidence strongly supports a direct relationship between residue packing and selective constraint for all protein residues.
In addition, we observed that TM residues evolve consistently more slowly than EM residues of a similar degree of solvent exposure, a phenomenon we attribute to an increase in the importance of residue packing in TM regions as a result of the decreasing importance of hydrophobic effects. This turns out to be a dominant force behind the lower overall evolutionary rate of TM regions relative to EM regions, although an increase in the fraction of buried residues also makes an important contribution (Oberai et al. 2009). Notably, we found no significant evidence of a direct link between the elevated hydrophobicity of TM regions and their tendency to evolve more slowly.
This improved understanding of the structure–evolution relationships of membrane proteins at the residue level has many important applications. Our quantitative residue-level structure–evolution model provides an improved baseline for evolutionary analyses of the EM and TM regions of membrane proteins. Such a baseline is critically important for detecting signs of differential selection, which may be used to identify surface sites with enhanced functionality (Adamian et al. 2011). Understanding the baseline constraints on the surfaces of membrane proteins is also crucial for predicting interaction interfaces of known or putative membrane protein–protein interactions (Miller et al. 2005; Xia et al. 2006; Babu et al. 2012). Additional applications of our model include prediction of the deleterious effects of SNPs in membrane proteins (Oberai et al. 2009) and 3D structure prediction of membrane proteins (Hopf et al. 2012).
Overall, our work reveals the universality of the linear relationship between residue burial and selective constraint across diverse solvent environments and quantifies the distinct evolutionary consequences at the residue level imposed by the unique biophysical properties of the membrane environment. Thus, our study highlights the importance of a high-resolution, quantitative approach that integrates structural with evolutionary proteomics in revealing general principles governing the biophysics and evolution of membrane proteins.
Note Added to Proof
After submission of this manuscript, we were made aware of a recently completed study by Spielman and Wilke (2013) where TM residues of mammalian G protein-coupled receptors (GPCRs) were compared with the corresponding EM residues on a per-protein basis. It was shown that the slower evolutionary rate of TM regions of mammalian GPCRs cannot be entirely explained by their higher average RSA, and thus the membrane environment must play an additional role in shaping membrane protein evolution. That study and our study together demonstrate the importance of rigorous statistical analysis in studying membrane protein evolution.
Supplementary Material
Supplementary table S1 and figures S1 and S2 are available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org).
Acknowledgments
This work was supported by the National Science Foundation grant CCF-1219007 to Y.X.
Literature Cited
- Adamian L, Liang J. Helix-helix packing and interfacial pairwise interactions of residues in membrane proteins. J Mol Biol. 2001;311:891–907. doi: 10.1006/jmbi.2001.4908. [DOI] [PubMed] [Google Scholar]
- Adamian L, Naveed H, Liang J. Lipid-binding surfaces of membrane proteins: evidence from evolutionary and structural analysis. Biochim Biophys Acta. 2011;1808:1092–1102. doi: 10.1016/j.bbamem.2010.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altschul SF, et al. Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res. 1997;25:3389–3402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Babu M, et al. Interaction landscape of membrane-protein complexes in Saccharomyces cerevisiae. Nature. 2012;489:585–589. doi: 10.1038/nature11354. [DOI] [PubMed] [Google Scholar]
- Berman HM, et al. The Protein Data Bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bloom JD, Drummond DA, Arnold FH, Wilke CO. Structural determinants of the rate of protein evolution in yeast. Mol Biol Evol. 2006;23:1751–1761. doi: 10.1093/molbev/msl040. [DOI] [PubMed] [Google Scholar]
- Bowie JU. Solving the membrane protein folding problem. Nature. 2005;438:581–589. doi: 10.1038/nature04395. [DOI] [PubMed] [Google Scholar]
- Bustamante CD, Townsend JP, Hartl DL. Solvent accessibility and purifying selection within proteins of Escherichia coli and Salmonella enterica. Mol Biol Evol. 2000;17:301–308. doi: 10.1093/oxfordjournals.molbev.a026310. [DOI] [PubMed] [Google Scholar]
- Cherry JM, et al. SGD: Saccharomyces Genome Database. Nucleic Acids Res. 1998;26:73–79. doi: 10.1093/nar/26.1.73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi SS, Vallender EJ, Lahn BT. Systematically assessing the influence of 3-dimensional structural context on the molecular evolution of mammalian proteomes. Mol Biol Evol. 2006;23:2131–2133. doi: 10.1093/molbev/msl086. [DOI] [PubMed] [Google Scholar]
- Conant GC, Stadler PF. Solvent exposure imparts similar selective pressures across a range of yeast proteins. Mol Biol Evol. 2009;26:1155–1161. doi: 10.1093/molbev/msp031. [DOI] [PubMed] [Google Scholar]
- Dill KA. Dominant forces in protein folding. Biochemistry. 1990;29:7133–7155. doi: 10.1021/bi00483a001. [DOI] [PubMed] [Google Scholar]
- Eilers M, Shekar SC, Shieh T, Smith SO, Fleming PJ. Internal packing of helical membrane proteins. Proc Natl Acad Sci U S A. 2000;97:5796–5801. doi: 10.1073/pnas.97.11.5796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eyre TA, Partridge L, Thornton JM. Computational analysis of alpha-helical membrane protein structure: implications for the prediction of 3D structural models. Protein Eng Des Sel. 2004;17:613–624. doi: 10.1093/protein/gzh072. [DOI] [PubMed] [Google Scholar]
- Franzosa EA, Xia Y. Structural determinants of protein evolution are context-sensitive at the residue level. Mol Biol Evol. 2009;26:2387–2395. doi: 10.1093/molbev/msp146. [DOI] [PubMed] [Google Scholar]
- Franzosa EA, Xia Y. Independent effects of protein core size and expression on residue-level structure-evolution relationships. PLoS One. 2012;7:e46602. doi: 10.1371/journal.pone.0046602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman N, Thorne JL, Jones DT. Assessing the impact of secondary structure and solvent accessibility on protein evolution. Genetics. 1998;149:445–458. doi: 10.1093/genetics/149.1.445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graur D. Amino acid composition and the evolutionary rates of protein-coding genes. J Mol Evol. 1985;22:53–62. doi: 10.1007/BF02105805. [DOI] [PubMed] [Google Scholar]
- Hopf TA, et al. Three-dimensional structures of membrane proteins from genomic sequencing. Cell. 2012;149:1607–1621. doi: 10.1016/j.cell.2012.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Illergard K, Callegari S, Elofsson A. MPRAP: an accessibility predictor for a-helical transmembrane proteins that performs well inside and outside the membrane. BMC Bioinformatics. 2010;11:333. doi: 10.1186/1471-2105-11-333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Illergard K, Kauko A, Elofsson A. Why are polar residues within the membrane core evolutionary conserved? Proteins. 2011;79:79–91. doi: 10.1002/prot.22859. [DOI] [PubMed] [Google Scholar]
- Jayasinghe S, Hristova K, White SH. MPtopo: a database of membrane protein topology. Protein Sci. 2001;10:455–458. doi: 10.1110/ps.43501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones DT, Taylor WR, Thornton JM. A mutation data matrix for transmembrane proteins. FEBS Lett. 1994;339:269–275. doi: 10.1016/0014-5793(94)80429-x. [DOI] [PubMed] [Google Scholar]
- Kauko A, Illergard K, Elofsson A. Coils in the membrane core are conserved and functionally important. J Mol Biol. 2008;380:170–180. doi: 10.1016/j.jmb.2008.04.052. [DOI] [PubMed] [Google Scholar]
- Kyte J, Doolittle RF. A simple method for displaying the hydropathic character of a protein. J Mol Biol. 1982;157:105–132. doi: 10.1016/0022-2836(82)90515-0. [DOI] [PubMed] [Google Scholar]
- Lehnert U, et al. Computational analysis of membrane proteins: genomic occurrence, structure prediction and helix interactions. Q Rev Biophys. 2004;37:121–146. doi: 10.1017/s003358350400397x. [DOI] [PubMed] [Google Scholar]
- Miller JP, et al. Large-scale identification of yeast integral membrane protein interactions. Proc Natl Acad Sci U S A. 2005;102:12123–12128. doi: 10.1073/pnas.0505482102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mokrab Y, Stevens TJ, Mizuguchi K. A structural dissection of amino acid substitutions in helical transmembrane proteins. Proteins. 2010;78:2895–2907. doi: 10.1002/prot.22809. [DOI] [PubMed] [Google Scholar]
- Oberai A, Joh NH, Pettit FK, Bowie JU. Structural imperatives impose diverse evolutionary constraints on helical membrane proteins. Proc Natl Acad Sci U S A. 2009;106:17747–17750. doi: 10.1073/pnas.0906390106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Overington J, Donnelly D, Johnson MS, Sali A, Blundell TL. Environment-specific amino acid substitution tables: tertiary templates and prediction of protein folds. Protein Sci. 1992;1:216–226. doi: 10.1002/pro.5560010203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perutz MF, Kendrew JC, Watson HC. Structure and function of haemoglobin: II. Some relations between polypeptide chain configuration and amino acid sequence. J Mol Biol. 1965;13:669–678. [Google Scholar]
- Popot JL, Engelman DM. Helical membrane protein folding, stability, and evolution. Annu Rev Biochem. 2000;69:881–922. doi: 10.1146/annurev.biochem.69.1.881. [DOI] [PubMed] [Google Scholar]
- Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical recipes: the art of scientific computing. Cambridge: Cambridge University Press; 2007. [Google Scholar]
- Ramsey DC, Scherrer MP, Zhou T, Wilke CO. The relationship between relative solvent accessibility and evolutionary rate in protein evolution. Genetics. 2011;188:479–488. doi: 10.1534/genetics.111.128025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rees DC, DeAntonio L, Eisenberg D. Hydrophobic organization of membrane proteins. Science. 1989;245:510–513. doi: 10.1126/science.2667138. [DOI] [PubMed] [Google Scholar]
- Richards FM. The interpretation of protein structures: total volume, group volume distributions and packing density. J Mol Biol. 1974;82:1–14. doi: 10.1016/0022-2836(74)90570-1. [DOI] [PubMed] [Google Scholar]
- Sanner MF, Olson AJ, Spehner JC. Reduced surface: an efficient way to compute molecular surfaces. Biopolymers. 1996;38:305–320. doi: 10.1002/(SICI)1097-0282(199603)38:3%3C305::AID-BIP4%3E3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- Spielman SJ, Wilke CO. Membrane environment imposes unique selection pressures on transmembrane domains of G protein-coupled receptors. J Mol Evol. 2013;76:172–182. doi: 10.1007/s00239-012-9538-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stevens TJ, Arkin IT. Are membrane proteins “inside-out” proteins? Proteins. 1999;36:135–143. doi: 10.1002/(sici)1097-0134(19990701)36:1<135::aid-prot11>3.0.co;2-i. [DOI] [PubMed] [Google Scholar]
- Tourasse NJ, Li WH. Selective constraints, amino acid composition, and the rate of protein evolution. Mol Biol Evol. 2000;17:656–664. doi: 10.1093/oxfordjournals.molbev.a026344. [DOI] [PubMed] [Google Scholar]
- Wallin E, von Heijne G. Genome-wide analysis of integral membrane proteins from eubacterial, archaean, and eukaryotic organisms. Protein Sci. 1998;7:1029–1038. doi: 10.1002/pro.5560070420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wapinski I, Pfeffer A, Friedman N, Regev A. Natural history and evolutionary principles of gene duplication in fungi. Nature. 2007;449:54–61. doi: 10.1038/nature06107. [DOI] [PubMed] [Google Scholar]
- White SH, Wimley WC. Membrane protein folding and stability: physical principles. Annu Rev Biophys Biomol Struct. 1999;28:319–365. doi: 10.1146/annurev.biophys.28.1.319. [DOI] [PubMed] [Google Scholar]
- Xia Y, Lu LJ, Gerstein M. Integrated prediction of the helical membrane protein interactome in yeast. J Mol Biol. 2006;357:339–349. doi: 10.1016/j.jmb.2005.12.067. [DOI] [PubMed] [Google Scholar]
- Yang Z. PAML: a program package for phylogenetic analysis by maximum likelihood. Comput Appl Biosci. 1997;13:555–556. doi: 10.1093/bioinformatics/13.5.555. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


