Measurement Error Case Series Models with Application to Infection-Cardiovascular Risk in OlderPatients on Dialysis

Abstract

Infection and cardiovascular disease are leading causes of hospitalization and death in older patients on dialysis. Our recent work found an increase in the relative incidence of cardiovascular outcomes during the ~ 30 days after infection-related hospitalizations using the case series model, which adjusts for measured and unmeasured baseline confounders. However, a major challenge in modeling/assessing the infection-cardiovascular risk hypothesis is that the exact time of infection, or more generally “exposure,” onsets cannot be ascertained based on hospitalization data. Only imprecise markers of the timing of infection onsets are available. Although there is a large literature on measurement error in the predictors in regression modeling, to date there is no work on measurement error on the timing of a time-varying exposure to our knowledge. Thus, we propose a new method, the measurement error case series (MECS) models, to account for measurement error in time-varying exposure onsets. We characterized the general nature of bias resulting from estimation that ignores measurement error and proposed a bias-corrected estimation for the MECS models. We examined in detail the accuracy of the proposed method to estimate the relative incidence. Hospitalization data from United States Renal Data System, which captures nearly all (> 99%) patients with end-stage renal disease in the U.S. over time, is used to illustrate the proposed method. The results suggest that the estimate of the cardiovascular incidence following the 30 days after infections, a period where acute effects of infection on vascular endothelium may be most pronounced, is substantially attenuated in the presence of infection onset measurement error.

1 Introduction

Infection and cardiovascular disease are leading causes of hospitalization and death in patients on dialysis in the United States (USRDS, 2010). Smeeth et al. (2004) found that infection is associated with an increased risk of cardiovascular events, using data from the United Kingdom General Research Practice Database (Walley and Mantgani, 1997), the largest source of ongoing data on illness and practice in the UK. More specifically, they showed that there is a 3- to 5-fold increase in risk (incidence) of a myocardial infarction or stroke after infection in the general population. Although the precise mechanisms by which infection may affect cardiovascular events are not fully known, infections may affect vascular endothelium (Mahmoudi, Curzen and Gallagher, 2007), create a chronic sub-clinical inflammatory state that affects atherosclerosis, (Zhu, Quyyumi, Norman et al., 2000), or may create a procoagulant state (Macko, Ameriso, Gruber et al., 1996; Sun, 2006).

Only recently has the association between acute infections and cardiovascular events been examined in the (U.S.) dialysis population, using data from the United States Renal Data System (USRDS) which captures nearly all (> 99%) patients with end-stage renal disease in the U.S. More specifically, Dalrymple et al. (2011) found an increased incidence of cardiovascular events, particularly in the first 30-day risk period after infection-related hospitalizations in older dialysis patients (age ≥ 65). Infection, or more generally the “exposure” of interest, was observed over time during the follow-up/observation period for each individual; therefore, the exposure was time-varying. The case series model, also called self-controlled case series model (Farrington, 1995), was utilized to estimate the association between the incidence of cardiovascular events and the time-varying exposure, namely infection. The approach uses only cases, i.e., individuals with one or more cardiovascular events. There are several important reasons and appealing aspects to this modeling choice. First, the case series method provides consistent estimates of the relative incidence (e.g., cardiovascular events during the 30-day risk period following an infection relative to the control period over the observation time) using only cases. Secondly, it implicitly controls for all fixed confounders, measured and unmeasured, such as genetics or co-existing illnesses. This later point is particularly relevant to the dialysis cohort from the USRDS as dialysis patients who do and do not acquire infections likely differ in important ways not easily measured; therefore, making adjustment in (e.g., Poisson) regression modeling infeasible. Third, the case series model is well-suited for this type of hypothesis-driven research because (1) it requires specification of the risk period(s) a priori and (2) leads to a specific time window to potentially examine more aggressive intervention monitoring, such as the first 30 days after exposure/infection, for cardiovascular risk reduction, in addition to implementation of overall infection control/prevention strategies and early treatment in this population.

The case series model was originally proposed in 1995 to investigate the association between an acute outcome and a time-varying exposure; more specifically, adverse events and vaccination. As mentioned above, only individuals with one or more events are sampled in the case series model. It is derived from an underlying non-homogeneous Poisson cohort model where events and exposure history are available on the observation period (a_i, b_i] for the ith case/individual and with incidence rate λ_ijk = exp(φ_i + α_j + β_k), where φ_i, α_j and β_k are the individual-specific, j^th age group and k^th risk group effects, respectively. The primary effects of interest are the β_k's. To take into account the deliberate sampling on cases only, the model likelihood is conditional on an event having occurred and the resulting kernel of the likelihood is multinomial with probabilities depending on the incidence rate λ_ijk. The “self-controlled” aspect of the method refers to the fact that individual effects φ_i cancel in the likelihood. The exposure history, i.e., the times when the exposures occurred, within the observation period of individual i, namely (a_i, b_i], is assumed to be known precisely. For example, in the original application of the case series model, there is little doubt as to when a vaccination occurs as those can be ascertained fairly accurately.

However, a major challenge associated with using the USRDS hospitalization data to address the infection-cardiovascular risk hypothesis is that the exact date or time of infection/exposure onset cannot be ascertained based on hospital claims data, although the discharge date is a surrogate marker for the time of infection as it reasonably assures that the infection has occurred by this date. Thus, our previous work used the date of infection-related hospitalization discharge as the observed time of infection (Dalrymple et al., 2011). Clearly, this is a conservative approximation to the true unknown date of infection, which most likely occurred sometime during hospitalization or prior to the start of hospitalization. From a more general perspective, this can be viewed as a problem of exposure onset measurement error, where one only observes a marker of the unknown time of exposure. The lack of an existing method that can handle this exposure onset measurement error leads us to propose the measurement error case series (MECS) model, in order to more thoroughly assess the infection-cardiovascular risk hypothesis in the dialysis population. Thus, the proposed MECS model in this work aims to target the true underlying relative incidences using imprecise exposure onset times and still retain the advantages associated with the original case series model.

We note that exposure onset measurement error is distinct from traditional measurement error in the form of mismeasured continuous or misclassified categorical variables (e.g., Carroll et al., 2006). There is indeed an extensive literature on methods for dealing with measurement error in the covariates, including time-varying covariates, in general regression modeling. For example, modeling measurement error in time-varying covariates, such as longitudinal dietary intakes (e.g., from food frequency questionaire (FFQ)) in linear mixed models and survival analysis were considered by Tosteson et al. (1999) and Liao et al. (2011), respectively. Measurement error in time-dependent covariates, such as growth hormone and binding protein levels, in pharmacokinetics nonlinear mixed-effects models were considered by Higgins et al. (1997). Other works include Huang and Wang (2000) and Tsiatis and Davidian (2004), both in the context of time-to-event data. In the literature on time-varying covariate measurement error, including the above referenced works, the main issue is that the longitudinal covariate measurements themselves, e.g., dietary/nutrient intakes or protein concentrations, are measured with error. The timing of the covariate measurements, such as when the FFQ's were administered or hourly measurements of serum protein concentration, is not in doubt. Our work here focuses on measurement error in the timing of when the exposures occur over time and to date there has been no work to handle measurement error in the timing of exposure onset in case series modeling. There are several works, unrelated to case series modeling and exposure onset measurement error, that involve the “timing error” of covariates, whose meaning differs completely from the current work. For example, in Higgins et al. (1997) this simply refers to covariates measured at different time points than the response measurement times. Li and Ryan (2004) considered “mistiming error,” which refers to using a covariate measured at a later known time, such as some known time after birth or baseline, in place of an intended covariate at birth, which is not available in a Cox regression model. See Keiding (1992), who also considered mistimed covariates. We note that in mistimed covariates, the timing of the covariate is not in doubt (error). One simply uses the covariate measured at a different known time; hence, the timing of the available covariate itself is not subject to error.

Some interesting case series applications involve antidepressant use and hip fracture (Hubbard et al., 2003) and prescription medications and motor vehicle crashes (Gibson et al., 2009), although the original novel proposal by Farrington (1995) was for investigating associations between time-varying transient exposures, specifically vaccinations, and adverse events. It is increasingly recognized as an important method in the analysis of data from biomedical and epidemiological studies. Excellent expository papers on the practice and implementation of case series modeling are provided by Whitaker et al. (2006, 2009).

The remainder of this paper is organized as follows. In Section 2, we introduce the measurement error case series model for exposure onset measurement error and investigate the bias when ignoring the measurement error. We also propose a bias-correction method in Section 2.3 that requires only fitting the ordinary case series model, ignoring measurement error. In Section 2.4 we examine the accuracy of the proposed bias-correction method in estimating the true relative incidence of interest. Effcacy of the proposed approach is examined in extensive simulation studies in Section 3 and these studies also reveal the nature of bias under different patterns of true exposure effects. We present, for the first time, an assessment of the infection-cardiovascular risk association in the dialysis population taking into account the imprecise exposure/infection onset data in Section 4. Finally, Section 5 provides a discussion of our proposed MECS models and findings.

2 Measurement Error Case Series Models for Imprecise Exposure Onset Times

2.1 The Model

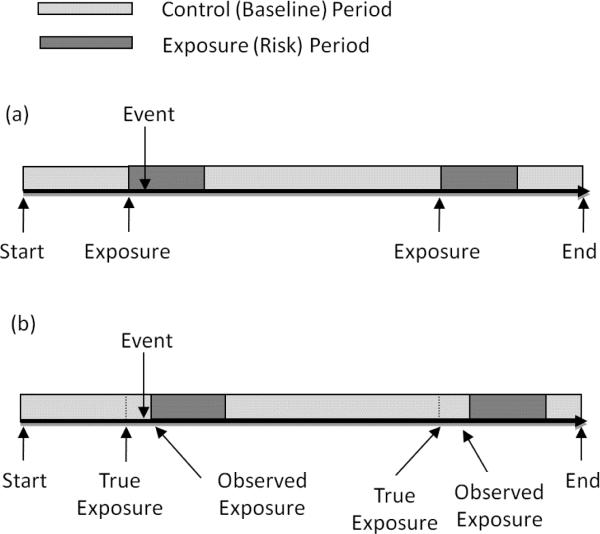
The self-controlled case series model was proposed by Farrington (1995) and was originally designed to estimate the relative incidence of acute events following transient exposures. It is a retrospective cohort method based on a conditional Poisson model requiring cases only and is self-controlled, since all time-invariant/age-independent confounders are implicitly controlled. The case series method is derived by conditioning on the occurrence of an event and the individual's exposure history during a fixed observation period, where event counts arise from a non-homogeneous Poisson process. For a cohort of N individuals (i = 1, …, N) with one or more events, let (a_i, b_i] denote the observation period over time for subject i (e.g., age in days) which is partitioned into age intervals (groups) j = 0, …, J and exposure risk periods k = 0, …, K. The baseline or control risk period corresponds to k = 0, which consists of all time periods outside of the exposure risk periods. Similarly, the reference age group is j = 0. For example, in the infection-cardiovascular example introduced earlier (Dalrymple et al., 2011), the risk periods are 1–30, 31–60, and 61–90 days (K = 3) after an infection (and the baseline period consists of observation times outside of the three risk periods). Figure 1(a) illustrates the follow-up data for a subject.

Figure 1.

Example of follow-up data for one subject (a) without and (b) with exposure onset measurement error. Note in (b) that when exposure onset measurement error is present, the event is now observed in the baseline period when in truth the event occurs in the exposure period, attenuating the relative incidence in this case.

The case series method compares the incidence within a risk period relative to the incidence in the baseline period, within each individual. Let the length of time individual i spends in age group j and risk period k be e_ijk. Given the exposure history over the observation period for individual i, the number of events in each interval, denoted n_ijk, is assumed to follow a non-homogeneous Poisson process with rate λ_ijk = exp(φ_i + α_j + β_k), i.e., n_ijk ~ Poisson(e_ijkλ_ijk). Here the parameters φ_i, α_j and β_k are, respectively, the individual-specific, j^th age group relative to age group j = 0 and k^th risk group relative to baseline period k = 0 effects, with α₀ = β₀ = 0. The parameters of primary interest are β_k, k = 1, …, K, the log relative incidences for the exposure risk periods. The case series model is obtained by conditioning on the event n_i.. = Σ_jk n_ijk ≥ 1, where n_i.. is the total number of events for individual i. As shown in Farrington (1995), the kernel of the case series likelihood is product multinomial, with the contribution from subject i given as

$$L_i(\alpha ,\beta )=\prod _{j,k}{\pi }_{ijk}^{n_{ijk}}$$ (1)

with probabilities

$${\pi }_{ijk}=\frac{e_{ijk}{\lambda }_{ijk}}{\sum _{rs}{e}_{irs}{\lambda }_{irs}}=\frac{e_{ijk}\text{exp}({\phi }_i+{\alpha }_j+{\beta }_k)}{\sum _{rs}{e}_{irs}\text{exp}({\phi }_i+{\alpha }_r+{\beta }_s)}=\frac{e_{ijk}\text{exp}({\alpha }_j+{\beta }_k)}{\sum _{rs}{e}_{irs}\text{exp}({\alpha }_r+{\beta }_s)},$$ (2)

β = (β₁, …, β_K) and = α (α₁, …, α_J). The individual effects φ_i cancel out, thus, selfcontrolling for all fixed covariates. We refer the reader to Farrington (1995) for details and also to the excellent expository papers by Whitaker et al. (2006, 2009) on the application of case series models, including study planning guidance and assessment of model assumptions.

Next, we introduce the model for exposure onset measurement error, motivated by imprecise infection onset when using USRDS hospitalization data. Because exposure onset measurement error is largely inconsequential to estimation of age effects, we focus here on the exposure effects of primary interest (i.e., the β′s); therefore, we drop subscript j. Also, we consider here, in more detail, a positive measurement error model because it is relevant to our current application, where we know that each exposure/infection must occur prior to the observed discharge date of an infection-related hospitalization. Thus, we consider the following positive additive exposure onset measurement error model,

$$w_{il}=v_{il}+u_{il},l=1,\dots ,L_i$$ (3)

where w_il is the observed exposure onset time, v_il is the true (unobserved) exposure onset time, u_il is a positive measurement error (u_il > 0) with mean μ_u = E(u_il) and variance ${\sigma }_u^2=\text{var}\left(u_{il}\right)$, and L_i is the number of exposures observed for individual i. For our current application w_il is the infection-related discharge time. Figure 1(b) illustrates the effects of exposure onset measurement error. We assume that the amount of measurement error in the exposure time (u_il) is less than the risk period length of interest. For example, if the relative incidence of events associated with the 30-day period after an infection is of interest, then the uncertainty in the time when the infection actually occurred should not exceed 30 days. If u_il > 30 days then one cannot estimate the relative incidence in the 30-day period after an infection, because u_il > 30 amounts to not having any reliable data for estimation. Thus, this assumption on the magnitude of the measurement error essentially ensures that there must be some amount of reliable data for estimation.

We refer to (1)–(3) as the measurement error case series (MECS) model. As in the case of classical measurement error problems, naive estimation ignoring measurement error will be biased. We characterize the target of the naive estimation, and hence the bias, in Section 2.2 below. For the MECS models, given u_i = (u_i1, …, u_iLi), ${\tilde{\mathbf{n}}}_i=({\tilde{n}}_{i0},\dots ,{\tilde{n}}_{iK})~Mult(n_{i.},{\tilde{\pi }}_i\left({\mathrm{u}}_i\right))$, where ${\tilde{n}}_{ik}$ is the observed number of (e.g., cardiovascular) events in risk period k (k = 0, …, K) and ${\tilde{\pi }}_i\equiv {\tilde{\pi }}_i\left({\mathbf{u}}_i\right)=\left({\tilde{\pi }}_{i0}\left({\mathbf{u}}_i\right),\dots ,{\tilde{\pi }}_{iK}\left({\mathbf{u}}_i\right)\right)$ are modified probabilities depending on measurement error u_i. More specifically, we show in the appendix that ${\tilde{\pi }}_{ik}$ is a function of the length of the kth risk period, the true underlying rate λ_ik, and a mixture of true rates corresponding to control and risk periods and measurement error.

We provide the following result (Theorem 1) needed to fully characterize the bias resulting from ignoring exposure onset measurement error in sections 2.2 and 3. For this purpose, we further introduce the following notation. Among individuals with L_i ≥ 2 exposures, let $L_i^{\prime }$ denote the number of (disjoint) risk segments ($L_i^{\prime }\le L_i$). For example, suppose that individual i has L_i = 5 infections, the risk period of interest is 1–30 days after an infection, infection 3 occurs within the 30-day risk period after infection 2 (i.e., the 30-day risk periods for infections 2 and 3 overlap), and similarly, infection 5 occurs within 30 days of infection 4. Then we have $L_i^{\prime }=3$ risk segments defined by infection 1, infections (2, 3), and infections (4, 5). We refer to the later two risk segments as “overlapping” risk segments. Thus, we have the following result for the general MECS model and a special case with potential overlapping risk segments. It is assumed that risk periods are adjacent following an exposure; for instance, 1–30, 31–60 and 61–90 days following an exposure. We defer the proof to the appendix.

Theorem 1. Under the general MECS model (1)–(3) with L_i exposures and non-overlapping risk segments,

$$E\left({\tilde{n}}_{ik}\right)=\{\begin{array}{cc}{n}_{i.}{\Delta }_i^{-1}\{e_{ik}{\lambda }_{ik}+L_i{\mu }_u({\lambda }_{i,k+1}-{\lambda }_{ik})\},\hfill & k=0,1,\dots ,K-1\hfill \\ n_{i.}{\Delta }_i^{-1}\{e_{iK}{\lambda }_{iK}+L_i{\mu }_u({\lambda }_{i0}-{\lambda }_{iK})\},\hfill & k=K\hfill \end{array}\phantom{\}},$$ (4)

where Δ_i = Σ e_irλ_ir. Furthermore, for MECS models with one risk period, individuals with multiple exposures, and possibly with overlaps, E(ñ_ik) in (4) holds with L_i replaced by $L_i^{\prime }$, the number of disjoint risk segments.

Remarks

Our studies in Section 3 below show that the MECS model with non-overlapping risk segments leads to the most severe bias on average; therefore, this case is of particular relevance to understanding the extent and nature of bias when ignoring exposure onset measurement error. Overlapping risk segments are relatively rare, although we also examine their effects on estimation bias as well. We discuss the above result for common MECS models (e.g., with K = 1 risk period) when there are possibly overlapping risk segments in the appendix. Also, although not directly applicable to our specific application in this work, the risk periods need not be adjacent in the case series model generally. Equation (4) can be extended to this case and we discuss this in the appendix section.

In the special case with one risk group (K = 1), we have that (4) reduces to

$$E\left({\tilde{n}}_{i1}\right)=n_{i.}\frac{e_{i1}{\lambda }_{i1}+L_i{\mu }_u({\lambda }_{i0}-{\lambda }_{i1})}{e_{i0}+e_{i1}{\lambda }_{i1}}=n_{i.}\frac{e_{i1}\text{exp}\left({\beta }_1\right)+L_i{\mu }_u(1-\text{exp}\left({\beta }_1\right))}{e_{i0}+e_{i1}\text{exp}\left({\beta }_1\right)}.$$

Thus, from the above equality, we note that lim_μu→0 E(ñ_i1) = n_i.π_i1, providing an approach to bias correction in Section 2.3.

2.2 Bias When Ignoring Exposure Onset Measurement Error

We consider here the bias that results from naive case series model estimation without accounting for exposure onset measurement error. Together with Theorem 1, the result described in this section is important for two purposes. First, it will be used to characterize the general nature of the bias when ignoring exposure time measurement error in Section 3. Secondly, it will be used to determine the accuracy of the proposed bias-correction method in estimating the true relative incidence of interest in Section 2.4.

Consider the observed data {${\tilde{n}}_i$, w_i, e_i}, where w_i = (w₁, …, w_Li) is the vector of observed exposure times for the i^th subject. The conditional maximum likelihood estimator (MLE) for the case series model, denoted ${\widehat{\beta }}^{\ast }$, is obtained as a solution to the set of likelihood equations

$$N^{-1}\sum _{i=1}^N({\tilde{n}}_{ik}-n_{i.}{\widehat{\pi }}_{ik}^{\ast })=0,k=1,2,\dots ,K,$$ (5)

where ${\widehat{\pi }}_{ik}^{\ast }=e_{ik}\text{exp}\left({\widehat{\beta }}_k^{\ast }\right)∕{\Sigma }_r{e}_{ir}\text{exp}\left({\widehat{\beta }}_r^{\ast }\right)$. Details are provided in the section Appendix: Estimation via Newton-Raphson. The MLE is consistent for ${\beta }^{\ast }$, which satisfies the estimating equations in (5) in expectation, i.e., β* is a solution to

$$N^{-1}\sum _{i=1}^N\{E\left({\tilde{n}}_{ik}\right)-n_{i.}{\pi }_{ik}^{\ast }\}=0,k=1,2,\dots ,K,$$ (6)

with ${\pi }_{ik}^{\ast }=e_{ik}\text{exp}\left({\beta }_k^{\ast }\right)∕{\Sigma }_r{e}_{ir}\text{exp}\left({\beta }_r^{\ast }\right)$. The bias of the naive case series model ignoring measurement error is the difference between β* (the target of ${\widehat{\beta }}^{\ast }$) and β. To solve (6), we note that substituting the expression for E(ñ_ik) from (4) gives

$$a_k\equiv N^{-1}{\Sigma }_{i=1}^N{n}_{i.}[{\Delta }_i^{-1}\{e_{ik}{\lambda }_{ik}+L_i{\mu }_u({\lambda }_{i,k+1}-{\lambda }_{ik})\}-{\pi }_{ik}^{\ast }]=0,k=1,\dots ,K-1$$

$$a_K\equiv N^{-1}{\Sigma }_{i=1}^N{n}_{i.}[{\Delta }_i^{-1}\{e_{iK}{\lambda }_{iK}+L_i{\mu }_u({\lambda }_{i0}-{\lambda }_{iK})\}-{\pi }_{iK}^{\ast }]=0,k=K.$$

This set of equations can be solved numerically for β* by the Newton-Raphson method where the update of β* at iteration t + 1 is β*^(t+1) = β*^(t) − (J^(t))⁻¹a^(t), with ${\mathbf{a}}^{\left(t\right)}={(a_1^{\left(t\right)},\dots ,a_K^{\left(t\right)})}^{\mathrm{T}}$ and J^(t) is a K × K matrix of partial derivatives evaluated at β^(t);

$$\frac{\partial a_k}{\partial {\beta }_k^{\ast }}=-N^{-1}{\Sigma }_{i=1}^N{n}_{i.}{\pi }_{ik}^{\ast }(1-{\pi }_{ik}^{\ast }),k=1,\dots ,K$$

$$\frac{\partial a_k}{\partial {\beta }_l^{\ast }}=N^{-1}{\Sigma }_{i=1}^N{n}_{i.}{\pi }_{ik}^{\ast }{\pi }_{il}^{\ast },k\ne l.$$

We use the above theoretical result to study the nature of bias due to exposure onset measurement error in the simulation studies of Section 3 for various patterns of exposure effects and realistic data scenarios. However, some insights are immediate from the above result with the simplifying assumption that the length of observation periods (and risk periods) and the number of exposures are the same for all subjects. For instance, we have from (6),

$$N^{-1}\sum _{i=1}^N{n}_{i.}\frac{e_{i1}\text{exp}\left(\beta \right)+L_i{\mu }_u(1-\text{exp}\left(\beta \right))}{e_{i0}+e_{i1}\text{exp}\left(\beta \right)}-N^{-1}\sum _{i=1}^N{n}_{i.}\frac{e_{i1}\text{exp}\left({\beta }^{\ast }\right)}{e_{i0}+e_{i1}\text{exp}\left({\beta }^{\ast }\right)}=0,$$

where a closed form expression for β* is possible under equal observation and risk periods for all subjects. Thus, in the simple, but illustrative, case where K = 1 (with L_i = 1; dropping subscript k), we obtain

$${\beta }^{\ast }=\text{log}\left\{\frac{e_1\text{exp}\left(\beta \right)+{\mu }_u(1-\text{exp}\left(\beta \right))}{e_0-{\mu }_u(1-\text{exp}\left(\beta \right))}\right\}-\text{log}(e_1∕e_0).$$ (7)

From equation (7), the bias in this special case is apparent; there is increasing attenuation of the true relative incidence, exp(β), as the mean of the exposure onset measurement error, μ_u, increases. However, the nature of the bias generally is not always attenuation, as we will demonstrate subsequently in Section 3. More precisely, if K = 1 the naive estimate will be attenuated, but with K > 1 risk periods the bias can be in either directions, depending on the pattern of the true relative incidences of the risk periods. We note that the target of the naive MLE ${\widehat{\beta }}^{\ast }$, namely β* given in (7), follows from (4), the law of large numbers and Slutsky's theorem, since it is straight-forward to show that ${\widehat{\beta }}^{\ast }=\log ({\tilde{n}}_{.1}∕{\tilde{n}}_{.0})-\log (e_1∕e_0)$. Here ñ_.k = Σ_iñ_ik, k = 0, 1.

2.3 Bias-corrected Estimation Procedure

To motivate our proposed bias-corrected estimation procedure, consider the target of the naive (conditional) maximum likelihood estimator, namely β* given in (7). Note that lim_μu→0 β* = β, the true unknown relative incidence parameter of interest. Thus, we propose a practical case series bias-correction procedure where the pattern of bias as a function of increasing amounts of exposure onset measurement error (μ_u) is determined/estimated and then extrapolated to the ideal case of no measurement error in the time of exposure. We assume that that an estimate of the average amount of exposure onset measurement error μ_u is available.

The simple steps of this correction procedure are as follows. First, obtain data sets with increasing exposure onset measurement error, i.e., with increasing mean μ_j = μ_u + τ_j, by adding a sequence of constants τ_j, j = 0, 1, …, M to the observed exposure times where 0 = τ₀ < τ₁ < … < τ_M and τ₀ refers to the observed data. Next, for each j, compute the naive maximum likelihood estimator, ${\widehat{\beta }}^{\ast \left(j\right)}$, by applying the standard case series model, ignoring exposure time measurement error. For a given estimate of μ_u, fit a least squares regression of ${\widehat{\beta }}_k^{\ast }={({\widehat{\beta }}_k^{\ast \left(0\right)},{\widehat{\beta }}_k^{\ast \left(1\right)},\dots ,{\widehat{\beta }}_k^{\ast \left(M\right)})}^{\mathrm{T}}$ on μ_j and the bias-corrected estimator is taken to be the extrapolated value at μ_j = 0, i.e., the regression intercept. More precisely, define the (M + 1) × (ν + 1) fixed predictor matrix by D_μ, then the estimated coefficient of the regression fit is ${\widehat{\alpha }}_k={\widehat{\alpha }}_{k0},{\widehat{\alpha }}_{k1},\dots ,{\widehat{\alpha }}_{kv}\mathrm{T}={\left({\mathbf{D}}_{\mu }^{\mathrm{T}}{\mathbf{D}}_{\mu }\right)}^{-1}{\mathbf{D}}_{\mu }^{\mathrm{T}}{\widehat{\beta }}_k^{\ast }$, k = 1, …, K. Thus, for bias-correction, we propose to use the extrapolated value at μ_j = 0, i.e.,

$${\widehat{\beta }}_k={\widehat{\alpha }}_{k0}={\mathbf{c}}^{\mathrm{T}}{\widehat{\beta }}_k^{\ast },k=1,2,\dots ,K,$$ (8)

where the vector of constants c = (c₀, c₁, …, c_M)^T is the first row of the (ν + 1) × (M + 1) matrix ${\left({\mathbf{D}}_{\mu }^{\mathrm{T}}{\mathbf{D}}_{\mu }\right)}^{-1}{\mathbf{D}}_{\mu }^{\mathrm{T}}$. As we will detail in subsection 2.4 below, it is adequate in practice to consider a quadratic regression fit (ν = 2) with D_μ containing predictors μ_j and ${\mu }_j^2$.

Note that although on the surface the proposed bias-corrected estimator appears to resemble the simulation and extrapolation (SIMEX; Cook and Stefanski, 1994) method for classical measurement error in the predictors (Carroll et al., 2006), it is quite distinct. SIMEX simulates additional data sets with increasing measurement error variance in the predictors. Such an approach is not appropriate for measurement error in the time of exposure onset This is clear when we consider a salient feature of the bias analysis described in Section 2.2, which is that the bias does not depend on the exposure time measurement error variance, as evident from (7). This facet generally holds, as illustrated in Figure 2, for the more general MECS model described above. Thus, a SIMEX approach is not appropriate to bias-correction for measurement error in the time of exposure. Secondly, note that there is no simulation involved in our proposed estimation.

Figure 2.

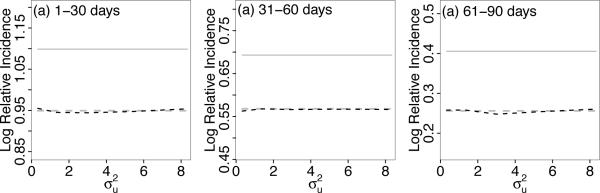
Property of exposure onset time measurement error. Bias does not depend on variance of the measurement error distribution. Dashed black curves denote naive case series estimates ignoring measurement error, which targets β* (dashed gray curves) instead of β (solid gray line).

We also note that given an estimate of μ_u based on auxiliary data or even knowledge of μ_u exactly, direct application of the case series model to the data where one subtracts this estimate from each observed exposure onset time will not correctly target the true relative incidences. For this reason, we developed the above estimator where extrapolation is made from a sequence of data sets with additively higher mean measurement error. We show this explicitly in the appendix and relate this to the more general cases of exposure onset measurement error where u is not strictly positive.

2.4 Accuracy of the Bias-Correction Method

In this section we evaluate the asymptotic accuracy of the bias-corrected estimation procedure to target the relative incidence θ_k ≡ exp(β_k) of interest. More precisely, we investigate the approximation error in using ${\widehat{\theta }}_k\equiv \text{exp}\left({\widehat{\beta }}_k\right)=\text{exp}\left({\widehat{\alpha }}_{k0}\right)=\text{exp}\left({\mathbf{c}}^{\mathrm{T}}{\widehat{\beta }}_k^{\ast }\right)$ as an estimator of θ_k. First, note that since ${\widehat{\beta }}_k^{\ast }$ is consistent for ${\beta }_k^{\ast }$, a solution to (6), we have that ${\widehat{\beta }}_k={\widehat{\alpha }}_{k0}={\mathbf{c}}^{\mathrm{T}}{\widehat{\beta }}_k^{\ast }$ is consistent for ${\mathbf{c}}^{\mathrm{T}}{\beta }_k^{\ast }$. Because ${\beta }_k^{\ast }$ is a solution to (6), note that it is a function of the true effects ${\beta }^{\mathrm{T}}=({\beta }_1,\dots ,{\beta }_K)$, the average exposure time measurement error μ_u and the observation lengths in the risk periods and baseline period {e_ik} across individuals i = 1, …, N. Thus, the accuracy depends on these parameters generally. Therefore, to assess accuracy in approximating the true relative incidence θ_k with the limit ${\theta }_k^{\ast }\left(\beta \right)=\text{exp}\left({\mathbf{c}}^{\mathrm{T}}{\beta }_k^{\ast }\right)$, we consider the maximum absolute relative approximation error (maxARE), defined as a function of the true relative incidences θ = (θ₁, …, θ_K),

$$\text{max ARE}=\underset{\beta }{\text{max}}\left\{\mid \frac{{\theta }_k-{\theta }_k^{\ast }\left(\beta \right)}{{\theta }_k}\mid ,k=1,\dots ,K\right\}.$$ (9)

Note that we used the notation ${\theta }_k^{\ast }\left(\beta \right)$ to emphasize the dependence on the true parameters β. We first consider the simple MECS model, with a single risk period K = 1, equal risk period e_i1 = e₁ and equal follow-up times, as it illustrates clearly the factors affecting the maximum approximation error. For this model (dropping subscript k), we have ${\beta }^{\ast \left(j\right)}=\text{log}(a+{\mu }_j)-\text{log}(b-{\mu }_j)-\text{log}(e_1∕e_0)$, where a = e₁ exp(β)/(1−exp(β)) and b = e₀/(1−exp(β)). Considering a third order Taylor approximation to log(·) at μ_j = 0 gives

$${\beta }^{\ast \left(j\right)}\approx \{\text{log}\left(a\right)+{\mu }_j∕a\}+\{\text{log}\left(b\right)+{\mu }_j∕b\}-\text{log}(e_1∕e_0).$$

It follows that for a quadratic regression fit (see Section 2.3 above), we have

$${\mathbf{c}}^{\mathrm{T}}{\beta }^{\ast }=\sum _{j=0}^M{c}_j{\beta }^{\ast \left(j\right)}\approx \text{log}\left(a\right)-\text{log}\left(b\right)-\text{log}(e_1∕e_0)=\beta ,$$ (10)

since a/b = (e₁/e₀) exp(β), ${\sum }_{j=0}^{M{c}_j=1}$ and ${\sum }_{j=0}^M{c}_j{\mu }_j={\sum }_{j=0}^M{c}_j{\mu }_j^2=0$.

The error in the above approximation involves ${\sum }_{j=0}^M{c}_j{\mu }_j^3$, ~ a⁻³ and ~ b⁻³. Thus, the error in (10) will depend on two main factors: the effect size β and the average level of exposure onset time measurement error relative to the risk period length μ_u/e₁, as well as the relative risk period length to the baseline period length e₁/e₀. Therefore, we examine the error in the approximation with respect to these parameters. We examine the maximum absolute relative error (maxARE) as given in (9). To encompass all reasonable relative incidences of interest in real applications, we evaluate the accuracy for a wide range of true relative incidences, ranging from a tiny effect size of 1% (θ = 1.01) to a very large effect size of 1,000% (10-fold; θ = 10). For equal observed risk length e₁ = 30 days after an exposure during 700 days of follow-up (e₁/e₀ ≈ 4.5%), and with the average level of exposure onset time measurement error of μ_u = 4, 6, and 8 days (i.e. μ_u/e₁ ~ 13.3%, 20% and 26.7%, respectively), the maxARE are 0.48%, 1.27%, and 2.84%; thus, even with the higher relative measurement error of nearly 27%, the maximum error of θ*(β) is less than 3% of the true relative incidence θ. We note that the 2.84% maximum error is associated with the extremely large effect size of θ = 10; therefore, the maximum relative error is quite low.

More generally, when allowing for varying lengths of the observed risk period for each individual and varying number of exposures per person, the maximum relative approximation error is similarly low compared to the simpler case of equal risk observation lengths considered above. For this, we solve equation (6) for β* using the Newton-Raphson method described in Section 2.2 and then evaluate (9) to determine the maximum error over the range of β values. Similar to the simple model considered above, the maxARE over all values of β are 0.52%, 1.34%, and 3.00% corresponding to moderate to high relative average exposure onset time measurement error, i.e., average μ_u/e₁ ~ 13.3%, 20% and 27%. The average time in the risk period across individuals is 48 days and the average percent of time spent in the risk period relative to the baseline period is ~ 7.5%. These parameters are similar to our data application in Section 4, where the relative incidences of cardiovascular events in the 30-days following infection were estimated to be ~ 1.5 to 1.8, corresponding to average exposure onset time measurement error of μ_u = 4 and μ_u = 8 days. Under this setting, the approximation error is negligible: 0.02% and 0.20% for for μ_u = 4 and 8 days, respectively.

The maximum approximation error is similarly low when extending to models with multiple risk groups, examined in more details in Section 3. For example, with average relative exposure time measurement error of 20%, the maximum relative error is ~ 5% for tiny effect sizes of θ = 1.01 to 1.05, and it reduces to ~ 1.5% otherwise. In summary, the limiting value ${\theta }_k^{\ast }\left(\beta \right)$ is close to the true effect θ_k for all reasonable range of β_k and average relative exposure onset time measurement error. However, ${\theta }_k^{\ast }\left(\beta \right)$ is not close to θ_k arbitrarily and particularly under impractical conditions in which we expect it not to perform well. For example, consider a situation in which there is excessive amount of measurement error on the time of exposure. For concreteness, consider the case where we are interested in the relative incidence of events in the 30-days risk period following an exposure with a very high exposure onset measurement error of μ_u = 15 days, so that on average we are uncertain as to when the true exposure actually occurred by 15 days within a relatively small 30-day risk window of interest (average 100×μ_u/e₁ = 50%). The maximum relative error is 25.7%. However, this reduced performance is expected since one cannot expect to be able to estimate the relative incidence of events during a fixed risk period following an exposure when one has excessive uncertainties regarding when the exposure actually occurred.

3 Simulation Study

3.1 Simulation Design

In this section, we implement a set of simulation studies to address two specific objectives: (1) characterize the general nature of bias as a consequence of data with exposure onset measurement error and (2) assess the efficacy of the proposed bias-corrected estimation procedure to target the true relative incidence in MECS models.

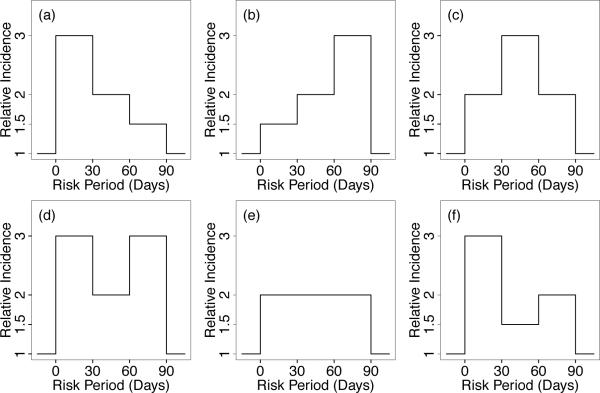
We consider various underlying patterns of true relative incidences over multiple risk periods. As illustrated in Figure 3, these patterns include decreasing, increasing, and constant relative incidences over risk periods (cases a, b, and e, respectively), as well as mixtures of increasing and decreasing incidences (cases c, d, and f). The log relative incidences corresponding to these patterns are provided in Table 1; e.g., β = (β₁, β₂, β₃) = (1.099, 0.693, 0.0405) for pattern (a). For each of these pattern of relative incidences, we generated the data as follows. The observation period [a_i, b_i] is uniformly generated with mean follow-up length of 700 days for i = 1, …, N = 1000 individuals and individual effects/baseline rates are set to φ_i = log(1/10000). Next, the marginal number of events, n_i., for the i^th individual is generated from a Poisson distribution, truncated at 1 to obtain cases/individuals with at least one event according to the case series model (Farrington, 1995) and these events are distributed within an individual's observation period according to the multinomial distribution with probabilities given in equation (2). The number of non-overlapping exposures L_i range from 0 to 3 with probability masses {0.2, 0.4, 0.25, 0.15} and true/unobserved exposure times v_il, l = 1, …, L_i, is uniformly distributed over the follow-up period. Next, positive measurement error u_il, for each exposure, is added to the true exposure times to obtain the observed exposure times, w_il = v_il + u_il. We consider uniform, normal and gamma distributed measurement error distributions with variances 1.33, 1.0 and 2.77, respectively.

Figure 3.

Patterns of true relative incidence (β) in contiguous risk periods studied in simulations, including (a) decreasing, (b) increasing, (e) constant, and both symmetric and non-symmetric mixtures of increasing and decreasing β_k's (pattern c, d and f).

Table 1.

Bias-corrected estimates $\widehat{\beta }$ and standard deviations over 200 replications for datasets (each with N = 1000) with three 30-day risk periods and for risk/effect patterns (a)–(f) described in Figure 3.

Pattern	True (β1)	Est.	SD	True (β2)	Est.	SD	True (β3)	Est.	SD
(a)	1.099	1.106	0.129	0.693	0.688	0.151	0.405	0.387	0.172
(b)	0.405	0.405	0.172	0.693	0.672	0.167	1.099	1.128	0.134
(c)	0.693	0.693	0.171	1.099	1.094	0.137	0.693	0.720	0.145
(d)	1.099	1.120	0.131	0.693	0.671	0.156	1.099	1.120	0.136
(e)	0.693	0.686	0.161	0.693	0.683	0.161	0.693	0.703	0.166
(f)	1.099	1.102	0.136	0.405	0.399	0.176	0.693	0.689	0.166

To characterize the general nature of bias due to exposure onset measurement error and illustrate how the bias depends on the average amount of measurement error μ_u as described in Section 2.2, we generated data with increasing μ_u = 4, 6, 8, 10, 12 or 14 days. All simulation results reported next are based on averages over 200 simulated data sets.

3.2 Results: Bias When Ignoring Measurement Error and Bias-corrected Estimation

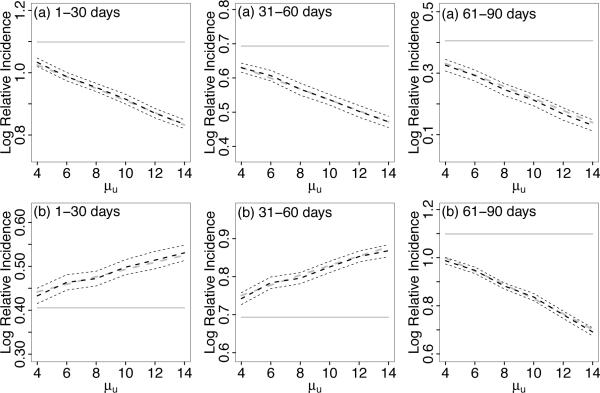
To describe the general nature of the asymptotic bias, we focus in more details on studies of decreasing and increasing effects patterns illustrated in Figure 3 (a) and (b), respectively. Also, for the description of the bias, we focus on the case with uniform measurement error and sample size N = 1000. Bias results for effect patterns (a) and (b) are shown in Figure 4 as a function of μ_u. Generally, and as expected, the bias increases with increasing average measurement error μ_u. As can be seen, the naive case series estimates (black dashed curve) target β* (dashed gray curve), which is obtained as the solution to equation (6) using the Newton-Raphson algorithm described in Section 2.2.

Figure 4.

Bias for (a) increasing and (b) decreasing true patterns of log relative incidence β(indicated by horizontal lines) over three risk periods. Dashed black curves denote naive case series estimates ignoring measurement error, which targets β* (dashed gray curves) instead of β. In pattern (a), all three risk period log relative incidence estimates are attenuated. In Pattern (b), the first two log relative incidence estimates are inflated and the third is attenuated. Also included are 95% confidence intervals (thin dashed lines). Given are averages over 200 simulated data sets.

When the risk is highest in the first 30 days and decreases with time, i.e., pattern (a), all estimates ignoring measurement error, ${\widehat{\beta }}_1^{\ast }$, ${\widehat{\beta }}_2^{\ast }$ and ${\widehat{\beta }}_3^{\ast }$, are attenuated. Conversely, when the true risk increases over time, i.e., pattern (b), ${\widehat{\beta }}_3^{\ast }$ is attenuated but ${\widehat{\beta }}_1^{\ast }$ and ${\widehat{\beta }}_2^{\ast }$ are inflated. This result is expected, since it can seen from (11) that the bias of the relative incidence in the k^th risk period is a function of the incidence in the next contiguous risk period, (k+1), for k = 0, 1, …, K − 1. Thus, if the true relative incidence in risk period k is greater than in risk period k+1, i.e., if β_k > β_k then ${\widehat{\beta }}_k^{\ast }$ will be attenuated. If β_k < β_k+1 then ${\widehat{\beta }}_k^{\ast }$ will be inflated. Note that ${\widehat{\beta }}_K^{\ast }$ will usually be attenuated if exposure onset measurement error is present since the relative incidence in the K^th risk period is a function of the incidence in the baseline period. Similar patterns of bias hold for different measurement error distributions, e.g., normal and gamma measurement errors. We provide details of these cases as supplemental materials in the file mecs_sup.pdf.

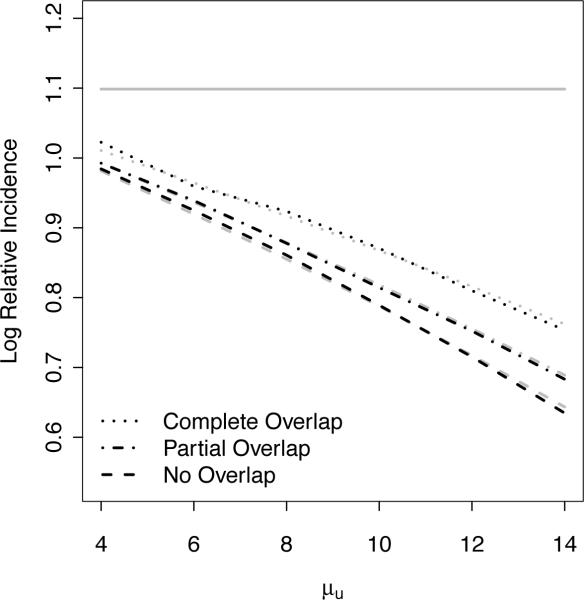
Next, in Figure 5, we compare the relative amount of bias as the average measurement error μ_u increases for data with no overlapping risk segments, partial overlapping risk segments, and complete overlapping risk segments. The simulation setting for Figure 5 is as described above with a 30 day risk period and uniformly distributed measurement error. As described earlier in Section 2.1, overlapping risk segments are observed in practice when a recurrent exposure occurs in the risk period of a previous exposure. For example, for a risk period of interest defined as 30 days after an infection and with the first and second infections occurring on days 10 and 35, the length of the risk segment is 55 days instead of 60 days since days 35 to 40 overlap. Although non-overlapping exposures, as described above, are vastly more common, we also illustrate here the relative differences in bias when there are overlapping risk segments. As illustrated in Figure 5, the bias is greatest when there are no overlapping risk segments, least when all risk segments overlap and intermediate when there are some/partial overlaps. Furthermore, the simulation results confirm the theoretical results described in Section 2.2 for realistic data with mixtures of non-overlapping and overlapping risk segments. Results for different measurement error distributions are similar and are not shown.

Figure 5.

Relative estimation bias when ignoring measurement error for data with (1) complete, (2) partial or (3) no overlapping risk segments. Bias is greatest when there are no overlapping risk segments, least when all risk segments overlap and intermediate when there is some/partial overlap. Dashed black curves denote naive case series estimates ignoring measurement error, which targets β* (dashed gray curves) instead of β (horizontal line).

We illustrate through extensive simulation studies the efficacy of the proposed bias-corrected estimation procedure for the MECS models described in Section 2.3. Table 1 shows results from the proposed bias-corrected estimation procedure, using the simple quadratic regression intercept estimate, under the more general MECS data scenarios for each true effect pattern in Figure 3 (a)–(f) with N = 1000. For each simulated data set with exposure onset time measurement error, increasing constants (τ_m = 0, 2, 4, …, 10 days) were added to each exposure time and estimates were computed by applying the case series model to each data set as detailed in Section 2.3. The proposed adjusted estimator performs well for the different patterns of risk (a)–(f) and targets the true parameter β. Table 2 presents the bias and mean square error (MSE) for the bias-corrected and the naive estimators. Overall, the MSE for the bias-corrected estimate is of similar order as the naive estimate MSE; however as expected, its bias is drastically reduced. On average, the reduction is ~ 9.4 folds across the simulations. We note that the simulation study assumes that μ_u is known; thus the results may be optimistic.

Table 2.

(A)Absolute bias for the proposed method and the ratio bias (naive/proposed) and (B) mean square error (MSE) of the naive and the proposed bias-corrected estimates corresponding to Table 1. See Table 1 caption for details.

(A) Bias	β 1		β 2		β 3
Pattern	Proposed	Ratio	Proposed	Ratio	Proposed	Ratio
(a)	0.008	8.125	0.006	11.167	0.019	4.105
(b)	0.003	12.333	0.016	3.562	0.020	4.300
(c)	0.008	5.000	0.004	15.500	0.008	12.000
(d)	0.019	4.526	0.031	0.581	0.005	24.200
(e)	0.008	2.125	0.010	1.700	0.010	7.700
(f)	0.003	29.667	0.007	1.143	0.004	21.000

(B) MSE
Pattern	Naive	Proposed	Naive	Proposed	Naive	Proposed
(a)	0.012	0.017	0.017	0.023	0.021	0.030
(b)	0.015	0.032	0.014	0.024	0.018	0.019
(c)	0.013	0.025	0.010	0.014	0.022	0.027
(d)	0.016	0.017	0.012	0.028	0.026	0.017
(e)	0.011	0.026	0.012	0.026	0.021	0.028
(f)	0.017	0.018	0.013	0.031	0.020	0.028

In addition to uniform exposure onset measurement errors, we also examined gamma and normally distributed measurement errors, as well as the performance for finite sample sizes. The adjusted estimates target the true parameters as expected and these additional results are available in the supplemental materials file mecs_sup.pdf. Also, at the suggestion of a reviewer, we provided more details on the performance as the variance of the measurement error distribution (${\sigma }_u^2$) increases in the supplemental materials (Table 7). This result illustrates the robustness of the bias-correction to the measurement error variance.

Finally, we remark on the choice of μ_M (i.e., the τ_j sequence) in the regression extrapolation. From our experiences, there is flexibility in the choice of the τ_j sequence and it is not a major factor in the quality of the estimator if chosen reasonably. In practice, the choice of the sequence ${\left\{\tau \right\}}_{j=0}^M$ will depend on the estimated average exposure onset measurement error (μ_u) relative to the a priori specified risk period of interest. For example, for the simulation study (and the data application) where the risk period of interest is the 30 day period(s) after infection/exposure, the choice of μ_M = μ_u + τ_M should not be excessively small relative to the risk period length. Figure 6 displays a regression fit through ${\widehat{\beta }}^{\ast \left(j\right)}$ versus μ_j = μ_u + τ_j with μ_u = 4 and μ_M = 14, demonstrating a very precise extrapolation (black lines). Here the interval μ_M − μ_u relative to the risk period is 1/3. We find that generally μ_M selected such that this relative length is about 1/3 to 1/2 to be adequate. To illustrate how the extrapolation accuracy declines, we chose μ_M = 10 so that the relative interval is only 20% of the risk period (gray lines). However, even with such a small interval where the regression is fitted, the extrapolation is able to correct for most of the bias relative to the naive estimate (asterisk). Since the computational cost of the naive case series estimator is trivial, we recommend a conservative approach to take M as large as feasible for a given dataset to capture the features of the quadratic regression fit in the extrapolation. In our applications, we find that it is adequate to take M to be 6–10.

Figure 6.

Illustration of the extrapolation from the regression fit to obtain the bias-corrected relative incidence estimates. Black lines are the regression fit using μ_M = 14 and the gray lines are based on μ_M = 10. Horizontal lines are the true β_k's; the asterisk marks the naive estimate; the square boxes indicate the bias-corrected estimates for μ_M = 14 (black) and μ_M = 10 (gray).

4 Application: Examining the Infection-Cardiovascular Risk Hypothesis for Patients on Dialysis

4.1 MECS Model for Infection-Cardiovascular Risk Using USRDS Data

As introduced in Section 1, a major challenge associated with using the USRDS inpatient hospitalization data to address the infection-cardiovascular risk hypothesis is that the exact date or time of infection onset cannot be ascertained precisely, although the observed discharge date is a good marker for the time of infection since it reasonably assures that the infection has occurred by this date. Thus, using the observed discharge time as a marker of the true infection time is a conservative approximation since the infection most likely occurred sometime during or possibly prior to the hospitalization. This modeling strategy leads to positive infection onset measurement error and thus we apply the proposed MECS model to determine the relative incidence of cardiovascular events in the risk period following infection. Provided in more details in Dalrymple et al. (2011), in the short period following an infection, specifically the approximate 30 days after infections, the effects of infection on vascular endothelium is hypothesized to be most pronounced. Thus, we focus on this risk period for illustrating the proposed MECS model. Cardiovascular events were defined as myocardial infarction, unstable angina, stroke, or transient ischemic attack and infections of interest included septicemia, bacteremia, peritonitis, endocarditis, soft-tissue, pulmonary, genitourinary, gastrointestinal, joint or bone infection. The source population included patients 65–100 years of age with end-stage renal disease who newly initiated dialysis between January 1, 2000 and December 31, 2002. Study follow-up ended December 31, 2004. We refer the reader to (Dalrymple et al., 2011) for further details on the study protocol. The cohort for the analysis reported below includes N = 16, 779 patients with one or more cardiovascular events.

Generally, external or auxiliary data sources are needed to reasonably estimate the measurement error parameter, namely μ_u. However, for our current application we can derive reasonable bounds on μ_u by using data on the length of hospitalization stay. If a hospitalization has an infection-related discharge diagnoses, it is likely that the infection occurred some time during the hospitalization stay, or in some cases possibly shortly before the start of the hospitalization. The median length of hospital stays is 8 days in our cohort. Thus, we used μ_u = 8 days as our intermediate estimate. We also used the lower estimate μ_u = 4, half of the length of a typical hospitalization stay, to illustrate the reduced biased corresponding to a lower average (optimistic) level of measurement error, as expected. Thus, we apply the bias-correction method for the MECS model to obtain adjusted estimates of the true relative incidence using these values of μ_u. Also, we note that due to the data violating the assumption of constant risk within a risk period, for illustration of the bias-correction method, we define the risk period as days 6–30 after an observed infection onset measured with error. The naive and bias-corrected log relative incidences are provided in Table 3. The naive relative incidence is 1.354 ($\widehat{\beta }=0.303$), i.e., the incidence of a cardiovascular event is 35% higher within the risk period after an infection compared to the baseline period. If we estimate that, on average, the observed date of infection is 4 days later than the true date of infection (μ_u = 4), then the relative incidence estimate is increased by 16% to 1.516 ($\widehat{\beta }=0.416$) after adjusting for infection onset measurement error. Similarly, if we instead consider the intermediate estimate of measurement error μ_u = 8, the median of the hospitalization length distribution, then the bias-corrected relative incidence estimate is 1.768 ($\widehat{\beta }=0.570$), an increase of 41% above the naive estimate.

Table 3.

Naive and bias-corrected estimates and standard errors for $\widehat{\beta }$. The naive estimate corresponds to applying the case series method to the observed USRDS data, ignoring the presence of measurement error. The bias-corrected estimates correspond to applying the proposed correction method and approximate standard errors were obtained using the bootstrap method (via resampling of subjects). Bootstrap confidence intervals (CIs) are provided for the bias-corrected estimates.

Estimation Method	Log Relative Incidence	Standard Error	95% CI
Naive	0.303	0.03	–
Bias-correction μu = 4	0.416	0.05	0.312–0.513
Bias-correction μu = 8	0.570	0.09	0.402–0.734
Bias-correction ${\widehat{\mu }}_u$ = 5.5	0.470	0.06	0.358–0.586

Thus, infection onset measurement error led to substantive attenuation of the direct case series estimate of the relative incidence of cardiovascular events following infection in patients on dialysis. However, from the standard error estimates provided in Table 3, it is obvious that all analyses lead to the same scientific conclusion that there is an increased risk of cardiovascular events following infection; only point estimates and precision are affected in this data. Reported standard errors for the bias-corrected estimation are based on 500 bootstrap data sets by resampling subjects, although SE estimates stabilize at ~ 100 bootstrap samples. Bootstrap confidence intervals (CIs) are also provided, showing that even under the extremely optimistic assumption of low measurement error (μ_u = 4) the CI is above the naive point estimate.

We note that for the USRDS data analysis above, we took a conservative approach by considering a low and intermediate value for μ_u because we do not have a direct estimate of the average amount of exposure onset measurement error. Instead, we arrived at this range based on the available data on the duration of hospitalization stay, where the median length of stay is 8 days. Examining both analyses, for μ_u = 4 and 8, allowed us to assess the degrees of attenuation of the true relative incidence for these two levels of measurement error. The analysis corresponding to μ_u = 4 can be interpreted as a reasonable approximation to the situation where the distribution of infection onset is highly skewed to the end of the hospitalization. This is unlikely and too optimistic, but it provides a lower estimate of attenuation in a very optimistic scenario. It is informative that for the USRDS data, even under this optimistic assumption about μ_u the relative incidence of cardiovascular events is increased by ~ 16%; and the increase is more likely to be in the 23% – 41% range, corresponding to μ_u = 5.5 to 8, for instance. However, similar to the theory of classical measurement error in the covariates, with a consistent estimate of μ_u, say ${\widehat{\mu }}_u$, which can be obtained from an internal subsample or external validation data sources generally, the proposed bias-correction method for the MECS model would target the true relative incidence. For our application here, if we assume equal likelihood of infection during a hospitalization stay, then u_i|l_i ~ U(0, l_i), where l_i is the duration/length of hospitalization. Thus, μ_u = E(u) = E{E(u_i|l_i)} and we can use the consistent estimate ${\widehat{\mu }}_u=0.5{\sum }_i^N{l}_i∕N~11∕2=5.5$ (which is between the 4 and 8 days range we considered above). For comparison, this analysis is also provided in Table 3.

4.2 Modeling of USRDS Infection-Cardiovascular Data via Simulation

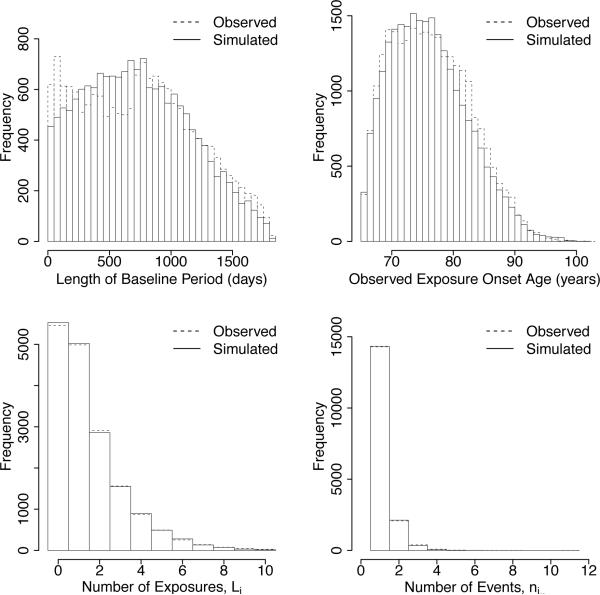
In this section we further analyze the infection-cardiovascular hypothesis and the effects of exposure onset measurement error by modeling the USRDS data characteristics relevant to case series modeling by simulating data that matches more precisely the key characteristics of the USRDS cohort. This allows for a more thorough study of the effects of measurement error since the unknown parameters are controlled and can be varied. More precisely, we simulated USRDS case series data by using the simulation approach described in Section 3 and matched key relevant characteristics of the USRDS data, including the distributions of the ages at the start and end of the observation period, the length of follow-up, the length of baseline and risk periods and the number of exposures per individual. The sample size is kept at N = 16, 779, as observed. The distribution of the number of exposures for each individual, L_i, was based on the distribution of the number of exposures in the observed data. We note that the number of exposures in the observed data ranged from 0 to 19. However, in the simulated data, we restricted the range to no more than 10 exposures as this captured > 99% of the original population and did not affect the analyses. We take the bias-corrected estimates of β in the previous section to model the USRDS data. Once the number of exposures were generated, the times of exposure were distributed uniformly across each individual's observation history. Figure 7 displays the observed and simulated distribution of the length of baseline period, observed exposure onset ages and number of exposures and events per individual. The characteristics of the simulated USRDS data closely track that of the observed USRDS data.

Figure 7.

Characteristics of observed USRDS data compared to simulated USRDS data.

We apply the case series model directly to both the data with true exposure times and observed exposure times. As done earlier, we assess the effect of measurement error generated from three different distributions: uniform, normal and gamma. Only results from the uniform distribution are presented here but results from the normal and gamma distributions are similar. Naive and bias-corrected estimates were obtained and averaged over 200 simulated datasets each for μ_u = 4 and μ_u = 8. When relatively modest measurement error was present, i.e., when μ_u = 4 days, namely when u_il ~ Uniform[1, 7], the average naive and bias-corrected relative incidence estimates were 1.433 and 1.525, respectively. For intermediate level of measurement error, i.e., u_il ~ Uniform[5, 11] (μ_u = 8 days), then the average relative incidence estimates were 1.518 and 1.784 for the naive and bias-corrected method, respectively. Thus, the results are similar to the percent increases observed in the analysis of the USRDS data of Section 4.1: the bias-corrected relative incidence estimates suggest a 9% (for μ_u = 4) and 27% (for μ_u = 8) increase over the naive relative incidence estimate on average, a significant difference in this high risk population.

5 Discussion

Motivated by using USRDS data to assess the infection-cardiovascular risk association in the dialysis population, where the precise times of infection cannot be ascertained, we proposed the measurement error case series model to take into account the imprecise exposure/infection onset data. We presented, for the first time, a novel analysis of infection-cardiovascular risk association in a national cohort, using the proposed MECS model. The results lend additional support to the hypothesis that the ~ 30-day period following infection is associated with a significantly increased risk/incidence of cardiovascular events. Through several different analyses of infection onset measurement error in Section 4, we confirmed the previously reported conclusion of an increased risk of cardiovascular events following infection-related hospitalization, based on the discharge date as a marker of the time of infection (Dalrymple et al., 2011); furthermore, the estimate of relative incidence was conservative when ignoring measurement error.

We also provided the asymptotic bias of the case series model that ignores exposure onset measurement error and proposed a feasible estimation procedure to correct for the bias when using the USRDS data. The method performs well in extensive realistic simulation studies, designed to match key characteristics of the USRDS data for the case series model. Also, an appealing aspect of the proposed MECS models is that no new computational tools are needed for estimation as they only involve repeated computation of the naive estimator.

We note that for general application of the MECS models, additional/auxiliary data is needed to estimate the mean of the exposure onset measurement error distribution. This is similar to the need for auxiliary data/information in regression modeling with traditional measurement error for mismeasured continuous or misclassified categorical variables. Depending on the specific application, additional data to estimate exposure onset measurement error mean can be obtained through retrospective review of a subset of subjects to determine true exposure onset times or follow-up data collection if feasible. In the absence of any additional data or if collection of new data is not practical, the tools developed in this work can be utilized in sensitivity analyses that assume specific values for the mean of exposure onset measurement error. For our specific application, which utilizes inpatient hospitalization data, a conservative marker of infection onset time is used and reasonable bounds for μ_u were determined based on additional data on the length of hospital stay.

Finally, in our application and the proposed MECS model framework, the precise onset of the cardiovascular events that we consider are reasonably measured with accuracy with respect to diagnosis and time. Although more rare, inevitably with the size of the sample analyzed, the timing of some events will not be accurate. However, although less applicable to our current hypothesis on cardiovascular outcomes/events, measurement error on the precise onset of events generally is possible, as pointed out by a reviewer. Case series modeling with measurement errors in both the precise onset of events as well as the timing of exposures presents significant challenges; it is an open problem at this time.

Appendix

Proof of Theorem 1

For the general MECS model with L_i exposures for individual i and with K adjacent risk periods, direct calculations yield

$${\tilde{\pi }}_{ik}\left({\mathbf{u}}_i\right)=\{\begin{array}{cc}{\Delta }_i^{-1}\{e_{ik}{\lambda }_{ik}+({\lambda }_{i,k+1}-{\lambda }_{ik})\sum _{l=1}^{L_i}{u}_{il}\},\hfill & k=0,1,\dots ,K-1\hfill \\ {\Delta }_i^{-1}\{e_{iK}{\lambda }_{iK}+({\lambda }_{i0}-{\lambda }_{iK})\sum _{l=1}^{L_i}{u}_{il}\},\hfill & k=K\hfill \end{array}\phantom{\}}$$ (11)

where Δ_i = Σ_r e_irλ_ir. To see that the denominator of ${\tilde{\pi }}_{ik}$(u_i) is Δ_i, denote the numerator in (11) by δ_ik for k = 0, 1, …, K. Then it can be directly verified that Σ_k δ_ik = Σ_k e_ikλ_ik. (Therefore, ${\sum }_k{\tilde{\pi }}_{ik}=1$.) Thus, $E({\tilde{n}}_{ik}\mid {\mathbf{u}}_i)=n_{i.}{\tilde{\pi }}_{ik}\left({\mathbf{u}}_i\right)$ since, conditional on u_i, ${\tilde{\mathbf{n}}}_i=({\tilde{n}}_{i0},\dots ,{\tilde{n}}_{iK})~Mult(n_{i.},{\tilde{\pi }}_i\left({\mathbf{u}}_i\right))$; $E\left({\tilde{n}}_{ik}\right)$ given in (4) follows. Next, we consider the more rare case in applications where two or more exposures may have overlapping risk segments within the risk period (MECS model with K = 1), as previously defined in Section 2.1. Suppose that there are L_i ≥ 2 exposures with $L_i^{\prime }$ disjoint risk segments ($L_i^{\prime }\le L_i$) as previously defined prior to Theorem 1. Denote the number of exposures that form the s^th risk segment by ζ(s), where ζ(s) ≥ 1 (s = 1, …, $L_i^{\prime }$). Overlapping risk segments correspond to ζ(s) > 1 and note that ${\sum }_{s=1}^{L_i^{\prime }}\zeta \left(s\right)=L_i$. The risk period length, e_i1, can be partitioned into disjoint risk segment lengths $e_{i1}^{\left(s\right)}>0$; thus, $e_{i1}={\sum }_{s=1}^{L_i^{\prime }}{e}_{i1}^{\left(s\right)}$. Similarly, the baseline period length, e_i0, can be partitioned into disjoint baseline segment lengths $e_{i1}^{\left(s\right)}>0$ (s = 1, …, $L_i^{\prime }$) and $e_{i0}^{\left(L_i^{\prime +1}\right)}\ge 0$, where the boundary is at the end of the observation period, $e_{i0}^{\left(L_i^{\prime +1}\right)}$, may be zero if the end of the observation period occurs within the last exposure risk segment. (Thus, $e_{i0}={\sum }_{s=1}^{L_i^{\prime +1}}{e}_{i0}^{\left(s\right)}$.) Also, denote the measurement errors associated with the ζ(s) exposures of the s^th risk segment by {u_isj; j = 1, …, ζ(s)}, for s = 1, …, $L_i^{\prime }$. Then the group probabilities, ${\tilde{\pi }}_{ik}$, can be shown to be linear functions of the underlying rates {λ_ik}, where the coefficients depend on risk segment lengths {$e_{i0}^{\left(s\right)}$} and {$e_{i1}^{\left(s\right)}$}, and the measurement errors {u_isj; j = 1, …, ζ(s)}. Similar to (11), the model probabilities for the risk and baseline periods (after simplification) are given by,

$${\tilde{\pi }}_{ik}\left({\mathbf{u}}_i\right)=\{\begin{array}{cc}{\Delta }_i^{-1}\{e_{i0}{\lambda }_{i0}+{\lambda }_{i1}\sum _{s=1}^{L_i^{\prime }}{u}_{i{s}_1}-{\lambda }_{i0}\sum _{s=1}^{L_i^{\prime }}{u}_{i{s}_{\zeta \left(s\right)}}\},\hfill & k=0\hfill \\ {\Delta }_i^{-1}\{e_{i1}{\lambda }_{i1}+{\lambda }_{i0}\sum _{s=1}^{L_i^{\prime }}{u}_{i{s}_{\zeta \left(s\right)}}-{\lambda }_{i1}\sum _{s=1}^{L_i^{\prime }}{u}_{i{s}_1}\},\hfill & k=1\hfill \end{array}\phantom{\}}.$$

Therefore, E(n_ik) is as given in (4) with L_i replaced by $L_i^{\prime }$. This completes the proof of Theorem 1.

For our application of the case series model to infection-cardiovascular association as well as other applications of this model, a heightened risk of adverse events following an exposure justifies the assumption of adjacent risk periods. However, the risk periods need not be adjacent in the case series model generally. In this case (for non-overlapping exposures) it can be shown that equation (4) becomes

$$E\left({\tilde{n}}_{ik}\right)=\{\begin{array}{cc}{n}_{i.}{\Delta }_i^{-1}\{e_{ik}{\lambda }_{ik}+L_i{\mu }_u({\lambda }_{i,0}-{\lambda }_{ik})\},\hfill & k=1,1,\dots ,K\hfill \\ n_{i.}{\Delta }_i^{-1}\{e_{i0}{\lambda }_{i0}+L_i{\mu }_u(\sum _{k=1}^K{\lambda }_{ik}-K{\lambda }_{i0})\},\hfill & k=0\hfill \end{array}\phantom{\}},$$

Estimation via Newton-Raphson

Fitting the case series (multinomial) model can be based on standard software (including SAS, Stata, and R; see http://statistics.open.ac.uk/sccs) that have routines for Poisson models with log link function and allow for an offset term log(e_ijk). For the MECS estimation proposed, no new computational tools are required; therefore, existing software can be used. However, it may be more efficient with the repeated applications for different μ_j to use the Newton-Raphson algorithm directly. We provide here the formulas for straight-forward implementation. Following the notations introduced in Section 2.1 we have that log(π_ijk/π_i00) = α_j + β_k + log(r_ijk), with r_ijk = e_ijk/e_i00. Thus, the log-likelihood for the i^th subject is

$${\ell }_i(\alpha ,\beta )=\sum _{j=0}^J\sum _{k=0}^K{n}_{ijk}\{{\alpha }_j+{\beta }_k+\text{log}\left(r_{ijk}\right)\}-n_{i..}\text{log}\left\{\sum _{r=0}^J\sum _{s=0}^K{e}_{irs}\text{exp}({\alpha }_r+{\beta }_s)∕e_{i00}\right\}$$

and the log-likelihood for N subjects with at least one event is $\ell (\alpha ,\beta )={\sum }_{i=1}^N{\ell }_i(\alpha ,\beta )$. (Note that the second term above is simply n_i.. log(1/π_i00).) Thus, direct calculations yield the J +K likelihood equations:

$$\frac{\partial \ell (\alpha ,\beta )}{\partial {\beta }_k}=\sum _{i=1}^N\sum _{j=0}^J(n_{ijk}-n_{i..}{\pi }_{ijk})=0,k=1,\dots ,K$$

$$\frac{\partial \ell (\alpha ,\beta )}{\partial {\alpha }_j}=\sum _{i=1}^N\sum _{k=0}^K(n_{ijk}-n_{i..}{\pi }_{ijk})=0,j=1,\dots ,J.$$

The needed second order partial derivatives are: ${\partial }^2\ell (\alpha ,\beta )∕\partial {\alpha }_j^2=-{\sum }_i{n}_{i..}{\pi }_{ij.}(1-{\pi }_{ij.})$, $j=1,\dots ,J;{\partial }^2\ell (\alpha ,\beta )∕\partial {\alpha }_j{\alpha }_l={\sum }_i{n}_{i..}{\pi }_{ij.}{\pi }_{il.}$, $j\ne l;{\partial }^2\ell (\alpha ,\beta )∕\partial {\beta }_k^2=-{\sum }_i{n}_{i..}{\pi }_{i.k}(1-{\pi }_{i.k})$, $k=1,\dots ,K;{\partial }^2\ell (\alpha ,\beta )∕\partial {\beta }_k{\beta }_l={\sum }_i{n}_{i..}{\pi }_{i.k}{\pi }_{i.l}$, $k\ne l;{\partial }^2\ell (\alpha ,\beta )∕\partial {\alpha }_j{\beta }_k=-{\sum }_i{n}_{i..}({\pi }_{ijk}-{\pi }_{ij.}{\pi }_{i.k})$. The Newton-Raphson update at iteration (t + 1) is θ^(t+1) = θ^(t) − (H^(t))⁻¹q^(t), where θ^(t) = (${\alpha }_1^{\left(t\right)},\dots ,{\alpha }_J^{\left(t\right)}$, ${\beta }_1^{\left(t\right)},\dots ,{\beta }_K^{\left(t\right)}$)^T, q^(t) is the vector of first order partial derivatives, and H^(t) is the (J + K) × (J + K) Hessian matrix, both evaluated at θ^(t).

Notes on Other Cases of Exposure Onset Measurement Error and Bias Correction

In this work, we focus on positive exposure onset measurement error because this model is directly applicable to our primary interest in analyzing infection-related hospitalizations data from the USRDS. However, for the proposed MECS models to be more broadly applicable, we provide here notes on the more general case where the variable u is not strictly positive. First, note that when exposure onset is strictly negative (i.e., u < 0), it can be shown that the expression for E(ñ_ik) given in (4) holds with μ_u replaced by E|u|. For the more general case, let p₀ = Pr(u < 0) and p₁ = Pr(u ≥ 0). For simplicity of notations, consider one exposure and risk period (L_i = 1, K = 1). Then it can be shown that

$$E\left({\tilde{n}}_{i1}\right)=p_0\{e_{i1}{\lambda }_{i1}+({\lambda }_{i0}-{\lambda }_{i1})E\left[\mid u\mid I(u<0)\right]\}{\Delta }_i^{-1}+p_1\{e_{i1}{\lambda }_{i1}+({\lambda }_{i0}-{\lambda }_{i1})E\left[uI(u\ge 0)\right]\}{\Delta }_i^{-1},$$

where I(E) denotes the indicator function for event E. Therefore, additional/auxiliary data is needed to estimate p₀, p₁, E[uI(u ≥ 0)], and E[|u|I(u < 0)]. Auxiliary data in some applications could be based on retrospective chart review of a subset of subjects to determine true exposure onset, for instance. Otherwise, sensitivity analysis can be performed for assumed values of these characteristics/parameters of the distribution of u.

Finally, we point out that the above expression for E(ñ_i1) explicitly shows that even when μ_u is known precisely, case series analysis of data whereby one simply subtracts μ_u from each observed exposure onset time with positive measurement error will not target β_k. It is clear that doing so, under positive exposure onset measurement error, will simply lead to the case of general measurement error.