Antagonism of Lidocaine Inhibition by Open-Channel Blockers That Generate Resurgent Na Current

Abstract

Na channels that generate resurgent current express an intracellular endogenous open-channel blocking protein, whose rapid binding upon depolarization and unbinding upon repolarization minimizes fast and slow inactivation. Na channels also bind exogenous compounds, such as lidocaine, which functionally stabilize inactivation. Like the endogenous blocking protein, these use-dependent inhibitors bind most effectively at depolarized potentials, raising the question of how lidocaine-like compounds affect neurons with resurgent Na current. We therefore recorded lidocaine inhibition of voltage-clamped, tetrodotoxin-sensitive Na currents in mouse Purkinje neurons, which express a native blocking protein, and in mouse hippocampal CA3 pyramidal neurons with and without a peptide from the cytoplasmic tail of Na_Vβ4 (the β4 peptide), which mimics endogenous open-channel block. To control channel states during drug exposure, lidocaine was applied with rapid-solution exchange techniques during steps to specific voltages. Inhibition of Na currents by lidocaine was diminished by either the β4 peptide or the native blocking protein. In peptide-free CA3 cells, prolonging channel opening with a site-3 toxin, anemone toxin II, reduced lidocaine inhibition; this effect was largely occluded by open-channel blockers, suggesting that lidocaine binding is favored by inactivation but prevented by open-channel block. In constant 100 μm lidocaine, current-clamped Purkinje cells continued to fire spontaneously. Similarly, the β4 peptide reduced lidocaine-dependent suppression of spiking in CA3 neurons in slices. Thus, the open-channel blocking protein responsible for resurgent current acts as a natural antagonist of lidocaine. Neurons with resurgent current may therefore be less susceptible to use-dependent Na channel inhibitors used as local anesthetic, antiarrhythmic, and anticonvulsant drugs.

Introduction

Upon depolarization, voltage-gated Na channels open and become nonconducting within milliseconds as the fast inactivation gate binds. In some cells, a distinct mode of inactivation occurs even more rapidly, as a separate protein blocks open channels. This endogenous blocking protein binds to open channels and is expelled by inward Na flux upon repolarization, resulting in “resurgent” Na current (Raman and Bean, 1997; Aman and Raman, 2010). The binding and rapid unbinding of the blocker support high-frequency repetitive action potential firing, largely by limiting fast inactivation (Raman and Bean, 2001; Khaliq et al., 2003). A likely candidate for the endogenous blocking particle, at least in some cells, is the Na_Vβ4 subunit, as the cytoplasmic tail of the protein can directly block open channels and its knockdown with siRNA can abolish resurgent current (Grieco et al., 2005; Bant and Raman, 2010).

Several clinically used compounds, such as lidocaine, also bind and block current through Na channels. Among these are the use-dependent blockers, which inhibit Na currents by several molecular mechanisms, including resting-state inhibition, open-channel block, and stabilization of inactivated states (Strichartz, 1973; Hille, 1977; Cahalan and Almers, 1979; Bean et al., 1983; Vedantham and Cannon, 1999; Sheets and Hanck, 2003, 2007). Unlike rapid recovery from blockade by the resurgent-current-inducing particle, recovery in the presence of lidocaine can take hundreds of milliseconds, thereby reducing, rather than promoting, rapid firing. The contrasting effects of the endogenous blocker and lidocaine raise the question of how neurons that produce resurgent current respond to use-dependent inhibitors.

More than 15 neuronal types, including Purkinje cells, have resurgent Na current and therefore must express an endogenous blocking protein (Raman and Bean, 1997; Do and Bean, 2003; Afshari et al., 2004; Cummins et al., 2005; Enomoto et al., 2006; Leão et al., 2006; Castelli et al., 2007a,b; Mercer et al., 2007; Gittis and du Lac, 2008; Kim et al., 2010; Ding et al., 2011). In cells lacking a native blocker, like CA3 hippocampal pyramidal neurons, a resurgent-like current can be generated by the putative blocking sequence from the cytoplasmic tail of Na_Vβ4 (the β4 peptide, KKLITFILKKTREKKKECLV) (Grieco et al., 2005). We therefore examined the influence of a resurgent current-inducing blocker on lidocaine inhibition, in CA3 cells with the β4 peptide, and in Purkinje cells, which have a native open-channel blocking protein.

Given the different affinities of lidocaine for different channel states, interactions between the β4 peptide and lidocaine are ideally probed with brief drug applications at fixed voltages. We therefore used rapid solution exchange techniques (Raman and Trussell, 1995) to measure lidocaine-mediated inhibition of TTX-sensitive Na channels in cells with and without resurgent current. Both the β4 peptide and the endogenous blocking protein antagonize inhibition of Na current by lidocaine. Furthermore, recordings in anemone toxin II (ATX), which slows the onset of fast inactivation, demonstrate that lidocaine is most effective at inhibiting fast-inactivated, rather than open or open-blocked, channels. These data suggest that neurons with resurgent current may have reduced sensitivity to local anesthetics and other use-dependent inhibitors.

Materials and Methods

Cell preparation.

All animal protocols conformed to institutional guidelines and were approved by the Northwestern University Institutional Animal Care and Use Committee. C57BL/6 mice of either sex were anesthetized with isoflurane and rapidly decapitated for acute dissociation either of neurons from the CA3 region of the hippocampus (P8-P11 mice) or of Purkinje neurons of the cerebellum (P14-P19) (Raman and Bean, 1997; Raman et al., 1997). For CA3 cells, the hippocampus was removed and sliced on a tissue chopper. For Purkinje cells, the superficial layers of the cerebellum were removed and minced. The tissue was incubated in oxygenated dissociation solution (82 mm Na₂SO₄, 30 mm K₂SO₄, 5 mm MgCl₂, 10 mm HEPES, 10 mm glucose, and 0.001% phenol red, pH 7.4 with NaOH, 31°C) with 3 mg/ml protease XXIII for 9 (CA3) or 7 (Purkinje) minutes. Tissue was microdissected in dissociation solution containing 1 mg/ml each of BSA and trypsin inhibitor, and then triturated in Tyrode's solution (150 mm NaCl, 4 mm KCl, 2 mm CaCl₂, 10 mm HEPES, 10 mm glucose, pH 7.4 with NaOH) with a series of polished Pasteur pipettes. Isolated cells settled in the recording chamber for at least 30 min before recording. CA3 neurons were identified by their pyramidal morphology, Purkinje cells by their large tear-shaped soma.

For preparation of hippocampal slices, mice (P12-P15) were anesthetized with isoflurane and transcardially perfused with ice-cold sucrose slicing solution containing 75 mm sucrose, 25 mm glucose, 85 mm NaCl, 2.5 mm KCl, 1.25 mm NaH₂PO₄, 25 mm NaHCO₃, 0.5 mm CaCl₂, 4 mm MgCl₂, and 1 mm kynurenic acid. Mice were decapitated, and the brain was removed and blocked. Transverse hippocampal slices (300 μm) were cut on a Leica VT-1200 vibratome at 4°C in sucrose slicing solution. Slices were then incubated at 30°C for 15 min and bubbled with carbogen. Over 15 min, the sucrose solution was exchanged for ACSF containing 2.5 mm KCl, 125 mm NaCl, 1.42 mm NaH₂PO₄, 25 mm NaHCO₃, 1.5 mm CaCl₂, 1 mm MgCl₂, 25 mm glucose, and 1 mm kynurenic acid. Slices were maintained in carbogenated ACSF at room temperature and used for experiments over a period of 2–4 h.

Voltage-clamp recording and analysis.

Borosilicate pipettes (1.2–3.5 MΩ) were wrapped with Parafilm and filled with an intracellular solution composed of 108 mm CsCH₃SO₃, 9 mm NaCl, 1.8 mm MgCl₂, 9 mm HEPES, 5 mm TEA-Cl, 48 mm sucrose, 14 mm Tris-CreatinePO₄, 4 mm MgATP, and 0.3 mm Tris-GTP (pH 7.37, with CsOH). Where indicated, 200 μm of the β4 peptide (KKLITFILKKTREKKKECLV, Open Biosystems), the first 20 amino acids from the Na_Vβ4 cytoplasmic tail, was included in the internal solution (Grieco et al., 2005). Whole-cell voltage-clamp recordings were made with a Multiclamp 700B amplifier and pClamp 9.0 (Molecular Devices), sampled at 50 kHz and filtered at 5 kHz. Series resistance was compensated >70%, and access resistance was monitored with a conductance pulse. Most cells either were exceptionally stable or deteriorated within seconds, such that no data were collected, and the few cells in which access resistance changed detectably were discarded. For rapid solution exchange studies, theta glass was pulled and cut to make each barrel opening ∼100 μm. TTX (without lidocaine) was applied through a single barrel of a matching theta pipette (to provide the same flow rate) that was attached to the theta pipette used for switching. The pipette array was mounted on an LSS-3000 ultrafast solution-switching piezoelectric device (EXFO Burleigh) that moved the theta glass tip by ∼30 μm. The angle between the theta pipette array and recording pipette was 150°, which minimized displacement of the cell from the recording pipette in the face of high flow rates. External solutions were driven through the theta-glass pipette with a pressure perfusion system (AutoMate Scientific). To maintain the cell while entering the flow, cells were moved into the plane of the pipette tip ∼1 cm away and then moved against the fluid stream to <50 μm of the pipette tip, near the interface of the fluid streams. To drive the piezoelectric device without ringing, a step voltage signal was filtered at 0.1 kHz. Complete exchange, measured by the change in open-tip junction potential, was accomplished in 300 μs.

Extracellular solutions applied through the theta glass pipette array consisted of control, lidocaine, ATX, and/or TTX solutions, with the following compositions: control (or “ATX-free”) extracellular solution contained 50 mm NaCl, 110 mm TEA-Cl, 10 mm HEPES, 0.3 mm CdCl₂, and 2 mm BaCl₂. In a few experiments (as noted), 100 mm TEA-Cl was exchanged for 100 mm NaCl to yield 150 mm external Na. Lidocaine-HCl (100 μm or 1 mm), ATX (300 nm), and/or TTX (900 nm) were added to control solutions as indicated. Lidocaine was selected as a representative local anesthetic because its extensively studied properties provide a good basis for examining its interactions with endogenous and exogenous open-channel blockers that produce resurgent current. The final pH of all extracellular solutions was 7.49 (adjusted with TEA-OH). In all fast-flow experiments, subsaturating TTX (2.5 nm) was used to decrease current amplitudes and improve clamp quality without further reducing extracellular Na, which has the additional effect of stabilizing binding of the resurgent current-inducing open-channel blocker at negative potentials (Aman and Raman, 2010). In experiments measuring activation and inactivation curves, 7.5 nm TTX was used. ATX was applied for at least 30 s before recordings were made.

To test solution exchange rate, the two theta pipes contained Tyrode's plus either 8 mm NaCl or 8 mm KCl (“high-K solution”), as well as TTX and Cd to block Na and Ca currents. For these experiments, the intracellular solution contained 120 mm KCH₃SO₃, 10 mm NaCl, 2 mm MgCl₂, 0.5 mm EGTA, 14 mmTris-creatine PO₄, 4 mm MgATP, and 0.3 mm Tris-GTP (pH 7.35 with ∼5 mm KOH, osmolarity adjusted to 305 mOsm with sucrose). Switching from one pipe to the other therefore changed E_K from ∼−90 mV to −61 mV. All drugs were from Sigma-Aldrich, except ATX and TTX (Alomone Laboratories). Recordings were made at room temperature.

In rapid solution exchange experiments, the solution switch occurred with a delay of 6.3 ms relative to the command to the piezoelectric driver, which was accounted for in designing protocols. The duration of lidocaine application was 34 ms, a value selected to provide an 8 ms gap before and after lidocaine application in the middle of a 50 ms depolarizing step. In this way, even considering the rise and decay of solution exchange, the lidocaine application could be reliably constrained to occur at a fixed voltage. Lidocaine applications ranged from 30 ms before to 18 ms after the onset of the conditioning step, which was taken as time 0. Start-to-start intervals were 4 s.

In all experiments, recordings were repeated in TTX, and TTX-sensitive Na current was isolated by subtraction, without additional p/n subtraction. Because the ionic composition of the solutions blocked K currents, Ca currents, and HCN currents, it was not necessary to include lidocaine in the TTX-containing solution. Activation curves were evoked by step depolarizations from −90 mV. Peak currents were converted to conductances by dividing by the driving force and normalized to the maximal conductance in control solutions, and conductance-voltage curves were fit by Boltzmann equations of the form G/G_max = 1/(1 + exp(−(V − V_1/2)/k)), where G is conductance, G_max is maximal conductance, V_1/2 is the voltage of half-maximal activation, and k is the slope factor. Inactivation curves were measured with step depolarizations to 0 mV after 200 ms conditioning steps to different voltages. Peak currents were normalized to the maximal current and fit with Boltzmann equations of the form I/I_max = 1/(1 + exp((V − V_1/2)/k)), where I is current, I_max is maximal current, V_1/2 is the voltage of half-maximal inactivation, and k is the slope factor. For isolated cell experiments, junction potentials were eliminated by means of a 3M KCl bridge connecting the recording chamber to a well containing the ground wire submerged in intracellular solution.

Current-clamp recordings.

Purkinje cell action potentials were recorded from P15-P18 acutely dissociated neurons at room temperature. The intracellular solution included 130 mm KCH₃O₃S, 3 mm NaCl, 5 mm Na-gluconate, 2 mm MgCl₂, 5 mm EGTA, 10 mm HEPES, 14 mm Tris-creatinePO₄, 4 mm MgATP, and 0.3 mm Tris-GTP, pH 7.4 with KOH (285 mosm). Spontaneous action potentials were recorded first in Tyrode's solution and then in Tyrode's with 100 μm lidocaine (pH 7.49, both solutions). Recordings were made only in cells that fired spontaneously for at least 1 s. In some cells, it was necessary to inject up to 40 pA hyperpolarizing current in control solutions to obtain regular spontaneous firing; in these cells, the same holding current was applied during lidocaine exposure. Firing rates are reported as the mean rate over a period of 1 s.

Action potentials from CA3 pyramidal neurons were recorded in slices. Slices were perfused with carbogenated ACSF ± 100 μm lidocaine at 35°C–37°C, with the pH of each solution adjusted to 7.49 with NaOH. Electrode resistance for these experiments was 2.5–4 MΩ, and the intracellular solution was identical to that used for current-clamp experiments in Purkinje cells. Because of the higher electrode resistance, in experiments with the β4 peptide, the peptide was allowed at least 6 min to diffuse into the cell before recordings were initiated, and only cells with <7 MΩ series resistance were used. Lidocaine was allowed at least 4 min to wash into the slice before spikes were recorded.

CA3 pyramidal cells were held near −70 mV, and action potentials were evoked with 1 s current injections in increments of 50 pA up to 500 pA, with a 2 s interval. To minimize confounds from premature depolarization block observed with the β4 peptide (see Results), action potentials were counted only in the first 500 ms of the step. Spikes were defined as events with a rise >10 V/s, and were counted for up to 400 pA above rheobase or until the maximum injection of 500 pA. Cells in which rheobase changed by >100 pA between control and lidocaine-containing solutions were excluded from the analysis. Recordings from slices are not corrected for a 4 mV junction potential.

Data were analyzed with Igor Pro 6.0 (Wavemetrics) and reported as mean ± SEM. Statistical significance was assessed by either Student's two-tailed t tests or 2-way ANOVA, as noted, and significance was taken as p < 0.05. Incompletely subtracted capacitive artifacts have been digitally reduced.

Results

To identify differences in the extent to which local anesthetics inhibit open, inactivated, and/or blocked Na channels, we made whole-cell recordings from isolated neurons and used rapid solution exchange methods to apply lidocaine briefly during voltage steps. First, to assess the speed of solution exchange around a whole neuron, we evoked voltage-gated K currents in a CA3 cell with a step depolarization from −90 to −30 mV, and switched into a high-K solution to reduce the driving force on K⁺ by 30 mV. The resulting change in current amplitude had a 10–90% rise time of 3.7 ms and fall time of 5.6 ms (Fig. 1A) and can be taken as an estimate of the time course of solution exchange around the whole-cell (Raman and Trussell, 1995).

Figure 1.

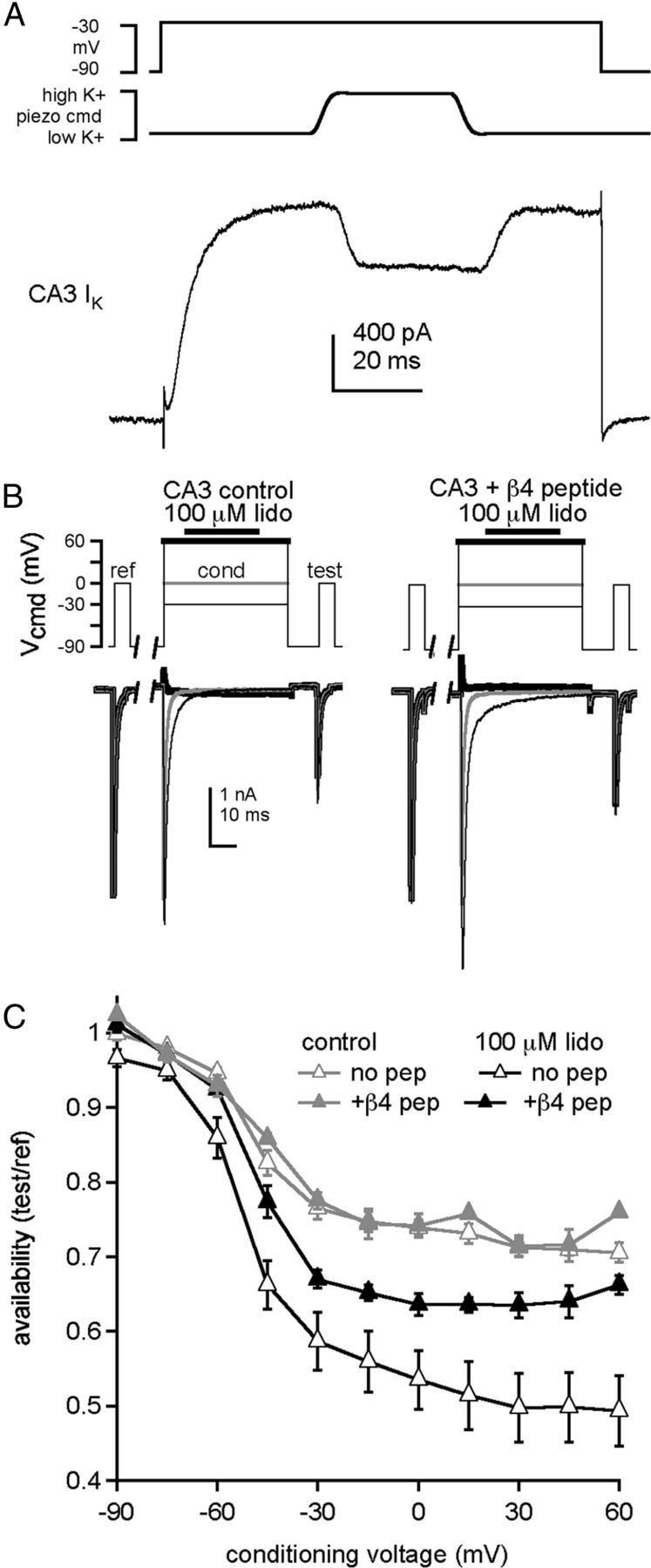
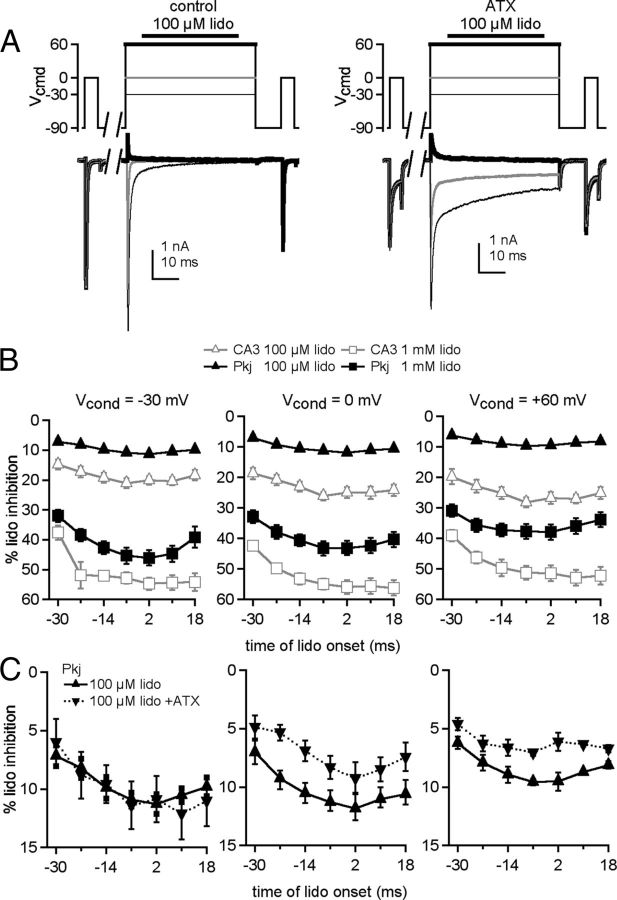
Open-channel block by the β4 peptide reduces lidocaine inhibition of Na currents. A, Voltage-clamp command (top), piezoelectric command voltage (middle), and whole-cell K current in a CA3 neuron during a 34 ms application of high-K⁺ extracellular solution (bottom). B, Left, CA3 Na currents evoked by the standard voltage protocol, consisting of a 5 ms reference step to 0 mV, a 1 s recovery interval at −90 mV, a 50 ms conditioning step during which 100 μm lidocaine was applied 8 ms after depolarization, a 10 ms recovery interval at −90 mV, and a 5 ms test step to 0 mV. Conditioning voltage: thin black line, −30 mV; gray line, 0 mV; thick black line, +60 mV. Right, Same protocol, with β4 peptide. C, Availability, measured as test current normalized to reference current, versus conditioning voltage (control, n = 4; lidocaine, n = 5). Data points are plotted as mean ± SEM. in all figures.

Next, we tested whether a single, brief application of lidocaine at depolarized potentials can inhibit Na currents evoked tens of milliseconds later. In isolated CA3 neurons, whose Na channels are subject to fast inactivation on this time scale but lack an endogenous open-channel blocking protein, TTX-sensitive Na currents were evoked by a series of three voltage steps from −90 mV (Fig. 1B). The first was a 5 ms “reference” step from −90 to 0 mV to measure the maximal transient Na current in each neuron. After a 1 s recovery interval at −90 mV, a 50 ms “conditioning” step to a potential between −90 and +60 mV was applied, with or without a 34 ms application of 100 μm lidocaine. After a 10 ms recovery interval at −90 mV, a 5 ms “test” step to 0 mV was applied to assay Na current inhibition that occurred during the conditioning pulse.

Because any loss of current during the test step could result either from normal inactivation or from lidocaine binding, experiments without exposure to lidocaine were used to assess the drug-independent decrease of Na current. In lidocaine-free control solution, the availability of Na channels during the test step (given as the test current normalized to the reference current) was >90% after conditioning at −75 and −60 mV, decreasing to ∼75% after conditioning at voltages >−30 mV (Fig. 1C, gray triangles, n = 4), consistent with the onset of inactivation during the conditioning pulse followed by a substantial but incomplete recovery during the 10 ms interval. When lidocaine was applied during the conditioning step, the availability was reduced relative to control. The difference in availability can be taken as an estimate of the inhibition by lidocaine, with the awareness that some recovery from lidocaine may have occurred after removal of the drug. Importantly, the current available after conditioning at the strongly hyperpolarized voltage of −90 mV was >95% after lidocaine exposure, indicating that the contribution of resting state inhibition to the total effect of lidocaine was minimal. The extent of lidocaine-dependent inhibition became progressively greater with depolarization, with availability falling to 50% by +60 mV (Fig. 1C, open triangles, p < 1e-11, 2-way ANOVA). These data are consistent with previous reports that lidocaine acts more effectively at more positive voltages (e.g., Strichartz, 1973). Furthermore, because the Na current has largely decayed by the time of lidocaine application, the results are also consistent with the idea that lidocaine binds effectively to channels that have already undergone fast inactivation.

Because the open-channel blocking protein responsible for resurgent Na current, likely Na_Vβ4 (Bant and Raman, 2010), appears to compete with fast inactivation (Raman and Bean, 2001; Grieco and Raman, 2004), we considered the possibility that such open-channel blockers might also compete with the action of lidocaine. We therefore repeated the protocol with 200 μm β4 peptide added intracellularly (Fig. 1B, right, C, closed triangles). This peptide mimics the action of the endogenous open-channel blocking protein, although CA3 Na channels bind to it with a lower affinity than do channels that normally produce resurgent current (Grieco et al., 2005; Bant and Raman, 2010; Lewis and Raman, 2011). In the absence of lidocaine, availability during the test step was unchanged by the peptide, relative to control. In contrast, with brief applications of lidocaine, the β4 peptide reduced inhibition, restoring availability to ∼65% after conditioning at any potential between −30 and +60 mV (n = 5). The increasing difference between the peptide and peptide-free condition at more positive potentials suggests that antagonism of lidocaine inhibition by the β4 peptide increased with depolarization. Because depolarization stabilizes binding of the open-channel blocker, the voltage-dependent effect of the peptide is consistent with the blockade of open channels directly preventing lidocaine binding.

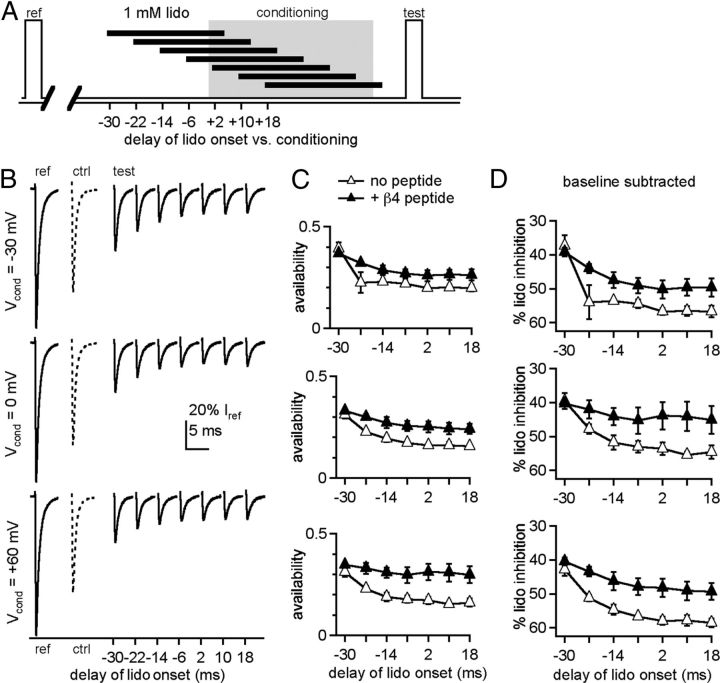
To compare the efficacy with which lidocaine inhibits inactivated, open, and blocked channels, we varied the time of application of lidocaine relative to depolarization (Fig. 2A). In this experiment, we used a high concentration of lidocaine, 1 mm, to maximize the likelihood that lidocaine binding would be favored. Reference and test responses after conditioning steps to −30, 0, or +60 mV are shown in isolation in Figure 2B (no peptide); a test response without lidocaine application is shown as a hyphenated trace. In the absence of the β4 peptide, availability during the test step tended to decrease with later applications of lidocaine (Fig. 2B,C, open triangles, n = 4). To isolate inhibition by lidocaine from differential inactivation stemming from conditioning at different voltages, we subtracted the test response after lidocaine from the test response without lidocaine (“baseline”) for each conditioning potential (baseline availability, no peptide, −30 mV, 77 ± 1%; 0 mV, 74 ± 1%; +60 mV, 71 ± 1%, n = 7; with peptide, −30 mV, 76 ± 2%; 0 mV, 73 ± 2%; +60 mV, 75 ± 1%, n = 5). The results are plotted at higher gain as the percentage lidocaine inhibition in Figure 2D and show that the percentage lidocaine inhibition increased with later applications at all potentials. This temporal profile may result from a differential interaction of lidocaine with different states and/or from channels recovering more with a larger gap between drug removal and the test step.

Figure 2.

Effects of lidocaine application time on inhibition of test currents. A, Schematic depicting application times of lidocaine during the standard protocol. B, Example traces from a CA3 neuron showing reference currents (left trace), control test currents with zero lidocaine (middle dotted trace), and test currents after 1 mm lidocaine application at different times, from earliest to latest (right solid traces), for conditioning: at −30 mV (top), 0 mV (middle), and +60 mV (bottom). All currents are normalized to the reference current for the sweep on which it was acquired. C, Normalized test currents recorded without (open triangles) and with (closed triangles) the β4 peptide versus delay of lidocaine onset relative to the conditioning step (n = 4, both conditions). D, Percentage current blocked by lidocaine (% lido inhibition), obtained by subtracting the zero-lidocaine (baseline) availability from the data in C, versus delay of lidocaine onset.

To test the former possibility, we included the β4 peptide in the pipette and remeasured the temporal profile of inhibition. At all voltages and at all but the earliest time of application, the β4 peptide decreased the percentage of inhibition by 1 mm lidocaine (Fig. 2C,D, closed triangles, n = 4). Thus, the amount of inhibition by lidocaine indeed decreases with the likelihood of channels being in an open-blocked state.

It remains a question, however, whether lidocaine acts preferentially at inactivated versus open (unblocked) channels, or whether it fails to discriminate between these states. To address this issue, we prolonged opening with the site 3 peptide toxin ATX. Site 3 toxins bind near the extracellular S3-S4 linker of domain IV (DIV) and slow the movement of the DIV voltage-sensing domain to the outward position, thereby slowing the onset of fast inactivation (Sheets et al., 1999; Sheets and Hanck, 2003; Hanck and Sheets, 2007). Neuronal Na currents and action potentials are also affected by ATX (Mantegazza et al., 1998; Brand et al., 2000; Brumberg et al., 2000; Miyawaki et al., 2002; Oliveira et al., 2004). Because effects of the drug can vary across cells, we first characterized the actions of ATX on voltage-clamped CA3 hippocampal Na currents.

CA3 Na currents were activated by step depolarizations (Fig. 3A), and the resulting conductance-voltage curves had a voltage of half-maximal activation, V_1/2, and slope factor, k, of −26.0 ± 2.0 mV and 5.6 ± 0.2 mV (n = 5) (Fig. 3C,E). In the same cells, in an approximately half-maximal concentration of ATX (300 nm) (el-Sherif et al., 1992), the activation V_1/2 shifted slightly negatively (to −29.9 ± 2.1 mV, p = 0.002, paired), the slope factor increased to 6.1 ± 0.2 mV (p = 0.011), and the G_max decreased to 75 ± 5% of control (p = 0.006). The reduced G_max is consistent with the induction of subconductances by ATX (Nagy, 1987, el-Sherif et al., 1992, Castillo et al., 1996). The most salient effect, however, was a slowing of inactivation (Fig. 3A). To capture effects on the fast and slow phases of inactivation, which varied in the number of exponential components necessary for a good fit, we measured the time required for the current evoked at 0 mV to decay by 25% (t_25%) and by 75% (t_75%). The t_25% increased from 0.32 ± 0.01 ms to 0.77 ± 0.2 ms in ATX (p = 0.04), and the t_75% increased from 1.3 ± 0.06 ms to 13.5 ± 3.5 ms in ATX (p = 0.025). This 10-fold increase reflects the slowed onset of inactivation. The steady-state inactivation curve, assayed with 200 ms conditioning steps, shifted slightly negatively, from a V_1/2 of −60.2 ± 1.6 mV in control to −66.1 ± 2.3 mV in ATX (p = 0.009) and a k of 6.5 ± 0.4 in control to 7.6 ± 0.3 mV in ATX (p = 0.13) (Fig. 3C,F). The steady-state (noninactivating) component, %_ss, increased from 4.2 ± 1.4% in control to 7.6 ± 1.3% in ATX (p = 0.04). Thus, ATX greatly slowed the onset of inactivation but only modestly decreased the equilibrium occupancy of inactivated states (Hanck and Sheets, 2007).

Figure 3.

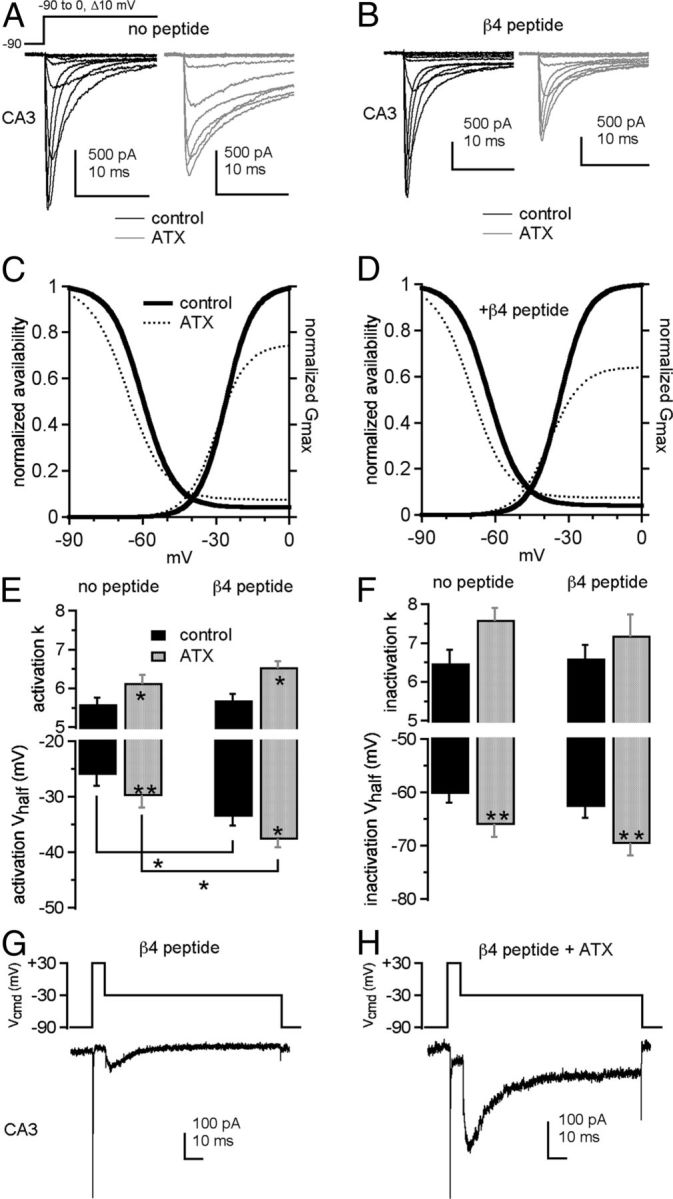
ATX slows inactivation and facilitates open-channel block by the β4 peptide in CA3 neurons. Na currents in CA3 neurons without (A, C) and with (B, D) the β4 peptide. A, B, Currents evoked by step depolarizations in control (black) and 300 nm ATX (gray). Each panel shows paired comparisons from a single cell. C, D, Activation and steady-state inactivation curves with mean values from Boltzmann fits of individual cells in control (thick black lines) and ATX (dotted lines). Activation curve (E) and inactivation curve (F) fit parameters without (left bars) and with (right bars) the β4 peptide in control (black) and ATX (gray) (no peptide: −ATX, n = 5, +ATX, n = 5; with peptide: −ATX, n = 6, +ATX, n = 6). G, H, β4 peptide-mediated resurgent current in a CA3 neuron evoked at −30 mV after a 15 ms step to +30 mV in control (G) and ATX (H). *p < 0.05. **p < 0.005.

In the absence of ATX, the β4 peptide alone hyperpolarized the activation V_1/2 relative to control solutions (with peptide V_1/2 = −33.6 ± 1.5 mV, k = 5.7 ± 0.2 mV, n = 6, p = 0.035, 0.36, vs control, unpaired), whereas the inactivation parameters were statistically unchanged (V_1/2 = −62.7 ± 2.1 mV, k = 6.6 ± 0.4 mV, %_ss = 4.1 ± 1.0%; p = 0.35, 0.36, 0.97; Fig. 3B,D,F). Adding ATX to β4 peptide-containing cells evoked effects similar to those in peptide-free cells: activation and inactivation shifted negatively and became less steeply voltage dependent (activation V_1/2 = −37.7 ± 1.3 mV, k = 6.6 ± 0.2 mV; inactivation V_1/2 = −69.7 ± 2.2 mV, k = 7.2 ± 0.6 mV, %_ss = 7.5 ± 1.8%; p = 0.0023, 0.029, 0.0003, 0.20, 0.008, vs ATX-free, paired), and ATX reduced G_max to 64 ± 5% of control. With peptide, the t_25% increased from 0.26 ± 0.02 ms to 0.34 ± 0.01 ms in ATX (p = 0.0003), and the t_75% increased only from 0.99 ± 0.06 ms to 1.9 ± 0.1 ms in ATX (p = 0.0002). The prolongation of current decay in ATX, although significant, was many times smaller than without the β4 peptide, as expected if this time course is largely determined by the rate of peptide block of open channels.

The β4 peptide induces a resurgent Na current upon repolarization from +30 mV to −30 mV (Raman and Bean, 1997; Grieco et al., 2005) (Fig. 3G). Like the site-3 toxin β-pompilidotoxin (Grieco and Raman, 2004), ATX greatly increased the amplitude of resurgent current (from 102 ± 21 pA to 226 ± 30 pA, p = 0.007, Fig. 3H). Although the rise time did not change (control, 6.0 ± 0.3 ms; ATX, 6.3 ± 0.4 ms, n = 6, p = 0.7), the decay time constant, thought to reflect entry into fast inactivated states at this potential, increased from 26 ± 1.1 ms in control to 32 ± 1.0 ms in ATX (p = 0.005; Fig. 3G). The increase in peak resurgent current amplitude presumably results in part from a higher occupancy of open-blocked channels during the depolarization, permitting more unblocking (opening) of channels upon repolarization. In addition, as channels unblock, they may pass current for longer times before inactivating, and the consequent overlap of open channels likely augments the peak current.

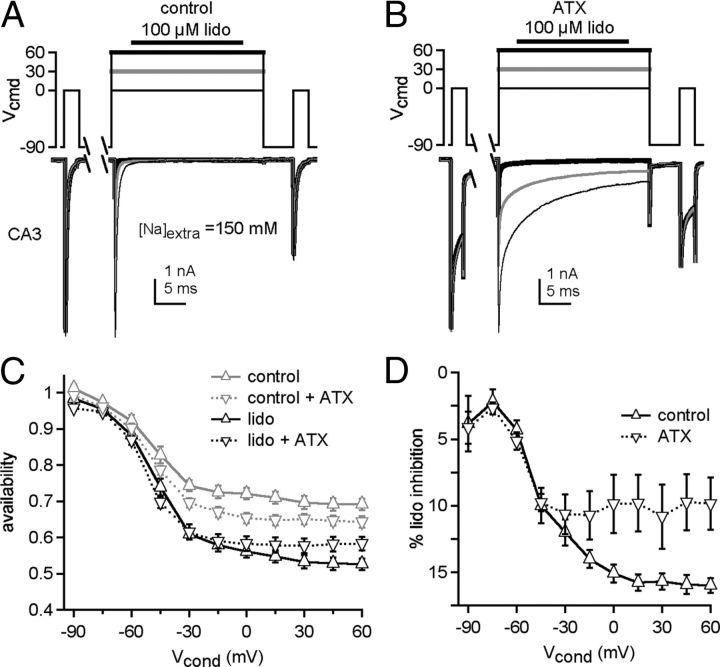
Given the slowed onset of inactivation of ATX-bound Na channels, we used this toxin to test the efficacy of lidocaine inhibition of Na channels that are biased toward open rather than inactivated states (Fig. 4A,B). In the first set of experiments, we used extracellular solutions containing 150 mm instead of 50 mm Na, to set E_Na to +75 mV so that Na current would flow inward at all conditioning voltages and also minimize any contribution of slow inactivation (Aman and Raman, 2007). As in Figure 1B, test currents were measured with or without 100 μm lidocaine during the conditioning step, as well as with and without ATX. The lidocaine-free records revealed that ATX alone consistently reduced the availability of Na channels during the test pulse, especially with conditioning steps >−45 mV (Fig. 4C, gray triangles). Lidocaine further inhibited test currents in this same voltage range, with inhibition in ATX-free solutions increasing at higher voltages, much as in lower concentrations of Na (compare withFig. 1C). This similarity indicates that slow inactivation and/or the direction of current flow during the conditioning pulse do not greatly affect lidocaine's action in this protocol. Subtracting the baseline responses showed that, at >−30 mV, ATX consistently decreased the extent of lidocaine-dependent inhibition (Fig. 4D, two-way ANOVA, p < 0.001). Moreover, unlike in ATX-free solutions, the amount of lidocaine inhibition in ATX was relatively constant at >−45 mV. Barring the possibility that the ATX-bound and ATX-free open states differ substantially in their affinities for lidocaine, the greater availability in ATX suggests that lidocaine is more effective at inhibiting inactivated than open channels, particularly at the most positive potentials.

Figure 4.

ATX reduces lidocaine inhibition of CA3 Na currents. A, B, Na currents elicited in CA3 cells in 150 mm extracellular Na, in control (A) or in ATX (B). Conditioning voltage: thin black line, −30 mV; gray line, 0 mV; thick black line, +60 mV. C, Na channel availability during test step, normalized to reference in control without lidocaine (gray) or with lidocaine (black). Control, solid lines, ATX (dotted lines). D, Percentage lidocaine inhibition (baseline-subtracted) in control (black, n = 7) and ATX (dotted, n = 7).

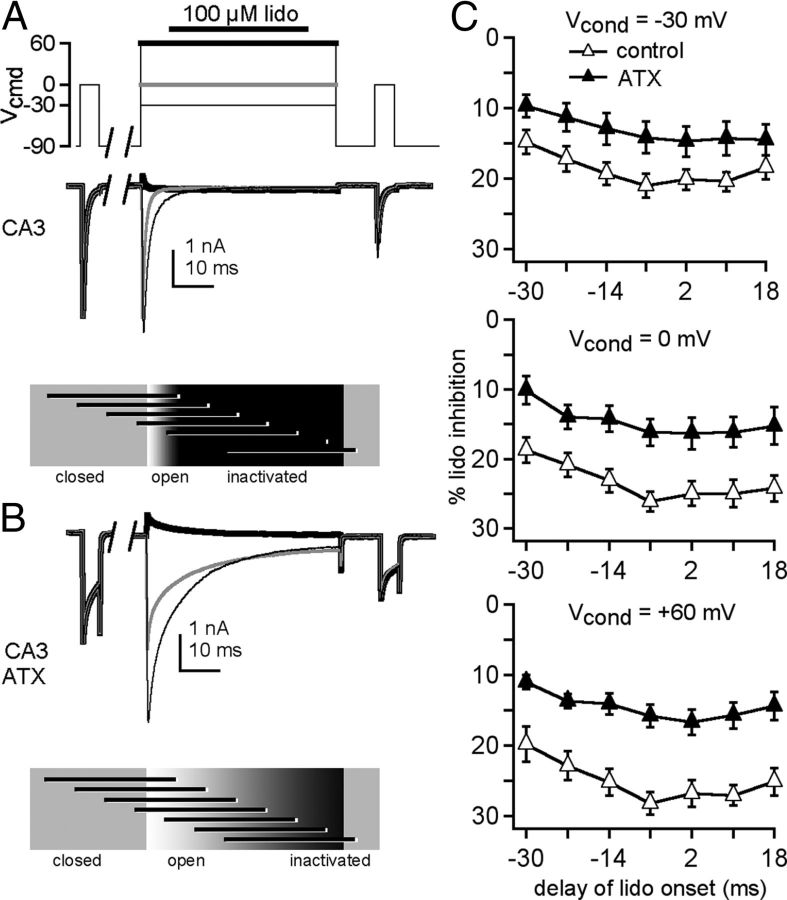
To explore the time dependence of the ATX effect, lidocaine (100 μm) was again applied in 50 mm Na at several times relative to the conditioning step, and recordings were made either with or without ATX (Fig. 5A,B). In control (ATX-free) solutions, inhibition of the test step after 100 μm lidocaine was approximately half that seen with 1 mm lidocaine (Fig. 5C, compare with Fig. 2D). ATX relieved lidocaine inhibition at all potentials, with the largest reduction at +60 mV (Fig. 5C, two-way ANOVA, −30 mV: p < 0.05, 0 mV: p < 0.001, +60 mV: p < 0.001). Indeed, with conditioning at +60 mV, the maximal inhibition by lidocaine in ATX was only approximately 10%. These data further support the idea that the channels' susceptibility to inhibition by lidocaine is reduced when opening is prolonged.

Figure 5.

Temporal profile of ATX-mediated relief of lidocaine inhibition in CA3 cells. A, B, Sample traces from a CA3 neuron, in control (A) and in ATX (B), in 50 mm extracellular Na, with conditioning: thin black line, −30 mV; gray line, 0 mV; thick black line, +60 mV, thick black line. C, Percentage lidocaine inhibition recorded without (closed triangles, n = 4) and with (open triangles, n = 6) ATX versus delay of lidocaine onset relative to the conditioning step.

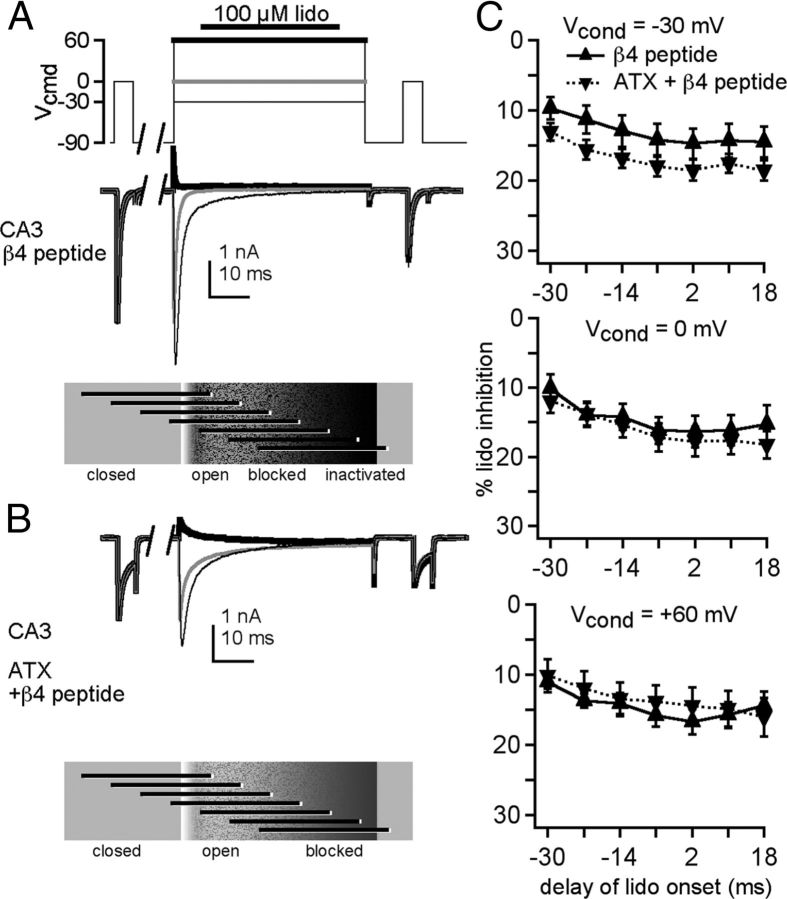
Because the β4 peptide and ATX each reduced the inhibition by lidocaine, we next examined the interaction between the two treatments. First, we verified that the β4 peptide reduced the extent of inhibition by 100 μm lidocaine during the test pulse after all conditioning voltages (Fig. 6A,B, up triangles, compared with Fig. 5; two-way ANOVA, −30 mV: p < 0.05, 0 mV: p < 0.01, +60 mV: p < 0.001). As with peptide-free solutions, the later the lidocaine application, the lower the availability. With ATX and the β4 peptide both present, the extent of inhibition slightly increased at −30 mV relative to the peptide alone, while remaining constant at 0 mV and +60 mV (Fig. 6C, −30 mV: p < 0.005, 0 and +60 mV: p > 0.2). The increased inhibition at −30 mV suggests that prolonging opening or restricting DIV-S4 movement may actually destabilize peptide binding at this voltage, favoring lidocaine inhibition. The lack of summation indicates that the β4 peptide occludes further relief of inhibition by ATX, supporting the idea that open-blocked channels are relatively lidocaine-resistant and that delaying inactivation with ATX has no further effect on lidocaine's action.

Figure 6.

ATX-mediated relief of lidocaine inhibition is largely occluded by the β4 peptide. A, B, Sample traces from a CA3 neuron with the β4 peptide, in control (A) and in ATX (B), in 50 mm extracellular Na, with conditioning: thin black line, −30 mV; gray line, 0 mV; thick black line, +60 mV. C, Percentage lidocaine inhibition recorded without (up triangles, n = 5) and with (down triangles, n = 6) ATX versus delay of lidocaine onset relative to the conditioning step.

Together, the data predict that neurons that contain an endogenous open-channel blocking protein will be only weakly affected by lidocaine. We therefore studied Purkinje cells to test whether the endogenous blocking protein also antagonizes inhibition by lidocaine and limits the effects of ATX. We first measured the influence of ATX and lidocaine on activation and inactivation of Na channels in Purkinje cells (Fig. 7A–F; paired comparisons are ± lidocaine). As in CA3 cells, ATX in Purkinje cells hyperpolarized the activation and inactivation curves and increased both the slope factor and noninactivating component of the inactivation curve (control vs ATX, activation V_1/2: −33.5 ± 0.9 vs −41.0 ± 0.8 mV; p = 0.0002; k: 5.9 ± 0.5 vs 6.7 ± 0.6 mV; p = 0.4; inactivation V_1/2, −61.7 ± 1.2 mV vs −65.5 ± 0.9 mV, p = 0.03; k: 5.4 ± 0.2 vs 6.6 ± 0.2 mV, p = 0.0004; %_ss: 2.7 ± 1.2% vs 7.3 ± 1.3%, p = 0.034, unpaired; n = 5 control, 5 ATX). Unlike in peptide-free CA3 cells, however, ATX only slightly changed the kinetics of Na current decay. The t_25% of the transient current was 0.19 ± 0.01 ms in control and was prolonged to 0.26 ± 0.02 ms by ATX (p = 0.007), whereas the t_75% increased from 0.59 ± 0.02 ms to 1.5 ± 0.17 ms (p = 0.003). The small but significant slowing of inactivation by ATX is consistent with the idea that channels that fail to enter fast-inactivated states rapidly in ATX are blocked by the endogenous blocking protein.

Figure 7.

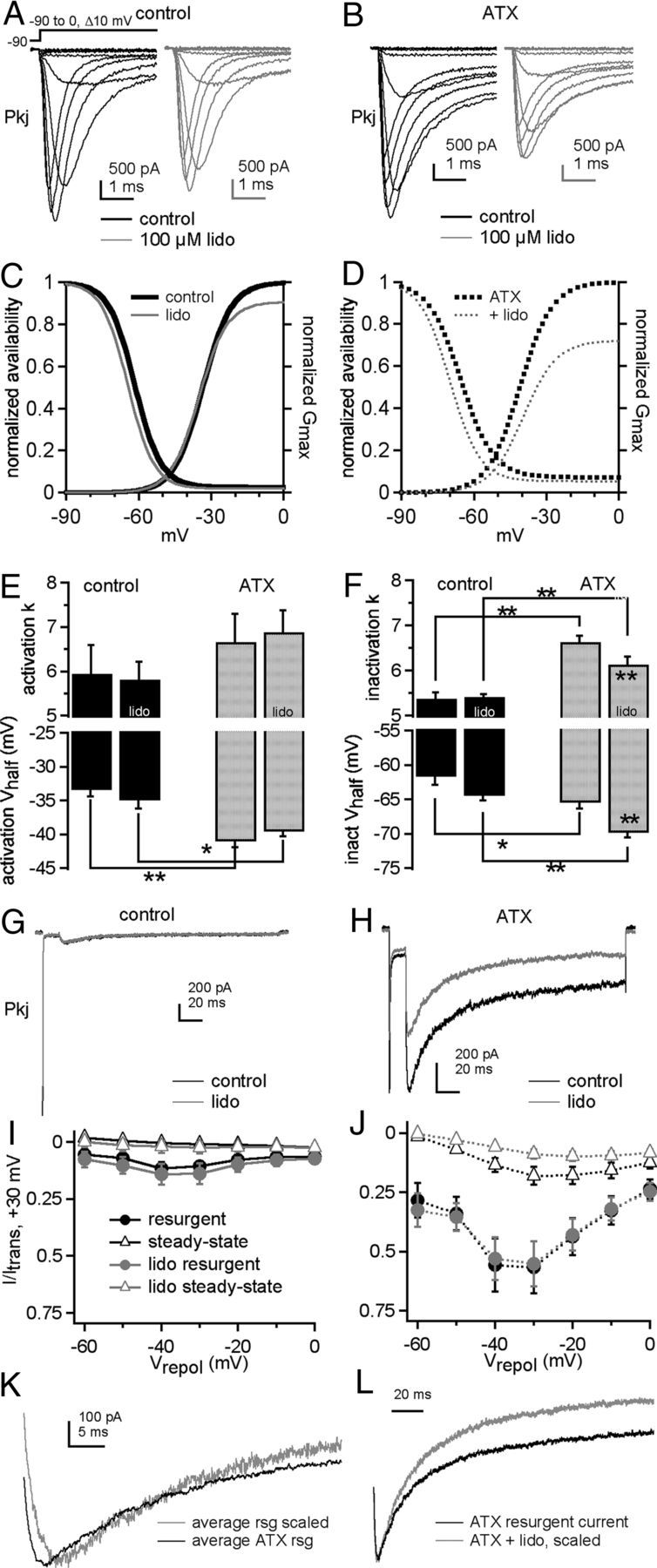
ATX and lidocaine effects on Na currents of Purkinje neurons. Na currents in Purkinje neurons without (A, C) and with (B, D) ATX. A, B, Currents evoked by step depolarizations in control (black) and 100 μm lidocaine (gray). Each panel shows paired comparisons from a single cell. C, D, Activation and steady-state inactivation curves with mean values from Boltzmann fits of individual cells in control (thick black lines) and lidocaine (gray lines). Activation curve (E) and inactivation curve (F) fit parameters without (black bars) and with (gray bars) ATX in control (left bar of each pair) and lidocaine (right bar of each pair). Control: −lidocaine, n = 4; +lidocaine, n = 5; ATX: −lidocaine, n = 4; +lidocaine, n = 5. G, H, Resurgent current in a Purkinje neuron evoked at −30 mV after a 15 ms step to +30 mV in control (G) and ATX (H) without (black) and with (gray) lidocaine. I, J, Current-voltage relationships for maximal resurgent (circles) and steady-state (triangles) Na current in control (I) and ATX (J), without (black, n = 5) and with (gray, n = 5) lidocaine. K, Averaged resurgent currents, enlarged and scaled to compare kinetics without ATX (gray, n = 5) and with ATX (black, n = 5). L, Averaged resurgent currents from five Purkinje cells, enlarged and scaled to compare kinetics without lidocaine (gray, n = 5) and with lidocaine (black, n = 5). *p < 0.05. **p < 0.005.

Constant application of 100 μm lidocaine had only modest effects on activation and inactivation parameters (Fig. 7A–F). In control solutions, lidocaine induced a small hyperpolarization of the activation V_1/2, with no changes in inactivation (with lidocaine: activation V_1/2: −35.0 ± 1.2 mV, p = 0.02; k = 5.8 ± 0.4 mV, p = 0.4; inactivation V_1/2: −64.5 ± 1.2 mV, p = 0.07; k: 5.4 ± 0.1 mV, p = 0.7; %_ss: 1.9 ± 0.7%, p = 0.2, paired). With ATX present, lidocaine did not affect activation but shifted the inactivation curve negatively and made it less steep (with lidocaine: activation V_1/2: −39.6 ± 0.7 mV, p = 0.15; k: 6.9 ± 0.5 mV, p = 0.4; inactivation V_1/2: −69.9 ± 0.6 mV, p = 0.00003; k: 6.1 ± 0.2 mV, p = 0.002; %_ss: 5.4 ± 0.5%, p = 0.1, paired). G_max was unchanged by lidocaine in control solutions. In contrast, in ATX, G_max was significantly reduced (G_max, ATX-free, without vs with lidocaine: 77 ± 8 vs 69 ± 9 nS, p = 0.09; ATX, without vs with lidocaine: 73 ± 7 nS vs 53 ± 5 nS, p = 0.009). Indeed, this reduction of total conductance in ATX was the most salient effect of lidocaine, suggestive of an ATX-dependent increased efficacy of resting state inhibition. Lidocaine did not significantly change Na current decay times in either control or ATX (p > 0.05, paired).

Resurgent current was greatly increased in ATX (Fig. 7G–J), but its rise time was briefer (Fig. 7K, at −30 mV, control, 6.2 ± 0.2 ms, ATX, 3.3 ± 0.02 ms, p < 0.0005). These data suggest that the toxin has two contrasting but compatible effects: It increases the occupancy of open-channel blocked states at positive potentials by delaying inactivation, setting the stage for more unblock and more resurgent current upon repolarization, but destabilizes open-channel block at least at voltages near −30 mV, permitting faster unbinding (Lewis and Raman, 2011). Also consistent with this idea, ATX increased steady-state current at potentials <0 mV (Fig. 7G–J). A faster rise of resurgent current in ATX was not evident in CA3 cells with β4 peptide, possibly because the β4-channel affinity is already relatively low and no further modulated by ATX, or because the extreme slowing of inactivation by ATX allows the current to rise for a longer time. Notably, however, the idea that ATX reduces open-channel block affinity at negative potentials even in CA3 cells is consistent with Figure 6C, in which ATX reduced the ability of the β4 peptide to relieve lidocaine inhibition at −30 mV.

Constant lidocaine had no effect on peak resurgent current amplitudes relative to transient current or on the rise time kinetics of resurgent current (Fig. 7G–J, gray symbols). It did, however, accelerate the resurgent current decay time and decrease the relative steady-state current, but only when ATX was present (Fig. 7L). This increased resurgent current decay rate, with no change in rise time, suggests that the lidocaine binds and inhibits channels that have become unblocked on the time scale of the repolarizing step.

With this information in hand, we investigated the interaction between lidocaine and the endogenous blocking protein with brief applications of lidocaine to Purkinje cells (Fig. 8A). With 100 μm lidocaine, inhibition of the test current was lower than in CA3 cells, remaining <12% at all times and all voltages (Fig. 8B). Given the weak action of 100 μm lidocaine in Purkinje cells, we tested the effect of 1 mm lidocaine. Not surprisingly, the higher concentration increased the inhibition of test currents in Purkinje neurons, but it was still less effective than the same concentration in CA3 cells (Fig. 8B). The least inhibition of Purkinje test currents was produced by the earliest application of lidocaine, and, as with CA3 cells, inhibition increased when lidocaine exposure occurred after channel opening. In Purkinje cells only, however, inhibition was actually reduced after the two latest applications of lidocaine, resulting in a U-shaped curve. These two applications occur after the onset of the conditioning depolarization, suggesting that, when lidocaine reaches channels after they have passed through the open state (and presumably become blocked), the channels are less susceptible to lidocaine's action. Such a U-shape is not clearly evident when the β4 peptide is added exogenously to CA3 neurons. This observation indicates that the free peptide added to CA3 cells is less effective at antagonizing lidocaine's action than the blocker in Purkinje cells, consistent with previous observations demonstrating that the β4 peptide has a lower affinity for CA3 Na channels than the endogenous blocking protein has for Purkinje cells (Lewis and Raman, 2011).

Figure 8.

Low sensitivity of Purkinje neurons to lidocaine inhibition. A, Sample traces from a Purkinje neuron, in control (left) and in ATX (right), in 50 mm extracellular Na. Conditioning steps: thin black line, −30 mV; gray line, 0 mV; thick black line, +60 mV. B, Percentage lidocaine inhibition after 100 μm (triangles, n = 5) or 1 mm (squares) lidocaine for Purkinje cells (black, n = 5). Data from peptide-free CA3 cells from other figures are included in gray for comparison. C, Percentage of lidocaine inhibition recorded without (up triangles, n = 5) and with (down triangles, n = 5) ATX versus delay of lidocaine onset relative to the conditioning step.

Application of ATX to Purkinje cells had a voltage-dependent effect on inhibition by lidocaine (Fig. 8C). At −30 mV, inhibition was unchanged (p = 0.18, 2-way ANOVA). At more depolarized potentials, lidocaine-mediated inhibition was further reduced by ATX, albeit slightly (0 mV, p = 0.0001; +60 mV, p = 0.0001). Thus, at +60 mV, with ATX, inhibition by lidocaine of Purkinje test currents was reduced to a few percentage (<7%). These results resemble the effects of ATX on CA3 cells with intracellular β4 peptide, except that the ATX data points are slightly upward-shifted relative to the data with blocker alone. This pattern would be expected if ATX's facilitation of blocker binding by delaying inactivation outweighs its apparent destabilization of the blocker-pore interaction in Purkinje cells but not in CA3 cells with peptide. This scenario is plausible because Purkinje channels have a higher apparent affinity for the native blocker than CA3 channels do for the β4 peptide (Lewis and Raman, 2011), making the endogenous protein of Purkinje cells more effective at antagonizing lidocaine inhibition.

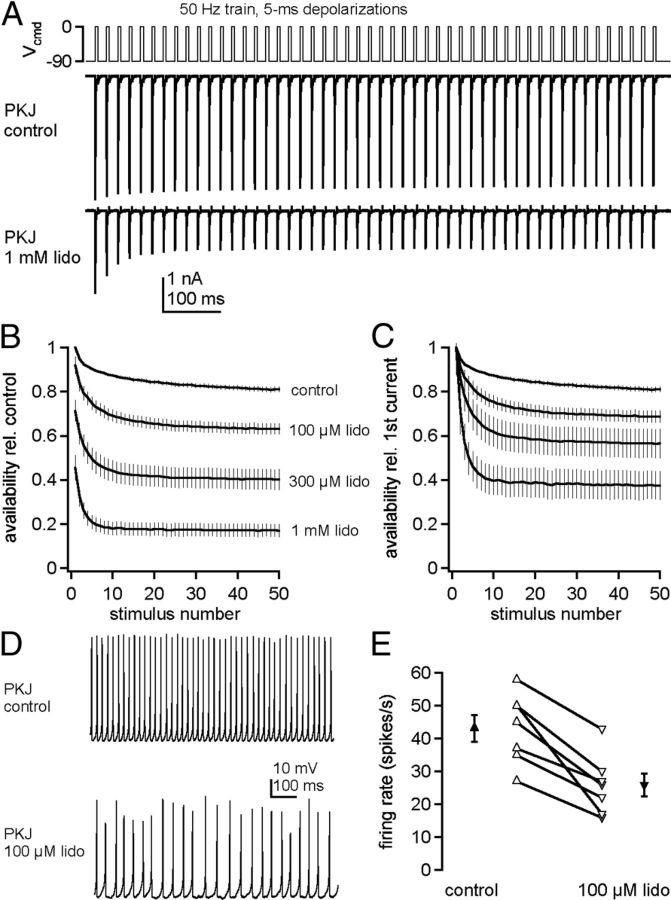
The relative insensitivity of Purkinje cell Na channels to lidocaine inhibition raises the question of how susceptible such channels are to use-dependent block by chronic lidocaine. We therefore evoked trains of Na currents with 5 ms step depolarizations from −90 to 0 mV, applied at 50 Hz for 1 s (Fig. 9A). Without extracellular lidocaine, currents decayed by 10% during the train. This stability of Na current amplitudes during repeated activation results partly from resurgent current and partly from a resistance of Purkinje Na channels to slow inactivation (Zhou and Goldin, 2004; Aman and Raman, 2007). In 100 μm, 300 μm, and 1 mm lidocaine, the resting inhibition decreased the first peak current by 5, 20, and 40%. During the train, however, the peak currents decayed only partially relative to the first peak current, by 27 ± 2% (n = 8) in 100 μm, 41 ± 5% (n = 7) in 300 μm, and 60 ± 4% (n = 8) in 1 mm lidocaine (Fig. 9B,C). Because Purkinje cells can fire repetitively with approximately half their Na channels blocked by TTX (Raman and Bean, 1999), these data suggest that firing may persist in lidocaine.

Figure 9.

Maintenance of Purkinje Na channel availability and firing in constant lidocaine. A, Voltage command of a 50 Hz, 1 s train of 5 ms step depolarizations (top) and Na currents (bottom) evoked in a Purkinje cell bathed in control or lidocaine solution. B, C, Availability, normalized to first peak current in lidocaine-free solution (B) and normalized to first peak current in lidocaine (C), versus stimulus number. Control, n = 12; 100 μm lidocaine, n = 7; 300 μm lidocaine, n = 7; 1 mm lidocaine, n = 7. D, Representative trace of Purkinje cells spontaneous firing in control and 100 μm lidocaine. E, Summary data of Purkinje firing rates in control and 100 μm lidocaine.

To test this possibility, we made current-clamp recordings from dissociated Purkinje cells. In control solutions, isolated cells fired regular spontaneous action potentials at 43 ± 4 Hz (n = 7), as in previous reports (Raman and Bean, 1999). In 100 μm lidocaine, spike heights decreased and the rate dropped to 25 ± 4 Hz (p = 0.007). Nevertheless, all cells continued firing spontaneously, confirming that, even with lidocaine continually present, Na channel availability remained sufficiently high to support sustained spiking (Fig. 9D,E). The extent to which the lidocaine-dependent decrease in firing rate can be attributed directly to inhibition of Na channels, however, is ambiguous because lidocaine at 100 μm can inhibit other channels that may be engaged during spiking, including blockade of TREK channels, HCN channels, and KV3 channels (Trellakis et al., 2006; Nayak et al., 2009; Putrenko and Schwarz, 2011).

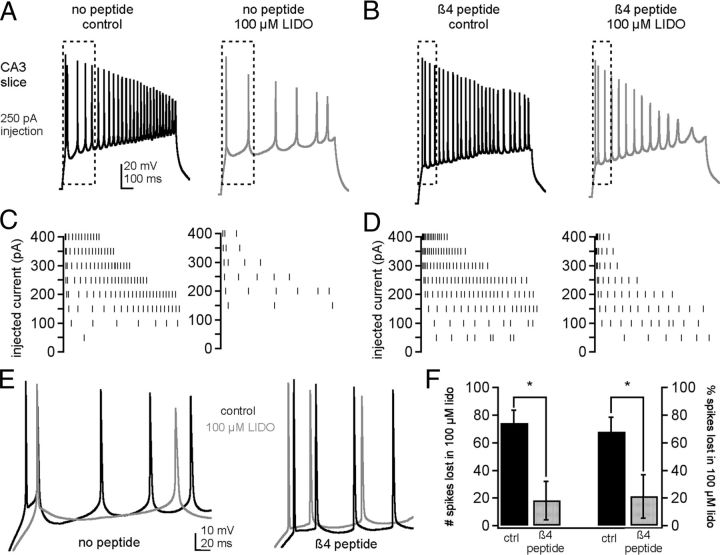
Therefore, to examine more directly whether the open-channel blocker responsible for resurgent Na current is sufficient to preserve spiking in the presence of lidocaine, we recorded action potentials in CA3 pyramidal neurons with and without the β4 peptide added to the intracellular solution. Because isolated CA3 pyramidal neurons do not fire action potentials readily (I.M.R. unpublished data), presumably because of a relatively low density of somatic Na and K channels and the loss of the initial segment (Lee et al., 2006; Meeks and Mennerick, 2007), recordings were made in hippocampal slices. Because CA3 neurons do not fire spontaneous spike trains, cells were held at −70 mV and action potentials were evoked with 1 s current injections in 50 pA increments (Fig. 10A, left, C, left). Including the β4 peptide in the pipette altered action potential waveforms as well as firing patterns (Fig. 10B, left, D, left, E). With the β4 peptide, the approach to threshold was more abrupt and the initial spike rate was accelerated, reflected in a decrease of the maximal interspike intervals. At the current injection that elicited the fastest spiking, the mean interspike interval of the first 6 spikes was 33 ± 12 ms (range 9–57 ms, n = 4) without β4 and 16 ± 5 ms (range 5–26 ms, n = 5) with β4 (F test for a change in variance, p = 0.055). Nevertheless, with β4, some cells tended to enter depolarization block more readily, resulting in fewer spikes, especially with bigger current injections. Because maintenance of the rapid firing induced by resurgent Na current depends on large, rapidly repolarizing K currents (Raman and Bean, 1999; Khaliq et al., 2003), it seems likely that the K currents of CA3 cells, which can be an order of magnitude smaller in the cell body alone (Khaliq et al., 2003; Lee et al., 2006), prevent CA3 cells from being able to exploit the properties of a resurgent current inducing blocking particle to produce sustained spiking at relatively depolarized potentials (Lee et al., 2006). We therefore quantified firing by counting the total number of action potentials in the first 500 ms of all steps. Peptide-free cells fired 114.3 ± 14.2 spikes (n = 4) and β4-peptide containing cells fired 56.8 ± 15.8 spikes (n = 5, p = 0.03, unpaired).

Figure 10.

Effect of β4 peptide on lidocaine-mediated suppression of firing in CA3 pyramidal neurons in slices. A, Action potentials in a peptide-free CA3 neuron evoked by a 250 pA current injection before (left) and after (right) perfusion of 100 μm lidocaine. B, Same as A in a different neuron containing the β4 peptide. C, Spike raster for multiple current injections for the cell in A. D, Spike raster for multiple current injections for the cell in B. E, Overlay of boxed regions in A and B, for control solutions (top) and lidocaine solutions (bottom). F, Summary of the number of spikes (left) and the percentage of spikes (right) lost in lidocaine for control (peptide-free) and β4 peptide-containing cells. * p < 0.05.

Perfusion of the slice with 100 μm lidocaine clearly reduced the total number of action potentials fired, quantified as the decrease in the number of spikes relative to control solutions (Fig. 10B, right, D, right, E). With peptide-free intracellular solution, 74.3 ± 9.5 spikes were lost in lidocaine (Fig. 10F). In contrast, with β4 peptide, only 16.6 ± 13.5 spikes were lost (p = 0.013). These correspond to lidocaine-induced decreases in firing of 68.0 ± 10.4% (peptide-free) and 21.3 ± 15.8% (β4 peptide, p = 0.045, Fig. 10F). Thus, the ability of lidocaine to inhibit firing is greatly reduced by a resurgent current-inducing open-channel blocker.

Discussion

Lidocaine and other use-dependent blockers bind Na channels with variable efficacy, depending on the channel states. By applying lidocaine rapidly and briefly to voltage clamped cells, we have restricted the exposure of lidocaine to channels in one or more known states. Consistent with studies in other preparations, lidocaine-dependent inhibition of Na current in CA3 neurons becomes more effective with depolarizations that favor fast-inactivated states. Inhibition is antagonized, however, by the β4 peptide, which acts as an open-channel blocker, as well as by ATX, which slows inactivation. Likewise, lidocaine inhibition of Na currents and of action potential firing is less effective in Purkinje neurons, which contain a native open-channel blocking protein, than in CA3 neurons, and the β4 peptide partially protects CA3 cells from lidocaine-induced spike suppression. These data suggest that lidocaine interacts strongly with inactivated channels and moderately with open channels, but only weakly with open-channel blocked channels. Because many clinical compounds, including local anesthetic, anticonvulsant, and antiarrhythmic drugs, act similarly to lidocaine, these data suggest that the interaction of such compounds with Na channels in different neurons may depend on whether the neurons express an endogenous blocking protein. As >15 classes of neurons are known to have resurgent current (i.e., express a native blocker), these cells may have a decreased sensitivity to use-dependent clinical agents.

Interaction of the open-channel blocker with lidocaine

Structurally, use-dependent inhibitors approach their binding sites through multiple pathways. In resting channels, they may gain access to the central cavity via hydrophobic fenestrations lateral to the closed pore (Payandeh et al., 2011); in open channels, they enter the pore from the cytoplasmic mouth. Many interact with the same sites in the inner pore, including hydrophobic and aromatic residues on DIII-S6 and DIV-S6 (Strichartz, 1973; Hille, 1977; Wang et al., 1987; Ragsdale et al., 1994; Catterall, 2002). Once bound, lidocaine stabilizes the S4 segments of DIII and DIV in their activated positions (Sheets and Hanck, 2003, 2007; Muroi and Chanda, 2009). Although not required for lidocaine inhibition, the inactivation gate increases lidocaine's affinity, keeping channels in a lidocaine-bound inactivated state (Cahalan, 1978; Wang et al., 1987; Sheets and Hanck, 2007).

The present data demonstrate that lidocaine can also bind directly to inactivated channels because test responses are inhibited even when drug is applied only after CA3 channels have become nonconducting after depolarization. Blocked channels, in contrast, are less sensitive to lidocaine inhibition, as conditioning protocols that favor open-channel block, either by the β4 peptide or by the native blocking protein, reduce lidocaine inhibition. Although lidocaine becomes more efficacious with depolarization, the relief of inhibition by the β4 peptide or the native blocker is greater at more positive potentials. Because the open-channel blocker binds more stably at higher voltages (Raman and Bean, 2001; Aman and Raman, 2010), these data suggest that the open-channel blocker and lidocaine compete to reach overlapping or otherwise mutually exclusive binding sites.

Three pieces of evidence hint that binding sites of lidocaine and the open-channel blocker share common features. First, brief exposure of Purkinje Na channels in inside-out patches to chymotrypsin, which cleaves aromatic residues, removes native open-channel block and disrupts use-dependent block by QX-314 (Grieco et al., 2005). Second, in Na_V1.5 channels with inactivation removed, mutating a phenylalanine in DIV-S6 disrupts binding of both lidocaine and the β4 peptide (Wang et al., 2006). Third, the phenylalanine in the β4 peptide is obligatory for open-channel block that generates resurgent-like current (Lewis and Raman, 2011) and is possibly analogous to the aromatic ring of lidocaine (Ahern et al., 2008).

Even when lidocaine is applied at −90 to −60 mV, however, the β4 peptide restores the test pulse to lidocaine-free amplitudes and hyperpolarized the activation curve, raising the possibility that the peptide also reduces resting-state inhibition by lidocaine. This idea is consistent with observations that the peptide depolarizes the steady-state inactivation curve and thus may interfere directly with fast inactivation (Bant and Raman, 2010). Nevertheless, the simplest interpretation of the peptide's effect is that, by occluding the permeation pathway, it restricts lidocaine's access via the central cavity to its binding site.

Kinetics of lidocaine inhibition

The extent of inhibition by lidocaine varied with its time of application. The temporal profile of inhibition is likely influenced by the amount of recovery from inhibition between drug removal and the test step, as well as channel states during lidocaine application. The basic observation, that lidocaine exposure during the conditioning pulse reliably reduced the test current, indicates that lidocaine entered the cell, associated with channels, and remained at least partly bound until the test pulse, despite the removal of free extracellular lidocaine. Lidocaine at 1 mm produced approximately twice the inhibition of 100 μm lidocaine, suggesting an IC₅₀ near 100 μm. Assuming diffusion-limited binding (1e7/M/s), however, such a low affinity predicts full recovery by the test pulse, which was not observed, suggesting the true affinity may be higher. Indeed, previous studies report affinities of tens of micromolars for inactivated channels (Bean et al., 1983; Chahine et al., 1992; Wright et al., 1997); some (free) lidocaine may also have remained trapped intracellularly until the test pulse. Lidocaine indeed washed out eventually, however, because complete recovery consistently occurred within the 4 s start-to-start interval, assayed by stability in the reference response. Thus, assuming greater lidocaine dissociation and recovery of channel availability for the longer intervals, the inhibition of the test response, although reliable, is probably underestimated, with the largest deviations for the earliest application times.

The channel state during drug exposure, however, appears more significant than affinity in determining lidocaine's effect because inhibition by high and low drug concentrations was preferentially relieved by modulating the proportion of channels in closed, open, inactivated, or blocked states. Inhibition was least when most channels were closed, as evident from the earliest applications, as well as from drug exposure at −90 mV. Inhibition was greatest at the most positive potentials, with lidocaine exposure occurring exclusively during the conditioning step. Blocking channels with the β4 peptide or favoring open states with ATX greatly reduced inhibition. Notably, although ATX relieved lidocaine inhibition in CA3 cells, especially at +60 mV, this reduced effect was occluded by the β4 peptide, as though delaying fast inactivation had no further effect on lidocaine binding if channels were already blocked. The response of Purkinje cells was unusual, as inhibition initially increased as drug application was delayed, but when lidocaine reached channels at the latest times, after they were likely blocked, inhibition decreased. Together, these data support the idea that the dominant variable setting the extent of inhibition is channel state during drug exposure.

Whether ATX reduces lidocaine's effect simply by prolonging opening remains a question, however. In Na channels with inactivation removed either pharmacologically or through mutagenesis, lidocaine and derivatives indeed inhibit Na current, although higher concentrations are necessary for maximal effects (Wang et al., 1987; Sheets and Hanck, 2007). ATX indeed slows entry into fast-inactivated states, but restricting DIV-S4 movement may itself reduce the efficacy of lidocaine, as lidocaine binding stabilizes this sensor in the outward position (Muroi and Chanda, 2009). Conversely, the ATX-modified open state, in which DIV-S4 movement is modulated (Sheets et al., 1999) and which has been reported to display subconductances (Nagy, 1987, el-Sherif et al., 1992, Castillo et al., 1996), may also hinder lidocaine's access to its binding site. Regardless of the precise mode of action, however, it is clear that ATX, which delays inactivation, has the measurable outcome of reducing lidocaine inhibition.

Physiological effects of use-dependent blockers

We find that Purkinje neurons are intrinsically less sensitive to lidocaine inhibition than CA3 neurons, and, based on CA3 responses with and without the β4 peptide, the difference likely results from the endogenous open-channel blocking protein. Even in Purkinje cells bathed in 1 mm lidocaine, ∼20% of Na current remained available after a 50 pulse, 50 Hz train of 5 ms depolarizations. Purkinje cells also fired spontaneous repetitive action potentials in chronic 100 μm lidocaine, although at rates lower than in control solutions. Thus, their firing likely persists even with clinically relevant concentrations of exogenous use-dependent blockers with modes of action that resemble that of lidocaine. Because many cerebellar and brainstem neurons express resurgent current, such neurons may be relatively resistant to lidocaine-like compounds, possibly explaining why brainstem regions critical for physiological function are not seriously disrupted by clinically used Na channel inhibitors. Conversely, because a subset of ventral hippocampal CA1 cells and dentate granule cells express resurgent current (Castelli et al., 2007a) and because the hippocampus is often implicated in epileptogenesis, a reduced sensitivity of these cells to use-dependent anticonvulsants may be pertinent to treating epilepsies. Finally, because resurgent current can be augmented under pathological conditions, contributing to sensory neuron hyperexcitability and pain hypersensitivity (Jarecki et al., 2010, Theile et al., 2011), channels may decrease their sensitivity to local anesthetic-like compounds in these conditions. Thus, the action of the endogenous blocker as a native antagonist of the local anesthetic receptor may well influence the effect of lidocaine and related drugs on the nervous system.