Local site preference rationalizes disentangling by DNA topoisomerases

Abstract

To rationalize the disentangling action of type II topoisomerases, an improved wormlike DNA model was used to delineate the degree of unknotting and decatenating achievable by selective segment passage at specific juxtaposition geometries and to determine how these activities were affected by DNA circle size and solution ionic strength. We found that segment passage at hooked geometries can reduce knot populations as dramatically as seen in experiments. Selective segment passage also provided theoretical underpinning for an intriguing empirical scaling relation between unknotting and decatenating potentials.

Closed DNA circles can be unknotted, knotted, or linked (catenated). Such topological entanglements of DNA molecules have important impact on biological processes [1–3]. Unlike “knots” in proteins that are resolvable without breaking their linear chains [4], knots in DNA circles cannot be disentangled by continuous deformation [5]. In the living cell, DNA topology is regulated by enzymes called topoisomerases, which function by transporting either a single-stranded or a double-stranded DNA (dsDNA) segment through another. We focus here on the unknotting and decatenating actions of type-II topoisomerases (topo IIs), which have the ability to pass one dsDNA through another [6,7]. Topo II disentangling is often compared against a baseline referred to as “topological equilibrium” in which the distribution of topological states is the same as if the chain segments of DNA circles were free to pass through each other. Rybenkov et al. demonstrated that topo IIs can reduce knot and catenane populations to steady-state values that are tens of times less than those at topological equilibrium [8]. This observation implies that topo IIs do not pass dsDNA segments randomly but, instead, selectively act on entangled molecules. How does a topo II recognize the topology of a DNA molecule that is much larger than itself?

In this paper, we evaluate a promising answer [9] to this puzzle. Several hypotheses have been proposed to meet the conceptual challenge [8–12], almost all of them envision the topo II actively deforming or probing the DNA to ascertain its topology (reviewed in Ref. [3]), like Maxwell’s demon [13]. In contrast, the hooked juxtaposition hypothesis [9] relies on pre-existing DNA conformational statistics. It stipulates that a simple rule of allowing segment passage only when a DNA juxtaposition is hooked (when the two segments curve toward each other, see top inset in Fig. 1) should account for many capabilities of topo II.

FIG. 1.

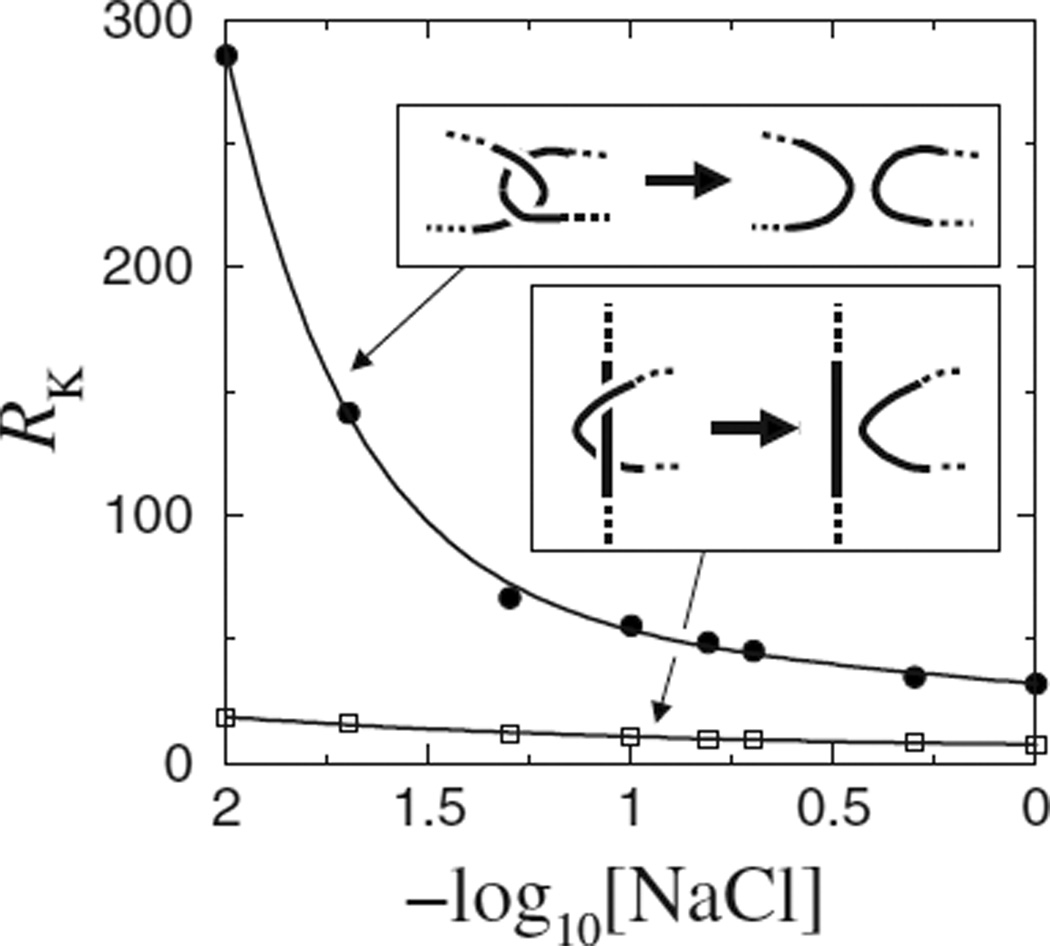
Modeled knot reduction factor (R_K) for 3.5 kb DNA circles varies with [NaCl] for selective segment passages (insets) at the hooked (dots) or the half-hooked (squares) juxtaposition. Throughout this paper, each data point was simulated using 6 × 10⁸–3 × 10⁹ attempted chain moves; curves through data points are merely guides for the eyes.

The hooked juxtaposition hypothesis is amenable to direct computational evaluation using a “juxtaposition-centric” algorithm that enumerates or samples conformations subject to the constraint of any given preformed two-segment juxtaposition of interest. Applications of this method to self-avoiding walks on the simple-cubic lattice have shown that the hypothesis can, in principle, lead to very significant disentangling [14,15]. An independent study using freely jointed chains reached a similar conclusion [16]. However, the biophysical viability of the hypothesis remains to be demonstrated using geometrically more realistic DNA models [17,18]. To do so here, we begin by comparing the effects of segment passages at the four specific juxtaposition geometries in Table I. Besides the hooked, the other juxtapositions are of interest because (i) the straight juxtaposition is useful as a baseline, (ii) the effect of the free juxtaposition is expected to be essentially opposite to that of the hooked juxtaposition [9,14,15], and (iii) the effect of the half-hooked juxtaposition is essentially equivalent to that predicted by an active bending model of topo II action [11] (see discussion in Ref. [15]).

TABLE I.

Knotting and unknotting as a function of juxtaposition geometry. 𝒥(j)’s are fractions of segment-passage events via a given juxtaposition geometry j that resulted in various transitions among unknotted (U) and knotted (K) states, computed for 3.5 kb DNA circles under ionic strength [NaCl] = 0.154 M in our model. R_K is the knot reduction factor.

Juxtaposition (j)		${𝒥}_{U\to U}^{(j)}$	${𝒥}_{U\to K}^{(j)}$	${𝒥}_{K\to U}^{(j)}$	${𝒥}_{K\to K}^{(j)}$	RK
	hooked	0.858	0.0028	0.1370	0.0023	48.9
	half-hooked	0.914	0.0077	0.0761	0.0025	9.8
	straight	0.954	0.0240	0.0198	0.0021	0.82
	free	0.894	0.1014	0.0027	0.0022	0.027

The lengths and shapes of our model juxtapositions were inspired by a recent x-ray crystal structure for a topo II–DNA complex showing that the interacting DNA segment has length ~10 nm and is bent into an ~150° arc [19]. Although this configuration might not be exactly that of DNA–topo II interaction in vivo or in solution, it is a good starting point for our analysis. Accordingly, the four juxtapositions in Table I were constructed as follows: each straight or curved segment has length l = 10 nm; each curved segment is a circular arc with subtending angle α = 150°; the midpoints of the two segments of a juxtaposition are separated by d =5 nm; and the two segments are perpendicular with crossing angle θ =90° (i.e., the scalar product of the segments’ midpoint tangents is zero). This set of parameters was used for Table I and Figs. 1 and 2 but later we investigate the consequences of varying these parameters.

FIG. 2.

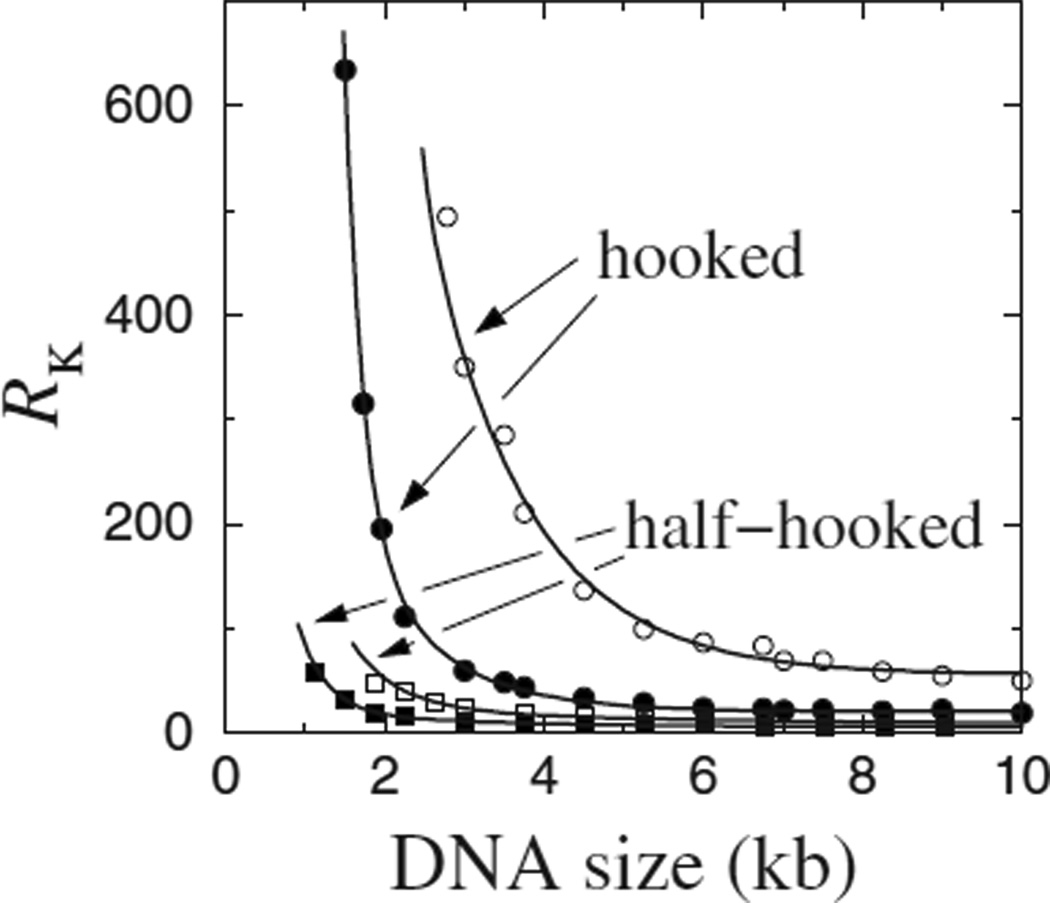
Knot reduction factor, R_K, varies with DNA circle size. Model results are shown for selective segment passages at the hooked and half-hooked juxtaposition geometries for [NaCl]=0.01 (open symbols) and 0.154 (filled symbols).

Here we use a wormlike DNA model [17] with a potential that includes stretching, bending, torsion, excluded volume terms, and an electrostatic interaction that depends on salt concentration [20,21]. In parallel with our lattice studies [14,15], preformed juxtapositions were imposed as constraints in Monte Carlo simulations. Following Ref. [17], we used the generalized Madras-Orlitsky-Shepp (MOS) moves to sample conformations across different topologies [22] and the length-changing T_± moves to sample conformations with the preformed juxtaposition situated at different locations of the model DNA circle. The topological state of each conformation was determined by computing its HOMFLY polynomial [23]. Mimicking topo II action, virtual segment passages [14,15], which change the crossing sign of the selected juxtaposition (see insets in Fig. 1), were performed on the conformations to ascertain the transition probabilities between various topological states.

In Table I, ${𝒥}_{U\to K}^{(j)}$ denotes the probability that a segment passage at juxtaposition j converts an unknot to a knot; 𝒥^(j)’s for other transitions are similarly defined [15]. We measure unknotting power by a knot-reduction factor

$$R_K=\frac{{(P_U)}_{\mathrm{s}\mathrm{t}}}{{(P_K)}_{\mathrm{s}\mathrm{t}}}\frac{{(P_K)}_{\mathrm{e}\mathrm{q}}}{{(P_U)}_{\mathrm{e}\mathrm{q}}},$$ (1)

where (P_U) and (P_K) are, respectively, the unknot and knot populations and the subscripts refer to topological equilibrium (eq) and the steady state (st) maintained by segment passage through the selected juxtaposition. Because knot populations are generally small [(P_U)_st, (P_U)_eq ≈ 1], R_K ≈ (P_K)_eq/(P_K)_st. A simple master-equation derivation [15] showed that $R_K={𝒥}_{K\to U}^{(j)}/{𝒥}_{U\to K}^{(j)}$.

Table I provides results under ~ physiologically relevant solution conditions ([NaCl]=0.154 M) for circles with equilibrium knot probability (P_K)_eq < 0.4%. If the circle contains a hooked juxtaposition, the knot probability is much higher at ${𝒥}_{K\to U}^{(j)}+{𝒥}_{K\to K}^{(j)}=13.9\%$, but an overwhelming majority ${𝒥}_{K\to U}^{(j)}/({𝒥}_{K\to U}^{(j)}+{𝒥}_{K\to K}^{(j)})=98\%$ of these knots are converted to unknots upon segment passage, resulting in ≈ 50 times reduction in knot population in the steady state $(R_K={𝒥}_{K\to U}^{(j)}/{𝒥}_{U\to K}^{(j)}=0.1370/0.0028=48.9)$. Remarkably, the topological information embodied in a small juxtaposition with two 10 nm segments is sufficient to effect such a significant knot reduction in relatively much larger DNA circles with chain length ≈ 1100 nm. Selective segment passages at the half-hooked juxtaposition also reduced knot populations, but much less effectively (R_K=9.8). The effect of selective segment passage at the straight juxtaposition was approximately neutral (R_K ≈ 1), as expected from its symmetric geometry. Finally, Table I shows that selective segment passages at the free juxtaposition promote rather than reduce knotting (R_K ≪ 1). Because we are primarily interested in unknotting, we will focus mainly on the hooked and half-hooked juxtapositions below.

The effective diameter of DNA and its knotting probability are affected by salt [24]. Recent studies of topo II action using lattice [14,15] and freely jointed [16] chain models correspond, respectively, to solution conditions with low and high salts [17]. The present simulations allow changes in salt concentration to be modeled by varying the electrostatic term [17,20,21] to explore how salt may affect the outcome of topo II action. For the hooked juxtaposition, the knot reduction factor (Fig. 1) shows a surprising salt sensitivity: R_K increases from ≈ 32 for [NaCl]=1 M to ≈ 150 and 280, respectively, for [NaCl]=0.02 and 0.01 M. In contrast, R_K for the half-hooked juxtaposition is generally low, ranging from 7.5 to 19.0 with [NaCl] varying between 0.01 and 1.0 M (Fig. 1). This clear difference in predicted variation of R_K with salt for the two juxtapositions may offer a test of the hooked juxtaposition hypothesis [9] and the active bending model [11] by future experiment.

Figure 2 shows knot reduction as a function of DNA circle size. For the hooked juxtaposition, R_K increases sharply when the DNA circle size decreases below ~4 kb. When DNA circle size increases, R_K first decreases then stabilizes for large circle sizes. This behavior, now obtained using a wormlike chain model with real DNA-like parameters, is consistent with lattice model results [15] and the original ansatz [9]. The robust trend supports the hooked juxtaposition hypothesis because it is in line with an experiment [8] showing that the R_K achieved by a particular topo II for a 10 kb DNA is 50 whereas that for a 7 kb DNA is 90. In Fig. 2, R_K≈ 22.0 for 10 kb DNA under physiological ionic strength ([NaCl]=0.154 M). This result is almost identical to that obtained using a 32-bead freely jointed chain model for the same DNA circle size [16]. It has the same order of magnitude as but is smaller than the experimental R_K=50 in Rybenkov et al. [8]. At lower salt, R_K is larger (≈ 57 for 10 kb DNA) and decays more slowly with increasing DNA circle size. In comparison, the R_K values for the half-hooked juxtaposition in Fig. 2—as in the lattice model [15]—do not show much increase with decreasing DNA circle size.

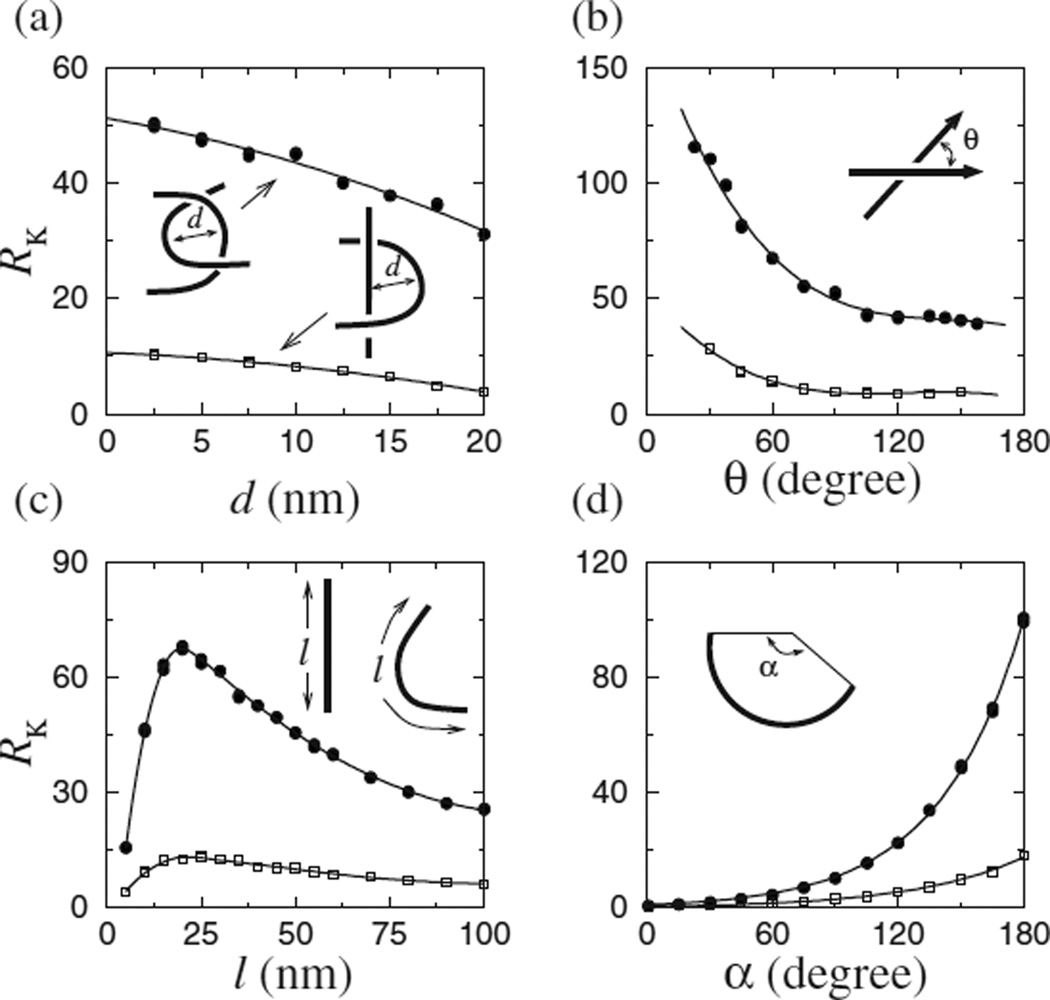
R_K varied tremendously for the different juxtapositions with fixed geometries (Table I). We next varied the geometrical parameters in Fig. 3 to study a spectrum of juxtapositions based on the hooked and half-hooked geometries. R_K is affected, to different degrees, by all four parameters. R_K increases with decreasing segment-segment separation d, but only mildly. Even for the hooked juxtaposition that shows more variation, R_K only increases from ≈ 32 to 50 for a decrease of d from 20 to 2.5 nm [Fig. 3(a)]. The crossing angle θ has a larger effect [Fig. 3(b)]. Because of the directionality of the segments (arrows), R_K is not symmetric with respect to θ=90°, showing an increase with decreasing θ. Interestingly, the structural data suggest that topo II does not act on juxtapositions with a 90° angle and this may rationalize the enzyme’s apparent chirality-sensing ability [25]. This question deserves future effort.

FIG. 3.

Effects of juxtaposition geometry on knot reduction. R_K for model 3.5 kb DNA circles, [NaCl]=0.154 M, was computed for variations of the hooked (dots) and half-hooked (squares) juxtapositions by changing the following parameters: (a) d is the midpoint separation between two equal-length segments of the juxtaposition, (b) θ is their crossing angle, (c) l is segment length, and (d) α is the arc angle subtended by the circular segment. Solid curves in (d) are single exponential fits. Except the parameter being varied in each panel, d=5 nm, α =150°, θ =90°, and l=10 nm.

Figure 3(c) shows that for the hooked juxtaposition, R_K increases sharply with segment length for l≲20 nm, which corresponds to a physically plausible regime given the size of topo II. For larger l, R_K decreases gradually. Among the geometric parameters examined, the arc angle α shows the most dramatic effect on R_K. Figure 3(d) shows an exponential increase in R_K with respect to α, which is consistent with the lattice results [15] showing a correlation between log R_K with the hookedness parameter H defined in Ref. [14] because H∝α. Taken together, Fig. 3 demonstrates that even subtle changes in the geometry of the selected juxtaposition can lead to large variations in R_K. These results may provide insight into the wide range of different R_K’s between 5 and 90 that have been observed among topo IIs from different organisms [8].

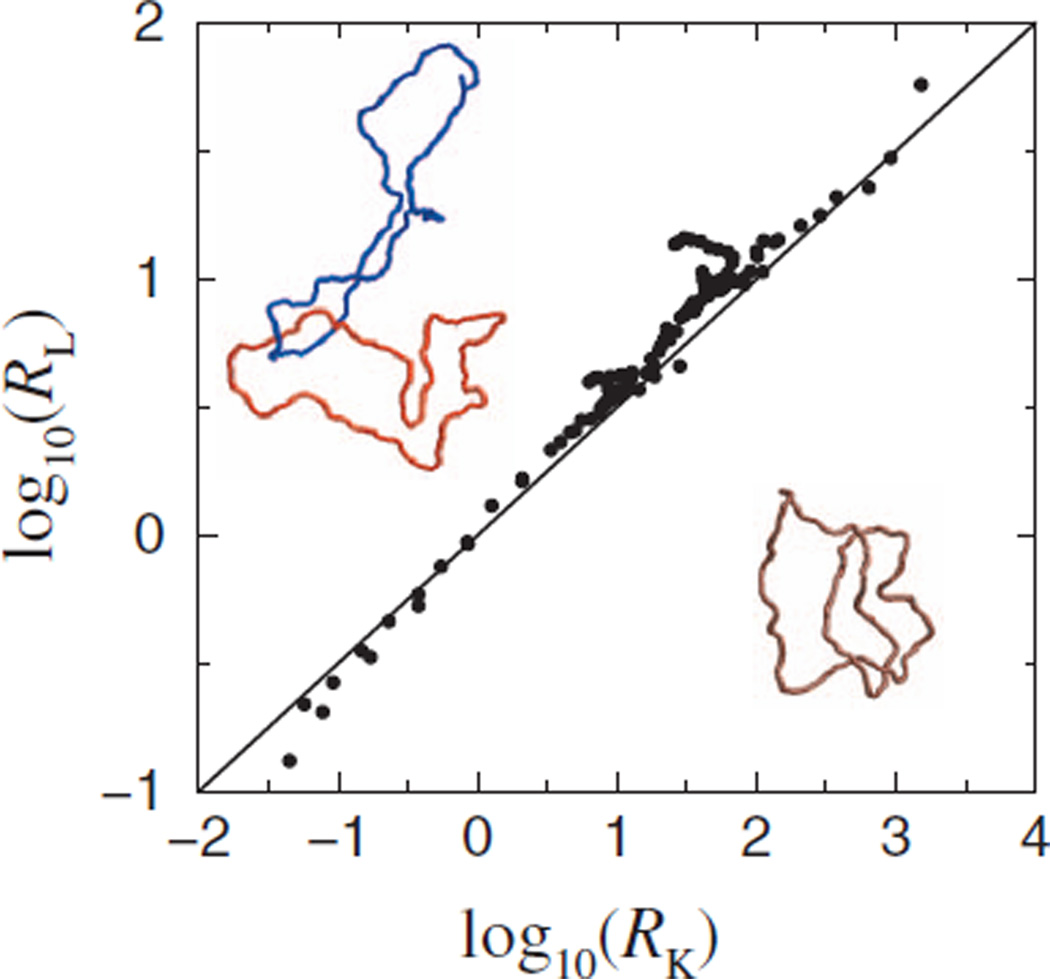
Although the disentangling powers of topo IIs from different organisms differ, experiments on six topo IIs suggest that their unknotting and decatenating potentials follow an approximate scaling law R_K≈ (R_L)^1.6, where R_L is the link (catenane) reduction factor [Fig. 3A of Ref. [8]]. Motivated by this finding, we examined (Fig. 4) the relationship between R_K and R_L in our model for the juxtaposition geometries studied in Figs. 1–3 plus others with α < 0 (e.g., the free juxtaposition) in which a circular segment curved away from the other segment. R_L in our model is defined in the same way as R_K in Eq. [1] except “U” now stands for unlinked and “K” (knotted) is replaced by “L” (linked); the corresponding 𝒥(j)’s were determined using two-circle juxtaposition-centric simulations [14]. The slope (=2) of the fitted line in Fig. 4 shows that our model data follow the power law R_K=(R_L)² to a good approximation. The same scaling was deduced from our lattice model [15]. The robustness of this behavior is suggestive of deeper mathematics yet to be discovered. To date, our results offer the only physical rationalization for the empirical scaling, despite a small ≈ 0.4 difference in the exponents, the resolution of which will require more extensive experimental data and perhaps further theoretical analyses.

FIG. 4.

(Color) Scatter plot reveals an approximate scaling law between models R_L and R_K computed for selective segment passages via a variety of juxtaposition geometries and for circles of various sizes (see text). Each data point is for a given juxtaposition and a given circle size. Also shown are two catenated circles (top left) and a knotted circle (bottom right) as example conformations in the wormlike DNA chain model.

In summary, using an improved wormlike model [17], we have shown that selective segment passage at juxtapositions with a hooklike geometry can lead to significant knot and link reduction. Because the wormlike model is reasonably realistic for DNA, our results demonstrate that the hooked juxtaposition hypothesis is a biophysically viable mechanism to account for topo II action. Many of the present results are very similar to those predicted by lattice [14,15] as well as freely jointed [16] chain models, pointing to underlying general principles governing the relationship between local conformational preference and global topology. Building on these advances, much biology and much physics remain to be learnt from topo II-mediated changes in DNA topology.