Helical Structure Determines Different Susceptibilities of dsDNA, dsRNA, and tsDNA to Counterion-Induced Condensation

Abstract

Recent studies of counterion-induced condensation of nucleic acid helices into aggregates produced several puzzling observations. For instance, trivalent cobalt hexamine ions condensed double-stranded (ds) DNA oligomers but not their more highly charged dsRNA counterparts. Divalent alkaline earth metal ions condensed triple-stranded (ts) DNA oligomers but not dsDNA. Here we show that these counterintuitive experimental results can be rationalized within the electrostatic zipper model of interactions between molecules with helical charge motifs. We report statistical mechanical calculations that reveal dramatic and nontrivial interplay between the effects of helical structure and thermal fluctuations on electrostatic interaction between oligomeric nucleic acids. Combining predictions for oligomeric and much longer helices, we also interpret recent experimental studies of the role of counterion charge, structure, and chemistry. We argue that an electrostatic zipper attraction might be a major or even dominant force in nucleic acid condensation.

Introduction

Interactions of nucleic acids at close separations play crucial role in some of the most fundamental biological reactions, including packing of genetic material in cells and viruses, homologous pairing, and RNA folding. Nucleic acid helices are among the most highly charged biological molecules (see Table 1). The ability of nucleic acids to overcome the repulsion caused by their extremely high charge density is generally attributed to counterion-induced (or mediated) attractive interactions, because specific counterions are needed to condense them into compact aggregates or structures (1).

Table 1.

Structural parameters and charge density of dsDNA (B-form), dsRNA, and tsDNA

Parameter	B-DNA	dsRNA	tsDNA
Helical pitch (Å)	33.8	30.9	38.4
Number of basepairs per helical turn	10	11	12
Groove half-width (rad/π)	0.4, 0.6	0.64, 0.36	0.36, 0.35, 0.29
Radius at the center of phosphate groups (Å)	9	8.5	9.5
Axial distance per elementary charge, lc (Å)	1.7	1.4	1.1
Average surface charge density of phosphates, σ (μC/cm2)	17	21	25

The physics underlying these attractive interactions is still debated (1–7). The proposed ideas include attractive hydration forces (8,9), bridging by shared counterions (10), correlated fluctuations in the density of condensed counterions (11), attraction between Wigner-crystal-like lattices of counterions (12,13), and zipper-like alignment of negatively charged strands of the sugar-phosphate backbone opposite to positively charged strands of counterions bound in nucleic acid grooves (14). For detailed analysis of these and other ideas, see, e.g., Kornyshev et al. (7) and references therein. Resolving which mechanisms of counterion-induced attraction contribute the most to interactions between nucleic acids is important not only for understanding the principles of nucleic acid behavior but also for rapidly expanding bioengineering applications of these molecules (15).

One of the most straightforward approaches to this problem is to examine how the propensity of nucleic acids to condense depends on their structure as well as on the charge and chemistry of the counterions. Experimental studies along these lines produced a number of challenging observations. Among the most puzzling: Oligomeric double-strand (ds) RNA helices, expected to be more susceptible to counterion-induced condensation due to their higher surface charge density, were found to resist condensation (16). Oligomeric triple-strand (ts) DNA molecules were found to be susceptible to condensation by Mg²⁺ and Ca²⁺ whereas their dsDNA analogs were not (17). No evidence of attractive interactions was detected between oligomeric dsDNA helices at counterion concentrations below the condensation threshold (18). These observations might be explained by different molecular mechanisms, as proposed in the original studies. However, the Occam’s Razor principle of simplicity (entities are not to be multiplied beyond necessity; see, e.g., Baker (19)) provides a compelling argument for seeking a more universal interpretation.

To examine whether these observations might indeed be different facets of a more general mechanism, here we extend an earlier theory of DNA-DNA interactions to oligomeric nucleic acids with different number and configuration of strands. We take into account that the total interaction energy for oligomers may not exceed the thermal energy k_BT by much, even at short distances between the molecules (k_B is the Boltzmann constant and T is the absolute temperature). In this case, thermal motions may produce important qualitative effects, necessitating a thorough statistical mechanical analysis, which is described in this article.

Our calculations rationalize different susceptibilities of oligomeric dsRNA, dsDNA, and tsDNA to condensation based on known differences in the helical structure of the molecules and preferential counterion adsorption in their grooves rather than possible differences in the underlying interactions. These results support the idea of zipper-like alignment of negatively charged phosphate strands with positively charged counterions bound in grooves of the opposing molecule as a mechanism of counterion-induced attraction between the molecules. We argue that this electrostatic zipper mechanism might also explain recently observed counterion charge, structure, and chemistry effects on condensation of longer nucleic acids. Other interactions might contribute to the condensation, but they are less universal in nature and cannot explain the entire data set.

To facilitate understanding of our results by readers who may be less interested in mathematical aspects of the theory than in the nature of the main results, we formulate the model and basic equations, and then concentrate on the physics of the predicted and observed effects. All mathematical derivations are appended in the Supporting Material. Because the statistical mechanics is different for oligomeric and longer nucleic acids and because relevant calculations for long dsDNA have been published already (20), here we focus on the calculations for oligomers. In Discussion, however, we consider recent experimental data for both oligomeric and longer molecules and evaluate more general principles for the electrostatic zipper mechanism of nucleic acid condensation.

Model

Basic approach

In this study, we calculate the free energy of electrostatic interactions between helical oligonucleotides in solution and in aggregates as a function of their interaxial separation. For simplicity, we focus on parallel-oriented oligomers and use the corresponding free energy for qualitatively evaluating whether differences in their helical structure and preferential binding of counterions might explain the experimental observations. This approach relies on previous studies of longer molecules, which suggest that chiral interactions between helices at small interaxial angles do not change the qualitative conclusions on requirements for intermolecular attraction and aggregation (7). Analysis of interactions at nonzero interaxial angles is much more complicated and lies beyond the scope of this study.

To clarify the underlying molecular mechanisms and physical principles, we develop an analytical theory that follows the general approach recently reviewed in Kornyshev et al. (7). Alternatively, this problem could be addressed by computer simulations based on explicit, all-atom solvent models or Poisson-Boltzmann solvent description. Such simulations are realistic for short oligonucleotide helices. Yet, they provide less clear delineation of different interaction mechanisms and they are still imprecise. They also utilize multiple simplifications and assumptions (interaction potentials for the atoms, summation of long-range interactions, effects of box size and boundary conditions, validity of the nonlinear Poisson-Boltzmann model in the immediate vicinity of the nucleic acid surface, etc.). Still, they are complementary to our approach and might be interesting to pursue.

Structure and charge state of nucleic acid helices

We model the helices as dielectric cylinders with charged groups at the cylinder/water interface (Fig. 1). To elucidate effects of the nucleic-acid structure and preferential counterion binding at specific sites that may play a crucial role in intermolecular interactions (7), we account not only for the average surface charge density but also for helical patterning of the charges (Fig. 1). In Table 1, we gather pertinent parameters of nucleic acid structure and charge distribution that appear in the theory. We describe negatively charged phosphate groups as point charges located along two helical strands in dsDNA and dsRNA or along three helical strands in tsDNA. We assume that the fraction θ of the total phosphate charge is compensated by bound counterions, which are treated as part of the nucleic acid charge. The net surface charge density of the molecule is (1–θ)σ, where σ is the surface change density of phosphates. The fraction f₁ of bound counterions is located in the center of the minor groove, the fraction f₂ is located in the center of the major groove in dsDNA and dsRNA or distributed equally between the centers of the two other grooves in tsDNA, and the remaining (1–f₁–f₂) counterions are bound at random locations. We describe the effects of other, free electrolyte ions within the Debye-Hückel (linearized Poisson-Boltzmann) theory. The advantages and drawbacks of this approach were discussed in detail in Kornyshev et al. (7).

Figure 1.

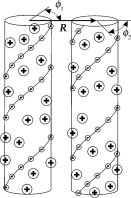
Model of electrostatic interaction between two parallel, double-stranded nucleic acids at close separations. The molecules are represented by dielectric cylinders with helical strands of point-like negative charges at the surface (small circles with the minus sign connected by helical lines). Bound counterions are modeled as point-like charges (large circles with the plus sign) at the cylinder surface, located randomly or in the middle between the strands of negative charges. Counterions responsible for the nonlinear screening of the nucleic acid charge are considered to be bound (7). Roughness of nucleic acid surfaces and poorly known dielectric properties of water in their grooves preclude evaluation of the effective cylinder radius with better than 2–3 Å accuracy from known molecular structures. For B-DNA, the effective radius that provides the best fit for the measured intermolecular forces is 11.2 Å, which is within the expected range between the 9 Å radius at centers and 12 Å radius at outer surfaces of phosphate groups (20). Because radii at the centers of phosphate groups in dsRNA and tsDNA are within 0.5 Å of that for B-DNA (Table 1), we use the same 11.2 Å effective radius for all three nucleic acids. It is important to emphasize that separation between nucleic acid surfaces in aggregates condensed by counterions is typically <10 Å (8,9), which is smaller than the separation between the strands of negative charges (Table 1). Therefore, it is essential to account for the discreteness and helical arrangement of the strands in any theory of such aggregates (7). Zipper-like juxtaposition of positively charged counterions bound in the grooves with negatively charged phosphate strands on the opposing molecule leads to electrostatic zipper attraction between the molecules, provided that bound counterions balance a sufficient fraction of the phosphate charges (14).

Pair interaction energy

We base our calculations on the theory of electrostatic interactions between molecules with helical charge motifs (7). Within this theory, the electrostatic interaction energy between two parallel helices of length L at large interaxial distances R may be approximated with

$$\frac{E_{\mathrm{int}}}{k_{\text{B}}T}\approx L\frac{2l_{\text{B}}}{l_c^2}\sum _{n=0}^{\infty }\left(2-{\delta }_{n,0}\right){\zeta }_n^2\left\{c_n^{im}\frac{\text{exp}\left(-2{\kappa }_{n}R\right)}{{\kappa }_{n}R}+{\left(-1\right)}^n{c}_n\frac{\text{exp}\left(-{\kappa }_{n}R\right)}{\sqrt{{\kappa }_{n}R}}\frac{1}{L}\underset{0}{\overset{L}{\int }}dz\text{cos}\left(n\left[\Delta \varphi \left(z\right)\right]\right)\right\}.$$ (1)

Here, l_B ≈ 7 Å is the Bjerrum length in water, and l_c is the axial length per phosphate group in the nucleic acid helix (see Table 1). The summation is performed over helical harmonics n of the interaction. δ_n,m = 1 at n = m δ_n,m = 0 at n ≠ m, ζ_n are helical harmonics of the density of the charged groups and bound counterions on nucleic acid surface (see Eq. S9 in the Supporting Material), e.g.,

$${\zeta }_n=\left[f_1+f_2{\left(-1\right)}^n+\left(1-f_1-f_2\right){\delta }_{n,0}\right]\theta -\text{cos}\left(n{\tilde{\varphi }}_s\right)$$ (2)

for double-stranded helices with the azimuthal half-width of the minor groove ${\tilde{\varphi }}_s$, and Δϕ(z) is the difference between the azimuthal orientations of the helices at point z along their length.

$${\kappa }_n=\sqrt{{\kappa }^2+{\left(\frac{2\pi n}{H}\right)}^2}$$ (3)

is the reciprocal decay length for each helical harmonic of the direct charge-charge interaction, κ is the reciprocal screening length in electrolyte solution, H is the helical pitch of the molecules, and c_n and $c_n^{im}$ are coefficients that depend only on κ_n and radius of the molecules, which are defined by Eqs. S7 and S8 of the Supporting Material. Note that Eq. 1 is a more transparent, simplified expression obtained by asymptotic expansion of Bessel functions at large R. More accurate Eqs. S1–S5, presented in the Supporting Material, were used in all of our calculations.

Each interaction harmonic consists of two contributions given by the two terms in the curly brackets in Eq. 1. The first one describes the energy of the dielectric core of each helix in the electric field created by the other helix, hereafter referred to as “image-charge interactions” (interaction of a charge with a dielectric may be represented by a sum of interaction of this charge with a set of images of this charge across the dielectric interface). The second one describes the energy of charges on one helix in the electric field created by the other helix, hereafter referred to as “direct charge-charge interactions”. It depends on mutual azimuthal orientation of the molecules which varies over the length of the molecules due to torsional fluctuations, as discussed in the next section.

Because κ_n linearly increases with n at large n and the energy associated with each harmonic n exponentially decreases with increasing κ_n, the sum over n in Eq. 1 rapidly converges. For dsDNA it is usually sufficient to retain only the terms with n ≤ 2 (7). For tsDNA, however, the term with n = 3 is also important. Thus, for consistency, here we retain the terms with n ≤ 3 for all nucleic acid helices.

Strictly speaking, Eq. 1 was derived for long helices (L >> R,H) and it neglects edge effects. Most of the experiments discussed in this study were performed with 25-basepair (bp) or longer oligonucleotides. For 25-bp helices L/R ≈ L/H ∼ 2, so that the predictions of the model based on this equation might be expected to be more qualitative than quantitative, which is important to keep in mind. Note also that the discreteness of the surface charges leads to additional harmonics in the electrostatic pair interaction energy that are not included into Eq. 1 (21,22). Because contribution of these harmonics is negligible for helices that have 10–12 charges per helical turn (7), we do not include them into our calculations.

Nonideality of the helical structure and thermal fluctuations

For ideal helices, the difference in the azimuthal orientations is the same along the entire length of the molecules, i.e., Δϕ is independent of z. In real nucleic acid molecules, however, sequence-related variations and thermal fluctuations in the stacking of basepairs result in variation of Δϕ with z. Because the interaction energy depends on Δϕ(z), the energetic cost of this variation contributes to the interaction free energy (23). This cost is described by

$$\frac{E_{\Delta \varphi }}{k_{\text{B}}T}=\frac{l_p^h}{4}\underset{0}{\overset{L}{\int }}{\left(\frac{d\left[\Delta \varphi \left(z\right)-\Delta {\varphi }_0\left(z\right)\right]}{dz}\right)}^{2}dz,$$ (4)

where Δϕ₀(z) describes intrinsic misalignment of nonidentical helices associated with sequence-related differences in their basepair stacking.

$$l_p^h=\frac{C_t{C}_s}{\left(C_s+{\left(2\pi /H\right)}^2{C}_t\right)k_{\text{B}}T}$$ (5)

is the helical persistence length of the molecules, and C_t and C_s are the torsional and stretching elasticity moduli, respectively (20). For B-DNA, k_BT/C_t ≈ $k_{\text{B}}T{\left(2\pi /H\right)}^2/C_s$ ≈ 1.4 × 10⁵ cm⁻¹ (24,25) and $l_p^h$ ≈ 350 Å. Here we consider only interactions between parallel, identical helices, for which Δϕ₀(z) = 0. This is the case in most experimental studies of oligonucleotide nucleic acids.

Interaction free energy

The free energy of pair interaction between two parallel helical oligonucleotides at an interaxial separation R may thus be calculated as

$$\frac{F\left(R\right)}{k_{\text{B}}T}=-\text{ln}\left[\frac{\int D\left\{\Delta \varphi \left(z\right)\right\}\text{exp}\left(-\frac{E_{\mathrm{int}}+E_{\Delta \varphi }}{k_{\text{B}}T}\right)}{\int D\left\{\Delta \varphi \left(z\right)\right\}\text{exp}\left(-\frac{E_{\Delta \varphi }}{k_{\text{B}}T}\right)}\right],$$ (6)

where D{Δϕ(z)} indicates functional integration over all possible trajectories of Δϕ(z) and the reference state for the free energy is at infinite R (E_int = 0). Calculation of these functional integrals, which follows the variational trial-function approach proposed in Lee et al. (20), is described in the Supporting Material.

To calculate the free energy of aggregates we utilize the approach proposed in Cherstvy et al. (26), which accounts for both pairwise-additive and nonadditive interactions (see Eqs. S40–S42 in the Supporting Material). In this case, it is also important to account for renormalization of the screening length κ due to increased concentration of free counterions in the aggregate compared to the surrounding solution (see Eq. S41 in the Supporting Material); we do this renormalization here using the scheme suggested in Cherstvy et al. (26).

Results

B-DNA

Fig. 2 illustrates main features of electrostatic interactions between nucleic acid oligomers predicted by our theory, using the example of 50-bp, double-stranded B-DNA. The interaction becomes attractive once a sufficient fraction of phosphate charge is neutralized by counterions bound in the grooves. The attraction results from zipper-like alignment of negatively charged phosphate strands with positively charged counterions bound in grooves of the opposing molecule (Fig. 1), as predicted earlier for long DNA double helices (7,14). Preferential counterion binding in the major groove favors the attraction between B-DNA helices (Fig. 2 B). Depending on the extent of phosphate charge neutralization and counterion partitioning between the grooves, the attraction may become strong enough to drive aggregation of the molecules (Fig. 2 D).

Figure 2.

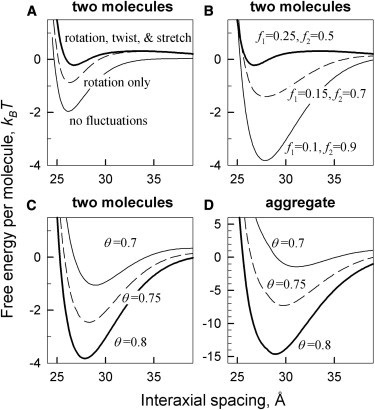
Free energy of interaction between 50 bp B-DNA double helices at 7 Å Debye screening length. (A) Effects of thermal rotation, twisting, and stretching of the helix on the pair interaction energy (θ = 0.8, f₁ = 0.25, f₂ = 0.5). (B) Effects of bound counterions partitioning between the middle of the minor groove (f₁), middle of the major groove (f₂), and random locations (1–f₁–f₂) on the pair interaction energy (θ = 0.8). (C and D) Interaction free energy per molecule in DNA pairs (C) and hexagonal, columnar aggregates (D) at different neutralization of DNA charge (θ) by bound counterions (f₁ = 0.1, f₂ = 0.9). (B–D) We accounted for thermal rotation, twisting, and stretching of the helix, using $l_p^h$ = 350 Å helical persistence length.

Thermal fluctuations in the helical pitch (twisting and stretching of the helices) diminish the attraction by disrupting the zipper alignment. For long helices, this effect of pitch fluctuations is small (7). For oligonucleotides, it may be large (Fig. 2 A). Depending on the oligonucleotide length and partitioning of bound counterions, it may completely wipe out the attraction. Because pitch fluctuations affect higher helical harmonics of the surface charge density more than lower harmonics, their effect depends on counterion partitioning between the grooves.

Thermal rotations of oligonucleotides as a whole about their long axes may diminish the attraction even more than pitch fluctuations (Fig. 2 A). Unlike pitch fluctuations, they do not involve costly elastic deformations. The cost of rotations is associated only with intermolecular interaction. It is proportional to the length of the molecules and becomes prohibitively high for long DNA molecules, but for shorter oligonucleotides it is comparable to or even smaller than the thermal energy, k_BT.

The conditions for energetically favorable formation of multimolecular aggregates are similar to those at which two molecules begin experiencing net attraction in solution (see Fig. 2, C and D). Hence, a simpler calculation of the threshold for pairwise attraction in solution is sufficient for qualitative evaluation of the conditions for counterion-induced aggregation. Yet, above this attraction threshold, the energy gain per molecule is dramatically larger in hexagonal, columnar aggregates, suggesting that oligonucleotide pairing should not occur below the aggregation threshold. The underlying reason is that six pairwise interactions result in larger net interaction energy per molecule and stronger suppression of thermal fluctuations in aggregates. This effect is partially counterbalanced by shorter effective screening length, 1/κ, due to counterion accumulation inside aggregates (26). The shorter screening length might significantly weaken attractive electrostatic interactions when a smaller fraction, θ, of DNA charge, is neutralized by bound counterions.

dsRNA

Fig. 3 compares the interaction free energy for a pair of B-DNA oligonucleotides with that for a pair of dsRNA, calculated for oligonucleotide lengths and electrolyte concentrations corresponding to the conditions of experiments reported in Li et al. (16). Based on the observed preferential binding of cobalt-hexamine (27–31), we plotted the predictions of our theory for 90% localization of the bound counterions in the major groove. Overall, B-DNA condensation is strongly favored whereas dsRNA condensation is not, as long as 70% or more counterions bind in the major groove. In contrast, dsRNA condensation is favored whereas B-DNA condensation is not by preferential counterion binding in the minor groove.

Figure 3.

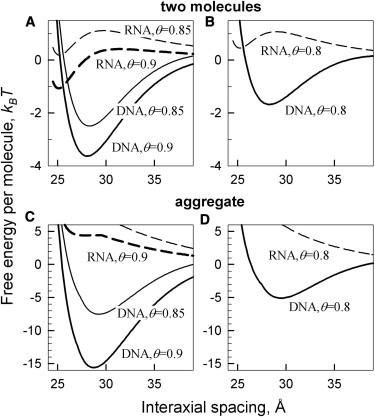
Preferential counterion binding in the major groove favors condensation of B-DNA but not double stranded A-RNA. (A) Interaction free energy per molecule in pairs of 25-bp A-RNA (dashed lines) and 25 bp B-DNA (solid lines) in 20 mM NaCl, 5 mM cobalt hexamine (cohex) calculated at 85% (θ = 0.85) and 90% (θ = 0.9) of DNA and RNA charge neutralization by cohex ions preferentially bound in the major groove (90% in the major groove and 10% in the minor groove). (B) Interaction free energy per molecule for the same pairs in 100 mM NaCl and 0.8 mM cohex, calculated assuming the same 90/10% partitioning of the ions between the major and minor grooves but lower θ. (C and D) Free energy per molecule in hexagonal, columnar aggregates of 25-bp A-RNA (dashed lines) and 25-bp B-DNA (solid lines) at the same conditions as in panels A and B, respectively.

The opposite behavior of B-DNA and dsRNA results primarily from the difference in the relative width of their minor and major grooves. The major groove of B-DNA is ∼50% wider than the minor one. The major groove of dsRNA is almost 50% narrower than the minor groove. Preferential localization of bound counterions in the middle of the wider groove results in a larger separation between positive and negative charges along the molecule, which leads to a stronger electrostatic zipper attraction. In addition, such counterion localization favors an azimuthal alignment of the molecules that is more compatible with the symmetry of hexagonal aggregates (7). The combination of these two factors promotes condensation of double helices upon counterion binding in the wider groove and inhibits the condensation upon counterion binding in the narrower groove. Counterion adsorption in the major grove thus induces condensation of double stranded B-DNA, whereas dsRNA resists condensation by such counterions.

tsDNA

Binding of the third oligonucleotide strand in the middle of the major groove of B-DNA, which produces tsDNA molecules, has two major effects on intermolecular interactions (Fig. 4):

Figure 4.

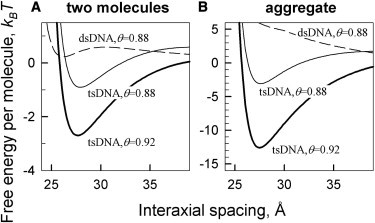
Preferential binding of Mg²⁺, Ba²⁺ and Ca²⁺ in the minor groove promotes condensation of triple-stranded but not double-stranded DNA. (A) Free energy of pair interaction per one molecule calculated for 10 mM divalent ion concentrations in 10 mM Tris, 1 mM EDTA, assuming that 60% of bound divalent counterions are located in the middle of the minor groove with the rest located at random sites on DNA surface. The ionic strength of the Tris/EDTA buffer has only a small effect on the interaction energy. The values of θ were calculated from the Onsager-Manning theory for divalent ions, $\theta =1-l_c/2l_{\text{B}}$, yielding θ ≈ 0.88 for double-stranded DNA (l_c ≈ 1.7 Å) and θ ≈ 0.92 for triple-stranded DNA (l_c ≈ 1.1 Å). The curve for tsDNA calculated at the value of θ expected for dsDNA is shown to demonstrate the relative contribution of the phosphate charge pattern in tsDNA condensation, but for practical purposes only the dashed and bold lines should be compared. (B) Free energy per molecule in hexagonal, columnar aggregates calculated at the same conditions as in panel A.

One effect is that the third strand increases the axial charge density by >50%, enhancing counterion condensation/binding to DNA surface. For instance, the value of θ predicted by the Onsawa-Manning theory at low ionic strength is θ = 1−l_c/ql_B, yielding θ ≈ 0.88 for B-DNA (l_c ≈ 1.7 Å) and θ ≈ 0.92 for tsDNA (l_c ≈ 1.1 Å) in the case of divalent counterions (q = 2). Stronger counterion condensation/binding promotes intermolecular attraction and aggregation of the molecules.

The other effect is that the third strand nearly equalizes the widths of the grooves (Table 1). In this case, preferential counterion adsorption in any one of the grooves favors intermolecular attraction and similar azimuthal orientation of all molecules, which can be easily accommodated in columnar aggregates.

These two effects might lead, e.g., to condensation of tsDNA by divalent counterions that preferentially bind in the minor groove, as discussed below.

Discussion

From the perspective of experimentally distinguishable predictions, it is useful to categorize proposed condensation mechanisms based on the following concepts of attractive interactions between nucleic acids that might be induced by counterions:

Bridging by counterions that are bound to two or more nucleic acid molecules (10) or form a condensed, liquid-like layer shared by these molecules (32). This interaction is most susceptible to changes in counterion dimensions. It is likely to be dominant in the case of very large counterions, such as poly(amido amine) dendrimers (33).

Counterion-correlation attraction between juxtaposed negatively charged phosphates and positively charged bound counterions that are spatially separated on the surface of each molecule due to repulsion between the counterions (12,13) or fluctuations in their density (11,34,35). This attraction originates from and depends strongly on interactions and resulting correlations between bound counterions that move freely along nucleic acid surfaces. Theoretically, it is expected to be dominant for point-like multivalent counterions that do not have strong preferential binding sites (7,36).

Electrostatic zipper attraction between juxtaposed helical phosphate strands and counterions in nucleic acid grooves (14). This attraction requires efficient zipper-like alignment of the strands with opposing grooves. It depends strongly on the nucleic acid structure and is expected to be dominant in the case of significant preferential counterion binding in nucleic acid grooves (7).

Our previous analysis of the published data suggested that preferential counterion binding in grooves might be the most prominent observed feature, likely responsible for differences in the ability of similarly charged but chemically or structurally different counterions to induce DNA condensation (7). Comparison of calculated and measured forces between B-DNA molecules supported the dominant role of this mechanism in DNA condensation by many counterions (20). Yet, interpretations of the same experiments based on the other two mechanisms could not be excluded (2–4,7).

Below we discuss studies of oligomeric dsDNA, tsDNA, and dsRNA as well as studies of counterion charge, structure, and chemistry effects on condensation of longer dsDNA, which are more recent and provide more data for discriminating between predictions of different theories. In our analysis, these studies show that zipper-like juxtaposition of phosphate strands with groove counterions is a major factor in nucleic acid condensation, although they do not resolve whether electrostatic or hydration forces, for which the predictions are similar (7,37), cause the zipper attraction.

Interaction between B-DNA oligonucleotides linked into pairs by flexible linkers at counterion concentrations below DNA condensation threshold

The authors of this study investigated effects of spermidine³⁺ on interactions between double helices within linked pairs of 12-bp oligonucleotides and linked pairs of 80-bp oligonucleotides (18). They observed aggregation of the pairs above a threshold spermidine³⁺ concentration, but no significant association between the helices within each pair below the threshold. For 12-bp oligonucleotides, they estimated that the lack of any observable association below the aggregation threshold means that the attraction between the helices within each pair must be <0.1–0.2 k_BT/bp. Bai et al. (18) hypothesized that “more than two neighboring helices are required to generate a pronounced attraction” needed for DNA aggregation observed in their own and multiple other studies.

Our predictions for the free energy per molecule in a pair (Fig. 2, B and C) and columnar aggregate (Fig. 2 D) provide a theoretical foundation for this idea, revealing the nature of complex many-body effects in aggregates. The aggregation occurs once the energy benefit per molecule exceeds several k_BT. Because the attractive energy per molecule is several times lower in a pair than in an aggregate (Fig. 2, C and D), the predicted pairwise attraction below the aggregation threshold is <1 k_BT per total length of the double helices (50 bp in the case illustrated in Fig. 2). This energy is consistent with the maximum attractive energy estimated in Fig. 6 of Bai et al. (18) and it is not sufficient to overcome the entropy loss upon the association of either 12- or 80-bp oligonucleotide pairs connected by flexible linkers.

Our calculations predict stable pairing below or near the aggregation threshold only for much longer DNA molecules, which are capable of forming braids that optimize chiral electrostatic interactions (38). For oligomeric molecules, stable association requires multiple pairwise attractions per molecule in columnar assemblies. Our calculations show that the cumulative effect of these attractions overcomes the entropy loss and the osmotic pressure of free counterions that make the aggregate electroneutral, provided that at least 80–90% of the DNA’s negative charge is compensated by bound counterions (as required for the condensation (1)).

Resistance of dsRNA to condensation at cobalt-hexamine³⁺ concentrations that condense dsDNA

This observation cannot be explained by theories of electrostatic interactions that do not account for the structure of nucleic acids and approximate them as featureless, homogeneously charged cylinders (16). In such theories, nucleic acid condensation propensity is determined by counterions, which are expected to exhibit stronger binding and correlations at surfaces of more charged molecules (see, e.g., Kornyshev et al. (7) and Grosberg et al. (36) and references therein). Both axial and surface densities of phosphate charge are higher in dsRNA than double-stranded B-DNA (Table 1), and bound counterions do appear to screen dsRNA charge more efficiently than B-DNA (39). Therefore, the observation of the resistance of dsRNA to condensation by cobalt-hexamine³⁺ prompted its authors to seek an alternative explanation. In particular, they suggested that this resistance might be related to cobalt-hexamine³⁺ binding inside the narrow cleft in the major groove of dsRNA, so that the counterions are buried deep inside the core of the molecules and cannot effectively balance the surface charge of phosphates (16). However, in view of the analysis presented above, there is no longer a need in this assumption.

The depth of cobalt-hexamine³⁺ location in the major groove may affect interactions between dsRNAs, but our calculations suggest an immediate, simpler explanation for the differences in the condensation propensities of dsRNA and B-DNA. This explanation is based on assuming that the stereochemistry of cobalt-hexamine³⁺ interaction with nucleic acid bases leads to its preferential binding in the major groove of both dsRNA, as reported in Davis et al. (27), Kieft and Tinoco (28), and Rüdisser and Tinoco (29), and B-DNA, as reported in Ouameur and Tajmir-Riahi (30) and Robinson and Wang (31). The difference in the condensation of these molecules by cobalt-hexamine³⁺ is then caused by the difference in the relative widths of their major grooves (Fig. 3). The condensation of oligomers (as well as longer nucleic acids) is promoted by counterion binding in the wider groove, which enhances the electrostatic zipper attraction. In B-DNA, the major groove is wider than the minor one. In dsRNA, the major groove is narrower than the minor one. Less favorable electrostatic zipper interaction upon cobalt-hexamine³⁺ binding in the narrower groove rationalizes why dsRNA resists the condensation (Fig. 3).

Condensation of tsDNA by Mg²⁺, Ba²⁺, and Ca²⁺ ions that do not condense dsDNA

This observation might be explained by several different contributing factors, as noted by its authors (17). Our calculations point to two such factors, which might contribute almost equally (Fig. 4):

The first factor is higher charge of tsDNA leads to stronger binding of divalent ions to its surface, weakening the repulsion associated with the net charge (charge of the molecules plus bound counterions) and enhancing the electrostatic zipper attraction associated with helical patterning of this charge. Enhancement of the zipper attraction is a straightforward consequence of more bound counterions, which are responsible for this force. The reason behind weakening of the repulsion between higher charged molecules is less intuitive. Onsager-Manning theory predicts counterion binding that ensures the same net axial charge density (phosphates plus bound counterions) regardless of the phosphate density (40). The same axial density means that the surface density of the net charge should be lower on tsDNA compared to dsDNA, because the former has a larger radius. Lower surface charge density leads to weaker electrostatic repulsion at the same surface-to-surface separation between the molecules.

The second factor is geometry of the three tsDNA grooves, which have similar yet not identical widths (Table 1). Counterion binding in the middle of one of these grooves is likely to provide more favorable salt-bridge interactions with phosphates, with which alkaline earth metal ions form poorly soluble salts. Provided that these ions do bind preferentially in the minor groove of B-DNA (41) and in one of the three grooves of tsDNA, we expect stronger electrostatic zipper attraction and condensation of tsDNA but not dsDNA oligonucleotides (Fig. 4). Interestingly, putrescine²⁺ ions do not condense either tsDNA (17) or B-DNA (42). Within our theory, this might be explained by insufficient preferential groove partitioning of these organic ions, which have very different chemical natures, structures, and interactions with phosphates than alkaline earth metal ions. Yet, we agree with the tsDNA study authors that further experiments are needed to unambiguously resolve the condensation mechanism.

We should note that bridging by divalent alkaline earth metal ions and side-by-side aggregation of 10-bp dsDNA oligonucleotides was predicted by computer simulations in Luan and Aksimentiev (43). However, experimental studies provide evidence only for end-to-end attraction and stacking of dsDNA oligonucleotides in solutions of these ions (44–46).

Condensation of short versus long nucleic acids

The only distinction of oligonucleotides in our theory is more pronounced independent thermal rotation of each molecule about its axis compared to longer nucleic acid molecules. Such rotations affect the zipper-like alignment of phosphates and counterions, altering the requirements for counterion-induced condensation. In the case of longer nucleic acids, they are suppressed by prohibitively large energetic cost associated with the loss of electrostatic zipper attraction.

Because the cost of thermal rotations depends not only on the length of the molecules but also on counterion binding and partitioning, the resulting differences in predictions for shorter and longer molecules are significant in some but not all cases. For instance, our calculations predict weak zipper attraction upon preferential counterion binding in the narrow groove, resulting in low energetic cost and a strong effect of thermal rotations on interactions between short double helices. The rotations further suppress the attraction, making 25-bp dsRNA molecules resistant to condensation by cobalt hexamine (Fig. 3). In contrast, preferential counterion binding in the wider groove strengthens the zipper attraction, increasing the cost and suppressing thermal rotations. We expect interactions between 25-bp B-DNA double helices and interactions between much longer B-DNA molecules to be similar in the presence of such counterions, e.g., consistent with observations for B-DNA condensation by spermine and spermidine (8,47,48).

It is also important to note that interactions between molecules shorter or comparable in length with the helical pitch (∼10 or fewer basepairs or triplets) might be affected by edge effects not incorporated into the theory. Nevertheless, our theory might work qualitatively even for these molecules, because of their tendency toward end-to-end stacking (44–46,49).

Effects of counterion charge, chemistry, and structure on condensation of long dsDNA molecules

Preferential counterion binding seems to explain not only how structures of different nucleic acid molecules affect their condensation but also how counterion structure and chemistry affect condensation of the same dsDNA molecules. In particular, we previously argued that preferential binding in the major groove might be responsible for the ability of divalent transition (versus alkaline earth) metal ions and some (but not all) polyamine ions to induce dsDNA condensation (7). A number of more recent observations lend further support to this hypothesis.

In particular, different effects of various chiral isoforms of methylated spermidine³⁺ and spermine⁴⁺ on DNA condensation (50) are difficult to explain without assuming preferential adsorption of these counterions at specific sites. Similar critical fraction of charge neutralization required for DNA condensation by ε-oligolysines with different length and charge (51) is consistent with the electrostatic zipper attraction, assuming similar partitioning of these ions between DNA grooves. It is not consistent with the other attraction mechanisms, because ε-oligolysines that vary from 3 to 31 residue length and from 4+ to 31+ charge are unlikely to exhibit similar counterion correlations and ability to bridge adjacent DNA molecules. Forces measured between DNA molecules condensed by polyarginines are also more consistent with predictions for zipper-like alignment and resulting electrostatic or hydration attraction between phosphate strands and counterions bound in the major groove (52,53).

Effects of intermolecular interaction on counterion binding pattern

Because preferential counterion adsorption significantly affects intermolecular interactions, the interactions might affect the counterion binding pattern as well (7,26). Here, we do not explicitly describe the latter effect, because we expect the interaction energy to be insufficient for overcoming the cost of relocating the counterions away from their preferential binding sites in most cases of nucleic acid condensation into hydrated aggregates. For instance, our calculations predict more favorable interactions between oligonucleotide double helices in hydrated aggregates when counterions are located in the wider groove (Fig. 3). Yet, they show that the interaction energy benefit of relocating to the wider minor groove of dsRNA is <1 k_BT per counterion and likely insufficient for overcoming preferential cobalt-hexamine binding in the major groove.

Counterions with weak or no preference for binding in a specific groove might relocate upon nucleic acid aggregation, e.g., such relocation might contribute to condensation of B-DNA by Mn²⁺ at elevated temperatures (26). However, detailed analysis of such counterion relocation is more complicated and beyond the scope of this study.

More importantly, intermolecular interactions might significantly affect counterion binding locations in nucleic acid crystals, in which these interactions are much stronger and favor different counterion binding patterns. In particular, our calculations show that interactions between very closely packed and immobilized B-DNA molecules in crystals are optimized by counterion binding in the narrower rather than wider groove, in contrast to hydrated aggregates. Smaller separation between the negative and positive charges upon narrow groove binding produces a shorter-range electric field that leads to more favorable electrostatic interactions in crystals. The corresponding energy benefit per ion is particularly large when longer polypeptides with multiple positively charged residues bind in the minor rather than major groove of B-DNA. It might explain, e.g., why arginine-containing polypeptides expected to bind in the major groove of fully hydrated DNA (52,53) are found in the minor groove of deformed DNA in nucleosome crystals (54).

Hybrid condensation mechanisms

X-ray structures of nucleosome crystals also illustrate that different mechanisms of counterion-mediated attraction between nucleic acids might sometimes represent different facets of the same interaction. These structures reveal zipper-like alignment of positively charged histone tails bound in the minor groove and phosphate strands on the opposing double helix surface (55,56). Yet, DNA packing in nucleosome crystals is so close that it is difficult to distinguish whether histone tails bind in the groove between two phosphate strands of one double helix and attract phosphate strands on the other helix or whether they bridge all strands together.

Overall, separation of distinct nucleic acid condensation mechanisms is certainly useful for conceptual clarity. However, depending on specific circumstances, several mechanisms might operate at the same time and even blend together. In another example, point-like 3+ or higher valence ions might mediate attraction by binding along helical strands of phosphate charges in a manner that blends together counterion-correlation attraction and zipper-like alignment of charges on opposing surfaces, as suggested by recent calculations (57–59).

Conclusions

• 1.Because of inaccuracies inherent in any theory, simulation, or measurement of mesoscopic phenomena, comparison of conceptual predictions and observations in a wider variety of nucleic acid condensation studies is more revealing than parsing of finer details of any specific calculation or experiment.
• 2.The common theme emerging from experimental studies is that condensation efficiency depends strongly on the nucleic acid structure and preferential counterion binding at specific sites, which are the distinguishing features of the electrostatic zipper attraction.
• 3.The concept of electrostatic zipper attraction appears to explain a wide variety of observations, including the most puzzling features of oligonucleotide condensation that are difficult to interpret otherwise.
• 4.The major role of this interaction in nucleic acid condensation does not exclude contributions from bridging by counterions or counterion-correlation attraction, which might become significant under some circumstances.

Revisiting the concept of electrostatic zipper attraction between helical molecules was motivated by the revival of interest in counterion-induced condensation of different nucleic acids, particularly oligomeric nucleic acids whose interactions can be better characterized experimentally and computationally. We believe that the statistical mechanical theory of interaction and aggregation of such molecules developed in this study provides a useful basis for interpreting the results of such studies.