Fractional Ca²⁺ Currents through TRP and TRPL Channels in Drosophila Photoreceptors

Abstract

Light responses in Drosophila photoreceptors are mediated by two Ca²⁺ permeable cation channels, transient receptor potential (TRP) and TRP-like (TRPL). Although Ca²⁺ influx via these channels is critical for amplification, inactivation, and light adaptation, the fractional contribution of Ca²⁺ to the currents (P_f) has not been measured. We describe a slow (τ ∼ 350 ms) tail current in voltage-clamped light responses and show that it is mediated by electrogenic Na⁺/Ca²⁺ exchange. Assuming a 3Na:1Ca stoichiometry, we derive empirical estimates of P_f by comparing the charge integrals of the exchanger and light-induced currents. For TRPL channels, P_f was ∼17% as predicted by Goldman-Hodgkin-Katz (GHK) theory. P_f for TRP (29%) and wild-type flies (26%) was higher, but lower than the GHK prediction (45% and 42%). As predicted by GHK theory, P_f for both channels increased with extracellular [Ca²⁺], and was largely independent of voltage between –100 and –30 mV. A model incorporating intra- and extracellular geometry, ion permeation, diffusion, extrusion, and buffering suggested that the deviation from GHK predictions was largely accounted for by extracellular ionic depletion during the light-induced currents, and the time course of the Na⁺/Ca²⁺ exchange current could be used to obtain estimates of cellular Ca²⁺ buffering capacities.

Introduction

Light activation of fly photoreceptors leads to the opening of two classes of Ca²⁺ permeable cation channels, transient receptor potential (TRP) and transient receptor potential-like (TRPL), via a G-protein-coupled PLC signaling cascade (1,2–4). Both the channels and upstream signaling elements are localized within the rhabdomere, a rod-like stack of ∼35,000 tightly packed microvilli, 1–2 μm in length and 60 nm in diameter. The Ca²⁺ influx associated with the light response accounts for virtually all of the light-induced Ca²⁺ rise in the photoreceptor (5–7) and is proposed to transiently reach near-millimolar levels within individual microvilli in response to single-photon absorptions (8,9). The Ca²⁺ influx is critical for response amplification, inactivation, and light adaptation, and mediates sequential positive and negative feedback via multiple molecular targets (10–12). These include the light-sensitive channels, which are both positively and negatively regulated by Ca²⁺ (12–14), and PLC (12,15) and metarhodopsin (16), which are both inhibited by Ca²⁺ influx. The resulting light response in flies represents the fastest known G-protein-coupled signaling cascade and has a huge dynamic range, from single photon responses (quantum bumps) to full daylight (17,18). This performance, which outstrips that of any vertebrate photoreceptor, has inspired a number of computational models that attempt to account for the light response in terms of the underlying molecular mechanisms (4,19–21).

A key parameter in such models is the amount of Ca²⁺ that enters into individual microvilli via the light-sensitive channels. This requires knowledge of the fraction of light-induced current (LIC) that is carried by Ca²⁺, i.e., the fractional Ca²⁺ current, P_f (22). P_f has never been directly measured, and previous estimates have relied upon theoretical values calculated from relative ionic permeabilities using the Goldman-Hodgkin-Katz (GHK) current equation (Eq. 1). However, it is questionable whether the independent mobility of ions, a central assumption of GHK theory (23), holds true for the light-sensitive channels, which show complex permeation and divalent ion block (24–26). In addition, the LIC can be so large that there may be significant changes in ionic gradients during the response.

For technical reasons, standard approaches for measuring P_f (22) are impractical for fly photoreceptors. In this study, we developed a novel (to our knowledge) approach that exploits the native electrogenic Na⁺/Ca²⁺ exchanger (CalX), which extrudes 1 Ca²⁺ ion for the entry of 3 Na⁺ ions (27–29). Using whole-cell recordings, we observed a distinct slow aftercurrent in response to bright flashes, which we attribute to electrogenic Na⁺/Ca²⁺ exchange. Under the assumption that this tail current represents the extrusion of Ca²⁺ that entered through the TRP and/or TRPL channels, we estimated empirical P_f values for TRP and/or TRPL channels from the ratio between the charge carried by the LIC and the exchanger current. Empirical P_f values for TRPL channels closely matched the simple GHK prediction (P_f ∼17%) but were somewhat below the prediction for TRP channels (empirical P_f ∼29%, compared with ∼45% for GHK-P_f). A detailed model incorporating intra- and extracellular geometry, ion permeation, diffusion, extrusion, and buffering suggested that the deviation from the GHK prediction could be largely accounted for by extracellular ionic depletion during the large LIC, and the time course of the Na⁺/Ca²⁺ exchange tail current could be used to obtain estimates of cellular Ca²⁺ buffering capacities.

Materials and Methods

Flies

Flies (Drosophila melanogaster) were reared at 25°C in the dark. The wild-type (WT) strain was Oregon. The mutants used included trp³⁴³ and trpl³⁰², null alleles of TRP and TRPL channels, respectively (30,31); calx^A, a loss-of-function mutation of the Na⁺/Ca²⁺ exchanger (29); and dSK, a deletion of the dSK gene encoding a small-conductance, Ca²⁺-activated K channel (32).

Whole-cell electrophysiology

Dissociated ommatidia were prepared from newly eclosed flies as described previously (33) and transferred to a recording chamber on an inverted Nikon Diaphot microscope (Nikon, Kingston-upon-Thames, U.K.). The standard bath contained (in mM) 120 NaCl, 5 KCl, 10 N-Tris-(hydroxymethyl)-methyl-2-amino-ethanesulphonic acid, 4 MgCl₂, 1.5 CaCl₂, 25 proline and 5 alanine, pH 7.15. The intracellular pipette solution was 110 Cs gluconate, 15 TEACl, 10 N-Tris-(hydroxymethyl)-methyl-2-amino-ethanesulphonic acid 4 Mg-ATP, 2 MgCl₂, 1 NAD, and 0.4 Na-GTP, pH 7.15 (adjusted with CsOH). Chemicals were obtained from Sigma-Aldrich (Gillingham, U.K.). Whole-cell voltage-clamp recordings were made at room temperature (20°C ± 1°C) at –70 mV unless otherwise stated (including correction for a –10 mV junction potential) using electrodes of resistance ∼10–15 MΩ. Series resistance values were generally <30 MΩ and were compensated to >80%. Data were collected and analyzed using an Axopatch 2D amplifier and pCLAMP9 software (Molecular Devices, Union City, CA). Photoreceptors were stimulated via green-light-emitting diodes, and intensities were calibrated in terms of effectively absorbed photons by counting quantum bumps at low intensities.

Measurement of P_f

Assuming that Ca²⁺ ions that enter through light-activated channels are all extruded by the CalX exchanger, the fractional Ca²⁺ current (P_f) can be calculated from the charge ratio of the total LIC and the extruded Ca²⁺. The onset of the Na⁺/Ca²⁺ exchange current is masked by the much larger LIC, and we estimated this hidden component by extrapolating an exponential fit back to the time of the peak response (Fig. 1 B). This would have introduced an error of <5% compared with more sophisticated modeling of the CalX current based on the overall response waveform (Fig. S2 in the Supporting Material). The charge integral of the LIC was calculated by subtracting the estimated CalX charge integral from the charge integral of the entire response. Assuming a stoichiometry of 3 Na⁺ to 1 Ca²⁺, the charge integral of the tail current was multiplied by two to correct for the divalency of the extruded Ca²⁺ ions and divided by the LIC charge integral to obtain an empirical estimate of P_f.

Figure 1.

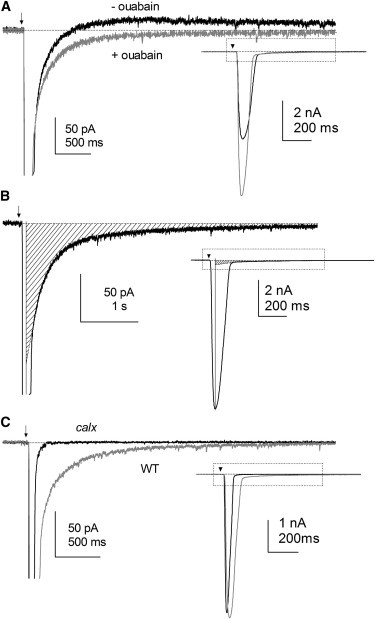
Light-induced tail currents in Drosophila photoreceptors. (A) Whole-cell voltage-clamped recording from WT photoreceptor at −70 mV to bright flashes (5 ms, ∼17,500 effective photons; arrow) in the presence (gray trace) and absence (black trace) of 100 μM ouabain in normal bath (1.5 mM Ca²⁺). A small, slow, outward aftercurrent (maximally ∼30 pA) due to electrogenic Na⁺/K⁺ ATPase, was eliminated by ouabain. Inset: scaled to show entire response. (B) Measurement of the Na⁺/Ca²⁺ exchange tail current in presence of ouabain (recording from the trpl mutant). The onset of the tail current is masked by the much larger LIC; this hidden component was estimated by extrapolating an exponential back to the time of the peak response and the charge integral measured (shaded area). (C) Responses to flashes containing ∼17,500 photons in WT and calx mutants in the presence of ouabain. The conspicuous tail current was absent in calx mutants.

Theoretical fractional currents

In the first instance, we compared the experimentally measured fractional Ca²⁺ current (P_f) values with theoretical predictions based on ionic permeability ratios using the GHK current equation (Eq. 1), which specifies the current (I) across the membrane carried by ion species S with charge z_s:

$$I_S=P_S{z}_S^2\frac{E_m{F}^2}{RT}\frac{{\left[S\right]}_i-{\left[S\right]}_o\text{exp}\left(-z_s{E}_{m}F/RT\right)}{1-\text{exp}\left(-z_s{E}_{m}F/RT\right)}$$ (1)

where E_m denotes membrane voltage, R is the gas constant, T is temperature (K), and F is the Faraday constant. [S]_i and [S]_o respectively denote the intra- and extracellular concentrations of ion S, and P_s is its permeability. [Ca²⁺]_i was taken as 160 nM in dark-adapted photoreceptors (7), other values from the experimental solutions. Under physiological conditions, the total LIC is carried by four main cations (Na⁺, K⁺, Ca²⁺, and Mg²⁺) (14):

$$I_{total}=I_{Na}+I_K+I_{Ca}+I_{Mg}$$ (2)

Table 1 shows theoretical P_f values for the WT and trp and trpl mutants in a standard bath based on Eq. 1 using published ionic permeability ratios (14,26).

Table 1.

Permeability ratios and theoretical P_f values of channels

Channels	PCa/PCs	Permeability ratios		a PK/PCs	Pf (%)
		PMg/PCs	PNa/PCs
TRP (in trpl)	57.0	15.8	1.27	1.27	45.2
TRPL (in trp)	4.3	1.4	0.84	0.84	17.0
TRP+TRPL (in WT)	27.6	5.7	1.16	1.16	41.6

Permeability ratios (P_X/P_Cs) derived from reversal potential data (14,26). TRP channels were measured in trpl mutants, and TRPL channels were measured in trp mutants. The final column gives the fractional Ca²⁺ current (P_f) predicted by the GHK current equation (Eq. 1) at –70 mV expressed as the percentage of total LIC. P_Na/P_K was assumed to be 1.0.

^aUnder the experimental conditions, intracellular K⁺ was substituted with Cs⁺; P_K was not directly measured due to the large voltage-sensitive K⁺ currents in Drosophila photoreceptors. However, increasing or decreasing the permeability ratio of K⁺ by 2-fold had a negligible effect on predicted P_f in otherwise physiological solutions.

Results

Na⁺/Ca²⁺ exchange tail current

In whole-cell, voltage-clamped recordings from Drosophila photoreceptors, the responses to brief, intense flashes exhibit a distinct slow, inward tail current of ∼100 pA (Fig. 1 A). Because the photoreceptors express high densities of an NCX electrogenic Na⁺/Ca²⁺ exchanger, encoded by calx (28,29,34,35), we suspected that this tail current was an electrogenic Na⁺/Ca²⁺ exchange current. A slowly inactivating depolarizing afterpotential with similar kinetics was previously reported in intracellular recordings from larger flies and also attributed to electrogenic Na⁺/Ca²⁺ exchange (36,37).

In principle, the charge integral of such an exchange current can be used to estimate the amount of Ca²⁺ that is extruded from the cell; however, this assumes that there are no other ionic fluxes that might otherwise overlap the putative Na⁺/Ca²⁺ exchange current. In fact, the tail current of the photoresponse is normally also associated with a small outward component that develops slowly and decays over several seconds. This current is attributable to a Na⁺/K⁺ ATPase (4,37,38) and was completely abolished by 100 μM ouabain (Fig. 1), which we therefore used in all quantitative experiments.

To test more rigorously whether the tail current represents CalX exchanger activity, we examined light responses in calx^A loss-of-function mutants. As previously reported (29), photoreceptors from calx^A mutants have reduced sensitivity to light and rapid response kinetics resulting from elevated resting cytosolic Ca²⁺ due to the failure of Ca²⁺ extrusion via CalX. Importantly, the slow inward tail current was absent in calx^A mutants, strongly supporting its identification as the exchanger current (Fig. 1 C).

An alternative explanation for the tail current could be persistent residual activation of the light-sensitive channels. If this were the case, it should show the characteristic pronounced outward rectification and reversal potential (E_rev) of the LIC (E_rev = +12 mV for TRP and –4 mV for TRPL). By contrast, Na⁺/Ca²⁺ exchange currents should show exponential inward rectification (39) and would not be expected to reverse in response to an imposed Ca²⁺ load (11,40). To measure the current voltage (I-V) relationship of the tail currents, we applied voltage steps at the onset of tail current and subtracted a template recorded in the dark (Fig. 2). For comparison, the I-V relationship of the LIC was also measured in response to continuous dim red light illumination. Consistent with the properties of an exchanger, the tail current was inwardly rectifying (Fig. 2 E) and clearly distinct from the strongly outwardly rectifying LIC (Fig. 2, E and F). Nevertheless, a small residual outward component was detected at depolarized voltages beyond +40 mV, possibly reflecting a residual, late inactivating light-induced component. However, this should not contribute significantly to the inward tail current at −70 mV, primarily because of the outward rectification and also because the kinetics of inactivation of the LIC are much faster at negative potentials due to the increased Ca²⁺ influx. Another potential contaminant of this current is the SK channel (small-conductance Ca²⁺-activated K channel), which was recently reported in photoreceptors (32). However, a significant SK contribution can be effectively excluded because the I-V curve of the tail current in sk null mutants (dSK⁻) was indistinguishable from that in the WT, whereas P_f values determined in dSK⁻ flies were similar to those obtained in the WT (see Figs. 4 and 5).

Figure 2.

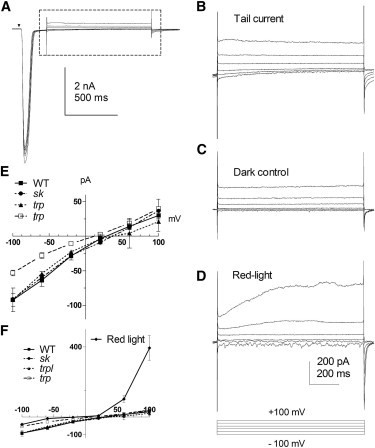
I-V relationships of tail currents. (A) Currents evoked by voltage steps from −100 mV to +100 mV (+40 mV steps) from a holding potential of −70 mV applied during tail currents of responses to flashes (5 ms, ∼17,500 photons) in a trpl mutant. (B) Tail currents from the region indicated on an expanded scale. (C) Dark control currents to the same voltage steps. (D) Under continuous red light illumination, the strongly outwardly rectifying characteristics of the LIC are apparent. (E) I-V relationship of the tail currents obtained after subtracting dark control traces (as in C). The predominantly inward I-V curves of the tail currents are distinct from the strongly outwardly rectifying LIC shown in panel F (including the same tail current data on a different scale). No significant difference was seen among WT (n = 8), dSK⁻ (n = 5), and trpl (n = 2); smaller currents with otherwise similar properties were observed in trp (n = 5).

Figure 4.

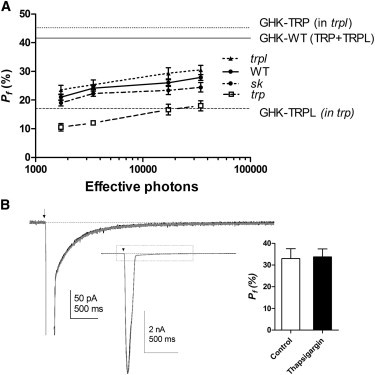
Measurement of fractional Ca²⁺ currents (P_f) through TRP and TRPL channels. (A) Mean P_f values (mean ± SE) are plotted as a function of intensity for TRP channels (isolated in trpl, n = 6), TRPL channels (isolated in trp, n = 8), native TRP+TRPL channels (in WT, n = 20), and TRP+TRPL channels (in dSK⁻, n = 12). Empirical P_f data were obtained from the charge integral ratio between the total LIC and the exchanger tail current (see Materials and Methods), and compared with P_f predictions using the GHK equation (horizontal lines). (B) Responses to 5 ms flashes containing 17,500 photons (arrow) in the trpl photoreceptor were unaffected in the presence of 10 μM thapsigargin for >2–3 min (gray trace) compared with control exposed to vehicle (0.1% DMSO; black trace). The bar graph shows that P_f values in the presence of thapsigargin were indistinguishable from controls (n =3).

Figure 5.

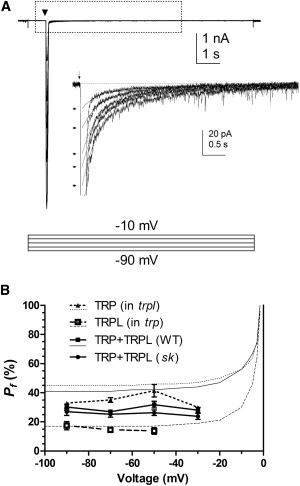
Voltage dependence of P_f. (A) Responses to bright 5 ms flashes (17,500 photons; arrow) in WT photoreceptor subjected to 10 s voltage steps (−90 mV to −10 mV in 20 mV steps) from a holding potential of −70 mV. Inset shows tail currents with exponential fits extrapolated back to time-to-peak of the LIC to estimate peak exchanger current (arrows). (B) P_f values (mean ± SE) as a function of membrane voltage in WT (n = 10), trp (n = 5), trpl (n = 4), and dsK⁻ mutants (n = 7) compared with GHK-P_f (continuous curves). Consistent with theoretical predictions, empirical P_f values were broadly similar over the measured voltage range.

The peak amplitude and charge integral of the inward tail current increased with flashes of increasing intensity (Fig. 3). The peak amplitudes (∼100 pA) activated in WT and trpl were in line with previous measurements of the Na⁺/Ca²⁺ exchange current (11). The peak amplitude of the tail current observed in trp was less than half of those (∼40 pA), as would be expected if TRPL channels had a lower P_f. In all cases, the current decayed with a similar time course, which presumably represents the rate of Ca²⁺ extrusion via the exchanger (Fig. 3 D). In all cases, the time course was well fitted by a single- or double-exponential time course with a dominant time constant (τ₁) of ∼300–400 ms and a minor slower component (τ₂ ∼2 s).

Figure 3.

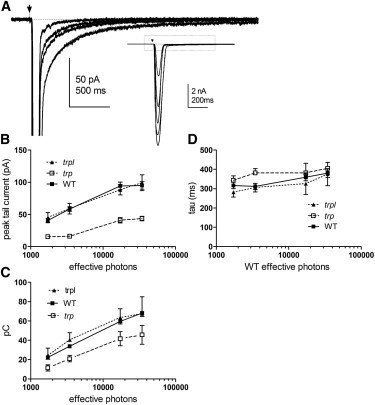
Intensity dependence of Na⁺/Ca²⁺ exchange tail currents. (A) Responses recorded in WT photoreceptor to flashes (arrow) of increasing intensity (350, 1750, 3500, 17,500 and 35,000 effective photons). The inward tail component and main LIC (see inset) both increased with light intensity. (B and C) Mean peak amplitude (B) and charge integral (C) of the tail currents plotted as a function of intensity in WT, trpl, and trp mutants. (D) The single exponential decay time constant (τ) of the inward tail current was similar at all intensities and in different genetic backgrounds (WT, trpl, and trp). Mean values (mean ± SE) for WT (n = 20 cells), trpl (n = 6 cells), and trp (n = 8 cells).

Fractional Ca²⁺ current, P_f

Our method for measuring P_f assumes that all Ca²⁺ entering the cell through light-sensitive channels is extruded by the CalX exchanger. Having identified the slow inward tail current as a Na⁺/Ca²⁺ exchange current, and assuming a stoichiometry of 3 Na⁺:1 Ca²⁺, which is generally accepted for NCX exchangers (27,41), we estimated P_f from the ratio between the total charge integral of the LIC and that of the CalX tail current (see Fig. 1 B).

Fig. 4 shows experimentally obtained values of P_f for TRP and/or TRPL channels from the WT and respective channel mutants compared with GHK predictions over a range of intensities. In principle, assuming the amount of Ca²⁺ extruded by Na⁺/Ca⁺ exchange equals the amount light-induced Ca²⁺ influx (42), P_f might be expected to remain constant with different intensities. However, we found that the empirical P_f values increased slightly with intensity. One factor that might contribute to this is that the exchanger is a low-affinity, high-capacity transporter that is expected to dominate Ca²⁺ homeostasis when Ca²⁺ levels are high: with lower Ca²⁺ levels associated with dimmer flashes, alternative higher-affinity transport and/or Ca²⁺ buffering mechanisms may prevent some Ca²⁺ ions from being immediately extruded by CalX exchange, leading to an underestimation of P_f. One such mechanism is sequestration of Ca²⁺ into smooth endoplasmic reticular (SER) stores by a SER Ca²⁺-ATPase (43). To exclude this possibility, we measured P_f in trpl flies after applying the SERCA pump inhibitor thapsigargin (10 μM) by puffer pipette. No significant differences were found in the properties of either the light response or the CalX-dependent tail current (Fig. 4 B). Nevertheless, we cannot exclude minor contributions of nonelectrogenic Ca²⁺ mechanisms (e.g., plasma membrane Ca-ATPase), mitochondrial Ca²⁺ buffering, or high-affinity buffers that do not release Ca²⁺ on the timescale of the experiments (although we suggest that these may be less significant at higher intensities, where they are likely to be saturated by the higher Ca²⁺ concentrations).

The larger light-induced responses at higher intensities are increasingly subject to series resistance error and deteriorating space clamp, which may result in poor voltage-clamp control (see Discussion). As a compromise, therefore, we used P_f values derived from flashes of submaximal intensity (∼17,500 photons, generating responses of <7 nA) from photoreceptors with optimal series compensation (>80%, R_s < 25 MΩ). On this basis, P_f for TRP channels, isolated in trpl mutants, was 29.3 ± 1.9% (mean ± SE, n = 6), which is substantial but still less than the simple GHK prediction of 45.2%. P_f for TRPL channels isolated in trp (16.6 ± 1.9% n = 8) was very close to the theoretical prediction (GHK-P_f = 17.0%). The WT current, which is mediated by both TRP and TRPL channels, yielded P_f values (26.1 ± 1.0%, n = 20) that were again below prediction (GHK-P_f = 41.6%). P_f in dSk null mutants (23.3 ± 1.5%, n = 12) was not significantly different from that in WT (p > 0.05). The results clearly confirm the higher fractional Ca²⁺ current mediated by TRP channels and support previous studies indicating that the WT LIC is largely carried by TRP under physiological conditions (14,31). Below, we consider the disparity between the empirical measurements and simple GHK predictions for TRP and WT currents by using a detailed modeling approach.

Voltage dependence of P_f

Thus far, P_f values were measured at resting potential (−70 mV); however, in vivo, photoreceptors depolarize in response to light. GHK theory predicts that P_f should vary with the membrane potential because each ion has its own unique reversal potential (E_rev). In addition, factors such as voltage-dependent divalent ion block (24) might influence P_f in a less predictable manner. We therefore measured P_f at different holding potentials. GHK theory predicts that P_f values should be almost constant at negative membrane potentials (−110 to −30 mV), but should tend to 100% near 0 mV as E_rev of monovalent ions is approached, while E_rev for Ca²⁺ remains positive. Unfortunately, we could not obtain accurate measurements at such positive potentials because the tail current was too small; however, within the range that could be tested, P_f was broadly independent of voltage in all genetic backgrounds, consistent with GHK theory (Fig. 5). This also implies that the high fractional Ca²⁺ current through the light-sensitive channels is maintained over most of the physiologically significant voltage operating range.

Ca²⁺ dependence of P_f

P_f is clearly predicted to increase with increasing extracellular Ca²⁺ concentration. To test this, we varied [Ca²⁺]_o without altering other cation concentrations by perfusing cells for 1–3 min using a puffer pipette before delivering test flashes. As previously reported, light responses in high [Ca²⁺]_o had faster time-to-peak and decay times (Fig. 6 A, inset) due to enhanced positive and negative feedback by Ca²⁺ (10). The peak amplitude of the exchanger current also significantly increased when [Ca²⁺]_o was raised, saturating above 3 mM at ∼200 pA in WT and TRPL while continuing to increase up to at least 10 mM in trp mutants (Fig. 6 B). We also noted a change in the kinetics of the tail current, which no longer decayed exponentially at higher [Ca²⁺]_o, but was initially ramp-like, probably indicating saturation of the exchanger rate (Fig. 6 A).

Figure 6.

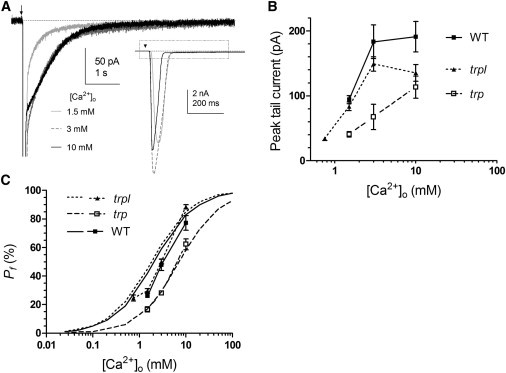
Ca²⁺ dependence of P_f. (A) Responses to 5 ms flashes (17,500 photons; arrow) recorded in different bath Ca²⁺ concentrations in trpl photoreceptors. Response kinetics became faster as Ca²⁺ was increased and resulted in a reduction of peak amplitude in most recordings. In addition to increasing in amplitude and area, the inward tail current was no longer well fit by an exponential at higher Ca²⁺ concentrations, but had an initial ramp-like phase indicative of saturation of the CalX exchanger. (B) Peak tail currents (mean ± SE) plotted as a function of [Ca²⁺]_o in WT, trp, and trpl mutants. (C) P_f values (symbols) at different Ca²⁺ concentrations compared with GHK-P_f predictions (continuous curves). Empirical P_f measurements increased in a Ca²⁺-dependent manner broadly as predicted by GHK theory, but values for trpl and WT deviated from the quantitative predictions.

The simple GHK model predicts a sigmoidal increase in P_f for both TRP and TRPL channels approaching 100% at high [Ca²⁺]_o. Our P_f measurements also increased in a Ca²⁺-dependent fashion broadly in line with the GHK model (Fig. 6 C). As before, empirical P_f values closely approximated the GHK predictions for TRPL channels (in trp) across the tested [Ca²⁺]_o range, but were generally below them for TRP channel (in trpl) and the native TRP and TRPL channels (WT).

Modeling of Ca²⁺ dynamics

Although we confirmed the high fractional Ca²⁺ contribution to the LIC and the greater Ca²⁺ influx via TRP channels, we observed significant discrepancies between the empirical P_f values and simple GHK predictions, assuming static ionic concentrations. To explore the basis for this, we extended an earlier model of Ca²⁺ dynamics (9) that considers the diffusion, influx, and efflux of the ions involved in the light response (Ca²⁺, Na⁺, K⁺, and Mg²⁺) and takes into account the large local and global changes in extra- and intracellular ionic concentrations. Although the model is detailed, it only aims to reproduce the ionic fluxes in and out of a patch-clamped fly photoreceptor, under the conditions of our experiments, for a bright flash, which effectively produces a quantum bump in each microvillus in the rhabdomere (∼35,000 effective photons). Using the model, we directly calculated estimates of fractional currents and tail currents caused by the Na⁺/Ca²⁺ exchanger, taking into account dynamic changes in ionic concentration (see Supporting Material for details).

To model the concentration changes during the light response, we reduced the photoreceptor cell and extracellular space to a one-dimensional (1D) geometry consisting of a single microvillus connected to a representative section of the cell body, and an extramicrovillar space connected to a representative section of the intraommatidial cavity (Fig. 7). By further compartmentalizing this geometry, we were able to model diffusion, local ionic fluxes, and local Ca²⁺ buffering. We estimated the currents associated with the TRP and TRPL channels from three representative measurements for WT, trp, and trpl flies by subtracting an estimated exchanger current from the total LIC (Fig. S2). Based on these estimated channel currents, the modeled local ionic concentrations, the measured relative ionic permeabilities, and the GHK equation, we calculated the ionic fluxes through TRP and TRPL channels in and out of the microvillus (Figs. S3 and S4). We subsequently modeled intra- and extracellular diffusion of ions, the extrusion of Ca²⁺ ions by the Na⁺/Ca²⁺ exchanger (Fig. S3A), and buffering of Ca²⁺ ions (Figs. S9 and S10). Because we used ouabain in all experiments, the model ignored any reequilibration of Na⁺ due to Na/K ATPase activity. We also ignored the dynamic reequilibration of Mg²⁺, about which nothing is known in terms of photoreceptors. The absence of any tail current in calx mutants (Fig. 3) indicates at least that there is no significant electrogenic component.

Figure 7.

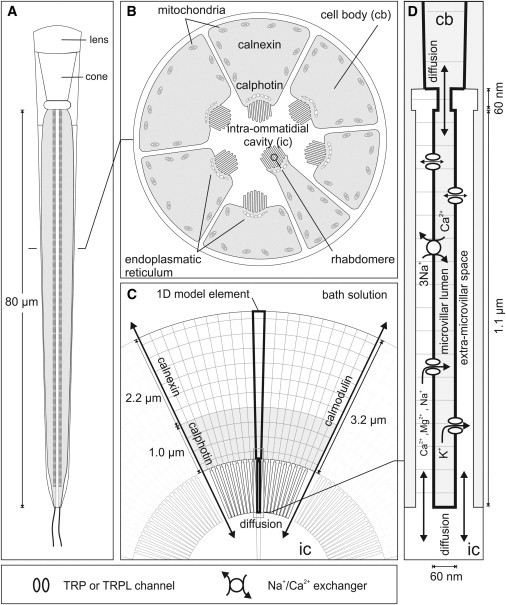
Photoreceptor geometry used for modeling. (A and B) Schematic of ommatidium in longitudinal view (A) and cross-section (B). (C) To model fluxes and diffusion, the geometry was reduced to a representative 1D element representing one microvillus and the associated section of cell body and extracellular space. (D) Schematic of microvillus with TRP/TRPL ion channels and Na⁺/Ca²⁺ exchanger. For further details and dimensions, see Fig. S1 and Table S1.

The ionic fluxes, diffusion, and buffering led to concentration changes in the four compartments (Figs. S5–S8). When the TRP and TRPL channels opened, Ca²⁺, Mg²⁺, and Na⁺ flowed into the cell, leading to a significant increase in the microvillus lumen and a delayed increase in the cell body after diffusion from the microvillus. Because Ca²⁺ ions are strongly buffered and have a lower diffusion coefficient than the other ions, Ca²⁺ showed a stronger peak in the microvillus, especially in WT and trpl flies, where influx was particularly high. Conversely, the concentration of Ca²⁺ ions decreased in the extracellular space, most notably in the extramicrovillar space and more moderately in the intraommatidial cavity. K⁺ concentrations changed in the opposite direction, but by smaller amounts because K⁺ has a high diffusion coefficient and its contribution to the LIC is small at −70 mV.

The Ca²⁺ concentration that is reached in the cell body depends strongly on the buffering power; therefore, we tuned the buffering power so that cell-body Ca²⁺ levels would peak around 50 μM in WT flies, as was previously measured using Ca²⁺ indicators (7). After Ca²⁺ influx, the exchanger extrudes the ions from the microvillus lumen into the extramicrovillar space in a concentration-dependent manner. The exchanger is assumed to saturate at high intracellular Ca²⁺ concentrations, with the concentration of half-maximal exchanger current tuned to a value of K_X = 30 μM. The maximal exchanger rate constant was adjusted to a value that is in agreement with the observed maximal exchanger current of ∼200 pA. Apart from these exchanger parameters, the apparent rate of extrusion is predicted to depend strongly on Ca²⁺ diffusion from the cell body to the microvillus/rhabdomere, which in turn is strongly influenced by the buffering power. Significantly, the same buffering parameters, which were tuned to reproduce the peak Ca²⁺ concentration in the cell body, also successfully modeled the time courses of the measured exchanger tail current, as well as Ca²⁺ concentration time courses previously measured using Ca²⁺ indicators (44,45).

The measured tail current exhibited a dominant fast component (τ ∼300–400 ms) and a minor slow component (τ ∼2 s). We explored several mechanisms to explain the second slow component, including diffusion from the pipette, mitochondria, and inhibition of the exchanger by intracellular Ca²⁺. None of these mechanisms seemed to robustly reproduce the slow component in a way that was consistent with other aspects of the measurements. However, adding a low-capacity, moderately high-affinity Ca²⁺ buffer also gave a slow component and seemed to be in better agreement with other aspects of the measurements.

Tuning of parameters was based on a representative WT measurement obtained in a bath solution containing 1.5 mM Ca²⁺. We subsequently used the same parameter set for the other simulations, in which we only varied the LIC (which was an input for the simulation); the relative permeabilities corresponding to WT, trp, and trpl flies; and the extracellular Ca²⁺ concentration. Because the measured integral of the LIC varies with extracellular Ca²⁺, we scaled the representative LICs for WT, trp, and trpl flies measured in a bath solution containing 1.5 mM Ca²⁺, with values of 0.6, 0.9, and 0.65 for simulations in which the Ca²⁺ bath concentration was 0.75, 3, and 10 mM, respectively.

Using the dynamic model, we calculated P_f values for WT, trp, and trpl flies for different extracellular Ca²⁺ concentrations and compared them with the measured values (Fig. 8 A). In similarity to the measured P_f values, we found that modeled P_f values in trp flies were hardly affected by dynamic changes in ion concentrations; however, for WT and trpl responses, we found that P_f was reduced close to measured values. During the peak of LIC, we predicted shifts in extra- and intracellular ionic concentrations (Figs. S6 and S7), which reduce the ionic gradients across the membrane and hence the driving force for ionic currents. The shifts were most notable in the confined extramicrovillar space and microvillus lumen. Although the gradients for Ca²⁺, Mg²⁺, and Na⁺ all became smaller, the effect on the more slowly diffusing Ca²⁺ combined with its large flux in WT and trpl flies was much more pronounced than that observed for Na⁺ and Mg²⁺, and this reduced P_f by increasing the relative contribution of Na⁺ and to some extent Mg²⁺ compared with Ca²⁺ (Fig. S4).

Figure 8.

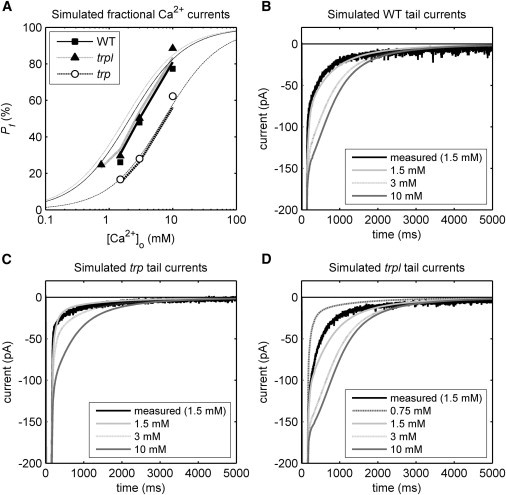
Dynamic modeling of fractional Ca²⁺ currents (P_f) and exchanger tail currents. (A) Comparison of simulated P_f values using the simple GHK model with static ionic concentrations (thin continuous curves replotted from Fig. 6), measured P_f values (data point symbols, replotted from Fig. 6) and the dynamic GHK model (thick lines, which fit well to the data points) for different extracellular Ca²⁺ concentrations in WT, trpl, and trp. With the dynamic GHK model, extracellular depletion of Ca²⁺ reduces the P_f calculated for WT and trpl flies compared with the simple GHK model. P_f values for trp flies are similar for both the simple and dynamic GHK models. (B–D) Measured tail currents for WT, trpl, and trp flies (black) with [Ca²⁺]_o = 1.5 mM, and modeled tail currents (gray) using the dynamic GHK model for different extracellular Ca²⁺ concentrations. The time course and amplitude of the tail currents are qualitatively consistent with measured tail currents. Notably, at higher extracellular Ca²⁺ concentrations, the tail currents for WT and trpl exhibit a ramp-like phase due to saturation of the exchanger, as also seen in measured tail currents (cf. Fig. 6).

Using the same dynamic model, we also calculated the exchanger tail currents for WT, trp, and trpl flies for the different extracellular Ca²⁺ concentrations (Fig. 8, B–D). The peak exchanger current just after LIC was comparable to measured values. We also found that the time course of the measured tail current qualitatively agreed with the modeled tail current for all genetic backgrounds and Ca²⁺ concentrations, including the ramp-like decay at high extracellular Ca²⁺ concentrations indicative of exchanger saturation (Figs. 6 A and 8, B and D).

Discussion

In this study, we characterize a light-induced tail current in Drosophila photoreceptors. We show that it is mediated by the CalX electrogenic Na⁺/Ca²⁺ exchanger and exploit its properties to provide quantitative estimates of the fractional contribution of Ca²⁺ to the LIC (P_f) through TRP and TRPL channels. Our data confirm that Ca²⁺ influx represents a major component (∼30%) of the LIC and is predominantly mediated by TRP channels, whereas TRPL channels mediate a more modest Ca²⁺ influx. The voltage and Ca²⁺ dependence of P_f are broadly in line with predictions of GHK theory, and the P_f for the TRPL channel closely matches that predicted by GHK theory. However, although the P_f of TRP channels (∼30%) was ∼2 times greater than that of TRPL, it was substantially lower than the simple GHK prediction (45%). A detailed model incorporating intra- and extracellular geometry, ion permeation, diffusion, extrusion, and buffering suggested that this deviation from the GHK prediction could be largely accounted for by extracellular ionic depletion during the large LICs.

Methodological considerations

The standard approach for measuring P_f involves loading cells with saturating levels of Ca²⁺ indicator dyes, which then must be calibrated, ideally using a pure Ca²⁺ current (22). This approach is impractical for Drosophila photoreceptors because of the huge Ca²⁺ fluxes, the extreme compartmentalization, and the lack of a pure Ca²⁺ current control for calibration. We therefore developed an alternative method based on the endogenous Na⁺/Ca²⁺ exchanger. This method assumes that all Ca²⁺ entering the cell is removed by the CalX exchanger during the time course of the tail current. In a strict sense, this is unlikely to be completely true (see below); however, there is a substantial body of evidence implicating the CalX exchanger as the principal mechanism of Ca²⁺ extrusion in Drosophila photoreceptors (29,42). The rapidity and high efficiency of Na⁺/Ca²⁺ exchange has also been demonstrated in Drosophila photoreceptors by a near-instantaneous inward exchange current that can be evoked by photolytic release of caged Ca²⁺ (11).

The method also assumes that the light-induced rise in Ca²⁺ is entirely due to Ca²⁺ influx through TRP and/or TRPL channels, and that other modes of raising cytosolic Ca²⁺ levels are negligible. This is strongly supported by studies using Ca²⁺ indicator dyes, in which it was concluded that Ca²⁺ influx vastly outweighs any release from intracellular stores (5–7,46). We also found that our estimate of P_f was unaffected by first depleting intracellular stores with thapsigargin. This result also excludes significant long-term Ca²⁺ sequestration by the SERCA pump as a source of error in our measurements.

Intensity dependence of P_f

In our experiments, we observed a slight intensity-dependent rise in P_f values (Fig. 4) that was not necessarily predicted, although a similar intensity-dependent difference between light-induced Ca²⁺ influx and Na⁺/Ca²⁺ exchange-dependent efflux has also been reported in blowfly photoreceptors (37). One possible explanation for the variation of P_f with intensity is a significant contribution of alternative, higher-affinity Ca²⁺ homeostatic mechanisms (e.g., buffers, stores, mitochondria, transporters) at lower intensities. It is possible that certain Ca²⁺-buffering/sequestering components have a slower release time constant and that some Ca²⁺ is not rapidly extruded by Na⁺/Ca⁺ exchange, but rather is released on a slower timescale and/or extruded by nonelectrogenic transporters such as the high-affinity plasma membrane Ca-ATPase. A significant contribution from any of these components would lead to an underestimation of P_f. With higher-intensity flashes, the empirical P_f estimate may approach its true value due to a greater proportion of high-affinity sites being occupied or saturated, leading to increased reliance on the low-affinity, high-capacity exchanger.

Another possibility is that the large currents elicited by brighter flashes were inadequately voltage-clamped, owing to series resistance (R_s) errors (maximally 40–50 mV) and/or poor space-clamp conditions. Both GHK theory and direct measurements suggest that the effect of voltage on P_f is minimal at hyperpolarized potentials below −20 mV (Fig. 5); however, P_f is predicted to increase sharply above −20 mV, and we cannot entirely exclude the possibility that voltage-clamp control of some of the largest responses may have deteriorated sufficiently to increase the P_f.

Finally, although the total LIC is smaller at low intensities, the local current density (number of channels activated per photon per microvillus) actually increases. Hence, in principle, local ionic depletion could be higher at low intensities, leading to greater deviation from the GHK prediction (i.e., the P_f value decreases at low intensity). However, this effect would be offset by less global depletion of the overall extracellular space, and the situation cannot be directly modeled by our assumption of a repeating 1D element (which strictly holds only for the case in which each microvillus is activated once).

Modeling Ca²⁺ influx and extrusion

Our experimentally obtained P_f values closely matched simple GHK predictions for TRPL channels but not for TRP channels. Although this might indicate that the GHK assumptions had been violated for TRP, a detailed model suggested that the discrepancy could be largely explained by extracellular ion depletion. Thus, a computational model that still uses GHK theory but calculates dynamic ionic concentrations by taking into account photoreceptor cell geometry was able to robustly reproduce the observed P_f values and Na⁺/Ca²⁺ exchanger tail currents over a range of extracellular Ca²⁺ concentrations and different genetic backgrounds. Because Ca²⁺ is a major charge carrier in WT and trpl flies, and also has the lowest diffusion coefficient, it is more strongly depleted in the extracellular space during the peak response than Na⁺ and Mg²⁺, resulting in a lower P_f in WT and trpl flies. In trp flies, the contribution of Ca²⁺ to the total current is lower and hence Ca²⁺ is less depleted, resulting in only a slightly smaller P_f value.

An essential feature of our model is the inclusion of Ca²⁺ buffering in the cell body. To obtain a realistic peak Ca²⁺ (50 μM) in the cell body, Ca²⁺ must be strongly (90–98%) buffered (without buffering, Ca²⁺ is expected to reach ∼0.5 mM in the cell body). Apart from controlling cell-body concentrations, buffering also slows down extrusion of Ca²⁺ and diffusion from the cell body to the rhabdomere. The time constant for free diffusion from the cell body to the rhabdomere is estimated to be approximately $\tau =4/{\pi }^2\times d_{cb}^2/D_{C{a}^{2+}}=4/{\pi }^2\times {3.2}^2/220$= 19 ms, but for buffered Ca²⁺ this can be ∼200–400 ms and even slower, suggesting that extrusion is partly diffusion limited. Significantly, the latter time constant matches the dominant time constant observed in the Na⁺/Ca²⁺ exchanger tail current. In other words, the introduction of a Ca²⁺ buffer with properties needed to account for measured cell-body Ca²⁺ concentrations also yields the observed extrusion time constant without further tuning. This interpretation of the effect of buffering on time constants is also consistent with a recent study that reported a similar time constant (∼350 ms) for the increase in cell-body Ca²⁺ after illumination, which was accelerated to ∼20 ms after genetic knockdown of the major cell-body Ca²⁺-binding protein calphotin (45).

To account for the maximal exchanger current of ∼200 pA, we modeled the exchanger using a Hill coefficient of one and a concentration of half-maximal exchanger current of K_X = 30 μM. Qualitatively, this yielded the correct time course and shape of the exchanger tail current for all extracellular Ca²⁺ concentrations and genetic backgrounds, including similar saturation characteristics (ramp-like decay) just after the peak currents recorded in high [Ca²⁺]_o (3 and 10 mM; cf. Figs. 6 and 8). The value for K_X is higher than the values reported for regulatory and transport binding sites for other organisms (41). However, it is likely that the apparent IC₅₀ values are different from specific binding sites, and, moreover, other ions or regulatory mechanisms may also affect the apparent affinity in vivo. From a physiological viewpoint, a relatively low apparent affinity of the exchanger for intracellular Ca²⁺ would be beneficial for cells that have to handle large Ca²⁺ influxes leading to concentration changes in the order of tens of micromolars. In some organisms at least, NCX exchangers can be modulated by [Na⁺]_o, [Na⁺]_i, or [Ca²⁺]_o (41,47). For simplicity, we ignored such regulatory sites because Drosophila CalX has not been fully characterized in this respect, and because these concentrations only undergo only relatively small changes during the light response compared with the massive changes in [Ca]_i.

Conclusions

To our knowledge, our results represent the first empirical measurements of the fractional Ca²⁺ current (P_f) of the light-sensitive channels in Drosophila. Because the TRP channel in particular shows complex permeation properties and divalent ion block, it is unlikely to strictly obey the assumptions (e.g., independent mobility of ions) of GHK theory. Despite this, our results indicate that to a good approximation, the fractional Ca²⁺ current follows the GHK prediction for both TRP and TRPL. It is only reduced from the simple GHK prediction for the case of TRP channels because of the depletion of Ca²⁺ ions that occurs during responses to bright flashes. Despite this reduction in P_f, Ca²⁺ influx is still massive. For example, assuming a single-channel conductance of 8 pS (48), a P_f of 30% represents a flux of ∼600 Ca²⁺ ions/ms per TRP channel at resting potential. Within the volume of a microvillus (∼3 × 10⁻¹⁸ liter), this represents an unbuffered flux of 350 μM/ms per channel. During the peak responses to the bright flashes used in this study, our model predicts that microvillar Ca²⁺ will transiently reach ∼0.5 mM in WT and trpl photoreceptors, and ∼0.15 mM in trp (Fig. S6). In response to these bright flashes, each effectively absorbed photon generates an average response of <1 pA. This is much smaller than the normal single-photon response (quantum bump), because the global rise in Ca²⁺ initiated by bumps with the shortest latencies already attenuates (light adapts) the majority of bumps that arise with longer latencies. Under dim illumination, single quantum bumps have an amplitude of ∼10 pA representing the opening of ∼15 channels in a single microvillus, and we predict that free Ca²⁺ transiently reaches levels of several millimolars within individual microvilli, as previously proposed (9). Under light-adapted conditions, each effectively absorbed photon may now only activate a single channel for a few milliseconds, but even this would be expected to raise microvillar free Ca²⁺ transiently well above 10 μM.

Although the model was specifically implemented to provide insight into the Ca²⁺ fluxes and exchanger currents associated with our bright-flash experiments, successful modeling of the exchanger tail current also provided insight into the cytosolic Ca²⁺ buffering of the cell body and microvilli. Particularly important are immobile cytosolic buffers, the most significant of which is probably the Ca²⁺-binding protein calphotin, which is localized in a band at the base of the microvilli (45,49,50). To account for both the measured exchanger time constant and the control of absolute cytosolic Ca²⁺ in the face of massive Ca²⁺ influx, the modeling suggests that the buffer (putatively calphotin) should have a relatively low affinity (∼1 mM) and high local concentration (20 mM). Future implementation of the model should provide the framework for gaining a more detailed understanding of Ca²⁺ homeostasis in microvillar photoreceptors under more physiological conditions, i.e., by considering reequilibration of Na⁺ via Na/K ATPase in the voltage domain rather than under voltage clamp, and responses to more physiologically relevant illumination.