Abstract
Joint impedance is an important property of the human muscular system and plays a role in the control of movement and posture Previous studies showed that joint impedance varies with the position of the joint and activation level of the surrounding muscles; however, it remains unknown how it varies during movement. Non-parametric algorithms that estimate time-varying impedance do exist; however these algorithms require hundreds of realizations of the same time-varying behavior. In this paper we develop a non-parametric algorithm that can estimate slowly time-varying impedance using multiple short data segments. Using simulated data we evaluate the desired data segment length and the number of realizations needed to yield accurate estimates.
I. Introduction
Joint impedance is an important property of the human muscular system and plays a role in the control of posture and movement. Joint impedance, also referred to as dynamic joint stiffness, relates the position of the joint and the torque acting about it. One source of joint impedance is the intrinsic properties of the joint and tissues such as the viscoelastic properties of the joint, muscles and connective tissues and limb inertia. Another source of joint impedance is the stretch reflex: the muscles respond to stretches by producing counteracting torques [1].
Previous studies showed that joint impedance varies with the position of the joint, as well as the activation level of surrounding muscles [2]. Other studies showed that joint impedance varies with time during cyclic and catching tasks [3, 4]. However, the analyses for those time-varying studies were performed using parametric methods; to our knowledge, no studies to date have estimated time-varying joint impedance using non-parametric methods. In contrast to parametric methods, non-parametric methods do not require a priori knowledge of the order of the system, thus are extremely useful for situations where the order of the system is unknown.
To estimate joint impedance during movement requires an algorithm that can estimate time-varying dynamics. Ludvig et al. [5] designed a non-parametric algorithm that can estimate time-varying joint impedance. However, their algorithm requires hundreds of realizations of identical movements. This is both time consuming and very demanding of the subject, as the subject must vary their joint impedance in nearly identical fashion hundreds of times. Furthermore, their algorithm produces impedance estimates at every sample point, and impedance may change very little between sample points.
In this paper, we present a novel algorithm to estimate joint impedance using multiple short segments of data. This non-parametric algorithm will have the advantage over time-invariant methods as it requires only short segments of stationarity over which impedance estimates will be generated; it will also have an advantage over the time-varying algorithm as only a limited number of realizations are needed to yield accurate estimates.
II. Multi-Segment Identification Algorithm
Previous studies [6–8] have estimated the intrinsic component of joint impedance by computing a 2-sided impulse response function (IRF) between the position and the intrinsic torque. This IRF can be estimated directly from the data; alternatively it can be estimated by computing the IRF between the position auto-correlation and the position-torque cross-correlation.
Under time-invariant conditions, the cross-correlation for each lag can be estimated by multiplying the lagged input with the output and then averaging along the entire data length. This can be formulated in discrete terms as
| (1) |
where ϕxy(k) is the cross-correlation at lag k, x(i-k) is the input at time i-k, y(i) is the output at time i, and N is the number of points. This cross-correlation assumes that the relationship between input and output does not vary with time, and thus cannot account for the correlations between the input and output that vary with time.
Under time-varying conditions, the cross-correlation is computed using multiple realizations of input-output data, where the behavior of the underlying system presents the same time-varying behavior. The discrete time-varying correlation can be formulated as
| (2) |
where ϕxy(i,k) is the cross-correlation at time i and lag k, x(ik, r) is the input at time i-k and realization r, y(i,r) is the output at time i and realization r, and R is the total number of realizations. In contrast to the time-invariant cross-correlation, the time-varying correlation averages the product of the input and output across the ensemble instead of along the data length.
The time-varying cross-correlation is a powerful method as it provides an estimate of the correlation between the input and output at each time point. However, it requires many realizations to perform the required averaging, and may result in very long experimental times. Furthermore, if the underlying system is only slowly time-varying, or has short periods where it is stationary—which we will refer to as quasi-stationary periods—then the time-varying algorithm will produce numerous redundant computations and is thus inefficient. Instead, we propose to combine both time-invariant and time-varying cross-correlations to estimate the behavior of the system during these quasi-stationary periods.
To estimate the correlation between the input and the output during these quasi-stationary periods, we averaged the product of the input and output both along time points during this period as well as across realizations. We define this cross-correlation as the multi-segment cross-correlation and is formulated as
| (3) |
where t is the beginning of the quasi-stationary periods and N is number of points in the quasi-stationary period. Similarly the multi-segment auto-correlation can be computed as in (3), except substituting the output y(i,r) with the input x(i,r).
The relationship between the multi-segment autocorrelation and cross correlation is given by
| (4) |
where h(j) is the IRF at lag j, and M1 and M2 are the minimum and maximum lag of the IRF. Thus, the IRF can be estimated by solving the following equation
| (5) |
where
III. Simulation Studies
A number of simulation studies were run to evaluate the performance of the multi-segment algorithm. The first two simulations were run on stationary data: the first compared the performance of the algorithm to both the time-invariant and time-varying algorithm; the second determined the length of time segments and the number of realizations needed to produce reliable estimates of the underlying system. The final simulation was run on time-varying data with goal of evaluating the performance of the algorithm in estimating time-varying systems.
A. Simulation Methods
The model shown in Fig. 1 was used to generate simulated data. The simulations were carried out using Simulink (The Mathworks inc.) running at a fixed rate of 1 kHz. Each simulation set consisted of a series of realizations of the same length; each simulation in a set contained identical parameters, but different random values were used for the position and noise signals. The joint impedance was simulated as a 2nd order differential equation shown in Fig. 1. The simulated position was Gaussian noise filtered with a single pole at 4 Hz, and having a standard deviation of 0.015 rad. The noise was Gaussian noise filtered at 5 Hz with an 8-pole Bessel filter. The power of the noise was set to produce a resultant signal-to-noise ratio of 10 dB. Following the simulation, the data were filtered by a 400 Hz, 8th order Chebyshev filter and then decimated to 100 Hz.
Fig. 1.
Schematic of simulations. Multiple realizations of simulated position signals were used to compute multiple realizations of simulated torque using the shown 2nd order differential.
Three different simulation sets were run. In the first set, 10 realizations of 0.1 s were simulated with the parameters of the impedance set to K = 75 Nm/rad, B = 0.63 Nm/rad/s and I = 0.0137 kgm2. These values were selected based on previous experiments at the ankle [2]. The purpose of this simulation was to compare the estimates produced by the multi-segment algorithm to those produced by the time-invariant and time-varying algorithms, for the same number of time points or number of realizations respectively. Therefore, the multi-segment algorithm computed a single IRF using all the data, while the time-invariant algorithm computed IRFs for each realization and the time-varying algorithm computed IRFs for each time point.
In the second simulation set, 100 realizations of 10 seconds were simulated with the parameters of the impedance the same as in the previous simulation set. The multi-segment algorithm was run on subsets of this data numerous times. The subsets were generated by systematically altering the segment length and number of realizations.
The third simulation set simulated a slow change in impedance. 20 realizations of 8 seconds were simulated, where K was simulated to vary with the following behavior
| (6) |
For this simulation set, the algorithm was run multiple times with segments of 3 different lengths: 0.1 s, 0.25 s and 0.5 s. For each segment length the data were segmented into windows spaced 0.05 s apart.
For the second and third simulations sets, the quality of the estimation was evaluated in two ways. First the %VAF between the torque predicted by the algorithm (T̂q) and the simulated noise free torque (Tq) is computed as
| (9) |
The quality of the algorithm was also evaluated by estimating the simulated steady-state impedance. This was done by integrating the impedance impulse response function.
B. Simulation Results
1) Algorithm Comparison
The first set of simulations compared the performance of the multi-segment algorithm to that of the time-invariant and time-varying algorithms. All algorithms were evaluated on the same set of stationary data. Fig. 2, shows the estimated IRFs from the three estimation methods along with the theoretical impulse response. The time-invariant IRF shown in Fig. 2 is the average of the IRFs computed for each realization; similarly, the time-varying IRF shown in Fig. 2 is the average of the IRFs computed for each time point. This ensured that all three methods had access to the same amount of data. It is clear that the multi-segment algorithm performed better than the time-invariant algorithm for the short segment lengths; similarly the multi-segment algorithm performed better than the time-varying algorithm when only a limited number of realizations were available.
Fig. 2.
Joint impedance IRFs. The multi-segment IRF (red) accurately estimated the impedance and matched the ideal IRF (black). The time-invariant (blue) and time-varying IRFs (green) produced estimates of impedance with greater variability, as evident by the larger standard deviations of the estimates (shaded regions equals ± 2 standard deviations).
2) Number of Data Points
The previous subsection showed that the multi-segment algorithm can outperform the time-variant and time-varying algorithm when only short segments and limited realizations are available. Thus, the next aspect of the algorithm that was tested was the minimum segment length and number of realizations needed to yield accurate results. Fig. 3A shows the %VAF of the multi-segment algorithm as a function of the segment length and the number of realizations. Clearly the performance of the algorithm improved with an increasing amount of data. However, under closer inspection it can be seen that for a given amount of data—the product of segment length and number of realizations, shown by black lines in the figure—the algorithm performed better with shorter segment lengths and greater numbers of realizations.
Fig. 3.
Performance of multi-segment algorithm. A) The algorithm accounted for more variance for a given number of points (black curves) when shorter segment lengths and greater numbers of realizations were used. B) The standard deviation of the K estimate decreased with the number of points, but there was no clear preference for longer segment lengths or greater numbers of realizations.
Fig. 3B shows the standard deviation of the K estimate; it decreased with increasing segment length and numbers of realizations. However, unlike the %VAF, the standard deviation of the K estimate did not show a strong preference for shorter segment lengths and greater numbers of realizations.
3) Estimation of Time-Varying Impedance
The previous subsection showed that with increasing segment lengths the algorithm performance improved. However, if the data segments are too long, the time-varying behavior of the underlying system may be missed. Thus, what is the best segment length?
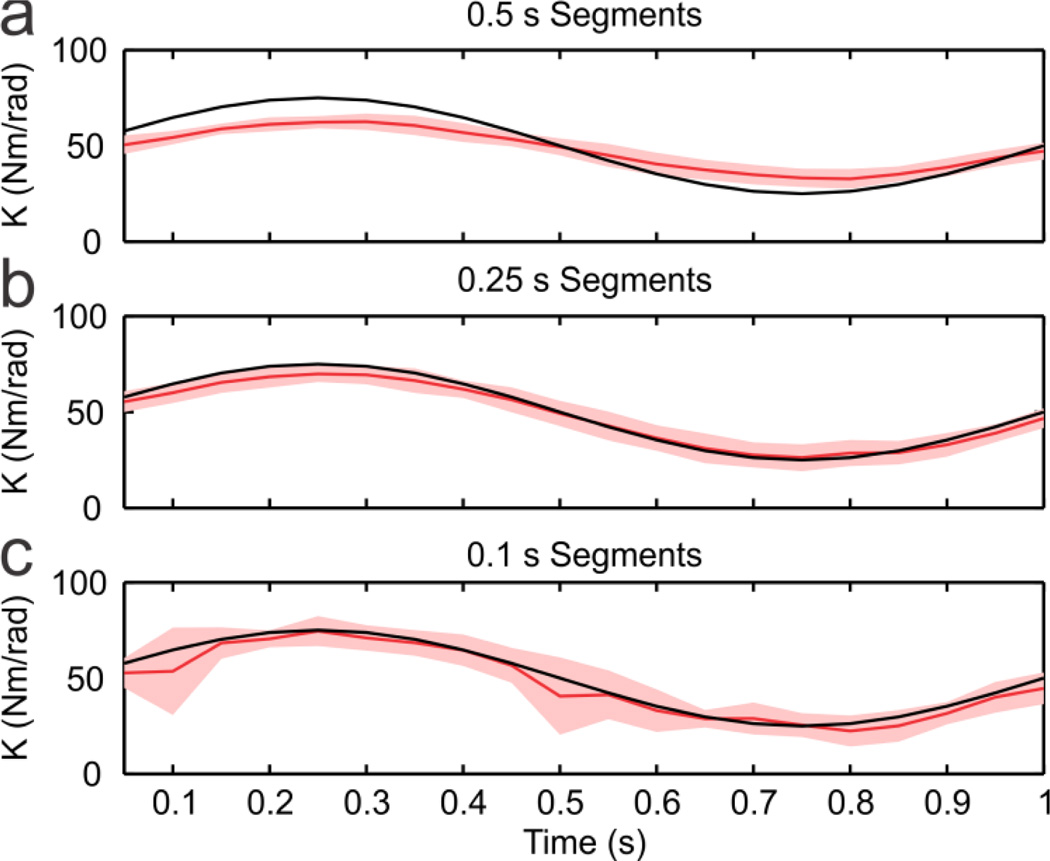
To assess this, we simulated K to vary sinusoidally with a frequency of 1 Hz. Fig. 4 shows K estimated with 3 different segment lengths. Longer data segments will benefit from better algorithm performance, as demonstrated in the previous section, but may miss the time-varying behavior. Shorter data segments will result in estimates that capture the time-varying behavior but will have increased random error. We can see that when the segments were 0.5 s long— half the period—the K estimate showed little variability, but it did not correctly estimate stiffness. When the segments were 0.1 s long, the algorithm correctly estimated K, but there was great variability in the estimates. Thus, under these conditions, using segments of 0.25 s long, resulted in estimates that were accurate and had low variability, and therefore the best of the three choices.
Fig. 4.
Estimation of time-varying behavior. Time-varying data was segmented into data segments of different length and the multi-segment algorithm was run on the data segments. The black lines show the simulated K, the red lines shows the K estimates and the shaded red regions show 1 standard deviation of the estimates.
IV. Discussion
In this paper, we presented a novel way to measure the joint impedance using multiple realizations of short data segments. We formulated auto and cross-correlations by averaging both along the data lengths and across the ensemble of realizations. Using these multi-segment auto and cross-correlations, we computed impulse response functions as estimates of joint impedance. We found that the performance of the algorithm improved as the segment length and number of realizations increased. Furthermore, for a given number of points, the algorithm accounted for a greater amount of torque variance when a greater number of shorter segments were used. Finally, we showed that using segments of properly selected lengths, the multi-segment algorithm can estimate time-varying impedance accurately.
A. Segment Length and Number
We showed that increasing the segment length and number of realizations improved performance, but taking segments too long may result in inaccurate estimates of time-varying impedance. So, how does one choose the proper values for segment length and number of realizations? The first step is to determine the dynamics of the time-varying behavior. In many situations these dynamics are unknown, thus a full time-varying analysis may need to be carried out to determine this time-varying behavior. In our simulation we found that the best performance was obtained by using segments one quarter of the period of the time-varying behavior.
Once the desired segment length is chosen, the number of realizations can be chosen based on the data shown in Fig. 3. This figure was generated for a SNR of 10 dB, and the exact number of realizations will depend on the SNR of the experiment.
B. Advantage of Non-Parametric Algorithm
The multi-segment algorithm has the advantage over the time-varying algorithm as it requires much less data. However, there are parametric algorithms that can estimate stiffness using the same limited amount of data [3, 4]. The multi-segment algorithm has the advantage of being nonparametric; this means that the multi-segment algorithm will still successfully estimate impedance even if the stiffness is not fully described by the 2nd order differential equation that the parametric approaches assume. A further benefit of the non-parametric approach is that it easily adapted to estimate other linear—and possible even non-linear—systems. One example where it could be useful would be to estimate time-varying reflex stiffness, which has been modeled as a Hammerstein system where the linear element can be 2nd or 3rd order [2].
C. Applications of the Multi-Segment Algorithm
We foresee a number of applications for the multi-segment algorithm. The first application would be to estimate slowly time-varying impedance. Since the impedance varies little between each sample time, producing impedance estimates at every time point is overkill. The multi-segment algorithm can estimate the general behavior of the time-varying impedance, however doing so with fewer data points.
Another application for the multi-segment algorithm would be to estimate the impedance of subjects in closed loop. By switching the environment from closed-loop to open-loop for short periods, it may be possible to estimate the subjects’ impedance prior to them altering their impedance in response to the change in environment.
Acknowledgments
This work was supported by the National Institutes of Health (grant R01 NS053813).
Contributor Information
Daniel Ludvig, Sensory Motor Performance Program, Rehabilitation Institute of Chicago, Chicago, IL 60657 USA (phone: 312-238-3381; fax: 312-238-2208; daniel.ludvig@mail.mcgill.ca).
Eric J. Perreault, Department of Biomedical Engineering and the Department of Physical Medicine and Rehabilitation at Northwestern University, Chicago, IL 60611 USA, and also with Sensory Motor Performance Program, Rehabilitation Institute of Chicago, Chicago, IL 60611 USA (e-perreault@northwestern.edu).
References
- 1.Kearney RE, Hunter IW. System identification of human joint dynamics. Crit Rev Biomed Eng. 1990;vol. 18:55–87. [PubMed] [Google Scholar]
- 2.Mirbagheri MM, et al. Intrinsic and reflex contributions to human, ankle stiffness: variation with activation level and position. Exp Brain Res. 2000 Dec;vol. 135:423–436. doi: 10.1007/s002210000534. [DOI] [PubMed] [Google Scholar]
- 3.Bennett DJ, et al. Tim, Time-varying stiffness of human elbow joint during cyclic voluntary movement. Exp Brain Res. 1992;vol. 88:433–442. doi: 10.1007/BF02259118. [DOI] [PubMed] [Google Scholar]
- 4.Lacquaniti F, et al. Time, Time-varying mechanical behavior of multijointed arm in man. J Neurophysiol. 1993 May;vol. 69:1443–1464. doi: 10.1152/jn.1993.69.5.1443. [DOI] [PubMed] [Google Scholar]
- 5.Ludvig D, et al. Identification of Time, Time-Varying Intrinsic and Reflex Joint Stiffness. IEEE Trans Biomed Eng. 2011 Feb 10; doi: 10.1109/TBME.2011.2113184. [DOI] [PubMed] [Google Scholar]
- 6.Kearney RE, et al. Identification of intrinsic and reflex, contributions to human ankle stiffness dynamics. IEEE Trans Biomed Eng. 1997 Jun;vol. 44:493–504. doi: 10.1109/10.581944. [DOI] [PubMed] [Google Scholar]
- 7.Perreault EJ, et al. Estimation of intrinsic and reflex contributions, to muscle dynamics: a modeling study. IEEE Trans Biomed Eng. 2000 Nov;vol. 47:1413–1421. doi: 10.1109/TBME.2000.880092. [DOI] [PubMed] [Google Scholar]
- 8.Westwick DT, Perreault EJ. Identification of apparently acausal stiffness models. Conf Proc IEEE Eng Med Biol Soc. 2005;vol. 6:5611–5614. doi: 10.1109/IEMBS.2005.1615758. [DOI] [PubMed] [Google Scholar]