Domain formation in membranes caused by lipid wetting of protein

Abstract

Formation of rafts and other domains in cell membranes is considered as wetting of proteins by lipids. The membrane is modeled as a continuous elastic medium. Thermodynamic functions of the lipid films that wet proteins are calculated using a mean-field theory of liquid crystals as adapted to biomembranes. This approach yields the conditions necessary for a macroscopic wetting film to form; its thickness could also be determined. It is shown that films of macroscopic thicknesses form around large (tens nanometers in diameter) lipid-protein aggregates; only thin adsorption films form around single proteins or small complexes. The means by which wetting films can facilitate the merger of these aggregates is considered. It is shown that a wetting film prevents a protein from leaving an aggregate. Using experimentally derived values of elastic moduli and spontaneous curvatures as well as height mismatch between aggregates and bulk membrane, we obtained numerical results, which can be compared with the experimental data.

I. INTRODUCTION

The classic fluid mosaic model [1] views the lipid environment of a plasma membrane as essentially homogeneous. But over the past decade it has been increasingly realized that nonhomogeneities in membranes are central to biological functions that depend on protein-protein interactions within membranes. Membrane nonuniformities must exist because lipid and protein interactions mediated by hydrophobic, Van der Waals, electrostatic, and chemical forces will cause some lipids and proteins to cluster into domains and others to repel. Over thirty years ago it was demonstrated by electron spin resonance that small spatial inhomogeneities existed [2]. It was found that “boundary lipids” surrounding a protein exhibit about a tenfold reduction in hop time compared to lipids that are not associated with proteins [2]. Around the same time it was shown that lipid diffusion is relatively fast [3,4], and so, although nonspecifically adsorbed boundary lipids are constrained, they do exchange rapidly with bulk lipids. In recent years, binding of specific lipids to particular proteins has been demonstrated [5]. Regardless of the mechanism by which the first layer of lipids adheres to a protein, short-range interactions can lead to a few additional lipid layers; the composition of these layers will approach that of the bulk membrane. Although the size of a single protein and its associated lipids is small, these units could also attract each other and associate to create a large complex through a number of different mechanisms. Large complexes could be created and stabilized by precise intermolecular interactions between ectodomains. Alternatively, the lipid bilayer portion of a membrane could elastically deform to accommodate the transmembrane domains of proteins and interactions between the deformed bilayers portions could yield larger stabilized domains. This type of deformation and aggregation would occur, for example, in the case of a significant hydrophobic mismatch between a protein and lipids. The consequences of hydrophobic mismatch on lipid deformation and protein agglomeration have been intensively investigated [6–18]. But whether the phase state of the lipids in this complex is the same as in the bulk membrane has not been considered: it has generally been tacitly assumed that they are the same, and this is equivalent to assuming that the lipid composition is laterally homogeneous. However, a computer simulation that has considered redistribution of lipids as a result of protein segregation suggested that lipids around a protein would be in a liquid-ordered (l_o) state [19,20]. In contrast, several years ago it was proposed that an extended lipid shell of definite and uniform composition could form around a membrane protein, implying that lipids in such shells are at the same phase state as in bulk membrane [21]. The shell model has only been considered in a qualitative manner; it has not been placed on solid physical and quantitative footings. A large body of work has thus led to the concept that the nonhomogeneities in lipid environments can be considered in terms of spatial and temporal hierarchies.

Currently, “rafts” are probably the most intensely studied domain in plasma membranes [22]. Rafts are generally thought to be domains that are enriched in sphingolipids and cholesterol in an l_o state and that contain particular membrane proteins, such as those that are glycoslphosphatidylinositol (GPI) anchored. However, a universal definition of lipid-protein rafts has not been agreed upon, although attempts have been made to standardize terminology [23]. Experimental data concerning basic properties of rafts in plasma membranes, such as size, composition, and dynamics are controversial. It has also been questioned whether rafts really exist in cell membranes [21]. But despite the many controversies, interest in rafts remains high because there is considerable indirect evidence that they intimately participate in protein trafficking, signaling, and many other vital cellular processes.

Data suggests that lipid-protein rafts are variable in size; estimates ranging from as little as a few nm in diameter [24] up to a couple of hundred nm [25]. Transmission electron microscopy of cell membrane sheets shows that large (up to 300 nm in radii) lipid-protein “islands” exist and it has been proposed that these islands are divided into raft and nonraft subregions [26]. Caveolae, relatively large domains of diameter 50– 150 nm that are rich in cholesterol and sphingolipids, could be considered to provide an example of such islands [27]. Raft composition has been inferred from that of membrane insoluble fractions extracted by nonionic detergents at 4 ° C. These fractions are rich in cholesterol, sphingomyelin, and glycolipids [22]. Domains in lipid bilayer model membranes that are enriched in these lipids are in a liquid-ordered state [28]. The bilayer region surrounding rafts, poorer in cholesterol and/or sphingomyelin, are in a different state, referred to as liquid disordered. Associations between lipid and proteins in a plasma membrane could give rise to more complex architectures and phase states.

Insight into a possible origin of rafts in cell membranes has been derived from studies in model lipid bilayers [28–32]. Fluorescence microscopy has shown that micron-sized cholesterol-sphingomyelin domains form when the temperature is low enough for the sphingomyelin to be supersaturated in the membrane. These micron domains are in liquid-ordered state [21]; they are circular, and extend through both monolayers of a bilayer [32]. It is also possible for lipid bilayers to contain nanodomains that are tens of nanometers in diameter [28,33]. It has been proposed that these nanodomains do not merge because their line tension is sufficiently small that the decrease in boundary energy upon merger does not fully compensate for the decreased entropy resulting from fewer domains [34]. In cell membranes, however, each lipid species is probably subsaturated at physiological temperature, so phase separation would not spontaneously occur. Because there are no indications of pure lipidic rafts in plasma membranes or of a global phase separation, it has been posited that a protein-mediated local phase transition is responsible for the formation of rafts [19].

The creation of lipid domains around a protein can be viewed from the perspective of surface chemistry. Here, one would consider the wetting of a protein by the surrounding lipid molecules. Wetting phenomena have long been studied in three-dimensional systems [35,36]. Wetting can be categorized as “complete” or “incomplete.” In complete wetting, the thickness of the film that condenses on the nucleating object is unlimited, ultimately leading to full, global phase separation. In incomplete wetting, only a thin film of a new phase condenses onto the surface. Several theoretical descriptions have been used to predict film thickness [37–39]. By using a general theory that treats Van der Waals forces arising from electromagnetic fluctuations [37], one can calculate the thermodynamic potentials, in terms of complex dielectric permeativities, for a liquid film formed on a solid surface. The chemical potential of the film is a function of its thickness and can exhibit a variety of properties: it can be positive or negative, monotonic or nonmonotonic. This richness leads to a “Lifshitz catalog” [38,39] of molecular and macroscopic films that can be stable, metastable, or unstable. The power of the approach is underscored by demonstrations that for simple liquids, Lifshitz theory and experiment are in perfect agreement [40]. However, this theory, developed for three-dimensional systems, is not applicable to biological membranes because it does not consider hydrophobic or structural forces, which are clearly critical for membrane structure and function. A more appropriate theory that utilizes thermal fluctuations has been developed to describe wetting of proteins in biological membranes. It is based on the concept that, within the plane of the bilayer, there are capillary waves at an interface between a thin wetting film and bulk membrane [20,41,42]. Capillary waves are unable to penetrate beyond the surface of the protein, and so there is an entropic confinement that creates a repulsive force between the fluctuating interface of the film and the protein wall. This force is sufficient to stabilize the film at very low line tension, γ, when the film interface exhibits appreciable fluctuations. But for large γ, mean-field approaches that describe bilayer membranes should be more appropriate.

In the present study, we treated the cell membrane as a continuous elastic medium subject to the deformations of splay and tilt. We define rafts as lipid-protein domains that have their lipids in an l_o state; compositions yielding this state are different from the composition of the bulk membrane. The lipid subsystem in a raft has different monolayer height and elastic parameters than the surround. These differences in mechanical properties mirror the differences in chemical composition between a raft and a bulk membrane. Using standard Hamiltonians originally developed for liquid crystals [43], and adapted to lipid bilayers [44,45], we calculated thermodynamic potentials for lipid films that wet proteins of various sizes in a membrane, for varied hydrophobic mismatches. We are thus employing a mean-field model to describe rafts, whereas the capillary wave model emphasizes in-plane fluctuations. A mean-field approach has been successfully used to describe a large variety of membrane phenomena, including membrane fusion and fission, as well as aspects of lipid-protein interactions [6–10,15,16,18,46–61]. We derived the conditions that determine whether a film will exist and numerically calculated properties of the films. Qualitatively, the catalog of films we obtained was similar to that obtained by Lifshitz theory to describe wetting, due to van der Waals forces, of a solid surface. We show that single proteins or small protein complexes are surrounded only by boundary lipids. But a macroscopic wetting film of thickness of several nanometers can surround a lipid-protein aggregate or “island” that is on the order of tens to hundreds nanometers in diameter.

II. STATEMENT OF THE PROBLEM

We consider a bilayer membrane containing proteins and m lipid species that would yield an l_o lipid domain if the temperature were lowered sufficiently (e.g., to 4 ° C). But at higher temperature (e.g., 37 ° C) the system is subsaturated, the bilayer is uniform, and a global phase transition cannot occur. However, in the presence of a protein, a thin film of a liquid-ordered lipid phase can locally condense to surround the transmembrane domain of the protein.

We assume that the protein has a cylindrically symmetric transmembrane domain of radius r_p (Fig. 1). The more general case of a protein with some number of transmembrane domains or an aggregate consisting of many proteins and lipids also will be considered. Then a radius r_p will describe a size of the whole complex; the system is assumed to be cylindrically symmetric. We will refer to a protein or lipid-protein aggregate, surrounded by liquid-ordered film of thickness l, as raft of radius r = l + r_p (Fig. 1). At equilibrium, the chemical potential of any lipid component is the same in the film and the surrounding bilayer. The lipid composition of the film is different from that of the surround, but we assume that the film is homogeneous and its composition is independent of film thickness. This assumption is formally equivalent to a film that increases its thickness by adsorbing lipids that always enter the film with a fixed lipid stoichiometry. One can thus conceptualize that rafts grow by the incorporation of multiple copies of an elemental structural unit of fixed composition. This unit is known as a “quasimolecule” [62,63]. Let a quasimolecule contain ν_i copies of each lipid for i = 1,2,…,m. The change in free energy of the entire system upon addition of a quasimolecule to the film is

FIG. 1.

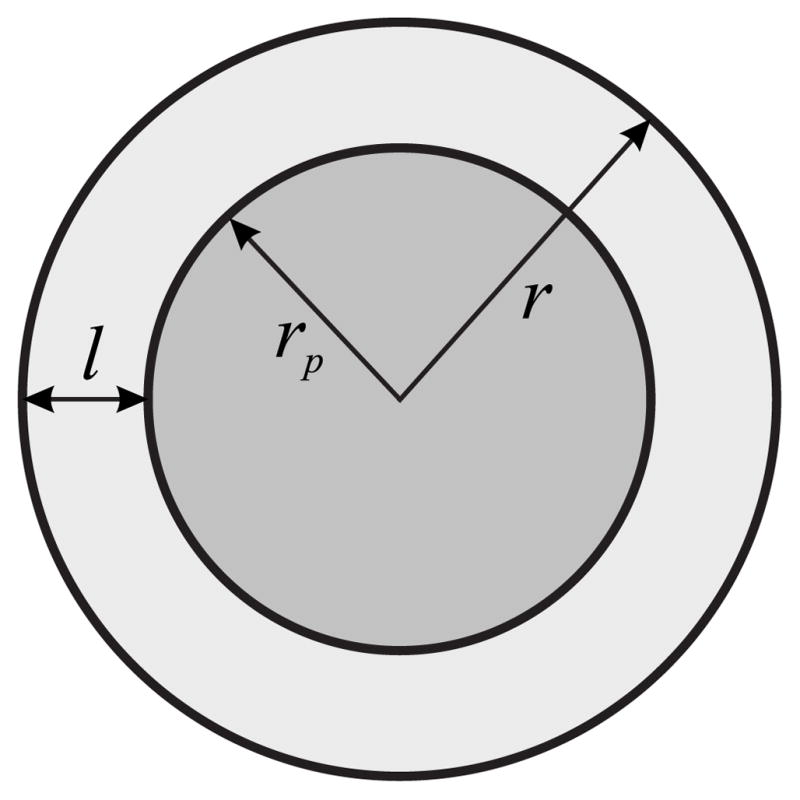
Schematic representation of a protein or an aggregate of radius r_p wetted by a lipid film of thickness l.

$$\mathrm{\Delta }\mu =\mu (r)-\sum _{i=1}^m{\nu }_i{\mu }_i,$$ (1)

where μ(r)is the chemical potential of a quasimolecule in the film and μ_i is the chemical potential of the ith component in the surrounding membrane. At equilibrium

$$\mu (r_e)=\sum _{i=1}^m{\nu }_i{\mu }_i=-kT\mathrm{\Delta },$$ (2)

where r_e is the external radius of the film at equilibrium. We will argue [by Eq. (33) and the description below it] that the variable Δ, defined by Eq. (2), is effectively the amount of subsaturation, expressed in terms of chemical potentials.

The chemical potential of a quasimolecule in the film is a function of the effective boundary energy, W, of the domain in which it resides. W is the grand potential, Ω, of the system. It is convenient to use the grand potential to describe surface phenomena and thin films because the independent variables of Ω are temperature, T, and chemical potential, μ, and each of them are the same in the two contacting phases. It is known that for two three-dimensional phases separated by a film of thickness much less than the radius of the interface Ω_s = σ_{ef f}A, where A is the area of a surface within the interface and σ_{ef f} is the “effective” surface tension that accounts for the film between the two phases [38]. It follows in an exactly analogous manner that for a film in two-dimensions, Ω_b = γ_{ef f}L, where γ_{ef f} is the effective line tension between two phases and L is the length of a boundary. In our particular case there are two boundaries: one between the protein and the lipid film (“protein-film”) and the other between the lipid film and the surrounding membrane (“film-surround”). Because these two boundaries have different lengths, it is more convenient to utilize the grand potential of the film, Ω_film, rather than an effective line tension γ_{ef f}. In this case Ω_film is the effective boundary energy for the inter-face between the protein and surrounding membrane when a lipid film intervenes between them. For a large film the two boundaries do not interact, and W is the sum of the boundary energies of the protein-film and the film-surround. We calculate W as the total energy of the elastic deformations at the boundary between the protein and the film. It follows from standard thermodynamic relations that for a film containing n quasimolecules,

$$n=-\frac{\partial {\mathrm{\Omega }}_{\mathit{film}}}{\partial \mu }=-\frac{\partial W}{\partial \mu }.$$ (3)

We introduce a as the mean area per quasimolecule in the film of external radius r, and rewrite Eq. (3) as

$$\frac{\pi (r^2-r_p^2)}{a}=-\frac{\partial W(r)}{\partial \mu (r)}=-\left(\frac{\partial W(r)}{\partial r}\right)/\left(\frac{\partial \mu (r)}{\partial r}\right).$$ (4)

A phase spontaneously forms at the point of a phase transition, and if the system is large, or connected to a reservoir of lipid, the thickness of a flat wetting film tends to infinity. (For curved surface film thickness will be finite due to Laplace forces.) At this transition point, we set the chemical potentials in the film and in the surrounding membrane equal to zero:

$$\mu (r\to \infty )=0,\text{and}\text{so}\mathrm{\Delta }\to 0.$$ (5)

Substituting Eq. (5) into Eq. (4), we obtain the dependence of the chemical potential on the external radius of the film,

$$\mu (r)={\int }_r^{\infty }\frac{a}{\pi (x^2-r_p^2)}\frac{\partial W(x)}{\partial x}dx.$$ (6)

Using Eq. (2), we obtain the final expression for the thickness of the film at equilibrium,

$$\mu (r_e)={\int }_{r_e}^{\infty }\frac{a}{\pi (x^2-r_p^2)}\frac{\partial W(x)}{\partial x}dx=-kT\mathrm{\Delta }.$$ (7)

Equation (7) takes on a convenient form at large r_p, because the effective line tension can be written as γ(r) = W(r)/(2πr). Substitution of this relation into the Eq. (7) yields

$${\int }_{l_e}^{\infty }\frac{a}{\pi [{(l+r_p)}^2-r_p^2]}\frac{\partial 2\pi r\gamma (r)}{\partial r}dl\to {\int }_{l_e}^{\infty }\frac{a}{2\pi l{r}_p}\left(2\pi (l+r_p)\frac{\partial \gamma (l)}{\partial l}+2\pi \gamma (l)\right)dl\to {\int }_{l_e}^{\infty }\frac{a}{2\pi l{r}_p}2\pi r_p\frac{\partial \gamma (l)}{\partial l}dl={\int }_{l_e}^{\infty }\frac{a}{l}\frac{\partial \gamma (l)}{\partial l}dl=-kT\mathrm{\Delta }.$$ (8)

To summarize the procedure for obtaining the thickness of the wetting film at equilibrium: Given the dependence of boundary energy W on raft radius r, we numerically calculate the dependence of the chemical potential of the quasimolecule in the film, μ, on r [see Eq. (6)]. By using Eq. (7), we obtain r_e.

III. CALCULATION OF BOUNDARY ENERGY

A. Model

To calculate W(r), we treat the film and the surrounding membrane as elastic media. The length of the hydrophobic transmembrane domain will generally be somewhat different than the thickness of the hydrophobic core of the membrane (Fig. 2). If the membrane did not deform near the protein boundary, the “hydrophobic mismatch” would expose a hydrophobic surface to water. But this exposure is energetically very unfavorable because the surface tension of a water-hydrocarbon surface is so high. The membrane should thus elastically deform near the protein molecule in order to decrease the area of the contact of a hydrophobic surface to water [56]. In model bilayer systems, experiments show that a liquid-ordered domain is generally thicker, by 0.6– 0.8 nm (per bilayer), than the liquid-disordered membrane that surrounds it [64], and so elastic deformations should occur between these two lipid phases [55]. For a multicomponent membrane, the hydrophobic mismatch between the protein molecule and the liquid-disordered surrounding membrane could potentially be compensated for in two ways:

FIG. 2.

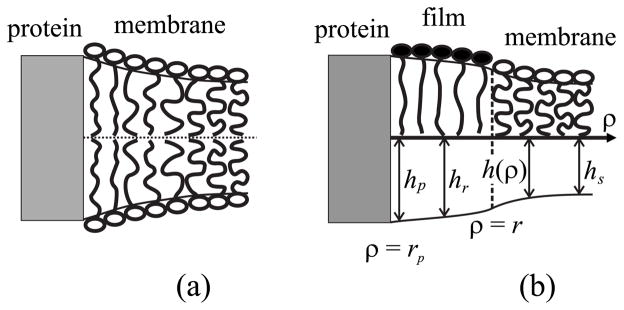
Compensation of hydrophobic mismatch between the surrounding bilayer membrane and a protein transmembrane domain (gray). (a) Compensation is achieved by deformation of the liquid-disordered membrane without formation of a film. (b) Compensation with the formation of a thin film. The film is in a liquid-ordered state. For both (a) and (b), the hydrophobic mismatch at the protein surface is completely compensated by membrane deformations. The notations are described in the body of the text.

1. The membrane remains laterally homogeneous in composition, but deforms near the protein [Fig. 2(a)].

2. A local phase transition takes place near the protein: a film of a liquid-ordered phase forms and elastic deformations occur at two boundaries (between the protein-film and film-surrounding membrane) to compensate for the hydrophobic mismatch [Fig. 2(b)].

The first possibility is the limiting case of the second for a film of zero thickness. We thus calculate the energy for a system consisting of a protein, a liquid-ordered film, and a liquid-disordered surrounding membrane under the condition that elastic deformations take place at the boundaries between the protein and the film as well as between the film and the surrounding membrane.

B. Deformations

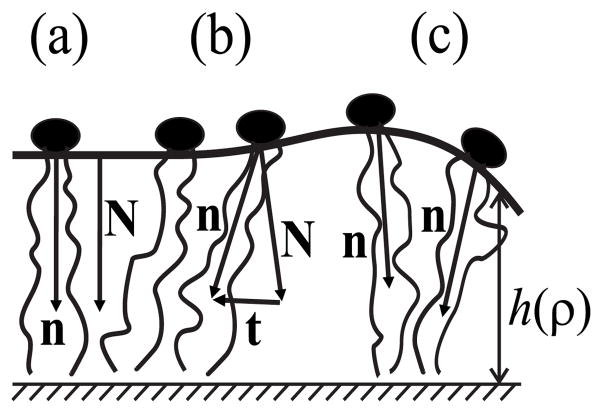
We assume that the membrane is symmetrical relative to its monolayer interface (midplane of the bilayer), and the deformations in both monolayers are identical. We thus consider a single flat monolayer. To treat the monolayer as a continuous elastic medium, we characterize the mean orientation of lipid molecules by a vector field of unit directors, n, defined relative to the neutral surface, a surface that is within the monolayer [45]. The vector field of unit normals, N, describes the shape of the neutral surface (Fig. 3). The initial unperturbed neutral surface is flat, so the directors and the normals are parallel to each other and perpendicular to the neutral surface [Fig. 3(a)]. We consider small deviations from the initial state and calculate the energy of the elastic deformations to second order (i.e., a quadratic approximation is used).

FIG. 3.

Deformations of elements of a monolayer: (a) the initial undistorted state, (b) the deformation of tilt, (c) the deformation of splay. See text for details.

Continuum membrane mechanics can characterize all known membrane deformations by a superposition of three fundamental deformations: area compression and/or stretching, splay, and tilt. However, membranes are almost un-stretchable and thus only the deformations of splay and tilt need to be considered. This is readily seen by using the elastic moduli to compare the characteristic energy surface densities (energy per area) necessary for each deformation: for compression and/or stretching, the energy density is E_a ~120 erg/cm² [65]; for splay, it is $B/h_m^2~10\text{erg}/{\text{cm}}^2$ for a monolayer thickness h_m ~ 2 nm [66,67]; and for tilt, it is K ~40 erg/cm² [6,45,68]. The energy to stretch (or compress) the area is even greater for cholesterol-enriched membranes, which have several-fold higher compression moduli [69–72]. Thus, lipids should deform at the boundaries through splay and tilt, with little contribution from area compression and/or stretching. The splay deformation [Fig. 3(c)] is given by div n along the neutral surface. Thus the magnitude of splay equals the rate of change of the angle between directors along the neutral surface. The tilt deformation [Fig. 3(b)] is characterized by the tilt vector t = n/(n · N)−N [45]; for small deformations, its magnitude at each point is equal to the angle between the normal and the director.

C. Energy of the elastic deformations

The energy of deformation per unit area of the neutral surface to second order is [45]

$$w_e=\frac{B}{2}{(\text{div}\mathbf{n}+J_0)}^2-\frac{B}{2}{J}_0^2+\frac{K}{2}{\mathbf{t}}^2,$$ (9)

where J₀ is the spontaneous curvature of the monolayer, B is the elastic splay modulus, and K is the tilt modulus. In our sign convention, the spontaneous curvature of lysoPC is positive. The first two terms in Eq. (9) account for the deformation of splay, and the last term describes the tilt deformation. The total energy of the deformations is

$$W_e=\int w_{e}dA,$$ (10)

where integration is performed over the total neutral surface of the monolayer. We assume that the deformations completely compensate for the hydrophobic mismatch between both the protein and the film and between the film and the surround. In other words, after deformation, polarizable and hydrophobic media do not contact each other.

We introduce a polar coordinate system, with origin O at the center of the axis of the cylindrically symmetric protein. Because of cylindrical symmetry, deformations at a point of the neutral surface depend only on the distance ρ from the point to the origin O. Thus, the vector variables, n, N, and t, are fully described by their projections onto the plane of monolayer interface. Explicitly, n_ρ= n, N_ρ= N and t_ρ= t. For small deformations, div n [see Eq. (9)] is given by

$$\text{div}\mathbf{n}=n^{\prime }(\rho )+\frac{n(\rho )}{\rho },$$ (11)

where the prime (the superscript) denotes a derivative with respect to ρ. Substituting the area element dA ≈ 2πρdρ and Eq. (11) into Eq. (10), we obtain

$$W_e=\int 2\pi \rho \left\{\frac{B}{2}{\left(n^{\prime }(\rho )+\frac{n(\rho )}{\rho }+J_0\right)}^2-\frac{B}{2}{J}_0^2+\frac{K}{2}t{(\rho )}^2\right\}d\rho .$$ (12)

D. Volumetric incompressibility

We assume that deformations do not alter the volume of any element of the hydrophobic interior of a monolayer (i.e., the monolayer is locally volumetrically incompressible). This assumption is standard in membrane mechanics [7,18,45,47] and is based on experimental measurements that show that the modulus to volumetrically compress a bilayer (which yields the energy necessary to change density) is very high, 10⁹ – 10¹⁰ J/m³ [73,74]. We denote the distance between the monolayer interface and the neutral surface as h(ρ) and refer to h(ρ) as the monolayer height (Fig. 3). The height of the initial unperturbed monolayer is denoted h₀. For small deformations, the condition of volumetric incompressibility is

$$h(\rho )=h_0-\frac{h_0^2}{2}\left(n^{\prime }(\rho )+\frac{n(\rho )}{\rho }\right)$$ (13)

[7,45]. Equation (13) quantifies the manner in which incompressibility restricts the possible deformations. We introduce the deviation of the monolayer height from h₀ as

$$\xi (\rho )=h_0-h(\rho ),$$ (14)

and write Eq. (13) as

$$\xi (\rho )=\frac{h_0^2}{2}\left(n^{\prime }(\rho )+\frac{n(\rho )}{\rho }\right).$$ (15)

We obtain the tilt-vector projection, t, with required accuracy, subject to Eq. (15), as equal to

$$t\approx n-N\approx n-h^{\prime }=n+{\xi }^{\prime }=n+\frac{h_0^2}{2}{n}^{″}+\frac{h_0^2}{2}\frac{n^{\prime }}{\rho }-\frac{h_0^2}{2}\frac{n}{{\rho }^2}.$$ (16)

Henceforth, we omit the argument ρ. Substituting Eq. (16) into the energy functional, Eq. (12), we obtain

$$W_e=\int 2\pi \rho \left\{\frac{B}{2}{\left(n^{\prime }+\frac{n}{\rho }+J_0\right)}^2-\frac{B}{2}{J}_0^2+\frac{K}{2}{\left(n+\frac{h_0^2}{2}{n}^{″}+\frac{h_0^2}{2}\frac{n^{\prime }}{\rho }-\frac{h_0^2}{2}\frac{n}{{\rho }^2}\right)}^2\right\}d\rho .$$ (17)

To calculate the boundary energy, we minimize the functional of equation (17) in both the region of the film (r_p <ρ<r) and the region of the surround (ρ>r) and solve the resulting Euler-Lagrange equation subject to the condition that the director and the monolayer height are continuous at the boundary between the film and the surround (ρ= r). If the monolayer neutral surface did not deform at the film-surround boundary, a discontinuity would arise because height mismatch would lead to a step difference in membrane thickness at the boundary. This would create an interface at the step that consists of the hydrophobic tails of the film’s lipids in contact with polar headgroups of the adjacent lipids within the bulk membrane. This interface has surface tension, σ. We used the algorithm described in [56] to estimate the minimum value of σ that would be necessary to provide continuity of a neutral surface. For a line tension at the film-surround interface of about 1 – 2 pN [75] and a height mismatch in the range of 0.3– 0.6 nm per monolayer, σ must exceed ~10 dyn/cm. For lower line tensions, even smaller values of σ would ensure continuity: for γ ~ 0.1– 0.3 pN [76], σ only has to exceed 0.7– 2 dyn/cm. We set the boundary conditions by matching the height and the director of the film to those of the protein at their boundary and require that the membrane remain undeformed far from the film. The energy that results from this calculation has a number of quantitatively unknown parameters. We determined them by minimizing the energy with respect to these parameters. We indicate all variables corresponding to the film by the subscript “f,” those for the surrounding region by the subscript “s,” and those for the protein by “p.” We denote the length of the protein transmembrane domain (per monolayer) as h_p, the height of the film monolayer as h_f, and the height of the surrounding monolayer as h_s (h_f >h_s). For the sake of simplicity, the elastic moduli of the film and of the surround are assumed equal (i.e., B_f = B_s = B, K_f = K_s =K).

The variation of the energy functional with fixed boundary conditions yields the Euler-Lagrange equation

$$h_0^4{n}^{(4)}+2h_0^4\frac{n^{(3)}}{\rho }+\left(4(h_0^2-l^2)-3\frac{h_0^4}{{\rho }^2}\right)n^{″}+\left(4(h_0^2-l^2)+3\frac{h_0^4}{{\rho }^2}\right)\frac{n^{\prime }}{\rho }+\left(4-4\frac{(h_0^2-l^2)}{{\rho }^2}-3\frac{h_0^4}{{\rho }^4}\right)n=0,$$ (18)

where l = (B/K)^1/2. The general solution of the equation is

$$n(\rho )=c_1{J}_1(p\rho )+c_2{Y}_1(p\rho )+c_3{J}_1(q\rho )+c_4{Y}_1(q\rho ),$$ (19)

where c₁, c₂, c₃, c₄ are arbitrary complex coefficients determined by the boundary conditions, and J₁ and Y₁ are the corresponding Bessel functions of first order. The parameters p and q are given by

$$p=\frac{\sqrt{2h_0^2-l^2}}{h_0^2}+i\frac{l}{h_0^2},q=\frac{\sqrt{2h_0^2-l^2}}{h_0^2}-i\frac{l}{h_0^2},$$ (20)

where $\pm i=\sqrt{-1}$. The four complex coefficients, c₁, c₂, c₃, c₄, have eight real number constants, which would overdeter-mine a differential equation of the fourth order. But the physical requirement that the director must be a real number for any ρ reduces the independent coefficients to four.

E. Elastic energy of the surround

The monolayer surrounding the protein and the protein’s associated film is situated in the region ρ>r. The spontaneous curvature of the surround is J_s. We denote the boundary director and height deviation as

$$n(r)=n_0,\xi (r)={\xi }_s.$$ (21)

The monolayer is unperturbed far from the boundary, so

$$h(\infty )=h_s,n(\infty )=0,n^{\prime }(\infty )=0,\text{etc}.$$ (22)

The solution of the Euler-Lagrange equation, Eq. (18), that satisfies the conditions of Eq. (22) is

$$n_s(\rho )=c_{s1}[J_1(p_s\rho )+{iY}_1(p_s\rho )]+c_{s2}[J_1(q_s\rho )-{iY}_1(q_s\rho )].$$ (23)

We determined the coefficients, c_s1 and c_s2, from the boundary conditions, Eq. (21), to obtain

$$\begin{array}{l}{c}_{s1}=\frac{\frac{2}{h_s^2}[J_1(q_{s}r)-{iY}_1(q_{s}r)]{\xi }_s-q_s[J_0(q_{s}r)-{iY}_0(q_{s}r)]n_0}{p_s[J_0(p_{s}r)+{iY}_0(p_{s}r)][J_1(q_{s}r)-{iY}_1(q_{s}r)]-q_s[J_1(p_{s}r)+{iY}_1(p_{s}r)][J_0(q_{s}r)-{iY}_0(q_{s}r)]},\\ c_{s2}=\frac{-\frac{2}{h_s^2}[J_1(p_{s}r)-{iY}_1(p_{s}r)]{\xi }_s-p_s[J_0(p_{s}r)-{iY}_0(p_{s}r)]n_0}{p_s[J_0(p_{s}r)+{iY}_0(p_{s}r)][J_1(q_{s}r)-{iY}_1(q_{s}r)]-q_s[J_1(p_{s}r)+{iY}_1(p_{s}r)][J_0(q_{s}r)-{iY}_0(q_{s}r)]}.\end{array}$$ (24)

Substituting Eqs. (23) and (24) into the energy functional, Eq. (17), and integrating over r <ρ<∞ yields the final expression for the energy of the surrounding monolayer,

$$\begin{array}{l}{W}_s=-2\pi {\mathit{rKl}}^2{n}_0{J}_s+\frac{i2\pi \mathit{rKl}}{p_s[J_0(p_{s}r)+{iY}_0(p_{s}r)][J_1(q_{s}r)-{iY}_1(q_{s}r)]-q_s[J_1(p_{s}r)+{iY}_1(p_{s}r)][J_0(q_{s}r)-{iY}_0(q_{s}r)]}\\ \times (m_s[J_0(p_{s}r)+{iY}_0(p_{s}r)][J_0(q_{s}r)-{iY}_0(q_{s}r)]n_0^2-2\{[J_0(p_{s}r)+{iY}_0(p_{s}r)][J_1(q_{s}r)-{iY}_1(q_{s}r)]\\ +[J_1(p_{s}r)+{iY}_1(p_{s}r)][J_0(q_{s}r)-{iY}_0(q_{s}r)]\}{\xi }_s{n}_0+\frac{2}{h_s^2}{m}_s[J_1(p_{s}r)+{iY}_1(p_{s}r)][J_1(q_{s}r)-{iY}_1(q_{s}r)]{\xi }_s^2),\end{array}$$ (25)

where $m_s=\sqrt{2h_s^2-l^2}$.

F. Elastic energy of the film

The film of spontaneous curvature J_r that surrounds the protein occupies the region r_p <ρ<r. We denote both the director and the deviation in height, at the boundary between the film and the surround as

$$n(r)=n_0\text{and}\xi (r)={\xi }_r,$$ (26)

and at the protein-film boundary as

$$n(r_p)=n_p\text{and}\xi (r_p)=h_r-h_p={\xi }_p.$$ (27)

The conditions imposed by Eqs. (21) and (26) ensure continuity in the director across the film-surround boundary; Eq. (27) states that the height of the film at its boundary with the protein is equal to the length h_p of the protein’s transmembrane domain (per monolayer). To obtain the elastic energy of the film W_r, we use the boundary conditions, Eqs. (26) and (27), and express the coefficients c₁, c₂, c₃, c₄ in terms of n₀, ξ_r, n_p, and ξ_p. By substituting the director distribution n(ρ) into the energy functional, Eq. (17), and then integrating over the film region, r_p <ρ<r, we obtain the final expression for W_r. The expressions are very lengthy, so rather than show them here, we employ them to derive the curves illustrated in Sec. IV.

G. Total energy minimization

The total boundary energy of the system is

$$W=W_s+W_r.$$ (28)

W depends on five boundary parameters: n₀, ξ_r, ξ_s, n_p, and ξ_p. The parameters n_p and ξ_p are completely defined by the shape of the protein’s transmembrane domain. The remaining three parameters have the one constraint equation that the monolayer height is continuous at the film-surround boundary, as given by

$$h(r-0)=h(r+0),\text{or},\text{equivalently},{\xi }_s={\xi }_r-(h_r-h_s)={\xi }_r-\delta .$$ (29)

This equation allowed us to express one of the boundary parameter (e.g., ξ_s) in terms of the remaining two, ξ_r and n₀. By minimizing W with respect to ξ_r and n₀, we obtained the boundary energy as a function of protein radius, r_p, and film radius, r. This minimization is equivalent to balancing the forces and torques at the film-surround boundary. Although the minimization procedure is straightforward, the final expression is again very lengthy. As above, we do not show it, but instead use it to graphically illustrate the dependence of the boundary energy on the film thickness (see Sec. IV). The full expression for the boundary energy is available from Ref. [92].

H. Values of elastic moduli

Splay, B, and tilt, K, moduli have been determined for liquid-disordered lipid phases. B increases fourfold, from 5 to 20 kT (kT ~ 4 ×10⁻²¹ J) for a monolayer as chain length increases from 13 to 22 carbon atoms [77]. K has been estimated to be ~40 mN/m based on analyzing the transition of dioleoylphosphatidylethanolamine (DOPE) from an H_II to a Q_II lipid phase [68]. This value is similar to that expected from the theoretical argument that the tilt modulus should be numerically close to the water-hydrocarbon surface tension, ~50 mN/m. According to this argument, the tilt modulus should be relatively independent of lipid composition, and we thus assume that K ~ 40 mN/m for all lipid monolayers, and not just for DOPE. The elastic moduli of lipid wetted films have not been experimentally measured. For simplicity, we set the moduli of the film equal to those of the surrounding membrane. That is, we set B_f = B_s = B = 10 kT and K_f =K_s = K = 40 mN/m.

I. System properties

We now consider the values of the physical parameters, other than elastic moduli, that enter our equations. The height of a monolayer increases from 1.7 to 2.2 nm on increasing the chain length of the hydrocarbon chains from 13 to 22 carbon atoms [77]. We use the height of dioleoylphosphatidylcholine (DOPC), ~2 nm (i.e., h_s = 2 nm) in our calculations, because it is often used in experiments studying rafts. In an analogous manner, the height of a raft depends on the chain length of its constituent sphingomyelins. The lengths of the variable chain of sphingomyelin vary from 16 to 24 carbon atoms (data from Ref. [93]). Atomic force microscopy (AFM) experiments have shown that for egg sphingomyelin (predominantly 16 carbon atoms) the monolayer height is 0.3– 0.35 nm greater than that of DOPC (18 carbon atoms) [64]. We will therefore vary the height of the film wetting a protein in the range of 2.3– 2.6 nm.

The boundary energy depends on the spontaneous curvatures of the monolayers of the film and surrounding membrane. The spontaneous curvature of a multicomponent lipid monolayer is typically set equal to the weighted average of the spontaneous curvatures of each component [78]. The radius of spontaneous curvature of DOPC is R_DOPC = −8.7 nm and that of cholesterol is R_Chol = −2.7 nm [79]. The radius of curvature has not been measured for any sphingomyelin, but because their acyl chains are generally saturated we assume R_Sm is positive, and we set R_Sm ~ 6 nm. For the compositions of the liquid-ordered and liquid-disordered phases that have been experimentally inferred [28], the spontaneous curvature of a liquid-ordered monolayer would vary in the range of ~ 0 to −1/14 nm⁻¹ and that of the surrounding membrane would be ~−1/8 nm⁻¹. We assume J_r is equal to either 0 or −1/14 nm⁻¹ and J_s is equal to −1/8 nm⁻¹. We also consider J_r = J_s = 0 for the sake of simplicity.

To obtain the area per quasimolecule, a, we set the sum of the stoichiometric coefficients to $1({\mathrm{\sum }}_{i=1}^m{\nu }_i=1)$. With this normalization, a is the average area per molecule in the film. We fix a = 0.5 nm². Because we assume that the hydrophobic transmembrane domain of a protein is cylindrical and perpendicular to the plane of the bilayer, its director projection n_p = 0. To capture the fact that the length of transmembrane domain depends on the particular protein, we let h_p vary in the range of 2 – 2.9 nm. To determine the dependence of film properties upon the radius, r_p, of the protein or upon an aggregate of proteins, we vary r_p over the range 5 – 30 nm.

IV. RESULTS

A. Chemical potential of a film for a protein and film of equal heights

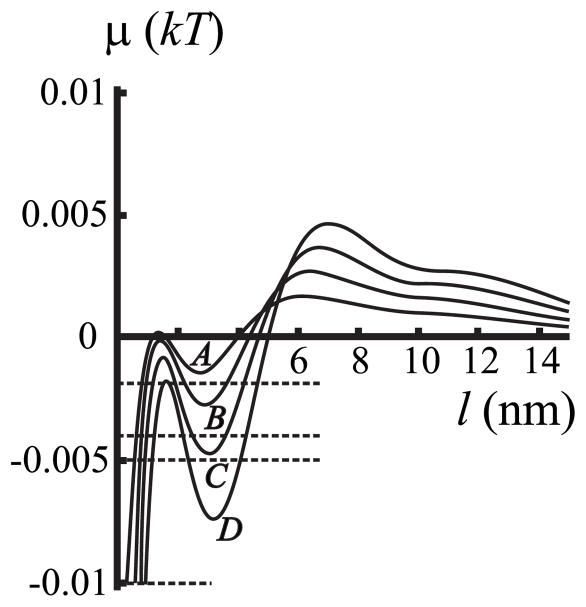
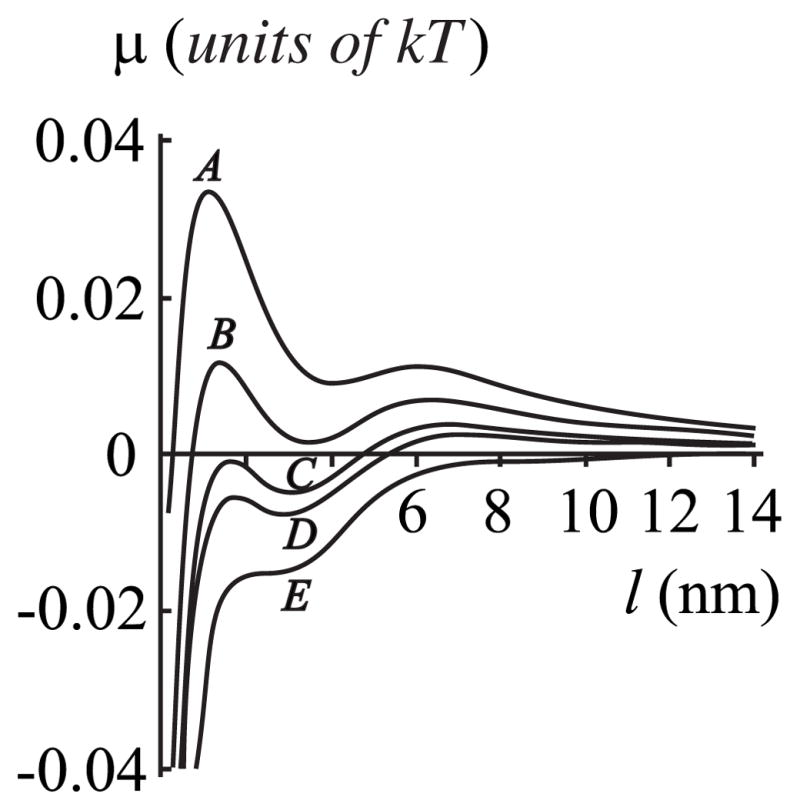
We first consider the case in which the length of the transmembrane domain of the protein and the film height are the same (i.e., h_p = h_r) and spontaneous curvature is zero everywhere (J_r = J_s = 0). However, there will be a hydrophobic mis-match between the film and the surrounding membrane. The dependence of chemical potential μ (l) in the film upon its thickness, l = r−r_p, is shown in Fig. 4 for different values of h_p = h_r (curves A – D), maintaining a radius of r_p = 20 nm for the lipid-protein aggregate.

FIG. 4.

The dependence of chemical potential of the film μ on film thickness l = r − r_p. Here, zero spontaneous curvatures J_r = J_s = 0 and zero protein-film mismatch h_p = h_r are assumed. This allows the influence of the mismatch between the film and surround on chemical potential to be directly illustrated by curves A – D: curve A, h_p = h_r = 2.3 nm; curve B, h_p = h_r = 2.4 nm; curve C, h_p = h_r = 2.5 nm; curve D, h_p = h_r = 2.6 nm. h_s = 2.0 nm and r_p = 20 nm for all four curves. The horizontal dashed lines correspond to the chemical potentials of the surrounding membrane at subsaturations Δ = 0.2%, 0.4%, 0.5%, and 1%.

According to Eq. (7), at equilibrium μ (r) in the film equals $-kT\mathrm{\Delta }={\mathrm{\sum }}_{i=1}^m{\nu }_i{\mu }_i$ in the surrounding membrane. We first consider the case that the surrounding membrane is an ideal solution of lipids. We can write the chemical potential for each component as

$${\mu }_i=\mathit{kT}ln\frac{c_i}{c_i^{eq}},$$ (30)

where c_i is the concentration of the ith component in the surrounding membrane, $c_i^{eq}$ is the equilibrium concentration of the ith component near a straight interface between a film and a surrounding membrane, and k is the Boltzmann constant. When the system is close to the phase transition point, we can expand the logarithm of Eq. (30), yielding

$${\mu }_i=kT\frac{c_i-c_i^{eq}}{c_i^{eq}}.$$ (31)

In accordance with prior investigators [62,63], the total amount of subsaturation for an ideal surrounding solution, Δ̃, is given by

$$\stackrel{\sim }{\mathrm{\Delta }}=\sum _{i=1}^m{\nu }_i\frac{c_i^{eq}-c_i}{c_i^{eq}}.$$ (32)

Equation (6) yields, subject to Eqs. (31) and (32),

$$\mu (r_e)=-kT\stackrel{\sim }{\mathrm{\Delta }}.$$ (33)

For an ideal solution, Δ= Δ̃. Thus, at equilibrium the chemical potential in the film is negative and its absolute value, in thermal units (kT), is equal to the total subsaturation Δ̃. Because $\mathrm{\Delta }=-{\mathrm{\sum }}_{i=1}^m\frac{{\nu }_i{\mu }_i}{kT}$ and the subsaturation $\stackrel{\sim }{\mathrm{\Delta }}={\mathrm{\sum }}_{i=1}^m{\nu }_i\frac{c_i^{eq}-c_i}{c_i^{eq}}$ are the same for an ideal solution, we refer to Δ as an effective subsaturation. Experimental data are not available for the value of Δ̃ or Δ. We therefore treat Δ as a free parameter. Because the values of Δ̃ and Δ are independent of the thickness of the wetting film, these parameters are displayed as horizontal lines in plots of μ (l) vs film thickness l (see Fig. 4).

Each line intersects the μ (l) curves at the film thicknesses indicated by the abscissa (Fig. 4); these films can be stable, metastable, or unstable. The horizontal line intersects the curves at either one or three intersection points at negative μ (l) (Fig. 4). If the effective subsaturation Δ is large (>0.75%), the horizontal line intersects μ (l) once and so only a single thin film can form. The intersection point on the left-most rising phase of μ (for either one or three intersection points) corresponds to a thin film that is referred to as an “adsorption film” (for our parameters l ~ 1 nm). Because the adsorption film has only about a single layer of lipids (for l = 1 nm), it is questionable whether our continuum model is applicable for the boundary energy. If, however, the effective subsaturation Δ is small, there can be three intersection points. In these cases, if the intersection is in a region in which μ (l) increases for increasing l, the film is either stable or metastable; the decreasing regions yield films that are unstable [38]. For example, for a subsaturation of ~0.5% and h_p = h_r = 2.3 nm, the film of ~1 nm thickness is stable (curve A). Similarly, stable or metastable films of ~1.5 nm and ~4 nm can form for h_p = h_r = 2.6 nm (curve D); but a film of ~2 nm thickness is unstable.

To determine, for small subsaturations, whether a film is stable or metastable in the increasing region of μ (l), we compare the two values of W evaluated at the two film thicknesses; the higher value yields the metastable film and the lower value yields the stable film. The values of W are not extrema (minima or maxima) at the thicknesses of stable, metastable, or unstable films. But the free energy of the system E(r) (the work needed to create a film of a thickness l = r − r_p) exhibits extrema for each of these films. For a constant chemical potential in the surrounding membrane, E(r) is

$$\begin{array}{l}E(r_0)={\int }_{r_p}^{r_0}\left(\mu (r)-\sum _{i=1}^m{\nu }_i{\mu }_i\right)dn\\ ={\int }_{r_p}^{r_0}[\mu (r)+kT\mathrm{\Delta }]dn\\ =F(r_0)-F(r_p).\end{array}$$ (34)

Because $dn=\frac{2\pi \mathit{rdr}}{a}$, we obtain

$$E(r_0)={\int }_{r_p}^{r_0}\frac{2\pi r}{a}[\mu (r)+kT\mathrm{\Delta }]dr.$$ (35)

Equation (35) quantitatively states that to change the radius from r to r + dr, one must transfer $\frac{2\pi \mathit{rdr}}{a}$ quasimolecules from the surround to the film; the energy of each transferred qua-simolecule changes from −kTΔ in the surrounding membrane to μ (r) in the film. Combining Eq. (2) and the difference in energy upon transfer of each quasimolecule, μ (r) − (−kTΔ ) = μ (r) + kTΔ, we obtain

$$\begin{array}{l}E(r_e)={\int }_{r_p}^{r_e}[\mu (r)+kT\mathrm{\Delta }]dn\\ =[\mu (r_e)+kT\mathrm{\Delta }]n_e-[\mu (r_p)+kT\mathrm{\Delta }]·0-{\int }_{r_p}^{r_e}nd\mu =0·n_e-0+W(r_e)-W(r_p)\\ =W(r_e)-W(r_p).\end{array}$$ (36)

Equation (36) demonstrates that rather than determining whether a film is stable, metastable, or unstable at equilibrium by comparing values of W, films can be identified from the extrema of E(r). Unstable films correspond to the maxima; a stable film resides at the global minimum; a metastable film resides at a local minimum of E(r). We use the parameters of Fig. 4, curve C, and plot E(r) for different degrees of subsaturation in Fig. 5. For a large degree of subsaturation, E(l) displays a single minimum and it occurs at l ~ 1 nm (curve A, Fig. 5), the same single value of l at which the horizontal line intersects μ (l) (Fig. 4). For smaller subsaturations, Δ= 0.4% (Fig. 5, curve B) or Δ= 0.2% (Fig. 5, curve C), the two minima and one maxima in E(l) correspond to the same values of l as the three intersection points (Fig. 4). As readily seen (Fig. 5), for Δ= 0.4% (curve B) the thicker of the two films (~4 nm) resides at a local minimum and is thus metastable. More work is required to create it than to create the stable thinner film (~2 nm). For Δ = 0.2% (Fig. 5, curve C), the opposite is the case: more work is needed to create the thinner metastable film than the thicker ~4 nm stable film. The barrier separating the stable and metastable film is small, ~1 – 2 kT.

FIG. 5.

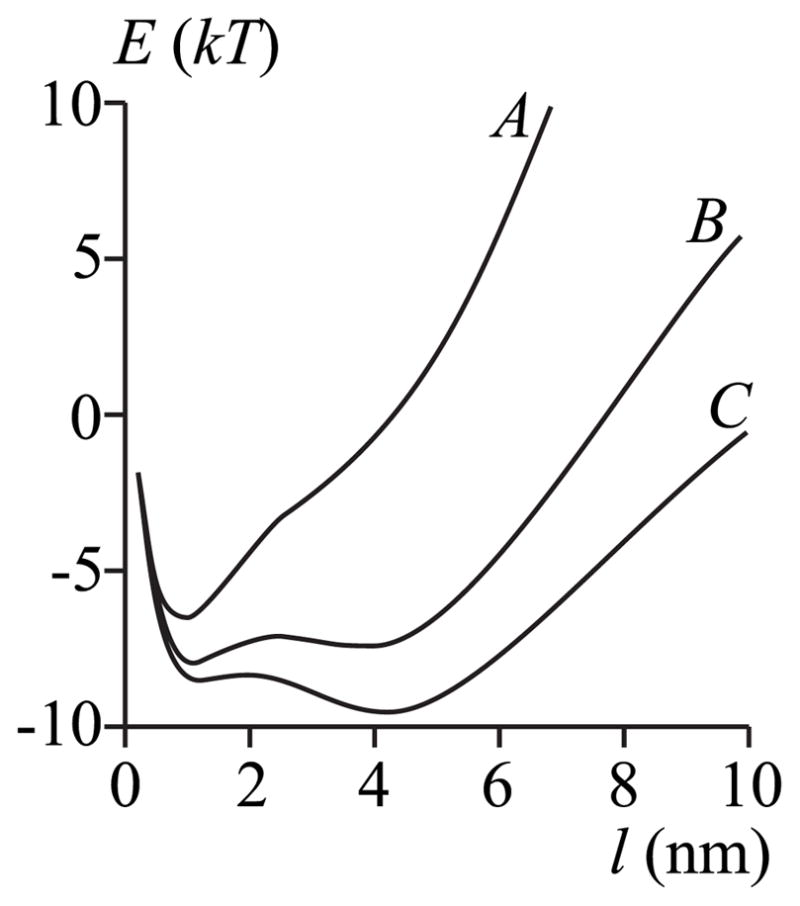
The work E to create a film of thickness l. Curves A – C represent different membrane subsaturations corresponding to those of the horizontal dashed lines in Fig. 4: curve A, Δ = 1%; curve B, Δ = 0.4%; curve C, Δ = 0.2%. The parameters are those of curve C of Fig. 4, J_r = J_s = 0, h_p = h_r = 2.5 nm, h_s = 2.0 nm, and r_p = 20 nm.

We now graphically illustrate W(l) and use its features to describe the dependence of chemical potential on film thickness (Fig. 6). For r → ∞, the boundary energy W(r) → 2πrγ > 0 where 2π γ is the constant slope at large l (Fig. 6). (Physically, γ is the effective line tension. ) Because ∂ W(r)/∂r is positive for large r, μ (r) is also positive [see Eq. (7)]. But W(r) is overall decreasing with r for r <7 nm (Fig. 6), and so μ (r) is negative over this region. A greater hydrophobic mismatch at the film-membrane boundary yields a greater |∂W(r)/∂ r|. This can be seen by noting that a greater height mismatch leads to a larger decrease in boundary energy W (e.g., compare curves A and D in Fig. 6). In other words, the chemical potential is lower for a large mismatch. This is readily seen by the lowering of chemical potential as the mismatch increases from curve A (smallest mismatch) to curve D (greatest mismatch) of Fig. 4. Consequently, a thicker film forms at a given subsaturation for larger mismatch; equivalently, a film of a given thickness can form for greater levels of subsaturation when the mismatch is larger (Fig. 4). For example, for l ~ 3 nm, films can form at equilibrium for a subsaturation down to ~0.2% if h_p = h_r = 2.3 nm, but a film will form for subsaturation as low as ~ 0.6% if h_p = h_r = 2.6 nm (Fig. 4).

FIG. 6.

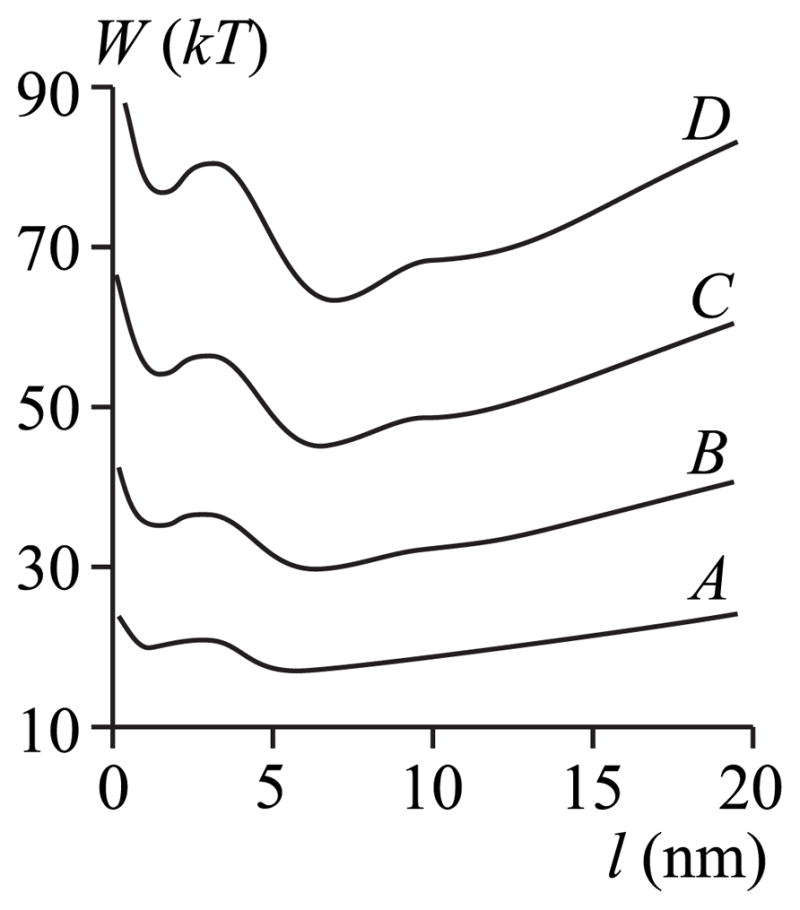
The dependence of boundary energy W (per monolayer) on l. All parameters for curves A – D are the same as in Fig. 4.

The oscillations of the chemical potential μ (l) (Fig. 4) are due to the oscillations of the boundary energy W(l) (Fig. 6), as given by Eq. (7). The splay deformation causes W(l) to oscillate for a monolayer that is locally volumetrically incompressible: substituting the projection of the tilt vector t = n − N and N ~ h′ into the equation of local volumetric incompressibility [Eq. (13)], an inhomogeneous equation for harmonic oscillations of monolayer height is obtained for r → ∞ [56]. If instead, r is finite, Eq. (13) yields the corresponding Bessel equation; its solution also oscillates. Physically, the elastic perturbations at each of the two boundaries (protein-film and film-membrane) oscillate and this generally drives the director distributions in different directions within the film. These oscillations directly lead to the boundary energy oscillations: when the directors of the two boundaries compete minimally, the energetic penalties are small and W is at its minimum; when the directors compete severely, W is at its maximum.

The characteristic lengths of decay and oscillations of deformations are defined by the real and imaginary parts of the parameters p and q in Eq. (20). The general solution, a sum of Bessel functions [Eq. (19)], of our Euler-Lagrange equation, Eq. (18), in the limit ρ→∞ provides expressions for the characteristic lengths. The Bessel function J₁(pρ), for example, may be written as

$$J_1(p\rho )~\partial e^{\pm Im(p)\rho }sin(Re(p)\rho )+\beta e^{\pm Im(p)\rho }cos(Re(p)\rho ),$$ (37)

where α and β are complex coefficients, and Re(p) and Im(p) are the real and imaginary parts of p, respectively. It immediately follows from Eq. (37) that the characteristic lengths of the decay, L_decay, and of the oscillation, L_osc, of deformations are

$$\begin{array}{l}{L}_{\mathit{decay}}=\frac{1}{Im(p)}=\frac{h_0^2}{l}~2-4\text{nm},\\ L_{\mathit{osc}}=\frac{2\pi }{Re(p)}=\frac{2\pi h_0^2}{\sqrt{2h_0^2-l^2}}~7.5-9.5\text{nm}.\end{array}$$ (38)

B. Dependence of chemical potential on film thickness for different lengths of a protein’s transmembrane domain

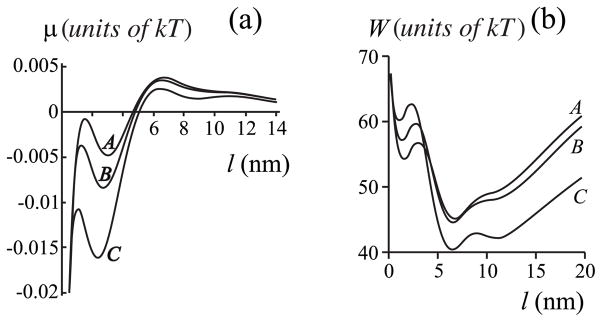
For h_p ≠ h_f (i.e., there is a protein-film hydrophobic mis-match), the chemical potential μ (l) exhibits damped oscillations around μ= 0 with increasing film thickness l [Fig. 7(a)]. These oscillations in μ (l) are again caused by the oscillations in the boundary energy W (l) see [Fig. 7(b) and Eq. (7)]. For very small subsaturations (<1 %), a relatively thick, metastable film of ~10– 12 nm can form if h_p >h_r [i.e., there is a local minimum in curve C for l ~ 12 nm, Fig. 7(a)]. But the stable film is thinner, l ~ 3 nm (Fig. 8). If the thick, metastable film forms, thermal fluctuations must have resulted in the system surmounting the high energetic barrier (maximum E at ~9 nm) of 15–20 kT that separates the energy minima at l = 3 nm and 12 nm. But the barrier for a metastable film to convert to a stable film is only ~kT (Fig. 8), and so once formed, the metastable film will quickly convert to a stable film. At large subsaturations, only an adsorption film can form with mismatch (h_p ≠h_r). This is similar to the case without mismatch between the protein and film (h_p = h_r) (Fig. 4). But with mismatch, the thickness of the adsorption film is somewhat larger: for 1% subsaturation, l_e ≤1 nm for h_p = h_r = 2.5 nm, while l_e ~ 2.5 nm for h_p = 2.7 nm, h_r = 2.5 nm [Fig. 7(a)].

FIG. 7.

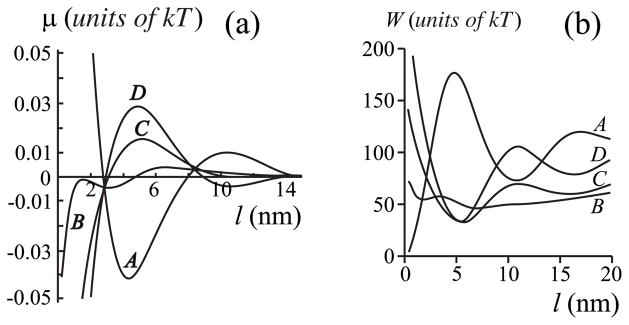
(a) The dependence of chemical potential of the film μ on film thickness l = r − r_p. The spontaneous curvatures are set equal to zero, J_r = J_s = 0, but in contrast to Fig. 4, the length of the protein transmembrane domain is varied to create a height mismatch between the protein and film. Curve A, h_p = 2.0 nm; curve B, h_p = 2.5 nm; curve C, h_p = 2.7 nm; curve D, h_p = 2.9 nm. (b) The dependence of the boundary energy W (per monolayer) on l. All parameters for curves A – D are the same as in (a). For (a) and (b), h_r = 2.5 nm, h_s = 2.0 nm, and r_p = 20 nm.

FIG. 8.

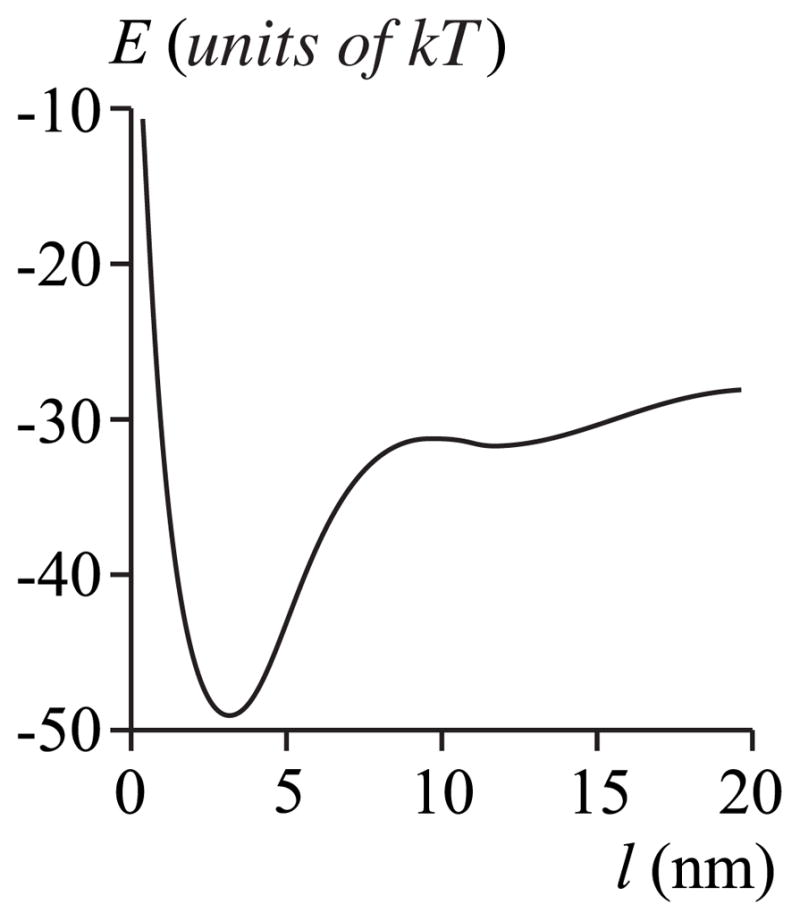
Work E for creating a film of thickness l for the case of curve C in Fig. 7: J_r = J_s = 0, h_p = 2.7 nm, h_r = 2.5 nm, h_s = 2.0 nm, and r_p = 20 nm. Zero subsaturation is assumed, Δ= 0%.

It may seem surprising that an equilibrium film of 4 – 8 nm thickness would form at all if the transmembrane domain length is less than the film height, h_s <h_p <h_r (or h_p = h_s) since it would clearly be energetically advantageous if the surrounding membrane deformed right up to the protein boundary [e.g., in curve A of Fig. 7 (a), μ increases and remains negative for l between 4 and 8 nm] rather than forming a film of greater height than the protein. But such a film would be highly metastable: For zero subsaturation (Fig. 9), a ~90 kT barrier must be surmounted to create the film and once formed, the 8 nm film is still unfavored by ~60 kT. If the subsaturation is not zero, the barrier is even higher. For h_p (2.0 nm) <h_r (2.5 nm, curve A of Fig. 7), the creation of an adsorption film is not favorable because μ (l) is positive for l <3 nm. We thus see that if the protein is shorter than (or has the same length as) the height of the surrounding membrane, a stable film will not form; if a film forms it is metastable.

FIG. 9.

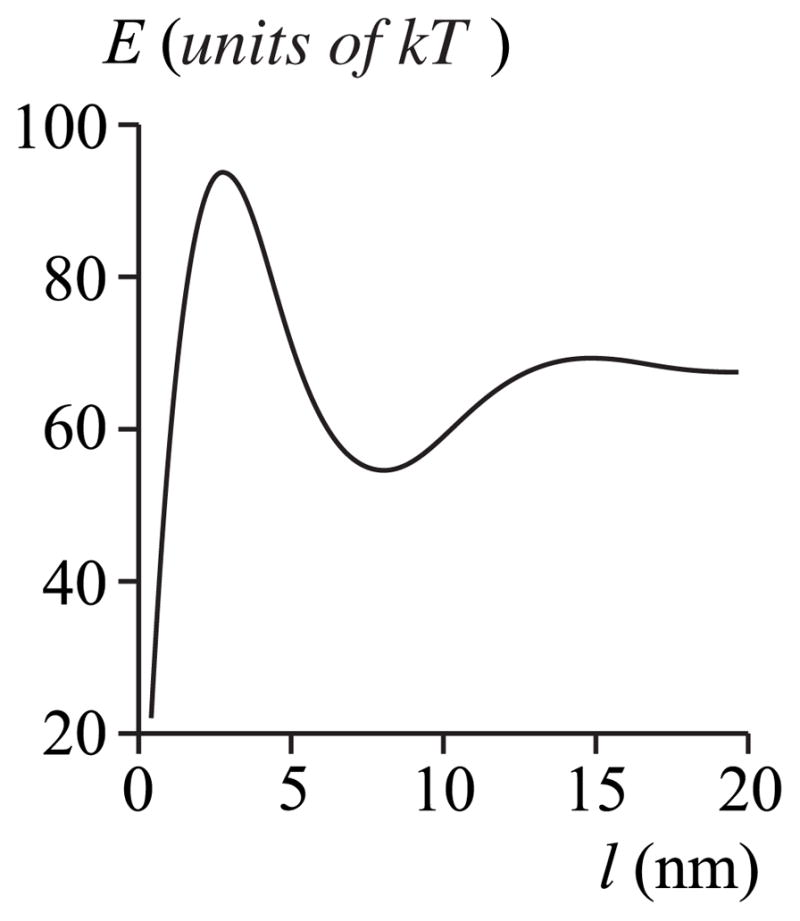
Work E for creating a film of thickness l for the case of curve A in Fig. 7: J_r = J_s = 0, h_p = 2.0 nm, h_r = 2.5 nm, h_s = 2.0 nm, and r_p = 20 nm. Subsaturation is Δ= 0%.

C. Dependence of film thickness on aggregate radius

To consider the dependence of the thickness of an equilibrium film on aggregate radius, we fix h_p = h_r = 2.5 nm and vary r_p to values of 5, 10, 20, and 30 nm (Fig. 10). Obviously, the thickness of the film increases for greater radii r_p. For example, l_e ~ 1 nm for r_p = 10 nm (curve B) and l_e ~5 nm for r_p = 30 nm (curve D). The films remain thin even if the system is saturated for finite aggregate radius. If r_p = ∞, an infinitely thick film would form if the system were saturated (curve E). But if the system is subsaturated at all, the film thickness remains relatively small even for r_p = ∞. The thickness is ~5 nm or less for 1% subsaturation. That is, only thin films can form if the system is subsaturated. For single proteins, only adsorption films will form.

FIG. 10.

The dependence of chemical potential of the film μ on film width l = r − r_p for varied protein radii r_p. Curve A, r_p = 5 nm; curve B; r_p = 10 nm; curve C; r_p = 20 nm; curve D; r_p = 30 nm, curve E, r_p = ∞. Spontaneous curvatures are zero, J_r = J_s = 0, and h_p = h_r = 2.5 nm, h_s = 2.0 nm.

D. Influence of monolayer spontaneous curvature on film properties

We have so far set to zero the spontaneous curvatures of the monolayers of the film and surrounding membrane. But the true values are generally not zero and this affects the boundary energy W (l) which in turn influences the chemical potential μ (l). We illustrate the consequences of nonzero spontaneous curvatures on the dependence of chemical potential [Fig. 11 (a)] and boundary energy [Fig. 11(b)] on film thickness by eliminating mismatch between the protein and the film.

FIG. 11.

(a ) The dependence of chemical potential of the film μ on film thickness l = r − r_p for varied spontaneous curvatures. Curve A, J_r = J_s = 0; curve B, J_r⁼ −1/14 nm⁻¹, J_s = −1/8 nm⁻¹; curve C, J_r = 0, J_s = −1/8 nm⁻¹. The equilibrium width of the film is largest for maximum |J_r − J_s|. (b) The dependence of the boundary energy W (per monolayer)on l. All parameters for curves A – D are the same as in (a). In all curves of panels (a) and (b), h_p = 2.5 nm, h_r = 2.5 nm, h_s = 2.0 nm, r_p = 20 nm.

For a given subsaturation, μ becomes more negative and the film equilibrium thickness becomes larger when the magnitude of the spontaneous curvature difference |J_r − J_s| is made greater [curve C in Fig. 11 (a)]. This occurs because the boundary energy for large films (l → ∞) contains a term proportional to − (J_r − J_s)² [56] and so the greater |J_r − J_s| becomes, the less is the boundary energy [compare curve A and curve C in Fig. 11 (b)].

The reason a difference in spontaneous curvature lowers boundary energy (and, thus, chemical potential) can be intuitively understood. For simplicity, assume that the spontaneous curvature of the monolayer of the film is zero and that of the surrounding membrane is negative. The membrane is then under mechanical stress. The film allows the stress to partially relax because the boundary director, n₀, can now reorient at the film-membrane boundary. In other words, the formation of a film creates an additional interface, and this provides an additional degree of freedom to the system. Additional degrees of freedom always allow stresses to relax, permitting films to form with less energy expenditure than in the case of equal spontaneous curvature over the entire membrane.

V. DISCUSSION

We have quantitatively analyzed the thickness and stability of a film that wets a membrane protein or its complexes. We found that only a few layers of lipids will coat a single protein molecule or small protein complexes. Although individual proteins and small protein complexes are only coated by boundary lipids, they can form large aggregates due to mutual attraction caused either by specific protein-protein or lipid-mediated interactions. For an aggregate of proteins (diameter, tens of nanometers) that contain lipids in a liquid-ordered state, an additional lipid liquid-ordered film will form around the aggregate. This film will be a few nm thick. We assume that a lipid film coating a protein is in an l_o state. Large complexes can also form by proteins that interact via the cell cytoskeleton. For example, electron microscopy has clearly shown that large “islands” of proteins and their associated lipids can be attached to cytoskeleton; the lipids in these islands could be in different phase states [26]. A quantitative analysis of aggregation of membrane proteins is undoubtedly dependent on particular protein-protein interactions and this has received considerable attention, but this is far outside the scope of this paper. However, even theoretical studies that have treated lipid-mediated protein-protein interactions have not considered the formation of a film around the proteins. The prior studies treated proteins within an l_d bulk membrane and, consequently, the variety of lipid phase states (raft or nonraft) has not been considered. Here, we qualitatively consider factors affecting physical mechanisms that could lead to formation of protein-lipid rafts.

We first consider the case when the transmembrane domains of aggregated proteins can pack tightly with each other (i.e., the ectodomains are not so large that they prevent tight packing). Ignoring specific attractions between ectodomains, the main driving force for aggregation between lipid-coated proteins is minimization of the total boundary energy of all the domains. A simple estimation shows that the free energy of an aggregate of r_p = 20 nm is ~40 times smaller than if the coated protein molecules of radius ~1 nm remained dispersed. Now consider the case of transmembrane domains that cannot tightly pack against each other (e.g., the ectodomains are too large to allow tight packing). The transmembrane domain of each protein will be coated by a few rows of lipid molecules; typically the thickness of the coat, L₀, would be on the order of a few nanometers [56].

Both calculations and computer simulations [19,20] show that there is a critical distance, L_c ~ 2L₀, between transmembrane domains of proteins. If the ectodomains allow the transmembrane domains to approach each other to a distance L <L_c, the lipids that coat the proteins can merge to form a common coat. If L <L_c, the concentration of proteins is great enough to cause lipids to locally phase separate. We classify these protein-lipid complexes with the surrounding lipid film in an l_o state as rafts. If the transmembrane domains cannot come closer than L_c, the lipid coats will remain separated and the lipids between the proteins (and their coats) would be in the same phase state as the surrounding membrane; these complexes could not be considered rafts. These proteins could move further apart unless attractive protein-protein interactions maintain them within a complex.

What functions could the lipid film surrounding the aggregate serve? Our results show that a surrounding lipid film prevents an individual protein from leaving an aggregate. If a protein does leave, the effective radius r_p of the aggregate decreases and the equilibrium film thickness will decrease as well (assuming a fixed subsaturation, see Fig. 10). We calculated the free energy E_min(r_p) of the equilibrium film of thickness l_e [e.g., see the curve E(l) in Figs. 5 and 8] for r_p varying between 15 to 30 nm [i.e., E(l = l_e), see Eq. (35)], for the parameters of Fig. 10 [i.e., J_r = J_s = 0, h_p = h_r = 2.5 nm, h_s = 2.0 nm] and an subsaturation Δ = 0.5%. The free energy of the equilibrium film, E_min(r_p), decreases for increasing r_p (Fig. 12). The physical reason is clear: the equilibrium film is created by the transfer of quasimolecules from the surrounding membrane; the chemical potential is less in the film than in the surround (see Fig. 10). Because E_min would increase if a protein left the aggregate, the film prevents this exit. Furthermore, E_min would decrease if a single protein or protein complex enters the aggregate, so the film would promote domain growth.

FIG. 12.

The dependence of the free energy E_min(r_p) of the equilibrium film on the radius of an aggregate r_p.

Merger of aggregates is thermodynamically favored, since it would lead to a decrease in their boundary energy [20]. However, the aggregates can be kinetically stabilized. The continuum elastic theory of membranes shows that the energy of interaction between two domains is nonmonotonic over separation distances. As a result, there is a significant energy barrier for a distance L ~ 3 nm between boundaries of two domains [56]. The height of the barrier depends strongly on the elastic properties of the domains; it is higher for a firm domain, and lower for a soft one. If, as seems reasonable, a protein aggregate is a more rigid structure than a liquid-ordered film, the energetic barrier hindering merger will be higher for aggregates lacking a lipid film. Estimates show that aggregates surrounded by films will merge with waiting times <1 s for radii of tens of nanometers, and with waiting times ~1 h for radii of hundreds of nanometers [34,56]. The rigid aggregates without wetting films will, in practice, not merge.

A. Assumptions of the model

We now consider the assumptions inherent in our model.

(1) We required the composition of the film to be independent of film thickness. This assumption is fairly standard when considering the kinetics of phase transitions of multi-component systems [62,63]. We have also assumed that the composition of the wetting film is similar to the lipid composition of rafts that form by lowering of temperature. There is experimental data that justifies this assumption for the case of model rafts in lipid bilayer membranes: for varying temperatures, the concentrations of the different lipids in liquid-ordered domains varied by only ~10% [28].

(2) Many molecular interactions—including hydrophobic, chemical, electrical, Van der Waals—contribute to the boundary energy. We considered only the “mechanical” contributions to free energy by treating a membrane as a continuous elastic medium. But because elastic moduli are affected by all molecular interactions, our treatment implicitly includes all interactions, at least to some extent. Clearly, the composition of a wetting film will generally be different from that of the surrounding bulk membrane and will be affected by molecular interactions differently than the surround. We allowed the values of these films’ spontaneous curvatures to vary from that of the surrounding bilayer, so the molecular interactions were somewhat accounted for.

We assume that concentrations of the components change abruptly at the film-surround boundary. More realistically, the composition will gradually change over the thickness of the interface. The gradual change should relax elastic stresses, and thereby lower the boundary energy. However, a gradual change in composition will also give rise to an additional “chemical” contribution to the boundary energy. Our calculations show (manuscript in preparation) that the chemical contribution and relaxation of elastic deformations roughly cancel each other.

A membrane can be considered a continuous medium as long as all characteristic lengths of the system are large compared with its molecular dimensions. Thus, continuum theory is justified for characteristic lengths greater than the lateral dimension of a lipid molecule, ~0.8 nm. But, the characteristic length of decay of the elastic deformations in the lipid film is about 3 nm, and this is not much larger than 0.8 nm. One may thus question whether continuum theory can be applied to narrow adsorptive films of thickness ≤1 – 2 nm. However, as a practical matter, macroscopic theory of elasticity is frequently employed for dimensions in the nm range and, as a rule, leads to reasonable results [46,47,54,68,80,81]. In fact, continuum theory has successfully described a reentrant phase transition in lipid bilayer membranes, using only experimentally measured values of elastic moduli and spontaneous curvatures, without any free parameters [80].

(3) We ignored features of cell membranes that are not captured in model bilayer membranes, such as asymmetry between inner and outer monolayers, and the presence of proteins in the surround. Also, as an approximation, we treated the membrane as an equilibrium system, even though a cell membrane is not at equilibrium. Cell membranes are part of an open dissipative system, which can exchange energy and matter with many compartments, including intrac-ellular structures [82]. Portrayals of cell membranes as open dissipative systems have been considered [83].

B. Comparison with other studies

We have employed the theory of deformations of liquid crystals [43] adapted to lipid membranes [44,45], which has been widely used to describe various membrane phenomena including: membrane fusion [46,47,54,84], fission [48–50], protein-protein interactions mediated by bilayer deformations [6,7,9,12,14,15,17,61,85], and formation of pores in membranes [86,87]. The deformations of bending (splay) and tilt have successfully been used to describe small objects—such as stalks and hemifission intermediates [46,47,54,88,89], and edges of bilayer pores [86,87]—with dimensions of a few of nanometers. This theory has also been applied to protein-induced deformations in membranes and to lipid-mediated interactions between protein molecules [6–10,12,14–17,59–61,85]. We have previously used the mean-field formalism employed in this study to calculate the energy of interaction between two membrane domains separated by a region of the background lipid, combining either the deformations of area compression and/or stretching and tilt [55] or tilt and splay [56]. These interactions had the same general form as interactions between proteins that were mediated by deformations in membranes induced by hydrophobic mismatch [6–10,12,14–17,59–61,85]. But in all these prior studies, the membrane was modeled as a continuous one-component elastic medium. In the present paper we have used the same formalism of membrane mechanics, but have considered a multicomponent lipid membrane that is subsaturated. The lipids alone would thus not phase separate, but the presence of proteins could induce local phase transitions and the formation of lipid wetting films. Because prior studies using membrane mechanics have not considered wetting films, we use the limiting case of a wetting film of zero thickness [see Fig. 2(a)] to compare our results with those of prior investigators. In all cases, the characteristic lengths of deformations are a few nanometers. Also, the monolayer pro-files and the boundary energies [see Figs. 6, 7(a), and 11(b)] oscillate in our multicomponent model; this is the case whenever the deformation of splay is allowed [9,15,18].

Two different concepts have been advanced for protein-mediated creation of domains when lipids are subsaturated: a lipid-shell model [21] and a wetting model [19,42]. The lipid shell model envisions that a lipid shell of definite composition coats a protein. But so far, it has been described only in qualitative terms, and the lipids in this shell have not been assigned a specific phase state. In contrast, the wetting model is explicit and has solid theoretical descriptions [19,20,41,42,90].

A wetting theory has been developed to describe lipid-protein domains in membranes [19,20,42]. It postulates that wetting of a protein is dominated by long-wavelength fluctuations of the interface (i.e., capillary waves) between the film and the bulk membrane. The equations for the energy of fluctuations were obtained by using scaling and functional renormalization [41]. Because capillary waves cannot cross the surface of the protein, entropy is reduced and a disjoining pressure is created. By balancing the disjoining and Laplace forces, the film thickness as a function of protein radius was obtained. In this wetting model, based on fluctuations of an interface, a film always formed and its width varied as $~\sqrt[3]{r_p}$. In our mean-field model, films exhibit much richer behavior than predicted by the long-wavelength fluctuating model. We found that films can have thickness of either molecular or macroscopic sizes, can be stable, metastable, or unstable, and a film is capable of transitioning between these states. These states are similar to the catalog of films that wet a solid surface as a result of Van der Waals interactions, which are described by the Lifshitz theory of electromagnetic fluctuations.

The discrepancy in predictions between our mean-field model and the previous wetting model, based on thermal fluctuations of the film-surround boundary, is caused by a difference in the choice of deformations that contribute to the free energy of the system. In the fluctuation theory [19,20,41,42], capillary waves of the interface of the lipid domains were the only mode of deformation. We used the deformations of splay and tilt, which reliably describe membrane mechanics. Our approach neglects the fluctuations of the interface; these fluctuations were the dominant driving force for creating a film in the earlier wetting models [20,42]. A mean-field approach is more applicable when the fluctuations are small. We show in the Appendix, Eq. (A10), that the fluctuations are small for a height mismatch δ >0.3 nm or γ>0.4 kT/nm; we made this estimate for standard values of membrane elastic moduli. For example, the interface fluctuates with average amplitude ~1.5 nm for a wetting film of l ~ 5 nm for δ= 0.6 nm [see Appendix, Eq. (A11)]. Values of the amplitude ~1.5– 2.5 nm are typical for a height mismatch in the range of 0.3 nm<δ<0.6 nm and small subsaturation, Δ ~ 0.1%. When the amplitude of the fluctuation is relatively small, the free energy of a wetting film arising from a capillary wave alone, V_fl(l), would obviously be small. Explicitly, using the equation for V_fl(l) from [20],

$$V_{fl}(l)=2\pi \times 0.948\frac{r_p{(kT)}^2}{\gamma l^2},$$ (39)

we obtain V_fl ~ 5 kT for γ= 1 kT/nm per bilayer (δ = 0.6 nm) and V_fl ~ 12 kT for γ= 0.4 kT/nm per bilayer (δ = 0.3 nm), assuming r_p = 20 nm and l = 5 nm. (The algorithm we used to obtain these values of line tension, γ, is described in the Appendix.) By comparison, the boundary energy in our model is much larger for the same values of r_p, l: the boundary energy, 2W, calculated for a bilayer, varies from ~40 kT for a height mismatch of δ= 0.3 nm to ~140 kT for δ= 0.6 nm (see Fig. 6 curves A – D). The different predictions of the two models becomes obvious by calculating the chemical potential of the film using the sum of energy of fluctuations V_fl [Eq. (39)], and interface energy, 2π (r_p + l) γ, instead of W in Eq. (6). (We use the parameters of Fig. 4, curve D to illustrate the differences.) At large subsaturations (see Fig. 13, lower horizontal dashed line), the thickness of equilibrium film calculated by the mean-field approach (Fig. 13, curve B) is larger, but close to that obtained by using the equation for energy of fluctuations (curve A). But for small subsaturation (see Fig. 13, upper horizontal dashed line), the thickness of equilibrium film obtained by the mean-field model is significantly larger than for the fluctuation model. In other words, deformations can maintain thicker films than can capillary waves. We are led to the conclusion that fluctuations can be ignored if the hydrophobic height mismatch is large. If, however, height mismatch is very small, δ ~0.1 nm, the boundary energy will be of the same order as V_fl, and here, in addition to the mechanical contribution, fluctuations of the interface should be taken into account.

FIG. 13.

The dependence of chemical potential of a film, μ, on film thickness l = r − r_p. Curve A calculated the chemical potential by using the energy of fluctuations, V_fl, at a boundary. Curve B (which is the same as curve D in Fig. 4) uses the mean-field theory. For both curves h_s = 2.0 nm and r_p = 20 nm.

Conceptually, our wetting theory quantifies some qualitative expectations expressed by other investigators. To list a few: The protein caveolin may be coated by lipids and these complexes may merge by mechanisms analyzed in the present study to create caveolae, aggregates of lipids and proteins in which r_p ~100 nm [21]. Membrane-associated proteins in T cells are clustered in “protein islands” of 30– 300 nm in diameter. In some cases the islands are attached to cytoskeleton [26]. Similar clustering has been identified in other cell types and it has been shown that the lipids of the cluster can be in a liquid-ordered state within distinct regions of the protein islands [26]. In all cases it appears that small aggregates of proteins could merge to form the larger clusters. Only large protein-lipid aggregates would be considered rafts or islands because a single, isolated protein could become lined by only a few layers of lipid, and this would not induce a substantial liquid-ordered wetting film. Our model has the virtue that it leads to explicit numerical results, which could be verified experimentally. For example, it should be possible to use spin-resonance and NMR spectroscopy to distinguish between boundary lipids and wetting films [91] and thus determine whether only large protein aggregates are surrounded by films, as predicted by our model.

In summary, we calculated thermodynamic functions of wetting lipid films by using well-known methods originally developed for liquid crystals and adapted to bilayer membranes. It was shown that either molecular or macroscopic films can form, depending on the values of parameters such as membrane thickness, hydrophobic height mismatches, spontaneous curvature of lipids, and protein radius. We have shown that a single protein of r ~ 1 nm is not large enough to induce a local phase transition to form a protein-lipid raft. But a macroscopic wetting film can form around a lipid -protein aggregate of more than tens of nanometers in diameter. We have assumed that the lipids in such aggregates are in a liquid-ordered state, analogous to wetting of solid surfaces The validity of this assumption is supported by calculations and simulations made in the context of the capillary wave model [19]. Wetting films that coat an aggregate could be quite important because they facilitate merger of domains. Also, a wetting film prevents a protein from leaving an aggregate and thereby promotes accumulation and clustering of proteins.

APPENDIX

Consider thermal fluctuations of the film–surround membrane boundary near its equilibrium position. Assume an initial circular shape of the boundary that becomes disturbed. We present the shape of the boundary as Fourier series in polar coordinates

$$r(\theta )=r_m+\delta r(\theta )=r_m+A_0+\sum _{n=2}^{\infty }[A_{n}sin(n\theta )+B_{n}cos(n\theta )],$$ (A1)

where r_m is initial equilibrium external radius of the film boundary; θ is polar angle; δr(θ) is local deviation of the boundary from its initial position. The sum in Eq. (A1) begins from n = 2 because fluctuation mode, corresponding to n = 1, leads to a shift of the film as a whole, i.e., to a shift of the center of mass of the system.

The initial equilibrium position of the film-surround boundary corresponds to the local minimum of the free energy E(r) at some radius r_m (Figs. 5, 8, and 9). It follows from the plots that the free energy becomes a linear function of the external film radius, r, for large r. In order to analytically calculate the change of the free energy, δw, resulting from the boundary shape disturbance, δr(θ), we approximate the dependence E(r) by the function E_app(r)—a sum of two functions: (1) linear function, 2π γr, which describes the behavior of E(r) at large r; (2) hyperbolic function, A/(r − r_p) −E₀ (A >0), which decreases with increasing r for r >r_p, and allows one to obtain local minimum of E_app(r). In such notations we have

$$E_{\mathit{app}}(r)=\frac{A}{r-r_p}+2\pi \gamma r-E_0.$$ (A2)

We determine A from the condition that E_app(r) has the local minimum at r = r_m,

$$\frac{\partial E_{\mathit{app}}(r_m)}{\partial r}=0\Rightarrow r_m=r_p+\sqrt{\frac{A}{2\pi \gamma }}\Rightarrow A=2\pi \gamma {(r_m-r_p)}^2.$$ (A3)

Substitution of A into Eq. (A2) yields

$$E_{\mathit{app}}(r)=2\pi r\gamma \left(1+\frac{{(r_m-r_p)}^2}{r(r-r_p)}\right)-E_0=2\pi r{\gamma }_{\mathit{eff}}(r)-E_0,$$ (A4)

where γ_{ef f}(r) is effective line tension, which depends on the film radius, r, and is equal to γ at large r.

Now we are able to calculate the change of the free energy, or minimal work, necessary to realize the boundary shape fluctuation δr(θ). It can be presented as:

$$\delta w={\int }_{-\pi }^{\pi }d\theta \{{\gamma }_{\mathit{eff}}(r)\sqrt{r^2+{(r^{\prime })}^2}-{\gamma }_{\mathit{eff}}(r_m)r_m\},$$ (A5)

where the superscript prime denotes derivative with respect to θ. Substituting γ_{ef f}(r) and γ_{ef f}(r_m) from Eq. (A4), and r = r_m + δr(θ), one can obtain from Eq. (A5) with necessary accuracy with respect of δr(θ) and δr′ (θ)

$$\delta w={\int }_{-\pi }^{\pi }d\theta \gamma \left(\frac{\delta r^2}{r_m-r_p}+\frac{2r_m-r_p}{2r_m^2}{(\delta r^{\prime })}^2\right),$$ (A6)

where the argument θ is omitted. Substitution of δr(θ) from Eq. (A1) and integration over θ results in

$$\delta w=\frac{2\pi \gamma }{r_m-r_p}{A}_0^2+\frac{\pi \gamma }{r_m-r_p}\sum _{n=2}^{\infty }(A_n^2+B_n^2)+\frac{\pi \gamma (2r_m-r_p)}{2r_m^2}\sum _{n=2}^{\infty }(n^2{A}_n^2+n^2{B}_n^2).$$ (A7)

In accordance with the thermodynamic theory of fluctuations [38], the mean square deviation of the film radius 〈δr²〉 at, for example, θ= 0 can be calculated as

$$\langle \delta r^2(0)\rangle =\frac{{\int }_{-\infty }^{\infty }\delta r{(0)}^2{e}^{-\delta w/kT}d\mathrm{\Gamma }}{{\int }_{-\infty }^{\infty }{e}^{-\delta w/kT}d\mathrm{\Gamma }},$$ (A8)

where dΓ= dA₀dA₂dA₃ …dA_n…dB₂dB₃ …dB_n… Substitution of $\delta r(0)=A_0+{\mathrm{\sum }}_{n=2}^{\infty }{B}_n$ from Eq. (A7) and integration in Eq. (A8) results in

$$\langle \delta r^2(0)\rangle =\frac{kT}{4\pi \gamma }(r_m-r_p)+\frac{kT}{2\pi \gamma }\sum _{n=2}^{\infty }\frac{\frac{2r_m^2}{2r_m-r_p}}{\frac{2r_m^2}{(2r_m-r_p)(r_m-r_p)}+n^2}.$$ (A9)

After calculation of the sum in Eq. (A9) and trivial transformations, one can obtain

$$\langle \delta r^2(0)\rangle =\frac{{\mathit{kTr}}_m(r_p-r_m)}{4\pi \gamma }\left(\frac{4r_m}{r_p^2-3r_p{r}_m+4r_m^2}+\frac{\sqrt{4+\frac{2r_p}{r_m-r_p}}}{2r_m-r_p}\times coth\left(-\sqrt{\frac{2}{(2r_m-r_p)(r_m-r_p)}}\pi r_m\right)\right).$$ (A10)

The mean amplitude of the fluctuations is square root of 〈δr²(0)〉. The unknown parameters r_m, γ, and E₀ could be determined from plots of E(r).

For example consider parameters, corresponding to curve D of Fig. 4, for subsaturation Δ= 0.1%. The plot of E(r) for this case is presented in Fig. 14. For this curve the parameters of the approximation are r_m = 25 nm, E₀ ~ 104 kT, γ ~ 0.47 kT/nm; all values are given per monolayer. One should substitute into Eq. (A10) the values multiplied by factor 2—per bilayer. For this set of the parameters, the mean amplitude of the fluctuations is

FIG. 14.

Dependence of the free energy of a film, E(r), on film thickness l = r − r_p. The parameters are the same as for curve D of Fig. 4, subsaturation Δ= 0.1%.

$$\sqrt{\langle \delta r^2(0)\rangle }~1.5\text{nm},$$ (A11)

which is smaller than the equilibrium thickness of the film, l = r_m − r_p ~ 5 nm.