Imaging the Fine Structure of a Magnetic Domain Wall in a Ni Nanocylinder

Abstract

We present the first experimental imaging of the internal DW structure in 55 and 85 nm diameter Ni nanocylinders, using electron holography combined with micromagnetic calculations. We demonstrate the magnetic transition from a hybrid magnetic state with both vortex and transverse DW in 85 nm diameter Ni nanocylinders to a pure transverse wall in thinner nanowires. This is particularly important as DWs in nanocylinders are model systems to go beyond the classical Walker limit.

The determination of the shape of domain walls (DW) in magnetic nanocylinders has become a very important topic in magnetism both for theoretical and technological issues. Indeed magnetic nanocylinders are expected to show a magnetic transition from vortex to transverse wall as the diameter is reduced,^1,2 reflecting the competition between dipolar and exchange energy. Moreover, their cylindrical symmetry prevents any change in the demagnetizing energy as the spins rotate during propagation^3,4 and should lead to a suppression of the Walker breakdown.⁵⁻⁷ This has been predicted in particular in the case of a transverse wall in a nanocylinder. The latter point is of particular interest for technological applications such as logic circuit or data storage,⁸⁻¹⁰ manipulating the walls by means of magnetic fields¹¹⁻¹⁴ or electric current,¹⁵⁻¹⁹ and for which the Walker breakdown is the main limitation on the DW velocities. Imaging and understanding the fine structure of the DW in nanocylinders is then of major importance to make these systems an interesting alternative to the usual flat nanostripes produced by lithography.

While magnetic DW have been almost exclusively studied experimentally in nanostripes, most of the research on nanocylinders has been carried out by means of micromagnetic calculations, and very few experimental studies of these structures have been performed up to now.^20,21 There are two major issues. The first is the difficulty to grow cylindrical magnetic nanostructures of good quality, and the second is the difficulty of studying the DW structure inside the object with sufficient spatial resolution. We bypass these two limitations by using template synthesis to grow high-quality Ni nanocylinders, and we use high spatial resolution off-axis electron holography to study the magnetic configuration of the DW. The internal structure of the DW is recovered, comparing the experimental magnetic phase shift image of the electron beam with the one calculated from micromagnetic simulations, taking into account the structural properties of the wire deduced from the transmission electron microscopy (TEM) studies. As the electrons cross the whole sample, electron holography offers direct information on the internal magnetic structure with a spatial resolution of about 5 nm as compared to other techniques such as magnetic force microscopy (MFM), for which the magnetic state is observed via its stray field, or magneto-optic Kerr effect (MOKE) or scanning electron microscopy with polarization analyzer (SEMPA)²²⁻²⁴ which are sensitive to surface magnetization and present spatial resolution of few tens of nanometers. Moreover, as compared to previous electron holography experiments on nanocylinders (ref (21)) showing the stray field of the DW, we optimize the observation conditions (see below) to study at higher magnification the magnetic state inside the wire.

Ni nanocylinders with diameters around 80 nm ±25 nm are grown by electro deposition in commercial 6 μm thick polycarbonate membranes.²⁵⁻²⁷ The membranes are then dissolved in CH₂Cl₂, and the Ni nanowires are recovered on a carbon foil for structural and magnetic TEM imaging. Figure 1a shows a TEM image of one of these Ni nanowires of about 90 nm in diameter with its corresponding diffraction pattern in Figure 1b. They both clearly demonstrate the polycrystalline structure of the wire with randomly oriented grains, leading to a random distribution of crystalline anisotropy and grain sizes roughly equal to the wire diameter.

Figure 1.

(a) TEM images of Ni nanocylinders grown by electrodeposition. Triangular shape crystalline domains are observed revealing a randomly distributed crystal orientation. (b) Diffraction pattern of the same area presented in a.

Off-axis electron holography experiments performed in a spherical aberration-corrected Tecnai F20 microscope are used to image the remanent magnetic configuration of single nanocylinders. Electron holography allows recovery of the phase of the electron beam that has been modified by interaction with magnetic and electrostatic fields inside and outside a nanostructure. The magnetic and the electrostatic contributions to the total phase shift are separated by subtracting two holograms where the sample has been inverted²⁸ (see Supporting Information). The magnetic phase shift can then be written as:

1

where z is the direction of the electron beam (perpendicular to the wire axis), r is a direction perpendicular to z, and B^⊥ is the amplitude of the magnetic induction perpendicular to both r and z. The isophase contour of the phase image then gives a direct representation of the projected induction field lines. However, as the phase shift is integrated over the entire path of the electron, the 2D recorded image contains all of the information about the internal structure of the domain wall projected along the z direction.

Before imaging at the remanence, a 2 T magnetic field was applied perpendicular to the nanowire axis (same direction than the electron path) using the electromagnetic objective lens of the microscope. We apply the field perpendicularly to the wire axis in order to favor transverse walls nanowires of smallest diameter. Then a single nanowire lying far from its neighbors is chosen in order to avoid magnetic interaction between them. We present in Figure 2a and b the amplitude image and magnetic phase image obtained from a 70 nm diameter Ni nanocylinder and few micrometers long in an area where no DW shows up. The induction field lines corresponding to the magnetic isophase contours are plotted inside the wire. They run parallel to the wire axis, meaning that the magnetization is uniformly aligned along the wire, without any stray field visible at this scale. This is the simplest magnetic configuration in such 1D structure as the shape anisotropy stabilizes the magnetization along the long axis. Figure 2c and d reports respectively a quantitative analysis of the amplitude of the projected induction field and the magnetic phase shift calculated for a uniform magnetic state (see details below). We observe a very good quantitative agreement between the experiment and the simulation. The small oscillations of the intensity in the magnetic induction profile on the edge of the wire come from the Fourier filtering used to reconstruct the phase images. This demonstrates the capabilities of electron holography coupled with micromagnetic simulations to obtain quantitative mapping of magnetic states in nanowires.

Figure 2.

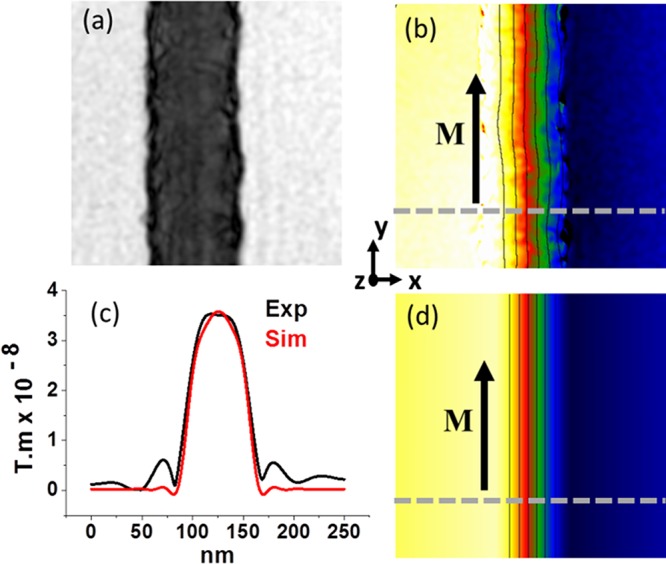
Magnetic phase shift of a uniformly magnetized nanocylinder. Amplitude (a) and (b) magnetic phase shift images in a piece of nanocylinder of 70 nm in diameter without DW. The lines in b corresponds to the isocontour of the phase shift and then to the induction field lines. (d) Calculated magnetic phase shift and isocontour from micromagnetic simulation. The isophase lines in b and d are separated by 0.6 rad. (c) Profile of the modulus of the projected induction in the cross section delimited by the dashed line in b and d.

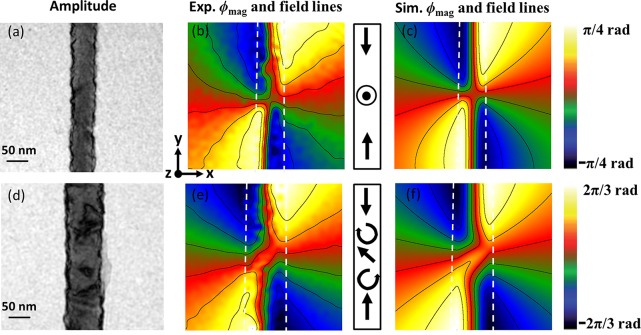
In contrast we show in Figure 3b and e the experimental magnetic phase shift image induced by DWs appearing in two nanocylinders of 55 and 85 nm diameter. Magnetic domain walls are evidenced by the stray field leaking outside the wire in each side of the DWs. Inside the wire, the magnetic flux at the DW position is found to be asymmetric as compared to the uniform case. Moreover, two different DW structures are found for two wires of different diameters. For the smaller one (Figure 3b), field lines are symmetric with respect to both the X and Y axis, and no magnetic induction is observed at the very center of the domain wall. It indicates that the magnetization at this location is either parallel to the +Z or −Z direction (the electron phase shift is only sensitive to the Bx and By components perpendicular to the e^– beam). This is the magnetic configuration expected for a pure transverse wall with the spins pointing in the direction of the saturation field (+Z). For the larger diameter wire (Figure 3e), the situation is different. Field lines are symmetric with respect to a (X,Y) plane tilted at about 45° from the Y direction. Once again it indicates that the spins within this plane are pointing in the ±Z direction. Note that such a magnetic DW configuration does not correspond to a vortex state as in such a case, the magnetic flux should be confined within the wire, with a perfect symmetry around the Y axis, and no stray field should be observed.

Figure 3.

Transverse DW and hybrid magnetic state in 55 and 85 nm nanocylinders. (a and d) Amplitude image of 55 and 85 nm nanocylinders, respectively. (b and e) Experimental magnetic phase shift and corresponding induction field lines. (c and f) Magnetic phase shift and corresponding induction field lines calculated from micromagnetic simulation. The difference of isophase contour is the same for the experiment and simulation, showing the quantitative agreement, and is set to 0.6 and 0.3 rad for 55 and 85 nm, respectively. The color bars on the right give the amplitude of the phase shift in radian. The dashed lines are a guide for the eye to position the wires. The arrows on the scheme represent a simplified view of the magnetization within the wire.

For a better understanding of these magnetic states, micromagnetic 3D calculations have been performed using the OOMMF code²⁹ to map the DW configuration for the two wires. To fit the electron holography experiments, we have calculated the electron beam phase shift images induced by the resulting magnetic state in the whole (X, Y, Z) space. The nanowire diameters used for calculation were deduced from the TEM amplitude images. As for the experiment, in the micromagnetic calculations, the magnetization is first saturated in the +Z direction (perpendicular to the wire axis) applying a magnetic field of 1 T. The polycrystalline structure has been implemented in homemade OOMMF script in order to be as close as possible to the real system (see methods for more details). The total area size is 600 × 600 × 4800 nm³, and the unit cell size is 2.5 × 2.5 × 2.5 nm³. The length of the wires was limited to 3.6 μm in order to limit the number of cells. Parameters used for the calculation are μ_0Ms = 0.485 T, magnetocrystalline anisotropy constant K₁ = −5.7 e^–3 J/m³, and exchange constant A = 9 e^–12 J/m. From the remanent magnetic configuration we calculated the magnetic induction B = μ₀(H_d + M) and deduced the magnetic phase shift from eq 1 in all of the simulated space. Results of the 3D micromagnetic calculations are shown in Figure 4 where only the part including the DW is reported as the rest of the wire is uniformly magnetized. The color representation depicts only the Mz component of the magnetization. The snapshots show the magnetization orientation in three different planes perpendicular to the wire.

Figure 4.

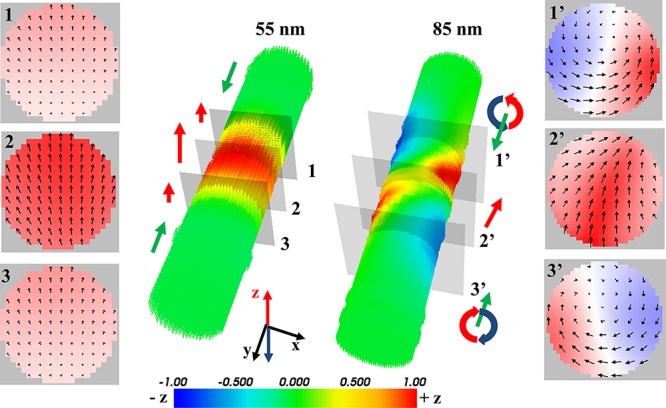
3D micromagnetic simulations for the 55 and 85 nm diameter nanocylinders. The snapshots present the magnetization at the different planes denoted on the 3D picture.

For the 55 nm diameter wire, micromagnetic calculations indicate a head to head transverse wall. The snapshots 1, 2, and 3 show that the spins at the center of the wall are aligned in the +Z direction, which result of the initial saturation of the sample. The corresponding calculated phase shift is reported in Figure 3c and is in very good agreement with the experimental one (Figure 3b). The shape of the field lines at the center of the wall indicates a slight tilt of the spins at the ±X edges of the wire, which point in opposite directions. The qualitative and quantitative agreements between simulation and experiment clearly prove the appearance of a transverse DW in the 55 nm nanowire.

Micromagnetic simulation indicates a more complex head-to-head DW in the 85 nm diameter wire. Snapshots 1′, 2′, and 3′ in Figure 4 show that at the start (1′) and the end (3′) of the DW, the spins rotate on the edge of the cylinder (as for a vortex), while at the center (2′) the spins are almost aligned parallel to +Z (i.e., in the direction of the saturation field) as for transverse wall. This “pseudo transverse wall” with spins roughly aligned in the +Z direction (red and yellow part in the 3D simulation) however lies at about 45° of the Y axis. The presence of such a “pseudo” transverse wall implies that the cores of the vortices are not centered along the wire axis as observed in 1′ and 3′. It also induces clockwise and anticlockwise rotation of the vortices on each side of it. As for the 55 nm diameter case, the phase shift calculated from this magnetic state (Figure 3f) is in perfect agreement with the experimental result (Figure 3e). As the cores of the vortices are not aligned with the Y axis, the resulting uncompensated flux closure induces the appearance of a stray field as experimentally observed. To our knowledge it is the first evidence of a magnetic transition in a cylindrical nanostructure from a pure transverse wall to a hybrid magnetic configuration whose fine structure has been clearly elucidated. It is different from previous works¹⁸ which showed that, for a field applied in the direction of the wire axis, a pure vortex state arises for wires diameter above 60 nm. We assume that such hybrid state strongly depends on the magnetic history of the nanostructure. In addition, we performed simulations for diameters up to 110 nm for which this hybrid state persists.

We must emphasize that saturating the magnetization perpendicular to the wire axis does not lead systematically to the pinning of a DW. As already stated, shape anisotropy tends to align all of the spins in the direction of the wire axis to stabilize a uniform magnetic state. We experimentally observed that most (∼60%) of the wires are uniformly magnetized and micromagnetic simulations also confirmed it is the most stable configuration since without considering the polycrystalline structure, DW nucleate but move and collapse at the edge of the wire leading to a uniform magnetic state. We then assume that the polycrystalline structure is responsible for the DW pinning most probably on grain boundaries as already reported in stripes.³⁰

In conclusion, we developed a method combining high-resolution electron holography with micromagnetism to obtain unprecedented resolution of the 3D structure of DW in a cylindrical ferromagnetic nanowire. We apply our method to demonstrate the occurrence of a magnetic transition at remanence from a transverse wall to a hybrid magnetic state as a function of the nanocylinder diameter. As transverse walls can be easily nucleated by saturating the sample perpendicular to the wire axis, they are perfect objects to test the massless DW concept which could be an important breakthrough to develop future spintronics devices.

Supporting Information Available

Description of the different experimental methods used for nanowire growth, electron holography experiments and 3D micromagnetic calculation of the magnetic phase shift. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.