Neutral forces acting on intragenomic variability shape the Escherichia coli regulatory network topology

Abstract

Cis-regulatory networks (CRNs) play a central role in cellular decision making. Like every other biological system, CRNs undergo evolution, which shapes their properties by a combination of adaptive and nonadaptive evolutionary forces. Teasing apart these forces is an important step toward functional analyses of the different components of CRNs, designing regulatory perturbation experiments, and constructing synthetic networks. Although tests of neutrality and selection based on molecular sequence data exist, no such tests are currently available based on CRNs. In this work, we present a unique genotype model of CRNs that is grounded in a genomic context and demonstrate its use in identifying portions of the CRN with properties explainable by neutral evolutionary forces at the system, subsystem, and operon levels. We leverage our model against experimentally derived data from Escherichia coli. The results of this analysis show statistically significant and substantial neutral trends in properties previously identified as adaptive in origin—degree distribution, clustering coefficient, and motifs—within the E. coli CRN. Our model captures the tightly coupled genome–interactome of an organism and enables analyses of how evolutionary events acting at the genome level, such as mutation, and at the population level, such as genetic drift, give rise to neutral patterns that we can quantify in CRNs.

A major cellular process underlying the central dogma of molecular biology is cis-regulation. This process involves the binding of specialized proteins, called transcription factors (TFs), to binding sites, in non-protein–coding DNA (ncDNA) regions upstream of target genes. The links between TFs and their target binding sites form the cis-regulatory network (CRN) in the cell. Reconstructing a CRN from experimental data, elucidating its dynamic and topological properties, and understanding how these properties emerge during development and evolution are major endeavors in experimental and computational biology (1–5).

The complexity of CRNs, coupled with observed “unexpected” trends in their properties, such as scale-freeness (6), high degree of clustering (7), and overrepresented subgraphs (3, 8–10), has led to several hypotheses of adaptive origins and explanations of CRNs and their properties. Central to most of these studies was the use of simplistic graph-theoretic models, such as randomly rewiring the connectivity of a biological network, to serve as a null model for CRN connectivity maps and their properties (11). However, it has been shown that when subjecting CRNs to the various neutral evolutionary forces and tracing their trajectory in time, many of these topological patterns may simply arise spontaneously due to the forces of mutation, recombination, gene duplication, and genetic drift (10, 12). These studies call into question arguments that were made in favor of adaptive explanations for the emergence and conservation of CRN properties (8, 13–15) and identify important parameters that may significantly affect the evolution of CRNs from a neutral perspective. Specifically (12), they highlighted the role that promoter length, binding-site size, and population size may play in forming certain topological patterns known as motifs. Nonetheless, a lingering question remains: Which specific parts of a CRN arise due to nonadaptive forces and, moreover, can we quantify these patterns to allow statistical testing?

To investigate this question, we developed a unique model of a CRN genotype that couples an individual’s CRN with its underlying genome. This coupling allows us to incorporate knowledge about genomes and their features, which is currently much richer than our knowledge of CRNs. In particular, an important insight into improving the quantifiability of neutral trends is that promoter length and the spontaneous gain and loss rates of TF binding sites (TFBS) vary substantially within a genome and that reducing each distribution to one value potentially eclipses important emergent properties and structure at the network level. Previous work assumed all promoters were the same length (10, 12, 15, 16), whereas the current work incorporates variability in promoter lengths. Finally, by subjecting a population of individuals whose genotypes are thus constructed to nonadaptive forces of evolution, we provide a simulation framework for generating data corresponding to a null model of only neutral forces. We leveraged this framework to analyze and quantify emergent properties in an Escherichia coli CRN.

It is important to note that graph-theoretic techniques, such as the edge-rewiring model, control for certain network properties, such as the number of edges, and in- and out-degrees, to produce an “acceptable” null model. One of the strengths of our model is that by incorporating well-studied and quantifiable information at the sequence level, network properties become emergent properties rather than control parameters.

Our analysis reveals surprising results. First, several subgraph types, such as the feed-forward loop, which were previously identified as network motifs, follow nonadaptive trends. Second, using our model highlighted other subgraph types that seem to arise unexpectedly with high frequency. Third, as a whole, the E. coli CRN follows neutral patterns, as reflected by the degree distribution, the number of edges, and clustering coefficient properties that are very similar to those emerging in our model at both the system and the operon level. Fourth, if we discard the information on the variability in promoter lengths and use, instead, a single length for all promoters (which is not supported by empirical data), all results change significantly. In summary, using our model, we established that nonadaptive forces, in combination with E. coli-specific genomic features, could explain much of the organization of the E. coli CRN.

Model

Our model consists of operons and transcription factors, where transcription factors are operons with additional binding-site motif information. For each operon, a nonzero promoter length is provided in base pair units, and for each transcription factor, its binding-site motifs are provided in International Union of Pure and Applied Chemistry (IUPAC) code from RegulonDB (17). IUPAC code describes ambiguous sites in a sequence motif, where each IUPAC character may correspond to one, two, three, or four nucleotide combinations. We define 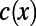to be the number of corresponding nucleotides for each IUPAC character x. Given a mutation in the binding-site region, we calculate the spontaneous binding-site gain and loss rates for each IUPAC sequence M of length N as

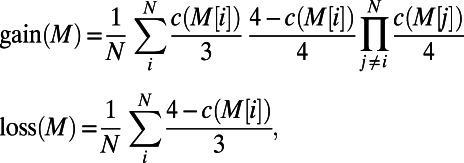where 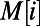denotes the character at the ith site in M. Because both 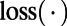and 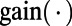are probabilities conditional on a base pair mutation, multiplying them by the base pair mutation rate u gives the individual loss and gain rates for each TF motif M: 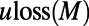and 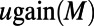. Further derivation details can be found in SI Text.

A promoter is encoded as an array of locations, where each location may or may not be occupied by a binding site. The number of locations is equal to the base pair length of the promoter, and the location of a binding site is interpreted as the distance from the transcription start site to its center position. We allow binding sites to overlap but not share the same center position. When a base pair mutation occurs at location x in the promoter, all binding sites whose locations fall within the range 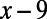to 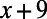are lost with a certain probability, based on their associated IUPAC sequence loss rate. Although we allow for unique loss and gain rates, we assumed, for the sake of computational efficiency, the same binding-site size of 20 bp, which is the average binding-site length from RegulonDB (Fig. S1). Once the last occupied binding site is lost in the promoter of an individual, that individual is rendered nonviable (i.e., all operons must be regulated).

Using the E. coli operon regulatory network (Materials and Methods) with the contents of promoters expunged, we generated initial random networks with a minimal binding-site set, where each promoter contains only one binding site. We used initial conditions similar to those in ref. 12, such that TF-encoding operons are autoregulatory and non-TF–encoding operons are regulated by a randomly chosen TF. This initial random network seeds a clonal population of 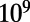cells that evolves for 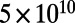generations. We observed that at about 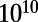generations, the number of edges in the simulated network plateaued. The specific value at which the number of edges plateaus is governed by the total amount of ncDNA represented in the promoters, the relative binding-site loss and gain rates, and stochastic forces. At the end of each simulation, we take the CRN that occurs with highest frequency in the extant population as the overall result for that simulation. We performed 1,000 replicate simulations to develop the null distribution of 1,000 regulatory networks according to the evolutionary model. Further details on the simulations can be found in Materials and Methods and SI Text.

Model Validation.

To validate our genotype model and evolutionary simulation settings, we compared the expected number of edges in the networks generated by our evolutionary model with the number of edges in the E. coli network. For the 545 operons represented in the E. coli network, the actual number of interactions is 1,039, which is within 2 SD (z-score = 1.73, P value = 0.04, n = 1,000) of the 989.5 interactions expected on the basis of the model. Because our model does not take into account many variables and processes that affect the evolution of interactions, we would not expect the null distribution generated by our model to match the E. coli network precisely; nonetheless, the low z-score shows that the sequence-level parameters provided to the model may explain a substantial portion of the network topology.

Simplifying Assumptions.

Although many evolutionary factors are simultaneously at play in shaping the topology of the regulatory network, we chose to focus on properties that were well studied with strong empirical support, were accurately quantifiable, and altered regulatory interactions through clear mechanisms. Because our goal was to create a null model that provided quantitative, rather than qualitative, results, the ability to accurately quantify rates was paramount. For this reason we constrained our model to sequence-level base pair mutation, high-confidence sequence annotation (e.g., promoters and operons in E. coli), and noncombinatorial transcription factors (i.e., no complexes). In addition, although we are simulating over timescales in which gene duplication and loss might occur, we simulated only the evolution of interactions while keeping the gene content unchanged. Similarly, our model assumes that the lengths of promoter regions are constant and that only binding sites within promoter regions change over time. The neutral processes that expand and contract promoters are known but difficult to quantify (e.g., the rate of transposon insertion and length). In essence, we assume that promoter length and coding DNA are under purifying selection, which is in keeping with neutral evolutionary theory.

Results

We begin by providing evidence that connects promoter length and regulatory network topology in the E. coli network, and then we leverage the null model to understand topological patterns of the E. coli network at the system, subgraph, and operon levels.

Role of Promoter Length in the E. coli CRN.

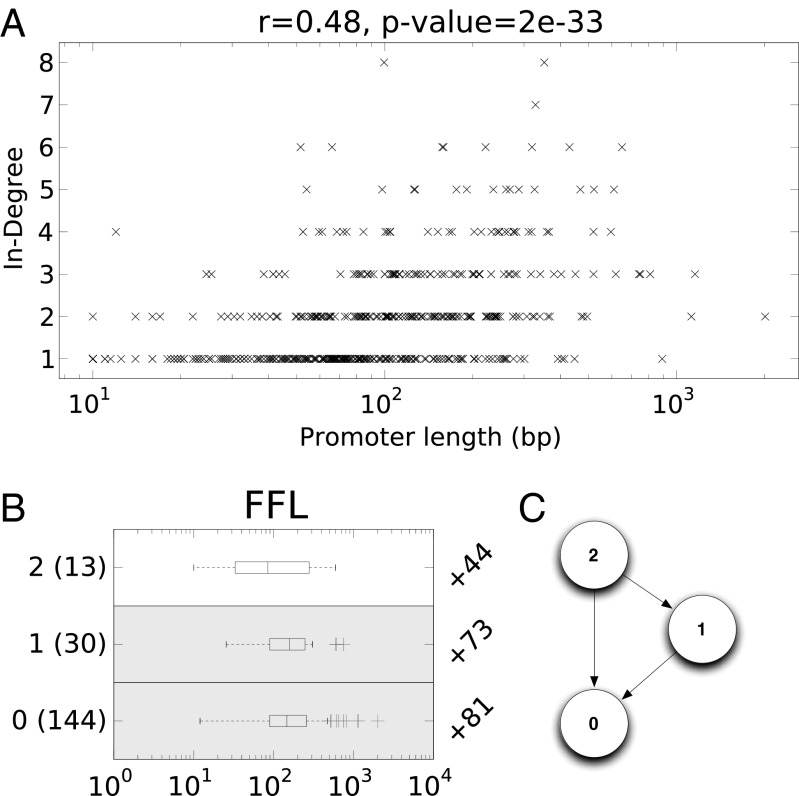
Each node (operon) in the E. coli regulatory network is annotated with the length of its promoter region and the sequence motifs for any TFs encoded by the operon, where a node with outgoing edges corresponds to a TF-encoding operon. With this annotated network, we investigated correlations between genomic and network-level properties (Fig. 1A and Fig. S2). We found that only promoter length correlated with in-degree (Pearson’s correlation coefficient 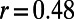), but otherwise the loss and gain rates of TFs poorly correlated with out-degree and with each other.

Fig. 1.

Significant promoter length signal exists in the E. coli regulatory network on both the system and the subsystem levels. (A) Each operon is plotted with its in-degree and promoter length; we report the Pearson correlation coefficient and significance above the plot. (B) The distributions of promoter lengths for operons that participate in feed-forward loops (FFL) are presented as boxplots per node. The left axis provides the node label, which corresponds to the node in the subgraph diagram C (e.g., 0 or 1), along with the number of distinct operons represented in that distribution. The difference in the average promoter length in the node distribution minus the average promoter length in the network is listed on the right axis in B. Distributions with significant uplift, assessed using a nonparametric Wilcoxon rank-sums test, are indicated with a gray background behind the boxplot (P values for 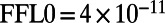and for ).

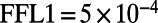To further understand the role of promoter length in the E. coli network, we enumerated the operons that participated in subgraphs that have been analyzed and studied extensively for their functional roles: feed-forward loop (FFL), single-input module (SIM), and bifan. A bifan is a directed graph on four nodes, two of which are designated target genes and each of the other two is designated as a regulator of both target genes. For each of these three subgraph types, we calculated the distribution of promoter length at each node in the subgraph (Fig. 1B for FFL and Fig. S3 for SIM and bifan). Although operons may arise multiple times in the enumeration of subgraphs (e.g., the regulator in the SIM), we count each operon only once in the distribution of promoter length.

Downstream nodes in the subgraph (that is, nodes with in-degree greater than 0) tended to be significantly overrepresented by operons with longer promoter regions (using Wilcoxon’s rank-sums test against all 545 operons). It is important to note that the operons that encode TFs, and would naturally be upstream in the motif, tend to have longer promoter regions than non-TF–encoding operons, although not significantly (Mann–Whitney nonparametric test, P value = 0.18). Consequently, the fact that downstream genes have longer promoter regions is not due to a predetermined bias. In the feed-forward loop, the operons that share a common regulator (nodes 0 and 1 in Fig. 1C) tend to have longer promoter regions than the common regulator. The downstream nodes in the FFL have promoter regions that are, on average, 73 and 81 bp longer than the overall average. Similarly, the nodes that share common regulators in the bifan (nodes 0 and 1) also tend to have longer promoter regions than the regulators, on average 67 and 62 bp longer. However, the single-input module is not enriched for longer promoters at the downstream nodes, due to the fact that nearly all operons (498 of the 545) participate in this pattern.

Quantifying Neutral Patterns.

We studied important properties of the E. coli regulatory network at the system (regulatory network), subsystem (regulatory patterns or subgraphs), and operon levels. To obtain statistically significant results, our analyses are based on 1,000 random networks generated by our model.

All of the initial networks that seeded the evolutionary simulations begin with 545 edges whereas the real E. coli network has 1,039. The numbers of nodes (545) in both the random and the actual networks are identical. The clustering coefficient for all initial networks, because all TFs are autoregulatory, is 0. The only subgraph present in the initial network is a single-input module, because TFs regulate themselves and other random non-TF–encoding operons. Each operon has an in-degree of 1, regardless of its promoter length. Therefore, any topological signal at the system, subgraph, and operon levels occurs during the course of the evolutionary simulations.

System Level.

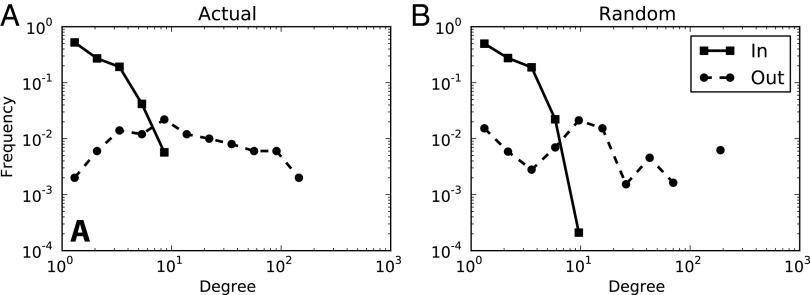
Two properties that are often investigated at the system, or network, level are the degree distribution and clustering coefficient of the network. Fig. 2 shows the in-degree and out-degree distributions of the actual E. coli network and the networks generated on the basis of our model.

Fig. 2.

(A and B) In-degree and out-degree distributions for the actual E. coli network (A) and the random networks (B) are compared side by side. Scatter points indicate the 12 logarithmic bins used to plot the lines. The discontinuity in the out-degree line in the random plot indicates that there are no nodes in the bin with a degree of around 100. We used a two-sample Kolmogorov–Smirnov test and found that all degree distributions did not differ significantly between the actual and the random distributions.

As Fig. 2 demonstrates, the in-degree and out-degree distributions of the actual E. coli network match the distributions found by our model (Kolmogorov–Smirnov test; in-degree, D = 0.029, P value = 0.75; out-degree, D = 0.031, P value = 0.65). Thus, our model provides an explanation for both degree distributions observed in the E. coli network.

Clustering coefficient is a graph-theoretic measure of the transitivity of the network. We compared the clustering coefficient of the actual network to the distribution expected by our model and found a strong agreement between the two. Specifically, the actual network has a clustering coefficient of 0.189 and the distribution based on our model has a mean of 0.162 and variance of 0.05 (z-score = 0.526; P value = 0.3).

We also compared the discretized joint distribution of in-degree and promoter length by subtracting the distribution under our model from that of the actual E. coli network (see Fig. S8). The in-degree of an operon is the number of unique regulatory interactions (equivalently, the number of distinct binding sites and their affinities in the promoter). We find that the distribution under our model accounts for about 91% of the interactions present in the actual network, leaving only 9% of the interactions to fall outside the model.

Subgraph Level.

Network motifs are subgraphs that are significantly overrepresented in the actual network compared with networks generated under a null model. In a seminal study (8), Alon reported on motifs and their distribution in the E. coli regulatory network. For their null model, the authors rewired the actual network randomly, while maintaining the in-degree and out-degree distribution, to obtain random networks. To identify certain subgraphs as motifs, the frequency of each subgraph (up to a certain subgraph size) in the actual network is compared with the mean and variance subgraph frequency found in random networks, resulting in a z-score and P value for each subgraph. For our evolutionary model, we calculate the mean and variance frequency by counting each subgraph topology in the 1,000 simulated networks.

For each subgraph, the z-scores, using both the random rewiring model of the original study (13) and our evolutionary model, are compared for three- and four-node subgraphs (Fig. 3). There is poor agreement between the two models, which is expected due to their fundamental differences. For three-node subgraphs, the FFL is highly significant according to the random rewiring model (z-score = 11.7) but is highly insignificant according to our model (z-score = 1.1). The SIM and the bifan subgraphs both occur with low z-scores under our model as well (−0.7 and −0.5, respectively). Many high-frequency subgraphs occur at significant levels according to our null model, including the three-node linear pathway and the feed-back loop and other subgraph topologies. Plots for other less-frequent four-node subgraphs can be found in Fig. S4.

Fig. 3.

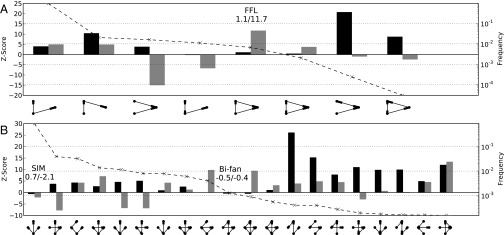
(A and B) z-scores for three- (A) and four (B)-node subgraphs are ranked according to frequency in the E. coli network. The left axis provides the scale for the z-score (bars) and the right axis measures the frequency (dashed line) of each subgraph. For each subgraph, the z-scores for our model (black) and the edge-rewiring model (gray) are graphed side-by-side. Both models used 1,000 random networks to calculate significance. Important motifs are annotated along with the precise z-score found by each model (left, our model; right, edge switching). Only the top 20 most frequent four-node subgraphs are shown.

Operon Level.

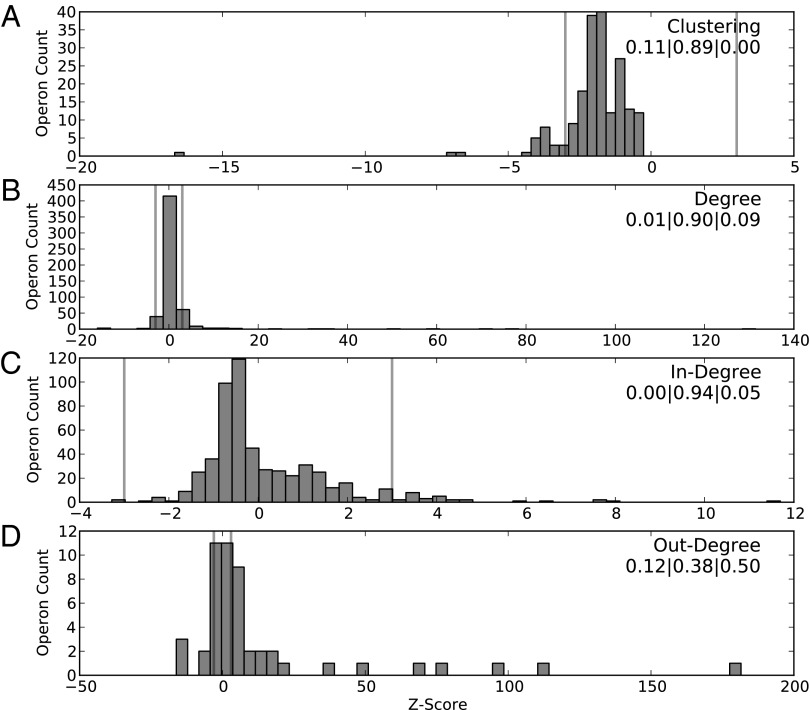
Because our null model makes use of the promoter length and IUPAC sequences for each operon in the E. coli network, it is possible to build distributions of network properties for any operon of interest. For instance, the null model can provide expected values for out-degree, in-degree, and clustering coefficient for the fis operon. We use this approach to identify operons that fit the model used in this study. We calculated the z-score for the clustering coefficient, in-degree, out-degree, and degree (sum of in- and out-degree) per operon and plot their distributions in Fig. 4. It is important to note that these network properties are dependent on one other, but in this analysis we decouple them by taking the distribution per operon across the 1,000 random networks. This is why, for example, the clustering coefficient plot in Fig. 4A presents only negative z-scores per operon but the z-score is positive for the average clustering coefficient per network.

Fig. 4.

(A–D) For each operon in the E. coli network, the distribution of significance (measured in z-score) is plotted for several local network properties: Clustering (A), degree (B), in-degree (C), and out-degree (D). Vertical bars indicate a z-score at ±3, separating each distribution into three categories. The percentages of operons in each of these three categories—significantly below, expected by, and significantly above—are listed underneath the name of the property. For instance, 89% of the operons have clustering coefficients as expected by the null model. In the out-degree distribution, only the 50 operons that encode TFs are included.

For each property, we classify each operon into three categories to gauge the agreement with the null model: having a z-score < −3 (underrepresented), between −3 and 3 (expected), and >3 (overrepresented). The various operon sequence and network properties used in this study, including the empirical and null model values, are reported in Dataset S1. The clustering coefficient, in-degree, and degree for operons have high agreement with the null model, with 89%, 94%, and 90% in the expected category, respectively. The few operons that are overrepresented in degree are the same operons that are overrepresented in out-degree. Out-degree has only 38% agreement with the null model, with 50% being overrepresented; however, out-degree applies only to operons that encode TFs.

We investigated operons that had absolute z-scores greater than 10. This set consists of 16 operons, only 1 of which did not encode a transcription factor, lending itself to the poor fit of out-degree. The operon ubiCA, which does not encode a transcription factor, has two interactions inferred from gene expression analysis that are not found in the promoter sequence and so potentially fall outside the regulatory model used in this study. This list also includes important global or pleiotropic regulators like H-NS, Fis, Fnr, CRP, and IHF, all of which have sequence motifs with low gain rates but nonetheless interact with many operons. On the other hand, MalT, important for maltose metabolism, and MetJ, a common repressor, have binding motifs with high gain rates but low out-degree compared with the null model. Both results are explainable by poor IUPAC sequences, functional conservation (in the case of the global regulators), or removal of detrimental binding sites by selection.

Homogeneous vs. Heterogeneous Promoter Lengths.

We performed additional simulations to measure the effects of the parameterization and initialization of our null model on the results. If instead we parameterize our model with homogeneous (average) promoter length and IUPAC sequences for all operons to generate a null distribution of 1,000 random networks, then all of the results presented in this study are in fact reversed (Figs. S5–S10). On the system level, the homogenous null model resulted in 5,232 interactions (z-score = −71.4), average clustering coefficient of 0.552 (z-score = −14.6), and significantly different in- and out-degree distributions. The distribution of promoter length and that of in-degree differed by 97%. Among many other differences in the subgraph distribution, the bifan and feed-forward loop subgraphs had z-scores 10 times and 3 times larger than those of the nonhomogeneous model. At the operon level, the majority of operons fell significantly outside neutral expectations, which emphasizes the significance of incorporating the promotor length distribution in the model.

We also investigated the robustness of the model to “biologically reasonable” changes in parameterization, specifically, an alternative initial condition and shorter binding-site length (7 bp). These alternate simulations yielded insignificant deviations from the results of the main study. However, when we performed additional simulations to measure the role of genetic drift, by using a smaller population size (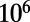) and random walks instead of population genetic simulations, we found large differences at the system, subgraph, and operon levels. This suggests that genetic drift is an important force for the patterns observed in this study. The details and results of these alternate simulations are described in SI Text.

Discussion

The results in this study demonstrate that, taking only a few important sequence characteristics and neutral evolutionary processes into account, it is possible to generate random networks that resemble the actual E. coli network at the system, subgraph, and operon levels. Due to their large effective population size and short reproductive cycles, bacteria are thought to be molded primarily by natural selection on the sequence and network levels (8, 18, 19); however, our model, which takes into account population genetic mechanisms, predicts that important features of the regulatory network for E. coli follow neutral patterns. With the recent technological advances that allow for expression and fitness analysis at a genomic scale, understanding the evolutionary origins of system-level properties will be important for interpreting trends in functional data.

Our results show that the degree distribution, the clustering coefficient, and the number of interactions all follow neutral patterns. Furthermore, the ability to quantify these neutral trends revealed the staggering portion of the E. coli network—nearly 90% for several important network properties—that occurs at frequencies expected by nonadaptive evolution. However, this does not mean that only 10% of the E. coli network derives from selective forces. Instead, our results serve as a guide for identifying more informative network properties that are enriched with adaptive signal. For instance, 94% of operons have in-degree within 3 SD of the null model, but only 38% of operons have out-degree that agrees with nonadaptive expectations (Fig. 4). Thus, although the number of unique regulatory interactions per operon may be neutral, transcription factors are wired considerably differently (about 62% according to out-degree) than expected by chance. Identifying this deviation is another strength of our model, because it guides the user to go back and understand the biology of the underlying system and highlights areas of further investigation.

The neutral trends in the local wiring of regulatory networks also challenge the prevailing adaptive perspective: Namely, are commonly accepted “motifs”, such as feed-forward loops, really motifs? A network rewiring model that preserves system-level properties was used to identify motifs—which have since been shown to execute highly functional temporal programs. These results have been adopted in the systems biology community to the point that “feed-forward loops”, “single-input module”, and “bifan” are synonymous with motif. Subsequent work has linked the ubiquity of these motifs to convergent evolution driven by functional requirements (14, 20). However, when using our evolutionary model, which accounts for events at the genomic level, it emerges that FFLs, SIMs, and bifans all occur within frequencies expected by neutral evolution. Without taking into account pathway dynamics, our null model accurately predicts the frequency of three important and highly functional subgraphs. Therefore, according to our model, these three subgraph topologies are not motifs, but rather topological patterns that would be expected to emerge by nonadaptive forces operating on sequences. The functionality of motifs, although an enabler of sophisticated cellular behavior, is not necessarily the cause or the explanation of their origin. This is not to say that regulatory network motifs do not exist; in fact, our model identified several three- and four-node subgraph topologies that were significantly over- or underrepresented in the E. coli network. However, accounting for true evolutionary processes, such as mutation and drift, rather than synthetically rewiring a network, might lead us in the direction of the true motifs.

Our study demonstrates the significant effect that distributions of promoter length can have on regulatory network properties. A major contribution of this work is the integration of distributions of promoter lengths and binding site sequences to understand their role in driving neutral patterns. Other studies have focused on single values for the promoter length and binding-site gain and loss rates (10, 12); however, when we applied a similar approach, the findings of the main study were reversed.

In our simulations, we assumed that promoter length was under purifying selection, but promoter regions are known to contract and expand and may even be under positive selection as a result of selection on genome size (21, 22). Regardless of the evolutionary origin of the promoter length, our results still explain network properties in terms of the neutral evolutionary forces of mutation and genetic drift.

Our results in general agree with other recent perspectives on regulatory evolution. Within a promoter, complex binding-site patterns like clustering, which were once thought to be adaptive, may in fact emerge from neutral evolution (23). At the subgraph level, commonly accepted motifs are poorly conserved across homologous genes (24); thus, convergent evolution of subgraphs (24, 25) is more simply explained as the result of neutral forces acting similarly in divergent species rather than as an adaptive response to environmental changes. Within a system, genome-wide expression and fitness experiments in bacteria have identified the suboptimal control at the genome level, which raises questions about the efficacy of selection to mold regulatory networks beyond direct interactions (26). The ability of selection to optimize the structure of a regulatory network is well studied in simulations (e.g., refs. 14, 20), but lacking in any in vivo observations beyond a few regulatory interactions (27). In fact, protein abundance is determined only in part by transcription, so regulatory network topology is significantly obfuscated from organismal-level selection, which is rarely taken into account in simulation studies (28). Indeed, a simpler explanation of all these observations, and in keeping with the results from our study, is that bacterial regulatory patterns are mostly explainable through neutral evolution acting on genomic properties.

Materials and Methods

Curating the E. coli Regulatory Network.

We compiled the E. coli regulatory network using data readily available from RegulonDB (17). Nodes represent operons and directed edges represent regulatory interactions between operons, where the source operon must encode a TF. Operons that encoded one part of a heterodimer TF (e.g., IHF) were merged together as one node in the network to avoid representation issues. The length of promoter sequences was measured by the amount of contiguous ncDNA that may harbor functional binding sites upstream of an operon, which was determined per operon by the maximum distance from the transcription start site for all identified functioning binding sites. We included only operons that had a clear contiguous upstream region and previously identified binding sites. TF sequence motifs are also available from RegulonDB for 50 TFs, provided in IUPAC format (29). We included only interactions in the regulatory network for which there existed a corresponding binding motif.

Evolutionary Simulations.

Population genetic simulations were used to understand the combined effect of binding-site mutation rate, population size, and promoter length on regulatory network evolution.

Regulatory networks.

Given a list of TF sequence motifs (here we use the TF and the operon encoding the TF synonymously), we represented regulatory networks as a collection of promoter sequences, such that each location in the promoter was either empty (“0”) or contained a binding site (nonzero index of the matching TF sequence motif). All binding sites were assumed to be 19 bp in length, such that they overlap with nine neighboring binding sites on each side. The average length of E. coli binding motifs used in this study is 20, but we use 19 so that distances can be measured symmetrically. The regulatory network, given the collection of promoter sequences, can be constructed by adding a node for each operon and an incoming edge for each binding site to the corresponding operon TF.

Population genetic simulations.

Simulations model a constant-sized, haploid, panmictic population of 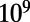cells, evolved over 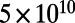generations. We simulate a Wright–Fisher model: Within each nonoverlapping generation, existing individuals are mutated to form a mutant pool that is then randomly sampled to select surviving individuals for the next generation. We used a scaling parameter of 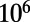to improve the computational efficiency of the simulations.

Mutation.

Given a regulatory network (which is a collection of promoter sequences), we model mutation as follows. We assume that there are sufficient locations in the promoters such that in one round of mutation, gain and loss do not conflict, which is a safe assumption with the size of the network used in this study (70,963 promoter locations). We calculate the probability of gain and loss of motifs given a base pair mutation in the binding site for each sequence motif provided to the simulator (see Model for the equations). Because we calculate the gain and loss rates given a base pair mutation, we begin the mutation process by calculating the number of base pair mutations in the promoter regions. For each base pair mutation, a random center location x is chosen from all promoters, such that each location is equally likely. Then, for each site y, such that 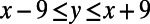and y is in the bounds of the promoter, a binding-site gain is calculated for each TF and, if y corresponds to a location occupied by a binding site for TF i, a binding-site loss is calculated for TF i.

Enumerating Subgraphs.

We used the Kavosh program with default parameters to both enumerate subgraphs and calculate motifs, using the random rewiring model, chosen for its speed, command line interface, and accessible output format (30). Significance scores for the random rewiring model used 1,000 random networks.