Abstract
Independent component analysis (ICA) is widely used in resting state functional connectivity studies. ICA is a data-driven method, which uses no a priori anatomical or functional assumptions. However, as a result, it still relies on the user to distinguish the independent components (ICs) corresponding to neuronal activation, peripherally originating signals (without directly attributable neuronal origin, such as respiration, cardiac pulsation and Mayer wave), and acquisition artifacts. In this concurrent near infrared spectroscopy (NIRS)/functional MRI (fMRI) resting state study, we developed a method to systematically and quantitatively identify the ICs that show strong contributions from signals originating in the periphery. We applied group ICA (MELODIC from FSL) to the resting state data of 10 healthy participants. The systemic low frequency oscillation (LFO) detected simultaneously at each participant’s fingertip by NIRS was used as a regressor to correlate with every subject-specific IC timecourse. The ICs that had high correlation with the systemic LFO were those closely associated with previously described sensorimotor, visual, and auditory networks. The ICs associated with the default mode and frontoparietal networks were less affected by the peripheral signals. The consistency and reproducibility of the results were evaluated using bootstrapping. This result demonstrates that systemic, low frequency oscillations in hemodynamic properties overlay the timecourses of many spatial patterns identified in ICA analyses, which complicates the detection and interpretation of connectivity in these regions of the brain
Keywords: Resting state networks, independent component analysis, low frequency oscillation, near infrared spectroscopy, BOTD fMRI, physiological noise
1. Introduction
Functional connectivity is commonly defined as the coordination of activity across brain regions. It has been widely investigated using functional MRI (fMRI), by detecting temporal correlations of the BOLD signal between brain regions during task activations and in resting state conditions (Friston et al., 1996). Resting state functional connectivity studies provide information regarding spontaneous activity that is generated intrinsically and naturally within the brain (Biswal et al., 1995; Fox and Raichle, 2007), and as it requires little participation, it is the preferred approach for studying functional brain activity among certain populations of individuals, including cognitively impaired patients who may not be able to perform tasks.
There are two widely used methods for analysis of functional connectivity in fMRI data (Rosazza et al., 2012). The first method is seed-based analysis (Biswal et al., 1995; Fox et al., 2006; Raichle et al., 2001; Vincent et al., 2008), in which a region of interest (ROI) or seed voxel is selected based on an a priori hypothesis of anatomical and/or functional relationships in the brain. The timecourse obtained from the ROI is correlated with that of other voxels in the brain. The second method is independent component analysis (ICA), a completely data-driven approach to separate the signals into statistically independent components (Beckmann et al., 2005; Calhoun et al., 2005; Damoiseaux et al., 2006; Kiviniemi et al., 2003; McKeown and Sejnowski, 1998). A number of studies have shown that these two methods yield results with significant similarities (Rosazza et al., 2012; Van Dijk et al., 2010). One benefit of ICA is that it does not require a priori anatomical assumptions or subjective selection of seed areas. Another benefit is that it can, to some extent, isolate sources of noise. In spite of these advantages, a major concern with ICA is that it requires the user to make a subjective determination whether a component represents a neuronal signal, another type of signal, or an artifact (Cole et al., 2010).
Many attempts have been made to develop methods to categorize ICA components accurately and objectively, but they have not been adopted as standard practice (Perlbarg et al., 2007; Sui et al., 2009; Tohka et al., 2008). Instead, visual inspection is the most commonly used method for component selection (Kelly et al., 2010). In order to improve this method and help reduce the false negative rate, criteria for identifying those independent components (ICs) representing artifactual noise were recently outlined and include irregular spotted patterns, extra-cerebral locations, and motion-related ring patterns (Kelly et al., 2010; Tohka et al., 2008). In addition, the timecourses corresponding to these components have easily recognizable features, such as temporal spikes, dominance in the high frequency region (>0.1 Hz), and high repeatability in a fixed pattern. However, beyond these easily identifiable “noise” ICs, there are many other ICs (especially from ICA group analysis), which have symmetrical patterns, reside mostly in the cortex, and have smooth timecourses that are dominated by energy in the low frequencies (≤0.1 Hz). Many of these ICs are commonly regarded as resting state networks (RSNs). Therefore, it is necessary and critical to understand the peripheral physiological contributions to these ICs.
Birn et al. (2008a) studied the effects of respiration-related low frequency oscillations (LFOs) on the RSNs derived from ICA of resting state data (Birn et al., 2008a). They found that ICA frequently confused the respiration-related IC with the default mode network (DMN), a widely accepted RSN. In most cases, the timecourse associated with DMN was significantly correlated with changes in the respiration volume per time. This work demonstrated that even the most accepted RSNs might have significant peripheral physiological contributions. Our recent work confirmed this idea with a concurrent near infrared spectroscopy (NIRS)/fMRI resting state study, which demonstrated that the BOLD fMRI signal obtained from many brain voxels is highly correlated with the LFOs (0.01 Hz~0.15 Hz) that were measured simultaneously at peripheral sites (e.g. fingertip) by NIRS (Tong et al., 2012a). Moreover, by using cross correlation between these two signals, we showed that the LFO is not static, but instead, travels with the blood circulation and arrives at different brain voxels at different times. Interestingly, the areas affected by this dynamic systemic blood fluctuation were shown to overlap significantly with many well-known RSNs. Since this systemic LFO corresponded to variations in parameters that directly affect the BOLD fMRI signal (e.g., blood flow, oxygenation, and volume), and these variations are in the same low frequency band as the RSN fluctuations, we postulated that many RSNs are likely to be influenced by this peripheral physiology.
Using the systemic LFO measured in the periphery (fingertip) by NIRS to identify the physiological component in RSNs (based on BOLD fMRI) offers several advantages: 1) Both the NIRS and the BOLD fMRI signals are blood-related, and therefore sensitive to changes in blood flow, volume and oxygenation; 2) The systemic LFO measured at the fingertip is a direct measurement of the physiological hemodynamic fluctuations within the same frequency band as BOLD fMRI (0.01–0.15Hz), but without any mathematical assumption or modeling; and 3) The systemic LFO identified by NIRS has no aliased contribution from respiratory or cardiac pulsation (i.e., due to the high temporal resolution of NIRS, we can filter out all the high frequency signals >0.2 Hz). Therefore, the effects arising only from this systemic LFO, which has been shown to have significant impact on BOLD fMRI, can be singled out and identified easily. Recently, functional connectivity has been investigated using functional NIRS (fNIRS) only (Lu et al., 2010; Mesquita et al., 2010; Sasai et al., 2011; Zhang et al., 2010b). Consistent RSNs have been found by both seed-based (Lu et al., 2010) and independent component (Zhang et al., 2010a) analyses. Due to the fact that fNIRS can only probe the networks on the surface of the cortex and is sensitive to the extracerebral systemic physiological fluctuations, the potential impact of our results on RSN studies using fNIRS alone may be even greater.
In the present concurrent NIRS/fMRI resting state study, we extended our previous research, in which we performed the resting state fMRI on healthy participants while using NIRS to measure the physiological signals at the fingertip, and combined it with a novel method to quantify the contribution of systemic LFO to a full set of RSNs identified by ICA in the resting state data. We also used a bootstrapping method to test the consistency and reproducibility of these physiologically correlated ICs and to assess the effects of dimensionality in the ICA process. To the best of our knowledge, the method we used is the first attempt to assess which RSNs are most affected by physiological signals originating in the periphery in an objective and systematic manner. Importantly, our results are not limited by the analytical method we used in this study (i.e., ICA) because the physiologically correlated RSNs we identified are consistent with well-established RSNs (Beckmann et al., 2005; Damoiseaux et al., 2006; Smith et al., 2009).
2 Materials and methods
2.1 Protocols and instrumentation
Concurrent NIRS and fMRI resting state studies were conducted in 10 healthy volunteers participating in an ongoing protocol (4M, 6F, average age ± SD, 30 ± 7 years). Participants were asked to lie quietly in the scanner and view a gray screen with a fixation point in the center. The Institutional Review Board at McLean Hospital approved the protocol and volunteers were compensated for their participation.
All MR data were acquired on a Siemens TIM Trio 3T scanner (Siemens Medical Systems, Malvern, PA) using a 32-channel phased array head matrix coil (200 time points, TR/TE=3000/30 ms, flip angle 90 degrees, matrix = 64 × 64 on a 224 × 224 mm FOV, 50 2.5 mm slices with 0.625 mm gap parallel to the AC-PC line extending down from the top of the brain). Physiological waveforms (pulse oximetry, and respiratory depth) were recorded using the scanner’s built-in wireless fingertip pulse oximeter and respiratory belt.
MRI-compatible NIRS optical probes, each with one collection fiber and one pair of illumination fibers (1.5 cm separation between collection and illumination fibers), were used to record NIRS signals. One probe was placed over the tip of left middle finger (the other hand was holding the “squeeze ball” to signal the MR technician), one probe was placed on the left big toe, and in 7 participants, an additional probe was placed on the right big toe, as shown in Figure 1 (a and b). NIRS data were recorded using an ISS Imagent instrument (ISS, Inc., Champaign, IL) at 690 and 830 nm. The sampling rate of the NIRS data acquisition ranged from 6.25 to 12.5 Hz (in all cases the cardiac waveform was fully sampled). FMRI data were collected for 10 mins; NIRS data were recorded continuously during this time, and before and after the resting state fMRI acquisition.
Figure 1.
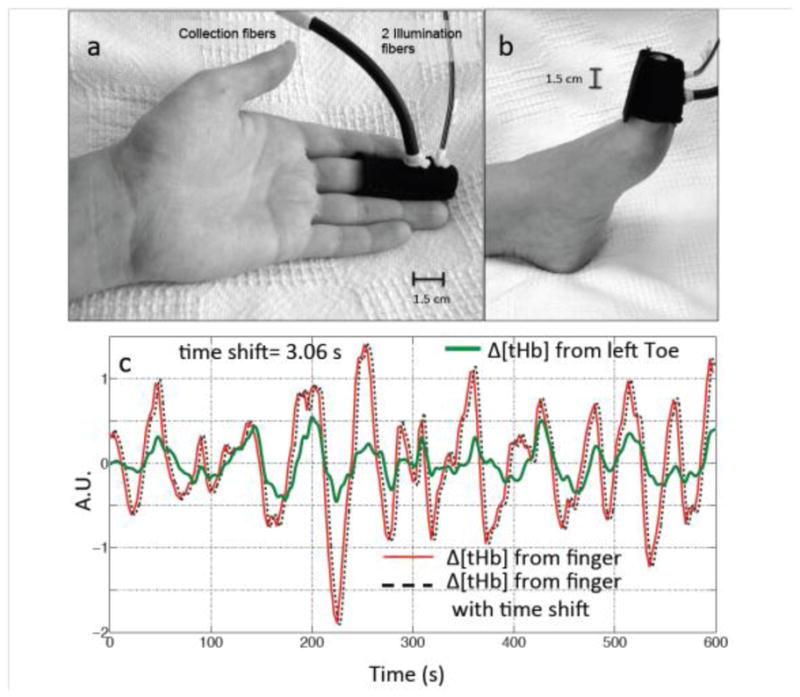
Experimental setup. NIRS probes (made in-house) with one source-detector (1.5 cm separation) pair was placed on the participant’s finger (a) and toe (b). The LFO signals (Δ[tHb]) of the finger (red) and toe (green) from one participant are shown in (c), together with a temporally shifted version of the finger data (dotted black line). A.U. is arbitrary unit.
Data preprocessing was conducted on both NIRS and fMRI data. For the NIRS data, each pair of raw NIRS timecourses (690 and 830 nm data) was converted into three timecourses representing temporal changes of the oxy-, deoxy and total hemoglobin concentration (Δ[HbO], Δ[Hb] and Δ[tHb], respectively) using the Modified Beer-Lambert law (Delpy et al., 1988; Kocsis et al., 2006) in Matlab (The Mathworks, Natick, MA). For the BOLD fMRI data, regular preprocessing steps in FSL (Smith et al., 2004), including motion correction, slice timing correction, and spatial smoothing (5mm) were performed.
2.2 Systemic Low Frequency Oscillation analyses
Previously we have established that LFOs measured at the fingertip by NIRS are systemic blood signals that travel to different body parts (including the brain) with different time delays (Tong and Frederick, 2010; Tong et al., 2012a). As a first step, we conducted the same analyses on these 10 participants. The detailed analytical procedure can be found in the previous work (Tong et al., 2012a). In short, a bandpass filter was used to isolate LFO signals (0.01~0.15 Hz) spectrally from simultaneously recorded NIRS data (i.e., Δ[tHb]) from the fingertip and the toe. In the studies of LFOs (including ours), the range of the low frequencies is commonly set to be 0.01~0.1Hz. However, recent studies indicated that BOLD resting state signals are more broadband than previously thought (Niazy et al., 2011). Since this work is to understand the impact of the LFOs on the RSNs, we expanded the frequency band to 0.01~0.15Hz. In our analyses we use Δ[tHb] because the LFO is closely associated with changes in blood flow and volume, which have been shown to be represented best by Δ[tHb] (Hoshi et al., 2001). Moreover, Δ[tHb] has much higher signal to noise ratio (SNR) than Δ[Hb]. Cross correlation was conducted between the Δ[tHb] recorded at the fingertip and toe to demonstrate LFOs travel in the periphery, while a set of time-shifted versions of the LFO signal (181 temporal traces covering −14.4 to +14.4 s with time shift 0.16s) was generated from the Δ[tHb] recorded at the fingertip, and downsampled to the TR of the fMRI data (3s) to demonstrate that LFOs travel in the brain. The large temporal span is chosen to compensate mainly for the delay of LFOs between the finger and the brain and variations in subjects’ peripheral blood circulations. A set of general linear model (GLM) analyses of the fMRI data (Figure 2) was performed to determine the relationship between the time shift and fit strength in each voxel with the fingertip. The results of this group of analyses (z-statistic maps) were combined (max z-statistics map) to visualize all the voxels that had been significantly affected at any time by the LFOs as they passed through the brain. As this systemic LFO travels further along the peripheral vasculature, it may have decreased magnitude and accumulate other physiological noise (leading to lower SNR), as seen in the comparison between fingertip and toe signal in Figure 1(c). Therefore, we only used the LFO (Δ[tHb]) recorded at the fingertip, instead of that from the toe, to study the correlation between the peripheral and the brain.
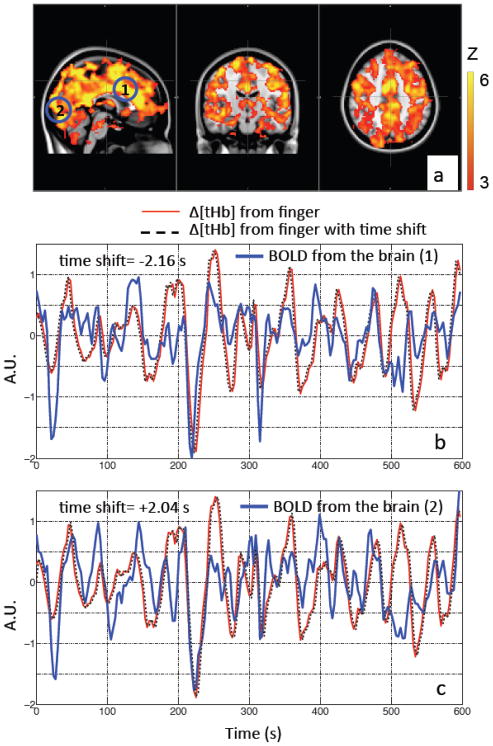
Figure 2.
Max z-statistics maps of the same participant (as in Figure 1) overlaid on the standard brain showing areas highly correlated with LFOs collected at the fingertip in (a). The color bar indicates the colors corresponding to the z value from 3 to 6. Two points (1 and 2) in the brain were chosen as shown in the blue circles (a), in order to compare the temporal traces at low frequency measured at the fingertip (by NIRS) and those measured at the brain (by BOLD fMRI). Their corresponding temporal traces of BOLD (in blue) were plotted in (b) and (c) with Δ[tHb] of the fingertip (in red) and its temporal shifted versions (in dotted black lines).
2.3 Combined RSN analyses
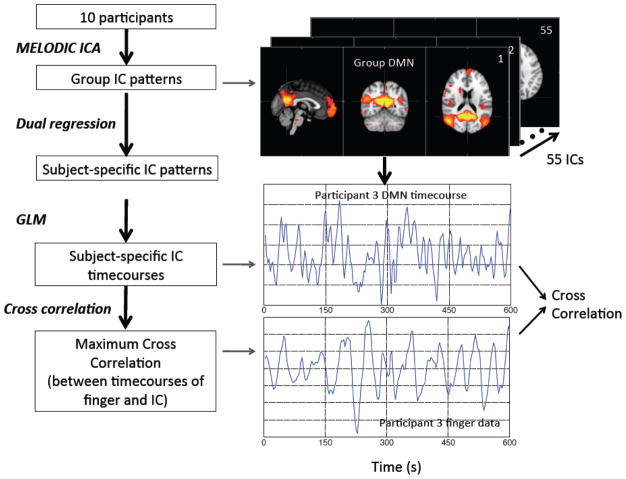
In order to evaluate whether these systemic LFOs affect different RSNs and to what extent, we conducted analyses in the following steps as shown in Figure 3. Multivariate Exploratory Linear Optimized Decomposition into Independent Components (MELODIC) ICA from FSL (Beckmann et al., 2005; Beckmann and Smith, 2004) was used on these 10 participants’ data sets. Fifty-five ICs were automatically generated by the ICA procedure. The dual regression method (Filippini et al., 2009) (from FSL) was then applied to the group results to calculate the corresponding subject-specific ICs for each participant. These subject-specific IC (i.e., 55 ICs) patterns were used as regressors in a spatial GLM to extract the corresponding subject-specific timecourse for each of the 55 ICs. The last step calculated the cross correlation between the subject-specific timecourse for each IC with downsampled NIRS Δ[tHb] recorded at the fingertip of the same participant (the max lag in the cross correlation is set to be ± 14.4s, that has been shown to fully cover the time delays between the NIRS Δ[tHb] and BOLD fMRI).
Figure 3.
The flow chart of the analytical process (together with corresponding intermediate results) to identify the ICs derived from group-ICA that have high correlations with the NIRS Δ[tHb] recorded at the finger.
The maximum cross correlation coefficient (MCCC) between each IC timecourse and Δ[tHb] from the fingertip was selected for each participant. The averaged MCCCs were obtained from 10 participants and were plotted in descending order with their corresponding standard deviations (std). To estimate the noise level in the calculation, cross correlation was also calculated between subject-specific timecourses for each IC and temporally-uncoupled NIRS Δ[tHb] recorded at the fingertip of the same participant, however at a much later time (480s later than the start of the fMRI scan). The resulting MCCCs were plotted in the same graph as comparison.
Lastly, we conducted the spatial correlation (R) between all 55 ICs with the well-known RSN templates (Beckmann et al., 2005; Smith et al., 2009) using fslcc from FSL. The threshold correlation in fslcc was set to 0.3 (R> 0.3).
2.4 Reproducibility analyses
The analyses described above were implemented to identify the ICs that have high MCCCs with the fingertip data (NIRS Δ[tHb]), or in other words, to identify those ICs that are greatly affected by systemic blood fluctuations. In order to demonstrate the reproducibility of the procedure for identifying the physiologically correlated ICs, we not only used a bootstrapping method according to Damoiseaux et al. (Damoiseaux et al., 2006), but we also tested the effects of choosing dimensionality other than 55 (in group ICA) on the spatial patterns of the physiologically correlated ICs.
The bootstrapping method (Damoiseaux et al., 2006) was employed as shown in Figure 4. Six participants were selected randomly (without repeat) to form a subgroup of the original base group of 10 participants. The analytical procedure in Figure 3 was applied to identify the top 10 physiologically correlated ICs (in terms of correlation value) from the subgroup. Then the spatial correlation (R; calculated by fslcc in FSL) was calculated between the top 10 ICs from the base group and those from the subgroup. An IC of the base group is considered to be reproduced if the magnitude of R (calculated between this IC and any other top 10 ICs from the subgroup) is greater than 0.3. The process was repeated 50 times between the base group and 50 unique subgroups (selected by bootstrapping, out of 210 possible combinations). The reproducibility (RP) of an IC from the base group is defined as RP= n/50, where n is the number of its appearances in the top 10 ICs of the subgroups, and 50 is the number of subgroups. In some instances an IC in the base group might be split into more than one IC in the subgroup, which would only be counted as one. The ICs from the base group with high reproducibility (RP> 0.8) are shown.
Figure 4.
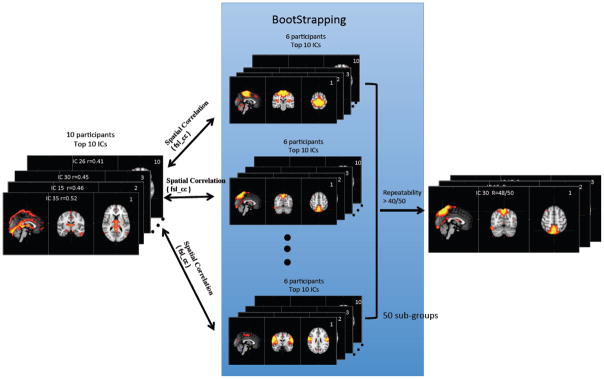
The illustration of the bootstrapping analytical procedure that calculates the reproducibility of the ICs that showed high correlations with the finger data.
To demonstrate that the analysis procedure for identifying physiologically correlated ICs is not limited to a dimensionality of 55, we tested the reproducibility of our results with dimensionality set to other values. Using the entire group (the original 10 participants), the dimensionality was varied to set the number of ICs equal to 25, 35, 45, 70, 85 and even 100, while the remainder of the steps in the analyses was kept the same.
2.5 Denoising using Regressor Interpolation at Progressive Time Delays (RIPTiDe)
In order to remove the effect of the peripheral physiological signal from the brain data, we used a modified version of the RIPTiDe physiological denoising method we have described previously (Frederick et al., 2012a). A temporally oversampled cross correlation followed by a Gaussian peak fitting was used to determine the maximum correlation time between the LFO component of the NIRS total hemoglobin waveform and the BOLD data at each voxel (Frederick et al., 2012b). This voxel specific time shift was then applied to the LFO (NIRS Δ[tHb]) regressor, and the timecourse was resampled to match the fMRI data. This generated a four dimensional dataset that was used as an input to film_gls as a voxel specific regressor. The four dimensional regressor file was then scaled by the resulting voxelwise beta values from the GLM fit and subtracted from the original data to generate a “denoised” dataset. Lastly, the analyses in Figure 3 were redone with the denoised fMRI data and the results were compared with the original ones.
2.6 Effects of cardiac pulsation
Given that other peripheral processes such as cardiac pulsation affect the BOLD fMRI signal, we determined if the analytical procedure outlined in Figure 3 could be used to identify the ICs that are mostly affected by cardiac pulsation (the respiration signal is not always detectable by the NIRS finger probe (Tong et al., 2012b), thus we were unable to apply this process to respiration). The cardiac pulsation data were extracted from the finger data (NIRS, Δ[tHb]), and it was downsampled according to the TR of fMRI (3s). However, this new temporal trace cannot be directly used in place of the LFO finger data in the process (Figure 3). This is because: 1) compared to systemic LFOs that influence the BOLD signal directly (i.e., 0.01~0.15 Hz), cardiac pulsation (~1Hz) is aliased in the BOLD signal (~0.33 Hz); 2) the cardiac pulsation wave is a dynamic wave that moves much more rapidly than the blood carrying it. The time step of the correlation calculation would be limited to that of the BOLD signal (3s, the same as the TR), far longer than the time it takes the cardiac pulse to travel through the whole brain (~1s), thus using one largely aliased temporal regressor will not be able to catch all the voxels on the passage of this wave in the brain (i.e. cross correlation). To estimate the correlation accurately, we used the following steps: 1) extract series (i.e. 25 timecourses) of temporally shifted cardiac pulsation data from the finger data (NIRS, Δ[tHb]) with the temporal shifts as small as 0.08s (thus the whole series covers about 0.08*25=2s); 2) downsample each temporal trace according to the TR of fMRI (3s); 3) calculate the correlation between each downsampled NIRS temporal trace and the temporal trace from each IC; 4) pick the maximum correlation coefficient for each IC. This maximum correlation coefficient is used to replace the MCCC. The ICs having significantly high correlation were identified as the ICs correlated to cardiac activity.
3 Results
3.1 Temporal correlations between LFOs from the periphery and brain
Figure 1(c) shows the LFOs (Δ[tHb]) recorded by NIRS at the fingertip (left middle finger, Figure 1 (a)) and the toe (left, Figure 1 (b)) of one representative participant. These two signals have high temporal correlation and a clear time-shift between these signals can be observed. The amount of time shift can be obtained by calculating the cross correlation. In the presented example the shift was 3.06 s, which indicates that the LFOs arrive at the finger 3.06 s earlier than they arrive at the toe. Similar observations were also made between NIRS measures of the LFOs in the fingertip and BOLD fMRI measures of those in the brain. Figure 2 (b–c) shows the LFOs (Δ[tHb]) recorded by NIRS at the fingertip and the BOLD signals from two example voxels, from the same participant. The correlation coefficients are high and the temporal shifts are t= +2.04 s and t= −2.16 s, respectively. This demonstrates that using the arrival time of LFO at the finger as reference, the LFO in the brain arrives at voxel one 2.16 s earlier, and at voxel two 2.04 s later.
3.2 Identified RSNs
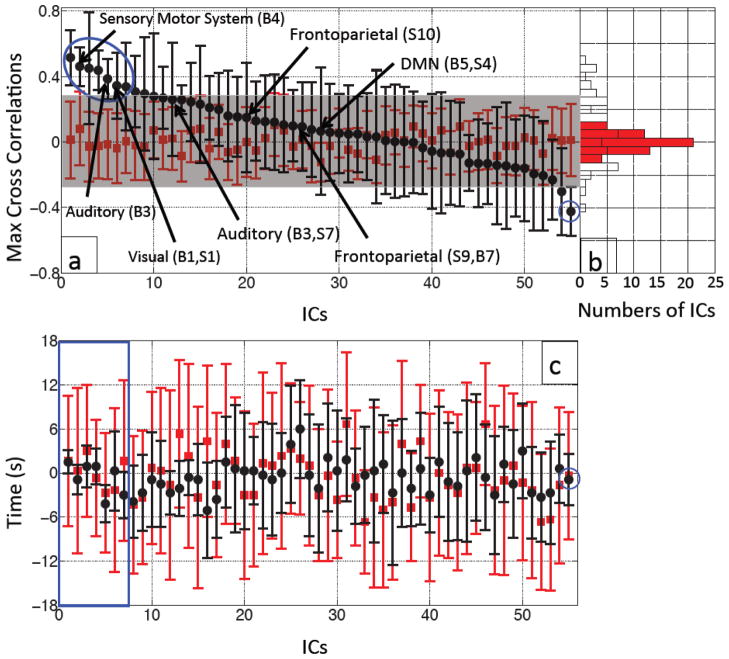
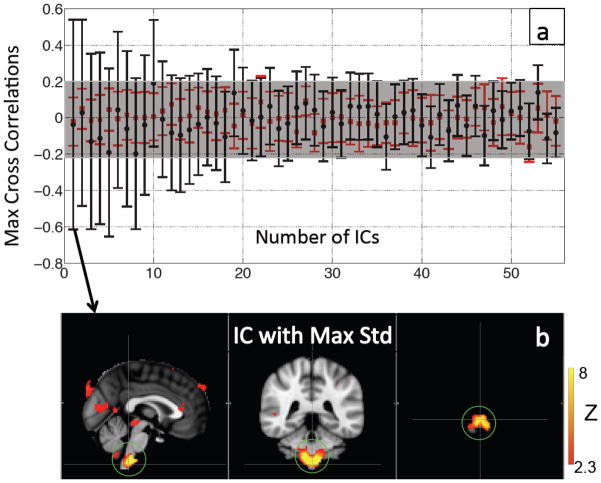
Figure 5(a) shows the averaged MCCCs (black dots, error bars indicate stds) between each IC timecourse and the within-subject Δ[tHb] from the fingertip in the 10 participants. The results are displayed in descending order. The estimated error (red) was calculated using the same procedure between each IC timecourse and the within-subject temporally uncoupled Δ[tHb] finger data. The resulting stds were within r= ±0.3, as indicated by the gray shade in the graph of Figure 5(a) (the mean and std of the red dots is 0.002±0.054). The top 7 ICs’ MCCCs represent correlations between IC timecourse and fingertip Δ[tHb] that are significantly different from the error (using false discovery rate (FDR) to correct for multiple comparisons between the averaged MCCCs from real data and those from uncoupled data, p< 0.05) (Benjamini and Yekutieli, 2001; Groppe et al., 2011). A subset of the ICs with high spatial correlations with previously described RSNs (Beckmann et al., 2005; Smith et al., 2009) is labeled in Figure 5(a). Among them, several well-known RSNs, including DMN and visual networks are listed. For example, when compared to Smith and colleagues’ RSN template (Smith et al., 2009), high correlations can be found between numerous ICs generated in our 55 component resting state analysis and their templates, including all visual RSNs (e.g. IC 26 (R= 0.73), IC 10 (R= 0.60) and IC 34 (R= 0.58)), the DMN (e.g. IC 44 (R= 0.56)), the auditory system (e.g. IC 49 (R= 0.50)), and both frontoparietal RSNs (e.g. IC 36 (R= 0.58) and IC 5 (R= 0.51)). Comparison with Beckmann’s template (Beckmann et al., 2005) showed high correlation with the medial visual cortical areas (e.g. IC 26 (R= 0.79)), the lateral visual cortical areas (e.g. IC 10 (R= 0.54)), the right lateralized dorsal visual stream (e.g. IC 36 (R= 0.50)), the visual-spatial (e.g. IC 44 (R= 0.62)) corresponding to the DMN of Smith (R= 0.79), the auditory system (e.g. IC 49 (R= 0.60), IC 17 (R= 0.30)), and the sensory motor system (e.g. IC 15 (R= 0.56), IC 17 (R= 0.35). A detailed table of the spatial correlation results is provided as supplemental materials (Table 1).
Figure 5.
Averaged MCCCs (black dots) between each participant’s IC timecourse (55 ICs) and Δ[tHb] measured at the fingertip were plotted in descending order with their error bars (a). To estimate the noise level, averaged MCCCs between the IC timecourses and temporally uncoupled Δ[tHb] (data collected 480 s later) were calculated for each IC (red squares in (a)). The blue circle marks the ICs with significant correlations with the data from the fingertip. The ICs that have high spatial correlations (R ≥ 0.5) with templates from Smith et al. (Smith et al., 2009) or Beckmann et al. (Beckmann et al., 2005) are labeled with the black arrows with their corresponding names. Figure 5(b) shows a corresponding histogram shows the distributions of the averaged MCCCs for the real (black line) and temporally uncoupled data (red blocks). Figure 5(c) shows averaged time delays (black dots) between each participant’s IC timecourse (55 ICs) and Δ[tHb] measured at the fingertip plotted with their error bars in the same order as in (a). The temporally uncoupled NIRS data was used to estimate the noise level (red squares and bars in (c)). The blue square in (c) marks the top 7 ICs with significant correlations with the data from the fingertip as shown in (a).
The histogram in Figure 5(b) shows the corresponding distribution of the averaged MCCCs calculated from the real data (white bars) and the noise estimates (red bars). We expected that the distribution of the average MCCCs would be Gaussian if there were no intrinsic correlations between the IC timecourse and the finger data. However, as our results in the histogram show, there are clearly distinct ICs with high averaged MCCCs. This validates the noise estimate procedure we employed (using participant’s own temporally uncoupled data instead of random noise), as the distribution of correlation values was neither Gaussian nor zero-mean.
Figure 5(c) shows the averaged time delays (black dots, error bars indicate stds) instead of averaged MCCCs between each ICs temporal trace and the LFOs from NIRS Δ[tHb] (averaged from 10 participants). The results are displayed in the order given in Figure 5(a). The estimated error (red) was calculated using the same procedure between each IC timecourse and the within-subject temporally uncoupled Δ[tHb] finger data, as in Figure 5(a). The stds of the delays calculated from the real regressors (black error bars, average std =2.3s) of the first 5 delays (in blue square) are much smaller than the estimates from the uncoupled data (red error bars, average std of noise estimate =10.2s) with the averaged time delays ranging from −4.2s to 1.5s. The reference for the time delay calculation is set to be zero, when the LFOs signal is detected at the fingertip. A negative time means the LFOs signal arrives earlier than it reaches the fingertip. The time delay of the last IC in Figure 5(c) is −0.9±3.5s.
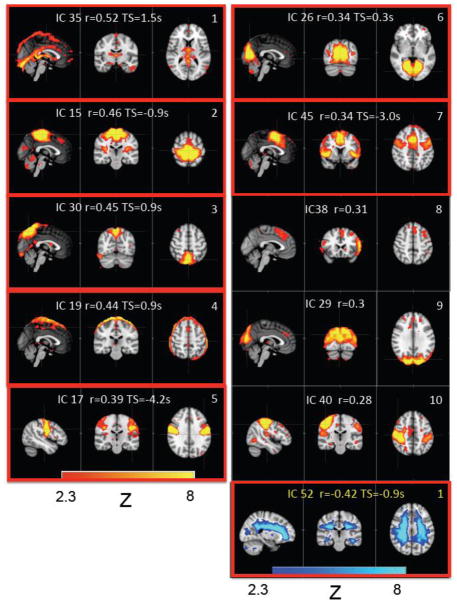
Figure 6 shows the spatial patterns of the top 10 ICs (identified in Figure 5; i.e., those that have the highest averaged MCCCs), together with their IC number as result of the MELODIC procedure and corresponding averaged MCCC values. The IC patterns enclosed in the red boxes are those that were significantly different from the noise estimate (corrected for multiple comparisons). Figure 6 also shows the IC spatial pattern with the highest negative MCCC with the finger data (as the lower right-most panel, numbered 1 with text in yellow). The spatial patterns of the top 5 ICs (those that have the highest averaged MCCCs) calculated with different dimensionalities (70 ICs, 85 ICs and 100 ICs) are shown as Figure 1 in the Supplemental Materials.
Figure 6.
The IC patterns corresponding to the first 10 ICs that show high positive correlations with the peripheral data (see Figure 5(a), blue circle). The IC pattern with the highest negative correlation with the peripheral data is also shown in the last panel. In each small graph, the IC number (generated by MELODIC), its corresponding averaged MCCC and averaged time delays are displayed. The graphs in the red box are the ICs that were significant different from the noise (corrected for multiple comparison by FDR).
3.3 Reproducibility
The ICs numbered 1–7 in Figure 5(a) have averaged MCCCs ranging from 0.34–0.52, and are significantly different from the estimates of noise. The ICs numbered from 8 to 10 in the same figure are not considered significant by the t-test. However, there are two reasons for including them in further analyses of reproducibility. First, the order of ICs shown in Figure 5(a) is from a single MELODIC analysis with one dimensionality (i.e. 55); repeating the same analysis with the same or different dimensionality can change the rank order slightly in Figure 5(a) or produce merged or split ICs. Multiple analyses have been run to confirm that the top 10 ICs in Figure 5(a) are representative and cover the variability associated with different ICA runs. Second, to estimate the noise of the MCCCs, we conducted the same analytical process (in Figure 3), now between subject-specific IC timecourse and participant’s own delayed finger data (instead of the simultaneously recorded finger data). The delay time was chosen to be 480 s in this case. However, if we change the delay time, the noise estimate (red dots) may change slightly, which will change the results of significance testing. Multiple tests have also been run with different time delays to confirm that these effects of time delay only affect the top 10 ICs. These slight differences in the analyses, make it necessary to include the top 10 ICs from both the base group and the subgroups into the bootstrapping procedure (introduced in Figure 4) to identify the physiologically correlated ICs with certainty.
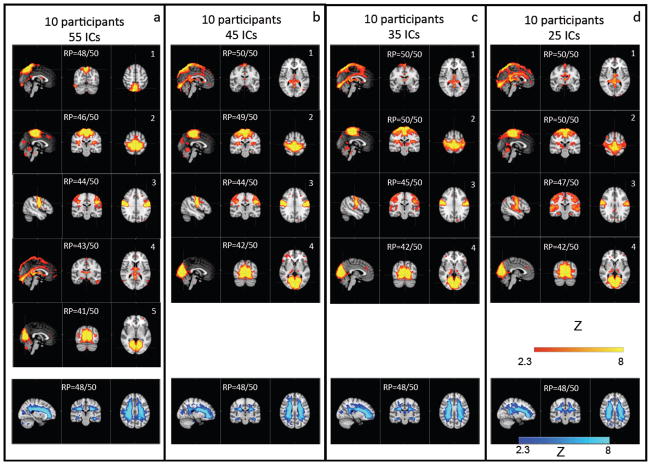
Figure 7 shows the ICs of the base groups that have been repeatedly identified in the 50 subgroups as physiologically correlated ICs. The four panels represent four sets of different results in which the dimensionality of the analysis of the base group were set differently. In each panel, the ICs with the high reproducibility (RP> 40/50) are shown with either the positive or the negative correlations with the fingertip data. In this analysis, the dimensionality was initially estimated by MELODIC automatically, yielding 55 ICs. In resting state analyses, dimensionalities of 20 to 120 ICs are commonly used (Beckmann et al., 2005; Smith et al., 2009). Higher dimensionality can separate ICs that might merge together when dimensionality is lowered. Since our goal was to separate the physiologically correlated ICs from the other ICs, it is logical to favor higher dimensionality analyses, which are better able to separate ICs that have similar signals. Therefore we used a fixed number of components, namely 55 ICs for all subgroups (six participants), which is the number of ICs automatically generated by MELODIC analysis when the dimensionality was not fixed. For the base group (10 participants), we next applied several commonly used dimensionalities (25, 35, 45, 55) to assess if and how the differences in dimensionality affect the physiologically correlated IC patterns. In Figure 7, we can observe that the similar set of IC patterns (panels a–d) was identified regardless of the different dimensionalities used in the base groups. For example, the similarity existed in 1) the second IC pattern in Figure 7(a) is visible as the second IC in all other panels (Figure 7(b–d)); 2) the third IC pattern in Figure 7(a) also returns as the third IC pattern in all other panels (Figure 7(b–d)); 3) the fourth IC pattern in Figure 7 (a) can be found as the first IC pattern in all other panels (Figure 7(b–d)); the fifth IC in Figure 7(a) is visible as the 4th IC in all other panels (Figure 7(b–d).
Figure 7.
The physiologically correlated patterns of the ICs, which are highly reproducible (RP> 40/50) as calculated from the bootstrapping method (panels a–d). Dimensionality was set to 55 (a), 45 (b), 35 (c) and 25 (d).
3.4 Denoising
Figure 8 shows the same plot as in Figure 5, but now using BOLD fMRI data that have been denoised by the RIPTiDe method using NIRS Δ[tHb] from the finger. Compared to Figure 5, the averaged MCCCs between each IC timecourse (after denoising) and the within-subject Δ[tHb] from the fingertip are much smaller (−0.26~0.15) and not significantly different from the noise estimate (−0.14~0.15). The positions of several ICs, which had high correlations in Figure 5 and had been repeatedly identified as in Figure 7, are labeled in Figure 8(a) by the black arrows. The histogram of Figure 8(b) shows the similarity of the distributions of the averaged MCCCs calculated from the real denoised data (white bars) and the noise estimates (red bars).
Figure 8.
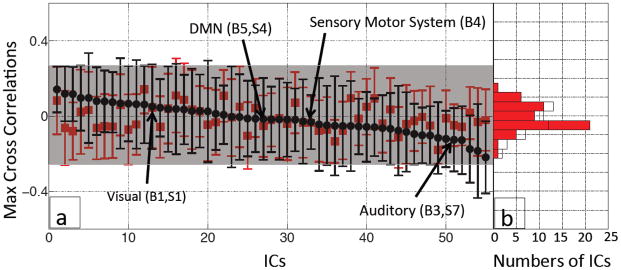
Averaged MCCCs (black dots) between each participant’s IC timecourse (55 ICs) after denoising procedure and Δ[tHb] measured at the fingertip were plotted in descending order (according to their MCCCs) with their error bars (a). To estimate the noise level, averaged MCCCs between the IC timecourses and temporally uncoupled Δ[tHb] (480 s late) were calculated for each IC (red squares in (a)). A corresponding histogram shows the distributions of the averaged MCCCs for the real (black line) and temporally uncoupled data (red blocks).
Table 1 compares the top 5 IC patterns identified in Figure 7(a) (analysis with dimensionality of 55 ICs) before and after the denoising procedure. All 5 ICs in Figure 7(a) were identified in the results of MELODIC analyses of denoised data (the left column in Table 1). The spatial correlations found between the corresponding ICs vary, ranging from R = 0.74 to 0.95, as shown in the middle column in Table 1. The percentage changes of the number of activated voxels between the corresponding ICs range from −31.7% to +22.7% (right column in Table 1). Negative percentage means the IC pattern from denoised data contains fewer voxels. The IC with the biggest change in area is marked in red.
Table 1.
Comparisons (in spatial correlation and number of voxels) between the corresponding ICs before and after the denoising procedure. The ICs displayed here are the same ICs as shown in Figure 7(a), in the same order.
| Corresponding ICs | Spatial Correlation (fslcc) between the corresponding ICs | Difference of the numbers of the voxels in the corresponding ICs |
|---|---|---|
| IC30 (IC32) | 0.88 | +22.7% |
| IC15 (IC34) | 0.95 | −12.4% |
| IC17 (IC45) | 0.95 | − 2.4% |
| IC35 (IC10) | 0.74 | −31.7% |
| IC26 (IC13) | 0.94 | +0.7% |
3.5 Impact of cardiac pulsation
The result of using the regressors generated from the timecourses of cardiac pulsation is shown in Figure 9(a), in which the averaged maximum correlation coefficients and their stds (10 participants) is plotted in descending order according to the stds. From Figure 9(a), there were no ICs with averaged maximum correlation coefficients that were significantly different from the noise estimate. However, the stds from some averaged maximum correlation coefficients were large. For instance, the averaged maximum correlation coefficients of the first 4 ICs in Figure 9(a) are not significant (from −0.11 to 0.03) yet their stds are much larger (from 0.47 to 0.58) than the noise estimate (average std of noise estimate = 0.13). The corresponding IC patterns (with highest std) are shown in Figure 9(b).
Figure 9.
Averaged MCCCs (black dots in (a)) between each participant’s IC timecourse (55 ICs) and series of temporally shifted Δ[tHb] downsampled from NIRS data (high-pass filtered, >0.6 Hz), were plotted in descending order according to their error bars (i.e. std). To estimate the noise level, averaged MCCCs between the IC timecourses and timely uncoupled Δ[tHb] (480 s late) were calculated for each IC (red squares in (a)). The pattern of the IC that had the highest variations in MCCCs (first IC in (a)) is shown in (b). The green circle highlights the medulla oblongata.
4. Discussion
4.1 Physiological correlation
The possible origin and characteristic of the systemic LFO have been discussed extensively in our previous work (Tong et al., 2012b). The main focus of this work is to understand its impact on the detection of the RSNs, especially the ones produced by ICA. The present results indicate that the timecourses of a number of BOLD fMRI ICs in the brain have significant correlations (both positive and negative) with the NIRS Δ[tHb] data collected from the finger, and therefore contain significant contributions from nonneuronal sources. In fact, the spatial pattern of the first IC (i.e., IC 35) in Figure 6 showed clearly recognizable regions involved in blood flow, including the superior sagittal sinus, straight sinus, and inferior sagittal sinus. Accordingly, this IC produced the highest averaged MCCC (r= 0.52) with the fingertip data, as expected, thus validating the sensitivity of the method of identification. Similar vascular patterns can also be found in IC pattern 3 (i.e., IC 30). Moreover, many ICs in Figure 5 could be identified with previously reported RSNs. For instance, our peripherally correlated IC15, IC17 and IC26 (see Figure 6), were also highly correlated (R > 0.3) with the sensorimotor, auditory, and visual RSNs characterized by Beckmann et al. (Beckmann et al., 2005) and Smith et al. (Smith et al., 2009). In contrast, the ICs consistent with executive control RSNs, such as DMN and the frontal parietal network, appear to be less correlated with the systemic LFO, suggesting that the effect of the systemic LFO on RSNs may vary widely. Therefore, of equal importance to distinguishing the ICs that have timecourses with large contributions from systemic LFO, a nonneuronal signal, this method also identifies which ICs have a smaller contribution from the systemic LFO, shown in Figure 5(a).
All the ICs identified in Figure 5 were derived from a single analysis. The ICs with high reproducibility (RP > 40/50) among 50 subgroups (bootstrapping) are shown in Figure 7. In addition to the IC that clearly represents the cerebral vasculature (the first and fourth IC pattern in Figure 7(a) and the first IC pattern in Figure 7(b–d)), the method identified three more ICs with high repeatability, corresponding to the sensorimotor (second IC pattern in Figure 7(a–d)), visual (fifth IC pattern in Figure 7(a) and fourth IC pattern in Figure 7(b–d)), and auditory RSNs (third IC pattern in Figure 7(a–d)). The commonality among these sensory RSNs is that they all have high blood capillary density (or vascular density (Biswal et al., 2007)). Harrison et al. demonstrated that density of blood vasculature is high in the primary sensory areas, including motor cortex, the speech related regions (Wernicke’s and Broca’s area) and visual cortex (Harrison et al., 2002). They also showed that the areas with high density are likely to be “activated” in functional tasks. In resting state studies, these same primary sensory areas are among the mostly identifiable networks using either seed-based analysis or ICA. Actually, the first resting state network ever found was the bilateral motor cortex (Biswal et al., 1995). Our contribution in this study is to point out that these same primary sensory cortices have high correlations with the systemic peripheral LFO in resting state. As we have shown previously (Figure 2) as well as in some of our other studies (Tong and Frederick, 2010; Tong et al., 2012a), the systemic LFOs are: 1) closely related to the blood signal (blood flow and volume); 2) moving through the brain dynamically, thus affecting different parts of the brain at different times. The high blood capillary distribution in the primary sensory cortices contributes to the high correlations by preferentially accentuating systemic hemodynamic fluctuations. Furthermore, the symmetry of these cortices on the cerebral vasculature results in the same time delays of the systemic LFOs arriving at these areas. For example, the time delays for the systemic LFOs in the left and right motor cortices are the same, due to the symmetry of the two bilateral motor cortices. However, the time delays are likely to be different when compared to other networks; for example, the visual cortex may be farther or closer to the source of the systemic LFO in the vasculature. This is also demonstrated by the work of Bright et al. (Bright et al., 2009). They showed the regional heterogeneity in the vascular response using a novel breathing paradigm. These are the reasons that the primary sensory networks can be identified easily and separately. In Figure 5(c) and 6, the ICs 2, 5, and 6 are associated with sensory motor, auditory and visual networks respectively. The averaged temporal delays of these ICs are −0.9s, −4.2s and +0.3s. This supports the argument that the LFOs arrive at different networks with different time delays. Moreover, it seems that the temporal order of arrival of the LFOs is auditory, sensory motor, then visual cortex, which matches the overall front to back pattern of LFO arrival time we see consistently in arrival time maps (Tong and Frederick, 2010).
These ICs in Figure 7 are still likely to have neuronal contributions. This is supported by the fact that the temporal traces from these areas, even though highly correlated with the systemic LFOs with different temporal shifts, are not temporally shifted copies of each other. This supports the existence of the local oscillations in addition to these systemic components. However, due to the significant impact of the systemic LFOs to these areas, the RSNs of these primary sensory networks are obscured. We employed our previously developed physiological denoising method (Frederick et al., 2012a), in hopes of understanding the nature of these physiologically correlated ICs, mainly located in the primary sensory cortices. The results are briefly discussed in the next session.
An interesting observation is the existence of an IC with a negative averaged MCCC (i.e., last IC pattern in Figure 6 and Figure 7). This IC is the only one that has been repeatedly identified as having the negative correlations with the systemic LFO (Figure 7). This IC pattern represents mostly white matter in the brain, but it is unclear why temporal oscillation of white matter as measured by BOLD fMRI is negatively correlated with the systemic blood fluctuation (for 55 ICs, the averaged time delay for this white matter IC is −0.9s as shown in Figure 6 last IC pattern). Aslan et al., have recently found that CBF in the white matter is inversely correlated with the gray matter’s temporal synchrony (Asian et al., 2011), which matches our finding. Although it is tempting to envision anticorrelation as resulting from a misalignment of two regular waveforms in time (knowing the vascular transit time in the white matter is longer than that in the gray matter(van Gelderen et al., 2008)), it is important to note that the LFO signal is a pseudorandom, multifrequency signal; as such there is no such thing as “180 degrees out of phase” – anticorrelation implies an actual negative correlation of the BOLD with the NIRS data, rather than a phase shift. Therefore we hypothesize that the mechanism by which the NIRS signal correlates with the white matter BOLD signal is different than that in the gray matter. One explanation consistent with the data is that the white matter serves as a cerebral blood reservoir, whose purpose is to meet the cerebral circulatory demands of the “more critical” gray matter. This means that less blood would flow to the white matter if the gray matter demands more. However, this is simply conjecture, and more studies are needed to clarify this issue. Lastly, even though the white matter IC has been consistently identified to have a negative correlation, its correlation coefficient is relatively low. This is probably due to the fact that the blood supply to the white matter is significantly lower (~25%) than that to the gray matter (Mezer et al., 2009), thus leading to lower SNR.
4.2 Physiological correction
The results in Figure 8 demonstrate the effectiveness of the RIPTiDe method in removing systemic LFOs from BOLD data. After the denoising procedure, no ICs have high correlations with the NIRS Δ[tHb]. Specifically, the ICs associated with motor, visual and auditory networks, which previously had quite high correlations with the systemic physiological signal, no longer rank high in Figure 8(a). Moreover, the distribution of maximum correlation coefficients, as shown in the histogram in Figure 8(b) shows no significant difference between the distribution of the MCCCs (after denoising procedure) and the random distribution of estimated noise calculated from the temporally uncoupled NIRS data.
Table 1 summarizes the differences of the top 5 ICs (from Figure 7(a)) before and after the denoising procedure. It is interesting to note that after the NIRS LFOs were regressed out from the BOLD fMRI using RIPTiDe, these IC patterns are still clearly identifiable. This is supported by the high spatial correlations (the middle column in Table 1) calculated between the corresponding ICs (before and after the denoising procedure). The most likely explanation is that these functionally linked areas of the brain also have similar vascularization; this will of necessity mean that there will be strong correlation within the networks due to the common physiological variation that will overlay, and to some degree obscure, the variation due to correlated neuronal activity.
The effect of removing the physiological noise affects all of these networks differently. One IC has a very significant decrease in size (−31.7%) (Table 1) - the IC that is very clearly outside the brain and associated with cerebral vasculature (IC4 in Figure 7(a)). This demonstrates that the systemic LFOs (identified by NIRS) effect on the BOLD signal, is most pronounced in voxels in and near the cerebral vasculature. However, the IC pattern (IC4 in Figure 7(a)) is still detectable, even with much smaller size. This is not surprising; there are doubtless other physiological fluctuations (from respiration, cardiac pulsations and arterial gas tension or concentrations) that affect the voxels of this primarily vascular IC similarly. These different physiological processes affect the BOLD fMRI through blood circulation independently, so while removing one of these effects (NIRS systemic LFOs) reduces correlation with the region, we are still able to detect the similar but smaller IC pattern. This idea is also supported by our previous study (Frederick et al., 2012a), in which we found the noise regressors generated from simultaneously recorded NIRS signal account for different portions of the variation in the BOLD fMRI than those from RETROICOR (Glover et al., 2000) and respiratory fluctuations (Birn et al., 2006).
For the remaining 4 ICs in Table 1, the changes in network size are both positive and negative, some of them quite significant (IC 30 increases in size by 22.7%). This is presumably accompanied by significant changes in network strength. More analyses and more subjects are needed to fully understand the issue, but the degree to which the overlying global vascular signal modifies the networks will depend on the specifics of the vascular networks within these brain regions; therefore removing the physiological signal will affect the quantitation of the underlying functional networks differently. The heterogeneity of the effect highlights the importance of removing this physiological noise – comparing the relative strengths of resting state networks between subjects or between states will be most sensitive when the confounding effects of overlying, global hemodynamic variations are removed. Moreover, as result, we found the improvements in the other networks too. For example, the DMN moved from IC 44 (before denoising) to IC 2 (after denoising), meaning more physiological variance has been removed.
4.3 Dimensionality
Varying the dimensionalities of the analysis of the complete subject group resulted in the identification of ICs that were consistent with those when the dimensionality was set to 55. For example, the ICs shown in Figure 7 (b–d) were almost one-to-one matches to those shown in Figure 7(a). Another observation made with the dimensionality analysis was that small dimensionality causes ICs to merge, as expected. For instance, the IC1 shown in Figure 7(b–d) appears to be the result of merging ICs 1 and 4 from Figure 7(a). This observation is supported by the spatial correlation analysis that was not shown. Moreover, IC3 and IC4 in Figure 7(b–d) are slightly larger compared to their counterparts IC3 and IC5 in Figure 7(a), likely due to this low dimensionality-related merging effect. While using a higher dimensionality (e.g., 70–100 as shown in the Supplemental Materials; Figure 1) creates less merging, similar ICs were identified as those seen in the 55-dimensionality analysis. Therefore, the peripherally correlated IC patterns identified are essentially the same regardless of the dimensionality. Altogether, these findings demonstrate the robustness of the peripherally correlated ICs.
4.4 Cardiac signal from NIRS
In our analyses on the effects of cardiac pulsation, there were no ICs with averaged maximum correlation coefficients that were significantly different from the noise estimate (Figure 9). However, beyond the facts that the cardiac pulsation wave is smaller than LFOs (1:4) and it is largely aliased into the BOLD fMRI, there is one major difference in the LFOs and cardiac pulsation wave, which is that the cardiac signal is highly periodic and oscillate at a much higher frequency (~1Hz). Thus, the maximum correlation coefficients calculated between the ICs’ temporal traces and a series of NIRS cardiac regressors (shifted by 0.08s) can be either positive or negative. This explains the large stds observed in Figure 9, since some subjects have high positive correlation coefficients while some have high negative ones; this is likely due to small variations in the temporal alignment of the heavily aliased cardiac variations with the BOLD signal in different voxels. In this case, the ICs with large stds are the ICs that have high correlations with the cardiac pulsation wave (but because of misalignment, vary between large positive and negative extremes – this effect is shown in Figure 2 in the Supplemental Material). Figure 9(b) shows the corresponding pattern for the IC with the largest std (the patterns for the top 4 ICs with largest stds are shown in Figure 3 in the Supplemental Materials). The area marked with the green circle (Figure 9(b)) mostly overlaps the medulla oblongata, a portion on the brainstem. The medulla oblongata controls autonomic nervous activity and regulates basic autonomic functions, such as respiration and heart rate. The fact that our method is able to identify ICs associated with the medulla oblongata as having a high correlation with the cardiac pulsation is extremely interesting. However, it is also well known that higher physiological fluctuations are also present in the brainstem (Beissner et al., 2011). This finding should be explored further using fMRI techniques with higher temporal resolution (see below) and effective denoising procedures.
4.5 Future studies
It is well known that the variations in heart rate (Chang et al., 2009; Shmueli et al., 2007) and respiration volume (Birn et al., 2006; Kastrup et al., 1999; Liu et al., 2002) also contribute to the BOLD signal in the low frequency band. Our future work will generate the LFOs corresponding to respiration volume changes (Birn et al., 2008b) as well as heart rate changes (Chang et al., 2009), and compare them with our systemic LFOs measured at the fingertip. We hypothesize that results from those studies will show empirically if these three effects are related or if they are distinct from one another. Furthermore, we will apply the denoising methods described in this paper to further remove the physiological fluctuations caused by respiration and cardiac pulsation from BOLD fMRI resting state data, in order to determine the extent to which the ICs are influenced by these physiological signals. Furthermore, resting state data using multiband EPI sequence (Feinberg et al., 2010) are now being collected. The much shorter TR (~0.4s) used in the scan would help dramatically in the denoising procedure, specifically for the physiological fluctuations from the respiration and cardiac pulsation due to the fact that these procedures are fully sampled in the fast sequence. Application of this method to high temporal resolution data may yield further insight into the interaction of physiological signals with BOLD data in the brain.
5. Conclusion
Using correlations between NIRS-measured concurrent systemic LFOs in Δ[tHb] from the fingertip and BOLD fMRI signal changes in resting state ICs, we have shown that not all the RSNs identified with ICA are affected by the systemic LFOs equally. Some of them were strongly correlated with the peripheral signals. A bootstrapping method has been used to confirm that physiologically correlated RSNs are mostly the RSNs associated with primary sensory cortices, including motor, auditory and visual cortex. Other RSNs associated with executive functions, such as DMN, are not strongly correlated with the systemic LFOs. We observe that these primary sensory RSNs contain significant contributions from the global blood-borne LFO signal due to their high blood capillary distribution and structural symmetry in the cerebral vasculature. We further show that RIPTiDe denoising can effectively reduce the influence of these signals on connectivity measurements.
Supplementary Material
Highlights.
Peripheral NIRS signals and BOLD fMRI data are highly temporally correlated.
Peripheral NIRS correlates strongly with some resting state networks.
Motor, visual and auditory networks are strongly correlated with peripheral NIRS.
The physiological correlations are consistent between subjects.
Acknowledgments
We thank Dr. Scott Lukas for meaningful discussions about this work, which was supported by the National Institutes of Health, Grants T32 DA015036 (YT), K25 DA031769 (YT), R21 DA027877 (BdeBF), K01 DA023659 (SCL).
Footnotes
Disclosure/Conflict of Interest
There are no conflicts of interest to declare.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Aslan S, Huang H, Uh J, Mishra V, Xiao G, van Osch MJ, Lu H. White matter cerebral blood flow is inversely correlated with structural and functional connectivity in the human brain. NeuroImage. 2011;56:1145–1153. doi: 10.1016/j.neuroimage.2011.02.082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckmann CF, DeLuca M, Devlin JT, Smith SM. Investigations into resting-state connectivity using independent component analysis. Phil Trans R Soc B. 2005;360:1001–1013. doi: 10.1098/rstb.2005.1634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckmann CF, Smith SM. Probabilistic independent component analysis for functional magnetic resonance imaging. IEEE transactions on medical imaging. 2004;23:137–152. doi: 10.1109/TMI.2003.822821. [DOI] [PubMed] [Google Scholar]
- Beissner F, Deichmann R, Baudrexel S. fMRI of the brainstem using dual-echo EPI. NeuroImage. 2011;55:1593–1599. doi: 10.1016/j.neuroimage.2011.01.042. [DOI] [PubMed] [Google Scholar]
- Benjamini Y, Yekutieli D. The control of the false discovery rate in multiple testing under dependency. The Annals of Statistics. 2001;29:1165–1188. [Google Scholar]
- Birn RM, Diamond JB, Smith MA, Bandettini PA. Separating respiratory-variation-related fluctuations from neuronal-activity-related fluctuations in fMRI. NeuroImage. 2006;31:1536–1548. doi: 10.1016/j.neuroimage.2006.02.048. [DOI] [PubMed] [Google Scholar]
- Birn RM, Murphy K, Bandettini PA. The effect of respiration variations on independent component analysis results of resting state functional connectivity. Human brain mapping. 2008a;29:740–750. doi: 10.1002/hbm.20577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Birn RM, Smith MA, Jones TB, Bandettini PA. The respiration response function: the temporal dynamics of fMRI signal fluctuations related to changes in respiration. NeuroImage. 2008b;40:644–654. doi: 10.1016/j.neuroimage.2007.11.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biswal B, Yetkin FZ, Haughton VM, Hyde JS. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magnetic resonance in medicine: official journal of the Society of Magnetic Resonance in Medicine/Society of Magnetic Resonance in Medicine. 1995;34:537–541. doi: 10.1002/mrm.1910340409. [DOI] [PubMed] [Google Scholar]
- Biswal BB, Kannurpatti SS, Rypma B. Hemodynamic scaling of fMRI-BOLD signal: validation of low-frequency spectral amplitude as a scalability factor. Magnetic resonance imaging. 2007;25:1358–1369. doi: 10.1016/j.mri.2007.03.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bright MG, Bulte DP, Jezzard P, Duyn JH. Characterization of regional heterogeneity in cerebrovascular reactivity dynamics using novel hypocapnia task and BOLD fMRI. NeuroImage. 2009;48:166–175. doi: 10.1016/j.neuroimage.2009.05.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun VD, Adali T, Stevens MC, Kiehl KA, Pekar JJ. Semi-blind ICA of fMRI: A method for utilizing hypothesis-derived time courses in a spatial ICA analysis. NeuroImage. 2005;25:527–538. doi: 10.1016/j.neuroimage.2004.12.012. [DOI] [PubMed] [Google Scholar]
- Chang C, Cunningham JP, Glover GH. Influence of heart rate on the BOLD signal: the cardiac response function. NeuroImage. 2009;44:857–869. doi: 10.1016/j.neuroimage.2008.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole DM, Smith SM, Beckmann CF. Advances and pitfalls in the analysis and interpretation of resting-state FMRI data. Frontiers in systems neuroscience. 2010;4:8. doi: 10.3389/fnsys.2010.00008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Damoiseaux JS, Rombouts SA, Barkhof F, Scheltens P, Stam CJ, Smith SM, Beckmann CF. Consistent resting-state networks across healthy subjects. Proceedings of the National Academy of Sciences of the United States of America. 2006;103:13848–13853. doi: 10.1073/pnas.0601417103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delpy DT, Cope M, van der Zee P, Arridge S, Wray S, Wyatt J. Estimation of optical pathlength through tissue from direct time of flight measurement. Physics in medicine and biology. 1988;33:1433–1442. doi: 10.1088/0031-9155/33/12/008. [DOI] [PubMed] [Google Scholar]
- Feinberg DA, Moeller S, Smith SM, Auerbach E, Ramanna S, Gunther M, Glasser MF, Miller KL, Ugurbil K, Yacoub E. Multiplexed echo planar imaging for sub-second whole brain FMRI and fast diffusion imaging. PloS one. 2010;5:e15710. doi: 10.1371/journal.pone.0015710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Filippini N, MacIntosh BJ, Hough MG, Goodwin GM, Frisoni GB, Smith SM, Matthews PM, Beckmann CF, Mackay CE. Distinct patterns of brain activity in young carriers of the APOE-epsilon4 allele. Proceedings of the National Academy of Sciences of the United States of America. 2009;106:7209–7214. doi: 10.1073/pnas.0811879106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Corbetta M, Snyder AZ, Vincent JL, Raichle ME. Spontaneous neuronal activity distinguishes human dorsal and ventral attention systems. Proceedings of the National Academy of Sciences of the United States of America. 2006;103:10046–10051. doi: 10.1073/pnas.0604187103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Raichle ME. Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nature reviews Neuroscience. 2007;8:700–711. doi: 10.1038/nrn2201. [DOI] [PubMed] [Google Scholar]
- Frederick B, Nickerson LD, Tong Y. Physiological denoising of BOLD fMRI data using Regressor Interpolation at Progressive Time Delays (RIPTiDe) processing of concurrent fMRI and near-infrared spectroscopy (NIRS) NeuroImage. 2012a;60:1913–1923. doi: 10.1016/j.neuroimage.2012.01.140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frederick B, Nickerson LD, Tong Y. Retrospective identification of global hemodynamic fluctuations from resting state fMRI. Biennial Conference on Resting State Brain Connectivity; Magdeburg, Germany. 2012b. [Google Scholar]
- Friston KJ, Frith CD, Fletcher P, Liddle PF, Frackowiak RS. Functional topography: multidimensional scaling and functional connectivity in the brain. Cerebral cortex. 1996;6:156–164. doi: 10.1093/cercor/6.2.156. [DOI] [PubMed] [Google Scholar]
- Glover GH, Li TQ, Ress D. Image-based method for retrospective correction of physiological motion effects in fMRI: RETROICOR. Magnetic resonance in medicine: official journal of the Society of Magnetic Resonance in Medicine/Society of Magnetic Resonance in Medicine. 2000;44:162–167. doi: 10.1002/1522-2594(200007)44:1<162::aid-mrm23>3.0.co;2-e. [DOI] [PubMed] [Google Scholar]
- Groppe DM, Urbach TP, Kutas M. Mass univariate analysis of event-related brain potentials/fields I: a critical tutorial review. Psychophysiology. 2011;48:1711–1725. doi: 10.1111/j.1469-8986.2011.01273.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrison RV, Harel N, Panesar J, Mount RJ. Blood capillary distribution correlates with hemodynamic-based functional imaging in cerebral cortex. Cerebral cortex. 2002;12:225–233. doi: 10.1093/cercor/12.3.225. [DOI] [PubMed] [Google Scholar]
- Hoshi Y, Kobayashi N, Tamura M. Interpretation of near-infrared spectroscopy signals: a study with a newly developed perfused rat brain model. Journal of applied physiology. 2001;90:1657–1662. doi: 10.1152/jappl.2001.90.5.1657. [DOI] [PubMed] [Google Scholar]
- Kastrup A, Kruger G, Glover GH, Neumann-Haefelin T, Moseley ME. Regional variability of cerebral blood oxygenation response to hypercapnia. NeuroImage. 1999;10:675–681. doi: 10.1006/nimg.1999.0505. [DOI] [PubMed] [Google Scholar]
- Kelly RE, Jr, Alexopoulos GS, Wang Z, Gunning FM, Murphy CF, Morimoto SS, Kanellopoulos D, Jia Z, Lim KO, Hoptman MJ. Visual inspection of independent components: defining a procedure for artifact removal from fMRI data. Journal of neuroscience methods. 2010;189:233–245. doi: 10.1016/j.jneumeth.2010.03.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiviniemi V, Kantola JH, Jauhiainen J, Hyvarinen A, Tervonen O. Independent component analysis of nondeterministic fMRI signal sources. NeuroImage. 2003;19:253–260. doi: 10.1016/s1053-8119(03)00097-1. [DOI] [PubMed] [Google Scholar]
- Kocsis L, Herman P, Eke A. The modified Beer-Lambert law revisited. Physics in medicine and biology. 2006;51:N91–98. doi: 10.1088/0031-9155/51/5/N02. [DOI] [PubMed] [Google Scholar]
- Liu HL, Huang JC, Wu CT, Hsu YY. Detectability of blood oxygenation level-dependent signal changes during short breath hold duration. Magnetic resonance imaging. 2002;20:643–648. doi: 10.1016/s0730-725x(02)00595-7. [DOI] [PubMed] [Google Scholar]
- Lu CM, Zhang YJ, Biswal BB, Zang YF, Peng DL, Zhu CZ. Use of fNIRS to assess resting state functional connectivity. Journal of neuroscience methods. 2010;186:242–249. doi: 10.1016/j.jneumeth.2009.11.010. [DOI] [PubMed] [Google Scholar]
- McKeown MJ, Sejnowski TJ. Independent component analysis of fMRI data: examining the assumptions. Human brain mapping. 1998;6:368–372. doi: 10.1002/(SICI)1097-0193(1998)6:5/6<368::AID-HBM7>3.0.CO;2-E. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mesquita RC, Franceschini MA, Boas DA. Resting state functional connectivity of the whole head with near-infrared spectroscopy. Biomedical optics express. 2010;1:324–336. doi: 10.1364/BOE.1.000324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mezer A, Yovel Y, Pasternak O, Gorfine T, Assaf Y. Cluster analysis of resting-state fMRI time series. NeuroImage. 2009;45:1117–1125. doi: 10.1016/j.neuroimage.2008.12.015. [DOI] [PubMed] [Google Scholar]
- Niazy RK, Xie J, Miller K, Beckmann CF, Smith SM. Spectral characteristics of resting state networks. Progress in brain research. 2011;193:259–276. doi: 10.1016/B978-0-444-53839-0.00017-X. [DOI] [PubMed] [Google Scholar]
- Perlbarg V, Bellec P, Anton JL, Pelegrini-Issac M, Doyon J, Benali H. CORSICA: correction of structured noise in fMRI by automatic identification of ICA components. Magnetic resonance imaging. 2007;25:35–46. doi: 10.1016/j.mri.2006.09.042. [DOI] [PubMed] [Google Scholar]
- Raichle ME, MacLeod AM, Snyder AZ, Powers WJ, Gusnard DA, Shulman GL. A default mode of brain function. Proceedings of the National Academy of Sciences of the United States of America. 2001;98:676–682. doi: 10.1073/pnas.98.2.676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosazza C, Minati L, Ghielmetti F, Mandelli ML, Bruzzone MG. Functional connectivity during resting-state functional MR imaging: study of the correspondence between independent component analysis and region-of-interest-based methods. AJNR American journal of neuroradiology. 2012;33:180–187. doi: 10.3174/ajnr.A2733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sasai S, Homae F, Watanabe H, Taga G. Frequency-specific functional connectivity in the brain during resting state revealed by NIRS. NeuroImage. 2011;56:252–257. doi: 10.1016/j.neuroimage.2010.12.075. [DOI] [PubMed] [Google Scholar]
- Shmueli K, van Gelderen P, de Zwart JA, Horovitz SG, Fukunaga M, Jansma JM, Duyn JH. Low-frequency fluctuations in the cardiac rate as a source of variance in the resting-state fMRI BOLD signal. NeuroImage. 2007;38:306–320. doi: 10.1016/j.neuroimage.2007.07.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Fox PT, Miller KL, Glahn DC, Fox PM, Mackay CE, Filippini N, Watkins KE, Toro R, Laird AR, Beckmann CF. Correspondence of the brain’s functional architecture during activation and rest. Proceedings of the National Academy of Sciences of the United States of America. 2009;106:13040–13045. doi: 10.1073/pnas.0905267106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TE, Johansen-Berg H, Bannister PR, De Luca M, Drobnjak I, Flitney DE, Niazy RK, Saunders J, Vickers J, Zhang Y, De Stefano N, Brady JM, Matthews PM. Advances in functional and structural MR image analysis and implementation as FSL. NeuroImage. 2004;23(Suppl 1):S208–219. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- Sui J, Adali T, Pearlson GD, Calhoun VD. An ICA-based method for the identification of optimal FMRI features and components using combined group-discriminative techniques. NeuroImage. 2009;46:73–86. doi: 10.1016/j.neuroimage.2009.01.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tohka J, Foerde K, Aron AR, Tom SM, Toga AW, Poldrack RA. Automatic independent component labeling for artifact removal in fMRI. NeuroImage. 2008;39:1227–1245. doi: 10.1016/j.neuroimage.2007.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tong Y, Frederick BD. Time lag dependent multimodal processing of concurrent fMRI and near-infrared spectroscopy (NIRS) data suggests a global circulatory origin for low-frequency oscillation signals in human brain. NeuroImage. 2010;53:553–564. doi: 10.1016/j.neuroimage.2010.06.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tong Y, Hocke LM, Licata SC, Frederick B. Low frequency oscillations measured in the periphery with near infrared spectroscopy (NIRS) are strongly correlated with blood oxygen level-dependent functional magnetic resonance imaging (BOLD fMRI) signals. Journal of biomedical optics. 2012a;17:106004. doi: 10.1117/1.JBO.17.10.106004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tong Y, Hocke LM, Licata SC, Frederick B. Low-frequency oscillations measured in the periphery with near-infrared spectroscopy are strongly correlated with blood oxygen level-dependent functional magnetic resonance imaging signals. Journal of biomedical optics. 2012b;17:106004. doi: 10.1117/1.JBO.17.10.106004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Dijk KR, Hedden T, Venkataraman A, Evans KC, Lazar SW, Buckner RL. Intrinsic functional connectivity as a tool for human connectomics: theory, properties, and optimization. Journal of neurophysiology. 2010;103:297–321. doi: 10.1152/jn.00783.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Gelderen P, de Zwart JA, Duyn JH. Pittfalls of MRI measurement of white matter perfusion based on arterial spin labeling. Magnetic resonance in medicine: official journal of the Society of Magnetic Resonance in Medicine/Society of Magnetic Resonance in Medicine. 2008;59:788–795. doi: 10.1002/mrm.21515. [DOI] [PubMed] [Google Scholar]
- Vincent JL, Kahn I, Snyder AZ, Raichle ME, Buckner RL. Evidence for a frontoparietal control system revealed by intrinsic functional connectivity. Journal of neurophysiology. 2008;100:3328–3342. doi: 10.1152/jn.90355.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H, Zhang YJ, Lu CM, Ma SY, Zang YF, Zhu CZ. Functional connectivity as revealed by independent component analysis of resting-state fNIRS measurements. NeuroImage. 2010a;51:1150–1161. doi: 10.1016/j.neuroimage.2010.02.080. [DOI] [PubMed] [Google Scholar]
- Zhang YJ, Lu CM, Biswal BB, Zang YF, Peng DL, Zhu CZ. Detecting resting-state functional connectivity in the language system using functional near-infrared spectroscopy. Journal of biomedical optics. 2010b;15:047003. doi: 10.1117/1.3462973. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.