Shape-Based Approach to Robust Image Segmentation using Kernel PCA

Abstract

Segmentation involves separating an object from the background. In this work, we propose a novel segmentation method combining image information with prior shape knowledge, within the level-set framework. Following the work of Leventon et al., we revisit the use of principal component analysis (PCA) to introduce prior knowledge about shapes in a more robust manner. To this end, we utilize Kernel PCA and show that this method of learning shapes outperforms linear PCA, by allowing only shapes that are close enough to the training data. In the proposed segmentation algorithm, shape knowledge and image information are encoded into two energy functionals entirely described in terms of shapes. This consistent description allows to fully take advantage of the Kernel PCA methodology and leads to promising segmentation results. In particular, our shape-driven segmentation technique allows for the simultaneous encoding of multiple types of shapes, and offers a convincing level of robustness with respect to noise, clutter, partial occlusions, or smearing.

1. Introduction

Segmentation consists of extracting an object from an image, an ubiquitous task in computer vision applications. It is quite useful in applications ranging from finding special features in medical images to tracking deformable objects; see [7, 14, 16, 17] and the references therein. The active contour methodology has proven to be quite valuable for performing this task. However, the use of image information alone often leads to poor segmentation results in the presence of noise, clutter or occlusion. The introduction of shape priors in the contour evolution process has been shown to be an effective way to address this issue, leading to more robust segmentation performances.

Many different methods which use a parameterized or an explicit representation for contours have been proposed [2, 15, 3]. In [4], the authors use the B-spline parametrization to build shape models in the kernel space [8]. These models were then used in the segmentation process to provide shape prior. The geometric active contour framework (GAC) (see [12] and the references therein) involves a parameter free representation of contours, i.e., a contour is represented implicitly by the zero level set of a higher dimensional function, typically a signed distance function [9]. In [7], the authors obtain the shape statistics by performing linear principal component analysis (PCA) on a training set of signed distance functions (SDFs). This approach was shown to be able to convincingly capture small variations in the shape of an object. It inspired other schemes to obtain shape prior described in [14, 11], notably, where SDFs were used to learn the shape variations.

However, when the object considered for learning may undergo complex or non-linear deformations, linear PCA can lead to unrealistic shape priors, by allowing linear combinations of the learnt shapes that are unfaithful to the true shape of the object. Cremers et al., successfully pioneered the use of kernel methods to address this issue, within the GAC framework [5]. In the present work, we propose to use Kernel PCA to introduce shape priors for GACs. Kernel PCA was presented by Scholkopf [8] and allows to combine the precision of kernel methods with the reduction of dimension in the training set. This is the first time, to our knowledge, that Kernel PCA is explicitly used to introduce shape priors in the GAC framework. In this paper, we also propose a novel intensity segmentation method, specifically tailored to allow for the inclusion of shape prior.

In the next section, we compare linear PCA to Kernel PCA, using SDFs and binary maps as representations of shapes. In Section 3, we propose an intensity-based energy functional in terms of binary shapes for separating an object from the background, in an image. These energies are qualitatively similar to the ones proposed by [1, 10] but quantitatively different. In Section 4, we present a robust segmentation framework, combining image cues and shape knowledge in a consistent fashion. The robustness of the proposed algorithm is demonstrated on various challenging examples, in Section 5.

2. Kernel PCA for shape prior

Kernel PCA can be considered to be a generalization of linear principal components analysis. This technique was introduced by Scholkopf [8], and has proven to be a powerful method to extract nonlinear structures from a data set. The idea behind Kernel PCA consists of mapping a data set from an input space ℐ into a feature space F via a nonlinear function φ. Then, PCA is performed in F to find the orthogonal directions (principal components) corresponding to the largest variation in the mapped data set. The first l principal components account for as much of the variance in the data as possible by using l directions. In addition, the error in representing any of the elements of the training set by its projection onto the first l principal components is minimal in the least square sense.

The nonlinear map φ typically does not need to be known, through the use of Mercer kernels. A Mercer kernel is a function k(․, ․) such that for all data points χ_i, the kernel matrix K(i, j) = k(χ_i, χ_j) is symmetric positive definite [8]. It can be shown that using k(․, ․) one can obtain the inner scalar product in F: k(χ_a, χ_b) = (φ(χ_a) · φ(χ_b)), with (χ_a, χ_b) ∈ ℐ.

We now briefly describe the Kernel PCA method [6, 8]. Let τ = {χ₁, χ₂, …, χ_N} be a set of training data. The centered kernel matrix K̃ corresponding to τ, is defined as

$$\mathbf{K̃}=(\phi ({\chi }_i)-\mathrm{\phi ̄}·\phi ({\chi }_j)-\mathrm{\phi ̄})=(\mathrm{\phi ̃}({\chi }_i)·\mathrm{\phi ̃}({\chi }_j))=\mathrm{k̃}({\chi }_i,{\chi }_j),\mathit{\text{for}}i\in [|1,N|]$$ (1)

with $\mathrm{\phi ̄}=\frac{1}{N}{\sum }_{i=1}^N\phi ({\chi }_i)$, φ̃(χ_i) = φ(χ_i) − φ̄ being the centered map corresponding to χ_i and k̃(․, ․) denotes the centered kernel function. Since K̃ is symmetric, using Singular Value Decomposition, it can be decomposed as

$$\mathbf{K̃}=\mathbf{U}\mathbf{S}{\mathbf{U}}^t$$ (2)

where S = diag(γ₁, …, γ_N) is a diagonal matrix containing the eigenvalues of K̃. U = [u₁, …, u_N] is an orthonormal matrix. The column-vectors u_i = [u_i1, …, u_iN]^t are the eigenvectors corresponding to the eigenvalues γ_i’s. Besides it can easily be shown that K̃ = HKH, where $\mathbf{H}=\mathbf{I}-\frac{1}{N}{\mathbf{11}}^t$. 1 = [1, …, 1]^t is an N × 1 vector.

Let C denote the covariance matrix of the elements of the training set mapped by φ̃. Within the Kernel PCA methodology, C does not need to be computed explicitly, only K̃ needs to be known to extract features from the training set [13]. The subspace of the feature space F spanned by the first l eigenvectors of C, will be referred to as the Kernel PCA space, in what follows. The Kernel PCA space is the subspace of F, obtained from learning the training data.

Let χ be any element of the input space ℐ. The projection of χ on the Kernel PCA space will be denoted by P^lφ(χ)¹. The projection P^lφ(χ) can be obtained as given in [8]. In the feature space F, the squared distance $d_F^2$ between a test point χ and its projection on the Kernel PCA space is given by [8]:

$$d_F^2[\phi (\chi ),P^l\phi (\chi )]={\Vert \phi (\chi )-P^l\phi (\chi )\Vert }^2=k(\chi ,\chi )-2\phi {(\chi )}^t{P}^l\phi (\chi )+P^l\phi {(\chi )}^t{P}^l\phi (\chi )$$

Using some matrices manipulations, this squared distance can be expressed only in terms of kernels as:

$$d_F^2[\phi (\chi ),P^l\phi (\chi )]=k(\chi ,\chi )+\frac{1}{N^2}{\mathbf{1}}^t\mathbf{K}\mathbf{1}-\frac{2}{N}{\mathbf{1}}^t{\mathbf{k}}_{\chi }+{\mathbf{k̃}}_{\chi }^t\mathbf{M}\mathbf{K̃}\mathbf{M}{\mathbf{k̃}}_{\chi }-2{\mathbf{k̃}}_{\chi }^t\mathbf{M}{\mathbf{k̃}}_{\chi }$$ (3)

where, k_χ = [k(χ, χ₁) k(χ, χ₂), …, k(χ, χ_N)]^t, ${\mathbf{k̃}}_{\chi }=\mathbf{H}({\mathbf{k}}_{\chi }-\frac{1}{N}\mathbf{K}\mathbf{1})$ and $\mathbf{M}={\sum }_{i=1}^l\frac{1}{{\gamma }_i}{\mathbf{u}}_i{\mathbf{u}}_i^t$.

2.1. Kernel for linear PCA

In [7], the authors presented a method to learn shape variations by performing PCA on a training set of shapes (closed curves) represented as the zero level sets of signed distance functions. Using the following kernel in the formulation of Kernel PCA presented above, amounts to performing Linear PCA on SDFs²:

$$k_{id}({\mathrm{\Phi }}_i,{\mathrm{\Phi }}_j)=({\mathrm{\Phi }}_i․{\mathrm{\Phi }}_j)=\int \int {\mathrm{\Phi }}_i(u,\upsilon ){\mathrm{\Phi }}_j(u,\upsilon )du․d\upsilon$$ (4)

for all SDFs Φ_i and Φ_j : R² ↦ R.

A different representation for shapes is to use binary maps, i.e., to set to 1 the pixels located inside the shape and to 0 the pixels located outside (see figure 1). One can change the shape representation from SDFs to binary maps using the Heaviside function $H\mathrm{\Phi }=\{\begin{array}{cc}\hfill 1\hfill & \mathrm{\Phi }\ge 0,\hfill \\ \hfill 0\hfill & \text{else}.\hfill \end{array}$

Figure 1.

Three training sets (Before alignment - Binary images are presented here). First row, “Soccer Player” silhouettes (6 of the 22 used). Second row, “Shark” silhouettes (6 of the 15 used). Third row, “4 words” (6 of the 80 learnt; 20 fonts per word).

Note that, in this case, the kernel allowing to perform linear PCA is given by k_id(HΦ_i, HΦ_j) = (HΦ_i․HΦ_j).

2.2. Kernel for nonlinear PCA

Choosing a nonlinear kernel function k(․, ․) leads to performing nonlinear PCA. The exponential kernel has been a popular choice in the machine learning community and has proven to nicely extract nonlinear structures from data sets. Using SDFs for representing shapes, this kernel is given by

$$k_{{\phi }_{\sigma }}({\mathrm{\Phi }}_i,{\mathrm{\Phi }}_j)=e^{-\frac{{\Vert {\mathrm{\Phi }}_i-{\mathrm{\Phi }}_j\Vert }^2}{2{\sigma }^2}},$$ (5)

where σ² is the variance parameter computed a-priori and ‖Φ_i − Φ_j‖² is the squared L₂-distance between two SDFs Φ_i and Φ_j. If the shapes are represented by binary maps, the corresponding kernel is

$$k_{{\phi }_{\sigma }}(H{\mathrm{\Phi }}_i,H{\mathrm{\Phi }}_j)=e^{-\frac{{\Vert H{\mathrm{\Phi }}_i-H{\mathrm{\Phi }}_j\Vert }^2}{2{\sigma }^2}}.$$ (6)

This exponential kernel is one among many possible choice of Mercer kernels: Other kernels could possibly be used to extract other specific features from the training set [8].

2.3. Shape Prior for GAC

To include prior knowledge on shape in the GAC framework, we propose to use the projection on the Kernel PCA space as a model and to minimize the following energy:

$$E_{\text{shape}}^{\mathrm{F}}(\chi )≔d_F^2[\phi (\chi ),P^l\phi (\chi )]$$ (7)

A similar idea was proposed in [13, 8], for the purpose of pattern recognition. In (7), χ is a test shape represented using either a SDF (χ = ϕ) or a binary map (χ = Hϕ) and φ refers to either id (linear PCA) or φ_σ (Kernel PCA). Minimizing $E_{\text{shape}}^{\mathrm{F}}$ amounts to driving the test shape χ towards the Kernel PCA space computed a priori from a training set of shapes using (2). In the GAC framework, the minimization of $E_{\text{shape}}^{\mathrm{F}}(\chi )$, can be undertaken as follows:

$$\frac{d\varphi }{dt}=-{\nabla }_{\varphi }{E}_{\text{shape}}^{\mathrm{F}}=-{\nabla }_{\chi }{E}_{\text{shape}}^{\mathrm{F}}·\frac{d\chi }{d\varphi }$$ (8)

The gradient of $E_{\text{shape}}^{\mathrm{F}}$ can be computed by applying calculus of variation and (3). For the kernel given in (6), the following result is obtained:

$${\nabla }_{\varphi }{E}_{\text{shape}}^{\mathrm{F}}=-\frac{{\Sigma }_{i=1}^N{g}_i(\varphi )k_{{\phi }_{\sigma }}(H\varphi ,H{\varphi }_i)\delta (\varphi )[H\varphi -H{\varphi }_i]}{{\sigma }^2}$$

with $[g_1(\varphi ),\dots ,g_N(\varphi )]=-\frac{2}{N}{\mathbf{1}}^t+2{\mathbf{k̃}}_{H\varphi }^t\mathbf{M}\mathbf{K̃}\mathbf{M}\mathbf{H}-4{\mathbf{k̃}}_{H\varphi }^t\mathbf{M}\mathbf{H}$

2.3.1 Linear PCA vs Kernel PCA

In this section we compare linear PCA with non-linear PCA for two different representations of shapes, i.e., SDF and binary map. Two training set of shapes were used: The first training set consists of various shapes of a man playing soccer and the second training set consists of various shapes of a shark (see Figure 1). These shapes were aligned using an appropriate registration scheme (see, [14]) to discard differences between them due to Euclidian transformations. The Kernel PCA space corresponding to each of the kernels presented in Sections 2.1 and 2.2 were then built for the two training sets. Starting from an arbitrary shape, Figure 2(a), the contour was deformed by running equation (8) until convergence: We will refer to this operation as “morphing”, in what follows.

Figure 2.

Morphing results of an arbitrary shape, obtained using Linear PCA and Kernel PCA applied on both Signed Distance Functions and binary maps. First row: Results for the “Soccer Player” training set, Second row: Results for the “Shark” training set. (a): Initial shape, (b): PCA on SDF, (c): Kernel PCA on SDF (d): PCA on binary maps, (e): Kernel PCA on binary maps.

Figure 2(b) shows the morphing results obtained by applying linear PCA on SDF. Figure 2(d) shows the morphing results obtained by applying linear PCA on binary maps. As can be noticed, results obtained for the SDF representation bear little resemblance with the elements of the training sets. Results obtained for binary maps are more faithful to the learnt shapes. Figure 2(c) and (e) present the morphing results obtained by applying nonlinear PCA on SDF and binary maps, respectively. In both cases, the final contour is very close to the training set and results are better than any of the results obtained with linear PCA.

Hence, Kernel PCA outperforms linear PCA as a means to introduce shape priors and binary maps seem to be an efficient shape representation. Besides, the learning process using Kernel PCA comes with no significant additional cost compared to linear PCA, thanks to the kernel formulation [8, 13]. Another advantage of using the exponential kernel, is that it enables to control the degree to which “mixing” is allowed between the learnt shapes, in the shape prior, larger σ’s allowing more mixing. This is shown in Figure 3. The choice of σ typically depends on how much the shapes vary within the data set: If the variation is large, a smaller value for σ is usually preferable.

Figure 3.

Influence of σ for the Kernel PCA method (exponential kernel) applied on binary maps. Morphing results of an arbitrary shape are presented for the “Shark” training set. (a): Initial shape, (b): Morphing result for σ = 3, (c): σ = 7, (d): σ = 9, (e): σ = 15,.

3. Intensity based segmentation

Different models [18, 1, 10], which incorporate geometric and/or photometric (color, texture, intensity) information, have been proposed to perform region based segmentation using level sets. In what follows, we present a novel intensity based segmentation framework aimed at separating an object from the background, in an image I. The main idea behind the proposed method is to build an “image shape model” (denoted by G_[I,Φ]) by thresholding the image I based on the estimates of the intensity statistics of the object (and background), available at each step t of the contour evolution: G_[I,Φ] is interpreted as the most likely shape of the object of interest, based on the available information. The contour at time t is deformed towards this “image shape model” by minimizing the following energy:

$$E_{\text{image}}≔{\Vert H\mathrm{\Phi }-G_{[I,\mathrm{\Phi }]}\Vert }^2={\int }_{\mathrm{\Omega }}{(H\mathrm{\Phi }-G_{[I,\mathrm{\Phi }]})}^{2}dxdy.$$ (9)

This energy functional amounts to measuring the distance between two binary maps, e.g.: HΦ and G_[I,Φ]. This is quite valuable in the present context, where shapes are represented using binary maps as in earlier sections. Thus, when the shape energy term described before is combined with the following formulation for image segmentation, all the elements are expressed in terms of shapes. This is one of the unique contributions in this work. In what follows, we describe two particular cases of this general framework.

3.1. Object and background with different mean intensities

As in [1, 18], we assume that the image is composed of two regions having different intensity means: μ_o (respectively μ_b) is the mean intensity of the object (respectively of the background). Given an initial guess for the shape of the object and representing the contour as the zero level set of a SDF Φ, one can calculate the mean intensity inside (μ₁) and outside (μ₂) the curve as ${\mu }_1=\frac{\int I(x,y)H\mathrm{\Phi }dxdy}{\int H\mathrm{\Phi }dxdy}$ and ${\mu }_2=\frac{\int I(x,y)(1-H\mathrm{\Phi })dxdy}{\int (1-H\mathrm{\Phi })dxdy}$. The goal is to deform this initial contour so that μ₁ = μ_o and μ₂ = μ_b. To achieve this, the “image shape model” G_[I,Φ] is generated at each step t, in the following manner:

$$\text{if}{\mu }_1>{\mu }_2,G_{[I,\mathrm{\Phi }]}(x,y)=\{\begin{array}{cc}\hfill 1\hfill & I(x,y){\ge }^{\frac{{\mu }_1+{\mu }_2}{2}};\hfill \\ \hfill 0\hfill & \text{else}.\hfill \end{array}\text{if}{\mu }_1\le {\mu }_2,G_{[I,\mathrm{\Phi }]}(x,y)=\{\begin{array}{cc}\hfill 1\hfill & I(x,y){\le }^{\frac{{\mu }_1+{\mu }_2}{2};}\hfill \\ \hfill 0\hfill & \text{else}.\hfill \end{array}$$

Notice that G_[I,Φ] is the image shape model (binary map) obtained from thresholding the image intensities so that values closer to μ₁ are classified as object (set to 1) and others are classified as background (set of 0). For numerical experiments, the function G_[I,Φ] is calculated as follows:

$$\text{if}{\mu }_1>{\mu }_2;G_{[I,\mathrm{\Phi },\epsilon ]}=\frac{1}{2}+\frac{1}{\pi }\text{arctan}\left(\frac{I-\frac{{\mu }_1+{\mu }_2}{2}}{\epsilon }\right)\text{else}{G}_{[I,\mathrm{\Phi },\epsilon ]}=\frac{1}{2}-\frac{1}{\pi }\text{arctan}\left(\frac{I-\frac{{\mu }_1+{\mu }_2}{2}}{\epsilon }\right)$$

where ε, a parameter such that G_[I,Φ,ε] → G_[I,Φ] as ε → 0.

3.2. Object and background with different variances

Following [10], we assume that the image is composed of two regions, with different variance in intensity. The mean intensities are computed as before, while the variances inside (σ₁) and outside (σ₂) the curve are computed as follows: ${\sigma }_1^2=\frac{\int {(I-{\mu }_1)}^{2}H\mathrm{\Phi }dxdy}{\int H\mathrm{\Phi }dxdy}$ and ${\sigma }_2^2=\frac{\int {(I-{\mu }_2)}^2(1-H\mathrm{\Phi })dxdy}{\int (1-H\mathrm{\Phi })dxdy}$. In this case, the image shape model G_[I,Φ] is obtained as follows:

$$\text{if}{\sigma }_1<{\sigma }_2,G_{[I,\mathrm{\Phi }]}=\{\begin{array}{cc}\hfill 1\hfill & I_2\ge I(x,y)\ge I_1;\hfill \\ \hfill 0\hfill & \text{else}.\hfill \end{array}\text{if}{\sigma }_1>{\sigma }_2,G_{[I,\mathrm{\Phi }]}=\{\begin{array}{cc}\hfill 1\hfill & I(x,y)\ge I_1\text{or}I(x,y)<I_2;\hfill \\ \hfill 0\hfill & \text{else}.\hfill \end{array}$$

where,

$$I_1=\frac{{\sigma }_2^2{\mu }_1-{\sigma }_1^2{\mu }_2-\alpha }{{\sigma }_2^2-{\sigma }_1^2}\text{and}{I}_2=\frac{{\sigma }_2^2{\mu }_1-{\sigma }_1^2{\mu }_2+\alpha }{{\sigma }_2^2-{\sigma }_1^2},\alpha ={\sigma }_2{\sigma }_1\sqrt{{({\mu }_1-{\mu }_2)}^2+2({\sigma }_1^2-{\sigma }_2^2)\text{log}(\frac{{\sigma }_1}{{\sigma }_2})}$$

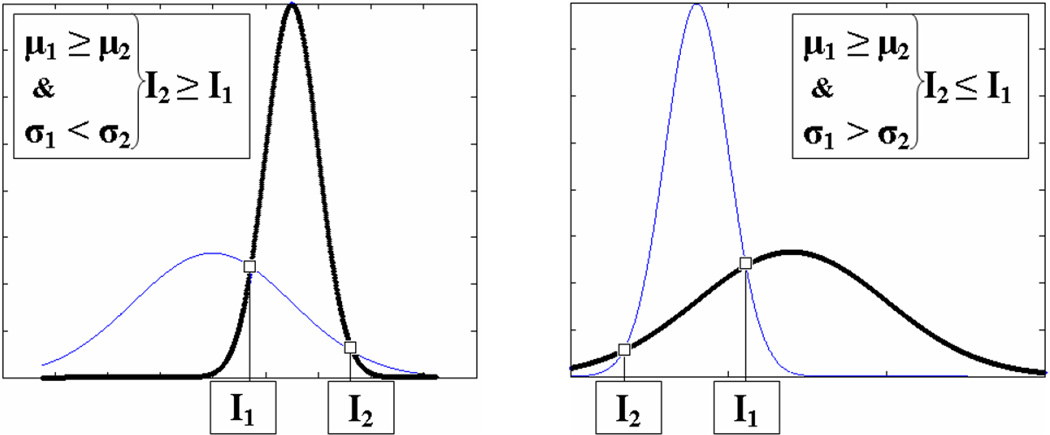
This thresholding ensures that pixels set to 1 in G_[I,Φ] correspond to pixels that are more likely to belong to the object of interest in the image, based on information available at step t. In the same way, pixels set to 0 in G_[I,Φ] correspond to pixels that are more likely to belong to the background. Figure 4 shows the different cases justifying the way thresholding is performed in equation (10).

Figure 4.

Probability density functions. Thick line: p(I ∈ Object); Thin line: p(I ∈ background). It is straightforward to see that p(I ∈ Object) > p(I ∈ Object) for I₁ ≤ I ≤ I₂, when σ₁ < σ₂ and for I ≥ I₁ and I ≤ I₂, when σ₁ > σ₂.

In numerical applications, the binary map G_[I,Φ] in (10) is computed as follows (for ε small):

$$\text{if}{\sigma }_1<{\sigma }_2;G_{[I,\mathrm{\Phi },\epsilon ]}=\frac{1}{\pi }\text{arctan}\left(\frac{I-I_1}{\epsilon }\right)-\frac{1}{\pi }\text{arctan}\left(\frac{I-I_2}{\epsilon }\right)\text{else}{G}_{[I,\mathrm{\Phi },\epsilon ]}=1-\frac{1}{\pi }\text{arctan}\left(\frac{I-I_2}{\epsilon }\right)+\frac{1}{\pi }\text{arctan}\left(\frac{I-I_1}{\epsilon }\right)$$

Figure 5, presents results obtained for each of the image shape models presented above.

Figure 5.

Segmentation results obtained using E_image, equation (9). Initial contour in black, final contour in white. Left: 1^st moment only. Right: second order moments (Two regions of same mean intensity and different variances)

4. Combining Shape Prior and Intensity information

In this part, we combine shape knowledge obtained by performing nonlinear PCA on binary maps with image information obtained by building an “image shape model”, within the GAC framework. As presented above, $E_{\text{shape}}^{\mathrm{F}}$ and E_image are squared distances between the shape of the current contour and a model. However, E_image is a squared distance in input space, whereas $E_{\text{shape}}^{\mathrm{F}}$ is expressed in the feature space. Thus, equilibrium would be hard to reach between “forces” extracted from $E_{\text{shape}}^{\mathrm{F}}$ and E_image³. This can be remedied by noticing that, for any SDFs ϕ_a and ϕ_b:

$$d_F^2({\varphi }_a,{\varphi }_b)=2-2k_{{\phi }_{\sigma }}(H{\varphi }_a,H{\varphi }_a)=2-2e^{-\frac{{\Vert H{\mathrm{\Phi }}_a-H{\mathrm{\Phi }}_b\Vert }^2}{2{\sigma }^2}}$$

By defining $E_{\text{shape}}=-2{\sigma }^2\text{log}(\frac{2-E_{\text{shape}}^{\mathrm{F}}}{2})$, a new shape prior energy functional is obtained⁴. This energy E_shape, like E_image, is homogeneous to a square distance in input space. This consistent description of energies allows for efficient and intuitive equilibration between image cues and shape knowledge, through the following energy functional:

$$E(\mathrm{\Phi },I)={\beta }_1{E}_{\text{shape}}(\mathrm{\Phi })+{\beta }_2{E}_{\text{image}}(\mathrm{\Phi },I)$$ (10)

4.1. Invariance to Similarity Transformations

Let p = [t_x, t_y, θ, ρ] = [p₁, p₂, p₃, p₄] be a vector of parameters corresponding to a similarity transformation; t_x and t_y corresponding to translation according to x and y-axis, θ being the rotation angle and ρ the scale parameter. Let us denote by Î(x̂, ŷ) the image obtained by applying the transformation: Î (x̂, ŷ) = I(ρ(x cos θ − y sin θ + t_x), ρ(x sin θ + y cos θ + t_y)). As mentioned above, the elements of the training sets are aligned prior to the construction of the space of shapes. Supposing that the object of interest in I differs from the registered elements of the training set by a similarity of parameter p, this transformation can be recovered by minimizing E(Φ, Î) with respect to the p_i’s. During evolution, the following gradient descent scheme can be performed for i ∈ [1, 4]:

$$\frac{d{p}_i}{dt}=-{\nabla }_{p_i}E(\mathrm{\Phi },Î)=-{\nabla }_{p_i}{E}_{\text{image}}(\mathrm{\Phi },Î).$$

5. Experiments

This section presents segmentation results obtained by introducing shape prior using Kernel PCA on binary maps and using our intensity based segmentation methodology: Equation (10) was run until convergence on diverse images.

5.1. Toy Example: Shape Priors Involving Objects of Different Types

Kernel methods have been used to learn complex multimodal distributions in an unsupervised fashion (see [8], and the references therein). The goal of this section is to investigate the ability of the proposed framework to simultaneously learn and accurately detect objects of different shapes. To this end, we built a training set consisting of four words, “orange”, “yellow”, “square” and “circle” each written using twenty different fonts. The size of the fonts was chosen to lead to words of roughly the same length. The obtained words (binary maps, see Figure 1) were then registered according to their centroid. No further effort such as matching the letters of the different words was pursued. The method presented in Section (2) was used to build the corresponding space of shapes for the registered binary maps.

We tested our framework on images where a corrupted version of either of the four words “orange”, “yellow”, “square” or “circle” was present (Figure 6, 1^st row). Word recognition is a challenging task and addressing it using geometric active contours may not be a panacea. However, the ability of the level set representation to naturally handle topological changes was found to be useful for this purpose: During evolution, the contour split and merged a certain number of times to segment the disconnected letters of the words. In all the following experiments, β₁ and β₂ were fixed in (10) and the same initial contour was used.

Figure 6.

Segmentation results for the “4 Words” training set. Shape Priors were built by applying the Kernel PCA method on binary maps as presented in Section 2. First row: Original images to segment, Second row: Segmentation results, Third row: shape underlined by the final contour (Hϕ), Fourth row: “Image shape model” (G_[I,ϕ]) obtained when computing E_image for the final contour.

Experiment 1: In this experiment, one of the words “square” belonging to the training set was corrupted: The letter “u” was almost completely erased. The shape thus obtained was filled with gaussian noise of mean μ_o = .5 and variance σ_o = .05. The background was also filled with Gaussian noise of same mean μ_b = .5 but of variance σ_b = .2. The result of applying our method is presented Figure 6(a). Despite the noise and the partial deletion, a very convincing segmentation is obtained. In particular, the correct font is detected and the letter “u” accurately reconstructed. In addition, the final curve is smooth even if no curvature term was used for regularization. Hence, using binary maps to represent shape priors can have valuable smoothing effects, even when dealing with noisy images.

Experiment 2: In this second experiment, one of the elements of the training set was used. A thick line (occlusion) was drawn on the word and a fair amount of gaussian noise was added to the resulting image. The result of applying our method is presented Figure 6(b). Despite the noise and the occlusion, a very convincing segmentation is obtained. In particular, the correct font is detected and the thick line completely removed. Once again, the final contour is smooth despite the fairly large amount of noise.

Experiment 3: Here, the word “yellow” was written using a different font from the ones used to build the training set. Additionally, a “linear shadowing” was used in the background (completely hiding the letter ”y”) and the letter ”w” was replaced by a grey square. The result of applying our framework is presented in Figure 6(c). The word “yellow” is correctly recognized and segmented. Also, the letters “y” and ”w”, were completely reconstructed.

Experiment 4: In this experiment, the word “orange” was handwritten in capital letters roughly matching the size of the letters of the words in the training set. The intensity of the letters was chosen to be rather close to some parts of the background. In addition, the word was blurred and smeared in a way that made its letters barely recognizable. This type of blurring effect is often observed in medical images due to patient motion. This image is particularly difficult to segment, even using shape prior, since the spacing between letters and the letters themselves are very irregular due to the combined effects of handwriting and blurring. Hence, mixing between classes (confusion between either of the 4 words) can be expected in the final result. In the final result obtained, the word “orange” is not only recognized but satisfyingly recovered; in particular, a thick font was obtained to model the thick letters of the word (Figure 6(d)).

Hence, starting for each experiment from the same initial contour, our algorithm was able to accurately detect which word was present in the image. This highlights the ability of our method not only to gather image information throughout evolution but also to distinguish between objects of different classes (“orange”, “yellow”, “square” and “circle”). Comparing the final contours obtained in each experiments to the final “image shape model” G_[I,ϕ] (last row of Figure 6), one can measure the effect of our shape prior model in constraining the contour evolution: The image information alone would lead to a shape that would bear very little resemblance with any of the four words learnt.

5.2. Real Images Example: Tracking of challenging sequences

To test the robustness of the framework, tracking was performed on two challenging sequences. A very simple tracking scheme was used: the same initial contour was used for each image in the sequence. This contour was initially positioned wherever the final contour was in the preceding image. The coefficients β₁ and β₂ were fixed throughout each sequence. Of course, many efficient tracking algorithms have already been proposed. However, convincing results were obtained here without considering the system dynamics, for instance. This highlights the efficiency of including prior knowledge on shape for the robust tracking of deformable objects.

5.2.1 Soccer Player Sequence

In this sequence (composed of 130 images), a man is jingling with a soccer ball. The challenge is to accurately capture the large deformations due to the movement of the person (e.g.: limbs undergo large changes in aspect), while sufficiently constraining the contour to discard clutter in the background. A training set of 22 silhouettes (Figure 1, first row) was used. The version of E_image involving the intensity means only was used to capture image information. Despite the small number of shapes used, successful tracking was obtained, correctly capturing the posture of the player.

5.2.2 Shark Video

In this sequence (composed of 70 images), a shark is evolving in a highly cluttered environment. Besides, the shark is oftentimes occluded by other fish and is poorly contrasted. To perform tracking, 15 shapes were extracted from the first half of the video (Figure 1, second row) and used to build shape prior. The version of E_image involving the variances was used to make up for the poor contrast of the shark in the images. Once again, despite the small training set, successful tracking performances were observed: The shark was correctly captured, while clutter and obstacles rejected.

6. Conclusion

In this work, we used Kernel PCA to introduce prior knowledge about shapes in the GAC framework. Better performance of Kernel PCA over linear PCA was demonstrated for two representations of shapes (binary maps and SDFs). We also developed a general approach to separate an object from the background using various image intensity statistics. In our algorithm, image information and shape knowledge were combined in a consistent fashion: both energies were expressed in terms of shapes. The proposed method not only allowed to simultaneously learn shapes of different objects but was also robust to noise, blurring, occlusion and clutter. In addition, even if the same parameters and same initial contour were used for each of the image of the sequences, successful tracking was obtained: This further highlights the robustness of the framework.

Figure 7.

Tracking results with the proposed method. First row: Soccer Player Sequence (Rightmost frame is the result obtained without shape prior; β₂ = 0 in (10)). Second row: “Shark” sequence (Rightmost frame is an original image from the sequence, reproduced here to assess the poor level of contrast).