Abstract
Cell-to-cell variability in molecular, genetic, and physiological features is increasingly recognized as a critical feature of complex biological systems, including the brain. Although such variability has potential advantages in robustness and reliability, how and why biological circuits assemble heterogeneous cells into functional groups is poorly understood. Here, we develop analytic approaches toward answering how neuron-level variation in intrinsic biophysical properties of olfactory bulb mitral cells influences population coding of fluctuating stimuli. We capture the intrinsic diversity of recorded populations of neurons through a statistical approach based on generalized linear models. These models are flexible enough to predict the diverse responses of individual neurons yet provide a common reference frame for comparing one neuron to the next. We then use Bayesian stimulus decoding to ask how effectively different populations of mitral cells, varying in their diversity, encode a common stimulus. We show that a key advantage provided by physiological levels of intrinsic diversity is more efficient and more robust encoding of stimuli by the population as a whole. However, we find that the populations that best encode stimulus features are not simply the most heterogeneous, but those that balance diversity with the benefits of neural similarity.
Keywords: generalized linear models, intrinsic biophysics, neural variability, stimulus coding, ion channels
Biological systems including brains must function efficiently under many constraints, including constraints on the numbers of individual neurons dedicated to a given task. Brain function therefore depends on an appropriate division of labor, with specific neurons dedicated to different functions. For example, different types of retinal ganglion cells represent visual information at different timescales (1), and distinct classes of cortical interneurons play diverse roles in coordinating network activity (2). Whereas attempts to understand how distinct classes of cells encode information have proven successful (1), the importance of within-type variability remains poorly understood (3, 4) although has recently become a topic of great interest (5–8).
Although neuron-to-neuron variability is often viewed as an epiphenomenon of biological imprecision (3, 4), having neurons of the same type that respond to different stimulus features may improve stimulus encoding. This variability may be leveraged to improve functions such as stimulus encoding if heterogeneous output of neurons of a single type is collectively used for population coding. Such populations of neurons could efficiently represent complex stimuli by collectively covering the relevant stimulus space (1, 9, 10). Network interactions could further increase the efficiency of information transmission by decorrelating neural responses and reducing the redundancy between their outputs (11–13). In contrast, eliminating redundancy (also referred to as biological degeneracy, ref. 14) may make stimulus coding less robust to noise or damage (15), thus we hypothesized that an optimal coding strategy would require balancing diversity with feature similarity or overlap.
Although theorists have previously explored this issue (12, 16, 17), analysis of the function of the diversity of real populations of neurons requires overcoming methodological hurdles associated with studying cell-to-cell variability (3, 4). Cell-level differences (that are typically averaged away) must be captured and quantified. Once these differences have been quantified, one must compare the functional output of populations differing in their variability. In the context of neural coding these issues translate to answering the questions: What properties of neurons determine their response to stimuli? How are these properties distributed? And how do these distributions of properties influence the encoding of stimuli by populations? Although previous experimental approaches have identified neuron diversity using standard receptive field analyses, these typically do not describe the full complexity of neural responses to stimuli (18–20), nor do they allow the source of the response heterogeneity to be identified as either synaptic or intrinsic. In addition, simplistic readouts of population spiking output may underestimate the richness of the underlying neural code (1, 10, 21). Our approach allows the influence of intrinsic diversity to be isolated from synaptic differences and captures the full potential of these diverse populations for stimulus encoding.
Specifically, we developed measures of neuronal population diversity based on statistical generalized linear models (18, 22) that accurately reproduce the responses of recorded individual olfactory bulb mitral cells (MCs). These cells have been shown to express significant biophysical variability from neuron to neuron (5–7). We then used the framework of model-based stimulus decoding (18, 23) to compare how populations varying in their diversity optimally encode varieties of stimuli. This approach enables us to determine whether specific advantages arise from the intrinsic diversity of these neurons, and how MC populations balance the competing benefits of diversity and feature similarity.
Results
Statistical Neuron Models Capture Mitral Cell Response Diversity.
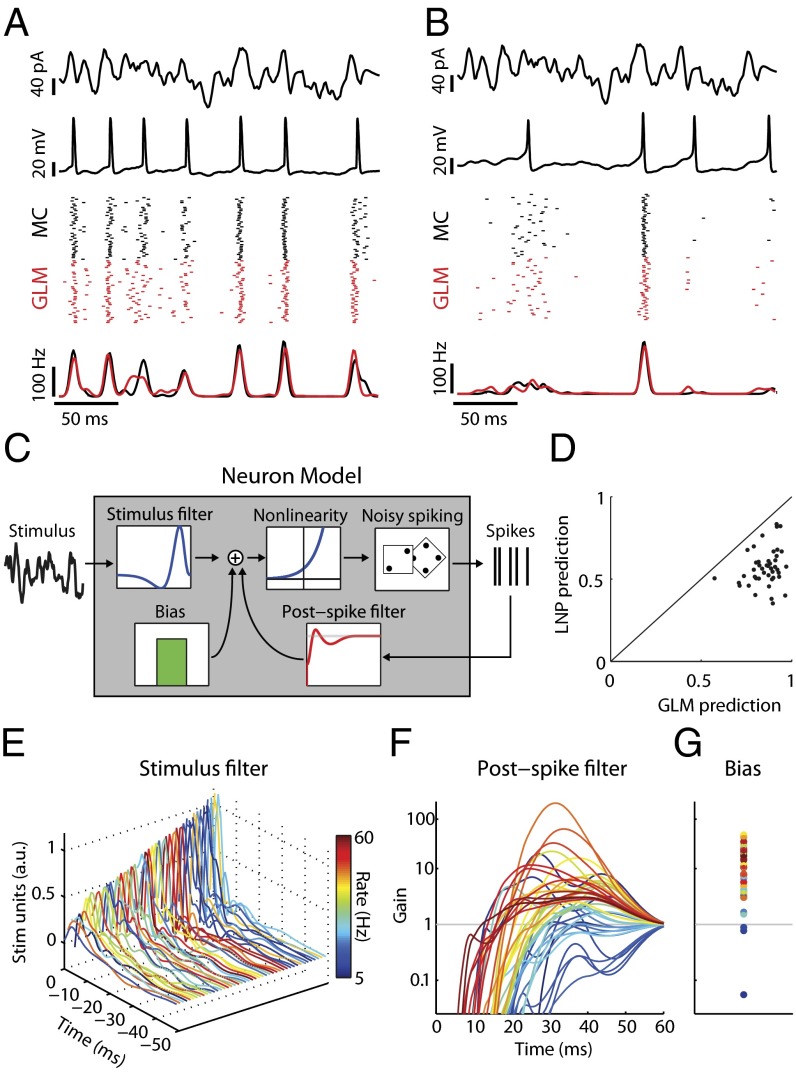
We generated models of individual MCs from data collected during in vitro whole-cell recordings in which somatic current injection of broad-band-filtered noise (5) evoked action potential trains (Fig. 1 A and B; n = 44 neurons). Synaptic transmission was blocked pharmacologically, so that differences in the cells’ spiking responses reflected only differences in their intrinsic firing properties (e.g., due to biophysical conductances and/or morphology). Each neuron’s spiking response to input current was fit by a generalized linear model (GLM). GLMs extend stimulus-based reverse correlation or linear–nonlinear–Poisson (LNP) models (20, 24) by including terms that describe how a neuron’s spike probability is modulated via its previous spikes (18, 22). Here each GLM had a constant (bias) term to match baseline firing, a linear stimulus filter determining the neuron’s stimulus preference, and a spike history function capturing the neuron’s refractory and bursting properties (Fig. 1C).
Fig. 1.
Simple models capture mitral cell stimulus-evoked responses and intrinsic diversity. (A) MC intrinsic properties are probed using filtered broadband stimuli (first row) injected somatically to evoke changes in membrane voltage (second row). Spike rasters (third row; black) and peri-stimulus time histograms (PSTH) (fourth row; black) for repeated stimulus presentations (n = 40 trials) show that this MC spikes to the stimulus with temporal jitter and displays a coarse stimulus preference. Model neuron rasters (Third Row, red) and PSTH (fourth row, red) show that the model accurately predicts MC activity on novel stimuli. (B) Same as A but for a different neuron. (C) Structure of the GLM neuron model. Model parameters describe a temporal stimulus filter, a postspike filter, and a constant bias term. An exponential nonlinearity defines an instantaneous spike rate and is used to draw noisy spikes. (D) GLM models accurately predict 86 ± 11% (mean ± SEM) of stimulus-evoked activity across all MCs, computed as the correlation coefficient between MC and model PSTH. For all neurons, the GLM fits were better than LNP models. (E–G) Model parameters for all MCs. Each line corresponds to parameters for a unique neuron and is colored by mean firing rate. (E) Temporal stimulus filters model differential stimulus specificity of neurons. (F) Exponentiated postspike filters, plotted as a multiplicative gain in spike probability following a spike at t = 0 ms. Values less (greater) than 1 indicate a decreased (increased) spike probability. (G) Bias terms also show considerable variation. Same y axis as F.
This approach captures the spiking responses of neurons without explicitly modeling the many ion channels expressed by individual cells (3, 5, 6) (Fig. 1 A and B). Furthermore, GLMs modeled MC activity better than a simpler model that did not include spike history effects (LNP; Fig. 1D and Fig. S1), indicating that postspike refractory and bursting effects substantially contribute to action potential generation in these neurons. Because the parameters of the GLM model emergent physiological features of the recorded neurons, comparing GLM parameters across neurons illustrates the diversity among MCs (Fig. 1 E–G). For example, the diversity reflected in postspike (i.e., spike history) filters potentially corresponds to a recently characterized variability in the rebound depolarization current of these neurons recorded in vivo (6). Furthermore, the interaction of each MC’s GLM parameters defines how it responds to stimuli and dictates the complex stimulus features that each neuron best encodes. We note that the efficacy of the GLM approach in capturing MC responses was not specific to the precise stimulus statistics delivered to the neurons here (Fig. S2).
Diversity Enables Efficient Stimulus Representation.
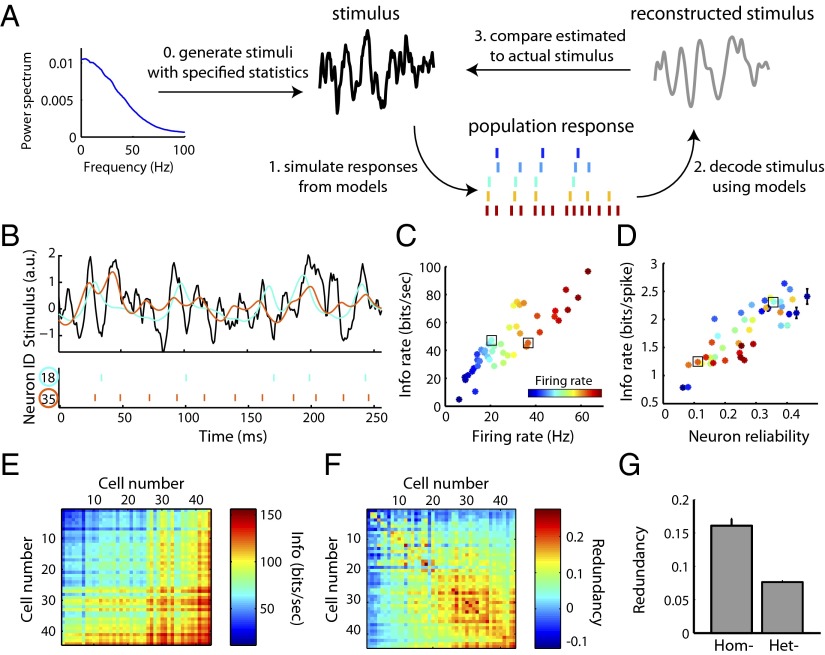
Because the GLM approach captures the intrinsic diversity across MCs, different model MCs generate unique spike trains when presented the same dynamic stimulus (Fig. 2B and Fig. S3). We used this model-based approach to ask which features of these individual neurons influence the amount of information about the stimulus that each neuron captures (Fig. 2A). Quantifying the quality of stimulus representation using information theoretic methods (23, 24), we found that neuron information rates were strongly correlated with firing rate (r = 0.87; Fig. 2C), in line with previous findings (25). However, we note that we found examples of neurons that had identical firing rates and yet differed almost twofold in their information rates, suggesting the importance of additional factors other than firing rate governing the amount of transmitted information. For example, neurons with spike times that were reliable across stimulus repeats and spikes that were strongly stimulus driven (i.e., minimal contributions from bias or spike-history terms) were more informative per spike (Fig. 2D and Fig. S3C). We note that the large range and diversity of firing rates observed among the MCs here is concordant with those found in vivo (26).
Fig. 2.
Using simulated ensemble responses to study stimulus representation in diverse neural populations. (A) Schematic of the paradigm used to study how neural populations represent stimuli. Following the generation of noisy stimuli, population spike responses were simulated using the MC models. Bayesian decoding was used to estimate the most probable stimulus given the population response and then compared with the actual stimulus. (B–D) Stimulus encoding by single neurons. Stimulus statistics and coloring of neurons same as in Fig. 1. (B) Stimulus (Top; black), spike trains (Bottom), and reconstructions (Top; cyan, orange) for two example neurons. These neurons encode the same stimulus differently, as evidenced by their unique spike trains and stimulus reconstructions. (C) Quantifying stimulus representation using mutual information (mean ± SEM, n = 44 cells) shows that a neuron’s information rate is strongly correlated with its firing rate (r = 0.87). Boxes indicate neurons shown in B. (D) As in C, but plotted as average information conveyed by single spikes as a function of neuron reliability. (E–G) Stimulus encoding by neuron pairs. (E) Mutual information for all neuron pairs with neurons ordered along axes by increasing firing rate. Values on (off) diagonal correspond to homogeneous (heterogeneous) pairs. (F) As in E but plotted as the normalized informational redundancy of the neuron pair. Positive (negative) values indicate population redundancy (synergy) where zero indicates independent stimulus encoding. 90% of pairs were redundant, yet overall redundancy values were small, indicating near-independent encoding. (G) Homogeneous pairs (Hom) are significantly more redundant than heterogeneous pairs (Het; P = 2.5*10−16, Wilcoxon, n = 44 and 946 pairs, respectively).
We extended this information-based framework to examine how populations of recorded MCs encode a common stimulus, considering two broad possibilities. First, stimuli might be best encoded by groups of highly similar neurons, suggesting that averaging across the population of recorded neurons can compensate for unreliable spiking in any single neuron (10). Alternatively, stimuli might be best encoded by groups of heterogeneous neurons, suggesting that maximizing the representation of temporal features of the stimuli is important (12, 27). We specifically chose to study how diverse groups collectively represent an identical stimulus to mimic features of the olfactory bulb, where 25–50 sister MCs projecting to the same glomerulus (5) each receive highly correlated stimulus- and respiration-driven synaptic input (26, 28–30).
We created populations of uncoupled virtual mitral cells by randomly selecting groups of model neurons (i.e., fit from the recorded MCs). Spiking responses in these virtual populations were then simulated using the GLM models, enabling us to probe ensemble responses to many more stimuli than could be delivered during experimental recordings. The neurons in these synthetic populations varied in the diversity of their GLM parameters, allowing us to determine how neuronal diversity influences the encoding of fluctuating stimuli. To this end, we used Bayesian model–based decoding, which optimally reconstructs the input to a population (i.e., its “perceived stimulus”) given its ensemble response (18, 23). This approach solves the high-dimensional problem of interpreting dynamic population responses (13, 23) without making undue simplifications or assumptions about the nature of the neural code (5, 10, 21). However, we note that we could have instead focused on alternative metrics of population output instead of stimulus representation efficacy.
We first used the analysis described above on populations consisting of pairs of simulated neurons. Homogeneous pairs, composed of two copies of the same model neuron (with identical stimulus filtering properties), encoded 73 ± 11% more informative about the stimulus than a single neuron copy alone (Fig. S4). In other words, because spiking is a stochastic process, decoding is improved by considering multiple spike trains from identical model neurons. This allows for “averaging out” the effect of any single neuron’s noise. Next, we considered both homogeneous and heterogeneous pairs of neurons, and quantified the informational redundancy of these pairs. This method compares the information of the pair relative to the sum of each neuron’s information independently (13), and gives an indication of the efficiency of information representation by the population. For example, do neurons together represent information redundantly (i.e., both neurons communicate identical or partially overlapping messages)? Or do they instead represent information synergistically (i.e., both neurons communicate more information together than both individually)? Although we found that most homogeneous and heterogeneous populations represented information redundantly (Fig. 2 E and F), homogeneous pairs were twice as redundant as heterogeneous pairs (16% versus 8% informational redundancy; Fig. 2G). Given that these neurons do not directly communicate, we note that the appearance of synergism among neurons pairs here is somewhat surprising and is likely due to limitations in our ability to estimate information rates among low firing rate neurons (see Materials and Methods for further explanation). Nonetheless, these results demonstrate that although pooling responses over multiple neurons even multiple copies of the same neuron is beneficial, the heterogeneity in intrinsic properties in actual mitral cells is beneficial for efficiently representing sensory information.
Intrinsic Diversity Enables Populations to Generalize Across Stimulus Types.
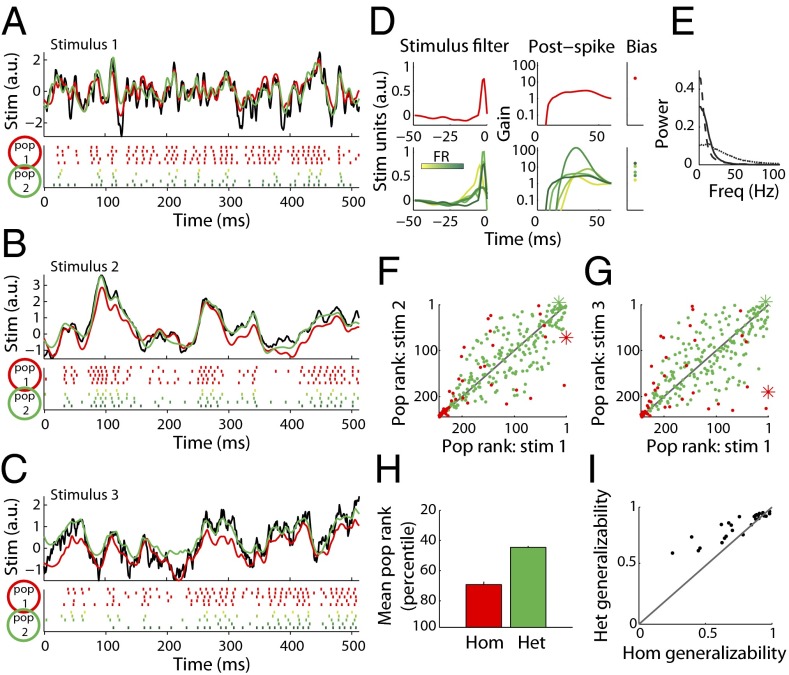
We next investigated the effect of diversity on stimulus coding in larger neuronal populations. In Fig. 3A we plot actual and reconstructed stimuli for two example populations: the first, a homogeneous group composed of five copies of the highest firing rate, most informative neuron from Fig. 2C; the second, a population composed of neurons with diverse parameters (Fig. 3D). Both populations encode stimuli composed of high frequencies with high fidelity (Fig. 3A); however, the diverse population is more effective in representing lower-frequency stimuli (Fig. 3E) than the homogeneous one (Fig. 3 B and C). Thus, although the diverse population has 45% fewer spikes than the homogeneous one, the diverse population better uses its allocation of five neurons by representing more of the relevant stimulus space with its (temporal) receptive fields.
Fig. 3.
Populations composed of diverse neurons effectively encode stimuli with very different frequency spectra. (A–C) Example stimulus (Top; black), rasters (Bottom), and reconstructions (Top) for a homogeneous population composed of five copies of the most informative neuron (pop 1, red) and a heterogeneous population composed of five neurons with diverse properties (pop 2, green) for three stimuli with different power spectra: stimulus 1, Gaussian white noise (GWN) convolved with an alpha function with τ = 3 ms (A); stimulus 2, GWN with alpha function with τ = 10 ms (B); stimulus 3, Ornstein–Uhlenbeck process with τ = 40 ms (C). Note that although both populations can represent the stimulus in A well, only population 2, the diverse population, can also represent the lower frequency stimuli in B and C. (D) Neuron GLM parameters for the populations in A–C. Top indicates parameters for population 1 and Bottom for population 2 (green shades indicate different neurons). (E) Power spectra for the three stimuli in A–C (dotted, solid, dashed respectively). (F and G) Relative rankings of stimulus reconstruction accuracy for all homogeneous (hom-, red) and 200 randomly sampled heterogeneous populations (het-, green) for stimuli 1 versus 2 (F) or 1 versus 3 (G). Populations in Top Right indicate those which represent both stimuli accurately. Asterisks indicate populations highlighted in A–C. Note that hom populations are among the bottom populations and are further from the unity line than het populations. (H) Average rank of het and hom populations across eight spectrally unique stimuli (Materials and Methods). Het populations are consistently ranked higher (more accurate) than hom ones (P = 0.002, paired Wilcoxon). (I) Plot of generalizability, defined as the correlation of population ranks on stimulus pairs, for hom and het populations across all pairs of eight stimulus types. Each dot corresponds to the generalizability between a pair of stimulus types (n = 28 total pairs). Het populations are significantly more likely than hom to generalize to novel kinds of stimuli (P = 1.5*10−4, paired Wilcoxon).
To extend this analysis we compared how 250 populations of randomly chosen five-neuron ensembles encoded stimuli with different frequency spectra (e.g., 1/fα noise with differing values of α, white noise, etc.; n = 8 stimuli total; shown in Fig. S5). These stimuli were chosen to cover a wide range of input frequencies including the range of frequencies these neurons likely receive in vivo (29, 31). We created homogeneous populations, each consisting of five copies of a single MC, and heterogeneous populations generated by randomly selecting five MCs from the recorded set with replacement. To compare population responses across stimulus spectra, we ranked the populations in order of increasing average reconstruction error for each kind of stimulus and compared ranks across different stimuli. Across pairs of stimulus types population ranks were correlated (Fig. 3 F and G; r = 0.80 and 0.71, respectively), meaning that those populations that represent one stimulus well also represent other kinds of stimuli well (termed generalizability). Heterogeneous populations were better than homogeneous ones not just at encoding stimuli on average (Fig. 3H), but also at generalizing across different stimuli (specific examples in Fig. 3 F and G and summary in I). Thus, the observed intrinsic diversity helps encode many kinds of stimuli, conferring representational robustness to MC populations.
Populations Optimized for Specific Stimuli Combine Diversity with Homogeneity.
Thus far, we have only considered sampling neurons randomly according to a particular rule (homogeneously versus heterogeneously). We next attempted to construct more optimal groups of neurons for encoding specific stimulus types. We liken this scenario to that of sister MCs associated with a single glomerulus, which receive inputs with a specific temporal structure (26, 32) based on olfactory receptor neuron (ORN) odorant binding kinetics, which differ across glomeruli and ORN subtypes (33, 34). Would the best population for a given stimulus be more diverse than selecting MCs at random from the physiologically based set? Or would the best population be more homogeneous than random, perhaps allowing the responses of unreliable neurons to be improved upon by selecting neurons coding for redundant (i.e., degenerate) stimulus features? To answer these questions, we implemented a greedy search algorithm (35) to build the best population of model MCs to encode a given stimulus by iteratively adding neurons one at a time such that the added neuron maximized the ability of the entire population to represent the stimulus (Fig. 4A). Although it is not guaranteed to find the global optimum, it is an efficient and intuitive method of finding neuron groups more informative than those generated through random sampling.
Fig. 4.
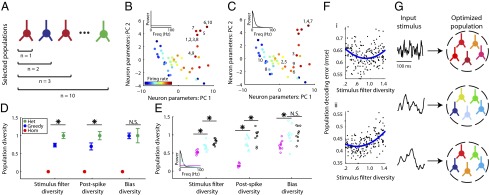
Populations optimized for stimulus representation combine homogeneity with diversity. (A) Cartoon of greedy search algorithm to estimate the population that best represents a particular type of stimulus. Neurons were iteratively added, one at a time, to the current population of neurons such that the neuron chosen maximized the population's reconstruction accuracy. To allow for homogeneity, neurons could be added more than once (e.g., two red neurons). (B and C) Visualization of the population selected to best represent a white-noise stimulus (B) or a low-frequency stimulus (C). Graphs show neurons (as dots) projected into a 2D space using principal component analysis (PCs). Population sizes vary from n = 1 to n = 10, numbers next to dots correspond to algorithm iteration step when each neuron was added. Note that certain neurons are chosen multiple times and that stimulus type dictates the selected population diversity. (D) GLM parameter diversity of the greedy-search-selected populations (blue) averaged over eight different choices of stimulus spectra relative to homogeneous (red) and randomly sampled heterogeneous populations (green), n = 10 neurons per population. Asterisks indicate where greedy search populations are significantly less diverse than heterogeneous (P < 0.05) and population diversity has been normalized to that of randomly sampled heterogeneous. Error bars indicate SEM (blue) and interquartile range (green). (E) Greedy-search population diversity for specific stimlus types. Colors indicate different stimulus types corresponding to inset power spectrum (magenta, stimulus as in B; cyan, Ornstein–Uhlenbeck process with τ = 10 ms; black, stimulus as in C), open circles indicate multiple runs of the greedy search algorithm (n = 10 per stimulus type), asterisks indicate significant differences in population diversity between stimulus types. (F) Population decoding error as a function of stimulus filter diversity for 200 randomly sampled populations (dots, n = 5 neurons per population) for stimulus 1 and 2 as in Fig. 3 (A and B, respectively). Least-squares fits using a second-order polynomial (blue) show that on average there is an intermediate level of stimulus filter diversity where decoding error is minimized (regression P < 0.01). (G) Cartoon showing that population diversity should be preferentially selected with respect to the specific incoming stimulus distribution.
Visualizing the makeup of these greedy-search-selected populations using dimensionality reduction (Fig. S6) reveals that they reflect a balance between diversity—consisting of neurons with different properties, and homogeneity, often including multiple copies of selected neurons (Fig. 4 B and C and Fig. S7). In addition, the stimulus type dictates the selection of specific neurons and the chosen level of population diversity. For example, the population selected to best encode a white-noise stimulus (Fig. 4C) was composed primarily of similar neurons with high firing rates; whereas, diversity in neuron properties was more important for encoding a more naturalistic stimulus with both rapidly and slowly varying temporal components (Fig. 4B). Using the greedy search algorithm to select populations for each of the eight stimulus types, we quantified the diversity of these populations and of randomly sampled heterogeneous and homogeneous populations (Fig. 4D). Surprisingly, greedy search populations were on average ∼25% less diverse than heterogeneous ones when considering either stimulus filter and postspike parameters. Furthermore, quantifying population diversity for MC groups selected to best encode different stimulus types reveals that they have varying levels of diversity (Fig. 4E and Fig. S8), suggesting that population diversity should be preferentially tuned to the afferent stimulus distribution.
To ensure that the previous findings are not solely the result of the greedy selection process, we performed additional simulations by randomly constructing populations with differing amounts of diversity and examining the relationship between population diversity and decoding accuracy. As predicted from the greedy search results, we found evidence for a U-shaped relationship between decoding accuracy and population diversity (Fig. 4F and Fig. S9), indicating that neural coding is optimized at intermediate levels of diversity. However, population size is also a relevant factor in the importance of population diversity, with diversity being more important to smaller populations than larger ones (Fig. S10). This suggests that heterogeneity will be more important to populations in which the number of neurons devoted to representing a stimulus is relatively small. Furthermore, we found the benefit of neural variability to not be solely dependent upon a single GLM filter dimension (Fig. S11), such as the stimulus filter or bias term.
Discussion
Here we apply the framework of generalized linear models to study how cell-to-cell differences in intrinsic properties of olfactory bulb mitral cells influence stimulus encoding. The statistical modeling approach that we have used accurately captures the neuronal properties determining spiking and avoids overfitting. It also avoids making specific but difficult-to-verify claims about channel densities or properties that can arise from underconstrained Hodgkin–Huxley models (36). We show that diverse populations offer the advantages of more efficient encoding (defined in terms of information per cell or information per spike) and more robust coding of different kinds of stimuli, such as stimuli with wide ranges of spectral properties. This is because neurons encoding partially overlapping (i.e., degenerate) stimulus features can work together to overcome neural spike-generation noise and also encode more stimulus features together than separate. We also show that populations selected to best represent stimuli with specific spectral properties have differing amounts of diversity, which suggests that population diversity should be selectively chosen with respect to the precise stimulus to be encoded. Although variants of this framework have been used to model neural responses previously [including in single neuron modeling competitions (37, 38)] we extend these methods to describe the systematic biological differences among neurons and their impact on population coding. Given the generality of this framework, we believe that this methodology can similarly be extended to describe electrophysiological differences across neuron types and to develop hypotheses about the distinct roles of different neuron types throughout the brain.
One of the key advantages of this approach is that it allows us to use Bayesian stimulus decoding to ask how neuron-to-neuron differences in stimulus filtering and postspike properties influence population coding of arbitrary stimuli. Bayesian decoding is advantageous because it offers an optimal, best-case view of neural encoding, making few assumptions that risk underestimating the complexity of the neural code (18, 23). Although we explored the relationship between stimulus encoding in diverse and homogeneous populations in a previous study (5), performing stimulus reconstruction here allows the identification of the relative importance of variation in specific features of the sets of recorded neurons. This approach also allows us to investigate stimulus encoding in a more general context by simulating responses to arbitrary stimuli. An obvious advantage of simulation approaches is that we are not limited to only analyzing data that we are able to collect during recordings.
Our results make specific, testable predictions on the role of MC intrinsic diversity for encoding olfactory information. First, we show that when populations need to represent a variety of stimulus types, then intrinsic diversity facilitates generalizing representations across stimulus types. Second, when populations need to represent a single kind of stimulus and are allowed to selectively choose their level of variability, populations choose a balance between complete homogeneity and diversity. That is, homogenizing the input received by a population of neurons should lead the population to be less diverse. This in silico finding is intriguing because it is consistent with recent experimental findings showing that sister MCs, receiving primary olfactory inputs from the same glomerulus and olfactory receptor subtype, are biophysically more similar to one another than sampling MCs at random (7). Furthermore, our work makes the additional hypothesis that the level of diversity across sister MCs should be adaptive with respect to the unique stimulus distribution that these neurons receive from their olfactory receptor subtype (32–34). Therefore, we predict that the levels of MC intrinsic diversity between sister MCs should be empirically different across glomeruli (Fig. 4G).
We note that we made multiple assumptions here for the sake of computational tractability. Because our focus was to study the functional role of MC intrinsic diversity, we chose not to include any of the effects of neural connections such as synapses between neurons in our experiments and simulations. Given that the olfactory bulb possesses extensive lateral circuitry (11), which has been shown to also diversify MC responses (11, 39, 40), we expect that bulbar circuit activity will work in conjunction with intrinsic diversity in vivo to further diversify MC responses (41). Furthermore, when decoding we took the perspective that the best populations were those that resulted in the most faithful reconstruction of the stimulus. However, the biological solution dictating the actual amount of diversity may use alternative criteria for optimality. For example, in vivo olfactory bulb MCs may seek to represent only odor-specific stimulus components or may try to maximize stimulus representation while also minimizing the number of spikes used to transmit the information (42). We chose to avoid assumptions about which features of ORN input are most important for MCs to represent and rather to take the agnostic view that MCs should try to represent the stimulus in its entirety. Our approach, however, can readily be adapted to tasks that require representation of specific stimulus components. Although these assumptions likely affect the quantitative details of our results, like specifying of the precise balance between diversity and feature similarity, our general finding that a precise stimulus-specific balance exists nevertheless likely holds.
We believe that our results generalize to other neural systems because this circuit motif in which multiple neurons receive highly correlated inputs occurs throughout the brain, including neocortex (43, 44). Thus, we predict that the observed degree of neuronal intrinsic variability plays a substantial role in tuning the output diversity (or redundancy) in these neurons’ spiking responses and in improving stimulus encoding. Furthermore, our findings may in part explain the substantial informational redundancy found in neural populations throughout the brain (1, 10). Given that the optimal networks here are neither maximally diverse nor maximally homogeneous, these results suggest similar design principles for other systems. By mixing diversity with neural feature similarity, complex systems can simultaneously maintain efficient functioning while remaining robust to uncertain events.
Materials and Methods
A detailed description of the methods is provided in the Supporting Information. In brief, whole-cell patch clamp recordings of mitral cells were obtained in vitro from mouse olfactory bulb slices (5). Spikes were recorded while stimulating neurons with 40 trials of a 2.5-s duration frozen noise stimulus, generated by convolving a white-noise current with an alpha function with τ = 3 ms. Point process models were fit from recordings via previously described methods (18). The models fit from physiological data were used to simulate neuron spike responses to stimuli not presenting during recording. Uncoupled populations were constructed by sampling neurons from the set of model neurons, where all neurons in a population received an identical stimulus. Population responses were decoded using the maximum a posteriori estimator (23) (posterior mode) to reconstruct the time series of stimulus input to the population. Population decoding performance was quantified using mutual information and root mean square error. To approximate the structure of the optimal population for best representing a particular kind stimulus, we implemented a greedy search algorithm (35). Unless otherwise indicated, all error bars indicate SEs and all statistical tests were Wilcoxon rank–sum tests.
Supplementary Material
Acknowledgments
We thank B. Doiron, R. Kass, A.L. Kumar, A. Schaefer, C. Shalizi, L. Paninski, and the Urban Laboratory for discussions and manuscript comments. We thank S. D. Burton for collecting the data shown in Fig. S2. Funding was provided by a National Science Foundation Graduate Research Fellowship/RK Mellon Foundation Fellowship (to S.J.T.); National Institutes of Health F32 DC010535 (to R.C.G); and National Institute on Deafness and other Communication Disorders Grant R01DC0005798 (to N.N.U.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1221214110/-/DCSupplemental.
References
- 1.Puchalla JL, Schneidman E, Harris RA, Berry MJ. Redundancy in the population code of the retina. Neuron. 2005;46(3):493–504. doi: 10.1016/j.neuron.2005.03.026. [DOI] [PubMed] [Google Scholar]
- 2.Moore CI, Carlen M, Knoblich U, Cardin JA. Neocortical interneurons: from diversity, strength. Cell. 2010;142(2):189–193. doi: 10.1016/j.cell.2010.07.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Marder E, Taylor AL. Multiple models to capture the variability in biological neurons and networks. Nat Neurosci. 2011;14(2):133–138. doi: 10.1038/nn.2735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Altschuler SJ, Wu LF. Cellular heterogeneity: do differences make a difference? Cell. 2010;141(4):559–563. doi: 10.1016/j.cell.2010.04.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Padmanabhan K, Urban NN. Intrinsic biophysical diversity decorrelates neuronal firing while increasing information content. Nat Neurosci. 2010;13(10):1276–1282. doi: 10.1038/nn.2630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Angelo K, Margrie TW. Population diversity and function of hyperpolarization-activated current in olfactory bulb mitral cells. Sci Rep. 2011;1(1):1–50. doi: 10.1038/srep00050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Angelo K, et al. A biophysical signature of network affiliation and sensory processing in mitral cells. Nature. 2012;488(7411):375–378. doi: 10.1038/nature11291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Graves AR, et al. Hippocampal pyramidal neurons comprise two distinct cell types that are countermodulated by metabotropic receptors. Neuron. 2012;76(4):776–789. doi: 10.1016/j.neuron.2012.09.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Marsat G, Maler L. Neural heterogeneity and efficient population codes for communication signals. J Neurophysiol. 2010;104(5):2543–2555. doi: 10.1152/jn.00256.2010. [DOI] [PubMed] [Google Scholar]
- 10.Schneider DM, Woolley SMN. Discrimination of communication vocalizations by single neurons and groups of neurons in the auditory midbrain. J Neurophysiol. 2010;103(6):3248–3265. doi: 10.1152/jn.01131.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Giridhar S, Doiron B, Urban NN. Timescale-dependent shaping of correlation by olfactory bulb lateral inhibition. Proc Natl Acad Sci USA. 2011;108(14):5843–5848. doi: 10.1073/pnas.1015165108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Tkačik G, Prentice JS, Balasubramanian V, Schneidman E. Optimal population coding by noisy spiking neurons. Proc Natl Acad Sci USA. 2010;107(32):14419–14424. doi: 10.1073/pnas.1004906107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Schneidman E, Bialek W, Berry MJ., 2nd Synergy, redundancy, and independence in population codes. J Neurosci. 2003;23(37):11539–11553. doi: 10.1523/JNEUROSCI.23-37-11539.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Edelman GM, Gally JA. Degeneracy and complexity in biological systems. Proc Natl Acad Sci USA. 2001;98(24):13763–13768. doi: 10.1073/pnas.231499798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Azouz R, Gray CM. Cellular mechanisms contributing to response variability of cortical neurons in vivo. J Neurosci. 1999;19(6):2209–2223. doi: 10.1523/JNEUROSCI.19-06-02209.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Stocks NG (2000) Suprathreshold stochastic resonance in multilevel threshold systems. Phys Rev Lett 84:2310–2313. [DOI] [PubMed]
- 17.Mejias JF, Longtin A. Optimal heterogeneity for coding in spiking neural networks. Phys Rev Lett. 2012;108(22):228102. doi: 10.1103/PhysRevLett.108.228102. [DOI] [PubMed] [Google Scholar]
- 18.Pillow JW, et al. Spatio-temporal correlations and visual signalling in a complete neuronal population. Nature. 2008;454(7207):995–999. doi: 10.1038/nature07140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Butts DA, et al. Temporal precision in the neural code and the timescales of natural vision. Nature. 2007;449(7158):92–95. doi: 10.1038/nature06105. [DOI] [PubMed] [Google Scholar]
- 20.Slee SJ, Higgs MH, Fairhall AL, Spain WJ. Two-dimensional time coding in the auditory brainstem. J Neurosci. 2005;25(43):9978–9988. doi: 10.1523/JNEUROSCI.2666-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Narayanan NS, Kimchi EY, Laubach M. Redundancy and synergy of neuronal ensembles in motor cortex. J Neurosci. 2005;25(17):4207–4216. doi: 10.1523/JNEUROSCI.4697-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kass RE, Ventura V. A spike-train probability model. Neural Comput. 2001;13(8):1713–1720. doi: 10.1162/08997660152469314. [DOI] [PubMed] [Google Scholar]
- 23.Pillow JW, Ahmadian Y, Paninski L. Model-based decoding, information estimation, and change-point detection techniques for multineuron spike trains. Neural Comput. 2011;23(1):1–45. doi: 10.1162/NECO_a_00058. [DOI] [PubMed] [Google Scholar]
- 24.Warland DK, Reinagel P, Meister M. Decoding visual information from a population of retinal ganglion cells. J Neurophysiol. 1997;78(5):2336–2350. doi: 10.1152/jn.1997.78.5.2336. [DOI] [PubMed] [Google Scholar]
- 25.Borst A, Haag J. Effects of mean firing on neural information rate. J Comput Neurosci. 2001;10(2):213–221. doi: 10.1023/a:1011225232120. [DOI] [PubMed] [Google Scholar]
- 26.Shusterman R, Smear MC, Koulakov AA, Rinberg D. Precise olfactory responses tile the sniff cycle. Nat Neurosci. 2011;14(8):1039–1044. doi: 10.1038/nn.2877. [DOI] [PubMed] [Google Scholar]
- 27.Atick JJ, Redlich AN. What does the retina know about natural scenes? Neural Comput. 1992;4:196–210. [Google Scholar]
- 28.Schoppa NE, Westbrook GL. Glomerulus-specific synchronization of mitral cells in the olfactory bulb. Neuron. 2001;31(4):639–651. doi: 10.1016/s0896-6273(01)00389-0. [DOI] [PubMed] [Google Scholar]
- 29.Spors H, Wachowiak M, Cohen LB, Friedrich RW. Temporal dynamics and latency patterns of receptor neuron input to the olfactory bulb. J Neurosci. 2006;26(4):1247–1259. doi: 10.1523/JNEUROSCI.3100-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Verhagen JV, Wesson DW, Netoff TI, White JA, Wachowiak M. Sniffing controls an adaptive filter of sensory input to the olfactory bulb. Nat Neurosci. 2007;10(5):631–639. doi: 10.1038/nn1892. [DOI] [PubMed] [Google Scholar]
- 31.Khan AG, Sarangi M, Bhalla US. Rats track odour trails accurately using a multi-layered strategy with near-optimal sampling. Nat Commun. 2012;3:703. doi: 10.1038/ncomms1712. [DOI] [PubMed] [Google Scholar]
- 32.Carey RM, Verhagen JV, Wesson DW, Pírez N, Wachowiak M. Temporal structure of receptor neuron input to the olfactory bulb imaged in behaving rats. J Neurophysiol. 2009;101(2):1073–1088. doi: 10.1152/jn.90902.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ghatpande AS, Reisert J. Olfactory receptor neuron responses coding for rapid odour sampling. J Physiol. 2011;589(Pt 9):2261–2273. doi: 10.1113/jphysiol.2010.203687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Nagel KI, Wilson RI. Biophysical mechanisms underlying olfactory receptor neuron dynamics. Nat Neurosci. 2011;14(2):208–216. doi: 10.1038/nn.2725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Russell S, Norvig P. Artificial Intelligence: A Modern Approach. Prentice Hall, Upper Saddle River, NJ; 2009. 3rd Ed. [Google Scholar]
- 36.Bhalla US, Bower JM. Exploring parameter space in detailed single neuron models: simulations of the mitral and granule cells of the olfactory bulb. J Neurophysiol. 1993;69(6):1948–1965. doi: 10.1152/jn.1993.69.6.1948. [DOI] [PubMed] [Google Scholar]
- 37.Gerstner W, Naud R. Neuroscience. How good are neuron models? Science. 2009;326(5951):379–380. doi: 10.1126/science.1181936. [DOI] [PubMed] [Google Scholar]
- 38.Jolivet R, et al. The quantitative single-neuron modeling competition. Biol Cybern. 2008;99(4-5):417–426. doi: 10.1007/s00422-008-0261-x. [DOI] [PubMed] [Google Scholar]
- 39.Dhawale AK, Hagiwara A, Bhalla US, Murthy VN, Albeanu DF. Non-redundant odor coding by sister mitral cells revealed by light addressable glomeruli in the mouse. Nat Neurosci. 2010;13(11):1404–1412. doi: 10.1038/nn.2673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Arevian AC, Kapoor V, Urban NN. Activity-dependent gating of lateral inhibition in the mouse olfactory bulb. Nat Neurosci. 2008;11(1):80–87. doi: 10.1038/nn2030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Chow S-F, Wick SD, Riecke H. Neurogenesis drives stimulus decorrelation in a model of the olfactory bulb. PLOS Comput Biol. 2012;8(3):e1002398. doi: 10.1371/journal.pcbi.1002398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Weber F, Machens CK, Borst A. Disentangling the functional consequences of the connectivity between optic-flow processing neurons. Nat Neurosci. 2012;15(3):441–448, S1–S2. doi: 10.1038/nn.3044. [DOI] [PubMed] [Google Scholar]
- 43.Poulet JFA, Petersen CCH. Internal brain state regulates membrane potential synchrony in barrel cortex of behaving mice. Nature. 2008;454(7206):881–885. doi: 10.1038/nature07150. [DOI] [PubMed] [Google Scholar]
- 44.Kerr JND, Greenberg D, Helmchen F. Imaging input and output of neocortical networks in vivo. Proc Natl Acad Sci USA. 2005;102(39):14063–14068. doi: 10.1073/pnas.0506029102. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.