Dynamic nuclear polarization-enhanced ¹³C NMR spectroscopy of static biological solids

Abstract

We explore the possibility of using dynamic nuclear polarization (DNP) to enhance signals in structural studies of biological solids by solid state NMR without sample spinning. Specifically, we use 2D ¹³C-¹³C exchange spectroscopy to probe the peptide backbone torsion angles (ϕ,ψ) in a series of selectively ¹³C-labeled 40-residue β-amyloid (Aβ_1–40) samples, in both fibrillar and non-fibrillar states. Experiments are carried out at 9.39 T and 8 K, using a static double-resonance NMR probe and low-power microwave irradiation at 264 GHz. In frozen solutions of Aβ_1–40 fibrils doped with DOTOPA-TEMPO, we observe DNP signal enhancement factors of 16–21. We show that the orientation- and frequency-dependent spin polarization exchange between sequential backbone carbonyl ¹³C labels can be simulated accurately using a simple expression for the exchange rate, after experimentally determined homogeneous ¹³C lineshapes are incorporated in the simulations. The experimental 2D ¹³C-¹³C exchange spectra place constraints on the ϕ and ψ angles between the two carbonyl labels. Although the data are not sufficient to determine ϕ and ψ uniquely, the data do provide non-trivial constraints that could be included in structure calculations. With DNP at low temperatures, 2D ¹³C-¹³C exchange spectra can be obtained from a 3.5 mg sample of Aβ_1–40 fibrils in 4 hr or less, despite the broad ¹³C chemical shift anisotropy line shapes that are observed in static samples.

Introduction

Experiments with biological solids in modern solid state NMR are mainly done under conditions of magic angle spinning (MAS). Nevertheless, a number of experiments with static samples provide useful structural information. For instance, multiple-quantum experiments were used to reveal the in-register parallel arrangement of 40-residue β-amyloid (Aβ_1–40) molecules in amyloid fibrils [1]. Double quantum-single quantum correlation (DOQSY) experiments showed that the polypeptide backbone is strongly oriented in silk fibrils, rather than forming an “amorphous” matrix [2]. Analysis of DOQSY spectra also allowed a distribution of backbone ϕ and ψ torsion angles to be determined [3]. NMR measurements on static solids were also applied in studies of non-biological materials. For instance, monomer conformations in non-crystalline solid polymers were studied using dipolar-CSA (chemical shift anisotropy) tensor correlation [4, 5], and orientational ordering in solid methanol was revealed through CSA-CSA correlation in a 2D ¹³C-¹³C exchange experiment [6], DOQSY approach was used to determine chain conformation in glassy polyethylene terephtalate[7]. The Carr-Purcell-Meiboom-Gill pulse sequence was used to determine the two bond lengths in C₆₀ molecules in the solid state [8]. Finally, studies of membrane proteins in magnetically or mechanically oriented lipid bilayers present the most conspicuous example for applicability of static NMR measurements [9–12].

The broad ¹³C NMR line widths in static samples, particularly for sites with large CSA such as carbonyl sites, make sensitivity a serious problem. In recent years, the phenomenon of dynamic nuclear polarization (DNP) has become a promising tool for boosting sensitivity in NMR experiments. DNP is a process where, by applying microwave (MW) irradiation to one of the electron spin resonance transitions in a system with unpaired electrons, the large Boltzmann electron spin polarization is partially transferred to coupled nuclei. To date, DNP-enhanced solid state NMR has been used for studies of numerous biological systems, including membrane proteins [13–17], amyloid peptides [18–20], oriented samples [21], and viral DNA [22], as well as for studies of surfaces of inorganic materials [23–26]. All these experiments have been carried out with MAS at temperatures of 80–100 K, and mainly employ the cross-effect DNP mechanism [27–31], requiring biradicals as polarizing agents [32, 33]. Such experiments also require high-power, high-frequency MW sources, such as gyrotrons [34], which now have become commercially available [35]. Alternatively, at lower temperatures attained by liquid helium cooling, one can use a low-power MW source. Recently, Tycko and coworkers have shown the feasibility of single frequency [36, 37] and double-resonance [38] solid state NMR measurements using a DNP system equipped with a tunable 30 mW MW source and quasioptical polarizing system. Nuclear polarization as high as 61% was recently obtained at 4.2 K in 7 T using a 70 mW power source[39]. Though employing different polarization mechanisms, the dissolution DNP field also routinely applies low power MW setups [40–42].

In this work, we demonstrate the feasibility of employing static DNP-enhanced 2D NMR experiments for deriving structural information about biological solids. We employ 2D ¹³C-¹³C exchange experiments [6, 43, 44] to record CSA/CSA correlation patterns for pairs of sequential backbone carbonyl ¹³C labels in Aβ_1–40 fibrils, as well as a non-fibrillar Aβ_1–40 sample. The 2D correlation patterns contain information about backbone torsion angles between the labeled sites. We analyze the experimental 2D patterns by comparing with numerical simulations, and emphasize the importance of including the effects of incomplete exchange, as discussed earlier by Dabbagh et al. [5].

Methods

Sample preparation

Selectively ¹³C-labeled Aβ_1–40 peptides were produced by solid phase synthesis. Two labeled peptides were made, with ¹³C labels at carbonyl sites of Val18 and Phe19 and the methyl site of Ala30 (called Aβ-VF), or with ¹³C-labels at carbonyl sites of Val24 and Gly25 and the methyl site of Ala30 (called Aβ-VG). The first batch of Aβ_1–40 fibrils was prepared by dissolving lyophilized Aβ_1–40 to a concentration of 200 µM in 10 mM pH 7.4 phosphate buffer and incubating overnight under gentle agitation. The growth was performed in a 50 mL tube filled with ~10 mL of solution and mounted horizontally on an orbital shaker (VWR DS-500E) oscillating at 40 rpm. The resulting fibrils were sonicated to produce short fibril fragments, which were used as seeds for later samples. Aβ-VF and Aβ-VG fibrils used in solid state NMR experiments were then prepared with the same growth conditions, except that seeds were added in a 1:20 molar ratio (based on Aβ_1–40 molecules). Negatively stained transmission electron microscope (TEM) images in Fig. S1 show that fibrils with slightly modulated width were predominantly produced by this method. These fibrils are similar in morphology to those observed by Paravastu et al. under quiescent conditions[45]. After 4 hr of growth, the fibrils were pelleted by centrifugation for 2 hr at ~56000 × g. The dry fibril sample discussed below was prepared by lyophilizing the pellet. Fibril samples in frozen solution were not lyophilized, but polarizing and glass-forming agents were added as follows. The wet pellet was resuspended in 0.2 M acetate buffer solution pH 3.0 containing 13.2 mM of DOTOPA-TEMPO, a triradical used as our DNP polarizing agent [36]. The fibrils were pelleted again, and later mixed with 60 wt% of ¹³C-depleted (99.95%) glycerol-d8 (Cambridge Isotopes), serving as glass forming agent. The final gel-like paste is estimated to contain ~6.6 mM of DOTOPA-TEMPO, assuming that the pellet density is 1 g/ml before adding glycerol

The non-fibrillar solution of disordered Aβ-VF peptides was prepared as follows: 4 mg of lyophilized Aβ-VF peptide was dissolved in 2 ml of hexafluoro-2-propanol and lyophilized. The resulting fluffy material was dissolved in 0.1 M HCl, containing 13.2 mM of DOTOPA-TEMPO, quickly mixed with 60 wt% ¹³C-depleted glycerol-d8 and flash frozen. The frozen sample was later mounted in the probe while immersed in a liquid nitrogen bath. Except as noted below, all samples had approximately the same volume of 40 µl, and contained ~3–4 mg of Aβ_1–40.

NMR measurements

NMR measurements were carried out at 9.39 T (400.8 MHz ¹H NMR frequency) using a Varian Infinity console and the double-resonance, low-temperature ¹H-¹³C NMR probe described previously [38], based on a variable-temperature cryostat with a cold-finger-in-vacuum design (Janis ST-200). MW irradiation at 264.0 GHz was provided by a 30 mW source (Virginia Diodes) mounted on a quasioptical polarizing system (Thomas Keating) [36]. The optimal MW frequency was determined earlier and corresponds to the maximum for cross-effect DNP. The sample temperature was set to 8 K for all experiments, except as noted below.

After mounting the sample in the NMR cryostat, the head of the cryostat was quickly plunged into liquid nitrogen to ensure good glass formation. The cryostat was then immediately evacuated and helium cooling was started. The sample stays frozen and, during the entire cooling process, its temperature, monitored by the Cernox sensor embedded in the copper block to which the sample is thermally anchored [38], does not exceed 140 K, which is well below the water/glycerol glass transition. The cryostat evacuation was done for ~ 1 hr at 100 K to remove residual gas that may cause NMR probe arcing, then the temperature was lowered for NMR measurements.

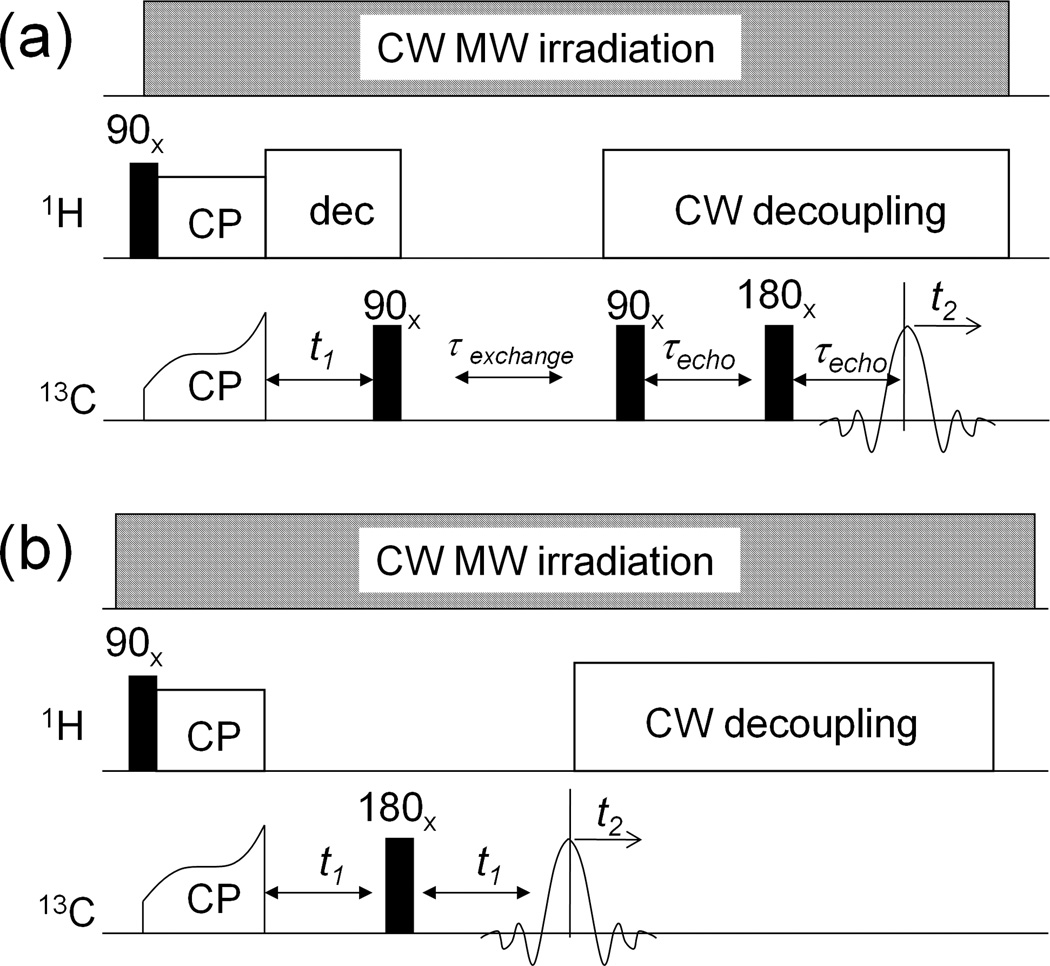
Fig. 1a shows the radio-frequency (RF) pulse sequence for 2D ¹³C-¹³C exchange experiments. ¹³C and ¹H RF field amplitudes were 80 kHz during cross-polarization. ¹H decoupling was done using continuous irradiation at 100 kHz RF amplitude. Fig. 1b shows the RF pulse sequence for measuring frequency-dependent ¹³C transverse decay curves required for calculation of the overlap integral (see below). It was carried out in a 2D manner by varying the interpulse delay in the Hahn echo sequence, without proton decoupling in the indirect dimension. Referencing of ¹³C chemical shifts was done by using the signal of 1-¹³C-labeled L-alanine powder at room temperature, for which the isotropic shift is 177.95 ppm relative to tetramethyl silane.

Fig. 1.

Pulse sequences used in this work. a) 2D spin exchange experiment; b) 2D transverse relaxation measurement experiment

Results

1D measurements

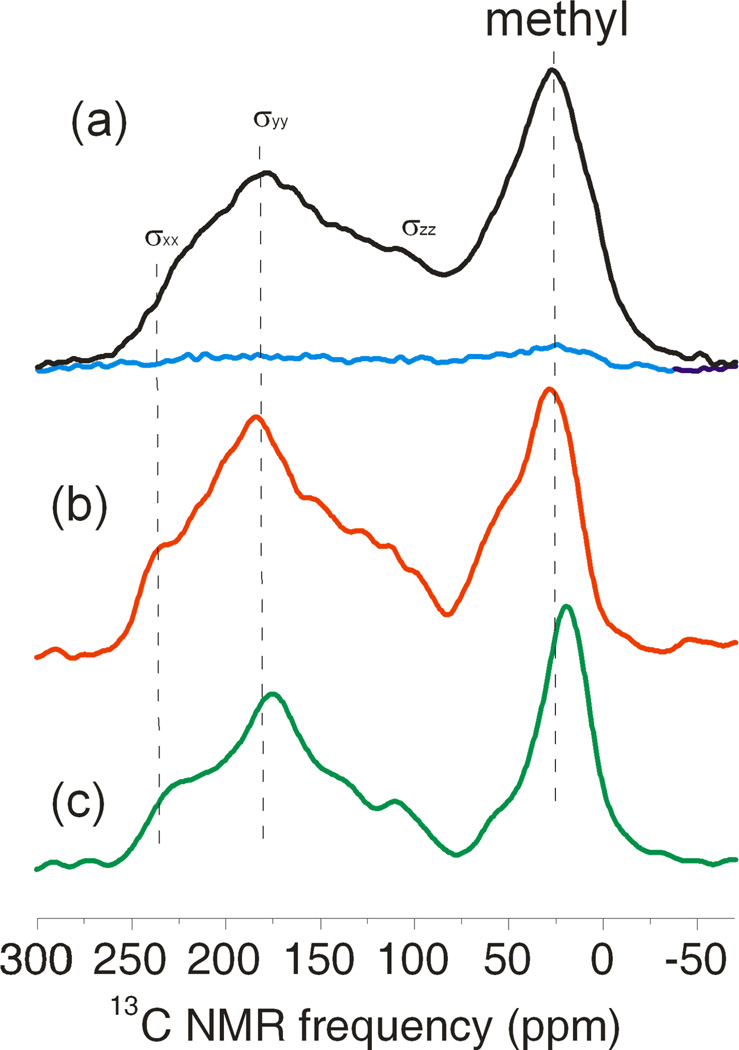
The cross-polarized ¹³C NMR spectrum of the Aβ-VF fibril sample with and without MW irradiation is shown in Fig. 2a. DNP enhancements observed for various samples are summarized in Table 1, with the largest enhancement factor being 21 for Aβ-VG fibrils. For fibrillar samples, we observed a significant difference in DNP build-up times (T_DNP, shown in Fig.S2) determined by observation of ¹H NMR signals or by observation of cross-polarized ¹³C NMR signals. The difference vanished only for the sample of non-fibrillar Aβ-VF peptide in frozen solution.

Fig. 2.

¹³C-cross polarization spectra. a) Aβ-VF fibrils in frozen solution 8 K with microwave irradiation (black line) and without microwave irradiation (blue line). Spectra taken at 4 scans; b) dry Aβ-VF fibrils at 8 K, 128 scans; c) dry Aβ-VF fibrils at room temperature, 512 scans. Dashed lines are drawn to give better reference for viewing the chemical shift change.

Table 1.

Summary of T_DNP, T₂ and polarization enhancements. Primary data are presented in Fig. S2.

	enhancement	TDNP (s), measured through cross- polarized 13C signals	TDNP (s), 1H signals observed directly	13C T2 (ms), with CW 1H decoupling
dry Aβ-VF fibrils at 8 K	-	4.6 (T1)	-	-
Aβ-VF fibrils in frozen solution	18	9.9	21	0.6
Aβ-VG fibrils in frozen solution	21	12.9	23	0.58
Aβ-VF peptide in frozen solution	16	13	13.9	0.6

The spectrum in Fig. 2a shows the CSA-broadened carbonyl line spanning from about 240 ppm to 90 ppm, and a methyl carbon line around 30 ppm. There is also a significant contribution from natural-abundance ¹³C signals. We expect natural-abundance carbonyl signals from unlabeled residues to account for about 17% of the total carbonyl signal. Natural-abundance signal from aromatic carbons may also overlap with carbonyl ¹³C lines. Additionally, natural-abundance ¹³C in ¹³C-depleted glycerol has a concentration of approximately 10 mM and therefore contributes signals with about 20% of the area of the signals from carbonyl labels. As shown in Fig. 2b, the carbonyl CSA principal values for a sample of dry fibrils at low temperature are somewhat different from the corresponding values for fibrils in frozen solution. While the σ_xx component of the carbonyl CSA tensor for dry fibrils (σ_xx=246 ppm) is shifted downfield relative to fibrils in frozen solution (σ_xx=235 ppm), the σ_yy component is almost unchanged (σ_yy=182 ppm in frozen solution and σ_yy=183 ppm in dry fibrils). For dry fibrils, spectra at low temperature and at room temperature (Figs. 2b and 2c) are also somewhat different. The chemical shifts determined from the centers of the powder pattern features are (σ_xx, σ_yy, σ_zz)=(243,174,94) ppm and (σ_xx, σ_yy, σ_zz)=(246,183,89) ppm for fibrils at room temperature and low temperature respectively. Upon cooling, the carbonyl CSA width (i.e., σ_zz − σ_xx) increases, while σ_xx − σ_yy decreases. The chemical shifts of the methyl label also undergo a significant change upon cooling. Chemical shift referencing in our work was based on measurements at room temperature. The overall shift of the spectrum upon cooling may result from a change in the magnetic susceptibility of the stainless steel cryostat.

The frozen solution spectrum in Fig. 2a exhibits more broadening of the carbonyl and methyl lines than spectra of dry samples, as can be seen from the narrower shoulders of the carbonyl CSA patterns in Figs. 2b and 2c. In order to determine the homogeneous contribution to this broadening, we performed transverse relaxation (T₂) measurements using a Hahn echo experiment, with results shown in Table 1. T₂ broadening would amount to ~500 Hz (~5 ppm), which is small compared to broadening observed in the experimental spectrum. The rest of the broadening is therefore inhomogeneous in nature, a more detailed discussion of which will follow below.

2D measurements

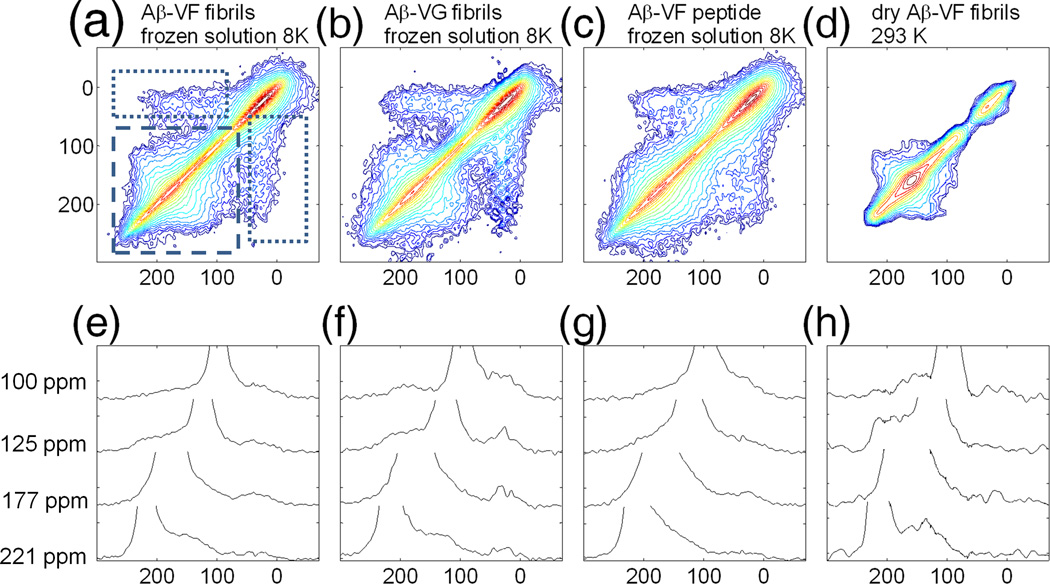
2D ¹³C-¹³C exchange spectra with a mixing time of 2.5 s are shown in Fig. 3 for frozen fibril solutions, non-fibrillar Aβ-VF in frozen solution, and dry fibrils at room temperature. The dashed square in Fig. 2a indicates the region of the 2D spectra where off-diagonal signal from carbonyl-carbonyl exchange is located. Additionally, some exchange between the Ala30 methyl carbon and the carbonyl sites shows up, marked by a dotted rectangle in Fig. 3a. 2D patterns in Figs. 3a–d, as well as the 1D slices shown in Figs. 3e–h, are clearly different from one another, suggesting structural differences.

Fig. 3.

2D ¹³C-¹³C exchange spectra obtained for various samples, exchange time in all experiments τ_exchange=2.5 s, the lowest contour in 2D plots is drawn at 6σ – standard deviation of noise in experimental spectrum. Each next level height is incremented by a factor of 1.3. a) Aβ-VF fibrils in frozen solution at 8 K, spectrum accumulation time ~4 hr with DNP enhancement. Dashed rectangle encloses the area of carbonyl-carbonyl correlation; dotted rectangle encloses the area of carbonyl-methyl carbon correlation; b) Aβ-VG fibrils in frozen solution at 8 K, spectrum accumulation time ~4 hr with DNP enhancement; c) Aβ-VF peptide in frozen solution at 8 K, spectrum accumulation time ~6 hr with DNP enhancement; d) dry Aβ-VF fibrils at room temperature, spectrum accumulation time ~ 4 days. ; e),f),g),h) represent slices made at specified values of chemical shifts in 2D plots a),b),c),d) respectively.

The samples used in this work represent different limiting cases. Aβ-VF and Aβ-VG fibrils are known to be well structured, and both the Val18-Phe19 and Val24-Gly25 segments of Aβ_1–40 should have well-defined ϕ and ψ angles. In these samples, exchange occurs between two sequential carbonyls within one Aβ_1–40 molecule, and possibly also between neighboring Aβ_1–40 molecules. Structural models of Aβ_1–40 fibrils [45, 46] (PDB accession codes: 2LMN,2LMO,2LMP,2LMQ) indicate the same orientation of carbonyl moieties in adjacent chains, due to the translational symmetry of their in-register parallel β-sheet structures. For this reason, CSA tensors of neighboring molecules have nearly identical orientation, so that intermolecular exchange does not contribute to the observed 2D exchange patterns. The observed 2D patterns arise only from exchange between sequential carbonyl ¹³C labels within one molecule.

In contrast, the sample of non-fibrillar Aβ-VF in frozen solution was prepared in a way that should produce a more conformationally disordered state of Aβ_1–40. For this sample, we expect that the ϕ and ψ angles are not well defined and may vary over a wide range. Although some evidence for oligomer formation under similar conditions has been reported [47], there is no evidence that those oligomers are well structured in the Val18-Phe19 segment. Additionally, no information is available concerning the observability of intermolecular exchange, even if Aβ_1–40 is not monomeric.

Simulation of 2D ¹³C-¹³C exchange spectra

The 2D ¹³C-¹³C exchange spectra report on the relative orientation of CSA tensors of two sequential ¹³C-labeled carbonyl sites, which can be described by a set of three Euler angles (α,β,γ). We assume that the carbonyl CSA tensor has a fixed orientation with respect to the peptide linkage frame. Typically σ_zz (the most upfield CSA component) makes a 5–10° angle with the direction of CO bond and σ_yy is perpendicular to the peptide plane, as shown in Fig. S3 [48, 49]. Given that variations in bond lengths and angles are small, and that the angle ω about the peptide bond is close to 180°, the set of three angles (α,β,γ) can be replaced by only two angles (ϕ,ψ) to describe the relative tensor orientations. Therefore, 2D exchange spectra carry information on peptide backbone torsion angles ϕ and ψ. By comparing the experimental 2D spectrum with simulated 2D spectra for various ϕ,ψ values, the correct ϕ and ψ values can in principle be found. Fig. S4 shows a variety of 2D spectra generated by our simulation program (vide infra) in a wide range of dihedral angles. Several ϕ,ψ pairs have quite similar 2D spectra, as illustrated by Fig. S4, which plots the root-mean-squared deviation between simulated 2D spectra for variable angles ϕ,ψ and the simulated 2D spectrum for fixed values ϕ₀,ψ₀. The similarity of 2D spectra for different choices of ϕ and ψ generally prevents determination of unique values. However, the experimental 2D exchange spectra are expected to place restrictions on the possible ϕ and ψ values, which can be combined with structural restraints from other sources.

Our simulation program calculates pairs of carbonyl ¹³C NMR frequencies for every possible direction of the magnetic field, given certain ϕ and ψ angles. The frequency of the first carbonyl for a particular field direction is:

$${\nu }_1=n_x^2{\sigma }_{xx}^{(1)}+n_y^2{\sigma }_{yy}^{(1)}+n_z^2{\sigma }_{zz}^{(1)}$$ (1)

where n⃗ = (n_x,n_y,n_z) is the unit vector in the direction of the magnetic field (in the CSA principal axis system of the first carbonyl site), and σ_xx⁽¹⁾, σ_yy⁽¹⁾, and σ_zz⁽¹⁾ are the CSA principal values. The frequency of the second carbonyl can also be calculated in a similar manner by replacing n⃗ by the magnetic field direction transformed into the principal axis system of the second CSA tensor: n⃗′ = R(ϕ,ψ)n⃗, where R(ϕ,ψ) is the transformation matrix. The frequency of the second carbonyl is then:

$${\nu }_2=n_x^{\prime 2}{\sigma }_{xx}^{(2)}+n_y^{\prime 2}{\sigma }_{yy}^{(2)}+n_z^{\prime 2}{\sigma }_{zz}^{(2)}$$ (2)

In order to simulate properly the exchange spectra, one has to account for the degree of exchange at each field direction. The theory suggests that the rate of spin exchange is given by [5, 50, 51]:

$$k_{exch}=d^2(\theta ){\int }_0^{\infty }d\tau \text{Re}[F_1(\tau )F_2^{-}(\tau )]$$ (3)

where $d(\theta )=\frac{1}{2}\frac{{\gamma }_1{\gamma }_2}{r^2(1-3{\text{cos}}^2\theta )}$, F_i(τ) is the free induction decay (FID) signal from spin i without proton decoupling, normalized to F_i(0) = 1, r is the distance between the two ¹³C labels (which is a function of the ϕ angle, assuming fixed bond lengths and angles, and ω = 180°), and θ is the angle between the ¹³C-¹³C internuclear vector and the magnetic field direction. The integral in Eq. (3) can be rewritten in terms of the spectral overlap integral using Parceval's theorem, giving:

$$k_{exch}=\frac{d^2(\theta )}{2\pi }{\int }_{-\infty }^{\infty }d\omega \text{Re}[G_1(\omega )G_2^{-}(\omega )]$$ (4)

Where G_t(ω) is the spectrum of spin I, normalized to ${\int }_{-\infty }^{\infty }d\omega G_1(\omega )=2\pi$. The spin exchange is driven by the dipolar interaction between ¹³C spins. However, the ¹³C NMR frequencies fluctuate, and the dipolar interaction is able to drive the transfer only when the frequencies are almost the same (i.e., Δω < d, where Δω is the instantaneous frequency difference). The overlap integral shows how likely is the coincidence of frequencies of different spin packets.

For a proper representation of off-diagonal intensities in the simulated 2D spectra, it is crucial to take into account the time-dependence of the intensity:

$$l_{1-2}(\tau )~\frac{1}{2[1-\text{exp}(-k_{exch}{\tau }_{exchange})]}$$ (5)

The simulation program uses Eq. (5) as the weighting factor for intensity at positions (ν₁, ν₂) and (ν₂, ν₁) in the 2D exchange spectrum. The exchange rate in Eq. (5) has a rather strong dependence on field direction relative to the peptide molecule. For instance, molecules for which the internuclear vector makes the magic angle with the magnetic field will not contribute to off-diagonal intensity, due to a vanishing dipolar coupling.

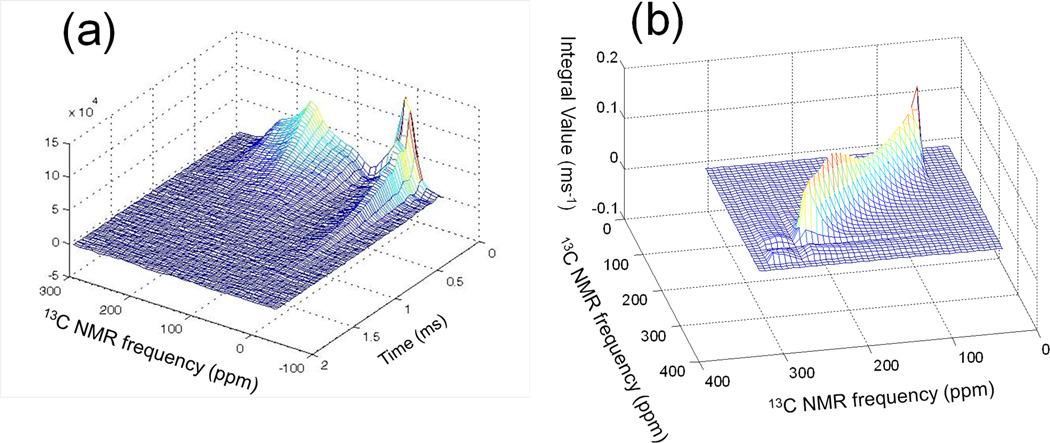
The spectral overlap integral in Eqs. (3) (or Eq. (4)) can be approximated from experimental data, through measurements of the signal decay (in the absence of proton decoupling) as a function of the ¹³C chemical shift, using the pulse sequence in Fig. 1b. Experimental data for dry Aβ-VF fibrils at room temperature are shown in Fig. 4a. For each chemical shift, the experimental signal decay was fit with a stretched exponential function a exp(−br^c), providing a very good fit to the data. The best-fit stretched exponential functions at each ¹³C chemical shift were used for evaluation of the integrals in Eq. (3). Fig. 4b shows the calculated overlap integral as a function of ν₁ and ν₂ for dry Aβ-VF fibrils at room temperature. As expected, the strongest overlap occurs for spin packets with closest frequencies, giving rise to a ridge along the diagonal, while the spin packets with very different frequencies overlap poorly, yielding a low value for the overlap integral. The ridge along the diagonal has varying height, which stems from a difference of transverse decay rates for various chemical shifts. This is not surprising, since spin packets corresponding to various chemical shifts have different local magnetic field environments.

Fig. 4.

Transverse relaxation decay and overlap integral determined for a sample of dry Aβ-VF fibrils at room temperature. a) Transverse relaxation measurement as a function of pulse delay recorded using the echo sequence shown in Fig. 1b; b) Overlap integral determined from transverse relaxation experiment on dry Aβ-VF fibrils at room temperature; $l_{12}={\int }_0^{\infty }d\tau \text{Re}[F_1(\tau )F_2^{-}(\tau )]$, where (1,2) are indices for spin packets with frequencies (ν₁,ν₂)

Except at the outer edges of the CSA patterns, signals at each ¹³C chemical shift include contributions from many different field directions (and from both carbonyl sites). Therefore, our use of experimental data as in Fig. 4a to evaluate overlap integrals for individual molecular orientations is an approximation. However, since carbonyl ¹³C nuclei have no directly-bonded protons, the experimental signal decays under the pulse sequence in Fig. 1b are due to long-range couplings to many protons. For this reason, we expect signal decays for each chemical shift value not to have a strong dependence on field direction.

Using a similar analysis we can explain the observation of polarization exchange between ¹³C labels at the Ala30 methyl site and the carbonyl sites. We estimate the characteristic transverse dephasing time of methyl signals from Fig. 4a as T₂~100 us, thus making homogeneous linewidth a factor of ~10 bigger compared to carbonyls. The value of overlap integral for a methyl-carbonyl pair can be estimated using a value of the integral for carbonyls with the same frequencies (I_{carb<−>carb}~0.1 ms⁻¹ as shown in Fig. 4b), taking into account difference in methyl linewidth we get I_{carb<−>methyl}~ I_{carb<−>carb} /10~0.01 ms⁻¹. The Aβ fibrils structural model (PDB accession code: 2LMP) features the closest distance of ~8.5 Å between Ala30 methyl group and the closest Phe19 carbons, allowing to estimate the exchange rate constant using eq. (4) as k_exch~0.1 s⁻¹. Therefore even within 2.5 s mixing time some noticeable exchange between methyl of Ala30 and carbonyl carbons takes place.

Comparisons of experimental and simulated 2D ¹³C-¹³C exchange spectra

2D exchange spectra, including the effects of incomplete exchange as described above, were calculated for a series of ϕ,ψ angles. One-bond ¹⁴N coupling to ¹³C was included by adjusting the effective ¹³C CSA tensors accordingly for each of the three ¹⁴N spin states of the two carbonyl sites and summing the resulting nine 2D exchange spectra. 2D frequency points were binned into a 2D frequency grid for plotting and comparison with experimental 2D spectra. Gaussian broadening in both dimensions was done after the main calculation was performed, with the amount of broadening adjusted for each spectrum individually judging by the width of ¹³C spectrum in the diagonal slice of the experimental 2D spectrum. For each simulated dataset, the reduced ${\chi }_{red}^2(\varphi ,\psi )$ characterizing the quality of fit to the experimental 2D spectrum was calculated as [52]:

$${\chi }_{red}^2(\varphi ,\psi )=\sum _t^N\frac{{(\lambda S_t(\varphi ,\psi )-E_t)}^2}{N{\sigma }^2}$$ (6)

where S_i and E_i are values of simulated and experimental data at the ith point of the 2D grid, consisting of N points (out of a total of 128×128=16384 points, N=1431 points from above the diagonal were chosen), λ is the scaling factor, and σ² is the mean squared noise in the experimental data. The scaling factor λ providing the minimal ${\chi }_{red}^2(\varphi ,\psi )$ was calculated as $-\frac{{\sum }_t^N{E}_t{S}_t}{{\sum }_t^N{S}_t{S}_t}$. Since the diagonal of the experimental spectrum contains contributions from natural abundance signals, only points with |ν₁−ν₂| > 3 kHz were included in Eq. (6). Ideally, a good fit to the experimental data is indicated by ${\chi }_{red}^2\approx 1$. In fact, as discussed below, minimum values of ${\chi }_{red}^2$ were significantly larger, due to various sources of systematic errors.

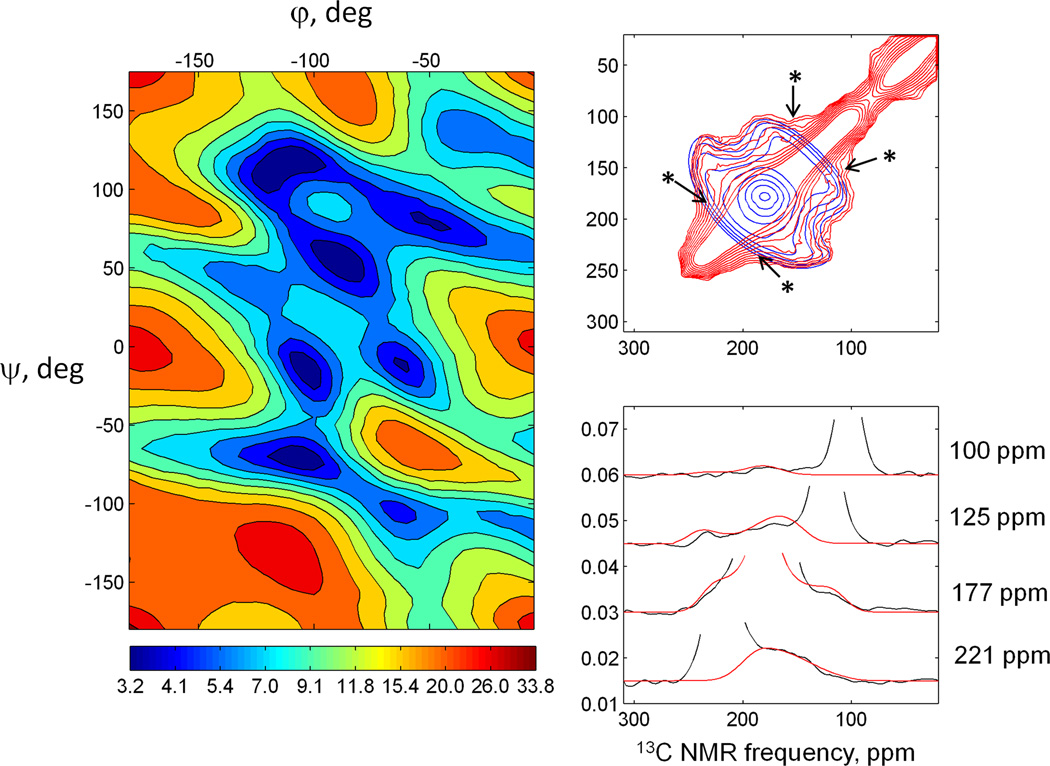
The 2D exchange spectrum of dry Aβ-VF fibrils with mixing time of τ_exchange = 2.5 s was used for benchmark calculations. Principal values of the carbonyl CSA tensor were taken from the diagonal of the experimental 2D spectrum. Since we cannot resolve the CSA patterns of the two labeled carbonyl sites, we assumed their CSA principal values to be equal in the simulation. Previous structural models of two-fold symmetric and three-fold symmetric Aβ_1–40 fibrils [45, 46] show that Val18 and Phe19 are located in a β-strand. Therefore the ϕ,ψ angles of Phe19 are expected to be in the β-strand region (ϕ ≈ −130° ± 20°, ψ ≈ 130° ± 20°). The ${\chi }_{red}^2(\varphi ,\psi )$ plot in Fig. 5a exhibits several minima. However, since we know that Phe19 is in a β-strand, the set of angles ϕ,ψ = −110°,120° is most relevant. The best-fit 2D spectrum with these angles is presented in Fig. 5b. A plot containing 1D slices from the 2D spectrum (Fig. 5c) shows how well the fitting with a single set of ϕ,ψ angles represents the experimental data. The minimum value of ${\chi }_{red}^2$ is about 3.8 in this case.

Fig. 5.

a) ${\chi }_{red}^2(\varphi ,\psi )$ plot for the spectrum of dry Aβ-VF fibrils; b) the best fit 2D pattern with (ϕ,ψ) = (−110°,120°) (in blue), overlaid onto experimental spectrum (in red), asterisks mark the features which could not be reproduced by simulations with a single set of (ϕ,ψ); c) slices made through experimental and best fit 2D patterns at various chemical shifts 221, 177, 125, 100 ppm.

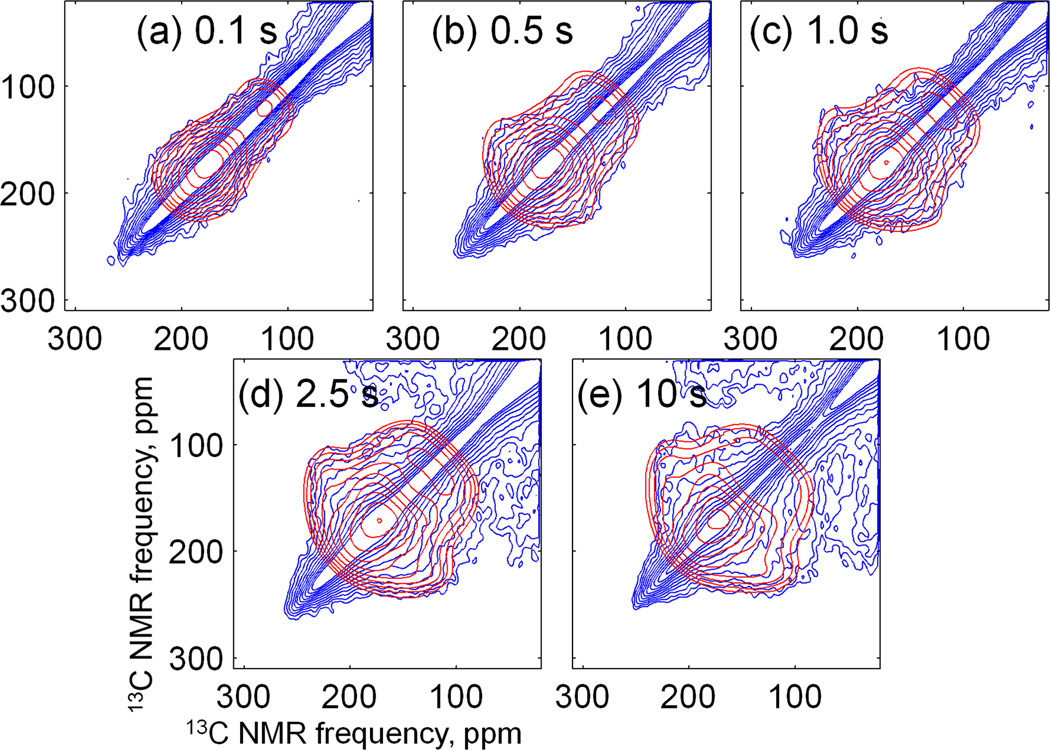
The importance of including the effects of incomplete exchange is demonstrated in Fig. 6, which shows experimental DNP-enhanced 2D spectra of Aβ-VF fibrils in frozen solution with mixing times τ_exchange from 0.1 s to 10 s. Even a 10 s mixing time does not result in a complete exchange, and intensity variations due to the orientation dependence of the ¹³C-¹³C dipolar interaction are still present. This fact was confirmed by simulations, where the experimental 2D spectrum with τ_exchange = 2.5 s was attempted to be fit by simulations with complete exchange. The agreement between simulations and experiment was rather poor (simulated data not shown).

Fig. 6.

Dependence of 2D exchange pattern on the exchange time for Aβ-VF fibrils in frozen solution. a) exchange time τ_exchange=0.1 s ; b) τ_exchange =0.5 s; c) τ_exchange =1.0 s; d) τ_exchange =2.5 s; e) τ_exchange =10 s. Blue contours – experimental data, red contours – simulations using τ_exchange = 2.5 s.

In order to fit the experimental 2D spectra in Fig. 6, σ_xx and σ_yy values were determined from the diagonal of the 2D spectra. Since the σ_zz value was obscured by other signals (see above), the total width Δ=(σ_xx − σ_zz) of the carbonyl CSA pattern was taken from the 1D spectrum of dry fibrils at low temperature (Fig. 2b) and σ_zz set equal to σ_xx −Δ. Fitting was performed for each τ value individually. The resulting ${\chi }_{red}^2(\varphi ,\psi )$ plots are shown in Fig. S5. By averaging the ${\chi }_{red}^2(\varphi ,\psi )$ plots for all values of τ, another plot was generated which allowed us to find the ϕ,ψ values that provide the best fit to the full set of 2D exchange spectra in Fig. 6. The resulting ${\chi }_{red}^2(\varphi ,\psi )$ plot is shown in Fig. 7a. Calculated 2D spectra as a function of τ_exchange, using ϕ,ψ = −110°,140° (values that correspond to the β-sheet region minimum of ${\chi }_{red}^2(\varphi ,\psi )$ in Fig. 7a), are superimposed on the experimental 2D spectra in Fig. 6. Overall agreement is satisfactory. It is especially noteworthy that the simulations, using the simple theoretical expression for the exchange rate in Eq. (3) and the experimentally-derived overlap integrals, accurately reproduce the growth of off-diagonal intensity with increasing τ_exchange.

Fig. 7.

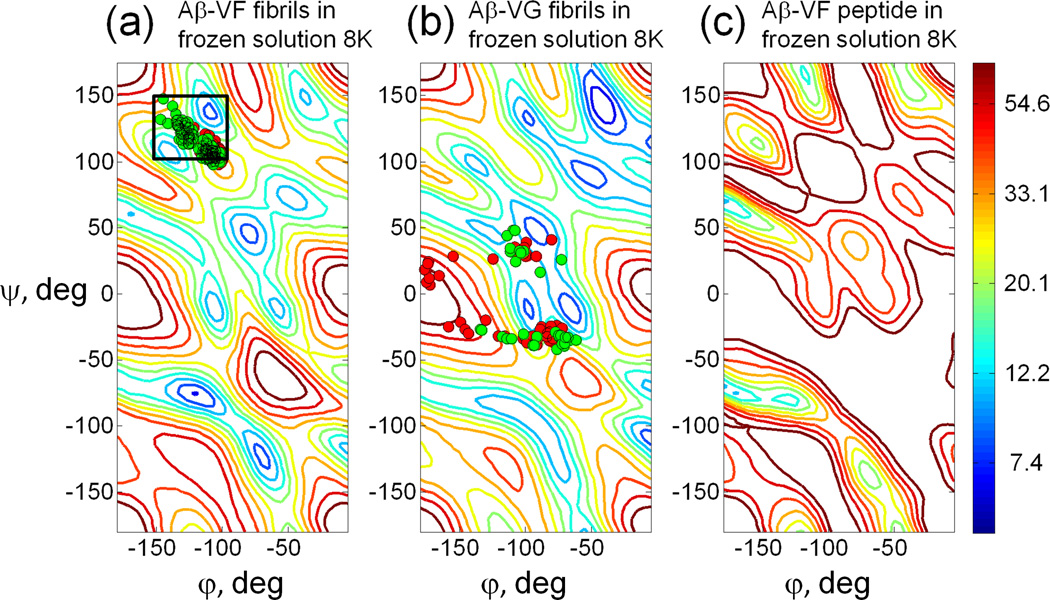
${\chi }_{red}^2(\varphi ,\psi )$ plots for three cases a) Aβ-VF fibrils in frozen solution at 8 K obtained by fitting exchange spectra with various τ_exchange altogether; b) Aβ-VG fibrils in frozen solution at 8 K obtained by fitting exchange spectra with τ_exchange = 2.5 s ; c) Aβ-VF peptide in frozen solution at 8 K obtained by fitting exchange spectra with τ_exchange = 2.5 s. Scattered markers in plot (a) and (b) denote (ϕ,ψ) angles obtained from various structural models for F19 and G25 respectively: red-three-fold symmetric positive stagger 2LMP, green – three-fold symmetric negative stagger 2LMQ. Black rectangle in plot (a) marks the range of (ϕ,ψ) angles for Phe19 in Aβ-fibrils as predicted by TALOS+ program.

Fig. 7b shows the ${\chi }_{red}^2(\varphi ,\psi )$ plot that results from fitting the experimental DNP-enhanced 2D spectrum of Aβ-VG fibrils in frozen solution. Although the position of some minima in the ${\chi }_{red}^2(\varphi ,\psi )$ plots in Figs. 7a and 7b are similar, the precise positions of minima and ${\chi }_{red}^2(\varphi ,\psi )$ values at those points are different. Similar locations for minima arise, because the patterns for some (ϕ,ψ) angle pairs may be similar to other patterns as illustrated in Fig. S6.

Fig. 7c shows the ${\chi }_{red}^2(\varphi ,\psi )$ plot that results from fitting the experimental DNP-enhanced 2D spectrum of non-fibrillar Aβ-VF peptide in frozen solution to simulations with single ϕ,ψ values. In this case, minimum values of ${\chi }_{red}^2(\varphi ,\psi )$ are larger than for the fibril samples, as expected if the peptide is more conformationally disordered at Val18-Phe19, so that the assumption of single torsion angle values is invalid.

Discussion

We observe a very clear 9 ppm shift downfield for the σ_yy component and 5 ppm upfield for the σ_zz component upon cooling of dry fibrils. The accuracy for determining the σ_zz component is somewhat limited due to overlap with aromatic natural abundance nuclei, but σ_yy has little overlap with other nuclei. The change of carbonyl ¹³C CSA principal values upon cooling apparently reflects the fact that at room temperature a significant amount of molecular motion affects the observed chemical shifts, possibly including librations of the whole peptide plane [53]. Such librations of the CSA tensor should not affect the isotropic chemical shift value. In our experiments we also observed a 2 ppm downfield shift in isotropic chemical shift upon cooling the sample of dry amyloid fibrils. Freezing out of stretching and bending vibrations may result in a change of the isotropic shift. This idea is indirectly supported by a recent computational study [54], which demonstrated that including corrections due to molecular motions on picosecond and microsecond time scales improves the accuracy of ¹³C chemical shift calculations for a crystalline tripeptide at room temperature. Changes to carbonyl CSA values might possibly be due to a temperature-dependent structural change, but we believe such changes to be minor. For example, it is well established by our previous experiments on Aβ_1–40 and other amyloid fibrils that rapid freezing in liquid nitrogen followed by lyophilization does not change their molecular structures significantly. A change of the apparent isotropic chemical shift may result from a change in magnetic susceptibility of the stainless steel cryostat and transfer line components upon cooling. Stainless steels of various grades are known to change their volume magnetic susceptibility upon cooling from room temperature to 4.2 K by a factor of Δχ=2–5×10⁻³=2000–5000 ppm [55]. However, it is hard to discriminate experimentally the physical mechanism mentioned before from this instrumental artifact.

The room temperature carbonyl CSA pattern has significant broadening (~2.8 kHz full width at half maximum as determined from the diagonal slice in the 2D exchange spectrum), which is largely due to the dipolar interaction between carbonyl ¹³C and ¹⁴N of the neighboring amide[49]. The unresolved triplet of lines should produce on average ~1.8 kHz broadening. Additionally, in processing of room temperature 2D exchange spectra, 1 kHz Gaussian broadening in both dimensions was applied.

At low temperatures under DNP conditions, the broadening due to ¹³C-¹⁴N coupling is complemented by other factors. Static dipolar interactions with deuterons of solvent should account for ~0.4 kHz, and small contributions may come from imperfect decoupling, intrinsic disorder of the sample, and slight variation in CSA tensor principal values of the two labeled sites. Our 1D spectra of frozen solution samples demonstrate a small contribution of homogeneous broadening (approximately 500 Hz in Aβ_1–40 fibril samples doped with DOTOPA-TEMPO) to the overall broadening of the ¹³C powder. Assuming uniform distribution of polarizing agent molecules over the sample volume, the broadening due to static interaction with unpaired electron spins amounts to ~440 Hz for [DOTOPA−TEMPO]=6.6 mM. Also, in processing of 2D spectra, a Gaussian broadening of 0.5 kHz was applied in both dimensions. All together these factors account for the ~3.6 kHz FWHM line broadening observed in experiments.

The build-up rates for DNP-enhanced ¹H NMR signals are smaller than those of cross-polarized ¹³C NMR signals in fibril samples in frozen solution. This most likely points to the effects of a relatively short intrinsic ¹H T₁ of fibrils, as can be seen from Table 1. While dry fibrils at 8 K have T₁ = 4.6 s, the bulk protons in glycerol/water solution have T₁ values of hundreds of seconds at 8 K in the absence of paramagnetic doping [36]. The observed difference in ¹H and ¹³C build-up rates could also reflect an affinity of the hydrophobic DOTOPA-TEMPO molecules for the fibrils. Our attempts to work with a dry sample containing only fibrils and DOTOPA-TEMPO (data not shown) failed because no significant DNP enhancements were obtained. A similar effect was observed previously in a solvent-free DNP study of a nitroxide labeled decapeptide [56].

The value of signal-to-noise (S/N) in a given measurement time represents well the sensitivity of an experiment. Relative to room-temperature measurements, our DNP-enhanced ¹³C NMR measurements at 8 K have a factor of ~750 signal gain in each scan, provided both by the DNP enhancement (ε_DNP ~ 20) and the Boltzmann factor (ε_Bolz ~ 37.5). This large enhancement produces a very large acceleration of experiments in frozen solution at low temperature. As an example, the 2D ¹³C-¹³C exchange spectrum of 3.5 mg of Aβ-VF fibrils in frozen solution presented in Fig. 3a was acquired in 4 hr, while the 2D exchange spectrum of 31 mg of dry Aβ-VF fibrils at room temperature in Fig. 3d was acquired in 4 days, the final 2D spectrum at room temperature has about 2.5 times worse signal-to-noise. The duration of one scan in the sequence was 3.5 s for room temperature measurements and 18.5 s for measurement at 8 K.

The overall carbonyl ¹³C CSA width is about 15 kHz at 9.39 T, while line widths under MAS for fibril samples are generally ~100 Hz. The line broadening for processing room temperature MAS experiments is usually ~50 Hz, while in our low-temperature measurements we used ~500 Hz, resulting in ~3.1 smaller root-mean-squared noise in the low-temperature measurements. Based on that DNP-enhanced static ¹³C NMR measurements at 8 K produce overall ~16 times greater S/N in one scan than MAS near room temperature.

On the other hand, structural information from CSA tensor orientations is lost under rapid MAS, but can be recovered by using relatively slow MAS. Previously, 2D exchange experiments under conditions of slow MAS were employed for obtaining relative orientations of CSA tensors of neighboring carbonyls [57, 58]. There the intensity is split among several sidebands. For example ~5 intense sidebands are observed at 2.5 kHz MAS frequency. This means that 1D static NMR with DNP at 8 K has ~80 times higher S/N compared to slow MAS measurements at room temperature in one scan. A 2D CSA/CSA correlation experiment under slow MAS requires shorter mixing times so that the duration of one scan determined by the recycle delay and the exchange time is ~1 s. At 8 K our measurements require 12–16 s for the recycle delay and 2.5 s for the exchange period. Still, all the mentioned factors lead to an overall sensitivity gain for DNP-enhanced static ¹³C NMR measurements at 8 K compared to room temperature MAS measurements by a factor of ~20.

Fits to the experimental data in Figs. 5 and 7 have ${\chi }_{red}^2(\varphi ,\psi )>1$, indicating discrepancies between experimental and simulated data larger than the noise in the experimental spectra. Several sources of discrepancy (i.e., systematic errors) may contribute. First, uncertainties in the carbonyl CSA tensors may be significant. Our simulations assume that the CSA tensors of the two labeled carbonyls have the same principal values. Solid state NMR measurements on microcrystalline protein GB1 by Wylie et al. have revealed a range of variation for carbonyl CSA principal values [59]. While the σ_xx and σ_zz components have almost constant values of 240 ppm and 100 ppm for many residues, the σ_yy component varies from 180 ppm to 200 ppm. Variation in the σ_yy component depends on residue type and secondary structure. In our measurements, the CSA principal values were determined from 1D line shapes, which do not allow the principal values of individual sites to be resolved. In frozen solutions, the carbonyl σ_zz value cannot be determined directly due to overlap with other ¹³C signals, and must be estimated from other data. In addition, our simulations assume a standard CSA tensor orientation with respect to the peptide linkage frame. However, this orientation has slight uncertainty for the direction of the σ_yy component, which varies over 10° in previous room-temperature measurements [48, 49]. The assumption that the σ_zz direction is strictly perpendicular to the peptide plane may not be precisely accurate, either. We are not aware of measurements which would precisely define the orientation of CSA tensor in the molecular frame at cryogenic temperatures.

Second, our analysis assumes that ϕ and ψ angles have unique values. Distributions of ϕ and ψ angles may arise either from local conformational disorder or from Aβ_1–40 fibril polymorphism. In the case of Aβ-VF, structural models derived from solid state NMR data [45, 46, 60] indicate that the Val18-Phe19 segment has a β-strand conformation in all polymorphs. Variations in ϕ and ψ are therefore expected to be ±15° or less. Examination of simulated 2D exchange spectra indicates that such variations could produce values of ${\chi }_{red}^2(\varphi ,\psi )$ as large as ~5–10.

Other sources of systematic errors may include non-uniform cross-polarization of ¹³C spins across the carbonyl CSA pattern and imperfect baseline correction during data processing of the broad 2D spectra. Furthermore, as discussed above, our calculations of overlap integrals are based on experimental transverse relaxation measurements that provide information about time dependences of undecoupled ¹³C signals (or undecoupled line shapes) of individual spin packets. However, a particular spin packet comprises an ensemble of molecular orientations. The molecules belonging to this ensemble may have somewhat different local field environments, which may affect the experimental exchange rates.

Nonetheless, despite these sources of uncertainty, fits of the experimental 2D ¹³C-¹³C exchange spectra give useful estimates of the ϕ,ψ angles. Detailed structural models have been developed for Aβ_1–40 fibrils with two-fold symmetry and a "striated ribbon" morphology in TEM images (PDB files 2LMN and 2LMO, for models with opposite "staggering" of β-sheet contacts), and for fibrils with three-fold symmetry and a gradually twisted morphology, indicated by modulation of the apparent fibril diameter with a 120 nm period (PDB files 2LMP and 2LMQ) [45, 46]. The TEM images obtained for our Aβ-VF and Aβ-VG fibrils resemble the images of three-fold symmetric fibrils, though for some fibrils the twist is hardly visible, either due to a difference in staining or due to a different morphology. In Figs. 7a and 7b, ϕ,ψ values extracted from PDB files 2LMP and 2LMQ are superimposed on the ${\chi }_{red}^2(\varphi ,\psi )$ plots. Each PDB file contains atomic coordinates for 10 specific models, with 18 Aβ_1–40 molecules in each model. The dihedral angles were calculated for all molecules except those capping the structure, and the values of ϕ,ψ are displayed in Fig. 7. For Aβ-VF, the ϕ,ψ values extracted from the structural models occur in a tight cluster that falls onto a weak local maximum between two minima in ${\chi }_{red}^2(\varphi ,\psi )$ (Fig. 7a). Apparent disagreement between minima in ${\chi }_{red}^2(\varphi ,\psi )$ and ϕ,ψ values in the structural models may be due to systematic errors discussed above, imprecision in local conformations in the structural models, or possibly real structural differences between our Aβ-VF fibrils and the three-fold symmetric fibrils originally studied by Paravastu et al. [45]. For Aβ-VG, the ϕ,ψ values extracted from the structural models are scattered over a large range (Fig. 7b), indicating that the backbone conformation at Gly25 is not well constrained in these models. Some of these values fall near minima in ${\chi }_{red}^2(\varphi ,\psi )$, while others do not. One could potentially include the ${\chi }_{red}^2(\varphi ,\psi )$ plots shown in Fig. 7 as potential energy functions in a molecular modeling program, which would penalize the candidate structures based on the value of ${\chi }_{red}^2(\varphi ,\psi )$.

In developing the structural models in PDB files 2LMP and 2LMQ, predicted ϕ,ψ ranges from the TALOS+ program, derived from ¹⁵N and ¹³C chemical shifts, were used as restraints on the ϕ,ψ values of F19. The predicted ranges are indicated by the rectangle in Fig. 7a. This rectangle contains the minimum in ${\chi }_{red}^2(\varphi ,\psi )$ at ϕ,ψ = −110,140, indicating consistency between the TALOS+ predictions and the 2D ¹³C-¹³C exchange data. On the other hand, TALOS+ predictions for G25 were not included in the structure calculations for PDB files 2LMP and 2LMQ.

Overall, the work described above demonstrates the feasibility of static 2D ¹³C experiments under conditions of DNP and the possibility of extracting structural information (i.e., constraints on ϕ,ψ torsion angles) from 2D ¹³C-¹³C exchange spectra of proteins in frozen solution. In future experiments, measurements of this type can be used to obtain local conformational constraints for systems with unknown structures. Future applications to static NMR experiments on oriented proteins in aligned membranes also appear promising.

• DNP allows for rapid accumulation of 2D exchange spectra

• Samples with varying labeling and structure show distinct 2D patterns

• 2D exchange orientation dependence can be included into simulation

• Comparison with simulations reveals allowed ranges of backbone torsion angles