OKVAR-Boost: a novel boosting algorithm to infer nonlinear dynamics and interactions in gene regulatory networks

Abstract

Motivation: Reverse engineering of gene regulatory networks remains a central challenge in computational systems biology, despite recent advances facilitated by benchmark in silico challenges that have aided in calibrating their performance. A number of approaches using either perturbation (knock-out) or wild-type time-series data have appeared in the literature addressing this problem, with the latter using linear temporal models. Nonlinear dynamical models are particularly appropriate for this inference task, given the generation mechanism of the time-series data. In this study, we introduce a novel nonlinear autoregressive model based on operator-valued kernels that simultaneously learns the model parameters, as well as the network structure.

Results: A flexible boosting algorithm (OKVAR-Boost) that shares features from L₂-boosting and randomization-based algorithms is developed to perform the tasks of parameter learning and network inference for the proposed model. Specifically, at each boosting iteration, a regularized Operator-valued Kernel-based Vector AutoRegressive model (OKVAR) is trained on a random subnetwork. The final model consists of an ensemble of such models. The empirical estimation of the ensemble model’s Jacobian matrix provides an estimation of the network structure. The performance of the proposed algorithm is first evaluated on a number of benchmark datasets from the DREAM3 challenge and then on real datasets related to the In vivo Reverse-Engineering and Modeling Assessment (IRMA) and T-cell networks. The high-quality results obtained strongly indicate that it outperforms existing approaches.

Availability: The OKVAR-Boost Matlab code is available as the archive: http://amis-group.fr/sourcecode-okvar-boost/OKVARBoost-v1.0.zip.

Contact: florence.dalche@ibisc.univ-evry.fr

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

The ability to reconstruct cellular networks plays an important role in our understanding of how genes interact with each other and how this information flow coordinates gene regulation and expression in the cell. Gene regulatory networks (GRN) have the potential to provide us with the cellular context of all genes of interest, as well as with a means to identify specific subnetworks that are malfunctioning in a given disease state (Cam et al., 2004; Jesmin et al., 2010).

A diverse suite of mathematical tools has been developed and used to infer gene regulatory interactions from spatial and temporal high-throughput gene expression data (see Bansal et al., 2007; Markowetz and Spang, 2007 and references therein). A fair comparison for the relative merits of these methods requires their evaluation on benchmark datasets, which the DREAM (Dialogue for Reverse Engineering Assessments and Methods) project (Marbach et al., 2009) provided. It aims to understand the strengths and the limitations of various algorithms to reconstruct cellular networks from high-throughput data (Stolovitzky et al., 2007). In addition to the choice of the algorithm, network reconstruction heavily depends on the input data type used. Data that measure the response of the cell to perturbations—either by knocking out or silencing genes—are particularly useful for such reconstructions because they offer the potential to obtain a detailed view of cellular functions. The downside is that obtaining large-scale perturbation data is expensive and relatively few methods have been proposed in the literature to infer regulatory networks from such data due to computational challenges (Gupta et al., 2011; Yip et al., 2010).

Data from time-course gene expression experiments have the potential to reveal regulatory interactions as they are induced over time. A number of methods have been used for this task, including dynamic Bayesian networks (Morrissey et al., 2010; Yu et al., 2004), Granger causality models (see Shojaie and Michailidis, 2010b and references therein) and state-space models (Perrin et al., 2003; Rangel et al., 2004). The first set of methods is computationally demanding, while the latter two use linear dynamics, hence limiting their appeal. Other approaches are based on assumptions about the parametric nature of the dynamical model and resort to time-consuming evolutionary algorithms to learn the network (Sîrbu et al., 2010). Moreover, in spite of the rich collection of methods used to solve the topology and dynamics of GRNs, certain types of errors continue to challenge the modeling efforts, implying that there is still significant room for improvement (Marbach et al., 2010; Smet and Marchal, 2010).

This study makes a number of key contributions to the challenging problem of network inference based solely on time-course data. It introduces a powerful network inference framework based on nonlinear autoregressive modeling and Jacobian estimation. The proposed framework is rich and flexible, using penalized regression models that coupled with randomized search algorithms, and features of L₂-boosting prove particularly effective as the extensive simulation results attest. The models used require tuning of a number of parameters, and we introduce a novel and generally applicable strategy that combines bootstrapping with stability selection to achieve this goal.

2 MODEL AND METHODS

2.1 Nonlinear autoregressive models and network inference

Let 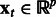denote the observed state of a GRN comprising p genes, with 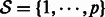. We assume that a first-order stationary model is adequate to capture the temporal evolution of the network state, which can exhibit nonlinear dynamics captured by a function 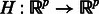; i.e. 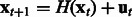, where 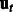is a noise term. The regulatory interactions among the genes are captured by an adjacency matrix A, which is the target of our inference procedure.

Note that for a linearly evolving network, A can be directly estimated from the data. However, in our setting, it can be obtained by averaging the values of the empirical Jacobian matrix J of the function H, over the whole set of time points. Specifically, denote by 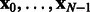the observed time series of the network state. Then, 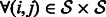, the empirical estimate of the Jacobian matrix of model H is given by

(1)

and an estimate of the adjacency matrix A of the network is given by 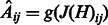where g is a thresholding function. Note that in the presence of sufficient number of time points (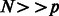) one can use the above posited model directly to obtain an estimate of A, provided that a good functional form of H is selected. However, the presence of more genes than time points makes the problem more challenging, which together with the absence of an obvious candidate functional form for H make a nonparametric approach an attractive option. Such an approach is greatly facilitated by adopting an ensemble methodology, where H is built as a linear combination of nonlinear vector autoregressive base models defined over overlapping subsets of genes (e.g. subnetworks). Let M be the number of subnetworks and (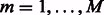) be the subset of genes that constitutes the m^th subnetwork. Each subnetwork has the same size k. We assume that H can be written as a linear combination of M autoregressive functions of the form 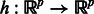such that

(2)

The paramater set 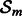defines the subspace of where h operates. This component-wise subnetwork approach is intended to overcome the intractability of searching in high-dimensional spaces and to facilitate model estimation. In our framework, subnetworks do not have any specific biological meaning and are allowed to overlap.

Efficient ways to build an ensemble of models include bagging, boosting and randomization-based methods such as random forests (Dietterich, 2000; Friedman et al., 2001). The latter two approaches have been empirically shown to perform well in classification and regression problems. In this study, we use an L₂-boosting type algorithm suitable for regression problems (Bühlmann and Yu, 2003; Friedman et al., 2001) enhanced with a randomization component where we select a subnetwork at each iteration. The algorithm sequentially builds a set of predictive models by fitting at each iteration the residuals of the previous predictive model. Early-stopping rules developed to avoid overfitting improve the performance of this algorithm.

Next, we discuss a novel class of base models.

2.2 A new base model

The ensemble learner is a linear combination of M base models denoted by h [Equation (2)]. Even though h works on a subspace of defined by 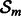, for the sake of simplicity we present here a base model 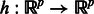that works with the whole set of genes, e.g. in the whole space . Here, we introduce a novel family of nonparametric vector autoregressive models called OKVAR (Operator-valued Kernel-based Vector AutoRegressive) (Lim et al., 2012) within the framework of Reproducing Kernel Hilbert Space (RKHS) theory for vector-valued functions. Operator-valued kernel-based models have been previously used for multitask learning problems (Micchelli and Pontil, 2005), functional regression (Kadri et al., 2010) and link prediction (Brouard et al., 2011).

OKVAR models generalize kernel-based methods initially designed for scalar-valued outputs, such as kernel ridge regression, elastic net and support vector machines, to vector-valued outputs. An operator (matrix)-valued kernel (as output space is , the operator is a linear application on vectors of and thus a matrix), whose properties can be found in Senkene and Tempel’man (1973), takes into account the similarity between two vectors of in a much richer way than a scalar-valued kernel, as shown next. Let 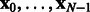be the observed network states. Model h is built on the observation pairs 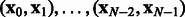and defined as

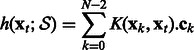(3)

where 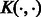is an operator-valued kernel and each 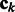() is a vector of dimension p. In the following, we will denote by 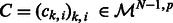, the matrix composed of the N – 1 row vectors 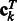of dimension p.

In this work, we define a novel matrix-valued kernel built on the Hadamard product of a decomposable kernel and a transformable kernel previously introduced in Caponnetto et al., 2008 (see details in the Supplementary Material): ,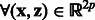

(4)

K depends on a matrix hyperparameter B that must be a positive semi-definite matrix. The term 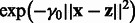is a classical Gaussian kernel that measures how a pair of states 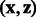are close. More interestingly, the term 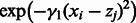measures how close coordinate i of state and coordinate j of state are, for any given pair of states 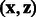.One great advantage of such a kernel is that it includes a term that reflects the comparison of all coordinate pairs of the two network states and does not reduce them to a single number. The matrix B serves as a mask, imposing the zeros. When b_ij is zero, the i-th coordinate of and the j-th coordinate of do not interact and do not play a role in the output of the model.

In other words, for a given gene 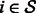, the output of the model writes as follows: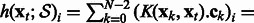

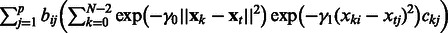
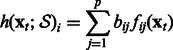(5)

Equation (5) shows that the expression level of gene i at time t + 1 is modeled by a linear combination of nonlinear terms 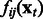that share parameter C. The function f_ij itself is a nonparametric function built from training data.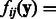 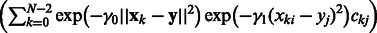. The function f_ij expresses the role of the regulator j on gene i. If b_ij equals 0, then gene j does not regulate gene i, according to the model. Matrices B and C need to be learned from the available training data. If B is fixed, C can be estimated using penalized least squares minimization as in (Brouard et al., 2011). However, learning B and C simultaneously is more challenging, as it involves a nonconvex optimization problem. We propose here to define B as the Laplacian of an undirected graph represented by an adjacency matrix W to ensure the positive semi-definiteness of B. Then, learning B reduces to learn W. In this work, we decouple the learning of W and C by first estimating W and then C.

2.3 OKVAR-Boost

The proposed algorithm is called OKVAR-Boost, as H models the temporal evolution between network states 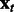with an L₂-boosting approach. As seen in Algorithm 1 and illustrated in Figure 1, it generates 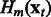, an estimate of 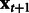at iteration m, and updates this estimate in a while-loop until an early-stopping criterion is met, or until the prespecified maximum number of iterations M is reached. In the OKVAR-Boost loop, 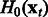is initialized with the mean values of the genes across the time points. The steps for estimating H in a subsequent iteration m are as follows: Step 1 computes the residuals 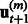for time points 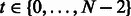. Computing the residuals in this step confers OKVAR-Boost its L₂-boosting nature. In Step 2, an early-stopping decision is made based on the comparison between the norms of the residuals and a prespecified stopping criterion ε. If the norms for all dimensions (genes) are less than ε, the algorithm exits the loop. In Step 3, a random subset 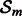of size k is chosen among the genes in 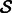, whose norm exceeds ε. This step constitutes the ‘randomization component’ of the algorithm. Step 4 uses the current residuals in the subspace to estimate the interaction matrix W_m and parameters 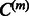. Subsequently, 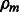is optimized through a line search. 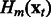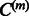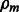The m^th boosting model is updated in Step 5 with the current W_m, and estimates. If the prespecified number of iterations M has not been reached, the algorithm loops back to Step 1. Otherwise, it exits the loop and estimates the adjacency matrix 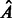by computing and thresholding the Jacobian matrix.

Fig. 1.

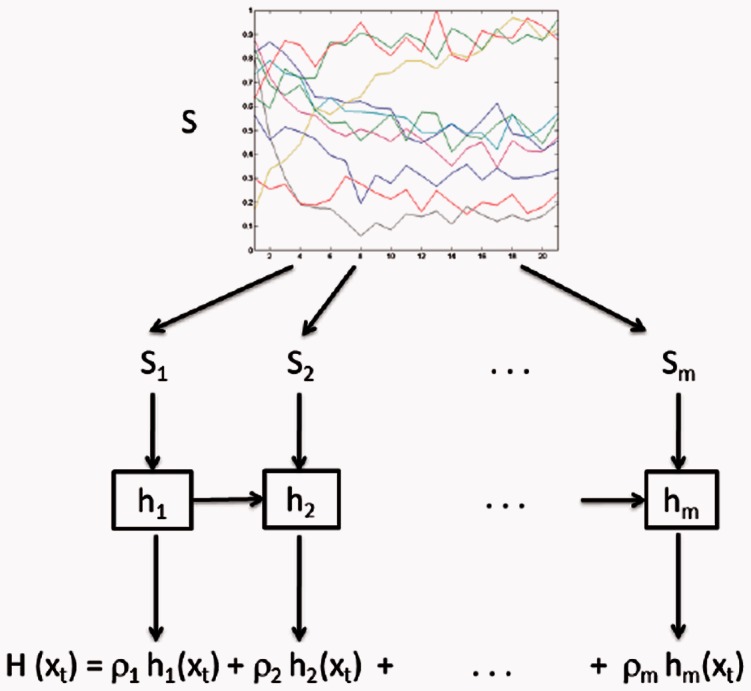
General scheme of OKVAR-Boost. The m^th learner is run on the residuals of the global model on a random subset of time series, denoted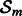

We next delineate how the interaction matrix W_m and model parameters 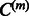and 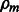are estimated from residuals in Step 4.

Algorithm 1 OKVAR-Boost.

Inputs:

 Network states: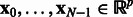

 Early-stopping threshold ε

Initialization:

 ,

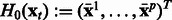
 Iteration m = 0, STOP = false

while 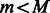and STOP = false do

 Step 0: Update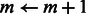

 Step 1: Compute the residuals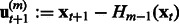

 Step 2: STOP: = true if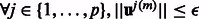

 if STOP = false then

  Step 3: Select 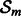, a random subset of genes of size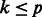

  Step 4: (a) Estimate the interaction matrix 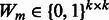from and compute B_m as the Laplacian of W_m, (b) estimate the parameters C_m and (c) estimate 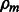by a line search.

  Step 5: Update the m^th boosting model: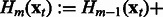

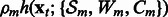
 end if

end while

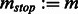
Compute the Jacobian matrix 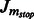of 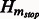across time points, and threshold to get the final adjacency matrix .

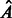2.4 Randomization and estimation of the interaction matrix

Combining features of random forests and boosting algorithms gave robust results in a previous study (Geurts et al., 2007). We use this approach and select, at each iteration m (Step 3) a random subset of genes denoted . Then, in (Step 4), we use partial correlation estimation, as a weak graph learner, on 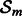to increase the robustness of the algorithm and reinforce its ability to focus on subspaces. The details of the statistical test for conditional independence based on partial correlations can be found in the Supplementary Material. Based on the matrix W_m resulting from this test, we define B_m as the Laplacian of W_m.

2.5 Autoregression using OKVAR

At each iteration m, an OKVAR model such as previously described in Equation (3) is defined to work in the k dimensional subspace associated with the subset 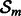. Denoted by 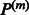the 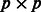diagonal matrix is defined as follows: 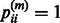if gene i belongs to 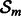, and 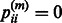otherwise. Formally,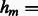 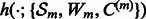has to be learnt from 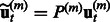instead of residuals 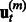. Then, we only need to complete Step 4(b) by learning parameters 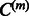. This estimation can be realized via the functional estimation of h_m within the framework of regularization theory, e.g. the minimization of a cost function comprising the empirical square loss and the square 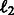norm of the function h_m, which imposes smoothness to the model. Moreover, our aim is 2-fold: we do not only want to get a final model H that fits the data well and predicts successfully future time points, but we also want to extract the underlying regulatory matrix from the model; therefore, the cost function to be minimized must also reflect this goal. Following Subsection 2.1, the adjacency matrix of the network A is estimated by the empirical Jacobian J(H), expressed in terms of the empirical Jacobian 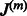of the base models h_m () using the observed data (not residuals): 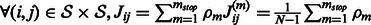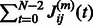where for a given time point t, the coefficients of the Jacobian, 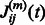, are given as follows:

The full expression of the instantaneous Jacobian when is chosen as the Gaussian matrix-valued kernel defined in Equation (4) is given in the Supplementary Material. Whatever is , when it is fixed, controlling the sparsity of the coefficients of will impact the sparsity of 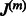and will avoid too many false-positive edges. Therefore, we add to the cost function previously discussed, an 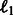term to ensure the sparsity of :

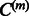(6)

The respective norms can be computed as follows:

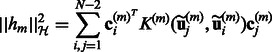and 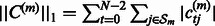. This regularization model combining 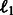and 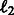penalties is known as the elastic net model (Friedman et al., 2001) and it has been shown that not only does it achieve sparsity like lasso penalized models, but also encourages grouping effects, which might be relevant in our case to highlight possible joint regulation among network variables (genes). We used a projected scaled subgradient method (Schmidt et al., 2009) to minimize the cost function.

3 IMPLEMENTATION

3.1 Data description

The performance of OKVAR-Boost was evaluated on a number of GRNs obtained from DREAM3 in silico challenges. Specifically, 4 and 46 time series consisting 21 time points corresponding, respectively, to size-10 and size-100 networks for Escherichia coli (2) and Yeast (3) were selected. The data were generated by simulating from a thermodynamic model for gene expression to which Gaussian noise was added. The multiple time series correspond to different random initial conditions for the thermodynamic model (Prill et al., 2010). The topology of the networks is extracted from the currently accepted E.coli and Saccharomyces cerevisiae GRNs, and exhibits varying patterns of sparsity and topological structure. Some summary statistics for the networks are presented in Supplementary Table S1. Yeast2 and Yeast3 have markedly higher average-degree, density and lower modularity for both size-10 and size-100 networks. Ecoli2 is seen to be different from Ecoli1 in that for size 10 is denser, less modular, has higher average-degree, whereas for size 100, these relations are reversed. Yeast1 is observed to be closer to the Ecoli networks for all three statistics.

In addition to these synthetic datasets, we applied OKVAR-Boost to two other datasets. The first deals with activation of T-cells (Rangel et al., 2004) and comprises 44 times series (replicates) for 58 genes. The second dataset comes from the In vivo Reverse-Engineering and Modeling Assessment (IRMA) experiment (Cantone et al., 2009), where a size-5 network was synthesized, with each gene controlling the transcription of at least another gene. Further, galactose and glucose are, respectively, used to switch on or off the network. In this study, we focus on time-series measurements (four switch-off series and five switch-on series) comprising 9 up to 20 time points.

3.2 Hyperparameters and model selection

Because the OKVAR-Boost algorithm depends on a number of tuning parameters, some of them were a priori fixed, with the remaining ones selected automatically with a new variant of stability criterion, appropriate for time series, called Block Stability. Let us first summarize the hyperparameters that we fixed a priori. They include a stopping criterion for the norm of the residual vector, set to 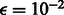, the size of random subnetworks k in Step 1 set to eight genes for size-10 networks, to 17 for size-100 networks, to six for T-cell and to four for IRMA (parameters based on a grid search) and in Step 4 the level of the partial correlation test is set to a conservative α = 5%. If the algorithm fails to find any significant interactions with the partial correlation test, the subnetwork is discarded and a new 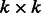subnetwork is randomly chosen. This procedure is repeated for a maximum of 100 iterations. In Step 5, the parameter of the Gaussian matrix-valued kernel 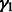Equation (4) is fixed to 0.2. As the role of the scalar Gaussian kernel of Equation (4) is not central in the network inference, 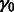is fixed to 0 in those experiments. For the other hyperparameters, we consider stability, which is a finite sample criterion that has been applied to select hyperparameters in various settings, such as clustering or feature selection in regression (Meinshausen and Bühlmann, 2010). The idea underlying stability-driven selection is to choose the hyperparameters that provide the most stable results when randomly subsampling the data. We propose a new selection criterion, called Block stability based on the block bootstrap. Block bootstrap resamples time series by consecutive blocks ensuring that each block of observations in a stationary time series can be treated as exchangeable (Politis et al., 1999). For the DREAM data, we chose a length of 12 and 15 time points for size 10 and size 100, respectively, and 7 for both the T-cell and IRMA datasets, while the number of pairs of block-bootstrapped subsamples was set to B = 20. We define the Block instability noted BIS for a pair of hyperparameters 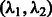by measuring how the two Jacobian matrices built from two models learnt from two different subsamples differ in average. The reader will find the expression of the BIS criterion in the Supplementary Material. When L time series are available, the criterion becomes 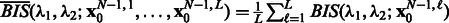. In the experiments, hyperparameters 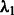and 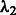were chosen as the minimizers of the block-instability criterion BIS when only a single time series was available and when multiple ones were provided.

3.3 OKVAR-Boost with multiple runs

As OKVAR-Boost residuals diminish rapidly, there is a risk that the potential regulators and their targets may not be fully explored by the random subnetwork procedure of the algorithm. To address this issue, the algorithm was run nRun = 10 times and a consensus network was built by combining the predictions from each run. Specifically, for each pair of nodes, the frequency with which the edge appears over multiple runs was calculated, thus yielding the final network prediction. If the frequency was above a preset threshold, the edge was kept, otherwise discarded.

3.4 Consensus network from multiple time series

In many instances, multiple (L) time series may be available, either because of multiple related initial conditions or due to biological and/or technical replicates. In this case, the procedure just needs to be repeated accordingly and the 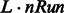obtained networks are combined as described above to provide a final consensus network. We set 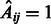if and only if 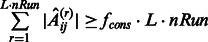, where 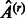is the estimated adjacency matrix for run number r and 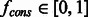is the consensus threshold level for edge acceptance.

When doing multiple runs, f_cons should be adjusted if prior knowledge about the size, density and modularity of the underlying network is available. In general, the larger the size of a biological network, the bigger are the combinatorial challenges for discovering true edges and avoiding false ones. Therefore, the consensus threshold should be set to smaller values for larger networks. For a fixed size, the threshold will depend on the density and modularity of the network. Denser and more modular networks have greater instances of co-regulation for certain genes, which lowers prediction accuracy for network inference algorithms (Marbach et al., 2010) and leads to a greater number of false positives. In our experience, lower consensus thresholds are also recommended for denser and more modular networks as well.

3.5 Network inference and evaluation

When ground truth is available for the network inference task, namely for simulated data from DREAM3 challenges and real data from the synthetic network IRMA, we evaluated the results according to the DREAM3 challenge assessment. In DREAM3 challenges, the target graph is directed but not labeled with inhibitions or inductions. The performance of the algorithm is assessed using the following standard metrics: the receiver operating characteristic curve (ROC), the area under ROC (AUROC) and the area under the precision-recall curve (AUPR). To extract the adjacency matrix from the Jacobian (see subsection 2.1), the hyperbolic tangent transformation applied to the normalized coefficients of the Jacobian was used (for a matrix Q, 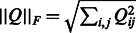is the Frobenius norm of Q): 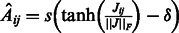, with 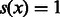if 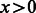and 0, otherwise and δ varying to get ROC and PR curves.

4 RESULTS

4.1 Numerical results for DREAM3 networks

Overall, the OKVAR-Boost algorithm succeeds in fitting the observed data and exhibits fast convergence. In Figure 2, results from the Ecoli2 networks (size 10 and size 100) are presented. Note that the algorithm is rich and flexible enough to have the mean squared error for genes diminishing fast toward zero in only 5–10 iterations. The performance of the OKVAR-Boost algorithm for prediction of the network structure is given in Tables 1 and 2 and Supplementary Table S3. The results show a comparison between the base learner alone when the true B is provided for DREAM3 size-10 networks (Table 1), boosting with multiple runs using a single time series and all the available time series. The base learner is an elastic-net OKVAR model learnt given the Laplacian of the true undirected graph and applied on the whole set 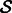of genes. The LASSO row corresponds to a classical linear least squares regression: 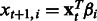, realized on each dimension (gene) 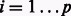subject to an 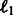penalty on the 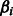parameters. An edge 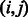is assigned for each nonzero 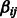coefficient. The LASSO was run on all the available time series and a final consensus network is built in the same fashion as delineated in section 3.4. The AUROC and AUPR values obtained strongly indicate that OKVAR-Boost outperforms the LASSO and the teams that exclusively used the same set of time-series data in the DREAM3 competition. The multiple-run consensus strategy achieved superior AUROC and AUPR results for all networks except for size-10 Yeast2. We particularly note that the OKVAR-Boost consensus runs exhibited excellent AUPR values compared with those obtained by teams 236 and 190. The consensus thresholds for multiple-run and bootstrap experiments were chosen taking into account network properties such as size, density, modularity, average-degree and topology. For size-10 networks, Yeast2 and Yeast3 have substantially higher density and average-degree suggesting lower consensus thresholds. In light of this information, we used a threshold of 50% for Ecoli1, Ecoli2, Yeast1, and 40% for Yeast2 and Yeast3 for multiple-run experiments. For size-100 networks, we made use of the prior information that Ecoli2 has a star topology composed of few central hubs that regulate many genes. Because it is more difficult to reconstruct such special modularities, one should expect to observe lower edge frequencies. Thus, a smaller consensus threshold would be appropriate. For the multiple-run experiments, we used 20% for Ecoli2 and 40% for all other networks.

Fig. 2.

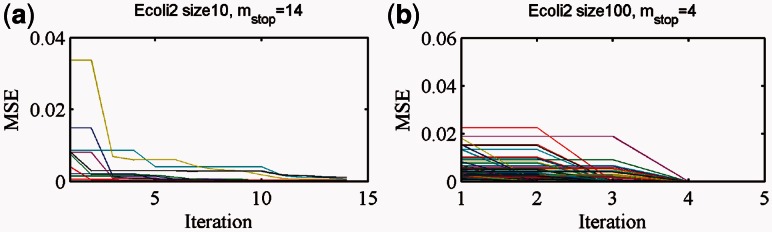
Mean squared error of OKVAR-Boost model for each gene using Ecoli2 datasets. (a) Size-10 Ecoli2 (b) Size-100 Ecoli2. The algorithm terminated after 14 and 4 iterations, respectively

Table 1.

AUROC and AUPR for OKVAR-Boost (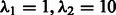 selected by Block Stability), LASSO, Team 236 and Team 190 (DREAM3 challenge) run on DREAM3 size-10 networks

Size-10	Ecoli1		Ecoli2		Yeast1		Yeast2a		Yeast3a
	AUROC	AUPR	AUROC	AUPR	AUROC	AUPR	AUROC	AUPR	AUROC	AUPR
OKVAR + True B	0.932	0.712	0.814	0.754	0.856	0.494	0.753	0.363	0.762	0.450
OKVAR-Boost (1 TS)	0.665 ± 0.088	0.272 ± 0.081	0.629 ± 0.095	0.466 ± 0.065	0.663 ± 0.037	0.256 ± 0.022	0.607 ± 0.049	0.312 ± 0.056	0.594 ± 0.072	0.358 ± 0.099
OKVAR-Boost (4 TS)	0.853	0.583	0.749	0.536	0.689	0.283	0.653	0.268	0.695	0.443
LASSO	0.500	0.119	0.547	0.531	0.528	0.244	0.627	0.305	0.582	0.255
Team 236	0.621	0.197	0.650	0.378	0.646	0.194	0.438	0.236	0.488	0.239
Team 190	0.573	0.152	0.515	0.181	0.631	0.167	0.577	0.371	0.603	0.373

Note: OKVAR-Boost results using one time series [OKVAR-Boost (1 TS)] (average ± standard deviations) and the four available time series [OKVAR-Boost (4 TS)] are from consensus networks. The numbers in boldface are the maximum values of each column.

^aConsensus thresholds for Yeast2 and Yeast3 are different due to their higher density and average-degree.

Table 2.

AUROC and AUPR for OKVAR-Boost (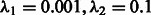 selected by Block Stability), LASSO and Team 236 (DREAM3 challenge) run on DREAM3 size-100 networks

Size-100	Ecoli1		Ecoli2a		Yeast1		Yeast2		Yeast3
	AUROC	AUPR	AUROC	AUPR	AUROC	AUPR	AUROC	AUPR	AUROC	AUPR
OKVAR-Boost	0.718	0.036	0.772	0.107	0.729	0.042	0.650	0.073	0.643	0.069
LASSO	0.519	0.016	0.512	0.057	0.507	0.016	0.530	0.044	0.506	0.044
Team 236	0.527	0.019	0.546	0.042	0.532	0.035	0.508	0.046	0.508	0.065

Note: All the results are obtained using the 46 available time series. The numbers in boldface are the maximum values of each column.

^aEcoli2 has a strong star topology, which suggests a different consensus threshold for this network.

A comparison between algorithms for size-100 networks (Table 2) shows that OKVAR-Boost again clearly outperforms Team 236, the only team that exclusively used time-series data for the size-100 challenge. It is noticeable that AUROC values for size-100 networks still remain high and look similar to their size-10 counterparts, while AUPR values in all rows have stayed lower than 10% except for size-100 Ecoli2. A similar decline is also observed in the results of Team 236. It can be seen that AUPR values can be impacted more strongly by the lower density of the size-100 networks, where the non-edges class severely outnumbers the edges class, rather than the choice of algorithm. Additionally, for such difficult tasks, the number of available time series may be too small to get better AUROC and AUPR. Although there is no information on the structure of team 236’s algorithm, its authors responded to the post-competition DREAM3 survey stating that their method uses Bayesian models with an in-degree constraint (Prill et al., 2010). This in-degree constraint may explain their particularly poor AUROC and AUPR performance for the high average-degree networks Yeast2 and Yeast3 (average-degree values in Supplementary Table S1). Team 190 (Table 1) reported in the same survey that their method is also Bayesian with a focus on nonlinear dynamics and local optimization. This team did not submit predictions for the size-100 challenge.

Interestingly, Supplementary Table S2 highlights that as expected, performance depends on the number of the training time series and that the use of all the provided time series allows to reach significant gains. This illustrates that the number of observations required to get good performance is related to the complexity of the dynamics in the state space. The optimal condition to use this nonparametric approach is to visit as many different initial conditions as possible. In practice, the user will also pay attention that the number of time points in a single time series is larger than the number of considered genes.

4.2 Results on IRMA datasets

OKVAR-Boost exhibits outstanding performance for the IRMA network (Supplementary Table S3). Specifically, for the switch-off series both AUROC and AUPR performance metrics exceed 80% (the inferred network is shown in Supplementary Fig. S1), while for the switch-on series they get a perfect score. The method clearly outperforms a Bayesian method using ordinary differential equations coupled with Gaussian processes (Äijö and Lähdesmäki, 2009) for the switch-on series and lags by a small margin for the switch-off series. The LASSO method gave fairly poor results.

4.3 Results on T-cell activation dataset

The reconstructed regulatory network using OKVAR-Boost is given in Supplementary Figure S2. The following hyperparameters were used: 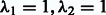and a threshold for the consensus network of 0.01. The resulting network contains 144 edges. As discussed in Rangel et al., 2004, the main functional categories involved in T-cell response are cytokines, apoptosis and cell cycle. Some important regulating and regulated genes include FYB, GATA3 and CD 9 (inflammation), CASP 7 and 8 (apoptosis) and CDC2 (cell cycle). All of them appeared in the reconstructed network. In addition, the algorithm identified CCNA2 involved in the cell cycle (Ody et al., 2000), SIVA involved in apoptosis (Gudi et al., 2006) and MKBNIA, which has been associated with T-cell immunodeficiency (Lopez-Granados et al., 2008), as key hub genes. Overall, the algorithm identifies previously known ones in T-cell activation, but also emphasizes the role of some new ones.

5 DISCUSSION

Gene regulatory inference has been cast as a feature selection problem in numerous works. For linear models, lasso penalized regression models have been effectively used for the task (Fujita et al., 2007; Perrin et al., 2003; Shojaie and Michailidis, 2010a). As an alternative to lasso regularization, an L₂ boosting algorithm was proposed in Anjum et al., 2009 to build a combination of linear autoregressive models that work for large networks. In nonlinear nonparametric modeling, random forests and their variants, extra-trees (Huynh-Thu et al., 2010), have recently won the DREAM5 challenge devoted to static data by solving p regression problems. Importance measures computed on the explanatory variables (genes) provide potential regulators for each of the candidate target gene. Compared with these approaches, OKVAR-Boost shares features with boosting and selected features of randomization-based methods, such as the use of a random subnetwork at each iteration. It exhibits fast convergence in terms of mean squared error due to the flexibilty of the OKVAR to capture nonlinear dynamics. Further, it uses an original and general way to extract the regulatory network through the Jacobian matrix of the estimated nonlinear model. The control of sparsity on the Jacobian matrix is converted into a constraint of the parameters of each base model h_m, for which the independence matrix W_m has been obtained by a conditional independence test. It should also be emphasized that prior information about the regulatory network can be easily incorporated into the algorithm by fixing known coefficients of the independence matrices used at each iteration. OKVAR-Boost also directly extends to additional observed time series from different initial conditions. Although we only showed one specific OKVAR model that is of special interest for network inference, other kernels can be defined and be more appropriate depending on the focus of the study.