Knotting of linear DNA in nano-slits and nano-channels: a numerical study

Abstract

The amount and type of self-entanglement of DNA filaments is significantly affected by spatial confinement, which is ubiquitous in biological systems. Motivated by recent advancements in single DNA molecule experiments based on nanofluidic devices and by the introduction of algorithms capable of detecting knots in open chains, we investigate numerically the entanglement of linear, open DNA chains confined inside nano-slits. The results regard the abundance, type, and length of occurring knots and are compared with recent findings for DNA inside nano-channels. In both cases, the width of the confining region, D, spans the 30 nm–1 μm range and the confined DNA chains are 1–4 μm long. It is found that the knotting probability is maximum for slit widths in the 70–100 nm range. However, over the considered DNA contour lengths, the maximum incidence of knots remains below 20%, while for channel confinement it tops 50%. Further differences of the entanglement are seen for the average contour length of the knotted region, which drops significantly below D ~100 nm for channel-confinement, while it stays approximately constant for slit-like confinement. These properties ought to reverberate in different kinetic properties of linear DNA depending on confinement and could be detectable experimentally or exploitable in nano-technological applications.

Introduction

Like other forms of entanglement, the abundance and type of knots in equilibrated DNA molecules depends on both intrinsic and extrinsic properties. The former include the chain contour length, the bending rigidity and chirality while the latter include spatial constraints such as confinement in narrow spaces [1–3].

A notable example of spatially confined DNA is offered by viral genome packaged inside capsids [1]. Typically, the viral DNA contour length exceeds by orders of magnitude the capsid diameter, resulting in a near crystalline density of the packaged genome [4–7]. Over the years, several numerical studies have accordingly tried to understand not only how the DNA filament is packaged inside the virus [4, 7–12] but especially how it can be ejected into the host cell through the narrow capsid exit channel without being jammed by self-entanglement [9, 13–15]. A solution to this conundrum was proposed in ref. [13], which reported that the ordering effect of DNA cholesteric self-interaction [16, 17] is responsible for keeping the entanglement at a minimum and compatible with an effective ejection process.

The effects of spatial constraints on DNA self-entanglement and the possible implications on DNA condensation, packaging, and translocation have been systematically addressed only recently, largely because of the introduction of suitable nano-devices and micro-manipulation techniques that allow for probing the properties of few confined molecules at a time [18–23].

In such contexts, a still largely unexplored research avenue is the characterization of the occurrence of knots in open, linear DNA molecules. In fact, theoretical and experimental studies of knot occurrence have largely focused on equilibrated chains where knots are trapped by a circularization reaction which ligates the two chain ends, thus forming a ring. The topology of such rings is clearly maintained until they open up, and therefore their knottedness is well defined.

This is not the case for open chains, where non-trivial entanglement cannot be permanently trapped because of the two free ends. Yet, we are all familiar with the fact that knots in open chains can be long-lived and can affect various physical and dynamical properties of polymers. In particular, in lab-on-chip experiments, the presence of knots in linear DNAs may interfere with the confinement elongation process of the molecules, an essential step for the detection of protein–DNA interactions [24] and also towards genome sequencing by pore-translocation [15, 25]. These considerations have stimulated a number of efforts aimed at suitably extending the algorithmic notion of knottedness to linear, open chains [26–28].

Building on these theoretical advancements and motivated by the upsurge of DNA nano-manipulation experiments [18–23], here we report on a numerical study of the knotting properties of linear DNA chains confined in nano-slits and nano-channels.

The investigation is based on a coarse-grained model of DNA and is a follow-up of two recent studies of the metric and entanglement properties that we carried out for closed and open chains in nano-slits and nano-channels [29, 30]. Specifically, the properties of knotted open chains confined in slits is reported here for the first time and is compared with the earlier results for channel confinement.

Methods

The model

Hereafter, we provide a brief, yet self-contained, description of the coarse-grained DNA model and simulation and numerical techniques used to characterize the topological properties in slit- and channel-like confining geometries.

By following the approach of ref. [31], linear filaments of dsDNA are modeled as semi-flexible chains of N identical cylinders.

The cylinders diameter is d = 2.5 nm, corresponding to the dsDNA hydration diameter, and their axis length is equal to b = 10 nm, i.e., a fraction of the nominal dsDNA persistence length, l_p = 50 nm.

A chain configuration is fully specified by the location in space of the normalised cylinders axes, t₁, t₂ . . . t_N and, in the unconstrained case, its energy is given by the sum of two terms:

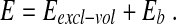1

The first term accounts for the excluded volume interaction of the cylinders. It is equal to “infinity” if two non-consecutive cylinders overlap and zero otherwise. The second term is the bending energy, 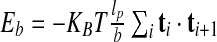with T = 300 K being the system temperature and K_B the Boltzmann constant. It is assumed that the DNA is in a solution with a high concentration of monovalent counterions, so that its electrostatic self-repulsion is effectively screened. Because non-local self-contacts of the DNA molecule are infrequent for two- and one-dimensional confinement we neglect both desolvation effects and the DNA cholesteric interaction [13, 32]. Finally, because linear chains can effectively relax torsion, the DNA torsional rigidity is neglected too.

The confinement of the DNA inside slits is enforced by requiring that the chain maximum span perpendicular to the slit plane, Δ, is lower than a preassigned value, D. Likewise, for channel confinement, it is required that the maximum caliper (diameter), Δ, measured perpendicularly to the channel axis is smaller than D.

The conformational space of confined chains was explored by means of a Monte Carlo scheme employing standard local and global moves (crankshaft and pivot moves). Following the Metropolis criterion, a newly generated trial conformation is accepted or rejected with probability given by . In the latter expression, μ represents an auxiliary parameter that couples to the chain span (or caliper size), Δ. Accordingly, by using different values of μ it is possible to bias the sampling of the configurations towards configurations with different average values of Δ. Next, because the biasing weight is set a priori, it is possible to remove it by using thermodynamic reweighting techniques and recover the canonical expectation values of the observables of interest. Advanced sampling and reweighting techniques (which are reviewed in detail in ref. [2]) are adopted here because a direct enforcement of the geometrical constraints in the Monte Carlo sampling would be inefficient due to the high Metropolis rejection rate.

We considered chains of N =120, 240, 360, 400, and 480 cylinders, corresponding to contour lengths L_c = Nb in the range 1–4.8 μm. Across the various values of μ we collected ~10⁵ uncorrelated configurations of chains that could be accommodated inside channels or slits with width D in the 40 nm–1 μm range. Notice that, because of excluded volume effects, the minimal width achievable by slits and channels in presence of a linear chain is d. It is therefore convenient to profile all properties in terms of the effective width D_eff = D − d.

Chain size and knot detection

To characterize the average size of the chain we consider its root mean square radius of gyration

2

where α runs over the three Cartesian components of the position vector r_i of the center of the ith cylinder of the chain, is the center of mass of the chain, and the brackets denote the canonical average over chains in equilibrium an confined in slits or channels.

Profiling the knot spectrum

The entanglement properties of the confined model DNA filaments were characterized by establishing the knotted state of the open chains and by measuring the knot contour length.

From a mathematical point of view, only circular chains have a well-defined topological knotted state since it cannot be altered by distorting or changing the chain geometry as long as the chain connectivity is preserved. To extend the concept of knottedness to open chains, it is therefore necessary to close them in a ring with an auxiliary arc [26, 27]. The knotted state of the closed ring is then assigned to the open chain. The auxiliary arc must clearly be suitably defined to ensure the robustness of the topological assignment; in particular, it must avoid interfering with the self-entanglement of the open chain. To this purpose we adopted the minimally interfering closure scheme introduced in ref. [27].

The position of the knot along the chain is next established by identifying the shortest chain portion that, upon closure, has the same knotted state of the whole chain. To minimize the chance of detecting slipknots [26], it is also required that the complementary arc on the closed chain is unknotted.

Figure 1 illustrates two knotted configurations of 2.4 μm-long open chains confined inside a slit and a channel. The knotted portion of the chains is highlighted.

Fig. 1.

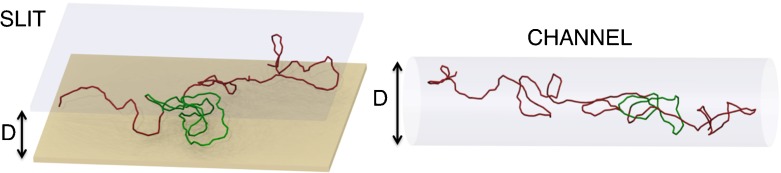
Linear knotted chain of length L_c = 2.4 μm confined inside a slit and a channel. In both cases, the confinement width is D = 70 nm and the chains accommodate a trefoil knot (highlighted in red)

Results and discussion

The metric properties of linear DNA chains for various degrees of slit-like confinement were systematically addressed in ref. [30]. Such study indicated that, for increasing confinement, the two principal axes of inertia of linear molecules first orient in the slit plane and next grow progressively as the chain spreads out in a quasi-two-dimensional geometry.

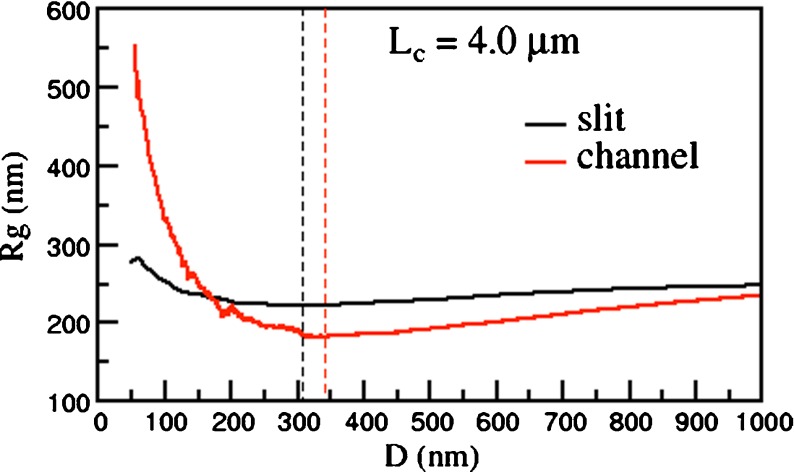
The interplay of the increase of the chain size projected in the slit plane, R_||, and the concomitant decrease of the transverse size, R_⊥, results in the non-monotonic behavior of R_g, as illustrated in Fig. 2. The data shows that R_g attains a minimum at an effective channel width, D^*, which is slightly larger then the average radius of gyration of the unconstrained, bulk case.

Fig. 2.

Average radius of gyration, R_g, of linear DNA with contour length L_c = 4.0 μm inside a slit and a cylindrical channel of effective width D_eff. Black and red dashed lines mark the location of the minimum of R_g, respectively, for slits and channels

For comparative purposes, in the same figure the average radius of gyration of equally long linear DNA chains confined in channels is shown. In this case, too, one observes the non-monotonic dependence of R_g on the width of the confining region, which attains its minimum at a channel width, D^* slightly larger that the slit case. However, the increase of R_g past the minimum is much more dramatic than for the slit case. This reflects the fact that the chain can elongate only along one direction rather than in a plane.

A relevant question regards the extent to which the dimensionality of the confining region (slits or channels) and its width can affect the incidence, complexity, and size of knots in linear chains. We accordingly applied the minimally interfering closure scheme to establish the knotted state of equilibrated linear chains and to locate the knot along their contour.

We first discuss the overall incidence of non-trivial knot topologies. The results for slit-confined chains are shown in Fig. 3a. As expected, for each fixed value of D_eff the knotting probability depends strongly on L_c [2]. In fact, going from L_c = 1 μm to 4.8 μm the knotting probability increases by one order of magnitude. By comparison, the knotting probability variations on D_eff (at fixed L_c) are smaller, though noticeable. More importantly, the knotting probability displays, as D_eff decreases, a non-monotonic behavior with a maximum enhancement peak at a width, D_e, that falls within the 50–100 nm range.

Fig. 3.

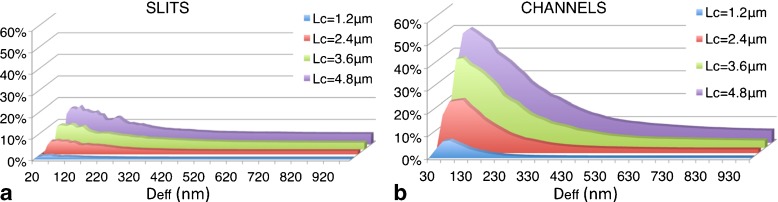
Percentage of knotted linear DNA chains inside slits (a) and cylindrical channels (b) of transversal effective size D_eff. Different curves refer to different DNA contour lengths. The estimated relative errors on the knotting probability are smaller than 1% for D_eff > 200 nm and about of 3–4% for D_eff < 200 nm. The knotting data for linear chains inside channels are based on the study of ref. [29]

In particular, the knotting probability varies by a factor of 2 going from the unconstrained case D~1 μm to D_e ~80 nm. As consistently indicated by analogous results of slit-confined rings [30], this knotting enhancement should be measurable experimentally by circularizing dsDNA molecules with complementary single-stranded ends inside slits.

As shown in Fig. 3b, the confinement-induced enhancement of non-trivial knots is even stronger for the channels case: at the largest contour length, L_c = 4.8 μm, the probability peak value is about ten times larger than the bulk one. One may anticipate that the maximum knot enhancement is attained for the same channel width, D^*, for which R_g is minimum (i.e., at the highest value of the overall chain density). This is, however, not the case since D_e is about one-third of D^* at all considered chain lengths.

Besides the overall knotting probability, it is of interest to examine in which proportion the various types of knots contribute to the overall knot population. The results for 4.8-μm-long chains inside slits are shown in Fig.  4. One notices that, at all explored values of D_eff, prime and composite knots with up to six crossings in their minimal diagrammatic representation account for at least 90% of the observed knot population. In particular, the simplest knot type, the 3₁ or trefoil knot, is by far the most abundant. For channel confinement, the predominance of simple knots is even stronger. In particular, the peak probability of the trefoil knot is, at D_eff = D_e about 23%, which is four times larger than for the unconstrained, bulk case.

Fig. 4.

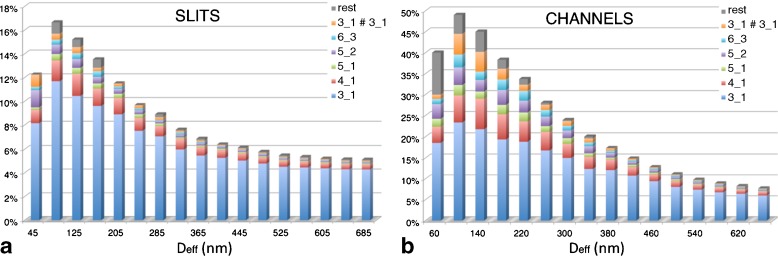
Knot spectrum as a function of D_eff for 4.8 μm-long linear DNA chains confined within slits (a) and channels (b). The knotting data for linear chains inside channels are based on the study of ref. [29]

The result is noteworthy for several reasons. Firstly, at variance with the case of three-dimensional isotropic confinement (cavity, capsids) of DNA rings [33], the knot spectrum of chains in slits and channels is dominated by the simplest knot types. This fact was recently established for closed chains in slits and channels and for open chains in channels only [29, 30]. The present results for open chains inside slits therefore complete the overall picture in a consistent way. Secondly, the percentage of simple knots (and in particular of the simplest one, the trefoil) found in two-dimensional confinement (slits) is at least doubled in one-dimensional confinement (i.e., channels).

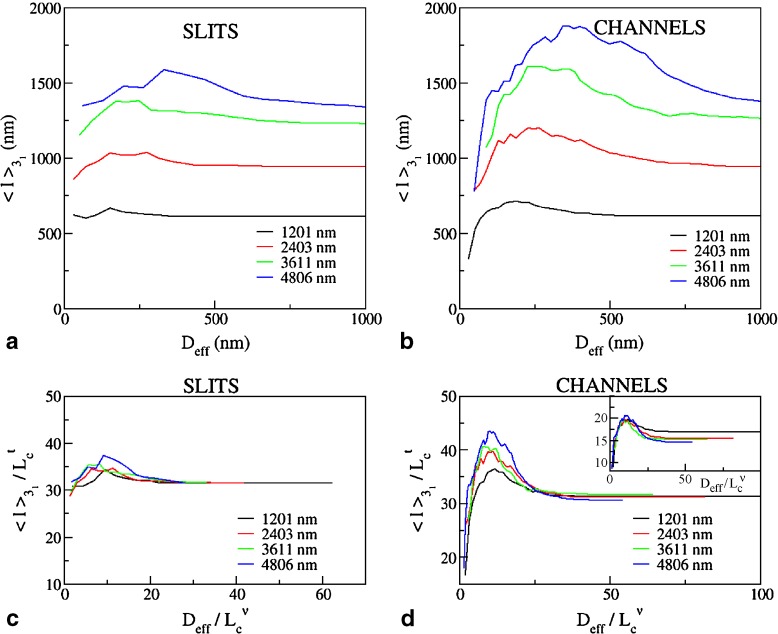
To profile the finer characteristics of the chain self-entanglement, we finally analyzed the average length of the chain portion that is spanned by the highly abundant trefoil knots, 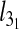. The results shown in Fig. 5 show that, at fixed L_c, 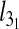is non-monotonic on D_eff for both slits and channels. However, one major difference is that the knot length decreases dramatically after the peak for channels while for slits it appears to approach a limiting value not dissimilar from the bulk one.

Fig. 5.

Average contour length of knotted arcs in linear DNA in slits (a) and channels (b) of effective transverse dimension D_eff. In (c) and (b), the data of (a) and (b) are rescaled by 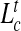for 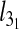and by 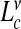with ν = 0.585 for D_eff. The main panels refer respectively to t = 0.62±0.05 while for the plot in the inset t = 0.74±0.01

For both types of confinement, 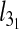depends strongly on L_c. For instance, the confinement width associated with the maximum knot length varies noticeably with L_c. In addition, the relative difference of the peak value of 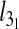with respect to the bulk case increases with L_c too (it ranges from 10% to 22% for slits and from 16% to 36% for the channels).

It is interesting to examine the observed dependence of 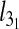on L_c in connection with earlier scaling studies on closed rings in various conditions (unconstrained, collapsed, stretched etc. [34–37]). In particular, we recall that knots in unconstrained rings are known to be weakly localized in that their contour length scales sublinearly with L_c. Specifically, for trefoils it was shown that for asymptotically long rings, 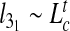with t ≈ 0.65 [36].

Motivated by these earlier findings, we analyzed the data in Fig. 5 and rescaled them so to collapse the 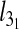curves for very weak confinement (D_eff > 800 nm). The optimal rescaling was obtained for the exponent, t = 0.62 ±0.05 for both slits and channels. For stronger confinement, the rescaled curves depart from each other. By contrast with the slit case, the channel data show a systematic upward trend for increasing L_c. As a matter of fact, the portion of the curve for 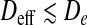shows a good collapse for t = 0.74±0.01.

This suggests that, as confinement increases, the knotted subregion of the chain remains weakly localized but it further swells along the unconstrained dimensions.

Conclusions

In polymer physics, there is an ongoing effort to understand the extent to which spatial constraints affect the probability of occurrence, the complexity, and size of topological defects in linear polymers. For DNA, this problem has various implications both for the understanding of some biological elementary processes (such as translocation and viral ejection) and for the development of efficient setups for DNA nano-manipulation protocols (such as sorting or sequencing).

Here we reported on a numerical study, based on advanced Monte Carlo simulations, thermodynamic reweighting, and scaling analysis of the equilibrium topological properties of a coarse-grained model of linear DNA confined in rectangular slits and cylindrical nanochannels. The investigation was carried out for linear chains with contour lengths ranging between 1.2 and 4.8 μm and confined within geometries whose transversal dimension D_eff span continuously the 30–1,000 nm range.

We found that, both for slits and channels, the knotting probability is a non-monotonic function of D_eff with a peak that occurs at a length-dependent confinement width D_e. Most importantly, and unlike DNA in capsids (i.e., under full confinement), the enhancement of the topological entanglement in slits and channels is not followed by a corresponding enhancement of the entanglement complexity. Indeed, despite that the peak knotting probability exceeds by several times the one in the bulk, most of the knots observed belong to very simple knot types. This effect is particularly evident for channel confinement. This suggests that nano-fluidic devices based on this or similar one-dimensional geometries may be very effective for producing a good population of linear DNA molecules with a simple knot tied in.

Finally, by using a robust algorithm for locating knots in open chains [27], we show that the typical contour length of the knotted region displays a non-monotonic behavior similar to the one observed for the knotting probability. Moreover, by looking at its scaling behavior as a function of the chain contour length, it is found that for the whole range of confinement and both for slits and channels, knots are weakly localized.