Impact of the topology of viral RNAs on their encapsulation by virus coat proteins

Abstract

Single-stranded RNAs of simple viruses seem to be topologically more compact than other types of single-stranded RNA. It has been suggested that this has an evolutionary purpose: more compact structures are more easily encapsulated in the limited space that the cavity of the virus capsid offers. We employ a simple Flory theory to calculate the optimal amount of polymers confined in a viral shell. We find that the free energy gain or more specifically the efficiency of RNA encapsidation increases substantially with topological compactness. We also find that the optimal length of RNA encapsidated in a capsid increases with the degree of branching of the genome even though this effect is very weak. Further, we show that if the structure of the branching of the polymer is allowed to anneal, the optimal loading increases substantially.

Introduction

A simple spherical virus consists of a protein shell known as the capsid that contains the viral genome, typically a single-stranded (ss) RNA molecule [1]. The capsid itself is a supramolecular assembly of multiple copies of the same or a few structurally similar coat proteins. Because of the underlying icosahedral symmetry of the arrangement of the proteins in the shell, the number of coat proteins making up virus shells equals 60 times the so-called T number of the virus, with T = 1,3,4,7,... and so on. Every virus has a specific T number associated with its well-defined size, although a few viruses come in more than a single T number [2].

A fair number of simple viruses have been reconstituted in vitro [2–11]. This includes rod-like viruses such as tobacco mosaic virus TMV [3, 4], the first virus reconstituted in vitro, and spherical viruses such as cowpea chlorotic mottle virus CCMV [8], the first spherical virus reassembled in vitro form its constituents. In fact, under the right conditions, virus coat proteins quite readily encapsulate the RNA of other viruses and even synthetic polyanions and charged nanoparticles [7–9, 12–15]. Interestingly, the purified capsid proteins of human immunodeficiency virus (HIV) also spontaneously assemble around the RNA of the virus, but in this case the formed capsids have a conical structure [16–19, 21–24].

The spontaneous reconstitution of viruses has led to the idea that virus assembly is a thermodynamic process [25], driven primarily (but not solely [26]) by electrostatic interactions between positive charges on RNA binding domains on the coat proteins and negative charges on the RNA molecules [27, 28]. This has spurred a flurry of theoretical work seeking to address questions relating to the distribution of RNA inside capsids and to fact that the total number of positive charges on the RNA binding domains, Q, that is linearly correlated with the number of charges on their ssRNA, M [29–39]. The latter equals the number of nucleotides of the genome. Recently, Belyi and Muthukumar [30] found that M ≃ 1.6 ×Q, implying that more charges are bound than necessary for charge neutralization. In polymer physics, this phenomenon is known as overcharging and is attributed to correlation effects between ions interacting with a charged surface, in this case caused by the connectivity of the charged polymeric chain [40].

For polyions such as RNA, overcharging is intuitive because charges that are away more than a Debye screening length or so from the charges on the RNA binding domains do not interact with them. These disordered domains, also known as arginine-rich motifs or ARMs, penetrate a few nanometers into the spherical cavity [30, 32]. The phenomenon of overcharging remains hotly debated in the polymer physics community and, not surprisingly, has lead to the application of quite different modeling approaches in the context of virus assembly [29–38, 41]. Intriguingly, virtually all of the calculations and computer simulations published to date rely on linear polyelectrolyte models representing the polynucleotide. An exception is the work of Lee and Nguyen, whose focus was on the radial density of RNA inside the capsid [42].

Even though single-stranded RNAs are linear polymers, they in fact resemble branched polymers in solution due to base pairing between complementary nucleotides that may or may not be far from each other along the primary sequence of the chain. In a ground-breaking study, de Gennes showed that the radius of gyration, R, of a model poly(dTA) RNA scales with molecular weight, M, as with a fractal dimension of d_f = d_G = 4 [43]. The Gaussian fractal dimension d_G is that of an ideal fractal object, i.e., one where excluded-volume effects are ignored. Since the fractal dimension of randomly branched polymers is also four [44–46], they are often thought to represent the statistical properties of ssRNAs in solution. Note that ideal randomly branched polymers are much more compact than ideal linear chains for the same molecular weight, because for the former d_G = 4 while for the latter d_G = 2.

More recent theoretical work on modeling ssRNAs give Gaussian fractal dimensions d_G = 3 − 4, depending on the temperature and nucleotide sequence [47–50]. Random nucleotide sequences, for instance, give d_G = 3 [50]. Base-pairing studies suggest that viral RNA sequences are unusual and might even have a Gaussian fractal dimension as large as five [49]. The compactness of viral RNAs has been linked to the presence of a large fraction of higher-order junctions in their secondary structure, i.e., junctions of functionality larger than three (Gopal et al., submitted). The primary sequence of viral RNAs may well have evolved to encode not only for proteins but also to attain as compact structures as possible, hence resulting to the secondary and tertiary structures. This would plausibly facilitate encapsulation by coat proteins and provide a competitive edge in their competition with cellular RNAs for encapsulation in infected cells [49].

The connection between Gaussian fractal dimension and the actual fractal dimension and the physical size of RNA is actually not all that straightforward. In fact, it is not even clear if single-stranded RNAs of viruses are indeed fractals, and if they are, whether they are indeed much more compact than other types of RNA with larger Gaussian fractal dimension. A simple estimate based on the application of Flory theory for self-avoiding fractal objects predicts a simple relation between the actual fractal and Gaussian fractal dimensions, d_f = 5 d_G / 2 (d_G + 1) [51], at least in three spatial dimensions. This then gives a fractal dimension d_f of 5/3 ≃ 1.67 for a linear chain with d_G = 2, and of 15/8 ≃ 1.88, 2 and 25/12 ≃ 2.08 for branched ones presuming d_G = 3, 4 and 5, respectively. The larger d_G the more compact the object, as expected, but excluded-volume interactions strongly diminish the impact of branching on the size of the object. In fact, the impact of branching on the physical size of a polymer becomes smaller still, if it is allowed to restructure or anneal in response to volume exclusion. For a randomly quenched branched chain that in essence consists only of branch points and end points and for which d_G = 4, we have d_f = 13/7 ≃ 1.86, at least within Flory theory [45, 52]. Single-stranded RNAs are thought to attain a different secondary structure inside of a capsid than in free solution [4], so they should behave in a way closer to an annealed branched polymer than a quenched one, i.e., one with a fixed branching.

As already noted, the focus of the work of Lee and Nguyen [42] was on the concentration profile of an annealed branched polymer in the spherical cavity of a model capsid, where the interaction with ARM region was modeled by a delta-peaked attractive interaction with the wall. No optimal loadings or free energies were presented as a function of the level of branching of RNA. Here, we study a much simpler and mathematically more tractable model based on a Flory theory for the encapsulation of fractal objects with arbitrary Gaussian fractal dimension. We extend our earlier work [36], focused on quenched polymers with Gaussian dimensions d_G = 2 and d_G = 4, to calculate the free energy and optimal chain encapsulate for RNAs with arbitrary Gaussian dimensions. Further, we now explicitly consider the effects of annealed branching for the case of d_G = 4.

We find that the optimal length of encapsulated polymer increases only weakly with Gaussian fractal dimension for given attraction to the ARM region of the capsid that we model by way of a square well potential. This means that branching does not significantly increase the optimal loading of the capsid. The equilibrium thickness of the adsorbed fractal polymer does decrease with d_G, in agreement with experimental observations on encapsulation of linear polymers and RNAs [4, 12]. The most significant result that we obtain is that the free energy gain upon encapsulation increases significantly with increasing fractal dimension, by as much as 60% on going from d_G = 3 (for random RNA sequences) to d_G = 5 (the upper limit for viral RNAs) [48, 49] (Gopal et al., submitted). For d_G = 4, annealing may increase the absorbed amount by as much as 30%. Our studies indicate that it is the structure rather than the length of RNA that has a huge impact on the free energy and in consequence on the efficiency of RNA packaging by capsid proteins, which is consistent with the recent studies of Stockley and coworkers on virus assemblies [26].

The remainder of this paper is organized as follows. In Section 2, we present our three-zone adsorption model and associated mean-field free energy. For this free energy we consider the fractal object (“manifold”) in free solution as a reference state. We optimize the free energy in terms of the thickness of the adsorbed layer and the total length of the polymer and find that the references free energy only weakly influences the outcome of our calculations. For weak interactions we are able to present analytical results. In Section 3 we discuss our results and present in Section 4 our main conclusions.

Theory

In our model, the RNAs are represented by polymeric objects of Gaussian fractal dimension d_G. We presume the branching to be quenched, i.e., fixed, and postpone a discussion of how to incorporate annealing into the model to the end of this section. The polymer segments of size l are thought to interact through a second virial coefficient (“excluded volume”) ν > 0 that includes the effects of electrostatic repulsion between them. For single-stranded RNAs, we expect l ≃ 1 − 2 nm [29, 49, 50]. Let the number of segments of the polymer be equal to M ≫ 1. We need to consider the free energy difference ΔF ≡ F_cap − F_free between the polymer confined in a capsid and that in free solution, described by the free energies F_cap and F_free, respectively. Electron microscopic images show that inside the capsid the genome forms a dense layer and seems to be adsorbed to the inner surface of the protein shell, where it makes contact with the positively charged ARMs of the coat proteins [30, 37].

For entropy reasons, we expect the layer thickness of the adsorbed polymer, D, to be larger than the thickness of the region, b, where the ARMS are located in the interior of the capsid [28, 38]. For the plant virus CCMV, we have the inner radius of capsid equal to R  _c ≃ 10 nm [27]. There is no precise value for the size of ARM region in the literature but, fortunately, b drops out the final resulting equations and as such we do not need to know its exact value.1 The polymer layer thickness D ≤ R  _c depends on the strength of the interaction between RNA segments and the RNA binding domains, described by a phenomenological free energy parameter ε (in units of thermal energy), the overall length of the polymer M and the degree of branching as expressed in the Gaussian fractal dimension d_G. The free energy gain ε > 0 of a polymer segment in the ARM region depends on the balance between attractive and repulsive interactions with the ARM. This includes the effect of volume exclusion, electrostatic attraction, and so on. Below we specify it for a particular model but for now we keep it as a free parameter driving the assembly of the virus particles.

In the spirit of Flory theory, we write down the free energy of the polymer inside the capsid as

1

in units of thermal energy, where c_i for i = 1,2,3 are numerical constants. This expression applies to three spatial dimensions. The first term describes the configurational entropy loss due to compression of the Gaussian reference polymer in a spherical annulus of width D ≤ R  _c with radius R  _c. It is accurate provided , and we verify this condition a posteriori. The expression can be obtained from a simple scaling Ansatz and formally derived within the so-called ground-state approximation for d_G = 2 and d_G = 4 from Edwards-Lifshitz theory for linear chains [53] and extension of it to randomly branched chains [44]. In principle, c₁ could depend on d_G but we for simplicity choose to ignore this. The other constants should be independent of d_G, because they refer to interactions between pairs of individual segments.

The second term describes the volume exclusion between the segments, including the influence of screened electrostatic repulsion between them. It should be noted (i) that 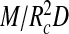is approximately the number density of RNA segments in the polymer layer, (ii) that 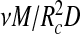must be proportional to a volume fraction in that layer, and (iii) that for low volume fraction we retrieve the familiar second-virial free energy (in units of thermal energy), 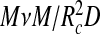. Hence, the second term in (1) goes beyond the usual second-virial treatment typical of Flory theory, but for simplicity we do approximate the volume fraction by replacing the exact volume of the spherical annulus, proportional to , by 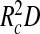. For our purposes this suffices, as this is accurate in both interesting limits of D ≪ R  _c and D = R  _c.

The last term of (1) accounts for the fraction of Mb/D of the segments interacting with the ARMs. As discussed, the ARMS are disordered domains located mostly on the C-terminal end but sometimes on the N-terminal end of the coat proteins [1]. These can be viewed as flexible linear polymers even though upon complexation with RNA, a short section may become α helical such as is the case with CCMV and BMV [54]. If we treat the ARM as a linear polymer and presume that the collection of ARMs lining the inner surface of the shell behave like a polymer brush [30], we find again from Flory theory that the interaction free energy per RNA segment must be equal to ε = − ν_±n / ab. Here, n is the number of segments making up an ARM, ν± < 0 is the second-virial coefficient between a RNA and an ARM segment and a the surface area per protein in a capsid. The latter is dominated by the attractive screened Coulomb interaction between them.

The free energy of the branched chain in free solution, F_free, is equivalent to that of (1), except that

2

where c₄ and c₅ are again constants of order unity. Note that here we plausibly presume that , i.e., excluded volume interactions swell the chain.

The optimal values of D and R minimize ΔF = F_cap − F_free. As we are interested in the optimal amount of RNA encapsulated, we also minimize the free energy with respect to M. The optimal values of the adsorption layer thickness D_*, size of the free chain R_* and molecular weight M_* we insert back into ΔF, in order to find the free energy of encapsulation ΔF_*. Associated with it is a Boltzmann factor that turns out to describe a critical mole fraction of coat proteins below which the ssRNAs and protein remain free in solution and above which co-assembly takes place, at least if the assembly is sufficiently co-operative [27]. The assembly is co-operative if the coat proteins interact strongly enough in the complete shell: this produces a significant rim tension in an incomplete shell that suppresses the intermediate structures. In that case, we only have appreciable concentrations of naked RNAs and/or completely encapsulated ones [36].

We can derive a similar free energy to (1) for an annealed randomly branched polymer with d_G = 4. This is most simply explained for a chain in free solution. Due to annealing of the branching, there is an additional entropy contribution proportional to L²/M relating to the number of segments L separating two endpoints, and the entropy loss upon stretching the (Gaussian) chain connecting those endpoints that scales as R  ²/l²L [46, 52]. Because L couples directly to the configurational entropy and only indirectly to the interactions between the segments, L optimizes the total free energy if L ≈ M  ^1/3R  ^2/3l^− 2/3. This gives a configurational free energy that scales as 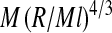. Hence, we obtain for the free energy of our self-avoiding annealed randomly branched chain in free solution,

3

as before in units of thermal energy with c₆ and c₇ constants. Here, we presumed that 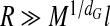with d_G = 4.

Applying similar scaling arguments to a chain in a spherical annulus, we find

4

with , and c₈ and c₉ constants. Comparing (1)–(4), it seems reasonable to presume that c₇ = c₅, c₉ = c₂ and c₁₀ = c₃. Note that the reshuffling of the branching is different in the chain in free solution from that in the capsid. The reason is that in one case the Gaussian chain is expanded while in the other it is confined (compressed). This leads to different fractal dimensions in the two cases.

The equilibrium values of D_*, M_* and R_* follow from the minimization of ΔF = F_cap − F_free. Inserting the equilibrium values of these quantities back into ΔF, gives the free-energy gain upon assembly, ΔF_*. Analytical results for all relevant quantities are presented in the next section for varying Gaussian fractal dimension. We also directly compare results for d_G = 4 for the cases of quenched and annealed branching.

Results and discussion

The optimal adsorption layer thickness D_* and size R_* in free solution for the optimal molecular weight M_* of encapsulated polymer that we find for the quenched case obey highly non-linear coupled equations that we do not reproduce here. It turns out, however, that in the limit of large enough capsids R  _c ≫ l and for sufficiently weak interactions εb/l < 1 we are able to obtain analytical results. For instance, in this limit we obtain for the optimal polymer size M_* encapsulated by the coat proteins,

5

where the constant of proportionality c₃/c₂ is omitted. Equation (5) shows that the larger the interaction, the longer the optimal length of the encapsulated polymer. Also, longer chains are encapsulated as the level of branching increases at fixed interaction strength although the effect is quite weak. Indeed, M_*(d_G = 5)/M_*(d_G = 3) = 10/9 ≈ 1.1, so the length of viral RNAs packaged is at most a mere 10% more than that of RNAs with a random nucleotide sequences. This implies that nucleotide sequence optimization as discussed in the introduction does not significantly help to increase the amount of genome encapsulation. For large values of εb/l ≫ 1, the conformational entropy becomes subdominant and the physics of the problem is dictated by the balance between attractive and repulsive interactions. In that regime, the fractal dimension of the chain becomes irrelevant.

Another important (observable) quantity is the optimal adsorption layer thickness for the encapsulated polymer with the optimal length M_*,

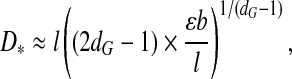6

where we have dropped a constant of proportionality . In order for (6) to take on reasonable values b ≤ D_* ≤ R  _c, we need to require that 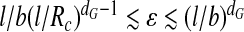. This puts fairly tight bounds on the strict applicability of the theory, in particular for small viruses. Granting these limits, D_* increases with increasing interaction strength, ε, between the segments of the polyanionic cargo and the polycationic ARM of the coat protein. This is due to the fact that as the strength of interaction increases, the optimal chain size increases and, because of this, the optimal thickness, D_*, increases. This has to be contrasted with what we find when the chain length M is fixed: in that case the layer thickness D decreases as ε increases, as expected. D_* also decreases with increasing d_G, i.e., with increasing degree of branching. So, the more strongly branched a polymer is, the more localized the adsorbed polymer is in the capsid. This is to be expected and agrees with what is seen in electron microscopic images of virus capsids containing linear polyanions and those containing ssRNA.

If we insert our estimate εb/l ≈ − ν_±n / al into (6), we find that it depends in essence only on the number of segments, n, and surface density 1/a of the individual ARM, the fractal dimension of the RNA and the strength of the interaction between the charges on the RNA and the ARMs as described by the parameter ν_± < 0. At the level of a Debye-Hückel approximation, we expect 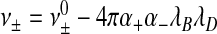, where is the “bare” excluded volume between the structural units of the ssRNA and the ARMs, and α₊ and α − are the number of charges per segment on the ARM ( + ) and ssRNA ( − ). Finally, λ_B ≈ 0.7 nm denotes the Bjerrum length and nm the Debye length of the aqueous solution, with c_S the molar concentration of 1-1 salt [51]. The larger the salt concentration, the smaller ε and D_*.

Another conclusion that we can draw from our analysis is that

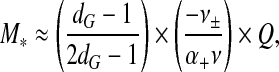7

if we insert our estimate for ε taken from the polymer brush model for the ARM region in (5) and again ignore the constant of proportionality. Here, Q is the total number of charges on the ARMs in the cavity of the capsid. So, we do find that M ∝ Q as discussed in the introductory section, except that the constant of proportionality seems to depend both on the level of branching of the polyanion and on the solution conditions via the excluded volumes ν_± < 0 and ν > 0. This means that more polymer can be encapsulated by reducing the solvent quality and hence ν, e.g., by adding multivalent cations that tend to condense ssRNAs by effectively lowering ν [55]. Adding simple 1-1 salt alters ν_± and ν in the same way, that is, both should become smaller in magnitude with increasing salt.

Indeed, for sufficiently low concentrations of added salt, we expect 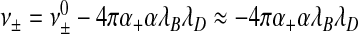to approximately hold, while 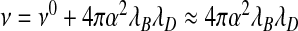. Here, and ν⁰ denote the “bare” volume exclusions between the various species. However, we do expect ν_± to change sign at sufficiently large ionic strength as electrostatic attraction becomes subdominant relative to, say, the effects of steric repulsion. This implies that at sufficiently large ionic strength, RNAs would not be encapsulated, which agrees with experimental observation [6]. All of this begs the question of whether the seemingly constant overcharging of 60% that was found by Belyi and Muthukumar [30] for a large number of viruses is real or just a coincidence. From our admittedly crude analysis, it certainly seems a coincidence, not least because the ionic conditions in different types of cell are not likely to be exactly the same. Our theory also explains why in encapsulation experiments of synthetic linear polymers the overcharging ranges from 0.6 and to 9 [12–14].

We have seen that branching does not significantly increase the optimal amount of encapsulated RNA. What branching does do, however, is increase the efficiency of encapsulation. In the limit R  _c ≫ l the free energy of encapsulation ΔF ≈ F_cap is dominated by the free energy of the polymer in the capsid, giving

8

apart from a constant of proportionality 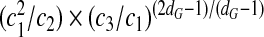that we have dropped. According to (8), the free-energy gain of encapsulation |ΔF| is an increasing function of the strength of the adsorption energy ε, but less so as the degree of branching d_G increases. Still, if we take the earlier discussed cases of d_G = 3 for RNAs with a random nucleotide sequence and the most extreme value d_G = 5 for viral RNAs, we obtain . If we consider the upper limit of εb / l ≈ 1 for (8) to be valid, we get ΔF(d_G = 5)/ΔF(d_G = 3) ≈ 1.6. In other words, the free-energy gain for a chain with d_G = 5 is more than 60% larger than that for a chain with d_G = 3 (if we ignore the unknown numerical prefactors). Note that because is on the order of 100, the free-energy enhancement can be substantial.

Finally, we consider the encapsulation of randomly branched polymers for both quenched and annealed cases. As we argued in the introduction, the statistical behavior of the annealed ones seems closer to single-stranded RNAs than that of the quenched ones. Even though d_G = 4 for both types of branched polymer, their fractal dimensions differ under good and poor solvent conditions [46]. There are a few interesting conclusions we can draw from our calculations. First, we find that the optimal packaging of annealed RNAs are larger than that of quenched ones, , in the regime where the second virial approximation is valid, i.e., . Here, the subscripts ann and que refer to the annealed and quenched degrees of disorder, respectively. This would imply that 30% more polynucleotide would be absorbed if RNA is allowed to restructure its branching. Annealing would therefore strongly increase the ability of the capsid to package genome.

If we consider the adsorbed layer thickness, however, then we find that 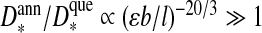if εb / l < 1. This is not entirely surprising, because (i) a longer annealed polymer is encapsulated than a quenched one for the same interaction strength and (ii) a self-avoiding annealed polymer in free solution is larger than a quenched one if their length is the same (see the introductory section). A more careful analysis shows, in fact, that unless the optimal annealed chain fills the entire cavity of the capsid, i.e., R_c = D_*. Interestingly, something similar was found in the more elaborate calculation of Lee and Nguyen [42]. As pointed out in Ref. [42], for some viruses this seems to be the case because the interaction strength between RNA and coat proteins is not strong and as such there is no well-defined adsorption layer.

On the other hand, we do find that the free energy of encapsulation for annealed randomly branched polymers to be less than that of quenched ones, unless εb / l > 1. In that case, the thickness layer D_* ≪ R_c and the the RNA sitting on the inner surface of the capsid is so dense that the second-virial approximation that we relied on in our analytical solutions to the governing equations fails. Clearly, a much more detailed study is needed to settle this issue. We leave for future work a direct comparison of the field-theoretical approaches for quenched and annealed branched polymers in the context of encapsulation.

Conclusions

In conclusion, we have shown that if the primary sequence of single-stranded RNA of viruses have indeed evolved to optimize their secondary structure so as to obtain higher levels of branching and hence compactness, as it has recently been suggested (Gopal et al., submitted), this does not necessarily lead to packaging of more RNA in virus capsids. However, according to our calculations, a higher level of branching considerably increases the free-energy gain of packaging of viral RNA rather than other types of RNA. More specifically, the secondary structure of RNA resulting from its branching has a significant impact on the efficiency of genome packaging. In head-to-head competition between viral and other types of RNA in co-assembly with virus coat proteins in infected cells, higher degree of branching could indeed give viral RNAs a competitive edge over other RNAs.