Analysis of DNA sequence variation within marine species using Beta-coalescents

Abstract

We apply recently developed inference methods based on general coalescent processes to DNA sequence data obtained from various marine species. Several of these species are believed to exhibit so-called shallow gene genealogies, potentially due to extreme reproductive behaviour, e.g. via Hedgecock’s “reproduction sweepstakes”. Besides the data analysis, in particular the inference of mutation rates and the estimation of the (real) time to the most recent common ancestor, we briefly address the question whether the genealogies might be adequately described by so-called Beta coalescents (as opposed to Kingman’s coalescent), allowing multiple mergers of genealogies.

The choice of the underlying coalescent model for the genealogy has drastic implications for the estimation of the above quantities, in particular the real-time embedding of the genealogy.

1. Introduction

Within the last decade, considerable attention has been turned to the explanation of the fact that intra-species DNA sequence variation yields shallow gene genealogies resp. low ratio between effective population size N_e and adult census size N in several marine species (see, e.g., [A04], [H94], [H05], [TWG02], [WT03]), as well as to the theory of mathematical models which may describe such genealogies in terms of so-called Λ-coalescents (see, e.g., [P99], [S99], [DK99], [MS01], [EW06], [BB08]).

Indeed, Hedgecock [H94] proposes a mechanism to describe substantial variation of reproductive success in marine species in terms of so-called “reproduction sweepstakes”, to be won by highly successful individuals within each generation, i.e, a few or even a single individual may replace a large fraction of the entire population. This requires great individual fecundity and high mortality early in life as well as “sweepstake-like chances of matching reproductive activity with oceanographic conditions conducive to gamete maturation, fertilization, larval development, settlement and successful recruitment to the adult spawning population”. As a result, Hedgecock claims that the variance in offspring numbers may be orders of magnitudes higher than what standard binomial or Poisson models predict, leading to a small N_e/N ratio. See also [HP11] for a recent overview.

However, if one tries to turn such a mechanism into a mathematical population model, it turns out that in order to make sense for large populations, sweepstakes whose size are a positive fraction of the present population cannot be too frequent, in fact, the probability of such an event in a given generation must approach zero for large population sizes. Otherwise, the model would predict vanishing genetic variability, in contrast to the empirical observations (as already suggested by Árnason in [A04]).

To circumvent such trivialities, we first discuss two rigorous mathematical population models in the classical “Cannings’ framework” ([C74], [C75]) that incorporate extreme reproductive events (due to Eldon and Wakeley [EW06] and Schweinsberg [S03]), which can be considered as simple models of Hedgecock’s sweepstakes, but still lead to non-vanishing variability. A classification result due to Möhle and Sagitov ([MS01]) then yields the required timescales for large population size, in a way that sweepstakes neither dominate (leading to vanishing genetic variability) nor become negligible.

It is important to note that the required time-scaling is mostly “non-classical” (i.e., unlike the Wright-Fisher model and its relatives, not a linear function of the model’s census population size) hence will also affect the scaling of the mutation rates and make the concept of the so-called (Kingman-) coalescent effective population size discussed in [SKK+05] void, since the existence of the latter depends on a linear change in time-scale.

The resulting limiting ancestral processes embedded in our population models (with extreme reproduction due to sweepstake-like behaviour) coincide with special cases of the so-called Λ-coalescents, i.e. exchangeable coalescents, which allow multiple collisions of lineages (extending the merely binary collisions in the Kingman-coalescent setup), but not simultaneous multiple collisions. Such processes were introduced and studied by Pitman [P99] and Sagitov [S99] and include the classical Kingman-coalescent as a special case. However, the class of Λ-coalescents is vast, in particular allowing for any type of probability distributions on the set of (random) sweepstakes sizes. An important pair of questions in each concrete scenario therefore is: What is the “right” distribution on sweepstakes sizes, what is the right timescale? In [EW06], Eldon and Wakeley discuss a simple model, in which sweepstake sizes are always the same fixed positive fraction of the population size. They then fit their model, using a maximum-likelihood method based on the number of segregating sites and total number of mutations, to mitochondrial data from Pacific Oysters (Crassostrea gigas), taken from [BBB94], with the result that the maximum-likelihood estimator for the fixed sweepstakes size is 8% of the living population.

To our knowledge, this was the first time that a Λ-coalescent based model has been calibrated to real data. However, there are a few issues that should be discussed. From the modeling perspective, there is no reason why there should be a fixed sweepstakes size. Still, it is certainly infeasible to infer from the full (non-parametric) class of Λ-coalescents. Parametric subclasses, which describe “realistic” mechanisms, would therefore be of interest (we use certain so-called “Beta-coalescents”, cf. e.g. [BB08], [BBC+05], see Section 2.1 and Section 4.3 for a discussion of this class of coalescents). Another important point is the adequacy of the equilibrium population assumption underlying the coalescent model used in [EW06]. As pointed out in [BBB94], the pacific oyster data are taken from a population which had only recently been introduced from Japan to Canada. The shallow genealogy might therefore also be explained by the presence of a relatively recent population bottleneck.

In the present article, we analyse several datasets obtained from Atlantic Cod (Gadus morhua), taken from geographically separated locations, under the Beta-coalescent model, taking the full information provided by the infinitely-many sites model into account (as opposed to [EW06] where the authors use summary statistics based only on the number of segregating sites and the total number of mutations).

As a result we report that in many cases, a neutral panmictic Kingman-based scenario can be rejected. Further, our maximum-likelihood estimators for the parameters of the Beta-coalescents and mutation rates are presented, as well as an estimated real-time embedding of the genealogy and in particular the expected time to the most recent common ancestor given the data. We finally discuss the question whether there is evidence for a sweepstake-based scenario in these datasets and propose and calibrate a potential candidate for the distribution of sweepstake sizes.

2. Methods

2.1. Exceptional genealogies and exchangeable coalescents

Since the early 80ies, models based on the Kingman coalescent have been successfully used to describe the genealogy of many biological populations. One of their distinguishing features is, together with exchange-ability, that only binary collisions are allowed. That is, at most two ancestral lineages may coalesce at a time (exchangeability meaning that all pairs of lineages are treated equal).

However, it turns out that many species seem to exhibit “exceptional genealogies”, for example “shallow genealogies”, (cf. e.g., [A04], [H94], [H05], [TWG02], [WT03]), which may be appropriately described by more general exchangeable coalescents, the so-called Λ-coalescents, which allow multiple collisions of ancestral lineages. Indeed, under a Lambda-coalescent, given a sample of size n, each k-tuple of ancestral lineages (where 2 ≤ k ≤ n) is merging to form a single lineage at rate λ_n,k, where

$${\lambda }_{n,k}={\int }_{[0,1]}{x}^k{(1-x)}^{n-k}\frac{1}{x^2}\mathrm{\Lambda }(dx),$$ (1)

for some finite measure Λ on the unit interval [0, 1], see [P99] or [S99]. Note that the family of Lambda-coalescents is rather large, and in particular cannot be parametrised by finitely-many real variables. Important examples include Λ = δ₀ (Kingman’s coalescent) and Λ = δ₁ (star-shaped genealogies). Here, we denote by δ_y the probability measure on [0, 1] with a unit point mass in y ∈ [0, 1]. Note that this means that (for continuous functions f)

$$\int f(x){\delta }_y(dx)=f(y).$$ (2)

From (1) and (2), one readily obtains

$${\lambda }_{n,k}={\int }_{[0,1]}{x}^{k-2}{(1-x)}^{n-k}{\delta }_0(dx)=0^{k-2}=\{\begin{array}{cc}1,\hfill & k=2,\hfill \\ 0,\hfill & k>2,\hfill \end{array}$$

in the Kingman case and

$${\lambda }_{n,k}={\int }_{[0,1]}{x}^{k-2}{(1-x)}^{n-k}{\delta }_1(dx)=\{\begin{array}{cc}1,\hfill & k=n,\hfill \\ 0,\hfill & 2\le k<n,\hfill \end{array}$$

in the star-shaped case. A little more generally, a single point mass at ψ ∈ (0, 1), say Λ = cψ²δ_ψ, c > 0, yields

$${\lambda }_{n,k}=c{\int }_{[0,1]}{x}^k{(1-x)}^{n-k}\frac{{\psi }^2}{x^2}{\delta }_{\psi }(dx)={\psi }^k{(1-\psi )}^{n-k}.$$ (3)

This has a simple interpretation via independent Bernoulli trials with individual success probability that determines which lineages participate in a given merger event. Also, forwards in time, it has a simple interpretation for the corresponding population model, namely, that on a macroscopic time-scale, at rate c > 0 a fraction of 100% of the living population is replaced by the offspring of single ancestor (by the strong law of large numbers). Such macroscopic reproduction events will be called “extreme reproductive behaviour”, and lead to multiple collisions in the genealogy. See, e.g., [BB09] for further details and references.

Of course, from a modelling point of view a restriction to a fixed fraction ψ appears unnatural, and the general case can be interpreted as a mixture over ψ’s. There are of course many possibility, and later, we will mainly be concerned with so-called Beta-coalescents, in particular the case where Λ has a Beta(2−α, α)-density, i.e.

$$\frac{\mathrm{\Gamma }(2)}{\mathrm{\Gamma }(\alpha )\mathrm{\Gamma }(2-\alpha )}{x}^{1-\alpha }{(1-x)}^{\alpha -1},x\in (0,1)$$

for some α ∈ (1, 2) (where Γ denotes Euler’s Gamma function). Even though this is not integrable for α = 2, the transition rates then correspond to the classical Kingman coalescent, which can in this way be included into the Beta(2−α, α)-class, and intuitively smaller α corresponds to stronger skew in offspring distributions. This class of multiple merger coalescents is mathematically distinguished (revealing a close connection to α-stable branching processes, see [BBC+05]); furthermore, many large-sample properties are determined by the shape of Λ near 0 (e.g. [BBL11]), by varying α we obtain a “natural” representative for each regularity index at 0. Finally, the Beta(2 −α, α)-coalescents appear as limiting genealogies for a “natural” class of reproduction models derived from a branching mechanism with “heavy tails”, see Section 2.3 below.

2.2. Population models with highly skewed offspring distributions leading to exceptional genealogies

We follow a classical framework of population genetics and regard neutral, non-overlapping discrete-generation population models with exchangeable offspring distribution, that is, Cannings models, see [C74], [C75]. Consider a (haploid) population of fixed size N, let t ∈ ℕ denote the t-th generation. Let ν^(t) ≔ denote the vector of offspring replacing the N individuals in the t-th generation, where ${\nu }_k^{(t)}$ is the number of children of individual k. We assume that the random vectors ν^(t), with t ∈ ℕ, are independent and identically distributed, and furthermore that, for fixed t, the random variables ${\nu }_1^{(t)},\dots ,{\nu }_N^{(t)}$ are exchangeable. We write ${\nu }_i={\nu }_i^{(t)}$ when speaking about distributional properties in a single generation, where t is irrelevant. Note that exchangeability and constant population size force that the expected number of offspring of each individual i is one, i.e. 𝔼[ν_i] = 1. Let

$$c_N≔\frac{𝔼[{\nu }_i({\nu }_i-1)]}{N-1}$$ (4)

(this is the probability that two randomly drawn individuals from the same generation are siblings). Note that the numerator equals the variance of the offspring distribution, i.e. ${\sigma }_N^2=𝔼[{\nu }_i(v_i-1)]$ and, of course, is independent of i due to exchangeability. A famous result by Kingman [K82] shows that if ${\sigma }_N^2\to {\sigma }^2\in (0,\infty )$ as N → ∞ (and suitable higher moment bounds hold), then the genealogy of a sample of size n taken from the limiting population (time-changed by 1/c_N) will be given by Kingman’s n-coalescent.

In [MS01], extending Kingman’s original result, Möhle and Sagitov provide the necessary and sufficient criteria so that a limiting Cannings population model has a non-trivial genealogy given by a Λ-coalescent. In particular, if we consider the population model on the time scale 1/c_N, then the limiting genealogy will be governed by a Λ-coalescent iff

• c_N → 0, as N → ∞,

• for all y ∈ (0, 1) with Λ ({y}) = 0, we have

  $$\frac{N}{c_N}\mathbb{P}\{{\nu }_1>N_y\}\to {\int }_{(y,1]}\frac{1}{x^2}\mathrm{\Lambda }(dx),\text{ as }N\to \infty ,$$ (5)

• and finally, for i ≠ j, 𝔼[ν₁(ν₁ − 1) ν₂(ν₂ − 1)]/(N₂c_N) → 0 as N → ∞.

Condition (5) shows how the distribution of the individual offspring numbers determines the measure Λ from (1) that governs the transition rates in the coalescent. Indeed, (5) can be interpreted as

$$\mathbb{P}\{\frac{{\nu }_1}{N}\approx y\}=\frac{c_N}{N{y}^2}\mathrm{\Lambda }(dy).$$

It in particular forces the offspring distribution to be “highly” skewed, i.e. there must be reproduction events where the number of offspring is of the same order as the total population size, which implies that the variance ${\sigma }_N^2$ of ν₁ blows up as N gets large. Note that this condition also implies that these extreme reproductive events need to happen on the time-scale 1/c_N, hence cannot be too frequent (an effect that has been pointed out, informally, in the introduction and also already in [A04]).

2.3. Examples for models with extreme reproductive behaviour

Several classes of Cannings models have been considered recently in the literature in this context. For example, in [EW06], Eldon and Wakeley discuss a model of size N where, in each generation, exactly one uniformly chosen individual reproduces and becomes parent of a fixed (non-random) positive fraction of the population, leading to a measure with an atom in (0,1].

If one is interested in a model with variable (random) sweepstakes sizes, one might consider Schweinsberg’s ([S03]) model, which leads naturally to Beta-coalescent based genealogies and is related to α-stable branching processes for some α ∈ (1, 2]. Again, consider a haploid population of size N. Reproduction is assumed to happen in two steps. First, each individual spawns (independently) ${\tilde{v}}_k^{(t)}$ offspring, according to a probability distribution with a power law tail-behaviour, i.e.

$$\mathbb{P}\{{\tilde{\nu }}_k^{(t)}\ge l\}~C{l}^{-\alpha },\alpha \in (1,2],C>0,$$ (6)

so that the amount of potential offspring has infinite variance. We denote the resulting vector of (potential) offspring by ${\tilde{\nu }}^{(t)}=({\tilde{\nu }}_1^{(t)},\dots ,{\tilde{\nu }}_N^{(t)})$. Note that the components do not (yet) sum up to N, but to some random Ñ typically much larger than N. Hence, in a second step, N individuals are chosen uniformly at random from the Ñ potential offspring particles, so that we obtain the new offspring vector ${\nu }^{(t)}=({\nu }_1^{(t)},\dots ,{\nu }_N^{(t)})$) where ${\nu }_i^{(t)}$ denotes the number of individuals drawn from the ${\tilde{\nu }}_i^{(t)}$ potential children of parent k.

This model has some resemblance of so-called “type-III survivorship”: high fertility leads to excessive amount of offspring, corresponding to the first reproduction step, whereas high mortality early in life is modeled in the second step.

2.4. Inference methods

Choosing a suitable limit of a Cannings population model (e.g. one of the models above) determines an explicit probabilistic mechanism for the ancestral process, i.e. the underlying class of Λ-coalescents. Still, one needs to calibrate the corresponding parameters to the observed DNA sample in questions, thus inferring “evolutionary parameters” like the mutation rate. We pursue a maximum-likelihood approach based on the full sample information. We assume that mutations occur according to the infinite-sites model, i.e., each new mutation hits a novel site.

A general probabilistic mechanism of obtaining DNA samples from a coalescent tree – which is our model for the gene genealogy of the ancestral limit process of our population models under consideration – is described in detail in [BBS11]. Here, we provide a quick overview. To obtain a sample of size n, first run an n-Λ-coalescent to obtain a rooted coalescent tree. On this rooted tree with n leaves (numbered from 1 to n), place mutations along the branches at rate r to obtain a gene genealogy (here, r is the scaled mutation rate). Then, label these mutations randomly: Given there are s mutations in total, attach uniformly at random the labels from 1,…,s to these mutations. An observed genetic type x is then given by the sequence of labels of mutations following its path backwards from a leaf to the root. When there are d different types, we enumerate them randomly, from 1,…, d. Note that d ≤ s, since each type has at least one unique mutation. We then let [t, n] = [(x₁,…x_d), (,₁,…n_d)] denote the pair consisting of the observed unordered d-tuple of types t and their respective multiplicities n. Note that [t, n] equivalently describes a tree, commonly referred to as a genetree. We will denote the distribution of such a data set or tree, depending on Λ and mutation rate r, by ℙ_Λ,r.

We may then compute the likelihood of observed data [t, n] under the “parameter” ϑ = (Λ, r), i.e. ℙ_ϑ([t, n]) ≔ ℙ_Λ,r([t, n]) recursively, conditioning on the last event in the coalescent history, see [BBS11, Section 1.3]. Such a recursionmay, for small sample sizes with few mutations, be solved numerically. However, for more complex samples, Monte-Carlo methods, for example Importance Sampling, need to be employed. Such methods are being discussed in detail in [BBS11] and implemented in the program MetaGeneTree.¹

3. Analysis of DNA sequence data

3.1. Description of underlying datasets

The Pacific Oysters dataset presented in [BBB94] was obtained as the result of a restriction-enzyme digest of mitochondrial DNA taken from 159 Pacific oysters (Crassostrea gigas) from British Columbia. This digest can (in an ad hoc fashion) be interpreted as sequence information resulting in 49 segregating sites or positions, where an enzyme either cuts or leaves the DNA-molecule intact, depending on the allele present. This pattern was then manually edited to resolve violations of the infinitely many sites model, resulting in the exclusion of four samples and five sites, see Appendix A for details. This dataset has also been analysed in [EW06], where the authors already pointed out the underlying genealogy might not be adequately modelled by Kingman’s coalescent.

The second set of DNA sequence data was discussed in [A04]. There, Árnason combined several datasets, published in other works, from a 250 bp region of the mitochondrial cytochrome b gene of the Atlantic cod (Gadus morhua). In [A04], he provided a discussion of the whole combined dataset which unfortunately turned out to be too large to be treated by our exact likelihood methods. For this reason we analysed the smaller component datasets described in [AP96, APP98, APKS00, CM91, CSHW95, PC93, SA03] separately. As Árnason pointed out these samples stem from various geographic locations throughout the Atlantic. In our analysis, we choose the most abundant type to represent the ancestral type, and we also consider summing out over all possible ancestral types. Again, some of the samples violated the assumptions of the infinitely many sites model. To cope with this, we considered the combined dataset of [A04] and introduced a consistent pattern of parallel mutations to resolve all violations (again, see Appendix A for details). This procedure lead to a dataset that corresponds to the phylogenetic maximum parsimony network from Figure 2 of [A04, p. 1875]. We then analysed the respective subsamples specified in the different publications. Table 1 and Table 2 show some characteristics of the datasets, and we refer to Appendix A for a more detailed description.

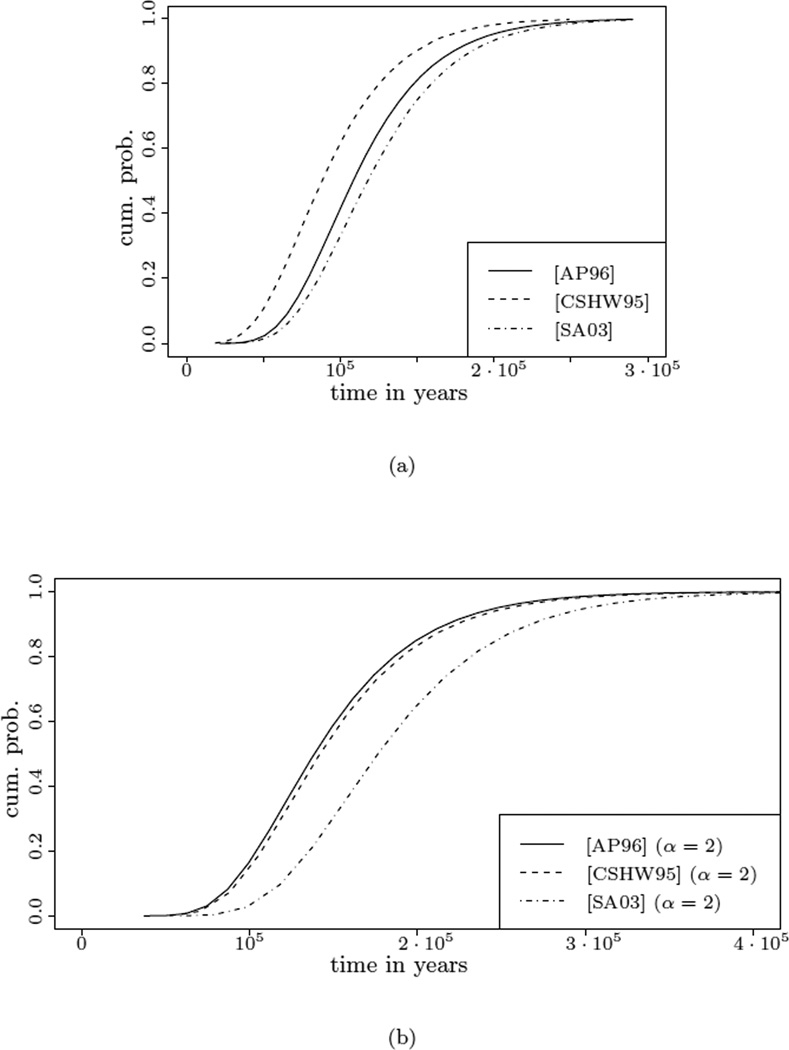
Figure 1.

Distribution functions for the time to the most recent common ancestor of the sample, given the data, for three of the cod data sets, in the Beta- and Kingman-case. (a) The Beta-case, where we used the inferred parameter α̂ from Table 4 as the underlying parameter. (b) The Kingman-case, where we used an underlying α = 2, as indicated in the legend.

Table 1.

Statistical tests reject Kingman hypothesis for Pacific Oyster data

Ref.	n	d	Tajima’s D	Δn	Sn	CI	Fu & Li’s D	ηi	ηe	CI
[BBB94]	155	40	−2.65 *	0.94	44	[−1.76, 2.10]	−6.6 *	14	30	[−2.38, 1.63]

Table 2.

Rejection of Kingman hypothesis for some Atlantic Cod datasets

Ref.	n	d	Tajima’s D	Δn	Sn	CI	Fu & Li’s D	ηi	ηe	CI
[AP96]	100	11	−0.66	1.44	10	[−1.78, 2.07]	−1.50	6	4	[−2.36, 1.61]
[APP98]	109	11	−0.89	1.23	10	[−1.78, 2.07]	−1.54	6	4	[−2.36, 1.61]
[APKS00]	78	12	−1.45	1.04	11	[−1.79, 2.06]	−1.83	6	5	[−2.38, 1.59]
[CM91]	55	12	−1.87 *	0.84	11	[−1.8, 2.05]	−2.24	5	6	[−2.45, 1.57]
[CSHW95]	236	16	−2.11 *	0.39	15	[−1.75, 2.11]	−2.24	9	6	[−2.25, 1.65]
[PC93]	103	10	−2.12 *	0.46	12	[−1.78, 2.07]	−3.07 *	5	7	[−2.36, 1.61]
[SA03]	74	15	−1.28	1.59	14	[−1.79, 2.06]	−2.88 *	6	8	[−2.38, 1.59]

3.2. Rejection of the “Kingman hypothesis”?

In several datasets, in particular the one discussed in [BBB94], standard tests reject the “Kingman hypothesis”, indicating that the genealogies underlying the observed datasets might not be adequately described by a Kingman-coalescent. In particular, we consider Tajima’s D and Fu & Li’s D in each case. Recall that for a sample of n sequences, Tajima’s D (see [T89]) is based on the normalized difference between the mean number of pairwise differences Δ_n and the weighted number of segregating sites S_n. In a neutral, Kingman-coalescent based scenario, D should be approximately 0. Small values of D indicate shallow genealogies, large values indicate long internal branches. Another standard test statistic is Fu & Li’s D (see [FL93]). Again, the test statistic is based on a standardized variable which is the difference between the number of mutations on external branches η_e, and the number of mutations on internal branches η_i, multiplied by a weighting factor. Values for approximate “confidence intervals” (CIs) for each D can be found in Table 2 of [FL93].

Table 1 and Table 2 show the observed values for each D and the corresponding 95% confidence intervals for the Pacific Oyster and Atlantic Cod datasets, respectively. Since both are always negative for all datasets, there is a consistent, sometimes rather weak, sometimes significant (marked by an asterisk) indication of a “shallow” genealogy.

3.3. Likelihood analysis

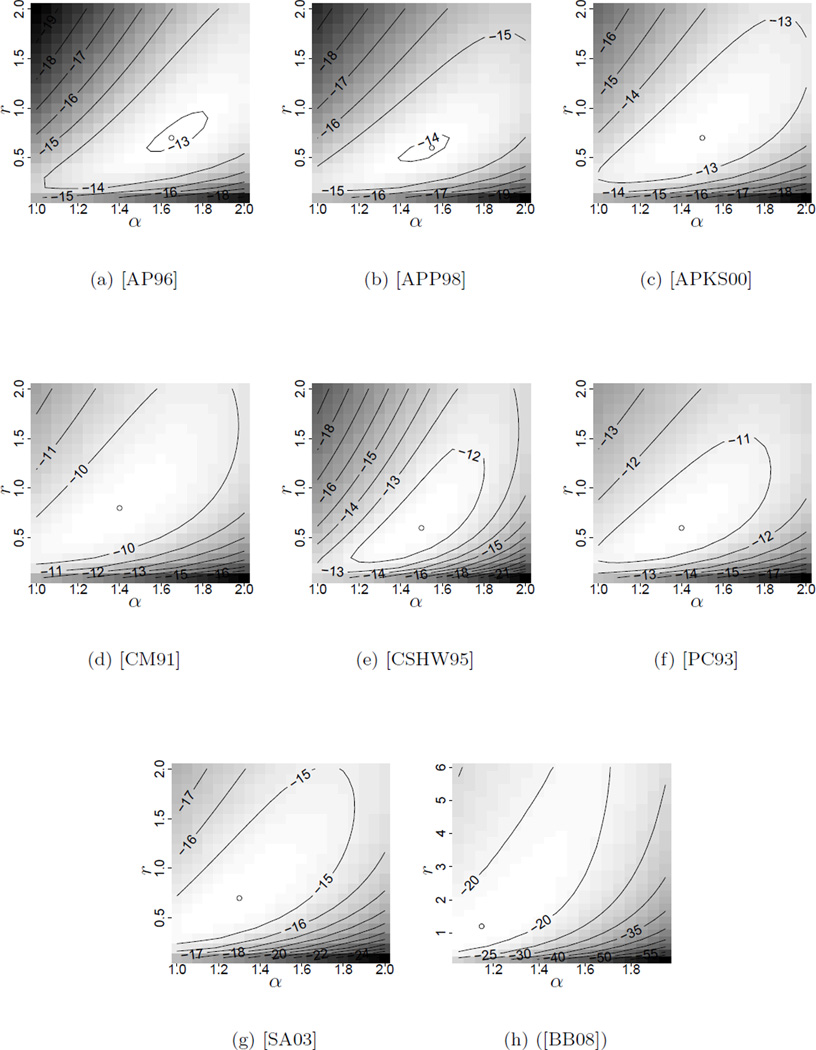
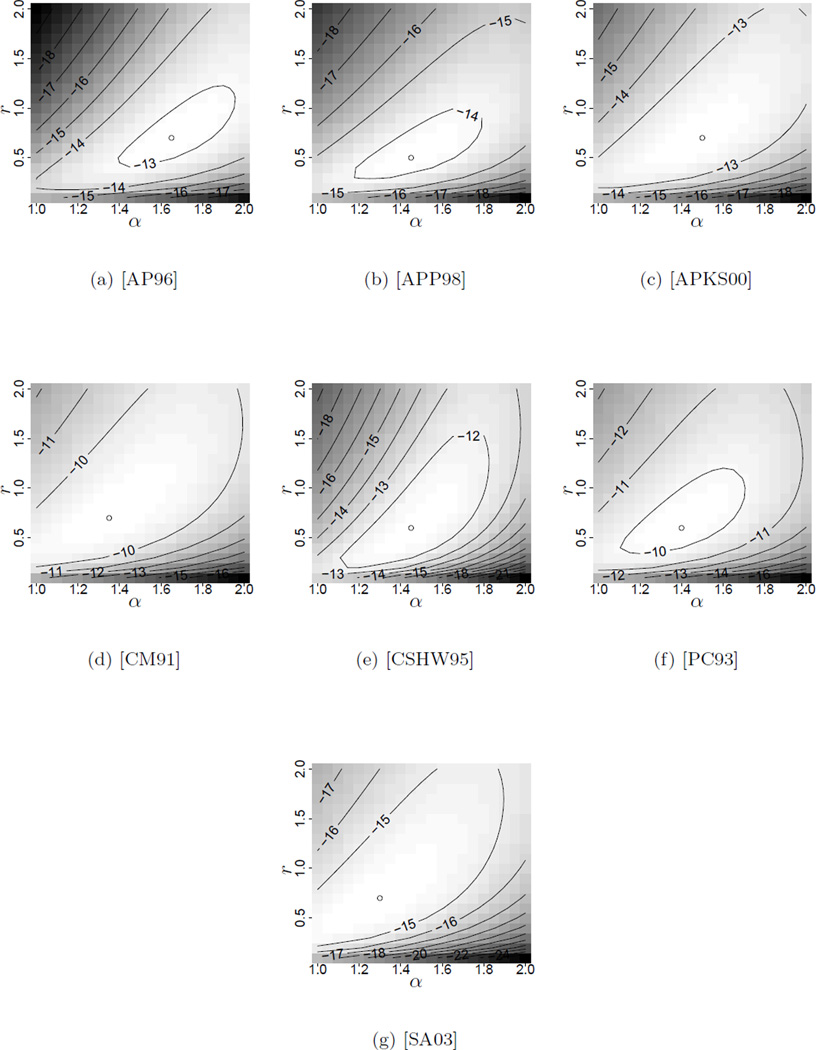
Figures 3 and 4 in Appendix B contain the likelihood surfaces for our pair of parameters (r, α), that is, the coalescent time mutation rate and the parameter of the underlying Beta-coalescent. Both the rooted and unrooted tree cases are presented, where in the former case we assumed the most frequent type to be ancestral. The results were obtained with the tool MetaGeneTree using the methods introduced in [BBS11] and [BB08], see Section 2.4. The surfaces were calculated on a discrete grid and the position of the maximum of the surface reported.

Figure 3.

Log₁₀-Likelihood surfaces for cod and oyster datasets. The argmax is indicated by a dot.

Figure 4.

Log₁₀-Likelihood surfaces for unrooted cod datasets. The argmax is indicated by a dot.

Table 3 shows the maximum likelihood estimate for the Pacific Oyster dataset. The surface was obtained on a discrete grid with spacing (0.2,0.05). For each gridpoint the likelihood was estimated by performing 108 independent runs of importance sampling using the proposal distribution [BBS11, Definition 2.11]. This proved sufficient to get an estimated relative error around 0.02. Note that our maximum likelihood estimate α̂ = 1.2 agrees well with a recently obtained estimate by [E11] of α̂ = 1.203 for the same dataset using methods based on the site frequency spectrum.

Table 3.

Estimate for r and α for the [BBB94] Pacific Oyster dataset, with the most abundant type considered ancestral.

Ref.	Location	(r̂, α̂)
[BBB94]	British Columbia	(1.2, 1.15)

The column called “rooted” in Table 4 shows the maximum likelihood estimates for the Atlantic cod datasets. The grid-spacing was (0.1,0.05), and all datasets except [CSHW95] could be analysed using the exact recursive formula. For the latter dataset we employed importance sampling with proposal distribution [BBS11, Definition 2.11] using driving values to estimate the likelihood on several gridpoints from a single run of the importance sampling, as detailed in [BBS11, Appendix A.3]. The grid-spacing for the driving values was chosen as (0.2,0.1) and we again used 108 independent runs. We calculated the likelihood for each true gridpoint whose euclidean distance is less then (0.4,0.2) of the respective driving value. After combining the results, this proved sufficient to estimate the likelihood for each true gridpoint with an estimated relative error of approximately 0.01.

Table 4.

Maximum likelihood estimates for the Atlantic cod datasets, for the “rooted” genetrees (most abundant type ancestral) and for the “unrooted” genetrees (summing over all possibilities of choosing ancestral types).

		(r̂, α̂)
Ref.	Location	rooted	unrooted
[AP96]	Norway	(0.7, 1.65)	(0.7, 1.65)
[APP98]	Baltic/ trans. area	(0.6, 1.55)	(0.5, 1.45)
[APKS00]	Greenland subsample	(0.7, 1.5)	(0.7, 1.5)
[CM91]	Norway/ Newfoundland	(0.8, 1.4)	(0.7, 1.35)
[CSHW95]	Newfoundland	(0.6, 1.5)	(0.6, 1.45)
[PC93]	Newfoundland	(0.6, 1.4)	(0.6, 1.4)
[SA03]	Faroe Islands	(0.7, 1.3)	(0.7, 1.3)

In the column titled “unrooted” we present the arg-maxima of the likelihood surfaces obtained by summing the likelihoods of all different samples obtained by choosing a different type to be the ancestral one (thus the likelihood for an unrooted genetree), following the methods introduced in [GT95, Section 2.1].

The maximum likelihood estimates for the tree-shape parameter α for both datasets range from 1.25 to 1.65. Recalling that α = 2 corresponds to Kingman’s coalescent, these results indicate consistently that the data is better explained by a genealogy allowing for multiple mergers than by a Kingman-based genealogy. We will briefly discuss possible explanations for this evidence of shallow genealogies in the next section. Again our estimates agree with the estimates of α̂ ≈ 1.55 in [E11] for the full dataset.

Note that the datasets used here contain no apriori-information about the ancestral type, so the likelihood of the unrooted trees should be used for estimation. However, as seen in Figures 3 and 4, the position of the maximum does not differ severely in both analyses. A closer inspection of the calculations reveals that the sum of probabilities of the different rooted trees is dominated by the probability of the tree with the most frequent type ancestral. Thus the root used in the “rooted”-case appears to be the most plausible choice. The only exception is given by dataset [PC93], where the sum is dominated by two summands, one of them being the tree with the root chosen due to abundance. The second tree, however, was not obviously set apart from the rest.

4. Discussion

4.1. Possible biological causes for shallow genealogies

The presence of “Hedgecock’s reproduction sweepstakes” is only one possible cause for violations of the Kingman framework produced by shallow genealogies. We will (non-exhaustively) address some effects that could account for the observed degree and pattern of variability here (following a discussion of Árnason in [A04, pp. 1882]). Apart from a recent population bottleneck for the Pacific Oyster data, the variability could be caused by selection, either acting directly on the observed part of the genome or in the “background”, the presence of frequent selective sweeps or geographical subdivision (resulting e.g. from glaciation events).

The observed mutations were synonymous or functionally equivalent replacements [A04, pp. 1882]. Thus, Árnason argues against direct selective effects as follows: Selection acting on RNA products etc. would be weak purifying selection, not positive selection required to explain the observed pattern; furthermore, it seems rather unconceivable “that by selecting at random a 250-bp fragment of a 16-kb chromosome one finds several selected sites and even balanced polymorphisms due to selection by the cellular machinery.”

Concerning indirect selection acting on the mitochondrial genome, [A04, p. 1883] writes: “[T]here might be frequent selective sweeps of mitochondrial variation, which through linkage have brought haplotypes to high frequencies.” Indeed, thinking e.g. of [DS04, DS05], recurrent selective sweeps could be a mechanism explaining multiple mergers in genealogies. [A04]’s answer is: “This explanation can account for the data but the main difficulty is to explain why there would be so much adaptive evolution going on for mitochondrial activity in cod.” Here a comparison of the mitochondrial genome and/or its protein products over several fish species might reveal that much is conserved, possibly arguing against frequent [and recent] selective sweeps.

Regarding the possibility of Population structure, either resulting from the population splitting into various subgroups in different refuges during the ice age(s) or due to local adaptations (which are linked to, but not visible in the observed region of the genome), resulting in overall balancing selection, [A04, p. 1883] writes: “The shallowness of the genealogy is evidence against these explanations.” He points to the divergence observed in [P01] to “calibrate” what shallowness means for the cod. Furthermore, concerning local refuges, Árnason argues that under this hypothesis, due to physical distance, one would expect the Baltic cod to have very different type configurations from the North Atlantic cod, which is not the case.

Finally, Árnason identifies a “sweepstake”-like mechanism as the most plausible cause, and as discussed above, population models with Beta-coalescent based genealogies are compatible with this explanation. If one believes in such a mechanism, this has significant implications for the estimation of parameters and the real-time embedding of various quantities, see Section 4.2.

The overview article of Hedgecock and Pudovkin [HP11] provides a further, more detailed discussion of the concept of “Sweepstakes reproductive success” (SRS) and of evidence for its presence in marine populations, together with a thorough literature review. Hedgecock and Pudovkin conclude that the “development of statistical tools to help decide between different coalescent models and to draw inferences about demographic and genetic parameters of interest” are welcome. In a similar spirit, [A04, p. 1883] writes “Studies of temporal variation are called for to test it and better resolve the differences between historical and contemporary factors influencing variance in offspring number and effective population sizes.” We will come back to these points asking for statistical studies in Section 4.3 below.

4.2. Age of the most recent common ancestor

Assuming that the Beta-coalescent and the estimated parameter values present a reasonable approximation to the real population mechanisms under consideration, we calibrate our models on the Atlantic cod data, using the method described in [GT94, Section 6] adapted to Λ-coalescents, see [BBS11], Appendix A.4. The maximum likelihood estimates from Table 4 can be used to estimate the time to the most recent common ancestor (T_MRCA) in coalescent-time units conditioned on the observed data. For comparison, we also estimated the time to the most recent common ancestor assuming that the Kingman coalescent is the appropriate model for the genealogy and using the corresponding estimate for the mutation rate at α = 2. In both cases, we estimated the value of the cumulative distribution function on a discrete grid with spacing 0.1 ranging from 0.3 to 4.0 using 108 independent runs of the Markov chain. The two columns in the middle of Table 5 and Table 6 show the approximation of the expected value based on the empirical distribution function, as well as the corresponding 95%-credibility interval assuming the Beta-coalescent respectively Kingman prior for the genealogy. For this we interpolated the distribution function using cubic splines in Mathematica 7.0 [W07] and reported the respective 0.025- and 0.975-quantiles. Independent replicates indicate that the variance due to the Monte Carlo method is negligible, data not shown.

Table 5.

Estimates for T_MRCA given the different datasets assuming the Beta-coalescent as the true underlying model. The respective estimated mean is given together with the corresponding credibility interval (CI), both in coalescent time units and embedded in real time, based on (r̂, α̂) from Table 4.

	coal. time		real time (in kya)
Ref.	est. mean	CI	est. mean	CI
[AP96]	1.59	[0.70, 3.07]	115.5	[50.9, 222.8]
[APP98]	1.82	[0.82, 3.47]	113.1	[51.0, 215.5]
[APKS00]	1.60	[0.68, 3.11]	116.0	[49.0, 225.7]
[CM91]	1.38	[0.55, 2.76]	114.8	[45.2, 229.0]
[CSHW95]	1.52	[0.55, 3.11]	94.7	[34.5, 193.1]
[PC93]	1.86	[0.75, 3.66]	115.5	[46.4, 227.6]
[SA03]	1.72	[0.77, 3.25]	124.6	[55.6, 235.9]

Table 6.

Estimates for T_MRCA given the different datasets assuming Kingman’s coalescent. The respective estimated mean is given together with the corresponding credibility interval (CI), both in coalescent time units and embedded in real time.

	coal. time		real time (in kya)
Ref.	est. mean	CI	est. mean	CI
[AP96]	1.19	[0.58, 2.22]	148.0	[72.7, 276.3]
[APP98]	1.29	[0.63, 2.41]	147.1	[71.6, 274.4]
[APKS00]	1.05	[0.51, 1.96]	151.7	[74.3, 284.3]
[CM91]	0.90	[0.45, 1.67]	158.0	[78.6, 293.4]
[CSHW95]	0.86	[0.43, 1.61]	151.8	[75.5, 284.2]
[PC93]	1.12	[0.53, 2.12]	162.8	[77.5, 307.6]
[SA03]	0.95	[0.49, 1.69]	186.7	[97.4, 333.6]

To embed these values into real time we use Árnason’s estimate ([A04, p.1873]) for the mutation/substitution rate of the mitochondrial DNA for the Atlantic cod µ̂ = 3.86 × 10⁻⁸/site/year. Since we consider a stretch of 250 bp in the analysis of the Atlantic cod data, the substitution rate for this stretch is given by µ̂ = 9.65 × 10⁻⁶/year. For the real time embedding of the coalescent time note that µ̂ ≈ #mut./year and r̂ ≈ #mut./coal.-time-unit. Thus the coalescent time can be transformed into real time by the relation

$$\text{coal.-time-unit}\approx \frac{\text{year}}{\widehat{r}}\widehat{\mu }.$$

The last two columns of Table 5 and Table 6 show the real time embeddings (in kya) of the time to the most recent common ancestor and the corresponding credibility intervals for the different samples, in the Beta respectively Kingman case. Some cumulative distribution functions are shown in Figure 1. We are not aware of any other estimates of T_MRCA for the presented Atlantic cod datasets in the literature, but it would be interesting to compare our results with results obtained by other methods.

More importantly, our results show that the choice of the prior distribution for the genealogy has a severe impact on the estimation of T_MRCA. The estimates under the Kingman coalescent are approximately 50% higher on average. This shows that, when estimating evolutionary parameters, it is crucial to verify the validity of Kingman’s coalescent as an appropriate model for the underlying neutral genealogy.

4.3. Further issues: Model-selection, allele-frequencies and statistical properties

It is a natural question to ask, if one finds that Kingman’s coalescent is not a suitable approximation, e.g. due to the the presence of Hedgecock’s “sweepstakes reproductive success” (SRS), which particular Λ-coalescents are of biological relevance. In order to do this, one needs to determine the distribution of the relative sizes of these reproduction sweepstakes to be won. This quantity typically depends in nontrivial ways on the offspring distribution of the species in question, but also on many other (ecological and demographic) factors which cannot be derived from simple assumptions from the outset (e.g. the geography of the habitat).

In [EW06], Eldon and Wakeley derived and used (to fit to data from [BBB94]) Λ-coalescents of the simple form Λ = α_ψ, thus positing a fixed relative sweepstake size ψ ∈ (0, 1], see Section 2.1 for an interpretation. This class has the advantages of conceptual simplicity and that it depends only on one real parameter. However, Eldon and Wakeley’s model raises the question why SRS should always be a fixed fraction of size ψ of the total population. As Hedgecock and Pudovkin point out: “It should come as no surprise, then, that just as recruitment success in marine fisheries fluctuates greatly, so too may severity of SRS fluctuate” ([HP11], p973).

In order to overcome this objection, while still keeping the statistical advantages of a class of coalescents parametrised by a single parameter, we chose the class of Beta(2−α,α) coalescents. They arise naturally as scaling limits of branching-type populations models, where each individual reproduces independently (subject to preservation of the total population size) and offspring numbers are heavy-tailed with a power-law decay, see (6) and the subsequent discussion, in particular the relation to “type-III-survivorship”.

Note that our scenario, motivated by Schweinsberg’s model, considers infrequent reproduction sweepstakes. This, together with a certain amount of independence between reproductive events and subexponential tail distributions, makes it highly unlikely to observe several “sweepstakes winners” within one generation (hence ruling out Ξ-coalescent like behaviour): Typically, if a family of the order of the total population size is produced, the amount of offspring of the most successful individual dominates the number of offspring of the second-most successful individual, thus ruling out, at least for large populations, the emergence of simultaneous multiple mergers.

However, in other scenarios, other Λ-coalescents might become relevant. Examples include Durrett and Schweinsberg’s models of recurrent selective sweeps [DS05] mentioned above. The presence of externally induced recurrent severe bottlenecks might even yield Ξ-coalescent based genealogies, admitting simultaneous multiple merger coalescents [BBM+09]. Often, as in the bottleneck scenario, simultaneous multiple mergers require drastic (externally induced) changes in the environment, which we do not consider here.

Of course, stochastic fluctuations in the ocean environment (see [HP11], p973), could potentially cause such bottlenecks. It will be an objective of future research to test whether deviations from Kingman’s coalescent seem to be induced predominantly by independent heavy-tailed reproduction, or by external stochastic fluctuations. However, such an analysis is clearly out of scope of this expository paper (in particular, there is a high risk of overfitting within the vast class of Ξ-coalescents).

Still, a way to assess the adequacy of the underlying coalescent models is to compare how well these models may be fitted to functions of the observed data such as frequency spectra. Indeed, in a recent presentation², Schweinsberg compared minimal-least-squares fits of the observed site frequency spectrum of the full atlantic cod dataset from [A04] (sample size n = 1278) to the expectation in Beta(2 −α, α)-models (using an asymptotically exact formula for the expected site frequency spectrum for the Beta(2−α,α)-case). The quality of the fit for the Beta-coalescent, with an estimated optimal α = 1.43, is striking and much better than for the Kingman-coalescent, making a strong point in favour of the use of Beta-coalescent models (the fit for the pacific oyster dataset from [BBB94] mentioned in the same presentation is worse, however, as already mentioned above, in this case the population history suggests a recent severe bottleneck, which is not literally compatible with any of the coalescent models considered here).

It is a very interesting question in how far the DNA sample data considered here allows a “retrospective” assessment of “sweepstake sizes” distributions, in particular whether a fixed sweepstake size ψ ∈ (0, 1] as in the models considered by Eldon and Wakely in [EW06] appears more or less plausible than the “random” one that is implicit in the Beta(2 −α, α)-models.

In preliminary computations, we computed likelihood values for the some of the component data sets considered here with Λ as in (3), varying ψ on a grid in (0, 1]. The maximal likelihood values, attained at ψ’s between 0.04 and 0.07, were sometimes comparable and sometimes one to two orders of magnitude smaller than those for the Beta(2−α, α)-coalescents (data not shown). In addition, we used the simulation algorithm described in [BB08] to estimate the expected site frequency spectrum under a coalescent with Λ as in (3) with n = 1278; the fit to the observed frequency spectrum of the total sample described in [A04] appeared much worse than that derived from the Beta(2−α, α)-coalescent described by Schweinsberg (data not shown). While this suggests that “non-fixed sweepstake sizes” might be indeed a more reasonable model, it also indicates that larger sample sizes and presumably also multi-locus data sets would be required for a reliable answer. This is beyond the scope of the present work.

Finally, it is still a largely open question to assess the statistical properties of the estimator employed here, which is based on methods described in [BBS11]. Some considerations in this direction can be found in [S09].

Appendix A. Detailed description of the datasets

We now describe the datasets analyzed in this paper in more detail. The datasets together with the scripts for handling the analysis are available from the authors upon request.

The input for our method has to be a valid genetree (cf. Section 2.4) under the infinitely-many-sites model, noting that DNA sequence data can only be transformed into this data structure if they satisfy the “four-point” condition [BB08, Equation (10)]. We now provide details on how we dealt with occasional violations of this condition in the datasets that we analysed.

Appendix A.1. Pacific Oyster dataset ([BBB94])

The dataset was taken from [BBB94], where the authors obtained the data as the result of a restriction-enzyme digest of mitochondrial DNA taken from 155 Pacific oysters (Crassostrea gigas) from British Columbia. The authors reported the fragment sizes resulting from 9 different enzymes in their Table 2 [BBB94, pp. 1612–1613].

We translated these lists of fragment length into pseudo-sequence data for every enzyme. Such a pseudo sequence is a list of zeros and ones for every reported type, specifying the presence or absence of a restriction enzyme binding site. The choice whether 1 denotes the presence of a binding site and 0 the absence or vice versa is determined uniquely once we specify an ancestral type later. Note that in [BBB94, Table 2] the authors report a type ‘C’ for the restriction enzyme ‘HincII’, however, this type is not reported in [BBB94, Table 1], so we omitted this type ‘C’ for the subsequent analysis.

Table 1 of [BBB94, page 1610] shows how the different observed haplotypes are composed of the sub-haplotypes, along with the respective abundance of a given type in the respective sub-populations. Note that in [BBB94, Table 1] type ‘HT32’ reports a sub-type ‘F’ for the enzyme ‘HAEII’, but this sub-type ‘F’ does not occur in the respective [BBB94, Table 2], thus we treated this sub-type as ‘E’ in the subsequent analysis.

We chose the most abundant type “PS2” to be ancestral, thus uniquely specifying which pattern of presence/absence of restriction sites corresponds to the all-zero pseudo-sequence. To remedy the violations of the infinitely-many-sites model present in the dataset, we deleted the sites for ‘HindIII.5’, ‘HaeIII.12’, ‘AvaII.1’, ‘HaeIII.11’, ‘HaeII.6’, and removed the types ‘HS45’, ‘PS10’, ‘HS44’, ‘DB40’. Note that these steps eliminate the only difference between PS1 and PS2, so that ultimately PS1 and PS2 are taken to be ancestral. After these steps, the data can be converted into a valid genetree as described in Section 2.4.

Appendix A.2. Atlantic Cod dataset(compiled in [A04])

The Atlantic Cod dataset is based on DNA sequence data taken from a 250 bp stretch of the mitochondrial cytochrome b gene of the Atlantic cod (Gadus morhua). In the numbering of the sites from [JB96], this stretch ranges from site 14,459 to site 14,708 (included). In [A04], Árnason took several cod datasets from different publications, combined them and provided an analysis of the whole dataset. However, since this combined dataset is too big to be treated by our method for computing likelihoods based on the full information, we analysed certain samples separately. As Árnason pointed out, the samples stem from various localities throughout the Atlantic, ranging from Newfoundland [CM91], [PC93] & [CSHW95], Greenland [APKS00], the Faroe Islands [SA03], and Norway [AP96] to the Baltic Sea [APP98].

The DNA sequence data of the different types present in the different samples can be found in Figure 1 on page 1874 in [A04]. The composition of the sample from [AP96] is {A: 35, E: 25, G: 14, D: 14, NI: 4, B: 2, C: 2, F: 1, GI: 1, DI: 1, BI: 1}, the sample from [APP98] is {E: 62, A: 19, G: 12, D: 6, DI: 3, H: 2, ES: 1, DK: 1, C: 1, EJ: 1, NI: 1}, the sample from [APKS00] is {A: 48, D: 6, E: 8, G: 7, C: 1, NI: 1, MI: 1, LI: 2, S: 1, PI: 1, GJ: 1, ED: 1}, the sample from [CM91] is {A: 36, B: 2, C: 2, D: 1, E: 4, F: 1, G: 4, H: 1, I: 1, J: 1, K: 1, L: 1}, the sample from [CSHW95] is {A: 201, B: 1, C: 2, D: 7, E: 4, H: 3, J: 2, N: 4, O: 1, P: 1, S: 3, T: 1, X: 2, Y: 2, Z: 1, a: 1}, the sample from [PC93] is {A: 84, G: 6, E: 4, P: 1, X: 1, U: 2, N: 2, M: 1, C: 1, J: 1}, and the sample from [SA03] is {A: 26, E: 13, D: 11, G: 10, MI: 3, H: 2, NI: 1, C: 1, GJ: 1, EY: 1, EX: 1, EL: 1, EK: 1, DO: 1, DL: 1}.

From [APKS00] we took the Greenland subsample and we restricted the sample from [APP98] to the Baltic and transition area. In [SA03], the authors provide the DNA sequence data of a larger 566 bp stretch from which we only took the information of the 250 bp fragment in question. Furthermore, in [CSHW95], the authors report the type ‘R’ which differs from the type ‘A’ only outside of the 250 bp segment we are considering. Thus we count this type as an ‘A’ type.

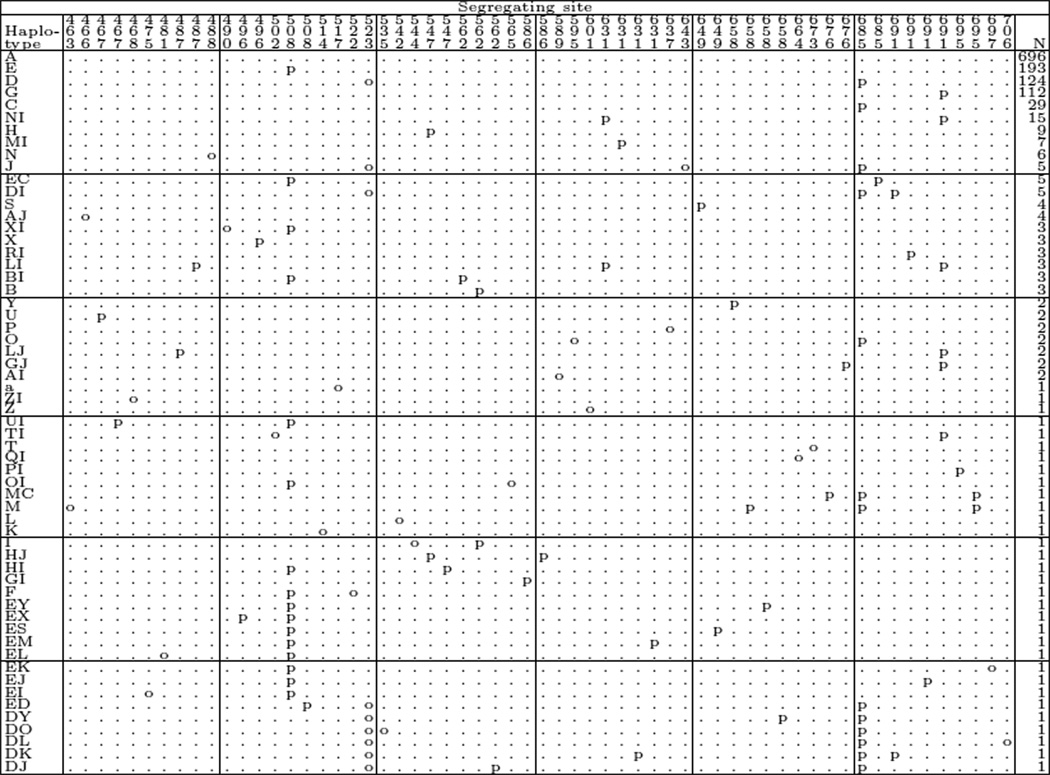
Since the full dataset from Figure 1 on page 1874 in [A04] contains violations of the infinitely-many-sites model, we solved these violations by introducing a consistent pattern of parallel mutations. This procedure replaced each mutation violating the infinitely-many-sites model by a certain number of mutations that were attributed to the different types in a non-violating pattern. The complete modified dataset with all parallel mutations is given in Figure 2.

Figure 2.

Árnason’s dataset with violations of the IMS model resolved through parallel mutations. Here ‘o’ denotes the original mutations (as in Árnason’s dataset), whereas ‘ p’ denotes the putative parallel mutations.

We then obtained the subsamples corresponding to the different publications by choosing the corresponding types in the corresponding quantities from this violation-free dataset, and then converted them into genetrees. We chose ‘A’ as the ancestral type for each dataset.

Appendix B. Likelihood surfaces

The log₁₀-likelihood surfaces for the cod and oyster datasets in the rooted case are shown in Figure 3, whereas Figure 4 shows the log₁₀-likelihood surfaces for the cod datasets in the unrooted case.