Generic theory for channel sinuosity

Abstract

Sinuous patterns traced by fluid flows are a ubiquitous feature of physical landscapes on Earth, Mars, the volcanic floodplains of the Moon and Venus, and other planetary bodies. Typically discussed as a consequence of migration processes in meandering rivers, sinuosity is also expressed in channel types that show little or no indication of meandering. Sinuosity is sometimes described as “inherited” from a preexisting morphology, which still does not explain where the inherited sinuosity came from. For a phenomenon so universal as sinuosity, existing models of channelized flows do not explain the occurrence of sinuosity in the full variety of settings in which it manifests, or how sinuosity may originate. Here we present a generic theory for sinuous flow patterns in landscapes. Using observations from nature and a numerical model of flow routing, we propose that flow resistance (representing landscape roughness attributable to topography or vegetation density) relative to surface slope exerts a fundamental control on channel sinuosity that is effectively independent of internal flow dynamics. Resistance-dominated surfaces produce channels with higher sinuosity than those of slope-dominated surfaces because increased resistance impedes downslope flow. Not limited to rivers, the hypothesis we explore pertains to sinuosity as a geomorphic pattern. The explanation we propose is inclusive enough to account for a wide variety of sinuous channel types in nature, and can serve as an analytical tool for determining the sinuosity a landscape might support.

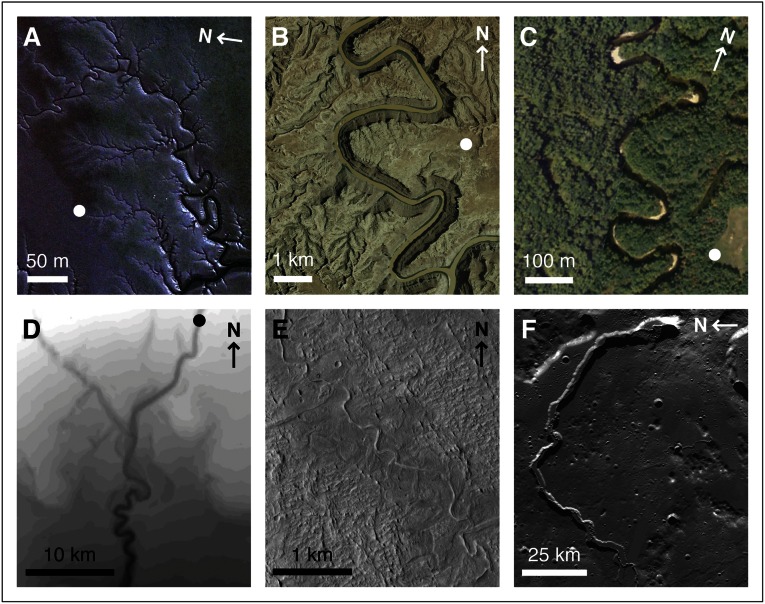
Sinuous, threadlike flows are ubiquitous features of landscapes on Earth and other planetary bodies (Fig. 1). Sinuosity is typically discussed as a consequence of channel migration processes in meandering rivers (1–9), where flow through a channel with modifiable boundaries and a curved planform sets up internal flow instabilities that drive spatial patterns of bank erosion and accretion, which change planform curvature. The physical mechanisms by which a nearly straight channel evolves into a freely meandering planform have been studied intensively and with great success. Strath terraces and meander bend cutoffs are evidence that even bedrock river channels can migrate, adjusting their sinuosity over time (10, 11). Despite their prominence, rivers with migrating meanders are a subset of the sinuous channel types that exist: lunar and Venusian rilles (12, 13) are sinuous, static patterns in lava channels; drainage channels in tidal mudflats that show little or no morphologic evidence of migration behavior can be characterized as quasi-static sinuous patterns (14–16). Sinuosity in some channels is described has having been “inherited” from a preexisting morphology (10, 14), but the nature of the antecedence tends to be unspecific or unexplained.

Fig. 1.

Sinuous channels in (A) intertidal mudflat channels near Seoul, South Korea; (B) river channels in bedrock southwest of Moab, Utah; (C) a migrating reach of the Ellis River in Maine; (D) digital elevation model of submarine channels offshore of Rio Doce, Brazil; (E) relict fluvial channel patterns in the Aeolis Planum on Mars; and (F) a lunar volcanic rille in the Vallis Schröteri. (See Table S1 for locations and image credits in this and other figures.)

If not all sinuous, threadlike flows evolve from effectively straight initial planforms, then planform sinuosity as a geomorphic trait is not inherently contingent upon a capacity to migrate. We present a generic theory for sinuosity in threadlike flows (which here we refer to as channel sinuosity for simplicity). We use an exploratory flow-routing model to show that changing the variance of flow resistance in the landscape (e.g., representative of local topographic roughness or vegetation density) relative to mean landscape slope produces a range of sinuous patterns with natural analogs. A surprising relationship between sinuosity and floodplain roughness relative to valley slope for 20 rivers from around the globe yields an independent test of the theory. We suggest that this ratio of flow-resistance variance (R) to slope (S) exerts a primary landscape control on path sinuosity (Ω) both in static and dynamic patterns of flow.

Numerical Model

Our model is a cellular topography in which flow finds a path of least resistance across a planar domain of slope S superimposed with random values between 0 and R (Fig. S1). Because slope imposes a preferred flow direction, the model employs the rules of a directed Brownian walk. Similar minimum-resistance simulations have been applied previously to mathematical structures and self-organization in natural fluvial systems and networks (17, 18), and have long-standing precedence in percolation theory (19) and theoretical material physics (20).

The domain landscape is the plane

where z is domain elevation and L is the length of the domain in the x direction (the plane extends in the y direction). Subtracting random topographic perturbations with values 0–R adjusts the elevation by

where r_i,j is the perturbation at a given cell (i, j). The results we present here are for a square domain of L = 100 with nonperiodic boundaries. (In terms of fluvial valleys, we are assuming that the domain length and downvalley length are the same.) We vary R and S at increments equal to 0.001 over the interval 0.001–0.1 to produce domains with R/S ratios between 0.01 and 100.

The flow path follows the local gradient between adjacent cells, occupying whichever of its eight neighbors has the lowest value. Length of the flow path (P) relative to the length of the domain (L) yields the path sinuosity (Ω = P/L). When the random perturbations are much smaller than the landscape gradient (R << S), the flow path always occupies one of three right-hand neighbor cells because their elevations are locally always the lowest. Conversely, when the magnitude of R overwhelms downslope differences (R >> S), the flow becomes effectively undirected. Rather than always traveling downslope, the flow path is as or more likely to occupy a lateral or rear-flanking neighbor and trace a more excursive (sinuous) route.

Three numerical artifacts arise from this model design. First, when R >> S, the lowest-neighbor rule can result in an arbitrary configuration of neighbors that traps the flow path in an infinite loop. To override this arbitrary trapping, flow-occupied cells are temporarily assigned the unperturbed cell elevation (Eq. 1), constituting a local high that discourages but does not prevent the path from recrossing itself. Recrossed cells are not double counted in the path length. The second artifact derives from the discretized cellular domain. A move to a cardinal neighbor adds unit length equal to 1 to the flow path; a move to an ordinal (diagonal) neighbor adds unit length equal to √2. Because flow moves to the lowest-elevation neighbor even when differences between downslope neighbors are infinitesimal, flow paths with Ω = 1 only occur in the absence of topographic perturbations (R = 0). Therefore, when 0 < R << S, the discretized domain always produces sinuosities 1 < Ω < 1.4 (occupation only of downslope, ordinal neighbors produces Ω = 1.4). At the other extreme, when R >> S, path sinuosity loses physical significance and becomes an undirected Brownian walk. Mathematically, sinuosity can be infinitely large, but highly sinuous natural channels, such as in rivers with freely migrating meanders, express Ω ∼ 3 (2, 21). We address this Brownian artifact of exaggerated sinuosity as follows. Once a flow path is complete, we assign the flow-occupied cells elevations according to

which ensures that the flow path contains the lowest local elevations in the domain (Fig. S1). We rerun the flow-path simulation for 10 iterations, updating the domain each time, so that the path adjusts to a minimum length for the specified conditions (Fig. S2). Flow paths through slope-dominated domains (R/S << 1) lock into their minimum sinuosity on the first iteration; highly excursive planforms through resistance-dominated domains (R/S >> 1) find less sinuous flow paths after a few iterations (Fig. S2). This rule is functionally analogous to meander cutoff in channels with migrating bends, but is not explicitly mechanistic.

Results

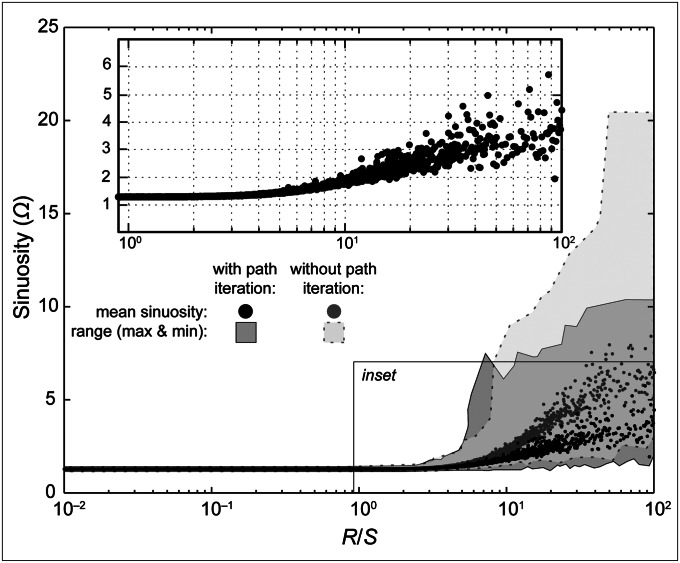
Ensemble results from over 40,000 flow-routing simulations (Fig. 2) show how path sinuosity (Ω) responds to changes in resistance variance relative to slope (R/S). When slope exceeds the resistance term (R/S < 1), paths find the lowest sinuosities allowed by the model’s discretized domain (mean sinuosity for all R/S < 1 is approximately Ω ∼ 1.28 ± 0.04). In the vicinity of R/S ∼ 1, Ω begins to increase; with increasing values of R/S > 1, the variance of Ω scales with mean Ω (Fig. S3A). Fourier analysis of flow paths shows no preferred wavelength in the modeled planforms (Fig. S3B). These characteristics reflect the model’s underlying Brownian mechanics, with the strength of resistance (R) relative to slope (S) driving the transition between directed and undirected random walks.

Fig. 2.

Semilog plot showing ensemble results of modeled sinuosity (Ω) versus relative resistance (R/S). Shaded regions illustrate the range (maxima to minima) of sinuosities produced by the model with (dark region) and without (light region) the iteration rule to shorten supersinuous paths. Black dots and gray dots show the mean sinuosities for both cases, respectively. Inset shows in greater detail mean sinuosities generated with the iteration rule. Additional statistical properties of the model are provided in Fig. S3.

It is interesting to note that the upper range of planform sinuosities we generate with and without our iterated, minimum-path procedure are consistent with results of other numerical planform models whose channel patterns, with and without meander cutoffs, derive from parameterization of in-channel flow (3, 4, 22). However, unlike in other models, our flow paths are static once formed. We do not route flow around contortions in curvature (8, 9) or explicitly treat means by which channel geometries evolve (17, 23). Our simulations may be interpreted as initial flow paths, perhaps most readily applicable to fixed flow planforms like volcanic rilles. Initial planforms can also arise anywhere initially unchannelized flow interacts with a mobile bed, incising a sinuous planform as a function of valley slope and flow resistance. Where planform patterns may be described as quasi-static, an original sinuosity may persist as a kind of legacy effect in planform evolution (10, 14, 24). In the special context of freely migrating channels, these initial planforms may be transitory patterns that hydraulic properties of in-channel flow subsequently rework.

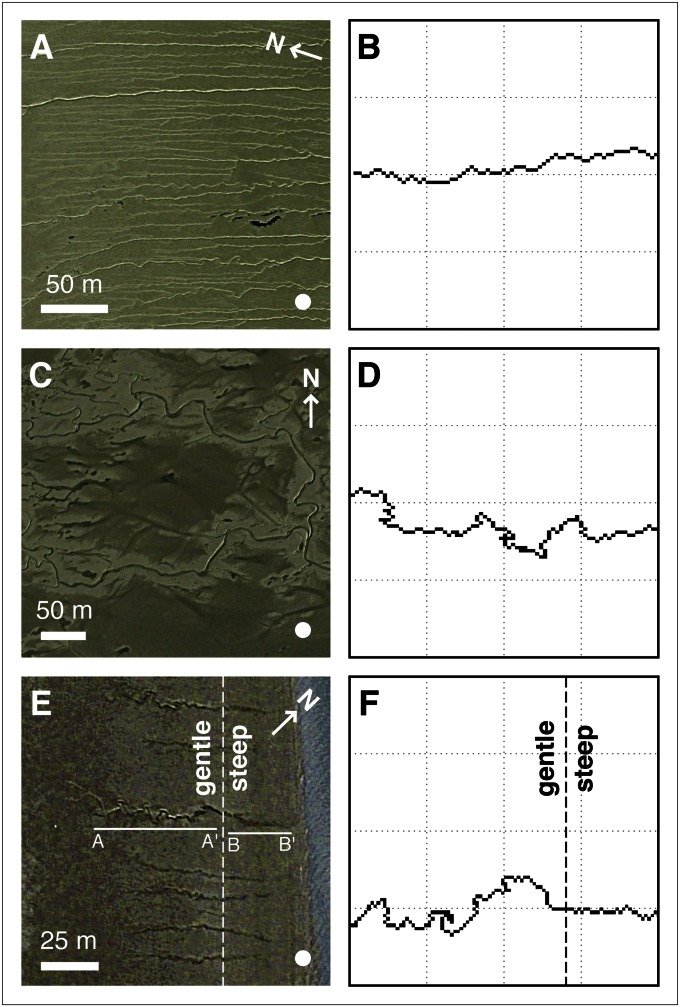
Channels in intertidal mudflats offer an illustration. Sinuous drainage channels can incise rapidly into a mudflat and persist for decades with little discernible change (14–16). Allowing the simplifying assumption that intertidal mudflats share broadly similar material properties (e.g., fine-grained, cohesive sediment), then to the first approximation we can compare channel paths in different mudflats on the basis of slope. For an arbitrary, low fixed resistance R, our model generates channel planforms on steep (R/S < 1; Fig. 3 A and B) and gentle slopes (R/S > 1; Fig. 3 C and D) that resemble channels in comparable mudflats, respectively. Likewise, simulations in which channel sinuosity adjusts across a break in slope are substantiated by examples in the field (25) (Fig. 3 E and F). For example, using a mean slope of S ∼ 0.005 from A to A′ (25) and a sinuosity of Ω ∼ 1.9 measured from A to A′ in Fig. 3E, we can apply the relationship of Ω to R/S in Fig. 2 to find an approximate value of R = 0.05. Entering these values for R and S into the model delivers a channel with sinuosity Ω = 2.0 between A and A′ (Fig. 3F). Relative to the steeper mean slope of S ∼ 0.04 between B and B′ (25), the same resistance R = 0.05 predicts a sinuosity of Ω ∼ 1.3. From Fig. 3E, sinuosity between B and B′ is approximately Ω ∼ 1.1; the corresponding modeled sinuosity in Fig. 3F is .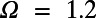

Fig. 3.

Comparisons of channels in intertidal mudflats and simulated planforms. (A) Low-sinuosity channels in an intertidal river bank and (B) a simulated low-sinuosity channel (R = 0.005; S = 0.01; R/S = 0.5). (C) High-sinuosity channels in an intertidal mudflat and (D) a simulated high-sinuosity channel (R = 0.005; S = 0.001; R/S = 5). (E) Intertidal channels that cross a break in slope (dotted line) from gentle (A–A′) to steep (B–B′), and (F) a simulated channel over a slope break based on (E) (25), where S ∼ 0.005 between A and A′ and S ∼ 0.04 between B and B′, using a resistance of R ∼ 0.05 derived from Fig. 2.

Using the relationship in Fig. 2 to back out a value for R based on measurements of S and Ω produces an intriguing comparison but does not constitute an independent test of the data. For that, we offer the following derivation. The relationship R/S is, in essence, a surrogate form of the Froude number, which likewise can be expressed in terms of slope and a parameter for flow resistance. The standard formulation of the Froude number (F) for open-channel flow is

where v is cross-sectional mean flow velocity, g is acceleration due to gravity (g = 9.81 m s⁻¹), and h is uniform flow depth. We can express v according to the Gauckler–Manning formula,

where S is slope and n is the empirically derived Gauckler–Manning coefficient, or Manning’s n (s m^−1/3). Substituting Eq. 5 into Eq. 4 yields an expression of the Froude number based on characteristics of the floodplain, rather than the channel:

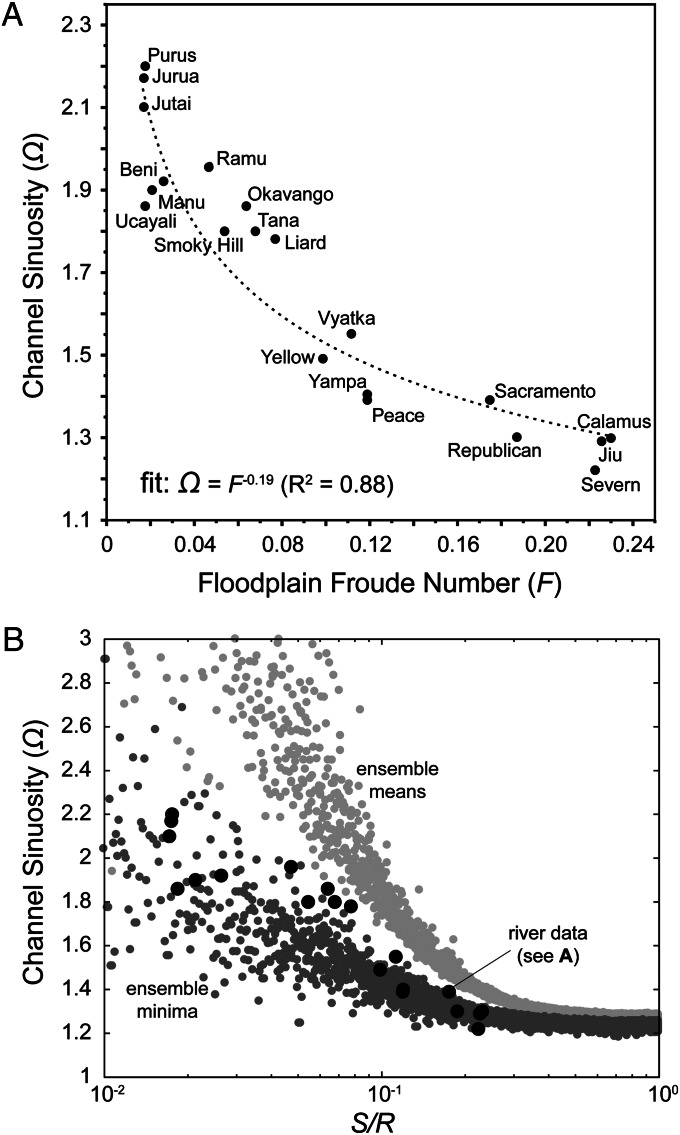
We estimate the floodplain Froude numbers for 20 meandering rivers around the world (Table S2), assuming steady, uniform flow conditions and the same depth of inundation across each floodplain (h = 1 m; h^1/6 makes F relatively insensitive to this simplification). Manning’s n has been calibrated for a variety of floodplain settings. Because F is sensitive to chosen values of n, we limit n to three possible values based on three generic, observable conditions of predominant floodplain vegetation (26): grasses or row crops (n = 0.05); brush and some trees (n = 0.10); or trees with dense understory (n = 0.15). Values for valley slope (S) were obtained from the literature. The resulting data (Fig. 4A) suggest that valley slope relative to resistance—the prevailing floodplain conditions S and n—explains ∼88% of the variability in planform sinuosity. These data fall neatly among the ensemble minimum sinuosities generated by the model (Fig. 4B) when the model data are inverted (expressed in terms of S/R) to match the Froude number convention. Artificially high sinuosity in the model when R/S >> 1 (or, equivalently, when S/R << 1) skews the mean sinuosity toward higher values, even with the path-iteration rule; we therefore expect better observational agreement with modeled sinuosity minima than with the means, especially given the rarity with which natural freely migrating meandering rivers exhibit Ω > 3.

Fig. 4.

(A) Sinuosity versus floodplain Froude number for 20 rivers around the world. Details regarding these data and their sources are available in Table S2. (B) Semilog plot of ensemble means (light gray dots) and minima (dark gray dots) of modeled sinuosity versus S/R, in keeping with the Froude number convention used in A and Eq. 6. Data from A are superimposed (large black dots).

Our abstraction of in-channel dynamics does not refute or discount the importance of secondary flow mechanics. Rather, the remnant of the initial planform may be statistical, retained more in the morphometry of the evolved planform than preserved in its morphology. Where meander-migration theory predicts a preferred meander wavelength for a channel, the random-walk mechanism in our model produces a broad spectrum of wavelengths resembling brown noise (Fig. S3B). This is consistent with empirical observations that not all rivers express a dominant wavelength (27, 28). Our model delivers the initial sinuosity of a new channel; that sinuosity may change with modifications to the channel planform driven by dynamics of in-channel flow. If resistance and slope set the initial planform condition that subsequent meander-migration dynamics amend, then the broad-spectrum properties of the initial planform mean that there will always be perturbations present with the wavelength (or wavelengths) that meander migration will tend to amplify. Even without incorporating the dynamics of in-channel flow that enable natural, single-thread fluvial systems to develop characteristic meander wavelengths, our model offers an explanation for the important implications of Fig. 4: that F is an important control on the long-term sinuosity that freely meandering rivers attain. In this setting, the flow paths in our model are more directly analogous to avulsions or overbank flows, extrachannel departures for which the effects of variable flow resistance might supersede in-channel dependencies, at least temporarily. The correlation between Ω and F in Fig. 4 reflects in part the role of overbank flows in modifying planform sinuosity. As in-channel dynamics lengthen the channel, incising overbank flows shorten it by finding new routes over the floodplain. Our model mechanics thus come into play during two phases of planform evolution in a freely meandering river channel: first during initial pattern formation, and again when overbank flow forces new interaction with the floodplain. Between these two phases, migration dynamics will dominate channel planform behavior.

The floodplain Froude number may extend to adjustments in channel sinuosity related to land-use changes that affect roughness characteristics of the floodplain. Studies of land-use history in the Pacific Northwest in the United States have linked deforestation in riparian corridors to morphological changes in fluvial channels (29). Similarly, historical maps and descriptions of the Sacramento River in California (30) indicate that before at least 1874, the river followed the sinuous channel (Ω = 2.2) shown in Fig. 5, and was flanked by natural riparian vegetation. That vegetation was subsequently cleared and replanted in orchards; by 1898, multiple incidents of meander cutoff had straightened the channel to the path shown in white (Ω = 1.4). Given the valley slope along this reach (S = 3.3 × 10⁻⁵) (31), the cutoff-driven change in sinuosity may be explained as a function of a change in resistance R, reflecting the transition from local riparian vegetation to orchard plantations (30, 31). In terms of our application of Manning’s n, this would represent a decrease from n = 0.10–0.15 to n = 0.05 (Fig. S4).

Fig. 5.

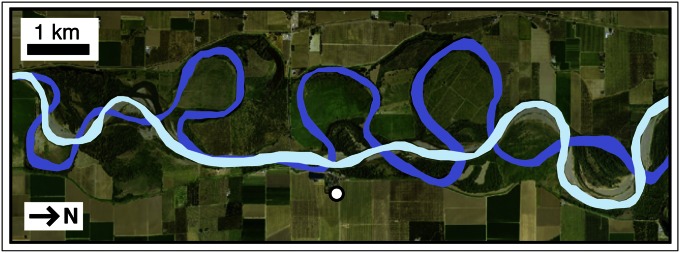
Land-use histories that change riparian vegetation density, thereby changing floodplain resistance, may affect channel sinuosity. On this reach of the Sacramento River (California), sinuosity decreased from Ω = 2.2 before 1874 (blue) to Ω = 1.4 by 1898 (white) after natural vegetation was replaced with planted orchards. For historical and present river conditions relative to data in Fig. 4B and Fig. S4.

Discussion

The resistance parameter R in our model is an abstraction of physical flow impediments but is not strictly theoretical: for a given surface, R might be determined from a high-resolution digital terrain map, such as a light detection and ranging (LIDAR) survey or laser scan of a laboratory flume. Investigations of lunar and Venusian rilles have suggested that rille sinuosity likely depends on preexisting conditions of landscape topography and slope (12, 13). Consider, as a conceptual example, the lunar landscape in Fig. 1F. A high-resolution topographic map would capture the subtle undulations in the surface underlying the rille. Subtracting mean slope of that surface from the elevation data leaves residuals that constitute the topographic variability; the maximum absolute value of those residuals is R, the upper limit of the range of topographic resistance 0–R. If mudflats are of interest, then a sensitive resolution of microtopography would likely allow a comparable analysis. LIDAR surveys of vegetated environments typically separate laser “first return” from “last return” as a way of distinguishing between the canopy and the ground (or “bare earth”). Calculating R solely from last-return measurements of topographic variability would neglect vegetation’s role in flow resistance, but measuring vegetation-density distributions in the first-return data as factors of floodplain resistance, beyond informing a Manning’s n classification, could produce a more comprehensive approximation of R. In a long-duration laboratory flume experiment in which floodplain vegetation (such as alfalfa sprouts) and the channel planform coevolve, R would change over time as a function of vegetation growth, which repeated topographic laser scans of the flume apparatus could record.

Like Manning’s n, the friction factor in the Darcy–Weisbach equation for head loss, or a drag force on woody riparian vegetation (11, 32), the resistance term R in our model is a flow-resistance term. We reiterate that R, as we have applied it, does not represent substrate erodibility. Substrate erodibility and bank stability, which can be functions of material properties and vegetation root systems, are certainly essential to the mechanisms that drive channelization and channel-migration behaviors. Positive correlation between erodibility and channel sinuosity suggests rock weakness is a primary control on sinuosity in bedrock rivers (7, 10). Recent laboratory attempts to isolate the conditions sufficient for sustaining a meandering, sinuous channel have highlighted the importance of increased bank strength relative to bed material, where bank strength is a function of sediment cohesiveness, stabilization by vegetation, or a combined effect (5, 6, 21). A channel-planform model based on flow resistance does not replace these elements, but can nevertheless inform investigations of planform origins even in systems where erodibility is important. Collectively, the sinuosities in our model derived from random walks constrained only by resistance and slope comprise a set of simplest-case explanations, a template of null hypotheses that help isolate and clarify more complicated, specific, or dynamic factors driving planform evolution.

Although this theoretical template does not explicitly predict the multichannel planforms (e.g., anastomosing, braided) that exist in nature, individual channel threads within such planforms—where individual threads can be differentiated—should share a similar dependence on local resistance and slope. Conventionally, sinuosity is a metric exclusive to single-thread channels. For example, it is unclear what would constitute a single-thread reach of a braided channel during normal flow conditions. A simple anastomosing pattern is perhaps a more manageable thought experiment: where flow divides among several intertwined routes, sinuosity for each determined “thread” could be calculated separately; together, those sinuosities would represent the sinuosity range the floodplain will support, as we use our model to suggest.

One practical application of relative resistance (R/S) could be to inform how floodplains of artificially straightened rivers are evaluated for restoring riparian ecosystems (33). Stream flow at the local scale of a channel bend and sinuosity at the larger scale of the river planform are both important to a river’s physical and ecological dynamics: even as internal flows amend the channel at a given bend, the overall planform sets the conditions for in-stream flow (9) and, by extension, in-stream habitats. Channel sinuosity will still reflect the characteristic resistance of the floodplain even in fluvial systems dominated by migration dynamics (e.g., Fig. 4). If a channel needs a large R/S to be highly sinuous, then even a channel engineered to be sinuous will tend to straighten if the R/S ratio of its floodplain is suppressed or inherently low and if overbank flows are allowed to mobilize the floodplain surface. Alternatively, increasing appropriate floodplain resistance might foster a channel more sinuous than extant hydraulic geometry may predict. Narrow rivers in densely forested regions, for example, appear to owe their channel patterns to log jams and other woody debris obstructions (29); log jams are thus an obstructive type of floodplain resistance that deforestation removes but reforesting can restore.

Conclusions

We demonstrate how two intrinsic properties of a floodplain or landscape surface—slope (S) and resistance (R)—can exert a first-order control on flow-path sinuosity. Paradoxical observations of static and dynamic flow patterns motivate our analysis: explanations for sinuosity that hinge on migration dynamics do not translate easily to static sinuous planforms; likewise, as others have noted (21), vegetation-driven explanations for planform sinuosity cannot extend to the same patterns in unvegetated environments. Although erodibility exerts a principal control on channelization and flow dynamics within a channel, flow resistance is arguably a more general condition applicable to a greater variety of single-thread flows. The resistance parameter R informs the range of possible sinuosities a given landscape might support. Independent of internal flow forces, R is potentially useful in remote-sensing applications and anywhere in-channel data are lacking or unobtainable. For example, determination of R might inform requisite conditions for sustainable sinuosity in engineered streams. The relationship we propose is an explication of sinuosity generic enough to account for the ubiquity of sinuous channel patterns in nature and not conflict with the various mechanistic processes from which specific channel types can derive.

Methods

The numerical model was written in Matlab (version R2013a). The model algorithm is described in full above. Schematic diagrams and figures of model operations, as well as the data supporting our floodplain Froude number calculations, are available in Supporting Information.