Frequent adaptation and the McDonald–Kreitman test

Abstract

Population genomic studies have shown that genetic draft and background selection can profoundly affect the genome-wide patterns of molecular variation. We performed forward simulations under realistic gene-structure and selection scenarios to investigate whether such linkage effects impinge on the ability of the McDonald–Kreitman (MK) test to infer the rate of positive selection (α) from polymorphism and divergence data. We find that in the presence of slightly deleterious mutations, MK estimates of α severely underestimate the true rate of adaptation even if all polymorphisms with population frequencies under 50% are excluded. Furthermore, already under intermediate rates of adaptation, genetic draft substantially distorts the site frequency spectra at neutral and functional sites from the expectations under mutation–selection–drift balance. MK-type approaches that first infer demography from synonymous sites and then use the inferred demography to correct the estimation of α obtain almost the correct α in our simulations. However, these approaches typically infer a severe past population expansion although there was no such expansion in the simulations, casting doubt on the accuracy of methods that infer demography from synonymous polymorphism data. We propose a simple asymptotic extension of the MK test that yields accurate estimates of α in our simulations and should provide a fruitful direction for future studies.

The relative importance of natural selection and random genetic drift in shaping molecular evolution is a matter of a longstanding dispute. Whereas the neo-Darwinian synthesis placed natural selection as the dominant force (1), from the late 1960s on it became popular to assume that the bulk of molecular variation is selectively neutral or at most weakly selected (2). The “neutral theory” of molecular evolution enabled development of analytical approaches, based on the diffusion approximation, for calculating the expected frequency spectra and fixation probabilities of polymorphisms of varying selective effect. Most of the currently available approaches for estimating selection and demography from population genetic data rest upon these results.

Recent studies have strongly challenged key assumption of the neutral theory. First, in many species the rate of adaptation appears to be very high with, for example, in Drosophila melanogaster more than 50% of the amino acid changing substitutions, and similarly large proportions of noncoding substitutions, driven to fixation by positive selection (3). Importantly, it appears that frequent adaptation strongly affects the genome-wide patterns of polymorphism (3–6). These results imply that the dynamics of a given polymorphism is not only affected by genetic drift and purifying selection acting at its particular site, but also by the so-called genetic draft (7), which describes the stochastic effects generated by recurrent selective sweeps at closely linked sites. Second, there is accumulating evidence that many polymorphisms in natural populations are slightly deleterious (8–11), and such polymorphisms are expected to generate another kind of interference among linked sites, known as background selection (12, 13). It is becoming increasingly clear that the assumption of independence between sites is violated in most cases in one way or another. What we do not yet fully understand is the extent to which these violations affect population genetic methods.

Here, we focus on the investigation of one of the primary methods to test the neutral theory and to estimate the rate of adaptation at the molecular level, introduced by McDonald and Kreitman in 1991 (14). The McDonald–Kreitman (MK) test contrasts levels of polymorphism and divergence at neutral and functional sites and uses this contrast to estimate the fraction of substitutions at the functional sites that were driven to fixation by positive selection. The MK test has been applied in many organisms with estimates of the rate of adaptation varying from extremely high in Drosophila (3) and Escherichia coli (15), to virtually zero in yeast (16) and humans (8, 17). These differences might reflect true variation in the rate of adaptation in different lineages or indicate that the test is biased to different extent, and possibly in different direction, in those lineages (18).

By using closely interdigitated sites, the MK test is robust to many sources of error, such as variation of mutation rate across the genome and variation in coalescent histories at different genomic locations. It can be confounded, however, by slightly deleterious mutations and demography (18). Much work has thus gone into the development of sophisticated extensions of the MK test that use the frequency distribution of polymorphisms to estimate the demographic history of the organism in question, to assess the distribution of deleterious effects at the functional sites, and to correct for both in estimating the rate of adaptation (8, 16, 19–26). However, all of these extensions are still based on the assumption that evolutionary dynamics at different sites can be modeled independently of each other. In light of the recent findings that genetic draft and background selection might often be important, it is essential to verify that these methods are robust to the linkage effects from advantageous and weakly deleterious polymorphisms and their interactions.

Results

The MK test compares the levels of diversity at neutral sites 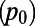and potentially functional sites (p) with the respective levels of divergence ( 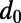and d) to evaluate whether neutral evolution can be rejected at the functional sites (14). An extension of the test can be used to estimate the fraction (α) of substitutions driven to fixation by positive selection at the functional sites (18, 27) (SI Text):

A known problem of this approach is slightly deleterious mutations. To minimize their impact, it has been proposed to exclude polymorphisms that are below a certain cutoff frequency (24, 28). More sophisticated extensions of the MK test attempt to infer the actual distribution of fitness effects (DFE) of new mutations at functional sites from the site frequency spectrum (SFS) of polymorphisms at those sites, and then correct the estimates of α accordingly (8, 9, 19–22, 25).

To study the effects of linkage and selection on MK-type approaches, we conducted forward population genetic simulations of a 10-Mb–long chromosome with realistic gene structure, evolving under mutation, recombination, and selection (Materials and Methods). The simulated chromosome resembles a moderately gene-rich region of the human genome with ∼4% of its sites assumed to be functional. Note that functional density varies strongly across eukaryotes, from a few percent of constrained sites in humans to upward of 50% in Drosophila, and the effects of linked selection should become more pronounced with higher functional density. Thus, if we find strong linkage effects in our scenario with only 4% functional density, we would then expect even stronger effects in the functionally denser genomes such as those found in flies. In this way, our scenario should be conservative for many eukaryotic species.

Mutations occurring at functional sites had their selection coefficients (s) drawn from a specified DFE, whereas every fourth site in exons represented a neutral, synonymous site. We assumed a mutation rate of 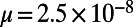per site and generation, a recombination rate of 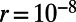, and a panmictic diploid population of size 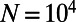(29, 30). These parameters are compatible with standard estimates for human evolution, such as heterozygosity at synonymous sites: 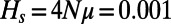. Note, however, that rather than the absolute values of μ, r, N, and s, primarily the products Nμ (specifying the overall rate at which new mutations arise in the population), Ns (specifying the effective strength of selection), and the ratio s/r (determining the region over which a selective sweep affects the genome) should matter in our analysis. We further required that the ratio of the substitution rate at functional sites versus synonymous sites be 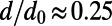, the value found in humans and similar to that of many other species. This condition sets bounds on the amount of purifying selection at functional sites. In our simulations, we estimated divergence from the mutations that fixed during a simulation run. Polymorphism levels and frequency distributions were estimated from population samples of 100 randomly drawn chromosomes, taken every N generations throughout a run.

The key observables in MK-type approaches are the levels of polymorphism and divergence at neutral and functional sites. Some approaches additionally take the SFS of polymorphism into account. In the following sections we study the effects of linkage and selection on these quantities individually, and the resulting effects on MK estimates.

Linkage Effects on Levels of Neutral Polymorphism.

It is well known that genetic draft and background selection can reduce the levels of polymorphism at linked neutral sites (13, 31). Analytical approximations have been derived for calculating the expected reduction due to background selection caused by strongly deleterious mutations (32, 33), as well as genetic draft (5, 34) (SI Text). To assess the accuracy of these results, we compared the level of heterozygosity at synonymous sites 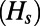in our simulation with the analytically predicted values. Functional mutations were of four types in our simulations: neutral, beneficial, deleterious, and strongly deleterious. Each type had a specific selection coefficient: 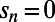, , 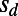, 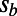and 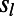, respectively. We assumed that 40% of functional mutations are always strongly deleterious (20, 22) and we set 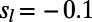. We chose 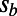, , 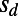and α as our free parameters, which allowed us to assess how different strengths of purifying selection (by varying the value of 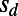), positive selection (by varying 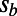), and rate of adaptation (by varying α) affect the results. Values of α in our simulations ranged from 0 to 0.5, 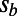from 0.001 to 0.05, and 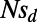from −1 to −100 (Table S1).

Fig. 1A shows that inferred and predicted levels of neutral heterozygosity are generally in good agreement. The amount by which linkage effects reduce 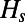is primarily determined by the product of rate and strength of adaptation (Fig. 1A, Inset). The contribution of background selection is typically less severe and appears most pronounced for the very weakly deleterious selection coefficients, as indicated by the observation that for the same value of 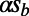, the simulation runs with the weaker deleterious selection coefficients (, darker points in the inset) yield stronger reduction.

Fig. 1.

(A) Observed levels of heterozygosity at synonymous sites in our simulations 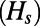compared with analytically predicted levels (SI Text) for each simulation run from Table S1. (B) SFS at functional and synonymous sites in three different simulation runs. Symbols show the observed numbers of polymorphisms per site averaged over all population samples taken throughout the run. Lines show the expected spectra under mutation–selection–drift balance (SI Text) using the value of 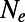inferred from heterozygosity at synonymous sites according to 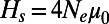. Expected spectra were corrected for binomial sampling. (C) Effective population sizes estimated from the observed fixation probabilities of deleterious mutations according to [2]. (Left) Three simulation runs with different rates of adaptation and 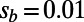. (Right) Three runs with weaker strength of positive selection 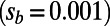. Dashed lines indicate the value of 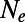inferred from the level of synonymous heterozygosity. Error bars are Pearson 95% confidence intervals, assuming that fixations of deleterious mutations are described by a Poisson process.

Linkage Effects on the SFS at Functional and Synonymous Sites.

Some heuristic extensions of the MK test simply eliminate low-frequency variants. Other, more sophisticated, extensions try to infer the actual DFE at functional sites from the SFS, based on the assumption of the mutation–selection–drift balance (SI Text). It is well known that genetic draft and background selection can distort the SFS from this expectation (6, 10, 34–39). What is not clear is whether the deviations are substantial under realistic evolutionary scenarios and whether this might affect methods based on the assumption of mutation–selection–drift balance. We measured the SFS at functional and synonymous sites in our simulations and compared it with the prediction under mutation–selection–drift balance given the DFE of the particular simulation run. In an attempt to account for the reduction in overall levels of diversity and reduced effectiveness of selection due to genetic draft and background selection, we replaced N in the formulas for mutation–selection–drift balance by an effective population size 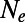, inferred from the level of heterozygosity at synonymous sites in each particular simulation run.

Fig. 1B (Left) shows the observed and expected SFS at functional and synonymous sites in our simulations for a scenario with no adaptation but high levels of background selection 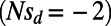. Expected and observed spectra are in good agreement, suggesting that for the chosen recombination rate and functional density the effects of background selection alone are well approximated by mutation–selection–drift balance with 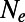being adjusted to the value obtained from the level of neutral heterozygosity.

However, already under moderately frequent adaptation substantial deviations emerge between observed and expected spectra (Fig. 1B, Middle and Right). These distortions do not fit any model of mutation–selection–drift balance with a constant effective population size. Methods based on mutation–selection–drift balance might therefore run into severe biases in the presence of even moderate levels of adaptation.

Linkage Effects on Fixation Probabilities of Deleterious Mutations.

Levels of divergence at functional and neutral sites are the other key parameters in MK-type approaches. Linked selection cannot affect the rate of neutral divergence, as it is always equal to the rate of mutation at neutral sites. The rate of divergence at functional sites, however, could be affected substantially. In the Wright–Fisher model under free recombination, a new mutation with selection coefficient s eventually fixes with probability:

Genetic draft and background selection are expected to increase the fixation probabilities of deleterious mutations: Under recurrent selective sweeps, deleterious mutations can hitchhike to frequencies they are unlikely to reach under mutation–selection–drift balance alone, increasing their chance of fixation over that expected without linkage (11, 40). Similarly, background selection renders purifying selection less effective by reducing the number of successfully reproducing individuals, thereby also increasing the fixation probabilities of deleterious mutations (13, 40, 41).

One common approach for addressing these issues is to assume that [2] can still be used but that N has to be replaced by a lower, effective population size 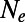. It is not clear though whether a single scalar 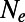applies over a range of selection coefficients. We tested this in our simulations by measuring the fixation probabilities of deleterious mutations with different selection coefficients 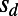and then inferring the corresponding values of 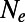according to [2] for the different selection coefficients in the same run independently. Every run had a particular rate (α) and strength 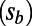of adaptation; deleterious functional mutations had selection coefficients 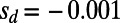, , 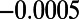, 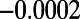and 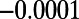, with all four classes being of equal proportion. The fraction of neutral mutations at functional sites was again tuned to .

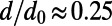Fig. 1C shows the inferred values of 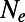according to [2] as a function of 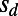. Our results confirm that genetic draft and background selection generally increase fixation probabilities of deleterious mutations, as indicated by the fact that the inferred 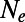is always smaller than the actual 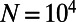. However, the fixation probabilities of mutations of different selection coefficients correspond to very different values of 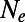. For example, in the simulation run with 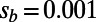and 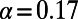, the mutations with 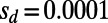fix with a probability that corresponds to 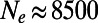, whereas the mutations with 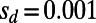yield 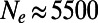. For stronger sweeps and higher α the discrepancies become even more pronounced. In none of the investigated scenarios we did we find a scalar 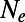that works for all four deleterious selection coefficients. Note that because N enters [2] exponentially, small differences in N can yield substantial differences in the actual fixation probabilities.

These results indicate that there is no scalar transformation of 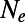that would allow us to estimate fixation probabilities across multiple fitness classes. Thus, even if we were to know the true DFE at functional sites, it would still be impossible to use mutation–selection–drift methods to predict the rate of fixation of deleterious mutations under scenarios that include even moderate amounts of genetic draft.

MK Estimates of the Rate of Adaptation.

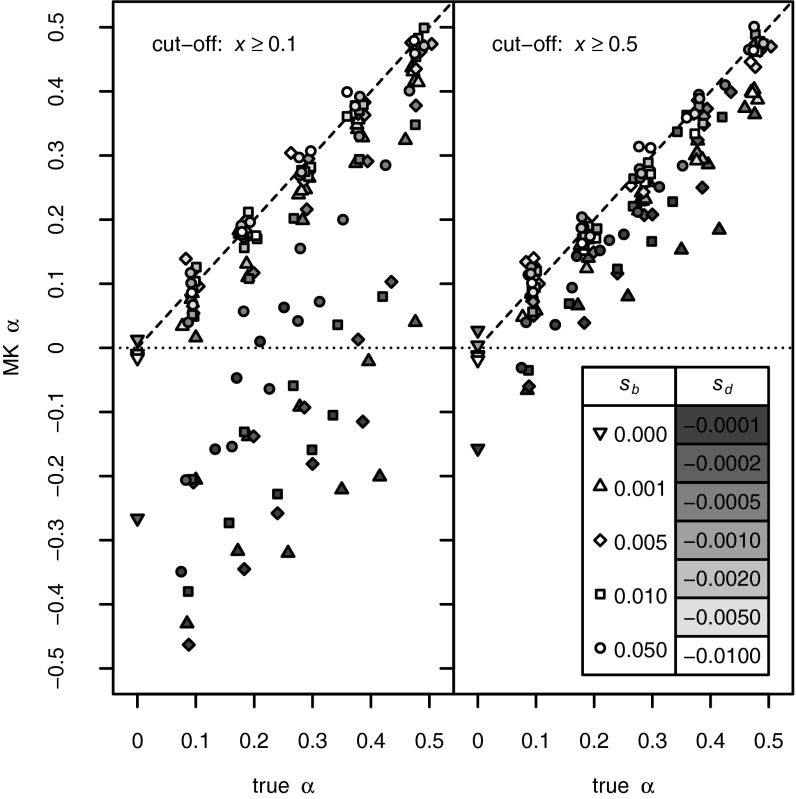
In the previous sections we have shown that linked selection can affect the key quantities in the MK test in complex ways that do not fit the predictions under mutation–selection–drift balance. However, some of the errors partially compensate for each other in the context of the MK test. For example, genetic draft might cause deleterious mutations to appear virtually neutral in the polymorphism data (they could be present at unexpectedly high frequencies) but would also elevate their probabilities of fixation close to that of neutral mutations. It is thus possible that the effects we described above might generally not affect MK estimates of α strongly. Our simulations allow us to explicitly test the accuracy of MK estimates of α inferred from [1]. Fig. 2 shows the comparison of true values and MK estimates for all simulation runs from Table S1. To minimize the bias generated by slightly deleterious polymorphisms, we considered only polymorphisms with a derived allele frequency of 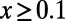(Fig. 2, Left) or 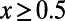(Fig. 2, Right) in the samples. Our results demonstrate that MK estimates of α under both cutoffs still tend to underestimate α, often substantially. For example, when the true α equals 0.4, the MK estimate using a cutoff yields a negative value of −0.2 for a scenario where 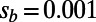and 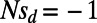. Increasing the cutoff from 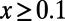to 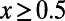reduces this discrepancy, but substantial errors remain. In the above scenario with 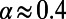the MK estimate still yields only .

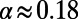Fig. 2.

Comparison of the true values of α and MK estimates according to [1] obtained from the observed levels of polymorphism and divergence at synonymous and functional sites in all simulation runs from Table S1. (Left) Results for a cutoff 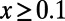. (Right) Results for a cutoff .

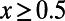The underestimation of α is generally more pronounced when deleterious mutations are only weakly deleterious than when they are strongly deleterious. This is consistent with weakly deleterious mutations having a higher chance of contributing to polymorphism than strongly deleterious mutations, but still having low probabilities of fixation. Strongly deleterious mutations contribute to neither polymorphism nor divergence and thus do not bias estimates of α. As strength of positive selection increases, the biases due to weakly deleterious mutations can be mitigated to some extent because now they become effectively neutral and contribute to both polymorphism and divergence.

DFE-Based Extensions of the MK Approach.

Several methods for correcting possible biases in MK estimates have been proposed that attempt to first estimate the DFE at functional sites and then calculate how many nonadaptive mutations are expected to become fixed given the inferred DFE (8, 9, 19–22, 25). Any excess of substitutions should be attributable to adaptation. Some approaches additionally aim to correct for possible effects of demography, which is first inferred from the SFS at synonymous sites and then used for correcting the SFS at functional sites (21, 22, 42).

One particularly popular such method is DFE-alpha by Eyre-Walker and Keightley (25). We investigated the performance of this method as a representative of the class of methods based on the same paradigm. DFE-alpha models the DFE at functional sites by a gamma distribution, specified by the mean strength of selection 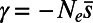, and a shape parameter β, allowing the distribution to take on a variety of shapes ranging from leptokurtic to platykurtic. DFE-alpha incorporates two simple demographic models: (i) constant population size and (ii) a single, instantaneous change in population size from an ancestral size 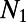to a present-day size 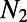having occurred t generations ago. Provided the SFS at both neutral and functional sites and the respective levels of divergence, DFE-alpha infers 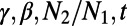, and α at functional sites.

We applied DFE-alpha to polymorphism and divergence data from our simulations (SI Materials and Methods). For this analysis, we modified our simulations such that the selection coefficients of the nonadaptive mutations at functional sites were drawn from a gamma distribution and thus the same distribution was used in the simulations as was assumed by DFE-alpha. We chose a shape parameter of 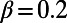, resembling empirical estimates from polymorphism data at nonsynonymous sites in humans (9, 21, 22). We varied α from 0 to 0.5 and investigated two scenarios with 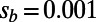or 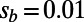. The mean of the DFE was tuned for each scenario such that 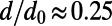. Throughout our simulations population size was always kept constant at 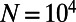individuals.

Table 1 shows the performance of DFE-alpha under its two demographic models. When using the correct model of constant population size, DFE-alpha systematically overestimates α and underestimates the strength of selection against deleterious mutations. The shape parameter β of the gamma distribution is overestimated by up to twofold. These biases are generally more pronounced for the scenarios with stronger sweeps than for those with weaker sweeps. Under the model with a population size change, the estimates of α and β become more accurate but the mean strength of selection against deleterious mutations is now overestimated. Strikingly, under this model DFE-alpha always infers a population size expansion although there was no such expansion in our simulation.

Table 1.

Performance of DFE-alpha under its two demographic models

Simulation parameters				DFE-alpha (constant)			DFE-alpha (step-change)
sb	α	γ	β	α	γ	β	α	γ	β	ξ	t
—	0.00	448	0.2	0.12	297	0.26	0.00	703	0.21	5.0	6.2
0.001	0.05	434	0.2	0.20	264	0.27	0.07	676	0.21	5.0	5.4
0.001	0.09	437	0.2	0.22	288	0.26	0.09	914	0.20	8.8	5.2
0.001	0.18	441	0.2	0.27	265	0.27	0.15	754	0.21	8.8	5.4
0.001	0.28	422	0.2	0.40	276	0.27	0.29	1,055	0.20	10.0	4.6
0.001	0.37	836	0.2	0.50	354	0.28	0.41	1,250	0.21	10.0	4.7
0.001	0.49	1,638	0.2	0.57	532	0.29	0.48	2438	0.21	10.0	4.2
0.01	0.06	424	0.2	0.24	233	0.27	0.11	635	0.21	5.0	4.9
0.01	0.09	424	0.2	0.26	217	0.29	0.12	675	0.22	10.0	4.7
0.01	0.18	381	0.2	0.40	152	0.31	0.24	654	0.21	10.0	3.5
0.01	0.27	339	0.2	0.49	109	0.34	0.31	618	0.21	10.0	2.8
0.01	0.36	652	0.2	0.58	158	0.35	0.43	1,113	0.22	10.0	2.6
0.01	0.47	1,154	0.2	0.68	182	0.38	0.53	1,802	0.22	10.0	2.1

Each row denotes a particular simulation run with the parameters specified in the left four columns. The average strength of purifying selection 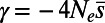was calculated from the mean of the DFE used in the simulation and 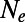inferred from heterozygosity at synonymous sites. The middle three columns show the estimates from DFE-alpha under the demographic model with constant population size. The last five columns show the estimates under the demographic model with a single population size change. 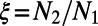is the inferred ratio between present and ancient population size; t is the estimated time since the population size change in units of 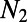generations.

This behavior of DFE-alpha is consistent with the fact that genetic draft leaves signatures in the SFS similar to those observed under a recent population size expansion, namely a skew toward low-frequency polymorphisms. The extent of this effect, however, is alarming, given that even for a scenario where α is only about 0.1, an almost 10-fold population size expansion is already inferred (reflecting a built-in limit of DFE-alpha as currently implemented). Note that even in the scenario with no adaptation, DFE-alpha still infers a fivefold expansion, implying that background selection alone can already bias demographic inference.

Discussion

In this study, we have used forward simulations that explicitly incorporate linkage and selection on a chromosome-wide scale to investigate quantitatively how linked selection can bias the MK test and its extensions to infer the rate of adaptation. Consistently with previous results (24), we found that MK estimates of the rate of adaptation can be severely biased in the presence of slightly deleterious mutations and generally underestimate α. Unfortunately, the standard approaches to address this known problem do not typically resolve it:

• i) Excluding low-frequency polymorphisms from the analysis renders MK estimates more accurate but substantial biases remain. The reason for this is that the dynamics of slightly deleterious polymorphisms under recurrent selective sweeps can be very different from the expectation under the diffusion model, which predicts that frequent mutations should have a realistic chance of eventually reaching fixation. However, under recurrent selective sweeps, a slightly deleterious mutation can easily hitchhike to substantial population frequencies, yet become unlinked during the late phase of a sweep. This deleterious mutation can then spend substantial time as a frequent polymorphism in the population while it slowly declines in frequency. At every stage of this process, the frequency of the mutation overestimates its fixation probability. Such mutations are not effectively removed from a population sample by excluding low-frequency polymorphisms.

• ii) Some methods aim to address the problem of slightly deleterious mutations by estimating the actual DFE of new mutations at functional sites. We found that these methods misestimate the mean and the shape of the DFE and, as a result, tend to overestimate α. This is not surprising given that such approaches infer the DFE by fitting the observed SFS to that predicted under mutation–selection–drift balance, which can be substantially distorted by linkage effects.

• iii) The most sophisticated extensions of the MK test available today additionally attempt to correct for demography. Interestingly, we found that such methods obtain accurate estimates of the rate of adaptation while inferring erroneous demography and also inaccurate estimates of the mean strength of purifying selection. This seeming contradiction reflects the fact that the distortions of the SFS at synonymous sites, which these methods interpret to be due to demography, can in fact be due to genetic draft. As we have shown in Fig. 1B, these distortions are very similar at synonymous and functional sites. Thus, by imposing a demographic scenario that corrects for distortions of the SFS at synonymous sites, the methods effectively also correct the SFS at functional sites.

This observation suggests a simple heuristic extension of the standard MK test that might already provide reasonable estimates without having to invoke demography. To illustrate such an approach, let us define 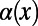as a function of the frequency of the derived mutations:

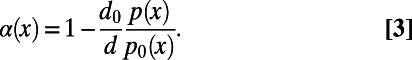Here, 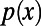and 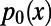are the levels of polymorphism at functional and synonymous sites, respectively, for the specific derived allele frequency x. Because 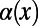depends only on the ratio 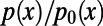, any biases affecting the SFS at functional and synonymous sites in the same way, regardless whether due to demography or genetic draft, effectively cancel out. Furthermore, we can extrapolate 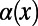to 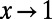, where it should converge close to the true α, assuming that adaptive mutations do not significantly contribute to polymorphism and that purifying selection has been sufficiently stable over time. As a proof of principle, we show in Fig. 3A and Fig. S1 that this simple heuristic approach indeed converges asymptotically to the true value of α in our simulations, even in a scenario with a high rate of adaptation 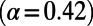, strong sweeps 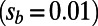, and slightly deleterious mutations .

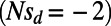Fig. 3.

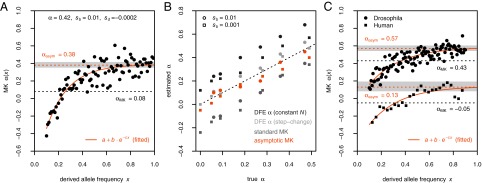
(A) Asymptotic MK estimation for a simulation run with 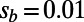, , 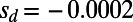and 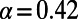. The standard MK estimate using a cutoff 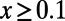yields 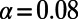(dashed black line). The asymptotic MK estimate yields 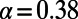and was obtained by fitting an exponential function 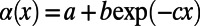for all 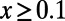using nonlinear least-squares and extrapolating to 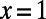(dashed red line). The gray bar denotes the area between the 5–95% quantiles obtained from 1,000 bootstrap samples [the observed values were resampled and the resampled sets were then fit]. (B) Comparison of true values of α for the simulation runs from Table 1 with DFE-alpha estimates under its two demographic models, standard MK estimates using a cutoff-frequency 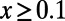, and asymptotic MK estimates. Circles show data for runs with 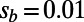; squares show data for runs with 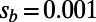. (C) Asymptotic MK estimation at nonsynonymous sites in humans and D. melanogaster. The dashed black lines show the respective standard MK estimates using a cutoff 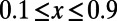. Gray bars denote the areas between the 5–95% quantiles obtained from 1,000 bootstrap replicates.

To obtain the asymptotic value of 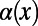in the limit 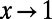, we fitted an exponential function of the form 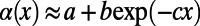to the data. This makes intuitive sense for the case where deleterious mutations all have the same selection coefficient, and levels of functional polymorphisms should thus decay approximately exponentially over the respective levels of neutral polymorphisms with increasing frequency. However, it is not clear which functional form should be fitted in scenarios where selection coefficients are drawn from a broader distribution, unless the specific DFE were known.

Fig. 3B shows that the simple exponential fit still works reasonably well even for the scenarios where deleterious selection coefficients were drawn from a gamma distribution. The asymptotic MK estimates obtained this way no longer suffer from a systematic downward bias due to deleterious mutations and are much more accurate than standard MK estimates obtained using a cutoff frequency of 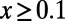, as well as estimates from DFE-alpha without the “demographic correction.” They are comparable in accuracy to estimates from DFE-alpha with the correction. Clearly, future analyses need to verify whether the asymptotic approach also works for a broader class of DFEs and complex demographic scenarios. However, neither is it clear whether DFE-alpha with the demographic correction would always work in such scenarios. One advantage of the asymptotic MK approach is that it provides an easy way to evaluate the goodness of fit of its estimates, as we have shown in Fig. 3 A and C.

We applied asymptotic MK to previously analyzed polymorphism and divergence data from D. melanogaster and humans (SI Materials and Methods). For the human data we obtained an asymptotic MK estimate of 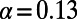(0.09, 0.19) (Fig. 3C), which is consistent with the range of 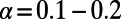estimated in ref. 22. Note that the standard MK estimate for these data when excluding all polymorphisms with sample frequencies below 10% yields a negative value 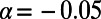. For D. melanogaster, we obtained an estimate of 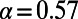(0.54, 0.60). This estimate is similar, although somewhat higher, than previously estimated values obtained from earlier polymorphism data sets in this species (3, 43).

The results presented in this study have important ramifications for the inference of evolutionary parameters from polymorphism and divergence data: The standard MK approach, with or without excluding rare polymorphisms, can produce severely biased estimates under many scenarios and even when adaptation is not pervasive. However, it appears that despite the complexity of the process we do have means of estimating the rate of adaptive evolution by using DFE-alpha like approaches with the demographic correction, or using the simple asymptotic MK approach we suggested above.

Unfortunately, estimation of the DFE, and especially of demography, tends to be severely affected by already moderate amounts of genetic draft and background selection. Estimating demography from neutral sites that are close to functional ones (such as synonymous sites) should in general lead to erroneous inference of population expansions.

Our analysis suggests that in the presence of genetic draft and background selection the evolutionary interactions among linked polymorphisms of different selective effects are complex and consequential. It is clear that the standard diffusion approximation that attempts to model evolution at different sites independently and wrap the complexity of linkage effects among sites into effective parameters, such as 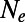, can introduce massive errors into the estimation of key population genetic parameters. We thus believe that new analytics need to be developed that correct for linkage effects. At the very least, one has to verify with forward simulations, such as the one presented here or similar programs (44), that commonly used heuristic and analytic methods in population genetics are robust to linkage effects.

Materials and Methods

Our simulations model the population dynamics of a 10-Mb–long chromosome on which genes are placed equidistantly with a density of 1 gene per 40 kb. Each gene consists of eight exons of length 150 bp each, separated by introns of length 1.5 kb. Genes are flanked by a 550-bp–long 5′ UTR and a 250-bp–long 3′ UTR. We assume that three out of four sites in exons and UTRs are functional sites. Every fourth site in exons and UTRs is used to model synonymous sites. We assume that mutations are codominant and that fitness effects at different sites in the genome are additive. A full description of the simulation is provided in SI Materials and Methods.